We use a modified De Bruijn sequence as the arrangement of color stripes to design the projected patterns. Suppose that D(k, n) denotes a k-array, n-order De Bruijn sequence; then, the element would be E = {0, 1, 2, 3, 4, 5}. Each element is assigned a color with a distance of 60° in hue value, as listed in Table 1. We consider that a neighbor stripe should differ by at least two channels in (R, G, B). With this constraint, only three nodes are allowed to follow one certain node. For element 0, the possible next following node should only be 1, 2 or 3. In this manner, a De Bruijn sequence with a length of 162 is generated. Figure 1 is the cut-out of the generated stripe patterns.

The color distortion caused by projector-camera color crosstalk is adjusted by a static color calibration, in which the parameters are stable for a pairwise projector-camera and measured in advance. The camera captures the reflected light through RGB channel sensors as an image. The model of this process was formulated as Equation (1) by Caspi et al. [17].

(1) [ c r c g c b ] ︸ I c = [ x rr x rg x rb x gr x gg x gb x br x bg x bb ] ︸ X [ a r 0 0 0 a g 0 0 0 a b ] ︸ A ( [ p r p g p b ] ︸ I P + [ o r o g o b ] ︸ O )where I_c is the observed color through the camera, and I_p denotes the corresponding projected color projected by the projector. O addresses the ambient light illumination. X indicates the projector-camera color crosstalk matrix, and A represents the albedo matrix of the object surface. During the static calibration process, the color crosstalk matrix X in Equation (1) is approximated by projecting solid color stripe patterns to a white planar board.

To recover the stripe's color with respect to the different albedos in the RGB channels and ambient light in the scene, the relative albedo is defined to calibrate the stripe color adaptively, as shown in Equation (2).

(2) A = [ a r 0 0 0 α a r 0 0 0 β a r ] = a r [ 1 0 0 0 α 0 0 0 β ]where a^r is the red channel reflectance ratio, α indicates the green channel relative reflectance ratio compared to the red channel, and β denotes the blue channel relative reflectance ratio.

In the stripe segmentation and color classification processes, I_p should be used as an input. Unfortunately, I_p is distorted by the crosstalk effect and albedo matrix. Given camera output I_c, we can compute the calibrated color through color calibration, which can be expressed as Equation (3).

(3) I p + O = A ˜ − 1 X − 1 I c = a − r [ 1 0 0 0 α ˜ 0 0 0 β ˜ ] − 1 X − 1 I cwhere Ã, compromised with α̃ and β̃, is the estimation of A. Then, the calibrated color I_a, defined Equation (4), is the input for stripe segmentation and color classification.

(4) I a = a r ( I p + O ) = [ 1 0 0 0 α ˜ 0 0 0 β ˜ ] − 1 X − 1 I c

The color crosstalk matrix X can be obtained from static color calibration. In the following section, we conclude that α̃ and β̃ can be estimated from the relative albedo estimation. The influence of ambient light O and a^r can both be canceled in the color classification and stripe segmentation processes.

We estimate α̃ by defining a relative albedo function between the red and green channels. Similarly, β̃ is estimated by comparing the red and blue channels. A histogram for each channel is produced. For example, the histogram of the red channel is expressed as Equation (5): (5) H r = { ( H 1 r , W 1 r ) , ( H 2 r , W 2 r ) , ⋯ , ( H n r , W n r ) }where H i r ( 1 ≤ i ≤ n ) is the histogram bin, and W i r ( 1 ≤ i ≤ n ) is the bin value. The superscripts r, g and b denote the red, green and blue channels respectively. To match H^r, H^g is transformed into H^g′, and a flow matrix f = {f_ij} (1 ≤ i ≤ n, 1 ≤ j ≤ n) is defined to represent the transition process. A specified f minimizes the overall cost function. The cost function is expressed as Equation (6).

(6) cost ( H g , H r ) = ∑ i = 1 n ∑ j = 1 n | j − i | f ijwhere f_ij denotes the flow from H i g to H j r and |j − i| denotes the flow distance, which implies that we encourage a flow from one bin in the histogram to another bin with a shorter distance. Equations (7)–(10) are the constraints of the process.

(7) f i j ≥ 0 for 1 ≤ i ≤ n , 1 ≤ j ≤ n (8) ∑ i = 1 n f ij ≤ W j r , 1 ≤ j ≤ n (9) ∑ j = 1 n f ij ≤ W i g , 1 ≤ j ≤ n (10) ∑ i = 1 n ∑ j = 1 n f ij = min ( ∑ i = 1 n W i g , ∑ j = 1 n W j r )

By adopting the Earth Mover's Distance (EMD) algorithm [18], which measures the least amount of work needed to match between two histograms through linear programming, a flow matrix f = {f_ij} from one histogram to another can be obtained. The f_ij is the pixel number transited from bin i in one histogram to bin j in another. Then, we propose a relative albedo function between the green and red channels as Equation (11) and obtain the estimated relative reflectance ratio α̃(i) for each grey level.

(11) α ˜ ( i ) = ( ∑ j = 1 n f ij ) i ∑ j = 1 n ∑ j = 1 n ( f ij j ) , 1 ≤ i ≤ n , 1 ≤ j ≤ n

The relative reflectance ratio β̃(i) can be estimated in a similar manner. After calibration, I_a serves as the input for stripe segmentation and color classification.

An M channel, which is a function of the RGB channels in I_a, is proposed in Equation (12) to suppress ambient light O.

(12) M ij = max ( C ij r , C ij g , C ij b ) − min ( C ij r , C ij g , C ij b )where C ij r in Equation (13) is the red channel value of pixel (i, j) in I_a, and the superscripts r, g and b denote the red, green and blue channels respectively.

(13) ( C ij r C ij g C ij b ) = a r ( p ij r + p ij g + p ij b + o ij r o ij g o ij b )

Given the assumption that ambient light is mostly white light, i.e., o^r ≈ o^g ≈ o^b, the M channel can be simplified as Equation (14).

(14) M ij = a r max ( p ij r + p ij g + p ij b + o ij r o ij g o ij b ) − a r min ( p ij r + p ij g + p ij b + o ij r o ij g o ij b ) = a r max ( p ij r p ij g p ij b ) − a r min ( p ij r p ij g p ij b ) = a r max ( p ij r p ij g p ij b )

Note that there is at least one invalid color channel in the designed stripe patterns. Thus, min ( p ij r , p ij g , p ij b ) is always zero. As a result, the M channel suppresses white ambient light. However, the red channel reflectance ratio a^r is still an interference.

Another advantage of the M channel is that it integrates the RGB color channels into one channel while maintaining the original characters, which facilitates further processing. Figure 2 is the M channel of Figure 3(e).

The stripe pattern is vertical, and we process the M channel horizontally. A stripe in a captured image means a peak in the M channel. Instead of segmenting stripes by illuminance value, we detect stripes by locating the intensity rising and falling edges in the M channel. The rising edge and falling edge information is derived by applying DTT in Equations (15,16).

(15) T ij = ∑ k = h + 1 j + N ∑ h = j j + N − 1 sign ( M ik − M ih )and (16) sing ( a ) = { 1 a > 0 0 a = 0 − 1 a < 0where T_ij indicates the local trend of pixel (i, j) in the M channel. The local trend measures the probability of an increasing or decreasing trend in a given window. The size of the window is controlled by N, which is typically assigned a value of less than half of the stripe width in the captured image.

In Equation (15), |k – h| ≤ N. Because N is a small number, we assume that the reflectance ratio is locally continuous, i.e., a ik r ≈ a ih r. Then, we obtain Equation (17).

(17) sing ( M ik − M ih ) = sing ( a ik r max ( p ik r p ik g p ik b ) − a i , h r max ( p ih r p ih g p ih b ) ) = sing ( max ( p ik ) − max ( p ih ) ) where p ik = ( p ik r , p ik g , p ik b ) T and p ih = ( p ih r , p ih g , p ih b ) T. Thus, Equation (15) can be rewritten as Equation (18). T_ij is only related to the projected pattern and is independent of the reflectance ratio and ambient light.

(18) T ij = ∑ k = h + 1 j + N ∑ h = j j + N − 1 sing ( max ( p ik ) − max ( p ih ) )

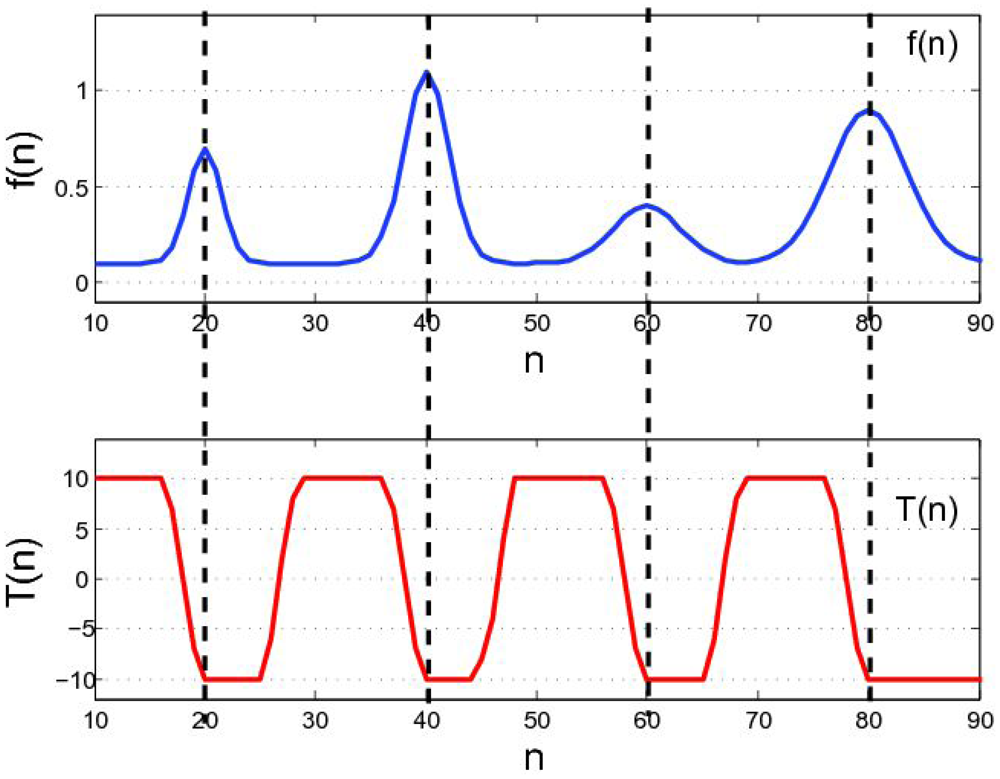
The DTT in Equation (18) works in the following manner:

at the falling edge in the M channel, T arrives its maximum N ( N + 1 ) 2 .

Figure 4 clarifies how DTT works. For example, f(n) is a scan-line in the M channel. If f(n) is locally monotonically decreasing in the window, then T achieves its maximum value N ( N + 1 ) 2. In contrast, T reaches its minimum value − N ( N + 1 ) 2 at f(n)'s rising edge. The values between the maximum and minimum denote that f(n) is neither monotonically increasing nor decreasing. The transition from the maximum to minimum values in T indicates a peak in the M channel. Thus, the max-to-min transition in T is searched for to locate the area of stripes. The rising edge in the M channel is marked as the start of a stripe area, and the falling edge in the M channel is marked as the end of a stripe area. The result of peak detection using DTT is illustrated in Figure 5. We can determine that DTT is more robust than the local adaptive threshold method [19] for weak stripes.

With the help of the M channel and DTT, there is no need to cut the foreground from the background. The standard of DTT detecting color stripes is a strict rising edge and strict falling edge in the M channel. The standard is so strict that very few points in the background are taken as candidate stripes after DTT. The robustness is enhanced by excluding the influence of the background.

Accurate sub-pixel peak localization must be estimated to derive the 3D point cloud. Some existing sub-pixel peak localization algorithms are detailed and compared in [20]. To estimate the peak position accurately, the maximum value M_max of the M channel is searched for in each stripe area, and its position is labeled as I_max. The estimated sub-pixel peak position I_estimated is proposed as Equation (19): (19) I estimated = ∑ I i ⋅ M i ∑ I i , for M i ≥ α M maxwhere I_i is the horizontal offset, M_i is the M channel's intensity value, and α is the related ratio, which defines the pixels related to M_max around I_max. In the following experiments, α is set to 0.8.

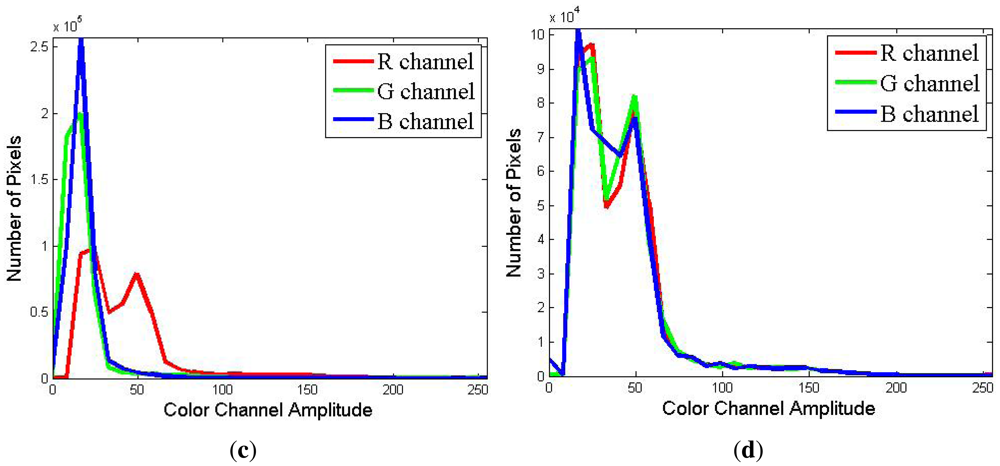
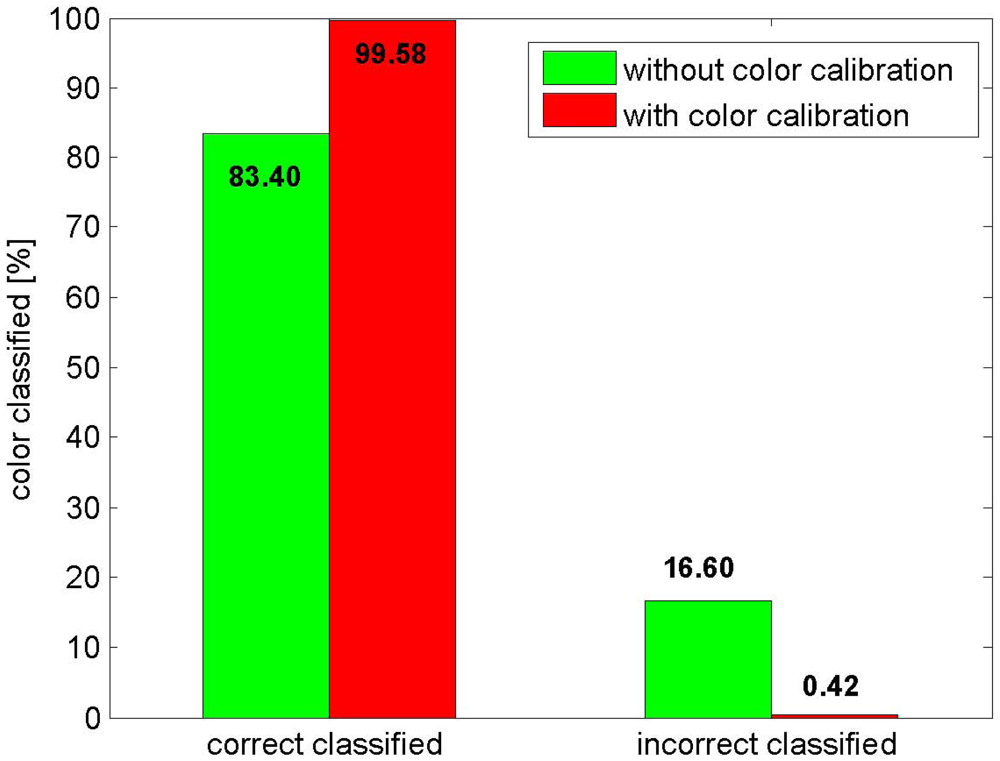
Adaptive color calibration is a crucial method for assuring the accuracy rate of color classification. This method can adjust a stripe's color adaptively with respect to the different albedos in the RGB channels. Figure 6(a,c) illustrates that the gain of the R channel is stronger than those of the G and B channels. After adaptive color calibration, the gains of the three channels are almost same in Figure 6(b,d). Some quantitative comparisons between the adaptive albedo calibration and non-adaptive calibration have been performed. The results in Figure 7 clearly show that adaptive albedo calibration increases the number of correctly labeled points (by more than 15%).

In this subsection, we mainly focus on analyzing the error of the estimated sub-pixel peak position. The performance of the traditional methods is compared with our method, which is referred to as the Max-Min Weighted Average Method (MMWA). Some traditional methods are listed as follows:

Max Method (MAX) [2]. Pages et al. use the maximum intensity value to define the M channel and choose localizations where the M channel reaches its maximum value as the estimated peak position.

(21) I i = max ( R i , G i , B i ) center = x where I x = max ( I i )

To simulate the captured stripes, we generate a designed color stripe pattern. As shown in Equation (23), the intensity of a valid color channel is consistent with the Gaussian Distribution and corrupted with noise. Each RGB channel is additionally polluted by some offset o simulating ambient light. For example, a red stripe compromises a valid red channel generated by Equation (23), while invalid Green and Blue channels contain offset o only.

(23) I ( n , c , σ , β , A , o ) = Ae − ( n − c ) 2 2 σ 2 + β A ɛ + owhere A denotes the amplitude of the color intensity, n is the measured pixel, βA is the noise amplitude and ε ∈ (0, 1). We consider different noise levels: SNR = 25 dB, 20 dB and 18 dB. c is the stripe peak position, σ controls the stripe width and o is the intensity offset.

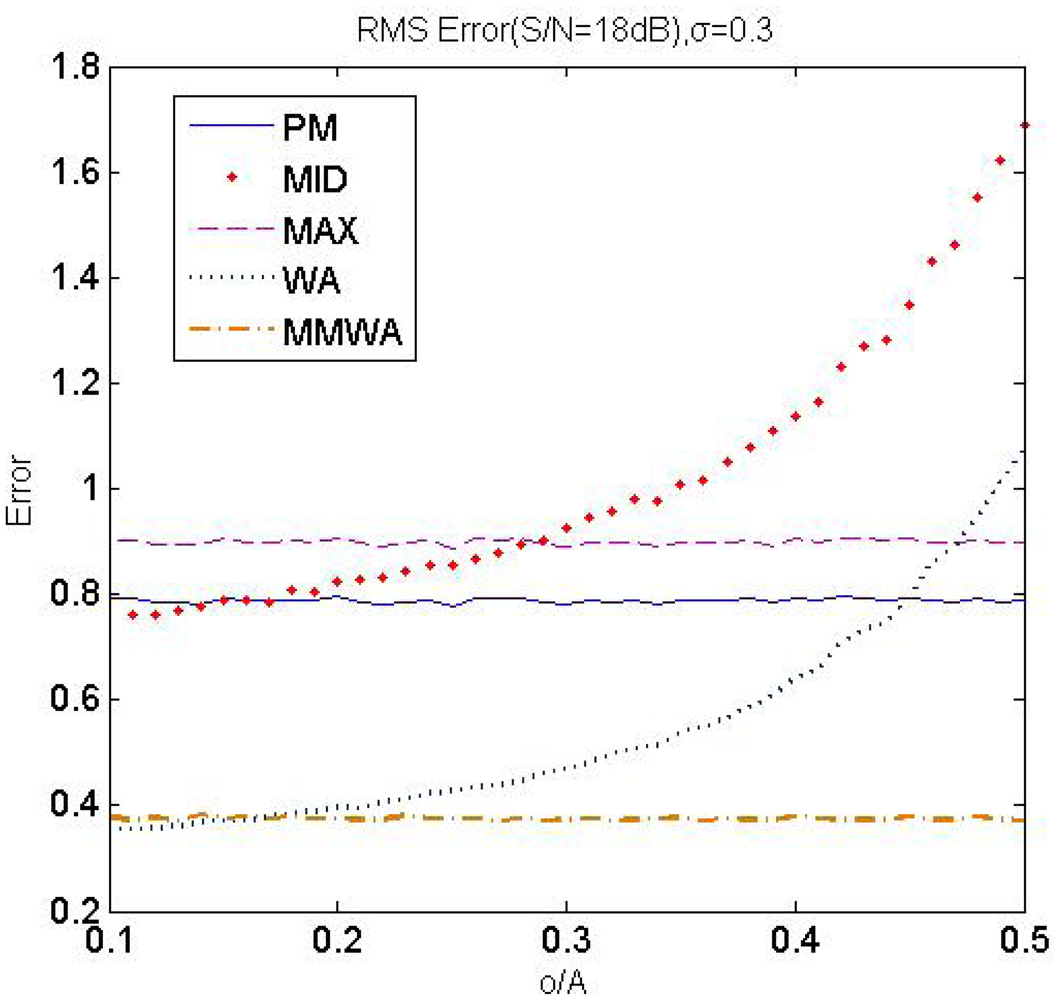
The RMS error of peak localization c, defined as Equation (24), is measured in each method by analyzing 10,000 samples. The average RMS error at the different noise levels are listed in Table 2, as σ changes from 0.3 to 0.6.

(24) RMS _ Error = ∑ ( c i − c i ′ ) 2 N

In all of the methods, the RMS error increases as the noise increases from 25 dB to 18 dB, while MMWA derives the least RMS error at the same noise conditions. Figure 8 depicts that WA and MID are sensitive to light offsets. Nevertheless, our method obtains a high level of accuracy, even in a strong ambient light environment, because the offset is suppressed when deriving the M channel. Form Table 2 and Figure 8, we can conclude that our method outperforms other methods in terms of RMS error with respect to noise, stripe width and ambient light.

Figure 3(a,c) demonstrates that the hand and face are projected with stripe patterns in a natural environment. With the presented methods, the color of the stripes could be classified correctly, the weak stripes could be detected effectively and the surfaces of the object could be reconstructed robustly, even when illuminated by such a strong ambient light, as depicted in Figure 3(b,d). Meanwhile, the reconstructed surfaces of the hand and face illustrate the richness in detail. Figure 3(b,d) contains 85,687 and 75,371 vertices respectively. Note that there is a hole near the nose in Figure 3(d), due to the occlusion in the captured image. Furthermore, Figure 3(e,f) demonstrates that the 3D shapes of multiple objects with different albedos in the same scene could be reconstructed simultaneously because color was calibrated adaptively according to the gray level and the stripes were segmented by DTT.