A Multi-Parameter Decoupling Method with a Lamb Wave Sensor for Improving the Selectivity of Label-Free Liquid Detection †
Abstract
: In this paper, a liquid multi-parameter decoupling method with only one Lamb wave sensor is presented. In a Lamb wave sensor, antisymmetric modes (A01 mode for low frequency, A03 mode for high frequency) and symmetric modes (S0 mode) are used to detect multiple parameters of a liquid, such as its density, sound velocity, and viscosity. We found they can play very different roles in the detections. For example, the A01 mode is very sensitive to the liquid's density but the A03 mode is sensitive to the sound velocity. Here, the A0 mode is used to identify the density of the detected liquid and with this density value we obtained the viscosity by the amplitude shifts of the S0 mode. This could be a way to distinguish an unknown liquid with high sensitivity or to solve the problem of selectivity of label-free detection on biosensors.1. Introduction
Acoustic sensors have been widely used in chemical/biological fields with the label-free detection method to detect the mass changes on the sensor surface [1–17]. However, the selectivity of this method is often poor due to the absorption of non-target molecules, which are difficult to distinguish using only one-parameter sensors [18,19]. This has been a common problem of all kinds of label-free biosensors. The detection of multiple parameters using a multi-mode acoustic sensor significantly improves the label-free detection method. Acoustic waves which travel in a medium can have multiple modes and this character has been successfully used in a combined detection of density and viscosity for high viscosity solutions [20]. However, for low viscosity solutions like aqueous electrolytic solutions or bio liquids, it is still a challenge [9,20–24].
The micro Lamb wave sensor is a powerful tool for liquid detection because it is easier to get multi-mode vibration, and it performs with high sensitivity and low attenuation [25–29]. The two well-known basic modes, the antisymmetric mode (A0 mode) and the symmetric mode (S0 mode), have already been used for solving the problem of temperature compensation on a chip by the authors of [26,30]. The A0 mode has been used to measure the concentration of bio/chemical liquids, such as the concentration of methanol for direct methanol cell applications [18]. However, it shows uncertain frequency shifts direction with the concentration changes of the liquid [18,31]. In fact, the parameters of a liquid, like the density, acoustic sound velocity and viscosity, will work together for a mode. So it's hard to decouple them with only one mode.
In this work, both the antisymmetric mode and the symmetric modes are used to decouple the liquid physical parameters. The characters of A03 mode, with a wavelength of about one-third of A01 mode (low frequency of A0 mode), are investigated with the liquid loading for the first time. In order to discuss the response of Lamb wave sensor to the liquid loading, two types of experiments were set up. The first experiment was used to measure the frequency shifts with the same type of solutions with different concentrations loaded on the sensors' surface, such as the solutions of NaCl. It shows that the characters of the modes are very different. Although both A01 and A03 modes belong to A0 mode, their frequency shifts showed an opposite behavior with the increase of the concentration of the loading solutions. The second experiment was used to measure the frequency changes with different types of solutions and different concentrations, such as solutions of KCl, NaBr and KBr. Although the tested objects are two different kinds of solutions with different concentrations, the frequency of A01 mode shows almost has no movement and A03 mode frequency shows a great difference. The frequency shifts of S0 mode for these solutions are not apparent. These will make it possible to be only sensitive to the liquid viscosity except for the environmental temperature. This essay attempts to decouple the functions of A01, A03 and S0 modes to obtain the basic physical parameters (density and sound velocity, viscosity) with different liquid loading responses. From the values which have been reported from literature [32] we can also determine the types of the solution. This work provides a selective, sensitive method for the measurement of physical parameters to an unknown solution. It can be useful for label-free biosensors.
2. Working Principle
Multi-mode wave, such as A01 mode, S0 mode and their harmonic ones (A03 mode, for example) can be excited in Lamb wave sensors and detected directly by using a pair of inter-digital transducers (IDTs) [33] located on the surface of the piezoelectric layer [34,35]. In liquid sensing, the liquid and IDT will be located on the two opposite sides of the membrane. For the A01 mode and the A03 mode, when the Lamb wave phase velocity is less than the liquid sound velocity, there are evanescent waves produced around the membrane-liquid interface. The phase velocity of the Lamb waves within the evanescent penetration field will be the same with the phase velocity inside the membrane. Taking account of the bending stiffness and the in-plane tension of the plate (Bi) for the A01 mode and the A03 mode, the phase velocity will be [31,36]:
In which, ρL is the detected liquid density. The evanescent penetration depth δEi obeys the following equation [37–39]:
By substituting the Equations (2) and (3) into the Equation (1), we will get the following formula:
In this formula, the constants Bi, λi, and M are independent of the liquid type; λi is determined by the structure of the device. With the implicit Equation (4), the density and sound velocity of the liquid on the sensor can be decoupled when the frequency response of the A01 mode and the A03 mode are obtained by the experiments.
In the measurement, the relative frequency shifts (Δf/f) will be used frequently. By taking the term cPi = fi λi into Equation (1) and deriving of the equation, the value of Δf/f) for the A01 mode and the A03 mode will be:
Obviously, the density and the sound velocity are the two factors affecting the relative frequency shifts. When the phase velocity is far less than the liquid sound velocity (cP « cL), such as the A01 mode, the values of δE and ΔδE approach λ/2π and 0, respectively. Then, in this situation the variations of the liquid sound velocity will have an almost negligible influence on the relative frequency shift. When the phase velocity is close to the liquid sound velocity, such as the A03 mode, the value 1 – (cP/cL)2 approaches 0. The influence of the terms δE and cL cannot be neglected any more. The liquid density and sound velocity will simultaneously affect the frequency shifts. The value of Δf/f can be positive or negative which depends on the sum of the value of ρLΔδE and the value of δEΔρL. Anyway, if we combine these two cases (A01 mode, A03 mode) simultaneously, we can get the values ρL and cL with high sensitivity.
For the S0 mode, when the wavelength of the Lamb mode is larger than the thickness of the plate, the phase velocity (cp) for the principal symmetric mode can be simplified as [40]:
Evidently, the effect of liquid on the propagation of the S0 mode does not change the real part of the phase velocity, but adds a very small attenuation of the amplitude [40]. This mode is suitable for the detection of attenuation. The amplitude (AL) response of an unknown solution can be expressed by:
In engineering, the insertion loss (dB) is widely used. The values of AL and AW can be transformed into values in dB scale which are denoted by ALdB and AWdB, respectively. Therefore, the attenuation difference (ΔAdB) between an unknown solution and water can be expressed in dB scale as follows:
3. Experiments for Liquid Detection
3.1. Experimental Setup
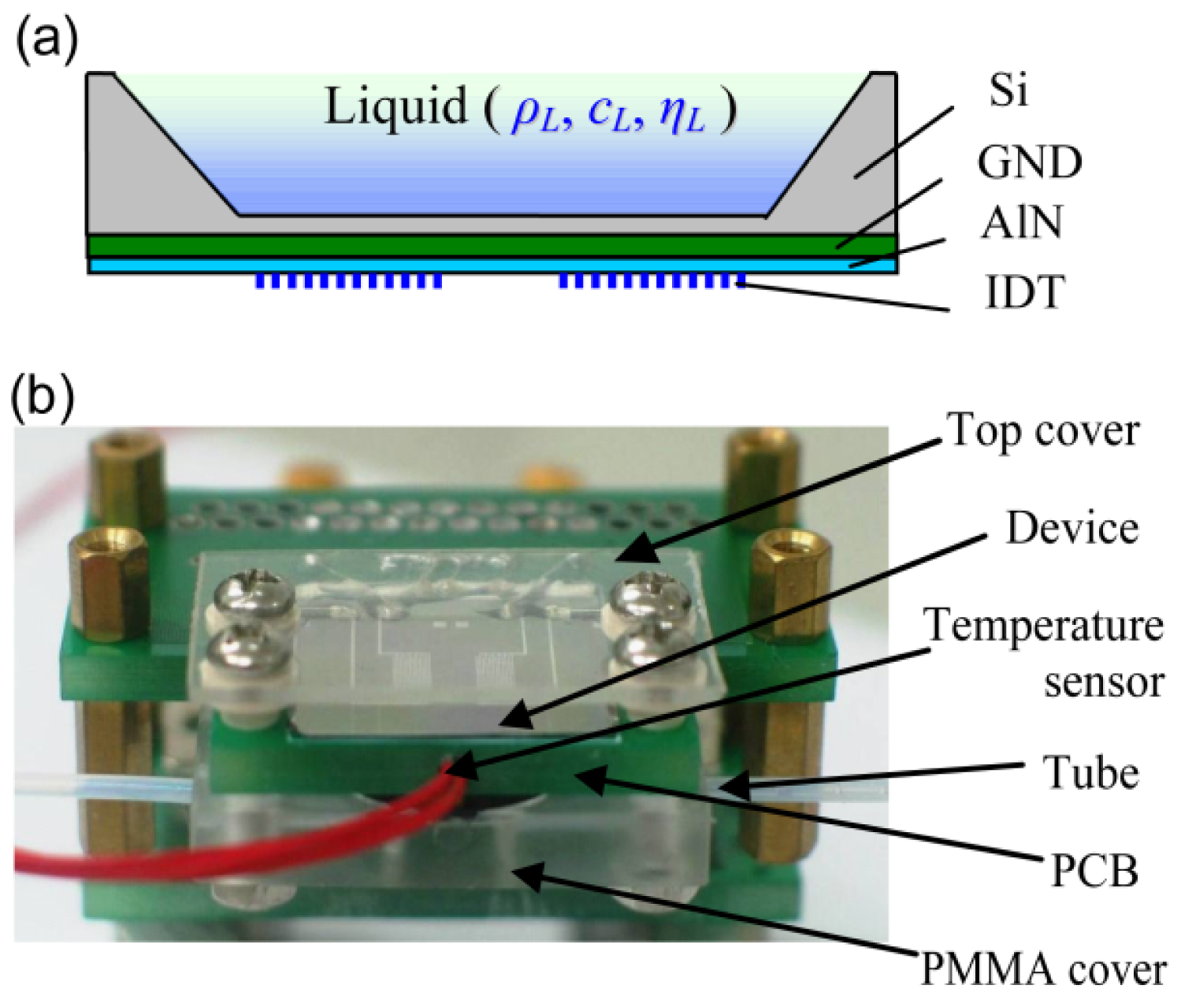
The micro Lamb wave device in Figure 1(a) contains a silicon membrane (length 7.8 mm, thickness ∼12 μm) with a ground layer (Ti/Mo, GND, ∼0.2 μm) and a piezoelectric layer (aluminum nitride, AlN, ∼1.8 μm). Lamb waves are excited and detected directly using bidirectional inter-digital transducers (IDTs) [33] located on the surface of the AlN layer. There are six pairs of fingers on bidirectional IDTs in each exciting and detecting transducer. The period of bidirectional IDT is about 400 μm. As waves are partly reflected at the end of length-limited membrane (∼7.8 mm), the device has strong signal without reflectors on both ends of the membrane. With the layers described as in [34], the mass per unit area of the membrane (M) is about 0.0355 kg/m2.
The micro Lamb wave device is packaged directly with the printed circuit board (PCB), as shown in Figure 1(b). The network analyzer (Agilent 4395A), connected with the PCB, is used to excite and receive the acoustic signals. The device is protected with one cover on top of the system. The tube is used to pass the liquid into/out of the chamber, which is sealed up with the polymethyl methacrylate (PMMA) cover under the PCB.
When the device is loaded with air or water, multi-modes can be excited and detected effectively, including the A01 mode, the A03 mode, and the S0 mode (Figure 2). As the A01 and A03 modes are harmonic, the wavelength of the A03 mode is about one third of the wavelength of the A01 mode. According to the positions of the A01 mode, A03 mode and S0 mode in the dispersion curves [41,42], the resonant frequencies (f) of these three modes should have the following relation: fA01 < fA03 < fS0. The measured resonant frequency of the A01 and A03 modes for water loading are 0.987 and 9.233 MHz, respectively. With the frequency (f) and the wavelength (λ), the corresponding phase velocities (fλ) of these two modes are 385 m/s and 1,200 m/s respectively. Although the phase velocity of the A01 mode is far less than the sound velocity of water (1,485.5 m/s), it is close to the sound velocity of water for the A03 mode. With the same water loading for the S0 mode, the measured central resonant frequency is about 20.86 MHz. The corresponding phase velocity of the S0 mode is about 8,135.4 m/s. Further experiments were conducted to investigate the response of multi-modes to the different solutions.
3.2. Experiments for One Species Solutions (NaCl Solutions) with Different Concentrations
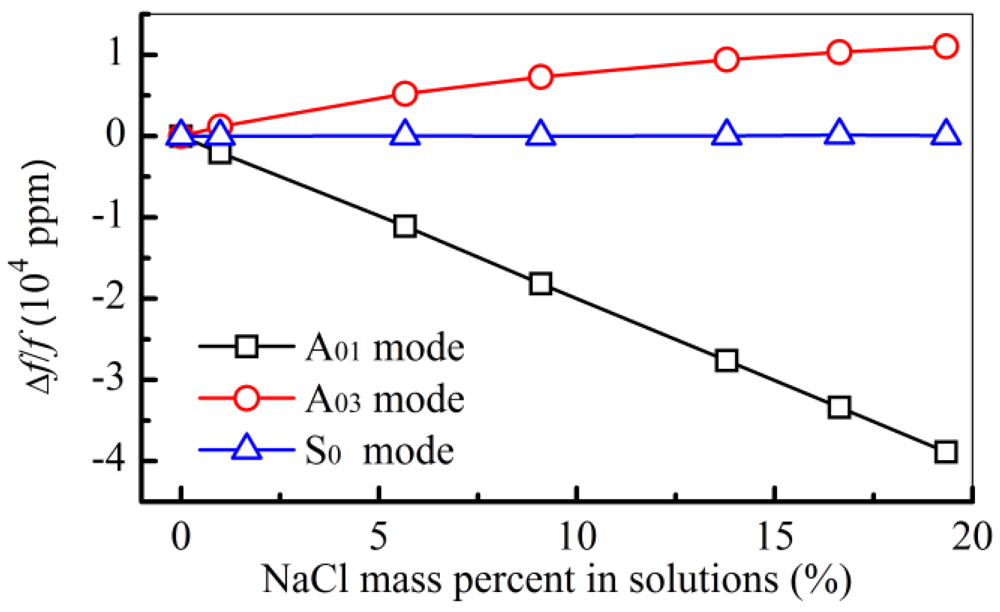
The first experiment was done to measure known solutions with different concentrations (Figure 3), such as NaCl solutions. When water is designated as the reference liquid, the relative frequency shifts (Δf/f = (fsolution − fwater)/fwater) with concentration are different for these three modes (A01 mode, A03 mode, and S0 mode), where fsolution and fwater are the measured frequencies for the solution and the water, respectively. The frequency of the A01 mode decreases with the concentrations and the A03 mode behaves oppositely. In the case of the A03 mode of NaCl solutions measured in Figure 3, the absolute value ρΔδE is bigger than the absolute value δEΔρ (Table 1). This causes the positive frequency shifts of A03 mode in NaCl solutions measurements. In any case, when the frequency shift is positive, this means the Lamb wave phase velocity is close to the liquid sound velocity. In this case, this phenomenon can be used to decouple the liquid sound velocity.
Compared with the frequency shifts measured with the A01 mode and A03 mode, the frequency of the S0 mode shows negligible shift with different concentrations (Figure 3).
3.3. Experiments for Three Different Unknown Species Solutions
The second experiment was done to measure the modes' responses to three different species of aqueous electrolytic solutions with different concentrations (Table 2). We will check the possibility of the method to decouple the density and the acoustic sound velocity of these solutions with the measurements of A01 mode and A03 mode. Three different species of aqueous electrolytic solutions are prepared, they are listed as solution A, solution B, and solution C respectively, as it is shown in Table 2. From No. 1 to No. 6 solutions, they are the solution A. No. 7 and No. 8 solutions are the solution B. No. 9 and No. 10 are solution C. In each kind of solution, the concentration increases with the serial number. The S0 mode is still insensitive to the solution changes compared with the measurement in water, and its values are not listed here.
In the case of solution A, the relative frequency shifts Δf/f of A01 mode and A03 mode have similar properties with the solution of NaCl measured in Figure 3. But for the solution B and solution C, the relative frequency shifts of A03 mode is negative. As it is indicated in Equation (5), the absolute value ρΔδE of solution B and solution C measured in Table 2 should be smaller than the absolute value δEΔρ.
Even for different kinds of solutions, such as the No. 6, No. 8, and No. 10 solutions, the values of Δf/f of the A01 mode are almost the same, but the values of Δf/f of the A03 mode are apparently different. This means only one antisymmetric mode measurement, such as A01 mode, can not determine the solution with high selectivity. In order to specify the liquid with high selectivity, it is better to decouple the liquid density and the liquid sound velocity with the measured relative frequency shifts of A01 mode and A03 mode. These will be analyzed in following section.
3.4. Viscosity Measurements with the S0 Mode
The responses of the S0 mode to the solutions of NaBr are similar to the ones of NaCl (Figure 3), the central frequency does not show apparent shifts due to their changing concentrations. However, the changes of the amplitude are related to the liquid's concentrations (Figure 4). It is because the frequency is mainly affected by the liquid density and sound velocity, which has no effects on the real part of the phase velocity of S0 mode (Equation (6)) [40]. The amplitude of the S0 mode in NaBr solution (Figure 4) shows that energy losses increase with the concentration, which is caused by the density and the viscosity of the liquid (Equation (7)). This can be used to decouple the density and the viscosity of the solution.
4. Results and Discussions
4.1. To Decouple the Density and the Acoustic Sound Velocity with the A01 Mode and A03 Mode
In order to specify the liquid with high selectivity, we attempted to decouple the liquid density and the liquid sound velocity with the measured frequency shifts of A01 mode and A03 mode. Based on the Equation (4), two steps are undertaken in order to decouple the density and the sound velocity of a liquid as follows:
Determine the constant Bi by measuring the frequency response of the reference liquid. Here, the water works as the reference liquid, the values of B1 and B3 are 14,767.3 N/m and 101,642.8 N/m respectively.
Get the physical parameters (ρL, cL) for a unknown liquid by measuring cPi. All other parameters (Bi, λi, M) in Equation (1) have already been calculated or measured.
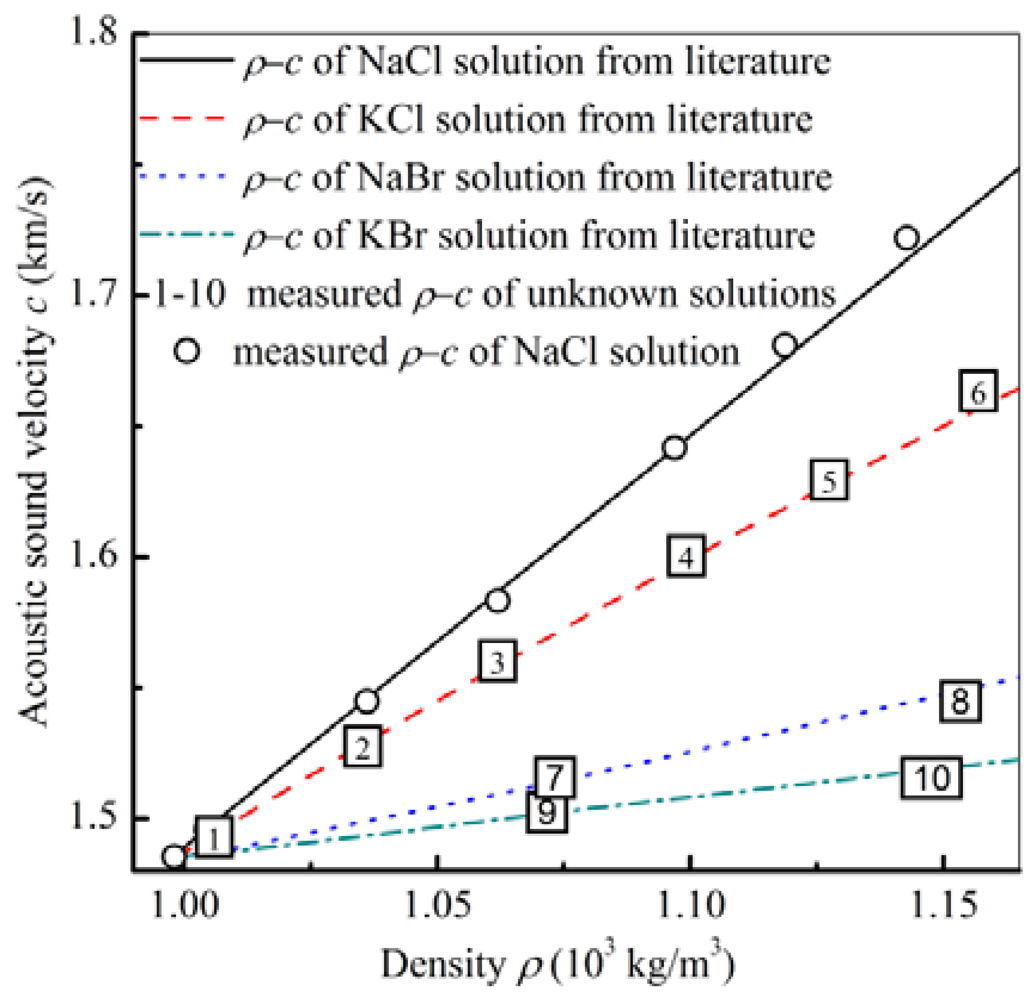
The first decoupled result using Equation (1) is the NaCl solution with different concentrations, as measured in Figure 3. Comparing the measured density and sound velocity with the values from the literature [32], the two results are close, as shown in Figure 5.
Based on the same process, the density and the sound velocity for other three different species solutions with different concentrations were also decoupled and are shown in Figure 5. Compared with the values from the literature [32], No. 1–No. 6 solutions are KCl solutions, No. 7 and No. 8 solutions are NaBr solutions, and No. 9 and No. 10 solutions are KBr solutions. Aside from decoupled density and sound velocity, the species of the solutions can be identified by comparing the measured values with the already known values [32]. After these density and sound velocity being decoupled using A01 mode and A03 mode, the liquid are determined with higher selectivity compared with only A01 mode measurement.
For Nos. 6, 8, and 10 solutions, the decoupled densities (Figure 5) are almost the same because the relative frequency shifts are very close (Table 2). For these solutions with adjacent density, sound velocities become the main factors affecting the frequency shifts in the A03 mode (Table 2). With the relations of the absolute frequency shifts: Δf/fNo.6 > Δf/fNo.8 > Δf/fNo.10 (Table 2), the decoupled sound velocity of these three solutions have the following relation: cNo.6 > cNo.8 > cNo.10 (Figure 5).
4.2. The Linear Response of (Density × Viscosity)0.5 Changing with the Item of Amplitude Shifts (ΔAdB) in S0 Mode
The item (density × viscosity)0.5 changes almost linearly with the item of amplitude shifts (ΔAdB), and the linear fitting coefficient is about 1.02 ± 0.09 (dB/(kg·m−2·s−0.5)), such as the NaBr and NaCl solutions (Figure 6). Beside the density and the viscosity, other parameters, such as the liquid's conductivity, affect the amplitude shifts. This is maybe the reason why the high linearity of (density × viscosity)0.5 doesn't change with the amplitude shift. However, by analyzing the amplitude shifts (ΔAdB) of the S0 mode, the viscosity of the solution can be derived. With the determined density by measuring the frequency response of the A01 and A03 modes, the viscosity will be determined by checking the amplitude response in the S0 mode.
5. Conclusions
In this study, for the first time to our knowledge, the density, sound velocity, and viscosity of the liquid are obtained simultaneously based on the measurements of the same solution sample volume with a Lamb wave sensor. When the frequency shifts of the A01 and A03 modes are combined, the density and sound velocity are decoupled. This happens because the phase velocity of the A01 mode is far from the sound velocity of the liquid and the phase velocity of the A03 mode is close to the sound velocity of the liquid. Viscosity is obtained by measuring the amplitude of the S0 mode, which is especially suitable for Newtonian fluids. Effects of the aqueous electrolytic solutions' conductivity on these three modes are not clearly observed. The term (density × viscosity)0.5 doesn't show high linearity as a function of amplitude shifts.
However, with this multi-parameter detection method, unknown solutions such as aqueous electrolytic solutions can be distinguished successfully and with high selectivity. Results clearly indicate that the multi-modes of a micro Lamb wave sensor are promising in the investigation of molecular thermodynamics, adiabatic compressibility, and molecular label free detection, among others.
Acknowledgments
The authors gratefully acknowledge the technical support from Engineers Jean-Yves Rauch of Femto-st, Pascal Blind of CTMN (Besançon), and Feng Li of CIOMP. Parts of the present work were financially supported by the National Natural Science Foundation of China (Nos. 11034007, 60971025) and the Chinese Academy of Sciences Innovation Program (KJCX2-YW-H18).
References
- Fu, Y.Q.; Luo, J.K.; Du, X.Y.; Flewitt, A.J.; Li, Y.; Markx, G.H.; Walton, A.J.; Milne, W.I. Recent developments on ZnO films for acoustic wave based bio-sensing and microfluidic applications: A review. Sens. Actuators B 2010, 143, 606–619. [Google Scholar]
- Hager, H.E. Fluid property evaluation by piezoelectric crystals operating in the thickness shear mode. Chem. Eng. Commun. 1986, 43, 25–38. [Google Scholar]
- Kondoh, J.; Shiokawa, S. Measurements of conductivity and pH of liquid using surface acoustic wave devices. Jpn. J. Appl. Phys. 1992, 31, 82–84. [Google Scholar]
- Lau, O.-W.; Shao, B.; Zhang, W. Evaluation of methods to minimize effects of liquid viscosity and density on the oscillating frequencies of thickness-shear-mode (TSM) piezoelectric resonators. Anal. Chim. Acta 1995, 312, 217–222. [Google Scholar]
- Arapan, L.; Alexieva, G.; Avramov, I.D.; Radeva, E.; Strashilov, V.; Katardjiev, I.; Yantchev, V. Highly mass-sensitive thin Film Plate Acoustic Resonators (FPAR). Sensors 2011, 11, 6942–6953. [Google Scholar]
- Sarvazyan, A.P. Ultrasonic velocimetry of biological compounds. Annu. Rev. Biophys. Biophys. Chem. 1991, 20, 321–342. [Google Scholar]
- Martin, S.J.; Ricco, A.J.; Niemczyk, T.M.; Frye, G.C. Characterization of SH acoustic plate mode liquid sensors. Sens. Actuators 1989, 20, 253–268. [Google Scholar]
- Montagut, Y.; García, J.V.; Jiménez, Y.; March, C.; Montoya, Á.; Arnau, A. Validation of a phase-mass characterization concept and interface for acoustic biosensors. Sensors 2011, 11, 4702–4720. [Google Scholar]
- Kovacs, G.; Vellekoop, M.J.; Haueis, R.; Lubking, G.W.; Venema, A. A love wave sensor for (bio)chemical sensing in liquids. Sens. Actuators A 1994, 43, 38–43. [Google Scholar]
- Newton, M.; Roach, P.; McHale, G. ST quartz acoustic wave sensors with sectional guiding layers. Sensors 2008, 8, 4384–4391. [Google Scholar]
- Länge, K.; Rapp, B.; Rapp, M. Surface acoustic wave biosensors: A review. Anal. Bioanal. Chem. 2008, 391, 1509–1519. [Google Scholar]
- Rocha-Gaso, M.-I.; March-Iborra, C.; Montoya-Baides, A.; Arnau-Vives, A. Surface generated acoustic wave biosensors for the detection of pathogens: A review. Sensors 2009, 9, 5740–5769. [Google Scholar]
- Voiculescu, I.; Nordin, A.N. Acoustic wave based MEMS devices for biosensing applications. Biosens. Bioelectron. 2012, 33, 1–9. [Google Scholar]
- Priego Capote, F.; Luque de Castro, M. Ultrasound in analytical chemistry. Anal. Bioanal. Chem. 2007, 387, 249–257. [Google Scholar]
- Cooper, M. Label-free screening of bio-molecular interactions. Anal. Bioanal. Chem. 2003, 377, 834–842. [Google Scholar]
- Rocha-Gaso, M.-I.; March-Iborra, C.; Montoya-Baides, Á.; Arnau-Vives, A. Surface generated acoustic wave biosensors for the detection of pathogens: A review. Sensors 2009, 9, 5740–5769. [Google Scholar]
- Rapp, B.; Gruhl, F.; Länge, K. Biosensors with label-free detection designed for diagnostic applications. Anal. Bioanal. Chem. 2010, 398, 2403–2412. [Google Scholar]
- Hino, R.; Esashi, M.; Tanaka, S. Antisymmetric-mode Lamb wave methanol sensor with edge reflectors for fuel cell applications. Proceedings of the 23rd IEEE International Conference on Micro Electro Mechanical Systems, Technical Digest (MEMS 2010), Hong Kong, 24−28 January 2010; pp. 871–874.
- Latif, U.; Mujahid, A.; Afzal, A.; Sikorski, R.; Lieberzeit, P.; Dickert, F. Dual and tetraelectrode QCMs using imprinted polymers as receptors for ions and neutral analytes. Anal. Bioanal. Chem. 2011, 400, 2507–2515. [Google Scholar]
- Raimbault, V.; Rebiere, D.; Dejous, C.; Guirardel, M.; Lachaud, J.L. Molecular weight influence study of aqueous poly(ethylene glycol) solutions with a microfluidic Love wave sensor. Sens. Actuators B 2010, 144, 318–322. [Google Scholar]
- Herrmann, F.; Hahn, D.; Büttgenbach, S. Separate determination of liquid density and viscosity with sagittally corrugated Love-mode sensors. Sens. Actuators A 1999, 78, 99–107. [Google Scholar]
- Doy, N.; McHale, G.; Newton, M.I.; Hardacre, C.; Ge, R.; MacInnes, J.M.; Kuvshinov, D.; Allen, R.W. Small volume laboratory on a chip measurements incorporating the quartz crystal microbalance to measure the viscosity-density product of room temperature ionic liquids. Biomicrofluidics 2010. [Google Scholar] [CrossRef]
- Mitsakakis, K.; Tsortos, A.; Kondoh, J.; Gizeli, E. Parametric study of SH-SAW device response to various types of surface perturbations. Sens. Actuators B 2009, 138, 408–416. [Google Scholar]
- Oita, I.; Halewyck, H.; Thys, B.; Rombaut, B.; Vander Heyden, Y.; Mangelings, D. Microfluidics in macro-biomolecules analysis: Macro inside in a nano world. Anal. Bioanal. Chem. 2010, 398, 239–264. [Google Scholar]
- Laurent, T.; Bastien, F.O.; Pommier, J.-C.; Cachard, A.; Remiens, D.; Cattan, E. Lamb wave and plate mode in ZnO/silicon and AlN/silicon membrane: Application to sensors able to operate in contact with liquid. Sens. Actuators A 2000, 87, 26–37. [Google Scholar]
- Jia, H.; Duhamel, R.; Manceau, J.F.; de Labachelerie, M.; Bastien, F. Improvement of Lamb waves sensors: Temperature sensitivity compensation. Sens. Actuators A 2005, 121, 321–326. [Google Scholar]
- Choujaa, A.; Tirole, N.; Bonjour, C.; Martin, G.; Hauden, D.; Blind, P.; Cachard, A.; Pommier, C. AlN/silicon Lamb-wave microsensors for pressure and gravimetric measurements. Sens. Actuators A 1995, 46, 179–182. [Google Scholar]
- Moll, J.; Golub, M.V.; Glushkov, E.; Glushkova, N.; Fritzen, C.-P. Non-axisymmetric Lamb wave excitation by piezoelectric wafer active sensors. Sens. Actuators A 2012, 174, 173–180. [Google Scholar]
- Rizwaan, A. Time-space analysis of a surface-bonded piezoelectric film's response with Lamb wave for diagnostics. Sens. Actuators A 2010, 161, 12–22. [Google Scholar]
- Li, F.; Wu, Y.; Manceau, J.-F.; Bastien, F. Temperature compensation of Lamb wave sensor by combined antisymmetric mode and symmetric mode. Appl. Phys. Lett. 2008, 92, 074101:1–074101:3. [Google Scholar]
- Martin, B.A.; Wenzel, S.W.; White, R.M. Viscosity and density sensing with ultrasonic plate waves. Sens. Actuators A 1990, 22, 704–708. [Google Scholar]
- Freyer, E.B. Sonic studies of the physical properties of liquids. II. The velocity of sound in solutions of certain alkali halides and their compressibilities. J. Am. Chem. Soc. 1931, 53, 1313–1320. [Google Scholar]
- White, R.M.; Voltmer, F.W. Direct piezoelectric coupling to surface elastic waves. Appl. Phys. Lett. 1965, 7, 314–316. [Google Scholar]
- Zhou, L.; Manceau, J.-F.; Bastien, F. Influence of gases on Lamb waves propagations in resonator. Appl. Phys. Lett. 2009, 95, 223505–223507. [Google Scholar]
- Zhou, L.; Manceau, J.-F.; Bastien, F. Interaction between gas flow and a Lamb waves based microsensor. Sens. Actuators A 2012, 181, 1–5. [Google Scholar]
- Chen, Z.; Han, T.; Shi, W.; Ji, X.; Li, L. Separate determination of liquid properties with Lamb wave devices. Proceedings of the 2006 IEEE International Frequency Control Symposium and Exposition, Miami, FL, USA, 4–7 June 2006; Volumes 1–2. pp. 322–327.
- Moroney, R.M.; White, R.M.; Howe, R.T. Microtransport induced by ultrasonic Lamb waves. Appl. Phys. Lett. 1991, 59, 774–776. [Google Scholar]
- Nguyen, N.T.; White, R.M. Design and optimization of an ultrasonic flexural plate wave micropump using numerical simulation. Sens. Actuators A 1999, 77, 229–236. [Google Scholar]
- Sayar, E.; Farouk, B. Acoustically generated flows in microchannel flexural plate wave sensors: Effects of compressibility. Sens. Actuators A 2011, 171, 317–323. [Google Scholar]
- Osborne, M.F.M.; Hart, S.D. Transmission, reflection, and guiding of an exponential pulse by a steel plate in water. I. theory. J. Acoust. Soc. Am. 1945, 17, 1–18. [Google Scholar]
- Leckey, C.A.C.; Rogge, M.D.; Miller, C.A.; Hinders, M.K. Multiple-mode Lamb wave scattering simulations using 3D elastodynamic finite integration technique. Ultrasonics 2012, 52, 193–207. [Google Scholar]
- Zhu, Z.; Wu, J.; Li, J.; Zhou, W. A general dispersion relation for Lamb-wave sensors with liquid-layer loading. Sens. Actuators A 1995, 49, 79–84. [Google Scholar]



| Concentration (%) | Density (103 kg/m3) | cP (m/s) | δE (μm) | δEΔρ | ρΔδE |
|---|---|---|---|---|---|
| 0 | 0.9981 | 1,200.30 | 35.12 | 0 | 0 |
| 0.99 | 1.0052 | 1,201.71 | 34.70 | 0.25 | −0.42 |
| 5.67 | 1.0389 | 1,206.55 | 32.81 | 1.34 | −2.39 |
| 9.09 | 1.0640 | 1,209.03 | 31.58 | 2.08 | −3.77 |
| 13.79 | 1.0995 | 1,211.59 | 30.01 | 3.04 | −5.62 |
| 16.64 | 1.1212 | 1,212.69 | 29.13 | 3.59 | −6.71 |
| 19.33 | 1.1425 | 1,213.53 | 28.40 | 4.10 | −7.67 |
| Solution A | Solution B | Solution C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No. of solutions | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Concentration (%) | 0.99 | 6.05 | 9.97 | 16.03 | 19.96 | 23.95 | 9.35 | 18.07 | 8.98 | 17.32 |
| Δf/f (A01 mode) (−1 × 104 ppm) | 0.236 | 1.09 | 1.846 | 2.886 | 3.654 | 4.434 | 2.243 | 4.474 | 2.216 | 4.356 |
| Δf/f (A03 mode) (104 ppm) | 0.027 | 0.216 | 0.357 | 0.373 | 0.325 | 0.287 | −0.649 | −1.422 | −0.876 | −1.848 |
- †Earlier version of this paper appears in the 16th International Conference on Solid-State Sensors, Actuators and Microsystems, Beijing, China, 5–9 June 2011.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhou, L.; Wu, Y.; Xuan, M.; Manceau, J.-F.; Bastien, F. A Multi-Parameter Decoupling Method with a Lamb Wave Sensor for Improving the Selectivity of Label-Free Liquid Detection. Sensors 2012, 12, 10369-10380. https://doi.org/10.3390/s120810369
Zhou L, Wu Y, Xuan M, Manceau J-F, Bastien F. A Multi-Parameter Decoupling Method with a Lamb Wave Sensor for Improving the Selectivity of Label-Free Liquid Detection. Sensors. 2012; 12(8):10369-10380. https://doi.org/10.3390/s120810369
Chicago/Turabian StyleZhou, Lianqun, Yihui Wu, Ming Xuan, Jean-François Manceau, and François Bastien. 2012. "A Multi-Parameter Decoupling Method with a Lamb Wave Sensor for Improving the Selectivity of Label-Free Liquid Detection" Sensors 12, no. 8: 10369-10380. https://doi.org/10.3390/s120810369




