A Critical Review of Published Data on the Gas Temperature and the Electron Density in the Electrolyte Cathode Atmospheric Glow Discharges
Abstract
: Electrolyte Cathode Discharge (ELCAD) spectrometry, a novel sensitive multielement direct analytical method for metal traces in aqueous solutions, was introduced in 1993 as a new sensing principle. Since then several works have tried to develop an operational mechanism for this exotic atmospheric glow plasma technique, however these attempts cannot be combined into a valid model description. In this review we summarize the conceptual and technical problems we found in this upcoming research field of direct sensors. The TG gas temperature and the ne electron density values published up to now for ELCAD are very confusing. These data were evaluated by three conditions. The first is the gas composition of the ELCAD plasma, since TG was determined from the emitted intensity of the N2 and OH bands. Secondly, since the ELCAD is an atmospheric glow discharge, thus, the obtained TG has to be close to the Te electron temperature. This can be used for the mutual validation of the received temperature data. Thirdly, as a consequence of the second condition, the values of TG and ne have to agree with the Engel-Brown approximation of the Saha-equation related to weakly ionized glow discharge plasmas. Application of non-adequate experimental methods and theoretical treatment leads to unreliable descriptions which cannot be used to optimize the detector performance.1. Introduction
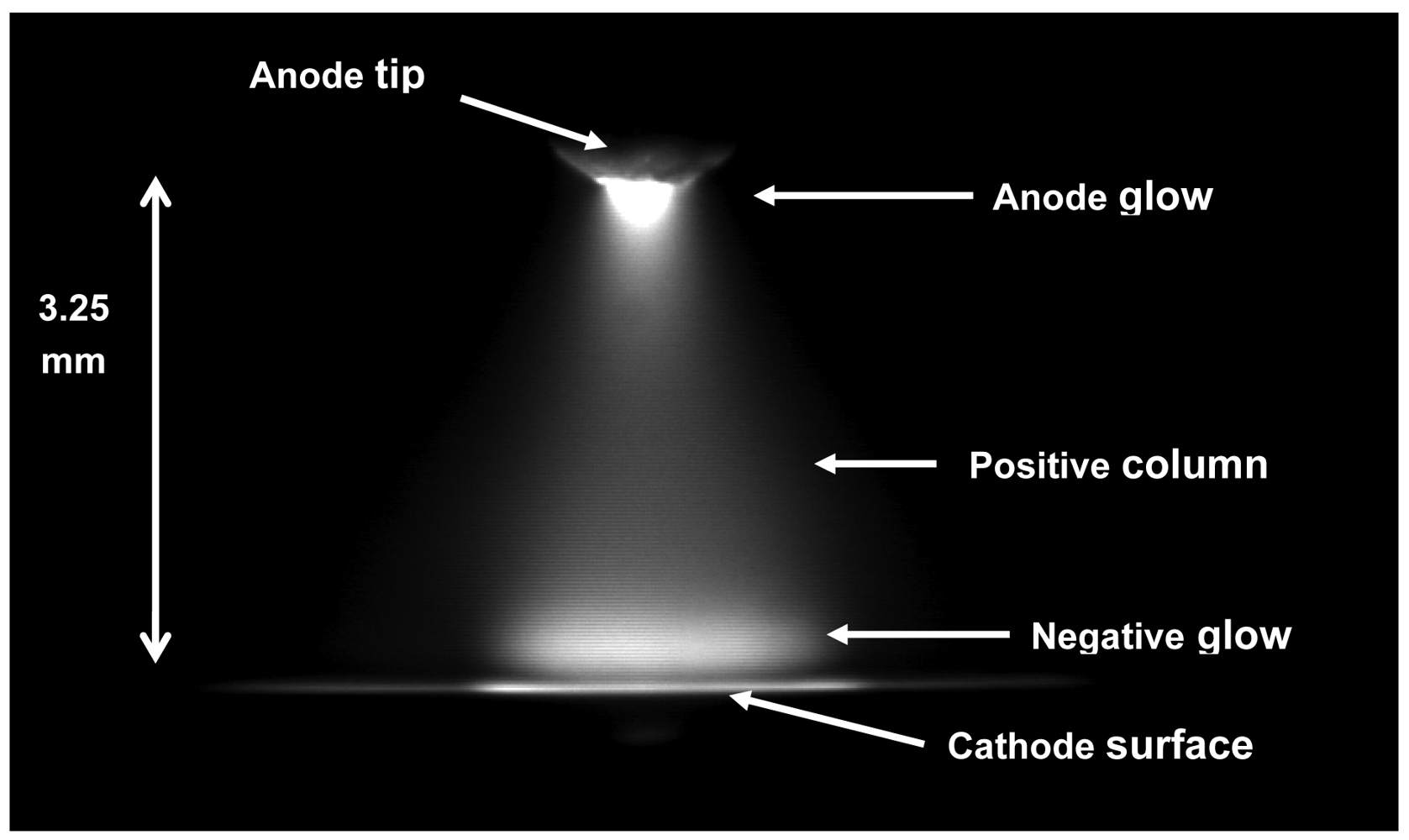
The electrolyte cathode atmospheric glow discharge (ELCAD) technique was invented for the direct measurement of metals (Zn, Cd, Cu, Ni, Cr, Pb, alkali and earth metals, Fe, Mn, etc.) in aqueous samples [1]. In the case of ELCAD, the sample solution is the cathode and a W-rod above it (3–5 mm) is the anode. Under atmospheric air pressure, a d.c. glow discharge is produced (Figure 1). The atomic lines of metals dissolved in the solution appear in the spectrum emitted by the ELCAD, and in this way the concentration of metals in a sample can be determined. Since the cathode sputtering consumes the sample solution, the maintenance of a constant electrode distance, thus a stable discharge operation requires a constant flow rate of cathode solution [1].
The atomic emission having very narrow emitted lines provides excellent possibilities for the simultaneous multimetal detection of up to 20–30 elements. In a flow injection analytical system, the capillary ELCAD detector reached approximately 1 ng mass detection limits (14–34 ng/mL) for heavy metals [2]. Later, in a continuous-flow method, the limits of detection are reported to be between 0.8–350 ng/mL for 16 metals ranging from Na to Hg [3].
The emitted intensity of the atomic lines of metals dissolved in the cathode solution, which have a maximum in the negative glow region, are determined by the pressure, the current and the solution pH, hence fall also on the cathode [4–6]. This was explained by the fact that the M+ positive metal ions leave the cathode solution due to the cathode sputtering. In the cathode dark space, these M+ ions are recombined by the reaction M+ + 2e → M + e. The rate of this recombination is inversely proportional to the kTe average electron energy [7]. The produced neutral M metal atoms diffuse into the negative glow, where they are mainly excited by electron impact [4–6].
On the other hand, the TG gas temperature and the ne electron density also influence the emitted intensity of the atomic metal lines. TG relates to the gas particle density, the collision number between the electrons and the gas particles, the mean free path of electrons and hence the electron energy gained in this distance [8–10]. In this way, the TG and the ne are two basic parameters of the ELCAD plasma determining the operation and the excitation mechanisms, hence the emitted intensities as well.
In the case of the ELCAD and its homologue plasmas, the TG was determined mainly by means of the emitted band of N2 molecule and OH radical, while the ne was studied by various methods. The published data, however, are very confusing, covering ∼3 orders of magnitude in ne values and ∼1 order of magnitude in TG values [3,4,6,11–20,21].
The evaluation of the available data was based on the following three conditions:
In order to offer an accurate method for the determination of TG, the gas composition of the ELCAD plasma was studied.
Since the ELCAD is an atmospheric glow discharge, hence for TG and Te electron temperature, TG = Te [22,23] or Te ≈ TG [24–26] can be expected. If Te is also measured, Te = TG or Te ≈ TG relation can be used for the mutual validation of the received values.
As a consequence of the Te = TG (or Te ≈ TG) relation referring to an local thermodynamic equilibrium (LTE) [22,23] (or a good approximation of it [24–26]), the corresponding values of TG and ne can be calculated from the Engel-Brown approximation [8,10] of the Saha-equation [27,28] related to the weakly ionized glow discharges with low charge densities.
2. The Published TG and ne DATA
The data presented in Table 1 are evaluated by means of the three conditions mentioned above.
3. The Evaluation of the Published TG and ne Data
3.1. The Investigation of the Gas Composition
To obtain the correct TG in the ELCAD plasma, the first necessary condition is the accurate knowledge of gas composition of the ELCAD plasma. From the measurement of the minimum flow rate of the electrolyte cathode, which can still sustain the discharge for at least 10 s, a cathode sputtering rate of 1,500 mg/min was obtained at a cathodic current density of 3.7 A/cm2, a current of 80 mA, and a pH = 1.55 (adjusted with HCl). This means, that 5 × 1022 H2O molecules leave the electrolyte cathode each minute due to the cathode sputtering. After the ELCAD plasma is ignited in the atmospheric air, the plasma composition is changing very fast by the cathode sputtering.
This sputtering rate is higher by 3–4 orders of magnitude than those observed on metal cathodes. Since this high flux of the sputtered matter must leave the discharge plasma through its boundary surface, an overpressure builds up in the core of the plasma. Due to this overpressure, the solution cathode surface is depressed [29] and a pressure gradient appears between the plasma core and the outer, ambient air. Therefore, a significant gas flow from the plasma core to the ambient air occurs. In ELCAD, the TG values of ∼8,000–5,000 K were found from the ratio of the measured intensity of the OH 306.5 nm, 306.8 nm and 308.9 nm unresolved band heads [6], hence the thermal water splitting effect appears producing H and OH particles [30]. This multiplies further the rate of outward gas flow. Thus, the OH radicals produced in the plasma core leave the core of the cathode dark space and the negative glow with a velocity of 5–10 m/s. This totally obstructs the diffusion of any component of the ambient gas atmosphere into the ELCAD plasma [31]. Because of this extensive flushing process the ELCAD plasma operates in a self-generated saturated water vapor internal atmosphere. This is supported by the measured intensity distributions:
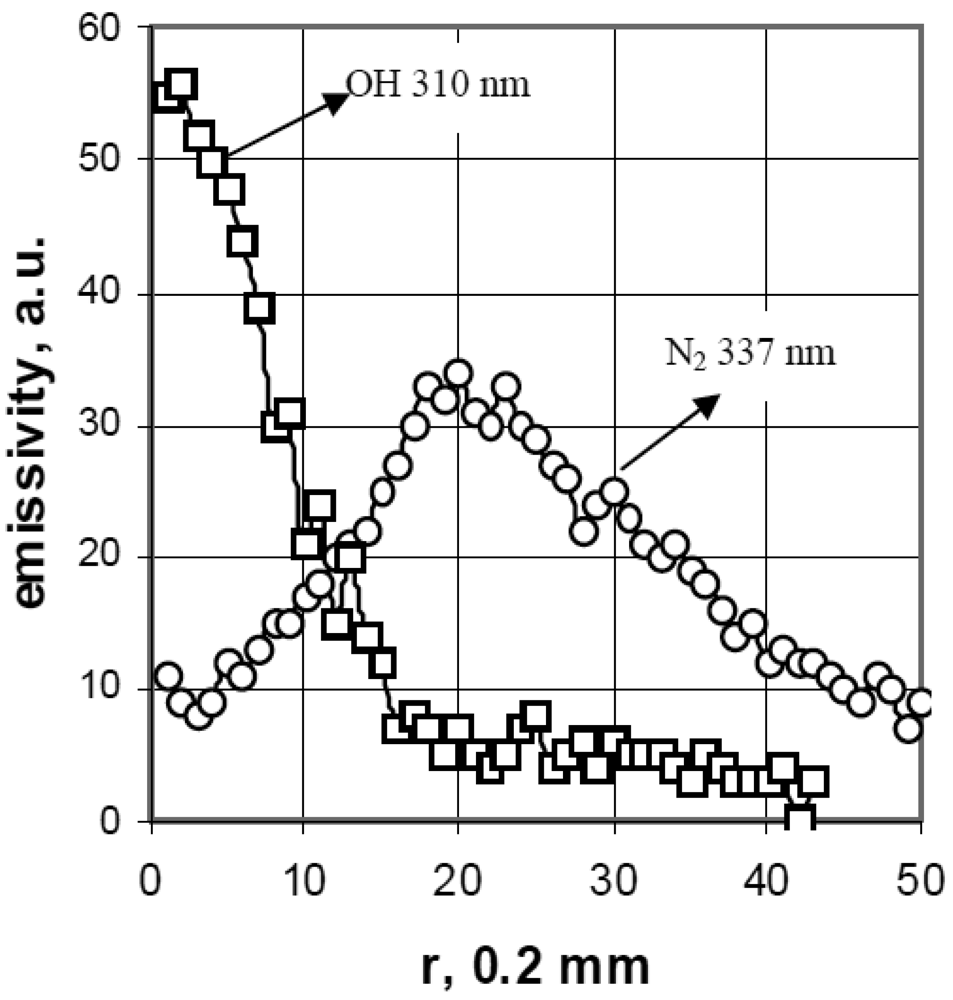
The intensity distribution of the OH-310 nm and the N2-337 nm bands in the ELCAD measured by an ultraviolet sensitive CCD camera using the corresponding interference filters (λ0 = 310 nm, λ0 = 337 nm, Δλ = 10 nm). The Abel-inversion processing of these plasma pictures show that in the near cathode region, the plasma contains dominantly OH radicals, while N2 can be observed only in the outer sheath of the plasma (Figure 2 [31]).
The axial intensity distribution of N2 measured as a function of the distance from the anode showed only a peak in the close anode region, while it was very low at the other segment of the discharge. N2 can diffuse into the ELCAD plasma only at the near-anode region, since there the outflow of the plasma gases is practically negligible [6].
Since the ELCAD operates in a self-generated saturated water vapour with an atmospheric pressure, therefore the intensity of the O+ (441–445 nm) lines, the Hβ-486.1 nm line, the OH ultraviolet bands and the atomic lines of metals dissolved in the liquid electrolyte cathode were found to be independent from the applied outer gas atmosphere [4–6]. Considering these facts, the correct TG values in the ELCAD plasma can be determined only from the emitted intensity of the OH bands.
Furthermore, the Trot rotational temperature of the ultraviolet OH (A2Σ, v = 0) → OH (X2∏, v = 0) band was found to be close to the TG [32], and Izarra demonstrated that this Trot can be obtained from the measured intensity ratio of the G0 = 306.5 nm, the G1 = 306.8 nm and the Gref = 308.9 nm (G0/Gref; G1/Gref) unresolved band heads [33]. He gave the Trot values in 100 K steps as a function of the spectral resolution of the applied monochromator. The received Trot values were verified by an independent, interferometric measurement [34].
The result of other methods (the Boltzmann-plot, the simulation of emitted spectrum as a function of TG), applied for determination of TG was not verified by an independent measurement [3,11–20]. Therefore, the Izarra method can be considered to be only a confirmed determination of the correct TG value in the ELCAD plasma.
3.2. The Te Electron and the TG Gas Temperatures
Since the ELCAD is an atmospheric glow discharge, thus TG ≈ Te can be expected [22–26]. This is valid only for the data in the first line of Table 1. In this case, TG is determined from the emitted intensity of the OH 306–309 nm bands with using of Izarra method, while Te is obtained from the ratio of measured intensity of the Cu-I 510.5 nm and 515.3 nm lines [4,6].
In all other cases, even if the TG determined from the emitted intensity of the OH bands, Te ≫ TG was obtained. This was attributed to that the discharge plasma is not in the local thermodynamical equilibrium, but this explanation is a self-contradiction, since the Maxwell-Boltzmann distribution was applied for determination of Trot by means of the Boltzmann-plot method and the simulation of the emitted spectrum of the OH bands.
The so called ionic temperature of Tion ≈ 4,623–5,038 K was determined from the Saha-Eggert equation with using the measured intensity of the Mg-I 285.2 nm and the Mg-II 279.5 nm lines [3,16]:
Equation (1/a) can be obtained from the Saha-Equation [27,28]
The conditions of Equations (2) and (4) can be applied for the ELCAD, since the excitations are mostly the electron impacts in it and it is an atmospheric glow discharge. Because of Equation (4), the received Tion ≈ 4,623–5,038 K is not the so called ionic, but this is really the common temperature of TG = Te. Therefore, the Trot ≈ 3,200–3,600 K gas temperature determined from the emitted intensity of the OH 306 nm band is inaccurate.
3.3. TG and ne Values and the Engel-Brown Approximation
The Saha-equation concerns the highly ionized plasmas with high charge densities [27,28]. But the glow discharges are weakly ionized plasmas, hence their charge densities are very low. Since the ELCAD is also a glow discharge, hence, instead of Saha-equation, the Engel-Brown approximation given for glow discharges [8,10] is used for checking the published TG and ne values:
The dependence of nn neutral gas particle density on the gas pressure and the gas temperature is [9]:
Combining the Equations (5) and (6) and taking into account that the ELCAD operates in a saturated atmospheric pressure water vapour, thus p = 760 torr and eUi = 2 × 10−18 J, we have:
The published TG and ne values are compared with the results obtained from Equation (7). The ne ≈ 2.1 × 1013 cm−3 value was estimated [4,21] at the end of the cathode dark space, where ne ≈ n+(= positive ion density) [8–10]. To obtain the ne value in the negative glow, this latter result needs a refinement due to the general charge density distributions.
For this saturated, atmospheric water vapour plasma, reliable simulated charge density distributions confirmed by experiments cannot be found in the literature. Therefore, the ne value in the negative glow can be estimated only on the base of two different general charge density distributions for glow discharges:
The von Engel distribution indicates that ne in the negative glow is higher by a factor of ∼1.5 than that at the end of cathode dark space [10]. Thus:
The Raizer distribution shows that ne in the negative glow is lower by a factor of ∼0.5 compared with that at the end of cathode dark space [9], hence:
In an ELCAD-type discharge, the radial distribution of the ne electron density was determined from the measured Stark-broadening of the Hβ-486.1 nm line. In the negative glow:
Applying Equation (7), the evaluation of the published TG and ne values presented in Table 1 can be summarized by a combined plot shown by Figure 3.
Figure 3 shows that the use of the N2 emission for investigation of the plasma core is misleading due to the fact that the plasma core in the negative glow does not contain components of the ambient atmosphere.
Except the TG ≈ 7,000 K and ne ≈ (1–3) × 1013 cm−3 values [6,21], the published ne electron density and the TG gas temperature data pairs are very far from the von Engel equilibrium curve (solid line) calculated for H2O vapor. In accordance with the usual, classical readings, the error of temperatures presented on Figure 3, is about ∼2,500–9,000 K. On the other hand, the published electron density values are higher with about two orders of magnitude compared with the expected one.
4. Conclusions
The evaluation of the published data performed by means of Equation (3) shows that in most of the cases, the obtained Trot rotational temperature and ne electron density values are not consistent with each other. Generally, the obtained Trot values are much lower, while the determined ne values are very much higher compared with those can be received from Equation (7). The main reasons of this are the following:
It is not yet widely understood that ELCAD plasmas operate in saturated H2O vapor due to the very intense sputtering of the aqueous cathode. Hence, the gas temperature determination based on the emitted spectrum of N2 molecule being only in the outer sheath cannot give the correct, real gas temperature data of the plasma.
For determination of TG (≈Trot) in the ELCAD technique, the method of de Izarra giving Trot from the ratio of the measured unresolved ultraviolet band heads of OH proved to be the only reliable method. These Trot values were verified by an independent, interferometric measurement [33,34].
A serious conceptual confusion can be found in the interpretation of the temperature results. The Te ≫ Trot values obtained from the emitted spectrum simulation and the Boltzmann plot method were attributed to the fact that the investigated ELCAD plasma is not in a local thermodynamic equilibrium. But this is a self-contradiction, since the Maxwell-Boltzmann distribution was applied for determination of the temperatures. These could be avoided if TG = Te are used for the mutual validation of the received temperature data. A thorough evaluation of the experiments and the simulations calculations could help to find the possible error sources causing these incorrect temperature values.
The experimental determinations of the ne electron density refer to that the limit of the applied experimental methods were not presented, since often they were not taken into account. In certain cases, the theoretical determination of ne is too complicated and confusing, moreover it neglects the basic properties of the ELCAD plasma.
Some investigations of this “exotic” plasma seem to be loaded with serious experimental errors:
ambiguous plasma conditions (e.g., distilled water cathode without recording of the steeply changing pH and conductivity values of the cathode solution during the plasma operation)
plasma probing with low spatial resolution technique (e.g., the received values cannot be linked to the relevant parts of this plasma of small physical dimensions, V ∼ 10 mm3)
considering the small physical dimensions of the plasma, a misaligned optical system can easily produce meaningless results.
Generally in the reviewed publications the prime rule of the experimental research is frequently missing: the experiment must be as precise as the theoretical base of the evaluation, in other words the quality of the measured data determines the reliability of the evaluation results. Without a strictly designed experimental setup using adequate techniques fitting to the characteristics of the specimen to be investigated, only conclusions of low validity can be derived, even with applying the most sophisticated theoretical treatments.
Acknowledgments
This work was supported by the Hungarian Scientific Research Foundation (OTKA) under the project number of K 68390.
References
- Cserfalvi, T.; Mezei, P.; Apai, P. Emission studies on a glow discharge in atmospheric pressure air using water as a cathode. J. Phys. D Appl. Phys. 1993, 26, 2184–2188. [Google Scholar]
- Cserfalvi, T.; Mezei, P. Subnanogram sensitive multimetal detector with atmospheric electrolyte cathode glow discharge. J. Anal. At. Spectrom. 2003, 18, 596–602. [Google Scholar]
- Webb, M.R.; Andrade, F.J.; Gamez, G.; McCrindle, R.; Hieftje, G.M. Spectroscopic and electrical studies of a solution-cathode glow discharge. J. Anal. At. Spectrom. 2005, 20, 1218–1225. [Google Scholar]
- Mezei, P.; Cserfalvi, T. Electrolyte cathode atmospheric glow discharges for direct solution analysis. Appl. Spectrosc. Rev. 2007, 42, 573–604. [Google Scholar]
- Mezei, P.; Cserfalvi, T.; Jánossy, M. Pressure dependenc of the atmospheric electrolyte cathode glow discharge spectrum. J. Anal. At. Spectrom. 1997, 12, 1203–1208. [Google Scholar]
- Mezei, P.; Cserfalvi, T.; Csillag, L. The spatial distribution of the temperatures and the emitted spectrum in the electrolyte cathode atmospheric glow discharge. J. Phys. D Appl. Phys. 2005, 38, 2804–2811. [Google Scholar]
- Massey, H.S.W.; Burhop, E.H.S.; Gilbody, H.B. Recombination. In Electronic and Ionic Impact Phenomena; Massey, H.S.W., Gilbody, H.B., Eds.; Clarendon: Oxford, UK, 1974. [Google Scholar]
- Brown, S.C. Introduction to Electrical Discharges in Gases; John Wiley: New York, USA, 1966. [Google Scholar]
- Raiser, Y.P. Gas Discharge Physics; Springer: Berlin, Germany, 1991. [Google Scholar]
- Von Engel, A. Ionized Gases; Clarendon: Oxford, UK, 1965. [Google Scholar]
- Afanasev, V.P.; André, P.; Barinov, Y.A.; Faure, G.; Kaplan, V.B.; Lefort, A.; Shkolnik, S.M. Theoretical and experimental investigation of a discharge with liquid nonmetallic electrodes in air at atmospheric pressure. Proceedings Contributed Papers of XXIII International Conference on Phenomena in Ionized Gases, Toulouse, France, 17–22 July 1997; Volume III. p. 104.
- Faure, G.; Shkolnik, S.M. Determination of rotational and vibrational temperatures in a discharge with non-metallic electrodes in air at atmospheric pressure. J. Phys. D Appl. Phys. 1998, 31, 1212–1218. [Google Scholar]
- André, P.; Barinov, Y.A.; Faure, G.; Kaplan, V.; Lefort, A.; Shkolnik, S.M.; Vacher, D. Experimental study of discharge with liquid non-metallic (tap-water) electrodes in air at atmospheric pressure. J. Phys. D Appl. Phys. 2001, 34, 3456–3465. [Google Scholar]
- André, P.; Aubreton, J.; Barinov, Y.A.; Elchinger, M.F.; Fauchais, P.; Faure, G.; Kaplan, V.; Lefort, A.; Rat, V.; Shkolnik, S.M. Theoretical study of column of discharge with liquid non-metallic (tap-water) electrodes in air at atmospheric pressure. J. Phys. D Appl. Phys. 2002, 35, 1846–1854. [Google Scholar]
- XinPei, L.; Leipold, F.; Laroussi, M. Optical and electrical diagnostics of a non-equilibrium air plasma. J. Phys. D Appl. Phys. 2003, 36, 2662–2666. [Google Scholar]
- Webb, M.R.; Chan, G.C.-Y.; Andrade, F.J.; Gomez, G.; Hieftje, G.M. Spectroscopical characterization of ion and electron populations in solution-cathode glow discharge. J. Anal. At. Spectrom. 2006, 21, 525–530. [Google Scholar]
- Bruggeman, P.; Liu, J.; Degroote, J.; Kong, M.G.; Vierendeels, J.; Leys, Ch. Dc excited glow discharges in atmospheric pressure air inpin-to-water electrode systems. J. Phys. D Appl. Phys. 2008. [Google Scholar] [CrossRef]
- Bruggeman, P.; Leys, C. Non-thermal plasmas in and in contact with liquids. J. Phys. D Appl. Phys. 2009. [Google Scholar] [CrossRef]
- Bruggeman, P.; Ribezl, E.; Maslani, A.; Degroote, J.; Malesevic, A.; Rego, R.; Vierendeels, J.; Leys, C. Characteristics of atmospheric pressure air discharges with liquid cathode and a metal anode. Plasma Source Sci. Technol. 2008. [Google Scholar] [CrossRef]
- Titov, V.A.; Rybkin, V.V.; Smirnov, S.A.; Kulentsan, A.L.; Choi, H.S. Experimental and theoretical studies on the characteristics of atmospheric pressure glow discharge with liquid cathode. Plasma Chem. Plasma Process. 2006, 26, 543–555. [Google Scholar]
- Mezei, P.; Cserfalvi, T. Charge densities in the electrolyte cathode atmospheric glow discharges (ELCAD). Eur. Phys. J. Appl. Phys. 2007, 40, 89–94. [Google Scholar]
- Houben, J.M.; Zaat, J.H. Analysis of a Plasma Torch. Available online: http://alexandria.tue.nl/repository/freearticles/604508.pdf (accessed on 24 April 2012).
- Meichsner, J. Introduction to Plasma Physics, Lecture on European Summer School Plasma Physics in Science and Technology. Available online: http://ppst-physik.uni-greifswald.de/Meichsner-PPST-2009-Prague.pdf (accessed on 24 April 2012).
- Massey, T.J. Constricted discharges in rare gases II. Analysis of the macroscopic properties of the discharges. J. Appl. Phys. 1965, 36, 373–380. [Google Scholar]
- Elenbaas, W. Ligth Sources; Crane Russak: New York, NY, USA, 1972. [Google Scholar]
- Penning, F.M. Electrical Discharges in Gases; Cleaver-Hume Press: London, UK, 1957. [Google Scholar]
- Simonyi, K. Physikalische Elektronik; Akadémiai Kiadó: Budapest, Hungary, 1972. [Google Scholar]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion; Plenum Press: New York, NY, USA, 2008; Volume 1. [Google Scholar]
- Mezei, P.; Cserfalvi, T. The investigation of an abnormal electrolyte cathode atmospheric glow discharge (ELCAD). J. Phys. D Appl. Phys. 2006, 39, 1–6. [Google Scholar]
- Boudesocque, N.; Vandensteendam, C.; Lafon, C.; Girold, C. Hydrogen production by thermal water splitting using a thermal plasma. Proceedings of 16th World Hydrogen Energy Conference (WHEC 16), Lyon, France, 13–16 June 2006.
- Cserfalvi, T.; Mezei, P. The radial emissivity distribution of N2-337 nm and OH-306 nm bands in the electrolyte cathode atmospheric glow discharge (ELCAD). Posters of the Colloqium Spectroscopicum Internationale XXXVI, Budapest, Hungary, 30 August–3 September 2009. Poster PW-85; CSI XXXVI compact disc.
- Pellerin, S.; Cormier, J.M.; Richard, F.; Musiol, K.; Chapelle, J. A spectroscopic diagnostic method using UV OH band spectrum. J. Phys. D Appl. Phys. 1996, 29, 726–739. [Google Scholar]
- De Izarra, C. UV OH spectrum used as molecular pyrometer. J. Phys. D Appl. Phys. 2000, 33, 1697–1704. [Google Scholar]
- Rabat, H.; de Izarra, C. Check of OH rotational temperature using an interferometric method. J. Phys. D Appl. Phys. 2004, 37, 2371–2375. [Google Scholar]

| Trot ≈ TG [K] | Te [K] | ne [cm−3] | type of discharge | Ref. |
|---|---|---|---|---|
| NAR: 6,000 PC: 4,800 NG: 7,000 OH emission, Izarra method | NAR: 6,000 PC: 5,500 NG: 7,000 Int. ratio of 510.5, 515.3 nm Cu lines | NG: 1013; 3 × 1013 Calculated from the operating parameters | Original ELCAD | [6,21] |
| NAR, PC: 1,000 NG: 2,000 N2 emission | 4,000 Intensity ratio of H-Balmer lines | PC: 4 × 1011 NG: 7 × 1011 Microwave absorption | liquid electrodes | [11–14] |
| 1,800 N2 emission | 7 × 1012 Calculated from current density, temperature | a.c. excited (v = 60 Hz) ELCAD like | [15] | |
| PC: 3,200 NG: 3,600 OH emission Boltzmann plot | PC: 2,500 NG: 5,000 from Fe-I lines, Boltzmann-plot; Saha-equation | PC: 2.5 × 1014 NG: 8.5 × 1014 Stark broadening of H-486.1 nm line | ELCAD type | [3,16] |
| PC: 3,250 NG: 3,400–3,600 OH emission PC: 3,250 NG: 2,200–2,800 N2 emission | 6,100 Intensity ratio of Hα and Hβ lines | NG:(5.5–9) × 1014 Stark broadening of H-486.1 nm | ELCAD like | [17–19] |
| 1,700 N2 emission 2,200–3,200 OH emission | 5,565 calculated from OH vibr. level population | 1013 calculated from current distribution | ELCAD like with distilled water cathode | [20] |
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mezei, P.; Cserfalvi, T. A Critical Review of Published Data on the Gas Temperature and the Electron Density in the Electrolyte Cathode Atmospheric Glow Discharges. Sensors 2012, 12, 6576-6586. https://doi.org/10.3390/s120506576
Mezei P, Cserfalvi T. A Critical Review of Published Data on the Gas Temperature and the Electron Density in the Electrolyte Cathode Atmospheric Glow Discharges. Sensors. 2012; 12(5):6576-6586. https://doi.org/10.3390/s120506576
Chicago/Turabian StyleMezei, Pál, and Tamás Cserfalvi. 2012. "A Critical Review of Published Data on the Gas Temperature and the Electron Density in the Electrolyte Cathode Atmospheric Glow Discharges" Sensors 12, no. 5: 6576-6586. https://doi.org/10.3390/s120506576




