With the development of mechatronics, automatic systems consisting of sensors for perception and actuators for action are more and more widely used in applications [1–4]. Besides the proper choices of sensors and actuators and an elaborate fabrication of mechanical structures, the control law design also plays a crucial role in the implementation of automatic systems especially for those with complicated dynamics. For most mechanical sensor-actuator systems, it is possible to model them in Euler-lagrange equations [4,5]. In this paper, we are concerned with the sensor-actuator systems modeled by Euler-lagrange equations.

Due to the importance of Euler-lagrange equations in modeling many real sensor-actuator systems, much attention has been paid to the control of such kind systems. According to the type of constraints, the Euler-lagrange system can be categorized into Euler-lagrange system without nonholonomic constraints (e.g., fully-actuated manipulator [6,7], omni-directional mobile robot [8]), and the system subject to nonholonomic constraint [9] (e.g., the cart-pole system [10], the under-actuated multiple body system [11]). For Euler-lagrange system without nonholonomic constraints, the dimension of inputs are often equal to the dimension of output and the system are often able to be transformed into a double integrator system by employing feedback linearization [12]. Other methods, such as control Lyapunov function method [13], passivity based method [14], optimal control method [15], etc., are also successfully applied to the control of Euler-lagrange system without nonholonomic constraints. In contrast, as the dimension of inputs is lower than that of outputs, it is often impossible to directly transform the Euler-lagrange system subject to nonholonomic constraints to a linear system and thus feedback linearization fails to stabilize the system. To tackle the difficulty, variable structure control based method [16], backstepping based control [17], optimal control based method [18], discontinuous control method [19], etc., are widely investigated and some useful design procedures are proposed. However, due to the inherent nonlinearity and nonholonomic constraints, most existing methods [16–19] are strongly model dependent and the performance are very sensitive to model errors. Inspired by the success of human operators for the control of Euler-lagrange systems, various intelligent control strategies, such as fuzzy logic [20], neural networks [21], evolutionary algorithms [22], to name a few of them, are proposed to solve the control problem of of Euler-lagrange systems subject to nonholonomic constraints. As demonstrated by extensive simulations, these type of strategies are indeed effective to the control of Euler-lagrange systems subject to nonholonomic constraints. However, rigorous proof on the stability are difficult for this type of methods and there may exist some initializations of the state, from which the system cannot be stabilized.

In this paper, we propose a self-learning control method applicable to Euler-lagrange systems. In contrast to existing work on intelligent control of Euler-lagrange systems, the stability of the close loop system with the proposed method is proven in theory. On the other hand, different from model based design strategies, such as backstepping based design [17], variable structure based design [16], etc., the proposed method does not require information of the model parameters and therefore is a model independent method. We formulate the problem from an optimal control perspective. In this framework, the goal is to find the input sequence to minimize the cost function defined on infinite horizon under the constraint of the system dynamics. The solution can be found by solving a Bellman equation according to the principle of optimality [23]. Then an adaptive dynamic programming strategy [24–26] is utilized to numerically solve the input sequence in real time.

The remainder of this paper is organized as follows: in Section 2, preliminaries on Euler-lagrange systems and variable structure control are given briefly. In Section 3, the problem is formulated as a constrained optimization problem and the critic model and the action model are employed to approximate the optimal mappings. The control law is then derived in Section 4. In Section 5, simulations are given to show the effectiveness of the proposed method. The paper is concluded in Section 6.

In this paper, we are concerned with the following sensor-actuator system in the Euler-Lagrange form, (1) D ( q ) q ¨ + C ( q , q ˙ ) q ˙ + ϕ ( q ) = uwhere q ∈ ℝⁿ, D(q) ∈ ℝ^n×n is the inertial matrix, C(q,q˙) ∈ ℝ^n×n, ϕ(q) ∈ ℝⁿ and u ∈ ℝⁿ. Note that the inertial matrix D(q) is symmetric and positive definite. There are three terms on the left side of the above equation. The first term involve the inertial force in the generalized coordinates, the second one models the Coriolis force and friction, the values of which depend on q̇ and the third one is the conservative force, which is in correspondence to the potential energy. The control force u applied on the system drives the variation of the coordinate q. It is also noteworthy that we assume the dimension of u is equal to that of q here. This definition also admits the case for u with lower dimension than that of q by imposing constraints to u, e.g., the constraint u = [u₁,u₂, …,u_n] with u₁ = 0 restricts u in a n – 1 dimensional space. Defining state variables x₁ = q and x₂ = q, the Euler-Lagrange Equation (1) can be put into the following state-space form: (2) x ˙ 1 = x 2 x ˙ 2 = − D − 1 ( x 1 ) ( u + C ( x 1 , x 2 ) x 2 + ϕ ( x 1 ) )Note that the matrix D(x₁) is invertible as it is positive definite. The control objective is to asymptotically stabilize the Euler-Lagrange system (2), i.e., design a mapping (x₁,x₂) → u such that x₁ → 0 and x₂ → 0 when time elapses.

As an effective design strategy, variable structure control finds applications in many different type of control systems including the Euler-Lagrange system. The method stabilizes the dynamics of a nonlinear system by steering the state to a elaborately designed sliding surface, on which the state inherently evolves towards the zero state. Particularly for the system (2), we define s = s(x₁,x₂) as follows: (3) s = c 0 x 1 + x 2where c₀ > 0 is a constant. Note that s = c₀x₁ + x₂ = 0 together with the dynamics of x₁ in Equation (2) gives the dynamics of x₁ as ẋ₁) = –c₀x₁ for c₀ > 0. Clearly, x₁ asymptotically converges to zero. Also we know x₂ = 0 when x₁ = 0 according to s = c₀x₁ + x₂ = 0. Therefore, we conclude the states x₁, x₂ on the sliding surface s = 0 for s defined in Equation (3) converge to zero with time. With this property of the sliding surface, a control law driving the states to s = 0 definitely grantees the ultimate convergence to the zero states. Accordingly, the stabilization of the system can be realized by controlling s to zero. To reach this goal, a positive definite control Lyapunov function V(s), e.g., V(s) = s², is often used to design the control law. For stability consideration, the time derivative of V(s) is required to be negative definite. In order to guarantee the negative definiteness of the time derivative of V(s), exact information about the system dynamics (2) is often necessary, which results in the model based design strategies.

About the Euler-Lagrange Equation (1) for modeling sensor-actuator systems, we have the following remark:

Remark 1 In this paper, we are concerned with the class of sensor-actuator systems modeled by the Euler-Lagrange Equation (1). Actually, the dynamics of mechanical systems can be described by the Euler-Lagrange equation according to the rigid body mechanics [4,5], which is essentially equivalent to Newton's laws of motion. Therefore, mechanical sensor-actuator system can be modeled by Equation (1). In this regard, the Euler-Lagrange equation employed in the paper models a general class of sensor-actuator systems.

Without losing generality, we stabilize the system (1) by steering it to the sliding surface s = 0 with s defined in Equation (3). Different from existing model based design procedures, we design a self-learning controller, which does not require accurate knowledge about D(q), C(q,q̇) and ϕ(q) in Equation (1). In this section, we formulate such a control problem from the optimal control perspective.

In this paper, we set the origin as the desired operating point, i.e., we consider the problem of controlling the state of the system (1) to the origin. For the case with other desired operating points, the problem can be equivalently transformed to the one with the origin as the operating point by shifting the coordinates. At each sampling period, the norm of s = c₀x₁ + x₂, which measures the distance from the desired sliding surface s = 0, can be used to evaluate the one step performance. Therefore, we define the following utility function associated with the one-step cost at the ith sampling period, (4) U i = U ( s )with (5) U ( s ) = { 0 | s 1 | < δ 1 , | s 2 | < δ 2 , … , | s n | < δ n 1 otherwisewhere s is defined in Equation (3) and s = [s₁,s₂, …, s_n]^T, |s_i| denotes the absolute value of the ith component of the vector s, the parameter δ_i> 0 for i = 1, 2,…, n. At each step, there is a value U_i and the total cost starting from the kth step along the infinite time horizon can be expressed as follows, (6) J k = J ( x ( k ) , u ¯ ( k ) ) = ∑ i = k ∞ γ i − k U iwhere x(k) is the state vector of system (1) sampled at the kth step with x ( k ) = [ x 1 T ( k ) , x 2 T ( k ) ] T γ is the discount factor with 0 < γ < 1, ū(k) = (u_k,u_k+1,…,u_∞) is the control sequence starting from the kth step. Note that for the deterministic system (1), the preceding states after the kth step are determined by x(k) and the control sequence ū_k. Accordingly, J_k is a function of x(k) and ū(k) with J_k = J(x(k), ū(k)). Also note that both the cost function J_k and the utility function U_k are defined based on the discrete samplings of the continuous system (1). Now, we can define the problem of controlling the sensor-actuator system (1) in this framework as follows, (7a) min u ( 0 ) , u ( 1 ) , … , u ( ∞ ) ∈ Ω J 0 = ∑ i = 0 ∞ γ i U isubject to: (7b) { x ˙ 1 ( t ) = x 2 ( t ) x ˙ 2 ( t ) = − D − 1 ( t ) ( x 1 ( t ) ) ( u ( t ) + C ( x 1 ( t ) , x 2 ( t ) ) x 2 ( t ) + ϕ ( x 1 ( t ) ) ) (7c) u ( t ) = u ( i ) for i τ ≤ t < ( i + 1 ) τwhere U_i is defined by Equations (4) and (5), τ > 0 is the sampling period, the set Ω defines the feasible control actions, J₀ is the cost function for k = 0 in Equation (6). It is worth noting that J₀ is a function of ū(0) = (u₀, u₁,…, u_∞) and x(0) according to Equation (6). The optimization in Equation (7) is relative to ū(0) with a given initial state x(0). Also note that in the optimization problem in Equation (7), the decision variable u(0),u(1), …,u(∞) are defined in every sampling period. The control action keeps the value in the duration of two consecutive sampling steps. This formulation is consistent with the real implementations of digital controllers.

Remark 2 There are infinitely many decision variables, which are u(0), u(1), …, u(∞), in the optimization problem in Equation (7). Therefore, this is an infinite dimensional problem. It cannot be solved directly using numerical methods. Conventionally, such kind of problem is often solved by using a finite dimensional approximation [27]. In addition, note that the dynamic model of the system appears in the optimization problem in Equation (7) and it will also show up in the finite dimensional relaxation of the problem, which means the resulting solution requires model information and thus is also model-dependent. In contrast, in this paper we investigate the model-independent variable structure control of sensor-actuator systems on the infinite time horizon.

In this section, we present the strategy to solve the constrained optimization problem efficiently without knowing the model information of the chaotic system. We first investigate the optimality condition of Equation (7) and present an iterative procedure to approach the analytical solution. Then, we analyze the convergence of the iterative procedure and the stability with the derived control strategy.

In this section, we consider the simulation implementation of the proposed control strategy. The dynamics given in Equation (1) model a wide class of sensor-actuator systems. Particularly, to demonstrate the effectiveness of the proposed self-learning variable structure method, we apply it to the stabilizations of a typical benchmark system: the cart-pole system.

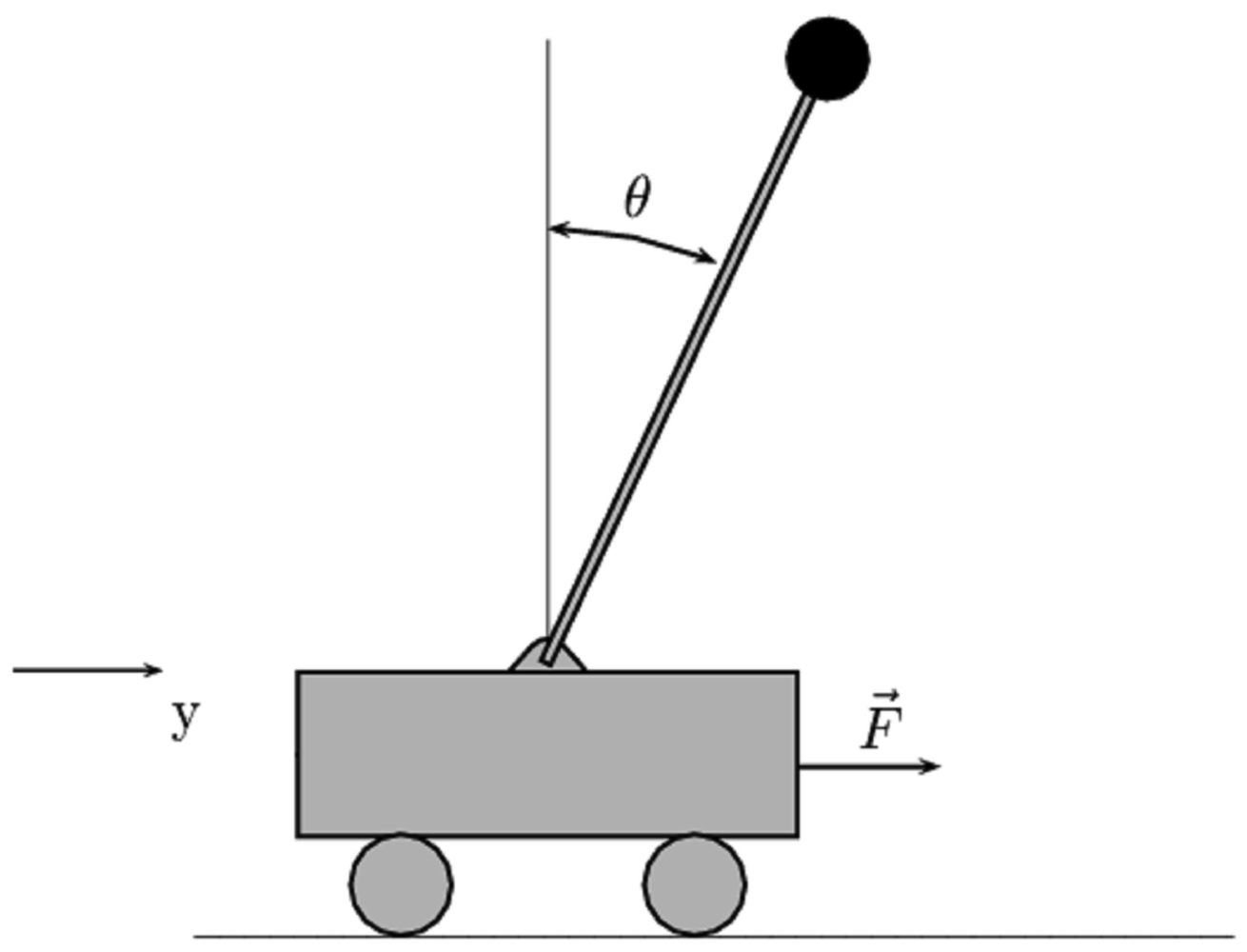
The cart-pole system, as sketched in Figure 1, is a widely used testbed for the effectiveness of control strategies. The system is composed of a pendulum and a cart. The pendulum has its mass above its pivot point, which is mounted on a cart moving horizontally. In this part, we apply the proposed control method to the cart-pole system to test the effectiveness of our method.

In this paper, the self-learning variable structure control is considered to solve a class of sensor-actuator systems. The control problem is formulated from the optimal control perspective and solved via iterative methods. In contrast to existing models, this method does not need pre-knowledge on the accurate mathematic model. The critic model and the the action model are introduced to make the method more practical. Simulations show that the control law obtained by the proposed method indeed achieves the control objective. Future work on this topic includes the theoretical proof of the convergence and exploration on the performance limit of the proposed strategy. Also, the control of other mechanical systems modeled by Euler-Lagrange system, such as manipulators etc., will be explored in our future work.