Recent advances in microelectronics have led to the development of autonomous tiny devices called sensor nodes. Such devices, in spite of their physical limitations, contain the essential components of a computer, such as memory, I/O ports, sensors, and wireless transceivers which are typically battery-powered. Once deployed (randomly or not) over a certain area, sensor nodes have the ability to be in touch via wireless communications with neighboring nodes forming a wireless sensor network (WSN). The great advantage of using WSNs is that they can be applied in important areas such as disaster and relief, military affairs, medical care, environmental monitoring, target tracking, and so on [1–3]. However, most of WSN applications are based on local events. This means that each sensor node needs to detect and share local phenomenons with neighboring nodes, implying that the location of such events (i.e., sensor locations) are crucial for the WSN application. In this way, sensor self-positioning represents the first startup process in most WSN projects. It is well known that using a GPS in each sensor node represents the primary solution to infer position estimates. However, this option is not suitable to be considered in all nodes if parameters like size, price, and energy-consumption in a sensor node are of concern [4]. In order to optimize such parameters, a good option consists of reducing to a small fraction of sensors with GPS, and the remainder sensors (i.e., unknown sensors), commonly above 90% of total deployed sensors, should use alternatives to estimate its own positions like radio-frequency transmissions or connectivity with neighboring sensors [5–7].

In order to provide position estimates many localization algorithms have been proposed, coming from different perspectives as described in [8,9]. Basically, localization algorithms can be categorized according to range-based vs. range-free methods, anchor-based vs. anchor-free models, and distributed vs. centralized processing [10,11]. Range-based methods consist of estimating node locations (using a localization algorithm) based on ranging information among sensor nodes. Range estimation between pairs of nodes is achieved using techniques of Time-of-Arrival (ToA), Receive-Signal-Strength (RSS), or Angle-of-Arrival (AoA) [12]. This approach has the disadvantage of requiring extra-hardware in each sensor board, increasing the cost per sensor. However, as far as is known, this approach provides the best cost-accuracy performance in localization algorithms. A less expensive but more inaccurate alternative consists of using just connectivity among sensor nodes to estimate node locations, called range-free [13]. On the other hand, if position estimates are obtained by considering absolute references (e.g., sensors with GPS or Anchors), the resulted position estimates (also with absolute positions) will be closely related to such reference positions, called an anchor-based model. By the contrary, if no reference positions are used to estimate locations, relative coordinates will be obtained, called an anchor-free model.

One of the most interesting and relevant aspects in WSN localization is associated with the way to compute the location of sensor nodes. For example, if all pairwise distance measurements among sensor nodes are sent to a central node to compute position estimates, the localization algorithm becomes centralized. This kind of central processing has the advantage of global mapping, but it has basically two important disadvantages which demerit its use in many cases when robustness and saving-energy have high priority in a WSN [14]. Some important centralized schemes are the next. In [15] an iterative descent procedure (i.e., Gauss–Newton method) is used in a centralized way to solve the Non-Linear Least-Square (NLLS) problem. Another interesting centralized scheme was proposed in [16] where the WSN localization problem is modeled as linear or semidefinite program (SDP), and a convex optimization is used to solve problem.

In contrast, when each sensor node estimates its own location using available information of neighboring nodes (e.g., range, connectivity, location, etc.), the localization process becomes distributed. Distributed processing is much less energy consuming in WSNs than centralized processing because centralized schemes need to collect relevant information from all nodes in the network which implies re-transmissions in multi-hop environments. Also, distributed algorithms are tolerant to node failures due to node redundancy. Thus, basically a distributed algorithm allows robustness, saving-energy, and scalability [14,17,18], which overcomes the limitations imposed by the centralized approach. In [19], a robust least squares scheme (RLS) for multi-hop node localization is proposed. This approach reduces the effects of error propagation by introducing a regularization parameter in the covariance matrix. However, the computational cost to mitigate the adverse effects of error propagation is too high at energy-constrained nodes. Similarly, [20] proposes two weighted least squares techniques to gain robustness when a non-optimal propagation model is considered however they failed to introduce a covariance matrix in the localization process that can effectively decrease the computational complexity. On the other hand, the authors of [21] propose a Quality of Trilateration method (QoT) for node localization. This approach provides a quantitative evaluation of different geometric forms of trilaterations. However, it seems to be that the main idea of this methodology depends on the quality or resolution of geometric forms (i.e., like image processing) which is impractical to be implemented in resource-constrained devices with limited memory and processing capabilities (i.e., nodes).

In this paper, we analyze a range-based bilateration algorithm (BL) that can be used in a distributed way to provide initial estimates for unknown sensors in a wireless sensor network (our analysis consider that each unknown sensor can determine its initial position communicating directly with several anchors). In this case, each node uses a set of two anchors and their respective ranges at a time to solve a set of circle intersection problems using a geometric formulation. The solutions from these geometric problems are processed to pick those that cluster around the location estimate and then take the average to produce an initial node location. Finally, we present a computational/accuracy comparison between the BL algorithm, based on closed-formulas, and a classical Least Squares (LS) approach for localization, based on the iterative Levenberg–Marquardt algorithm (LM).

The outline of this paper is as follows. In Section 2 we examine a popular ranging technique for WSNs used in our simulations. In Section 3 we explore the localization problem from the Least Squares point of view. In Section 4 we analyze in detail the BL algorithm. In Sections 5 and 6 we evaluate the accuracy and computational-complexity performance respectively between the bilateration algorithm vs. LS schemes. Finally, we present our conclusions.

This section presents a brief overview of an existing ranging technique used to estimate the true distance between two sensor nodes using power measurements, called Received Signal Strength (RSS). This technique is popular because sensor nodes do not require special hardware support to estimate distances. As a first approximation, considering the free space path loss model, the distance d_ij between two sensors s_i and s_j can be estimated by assuming that the power signal decreases in a way that is inversely proportional to the square of the distance ( 1 / d ij 2 ). However, in real environments the signal power is attenuated by a factor d^−η_p. The path-loss factor η_p is closely related to geometrical and environmental factors, and it varies from 2 to 4 for practical situations [22]. In noiseless environments the power signal traveling from a sensor s_j to a sensor s_i can be measured according to the relation [23] (1) P ij = P 0   ( d 0 d ij ) η pwhere the path-loss factor (η_p) depends directly on the environmental conditions. P₀ is the received power at the short reference distance of d₀ = 1m from the transmitter. Also, P₀ can be computed by the Friis free space equation [24]. The log-distance path loss model (2) P ¯ L ( i j ) ( dB ) = P 0 − 10 η p log d ij d 0measures the average large-scale path loss between sensors s_i and s_j. The actual path-loss (in dB) is a normally distributed random variable: (3) P L ( ij ) ∼ 𝒩 ( P ¯ L ( ij ) , σ SH 2 )where σ_SH is given in dB and reflects the degradations on signal propagation due to reflection, refraction, diffraction, and shadowing. It can be seen that the linear measurements and distance estimates have a log-normal distribution with a multiplicative effect on the measurements. The noisy range measurement R_ij can be obtained from Equations (2) and (3) as (4) R ij = 10 P 0 − P L ( ij ) 10 − η p

In this section, we describe multilateration schemes that provide solutions to the Least-Square (LS) problem for location estimates using noisy ranging information derived from ToA or RSS ranging techniques. Consider a set of N wireless sensor nodes S = {s₁, s₂,..., s_N}, randomly distributed over a 2-D region whose locations are unknown. We represent these unknown locations with vectors z_i = [x_i, y_i]^T. Further, we assume the presence of a set A = {a₁,a₂,...,a_M} of M reference or anchor nodes with known position q_j = [x_j, y_j]T. Anchor nodes, a_i, are equipped with GPS or a similar scheme to self localize. Also, for practical situations M ≪ N with M > 2. We develop our discussion assuming a 2-D scenario, but it can be easily generalized to the 3-D case.

Moreover, we assume that any sensor can estimate pairwise ranges with its neighbors using time-of-arrival (ToA) or radio signal strength (RSS) techniques [24]. Denote the range estimate between the node s_i and anchor a_j as (5) R ij = d ij + e ijwhere d_ij is the true distance between a_j and s_i, and e_ij represents the measurement error introduced by environmental noise, propagation distortion, and the ranging technique. Then the solution to the localization problem for a node s_i consists of minimizing the sum of certain weighted error-distance function e_w(·) as follows: (6) p i = arg min x ∑ j = 1 M e w ( ‖ q j − x ‖ − R ij ) = arg min x   𝒡   ( x )where p_i = [x_i,y_i]^T represents the most likely position for the sensor s_i that minimizes 𝒡, ‖ · ‖ represents the Euclidean norm, and e_w(x) represents a function that provides a specific weight to the argument x (i.e., error distance). For example, the function e₂(x) = (x)², the LS formulation, is commonly used to solve Equation (6) due its tractability and efficiency in both mathematical and computational analysis. The LS problem can be solved either by closed-form solutions or by iterative methods. Next we describe both methodologies in detail.

In this section we present the bilateration method for WSN localization which can be used as the initialization step for iterative localization schemes. This algorithm avoids iterative procedures, gradient calculations, and matrix operations that increase the internal processing in a constrained device. This research was done independently of the work presented in [36]. Even though both schemes share the same idea (i.e., bilateration), the procedure and the scope of both works are different as shown in Subsection 4.1. We show that it is possible to obtain a position estimate by solving a set of bilateration problems between a sensor node and its neighboring anchors, and then fusing the solutions according to the geometrical relationships among the nodes. Our aim is to find a scheme that can be deployed on a computationally constrained node. We argue that bilateration is an attractive option as the localization problem is divided on smaller sub-problems which can be efficiently solved on a mote. Next we start our development by introducing the typical assumptions and definitions considered in a WSN localization problem.

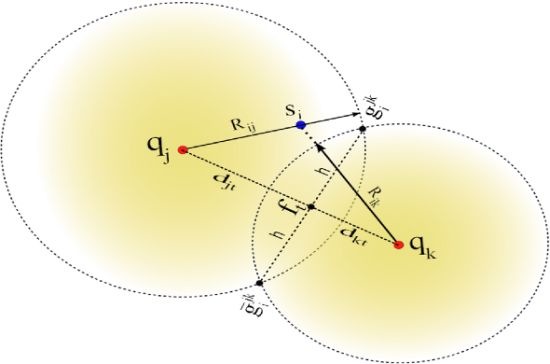
Let us define anchor subsets A_jk ⊂ A such that A_jk = {a_j, a_k} with j ≠ k. Hence, there is a total of Q = ( M 2 ) anchor subsets. Without loss of generality, consider the case for one node s_i that receives from a subset A_jk the anchor positions q_j and q_k, and computes the respective ranges R_ij and R_ik using RSS or ToA measurements. A possible geometrical scenario for this configuration is shown in Figure 1. We can appreciate from this example that the range estimates R_ij is larger than d_ij and R_ik is shorter than d_ik. Now, consider the two range circles shown in the figure; one with its origin at q_j and radius R_ij, and the second with center in q_k and radius R_ik. Next, define the two circle intersection points as g i jk and g ¯ i jk, where g ¯ i jk is the reflection of g i jk with respect to the (imaginary) line that connects q_j and q_k. In this case, the superscript jk represents the anchor subset A_jk. To simplify our discussion, we drop the superscripts, and only use them when more than one anchor subset is involved in our discussion.

In our approach, node s_i determines the circle-circle intersections (CCI) g_i and ḡ_i by solving the closed-form expression reported in [37]. For instance, consider the two right triangles formed by the coordinates (q_j,g_i,f_t) and (q_k,g_i, f_t) in Figure 1, which satisfy the following relationships: (24a) d jt 2 + h 2 = R ij 2 (24b) d kt 2 + h 2 = R ik 2respectively. The distance d_jt can be obtained by solving for h² in Equations (24a) and (24b): (25) R ij 2 − d jt 2 = R ik 2 − d kt 2and letting d = ‖q_j − q_k‖ = d_jt + d_kt resulting in (26a) R ij 2 − d jt 2 = R ik 2 − ( d − d jt ) 2 (26b) R ij 2 = R ik 2 − d 2 + 2 ⋅ d ⋅ d jt (26c) d jt = R ij 2 − R ik 2 + d 2 2 ⋅ dwhere the position f_t = [x_t, y_t]^T is obtained as follows: (27) f t = q j + d jt d ( q k − q j )Finally, the circle intersection g_i = [x_i,y_i]^T is computed as (28a) x i = x t ± h d ( y k − y j ) (28b) y i = y t ∓ h d ( x k − x j )where q_j = [x_j,y_j]^T, q_k = [x_k, y_k]^T, and h is easily obtained from Equation (24). The complementary signs of Equations (28a) and (28b) are used to obtain the solution for ḡ_i.

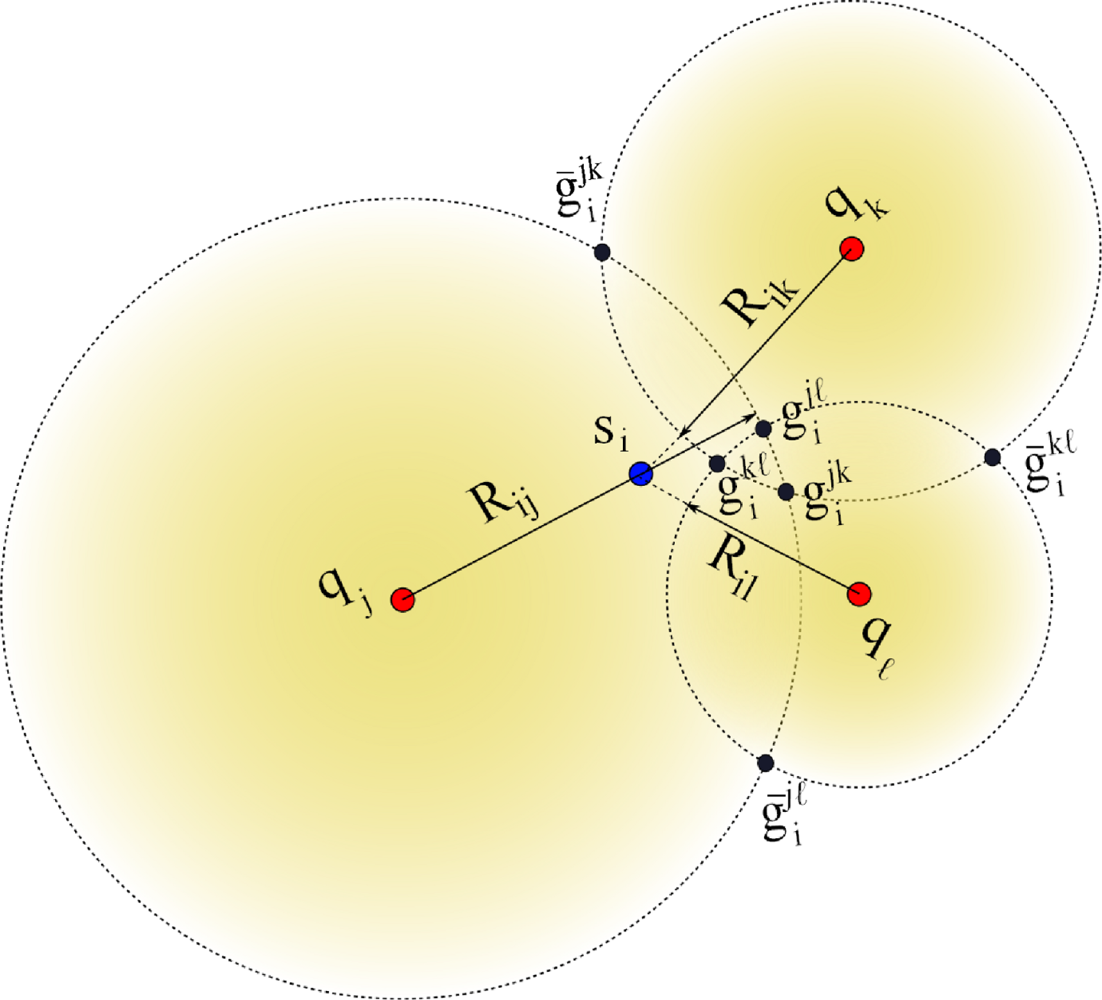
Each node s_i applies the CCI procedure using all Q subsets A_jk. For instance, g i jk and g ¯ i jk are obtained from the subset A_jk, g i j ℓ and g ¯ i j ℓ are obtained from the subset A_jℓ, and so on. Hence, a sensor node will have 2Q possible initial position estimates where half are considered mirror solutions which should be eliminated through the selection process described next. Geometrically, we expect that the true location will be located around the region where solutions form a cluster (i.e., half of the circle intersections should ideally intersect at the solution). Let us to consider the example shown in Figure 2.

There are three anchors named a_j, a_k and a_ℓ and a node s_i that needs to be localized. The range estimate R_ij is larger than d_ij, the range estimate R_ik is shorter than d_ik, and the range estimate R_iℓ is shorter than d_iℓ. Hence, s_i computes a set of of six location candidates given by { g i jk , g ¯ i jk , g i j ℓ , g ¯ i j ℓ , g i k ℓ , g ¯ i k ℓ }. As seen in the figure, all the mirror circle intersection estimates will tend to be isolated while the correct circle intersections will tend to cluster around the node location. For example, to decide between g i jk and g ¯ i jk candidate positions, generated using the anchors (a_j, a_k), the sensor s_i obtains the minimum Square Euclidean sum from the location g i jk to each pair of candidate positions as follows: (29) ψ = min   ( ‖ g i jk − g i j ℓ ‖ 2 , ‖ g i jk − g ¯ i j ℓ ‖ 2 ) + min   ( ‖ g i jk − g i k ℓ ‖ 2 , ‖ g i jk − g ¯ i k ℓ ‖ 2 )

On the other hand, the sensor s_i also obtains the minimum Square Euclidean sum from the location g ¯ i jk to each pair of candidate positions as follows: (30) φ = min   ( ‖ g ¯ i jk − g i j ℓ ‖ 2 , ‖ g ¯ i jk − g ¯ i j ℓ ‖ 2 ) + min   ( ‖ g ¯ i jk − g i k ℓ ‖ 2 , ‖ g ¯ i jk − g ¯ i k ℓ ‖ 2 )

Finally, the lowest value of ψ and φ helps to decide between choosing g i jk or g ¯ i jk. The process is repeated for all Q solution pairs to generate a set of disambiguated locations.

Referring to our example, once node s_i removes the mirror locations, then an estimate of the node position can be formed by taking the average of the disambiguated set G = { g i jk , g i j ℓ , g i k ℓ }.

The complete bilateration scheme is described in Algorithm 2. This is a distributed localization algorithm in the sense that each node can implement it and determine its position estimate, given the anchor positions and the range estimates R_ij between each node and all the anchors. Since Algorithm 2 uses only anchor measurement, it can be used as an initialization step to generate a set of position estimates that can be used with algorithms that integrate more information from anchor and non-anchor nodes (i.e., iterative distributed algorithms).

There are some anomalous cases which should be considered in the bilateration algorithm. In order to get its initial estimation p i 0, it is essential that every sensor s_i gets the two location estimations from each one of the Q subsets even if the solutions are not feasible. For example, assume the two special cases shown in Figure 3. If we consider the left-side case on the figure, R_ik is shorter than d_ik, and R_ij is shorter than d_ij, clearly the triangle inequalities are not satisfied since (31) R ij + R ik > ‖ q j − q k ‖ R ij + ‖ q j − q k ‖ > R ik R ik + ‖ q j − q k ‖ > R ijAs a consequence, the sensor s_i will not be able to find any solution to Equation (28). In other words, if the two circles do not intersect with each other, it will not be feasible to find the circle intersections g_i and ḡ_i. Therefore, a relaxed estimation should be generated as described next. Considering that ‖q_j − q_k‖ is a constant distance between the anchors in set A_jk, the node s_i takes two steps to estimate the locations g i jk and g ¯ i jk. First, a location x₁ is obtained by fixing R_ik and making R_ij = |‖q_j − q_k‖ − R_ik| in order to satisfy the triangle inequality. Next, the sensor s_i should use the CCI procedure to solve for x₁. Similarly, a second location estimate x₂ is obtained by fixing R_ij, choosing R_ik = |‖q_j − q_k‖ − R_ij| to satisfy the triangle inequality and solving the problem through the CCI procedure. Finally, both g i jk and g ¯ i jk are generated as the average x 1 + x 2 2 implying that when the triangle inequality is not satisfied, there will be a single solution that falls over the line y. A similar procedure can be derived for the second case as depicted in Figure 3.

In this section we analyze the accuracy performance of both methodologies, optimized and closed-formula schemes. Even though the strength of a closed-formula for solving the WSN localization problem is its low complexity compared with an iterative algorithm, closed-formulas can present large errors in the presence of inaccurate ranging measurements. However, in many cases it is desirable to sacrifice accuracy to save energy (i.e., increase battery lifetime). On the other hand, the weakness for closed-form methods (i.e., noise sensitivity) represents the strong point for iterative methods and vice versa. The goal of both methodologies seems to be in opposite directions. However, the main effort in WSN localization research is focused on developing an strategy that can join the strength of both methodologies to create an efficient algorithm that can save energy providing the best accuracy in the estimated positions.

Next we present an evaluation of accuracy between closed-formulas and iterative methodologies. For the former methods we are considering the classical LS Multilateration, the Min-max method (The Min-max approach is based on the intersection of rectangles instead of circle intersections. It provides a more simple technique than lateration schemes to obtain position estimates at the expenses of accuracy) [38,39], and the bilateration algorithm. For iterative methodologies we are considering two algorithms to solve the NLLS: the LM and the TRR algorithms.

For the simulations that follow, we consider 20 different sensor networks where each one is composed by N = 96 unknown sensors, randomly distributed over 100 m by 100 m area. Also, we add M = 4 non-collinear anchors with full-connectivity on every realization as shown in Figure 4.

For each network, we add noise to the true distances between anchors and nodes using the log-distance path loss model described in Equation (4). The estimated distances are simulated using σ_SH = 6_dB and η_P = 2.6, typical parameters for the propagation models on outdoors scenarios, and P₀ = −52_dB is selected according to current commercial specifications for wireless motes [40]. Finally, we assume that all nodes have the sensitivity to detect any RF signal coming from anchors.

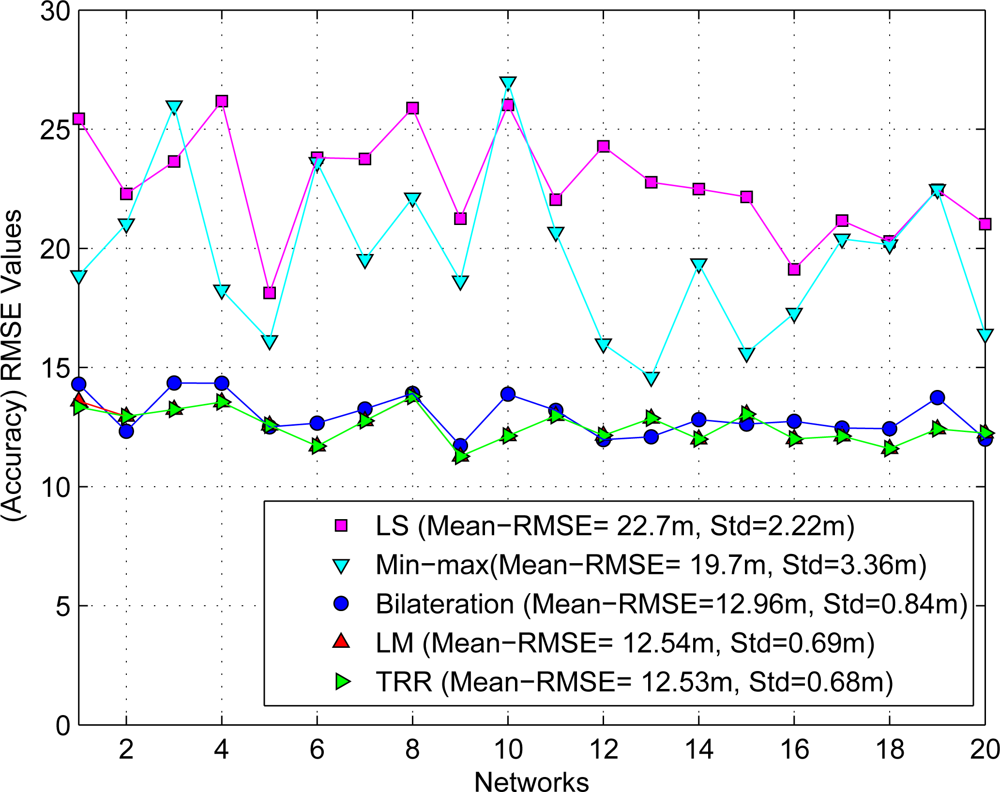
To compare the accuracy performance between both methodologies it was necessary to use the same set of range measurements for each closed-form method and iterative algorithm. Figure 5 summarizes the initial estimates obtained by both methodologies using the RMSE metric as shown the next equation: (32) RMSE = 1 N ∑ i = 1 N ‖ p i 0 − z i ‖where p i 0 represents an initial position estimate for a sensor s_i and z_i its true position.

As can be seen, the closed-form LS approach provides the least accurate initial estimates (mean = 22.7 m and standard deviation = 2.22 m) compared with iterative algorithms as expected due to the noisy ranging measurements. In a similar way, the Min-max scheme also provides large errors (mean = 19.7 m and standard deviation = 3.36 m). On the other hand, we can appreciate that both iterative algorithms, the LM and the TRR, provide practically the best and similar results for initial estimates (mean = 12.54 m and standard deviation = 0.69 m) as expected, and finally the bilateration algorithm presents very acceptable initial estimates compared with the last two algorithms (mean = 12.96 m and standard deviation = 0.84 m). However, we should consider that the computational complexity for the LM and the TRR algorithms is significantly larger than the bilateration algorithm. This discussion will be expanded in the next section.

Also, we tested the SX, SI and GSLS algorithms [25] using the same set of networks. The estimated positions presented large errors under this scheme as indicated by [26]. Then, these results were disregarded in our analysis.

The efficiency of an algorithm can be described in terms of the time or space complexity [41]. Time complexity refers to the relation between the number of required computations for a given input. The space used for a given input provides the space complexity of an algorithm. The computational complexity of an algorithm could be described as the number of operations that it takes to find a solution [42].

In this section we provide an operation count on the number of additions (ADDs), multipliers (MULs), divides (DIVs), and square roots (SQRTs) exactly in the way that DSP algorithms are described [43]. This will allow an “apple-to-apple” comparison. Moreover, an accurate description lends itself to a cycle accurate description for any microprocessor and more significantly, the use of energy models based on computing cycles to estimate the energy consumption for a given algorithm. An energy analysis will be a discussion of a future work. In next subsections we present the computational complexity analysis for the iterative LS and the bilateration algorithm.

In this research, we analyzed a localization algorithm that can be realistically deployed over real WSNs which can provide good accuracy performance with low computational complexity. The bilateration algorithm is a distributed scheme that can be used as an initialization stage to find an initial set of locations.

Most initialization algorithms demand very high computing power to provide a set of initial estimates for an N-node WSN. The analyzed algorithm is capable to provide competitive initial estimates at low processing power. This approach is basically formed by two stages. The first stage consists of finding all circle intersections formed by anchor positions and their respective range estimates to a sensor node, obtained by ranging techniques like ToA or RSS. The great advantage of this approach is to use “closed-formulas” to find all circle intersections (i.e., candidate positions) using two anchors at a time. In the second stage, the algorithm uses a sorting algorithm to find the cluster of candidate positions that tend to be closer to each other around the true location. The cluster with the nearby candidate positions is averaged to finally obtain the initial location. This scheme can be used by any WSN localization algorithm that needs initial approximations. Also, it is implementable in constrained devices with low processing and memory capabilities (i.e., motes). Results show that this initialization algorithm is well behaved (e.g., computational and accuracy performance) in comparison with other well known algorithms like LS methodologies.

Finally, we are interested in exploring iteratively, at the refinement process, the Levenberg–Marquardt approach for node localization. We believe that this methodology can play a crucial role in producing excellent position estimates with high accuracy and low energy consumption due to the rate of convergence associated with this optimization technique.