1. Introduction
Inertial navigation systems (INS) require at least three accelerometers and three gyroscopes to calculate the navigation information such as the position, velocity and attitude. However, the use of redundant sensors is preferable to ensure their reliability and enhance their navigation accuracy and, thus, the problem of the proper placement of the redundant inertial sensors has been studied since the 1970s. For over four decades reliability has been a subject of interest in various complex systems, such as industrial process systems and power systems, as well as in safety-critical systems such as nuclear power systems and the control of military and space aircraft. Hardware redundancy has been studied from the early stages of the introduction and development of FDI (fault detection and isolation). The various FDI approaches to hardware redundancy include the following methods: the squared-error (SE) [
1], generalized likelihood test (GLT) [
2], minimax [
3], sequential [
4], optimal parity test (OPT) [
5], multiple parity vectors [
6], and double fault isolation method [
7]. Wilcox [
8] compared the results of some FDI methods. Gai
et al. [
9] analyzed the FDI performance of two redundant sensor configurations. Yang
et al. [
10] suggested the best sensor configuration and accommodation rule for an INS with seven inertial sensors
The optimal configuration problem of redundant inertial sensors was studied in [
11], where redundant MEMS-IMU integration with GPS is considered. Recently, finding the optimal sensor configuration for passive source localization [
12] or mobile sensor networks [
13] has attracted considerable attention. One of the main applications of modern source localization is the surveillance and protection of military, industrial or strongly populated areas [
12]. The optimal sensor configuration is necessary to optimize the passive source localization. It is interesting to note that the condition of the optimal sensor configuration for passive position estimation in [
12] is the same as the optimal configuration for the redundant inertial sensors in [
14].
In the early 1970s, nine inertial sensors were employed in aircraft, with three sensors in each axis, since it was not known how to optimally configure the sensors. One of the earliest references to redundancy in inertial units uses two sets of orthogonal triads skewed against one another [
15]. Gilmore
et al. [
1] suggested a symmetric configuration with a dodecahedron and Pejsa [
16] suggested optimal configurations for four, five, and six inertial sensors. Much additional research into the optimal configuration of redundant sensors in INS was subsequently performed [
1,
13,
14,
16].
Harrison
et al. [
14] suggested the use of figures of merit to evaluate the sensor orientations for navigation performance and FDI capability. With the figure of merit of the navigation performance, the optimal condition for the sensor configuration is obtained and, with the figure of merit of the FDI performance, alternative sensor orientations are evaluated and compared with each other. The condition required to obtain the optimal navigation performance is well-known nowadays, while the condition for the optimal FDI performance is not known yet. Platonic solids (or regular polyhedrons) are known to be the optimal configuration for both the navigation and FDI performance. Thus, when the number of sensors is six or 10, dodecahedrons and icosahedrons are the best sensor configurations for the navigation and FDI performance, respectively. However, when the number of sensors is other than six or 10, such as five, seven or eight, the optimal configuration for both the navigation and FDI performance remains unknown.
In this paper, we focus on hardware redundancy in INS and especially on the optimal configuration and suggest a figure of merit for a sensor configuration considering both the navigation and FDI performance. The proposed figure of merit can be used to compare the alternative sensor configurations and, thus, it is possible to obtain the optimal configuration of the redundant sensors considering both the best navigation and FDI performance. Section 2 discusses the condition of the optimal sensor configuration for the navigation performance and gives some sensor configurations providing the best navigation performance, and Section 3 discusses the FDI performance of the sensor configurations with respect to the number of sensors and the angles between them. Section 4 discusses the main results of this paper and suggests a figure of merit for a sensor configuration considering both the navigation and FDI performance. Section 5 shows some simulation results to confirm the validity of the suggested method and in Section 6 we give our conclusions.
6. Conclusions
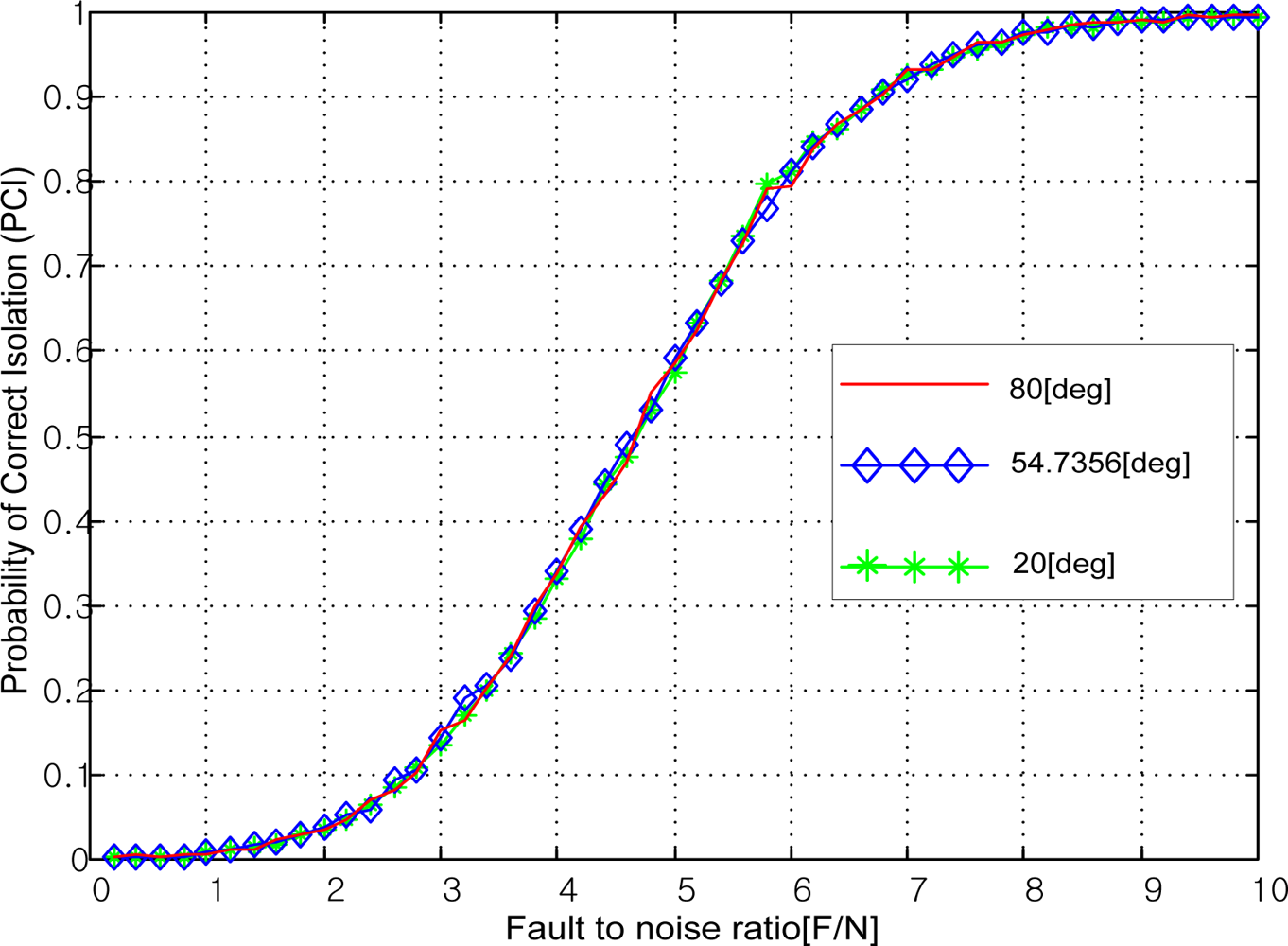
This paper considers the optimal sensor configuration for inertial navigation systems which have redundant inertial sensors. We show that the condition which affords the optimal sensor configuration for the best navigation performance is a necessary and sufficient condition, and enumerate some of the best sensor configurations for navigation performance. We suggest a figure of merit to determine the optimal sensor configuration which considers both the navigation and FDI performance. The main criterion is that among the configurations providing the best navigation performance, the optimal configuration is the one which makes the angle between the nearest two sensors the largest
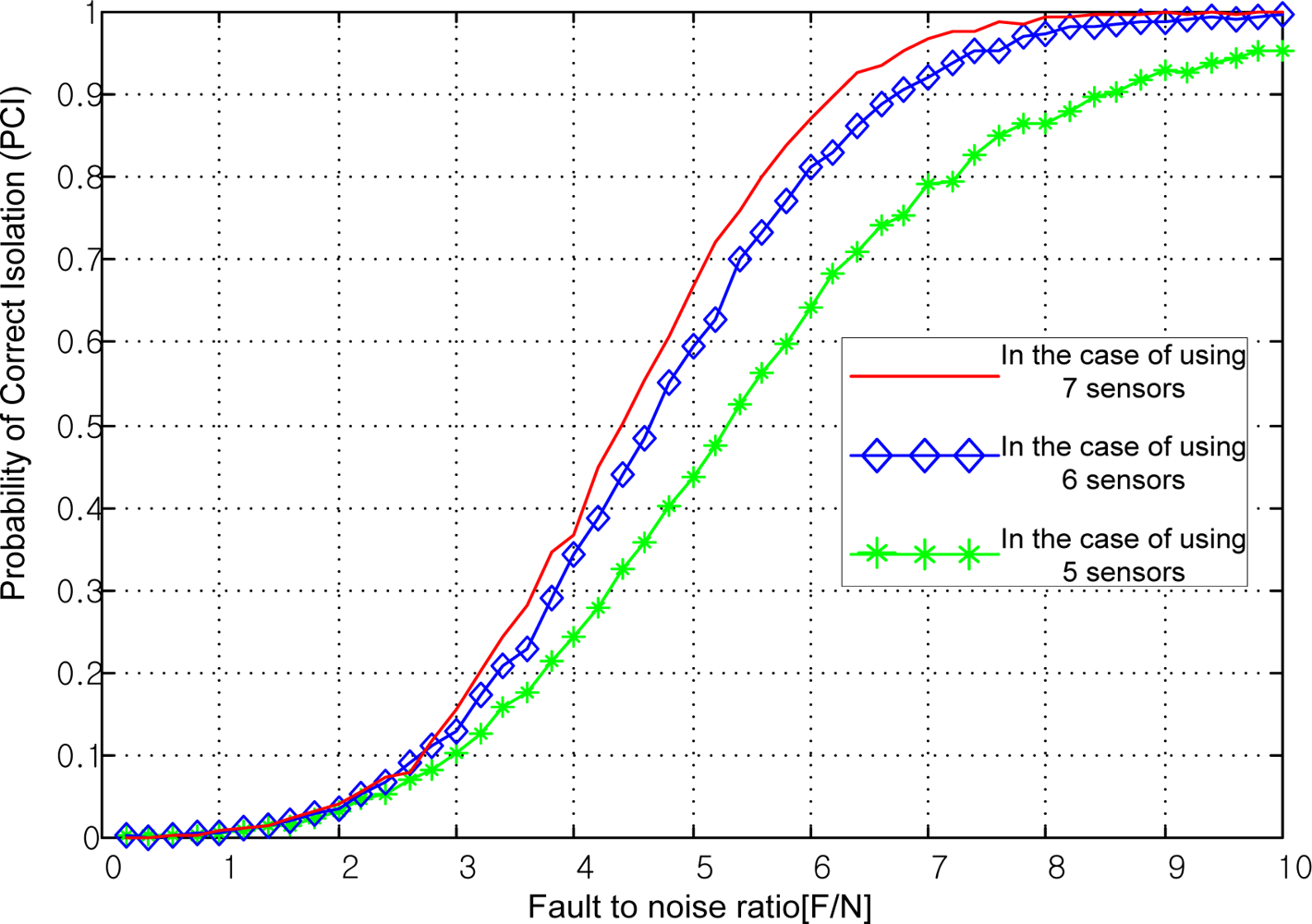
Monte Carlo simulations are performed to demonstrate the performance of the suggested optimal sensor configuration method. For the FDI performance, the probability of correct isolation is used. To obtain one PCI value in the table, 3,000 Monte Carlo simulation runs are performed and the resulting 3,000 values are averaged. The results of the Monte Carlo simulations were found to be the same as those of the suggested method. The figure of merit (FOM) for the FDI performance suggested in [
6] is used to reconfirm the performance of the suggested method, and the FOM results were identical to those of the Monte Carlo simulations.