In this section, we analyze the proposed ACS algorithm based on the IEEE 802.15.4 slotted CSMA/CA in the case of acknowledged uplink data transmission with unsaturated traffic conditions. We consider a single hop with star topology consisting of a coordinator and N sensor nodes under the assumptions of ideal channel conditions without hidden nodes and capture effects. We assume that data packets arrive at each sensor node according to the Poisson process with rate λ for uplink transmission. According to the IEEE 802.15.4 specification, an aUnitBackoffPeriod (UBP) contains 20 symbols, and one symbol contains 4 bits, i.e., a UBP contains 80 bits. We also assume that the length of data packet Ld is fixed and occupies 12 UBPs for transmission, while tACK and the length of the acknowledged packet LACK occupy 1 and 2 UBPs, respectively. We derive the stationary probability that a node attempts the first carrier sensing in a random chosen UBP, and analyze throughput, MAC delay and the number of CCAs sent before transmission to understand the energy consumed by CCAs.
3.1. System Model and Throughput Analysis
Let
s(t),
c(t),
b(t) and
y(t) be the stochastic processes representing the backoff stage, CW value, backoff counter and transmitting slot at the boundary of slot
t for a given sensor node, respectively. We have
s(t) ∈ {0,1,…,
m} by assuming that
m is the maximum backff stage and is equal to
aMaxBE − aMinBE. Since CCA detection occurs three times in the ACS algorithm, we have
c(t) ∈ {0,1,2,3}. The backoff counter in backoff stage
i will be uniformly selected from [0,
Wi − 1] where
Wi = 2
(aMinBE + i) and 0 ≤
i ≤
m; then we have
b(t) ∈ {0,1,…,
Wi − 1}. Since
Ld is the total transmission slots, we have
y(t) ∈ {1,…,
Ld}, where the state
y(t) = 0 represents nothing for transmitting or receiving. The set of processes {
s(t),
c(t),
b(t),
y(t)} defines the state of a node at the boundaries of time slots. The behavior of a single device is described by the discrete-time Markov chain shown as
Figure 2. This Markov chain model combines Jung’s model [
13] with Pollin’s model [
14] and further considers the CCA3 operation. In the Markov chain model, the state {0} represents the idle state whenever a node has no data packet for transmission. In
Figure 2, p
c is the collision probability caused by at least one of N − 1 remaining nodes to senses successfully and transmits; p
b1 is the probability of detecting a busy channel in CCA1, while p
b2 and p
b3 are probabilities that a node detects a busy channel before performing CCA2 and CCA3, respectively, given that the channel is idle by performing CCA1 and the previous CCA2 is failed, respectively. The term α represents the transition probability of data packet arrival as obtained by
Equation (1) [
13], where
Tslot is the duration of a time slot:
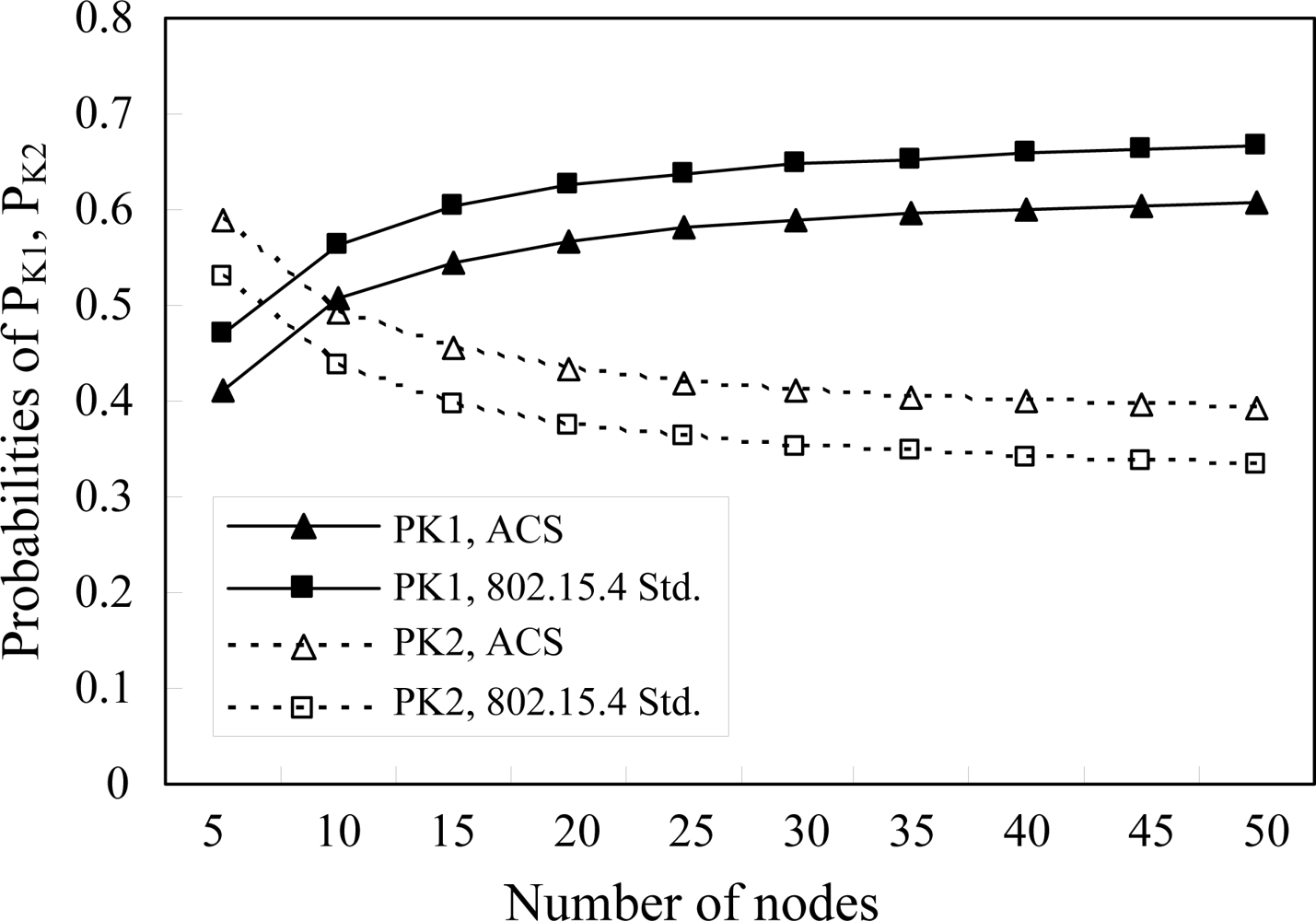
Let us denote PK1 and PK2 to be the probabilities of entering the next backoff stage and transmitting a data packet from a node in a certain backoff stage, respectively, where PK1 and PK2 can be further obtained by PK1 = pb1 + (1 − pb1)pb2pb3 and PK2 = (1 − pb1)[(1 − pb2) + pb2(1 − pb3)]. The other transition probabilities associated with the Markov chain are presented as follows.
Equation (2) states the probability that the backoff counter is decreased after each slot.
Equation (3) gives the probability of finding a busy channel in CCA1 or CCA3 and a node uniformly selects a state in the next backoff stage.
Equation (4) gives the probability to uniformly choose a state for starting a new transmission when the previous transmission is successful or retransmission attempt after the previous transmission failure or reaches to the maximum backoff stage.
Equation (5) states the probability of the decreased backoff counter to perform CCA3.
Equation (6) states the probability of transmission after the backoff counter reaches zero.
Equation (7) states the probability of transmitting in the next slot.
The closed-form solution of the Markov chain can be obtained by
Equations (2)–
(7) with the chain regularities as follows. Let
bi,j,k,l be the stationary distribution of the Markov chain,
i.e.,
for
i ∈ [0,
m],
j ∈ [0,3],
k ∈ [0,
Wi − 1],
l ∈ [0,
Ld], where
b0 =
P{0}. By using
Equation (3), we can obtain b
i,3,0,0 shown as
Equation (8). The steady-state probabilities to perform CCA2 and CCA3 can be obtained by
equations (9) and
(10), respectively.
b0,0,0,1 and
b0 can also be obtained by
equations (11) and
(12), respectively. Consequently,
b0,3,k,0 and
bi,3,k,0 can be expressed by
equations (13) and
(14), respectively.
Since the sum of probabilities in the Markov chain must be equal to one, we have:
Therefore,
b0,3,0,0 can be obtained by the expression of
pb1,
pb2,
pb3 and
pc as shown in
Equation (16):
Let
φ be the probability that a node performs CCA1 in a random chosen time slot when the backoff counter reaches zero without considering the backoff stage and independent across nodes, where
φ can be expressed as
Equation (17):
Accordingly, let
Pt be the transmission probability that at least one node senses the channel successfully, while
Ps is the successful transmission probability that a node senses the channel successfully and the others are not, which can be expressed by
equations (18) and
(19), respectively:
Let
Pcoll be the collision probability of the entire system that can be obtained and shown as
Equation (20):
The closed forms of
pb1,
pb2,
pb3 and
pc can be obtained by solving
equations (17)–
(20).
pb1 is the probability that a performing CCA1 node detects a busy channel caused by at least one of N-1 remaining nodes transmitting data packets or receiving ACK packets, shown as
Equation (21) [
14]:
The formula of
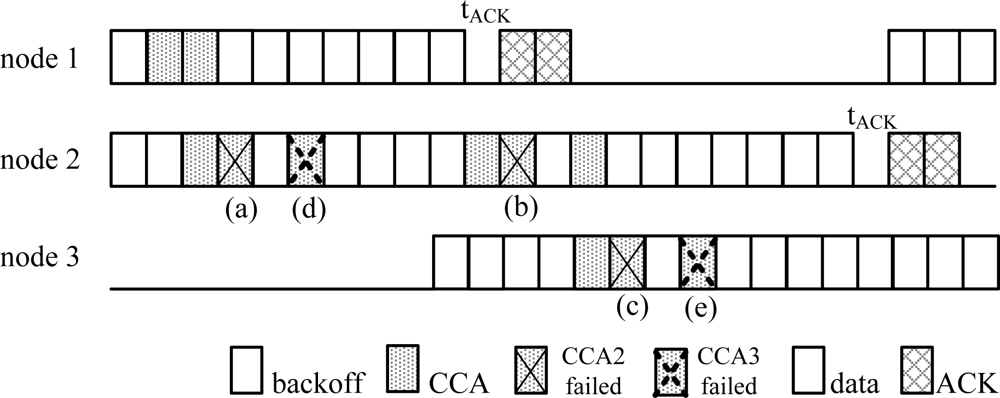
pb2 in the standard edition of IEEE 802.15.4 consists of two terms derived by the unacknowledged and acknowledged modes corresponding to slots (a) and (b) in
Figure 3, respectively [
14].
In the ACS algorithm, we still need to consider the other conditions that cause CCA2 to fail, that is, at least one of N-1 nodes successfully detects an idle channel in CCA3 whenever the target node is performing CCA1 at the same time. Consequently, the node performing successful CCA3 will start transmission in the next slot and further causes the target node to detect a busy channel in CCA2. In
Figure 3, we know that CCA2 failed not only at slots (a) and (b), but also at slot (c). Besides, the probability of CCA2 failure occurring at slot (c) is the same as at slot (b). Thus,
pb2 can be obtained by
Equation (22). Moreover, both events in the slots (d) and (e) are the only two cases that cause CCA3 failure. Clearly, the events in the slots (d) and (e) only follow the events in the slots (a) and (c), respectively, which means
pb3 is the combination of the events in both slots (a) and (c) and can be obtained by
Equation (23). Finally
pb1,
pb2,
pb3 and
pc can be obtained by solving the above four non-linear
equations (21)–
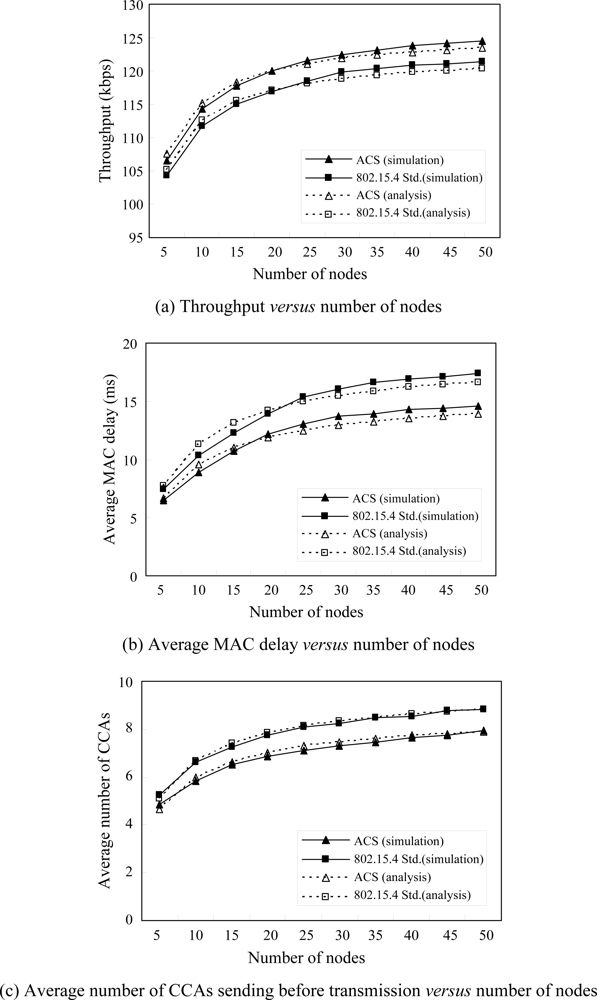
(24). Furthermore throughput
S can be simply expressed by
Equation (25) if
B is denoted to be the bandwidth of the channel:
3.2. Analysis of Average MAC Delay
In this subsection, we analyze the average MAC delay for each node. The MAC delay is defined as the time between packet arrival and transmission, so it can be obtained by simply counting the average number of states that a node experiences in the Markov chain. The average number of states also implies how many slots on average are experienced for a transmission whenever a new packet arrives.
Let
di be the average backoff counter in backoff stage
i and also be the average number of states (slots) experienced by a node to perform backoff countdown procedure in backoff stage
i, where
di = Wi/2. In
Figure 2, a node may have two different paths, e.g., path1 and path2, to enter the next backoff stage with probabilities
PC1 and
PC2, respectively, whenever it senses a busy channel in the current backoff stage, where
PC1 = pb1,
PC2 = (1 − pb1)pb2pb3. Therefore, a new arrival packet has in total
2i different paths to enter the
ith backoff stage. Moreover, a node entering the next backoff stage by path2 will experience 3 more states than by path1,
i.e., it causes it to perform CCA3 three more times. Similarly, a node may have two different paths, e.g., path3 and path4, to successfully sense the channel and transmit in a certain backoff stage with probabilities
PC3 and
PC4, respectively, where
PC3 = (1 − pb1)(1 − pb2), and
PC4 = (1 − pb1)pb2(1 − pb3). Therefore, a new arrival packet will have 2
i + 1 different paths to successfully sense the channel and transmit in the
ith backoff stage. Furthermore, a node which senses the channel successfully and transmits by path4 will experience two more states than by path3,
i.e., it causes CCA3 to be performed two more times.
Let
Di be the average number of states that a node experiences to successfully sense the channel and transmit in backoff stage
i, and
D1 can be obtained by
Equation (26):
In the right hand side of
Equation (26), the first two terms represent that a node fails to sense the channel in backoff stage 0 and enters backoff stage 1 with probability
PC1, then it experiences
d0 + d1 + 1 or
d0 + d1 + 3 states for successfully sensing the channel and transmission with probability
PC3 or
PC4, respectively. Furthermore, as mentioned above, the average number of states via path1 and path4 is
d0 + d1 + 3, which includes two more states to perform a CCA3 than that via path1 and path3,
i.e.,
d0 + d1 + 1. Similarly, the last two terms represent a node entering backoff stage 1 with probability
PC2 and experiencing
d0+3+d1+1 or
d0+3+d1+3 states for successfully sensing the channel and transmission with probability
PC3 or
PC4, respectively. The average number of states via path2 and path4 includes two more states to perform a CCA3 than that via path2 and path3. Summarily,
Di can be obtained by
Equation (27), where the exponents of
q and
r are the remainder of
j/2 and
(j + 1)/2, respectively, while
v and
u are the number of paths via path1 and path2, respectively. Since path1 and path2 are mutually exclusive, there are totally
2i different paths to enter the
ith backoff stage for a new arrival packet as the mentioned above. The term
u represents the number of paths via path2, which can be obtained by counting the number of 1s in the binary format of ⌊
j/2⌋, and
v is equal to
i−
u. Let
Ds be the summation of
Di for
i ∈ [0,
m] shown as
Equation (28), where
Xj is a sequence representing the number of states caused by different possible paths to transmit in the
ith backoff stage shown as
Equation (29) for
j ∈[0,2
i+1−1]. Finally, the average MAC delay
Dav can be obtained by
Equation (30).
To consider if the additional CCA3 consumes more power, we can simply count the average number of CCAs sent by each node between packet arrival and transmission to see the power consumption caused by all sent CCAs. Clearly, it is very similar to obtaining the average MAC delay; the number of CCAs can be obtained and shown as
Equation (31) by using the backoff stage instead of the average backoff counter in
Equation (27), where
Yj is a little different from
Xj in
Equation (29) and shown as
Equation (32) if we only consider the average number of CCAs and neglect the single slot backoff in CCA3. Therefore, the average number of CCAs sent before transmission,
Nav_CCA, is given by
Equation (33):