1. Introduction
Since the early eighties, the Advanced Very High Resolution Radiometer (AVHRR) sensors onboard the National Oceanic and Atmospheric Administration (NOAA) satellite series have been capturing daily images of the world, providing spectral information to monitor atmospheric, oceanic, vegetation, and land properties of the Earth. To date, three versions of the AVHRR sensor have operated: AVHRR/1 (with four channels, operating between 1979 and 1994 onboard the NOAA-6, -8, -10 satellites), AVHRR/2 (with five channels, operating between 1981 and 1999 onboard the NOAA-7, -9, -11, -12, -13, -14 satellites), and AVHRR/3 (with six channels, operating since 1999 to present onboard the NOAA-15, -16, -17, -18 satellites) (
http://goespoes.gsfc.nasa.gov/poes/project/index.html, January 2010). A long-term (1981-present) time-series of global AVHRR daily images has been stored at degraded resolution in the Global Area Coverage (GAC) archive. The GAC images are a resample of the full 1.1 km resolution AVHRR images by averaging four out of every five samples along the scan line and processing only every third scan line. The final resolution is 1.1 × 4.4 km at the subpoint, although it is generally treated as 4 km resolution. Repeated efforts have processed the GAC archive attempting to produce datasets of consistent time-series of surface reflectance and spectral indices with enough quality to study the long-term dynamics and trends of different properties of the Earth. Despite the images were captured by similar AVHRR sensors, many issues have to be considered to avoid artifacts that may lead to missing or detecting trends in the time series that are or are not related to actual changes in important spectral properties of the Earth (e.g., [
1,
2]).
One of the important spectral indices that shows dissimilar long-term trends between different AVHRR-derived datasets is the Normalized Difference Vegetation Index (NDVI) (e.g., [
3,
4]). The NDVI is calculated from the reflectance in the AVHRR red (channel 1, 580–680 nm) and near infrared (channel 2, 725–1,100 nm) bands as follows [
5,
6]: NDVI = (NIR − R)/(NIR + R). This spectral index is strongly related to the fraction of the incoming photosynthetically active radiation intercepted by green vegetation [
7] and it is widely and satisfactorily used for monitoring changes in ecosystem structure and function [
8], detecting long-term trends in vegetation growth and phenology [
9,
10], providing inputs for primary production [
11] and global circulation [
12] models, and providing a reference to model the carbon balance worldwide [
13–
15].
Since the AVHRR sensor series were not originally designed for vegetation monitoring (but rather meteorological studies) and suffer from lack of onboard calibration and navigation/georeferencing problems, they have several shortcomings for this purpose [
16–
19]. To achieve a consistent NDVI time-series, the different processing efforts of the GAC archive had to deal with a wide range of factors affecting the NDVI. Van Leeuwen
et al. [
1] showed how multi-sensor NDVI time-series would significantly benefit if atmospheric corrections were adequately addressed. For instance, the AVHRR near-infrared band (channel 2) overlaps a wavelength interval in which there is considerable radiation absorption by water vapor in the atmosphere, which significantly decreases observed NDVI [
20,
21]. Other atmospheric corrections must also include ozone absorption, Rayleigh scattering, tropospheric aerosol optical thickness, and presence of aerosols in the stratosphere after major volcanic eruptions (e.g., El Chichón and Pinatubo). In addition to atmospheric corrections, the NDVI signal must be corrected for the variation in the solar zenith and viewing angles due to the orbital drift through the lifetime of the satellites [
22]. Finally, AVHRR reflectance and NDVI data must also be corrected for sensor degradation and cross-calibration due to inter-sensor differences in spectral response functions of different sensor red and near-infrared bands [
1]. In the case of the AVHRR GAC archive, an additional source of uncertainty may impact the quality of the data: it consists of the data reduction methodology used for transforming the 1.1 km resolution AVHRR data into the coarse resolution of the GAC archive [
23,
24].
Depending on the different corrections applied and processing streams and algorithms used, successive efforts have produced different coarse resolution AVHRR NDVI datasets from the original GAC data. The most common and broadly used ones are, from the earliest to the foremost, Pathfinder AVHRR Land (PAL I and II) [
24,
25], Fourier-Adjustment, Solar zenith angle corrected, Interpolated Reconstructed (FASIR) [
26], Global Monitoring and Mapping Studies (GIMMS) [
27], and Land Long-Term Data Record (LTDR) [
28] datasets. Several studies have evaluated the consistency of the NDVI trends across the PAL, FASIR, and GIMMS AVHRR datasets in different regions of the world (e.g., [
29,
30]), and have also compared them to those derived from SPOT VEGETATION and MODIS Terra sensors (e.g., [
31]). In some of these regions, the NDVI trends have been consistent across datasets and sensors, for instance, in the humid Sahel (but not in the driest; [
31]), or the Chilean arid zones [
4]. Contrary, in other regions, the use of different datasets has led to conflicting findings, potentially due to differences in the processing and corrections applied to the GAC data [e.g., 3,4,32,33]. Despite the LTDR dataset is the most recently produced one and incorporates much of the learning from the previous efforts, it does not still exist any published study that includes this dataset to evaluate the consistency of the NDVI trends.
This is also the case of the Iberian Peninsula (Spain and Portugal), where previous studies have calculated the NDVI trends based on AVHRR datasets at the regional [
34–
37] and local [
38–
40] scales, but none have evaluated their consistency across different datasets. Following up the suggestions of recent works [
3,
4,
31], in this article we evaluate the spatial consistency of four AVHRR NDVI datasets to detect NDVI trends in the Iberian Peninsula, with a special focus on the recently released LTDR dataset. We also evaluated the error budget of the NDVI trends from the different slopes obtained across datasets. As far as we know, this is the first evaluation of the performance of the new LTDR dataset to detect NDVI trends.
3. Results
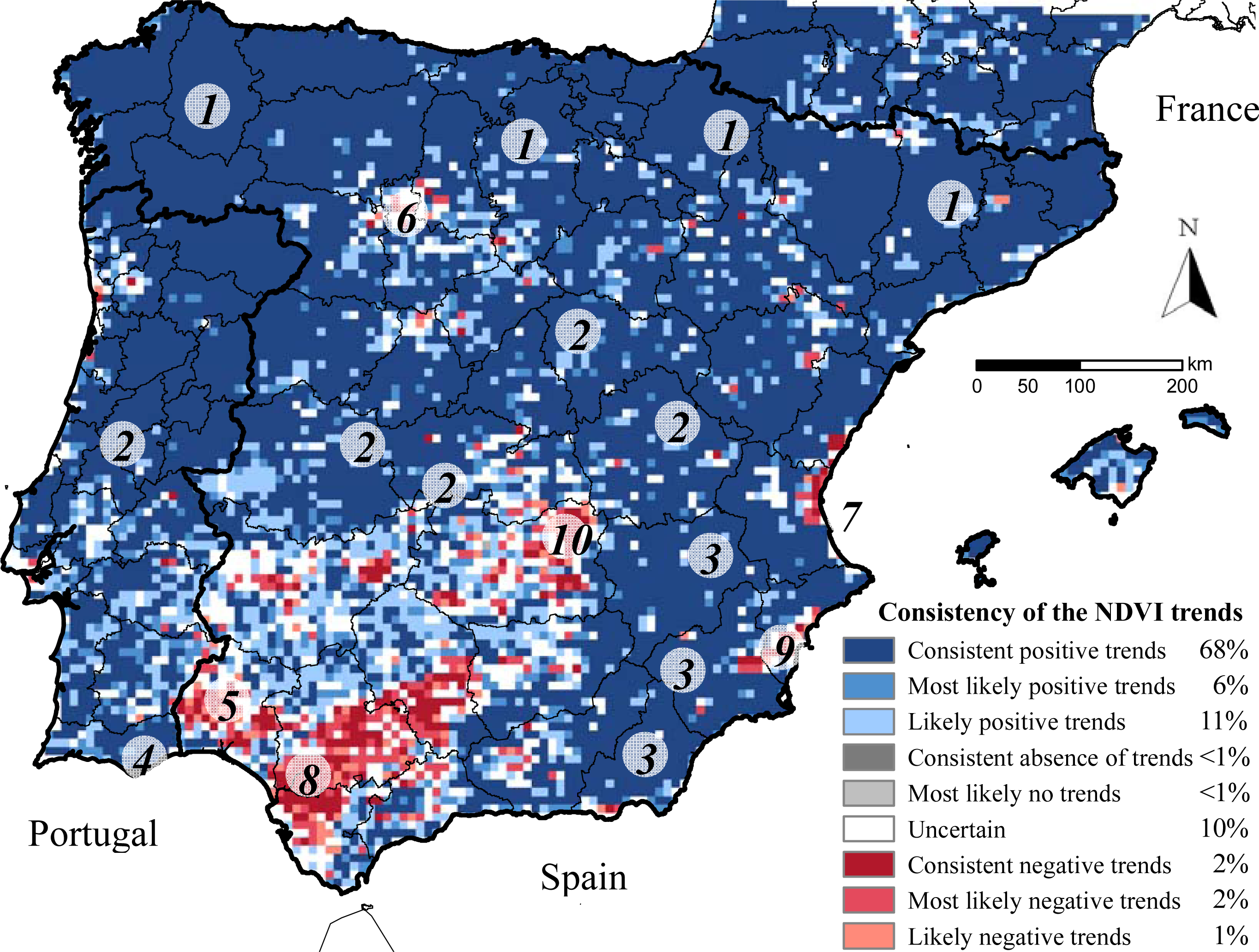
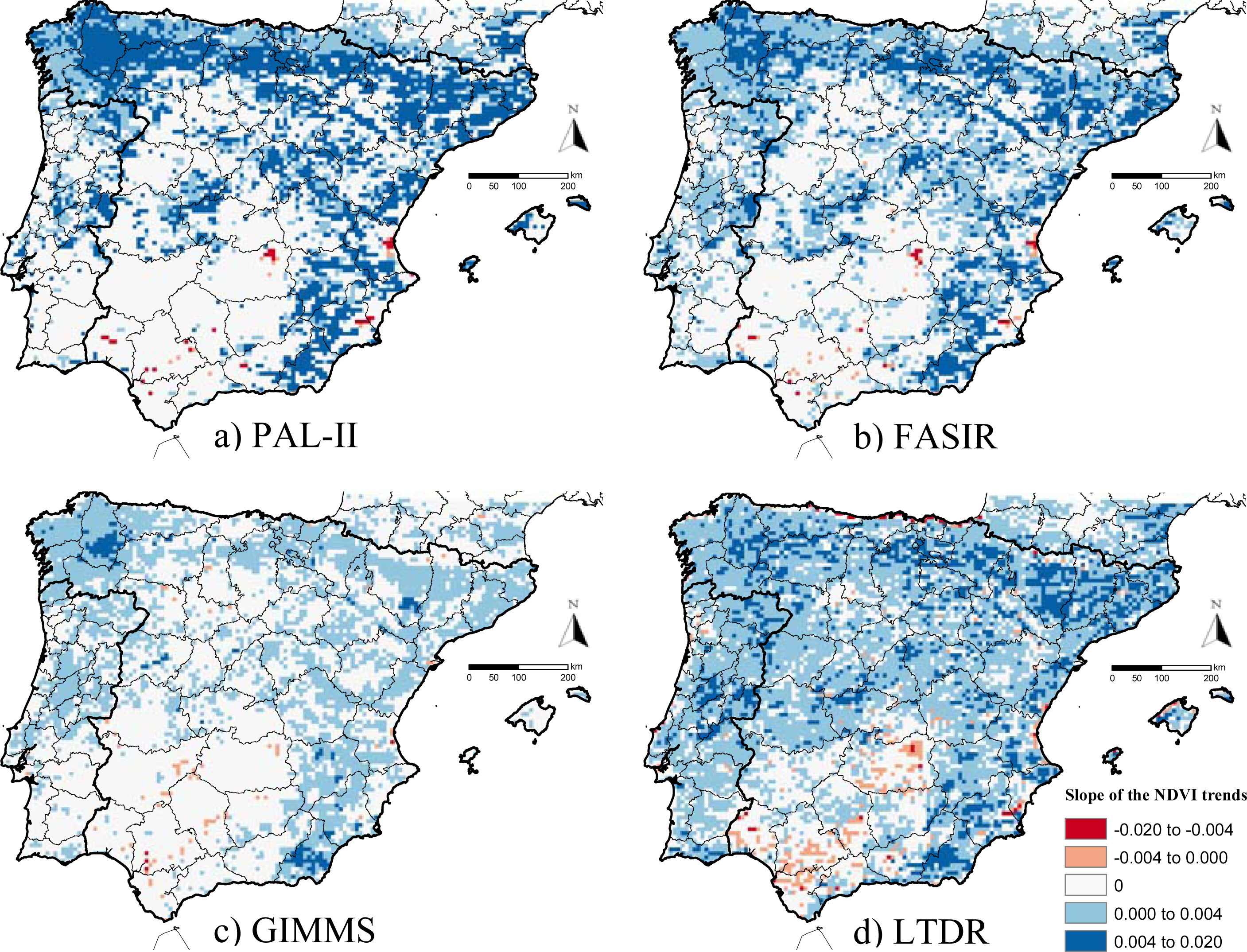
The AVHRR datasets showed that most of Iberia experienced either positive or no trends in NDVI during the 1982–1999 period. The areas with negative trends are small and isolated, despite the dataset considered (
Figure 1,
Table 4). Datasets, though, differed in the magnitude of the NDVI trends (
Figure 1,
Table 3). The mean NDVI trend of the whole Iberian Peninsula was similar and positive for PAL-II, FASIR, and LTDR datasets (
Table 3), though it was half in magnitude for the GIMMS dataset. When the means for positive and negative significant trends were calculated separately, the PAL-II dataset showed the steepest trends (
Table 3), while the GIMMS datasets showed the weakest ones (half in magnitude than PAL-II).
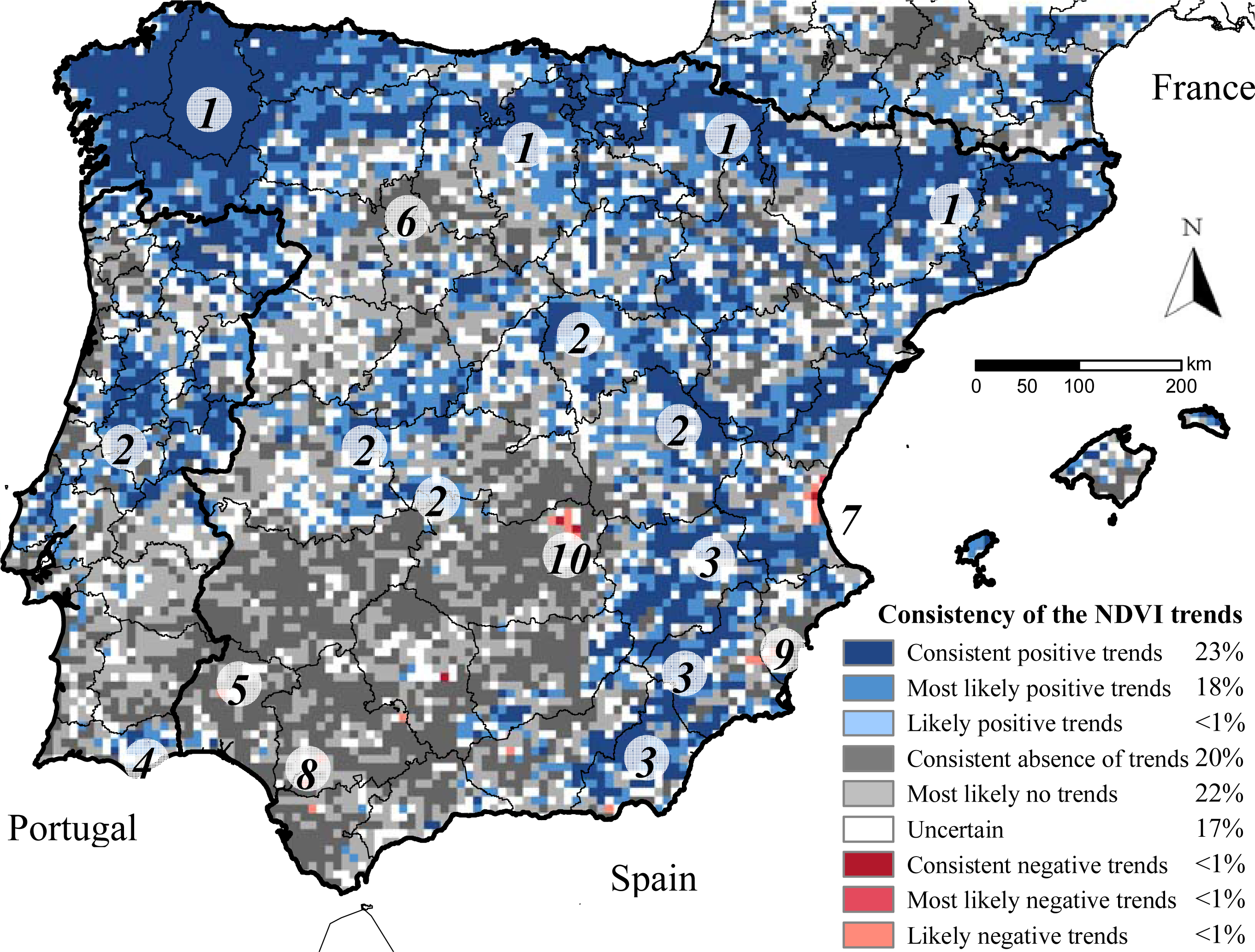
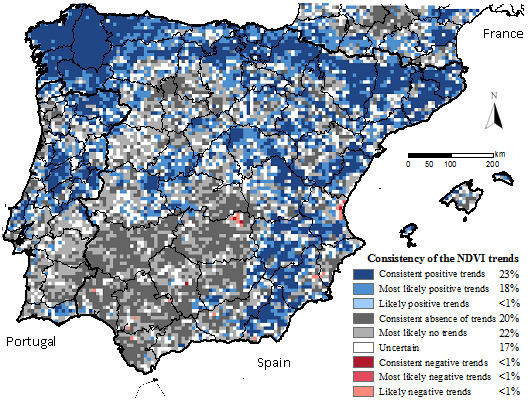
The consensus map (
Figure 2) showed that in 20% of the Peninsula the four datasets exhibited absence of significant trends (pixels distributed across the southwestern quarter of the Peninsula and the agricultural high plains of the Duero basin) (
Table 4).
In an additional 22% of Iberia, three databases did not detect significant trends (most likely no trends in
Figure 2). A 23% of the Peninsula showed positive and significant NDVI trends across the four datasets (areas along the northern, central, and southeastern mountain ranges) and an additional 18% across three databases (most likely positive trends in
Figure 2). Consistent significant negative NDVI trends across the four datasets occurred in less than 1% of the Peninsula (isolated pixels in Aracena mountains and in agricultural areas in the Guadalquivir and Segura basins, La Mancha plains, and Valencia). The LTDR dataset showed the greatest percentage of pixels with significant NDVI trends (
Table 4), while the GIMMS dataset showed the lowest (LTDR detected significant trends in 32% more pixels than GIMMS) (
Table 4). In Spain, the percentage of pixels exhibiting consistent significant NDVI trends across all datasets was 7.8% greater than in Portugal, though it varied depending on the dataset (e.g., for PAL, Spain showed 15% more pixels with significant trends than Portugal, while for LTDR, Portugal showed 6.7% more trending pixels than Spain) (
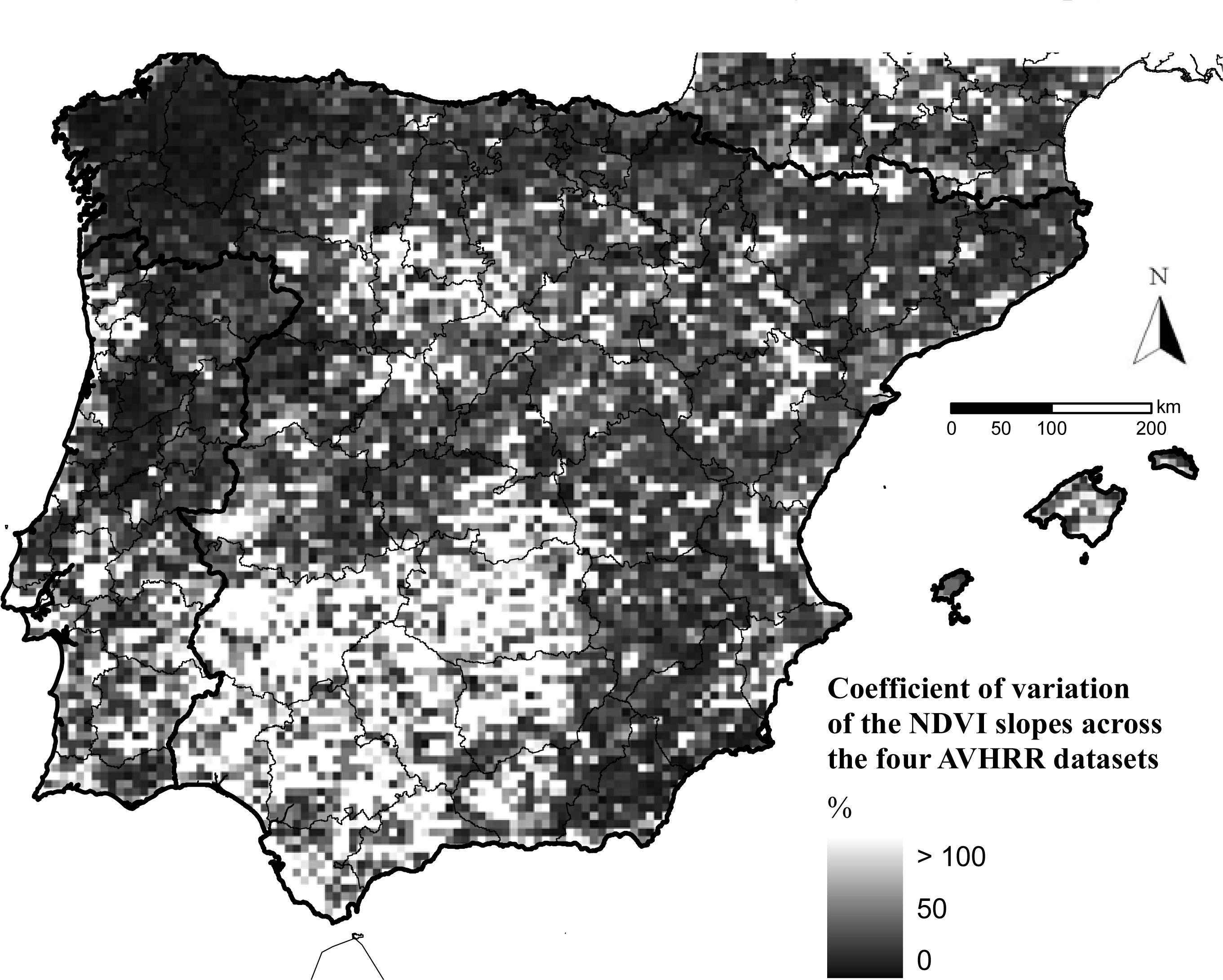
Table 4). The relative error budget of the NDVI trends, evaluated by means of the coefficient of variation of the slopes across the four datasets, showed a similar spatial pattern to the consensus map. Those areas showing consistent positive or negative significant trends across the four datasets differed on average by less than 50% in the magnitude of their slopes, while in areas showing non-significant trends, the magnitude and sense of the slopes largely varied across datasets by more than 100%.
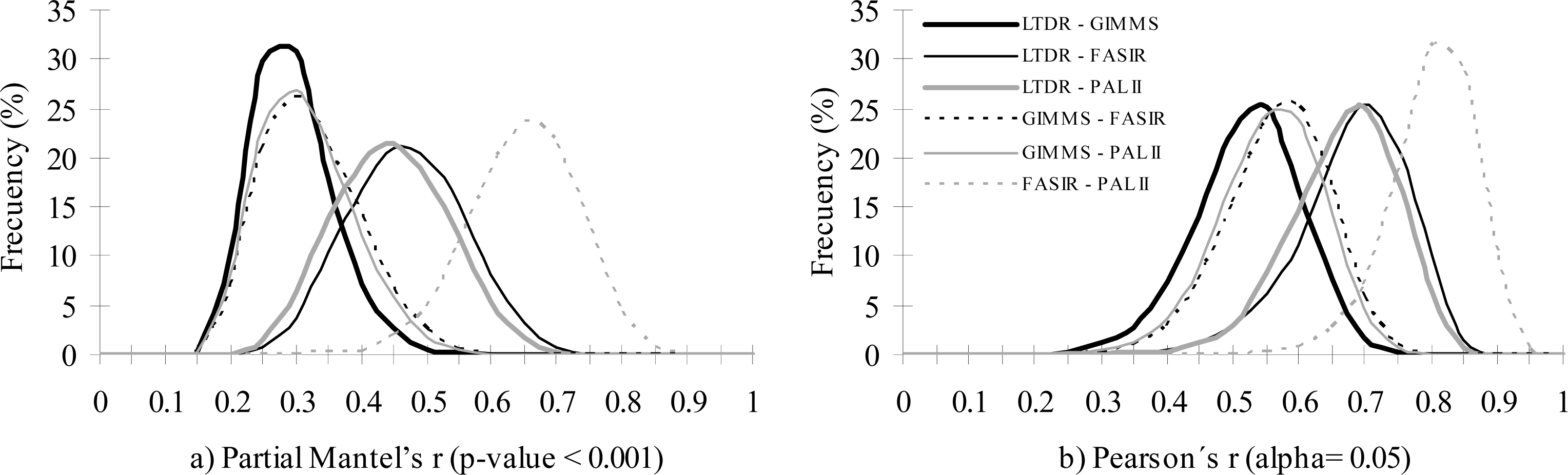
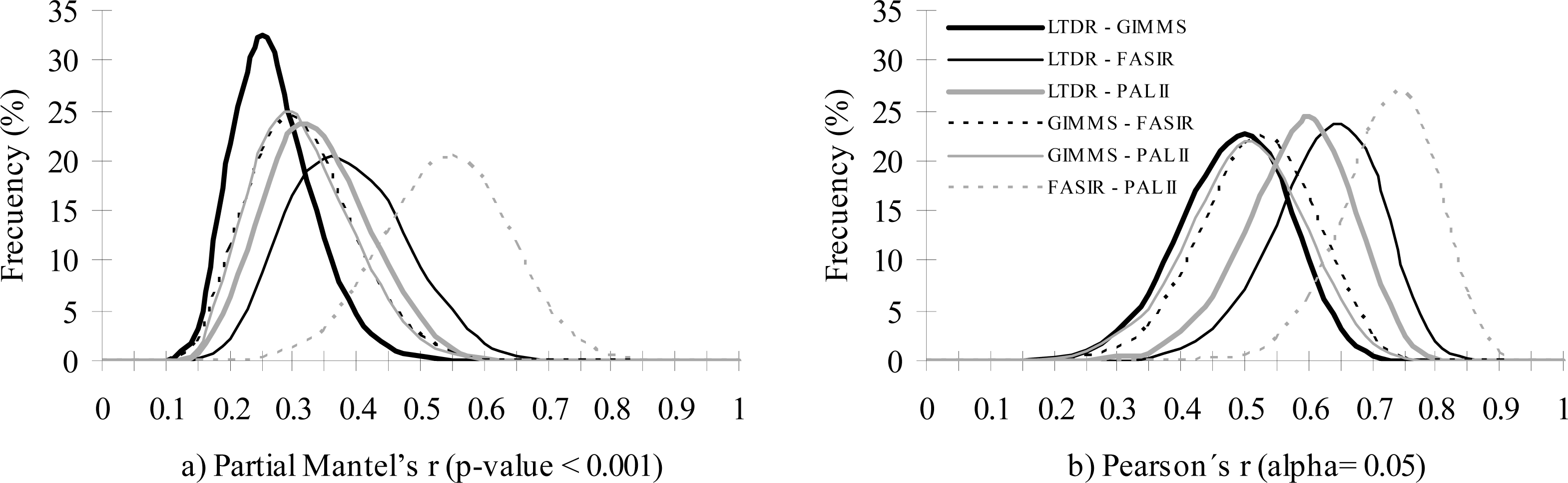
From the four AVHRR datasets, spatial similarity and correlation of significant NDVI trends was the greatest between FASIR and PAL datasets, and the lowest between GIMMS and LTDR (
Table 5,
Figure 3). The rest of the comparisons of the spatial distribution of significant NDVI trends showed comparable partial Mantel’s r and Pearson’s r (
Figure 3), and percentage of consensus in the contingency table (
Table 5). The GIMMS dataset showed the lowest correlation with the other three datasets, while the LTDR datasets showed a moderate correlation with PAL-II and FASIR (but not with GIMMS dataset).
4. Discussion and Conclusions
Coarse-resolution satellite datasets of the NDVI derived from the AVHRR GAC archive are one of the most valuable sources to evaluate temporal trends of carbon gains at the global, regional, and national scales. In carbon budget assessments, countries often make use of these satellite datasets to estimate both vegetation uptake and land-use change related release [
14]. In our study for the Iberian Peninsula, the AVHRR datasets clearly showed that the area showing significant positive NDVI trends is important (23% and an additional 18% of Iberia showed consistency across four and three datasets respectively) and much larger than the proportion with decreasing trends (only 0.1% of Iberia). The area without significant trends was also important (consistently in 20% and an additional 22% of Iberia across four and three datasets respectively). However, although clear consistent patterns may emerge at the country level or regional scale, local analyses must consider that the area showing significant trends can vary depending on the analyzed dataset. For instance, in the whole Iberian Peninsula, it varied from 37 to 67% of the area for positive trends, and from 0.6 to 3.6% for negative trends, and these differences were much larger for Portugal than for Spain (
Table 4). Our study quantified a large portion of the territory (57% of pixels for the Peninsula, 66% for Portugal, and 55% for Spain) where the use of different NDVI datasets may lead to inconsistent NDVI significant trends (though it decreased to just 30%, 37%, and 38% respectively when only the sign of the slope but not the significance was considered (
Appendix 3)). For agreements across just two datasets (contingency tables of
Table 5 and
Appendix 5), the spatial inconsistency was much lower (even just 20% in the comparison between PAL and FASIR;
Table 5). In addition to the differences in the magnitude of the NDVI trends between GIMMS and LTDR (
Table 3), they showed the lowest percentage of agreement in the contingency table (
Table 5). However, their spatial consistency largely increased when non-significant slopes were also compared (
Appendix 5), due to the lower sensitivity of GIMMS to detect both positive and negative NDVI trends.
Regarding the spatial distribution of the NDVI trends in the Iberian Peninsula, increases in vegetation greenness (consistent and most likely positive trends) were largely observed along mountain ranges in the north, center, and southeast of both Spain and Portugal, mainly occupied by natural forests and tree plantations. This increase in the photosynthetic activity agrees with the general trend observed in Europe due to the increase in the forested area, the juvenile age structure, CO
2-fertilization, elevated atmospheric nitrogen deposition, and climate change [
14]. NDVI increases were also aligned along the Ebro river margins, where irrigation expansion over drylands has increased productivity [
34,
36]. Decreases in vegetation greenness were scarce and localized mainly on agricultural lands along the southern and eastern river valleys (
Figures 1 and
2, and
Appendixes 1 and
3) and were largely related to land-use changes on croplands: in Valencia, NDVI decrease was related to urban expansion and
Citrus crop abandonment [
36,
37]; in La Mancha, it was related to the abandonment of vineyards and unsustainable irrigation due to the drop of groundwater tables [
36,
64]; in the Segura river valley, it may be due to both urban expansion and abandonment of unsustainable irrigation [
64,
65]; in the Guadalquivir river valley, NDVI decreases seem to be caused by a decrease in irrigation and rainfall both originated by lower precipitations determined by a trend towards positive phases of the North Atlantic Oscillation (NAO) [
34,
37]. In the woodlands of Sierra de Aracena, NDVI decreases also seem to be caused by lower precipitations related to the NAO dynamics [
34,
37]. The regional control of the NAO dynamics over the NDVI trends of the southwestern quadrant is also suggested by the high local spatial autocorrelation in this region (
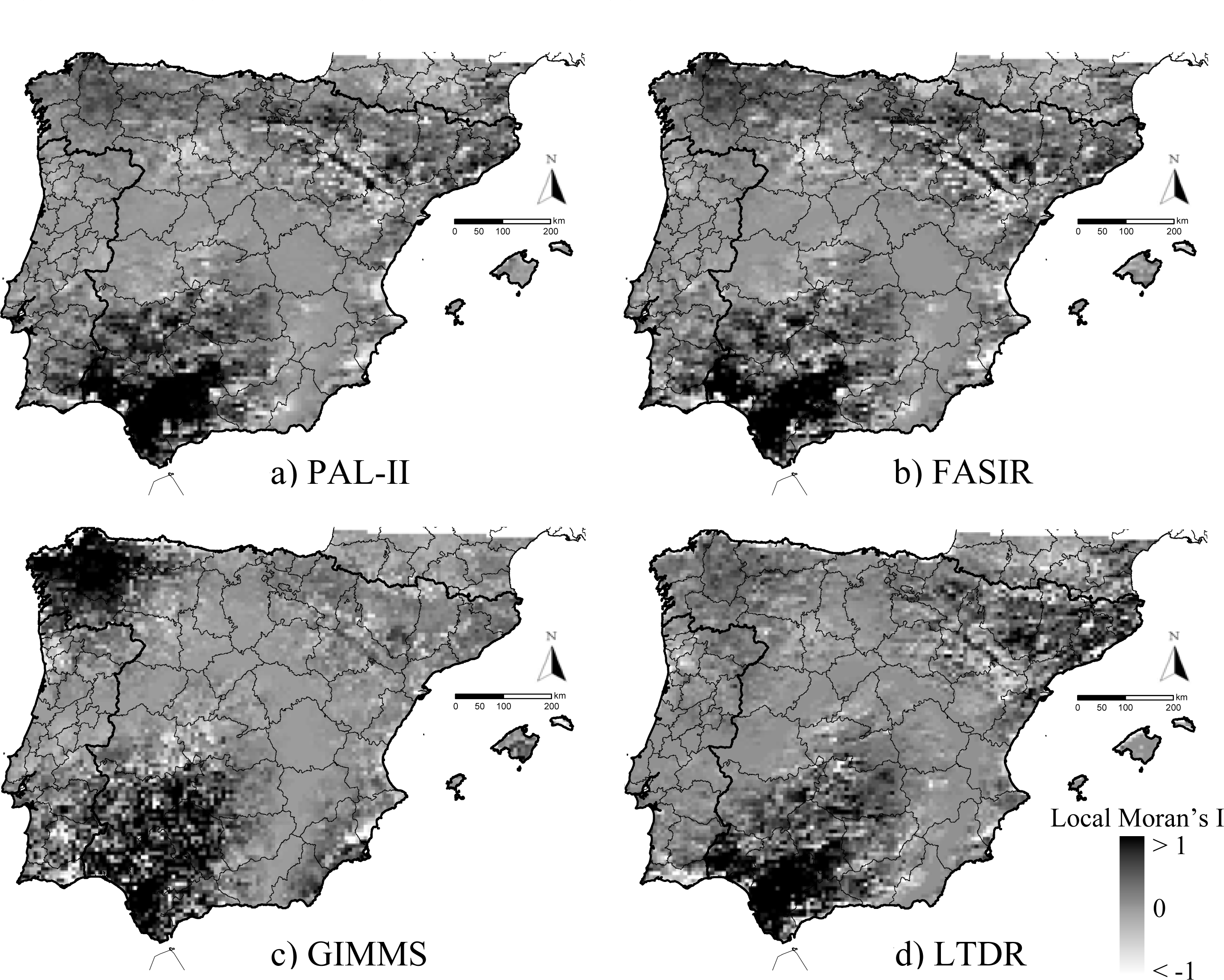
Appendix 7), which should be further investigated. The PAL, FASIR, and LTDR (but not GIMMS) datasets also displayed high spatial autocorrelation in the north and northeastern regions and along the river Ebro valley. Only the GIMMS dataset showed very strong autocorrelation in NW Spain (
Appendix 7).
Many factors may be responsible for the retrieval of different significant NDVI trends across datasets, such as differences among their corrections schemes, projection systems, temporal resolution, or geolocation errors. For instance, the PAL dataset is known to be strongly affected by both satellite drift and volcanic aerosols, while GIMMS does not explicitly address atmospheric corrections [
2], and LTDR still lacks complete atmospheric correction [
2]. In the case of temporal resolution, datasets with longer composite periods (e.g., GIMMS and LTDR) are less affected by cloud noise [
20] but, since they also have fewer composites per year, they may offer less power to retrieve significant trends. Hence, in our analysis, it would be expected to have less power in the retrieval of significant trends using datasets with fewer composites such as GIMMS and LTDR (24 composites per year), than with more composites such as PAL and FASIR (36 composites per year). However, this only happened with the GIMMS dataset, the one showing the lowest percentage of significant trends, while the LTDR dataset cumulated the greatest percentage of significant trends (
Table 4). Additionally, the differences in projections and geolocation error, seem to be partially responsible of the very low spatial correspondence of significant negative NDVI trends since they were mainly local (occupying a few pixels) and along river valleys (
Figure 1,
Appendix 1). From our findings, in addition to quantifying the area affected by consistent trends in vegetation greenness, carbon budget evaluations should also assess the differences in magnitude of the NDVI trends, which can largely vary across datasets. In the case of Spain and Portugal, the maximum difference across datasets was more than double both for the global mean, and for positive and negative trends separately.
C gains estimates had historically relied on forest inventories or land use–land cover changes [
15,
66,
67]. Remotely sensed data has been incorporated as a tool to derive C gains for non-forested areas and for areas without previous inventories [
68–
70]. From our and previous studies [
3,
4], it is recommended that evaluations of the carbon balance based on regional NDVI trends derived from coarse-resolution AVHRR sensor datasets are compared across several datasets to minimize the broad effects that potential local or regional biases in one of them may cause into national carbon budgets. Currently, the PAL and FASIR datasets have been mostly substituted by the GIMMS dataset as reference to model the carbon balance worldwide [
13,
15]. Since the LTDR dataset has been produced as the first component of a cross-sensor long-term NDVI record (to be continued by the MODIS and VIIRS sensors), it is expected that LTDR will also replace all previous AVHRR datasets in this type of studies. However, in our analysis, GIMMS and LTDR, the two “most improved” and newest AVHRR global datasets, showed the lowest consistency between each other. This strongly suggests that the LTDR NDVI trends should also be compared across several AVHRR datasets and, ideally, with independent sensors (such as VEGETATION SPOT or MODIS) to seek for consistencies that reduce as much uncertainty as possible. Future long-term NDVI datasets (e.g., coming versions of LTDR) should contain global estimates of their errors (as Nagol
et al. also suggest [
2]) and, whether possible, spatially and temporally explicit estimates of uncertainty. As an example of the spatial differences in error budgets,
Appendix 8 expresses the relative uncertainty of the 1982–1999 NDVI trends throughout the Iberian Peninsula as the absolute value of the coefficient of variation of the NDVI slope across the four AVHRR datasets. Despite our error analysis being incomplete, it gives a sense of the relative level of uncertainty to consider when using NDVI trends to estimate carbon gains at the regional level.
A proper evaluation of satellite datasets should not only restrict to the physical and mathematical assumptions of image processing but it should also test them at the level of predictions, e.g., comparing trends derived from spectral data with independent observation of change [
3,
4]. Identified areas with extreme land cover changes that cover a substantial portion of a 64 km
2 pixel (e.g., deforested areas in South America and expansion of center pivot agricultural systems over drylands) are ideal places to contrast remotely sensed trends with observed changes.