1. Introduction
Sensor networks are typically characterized by limited power supplies, low bandwidth, small memory sizes and limited energy [
1,
2]. Thus the resource-starved nature of sensor networks poses great challenges for security, since wireless networks are vulnerable to security attacks due to the broadcast nature of the transmission medium [
2–
15].
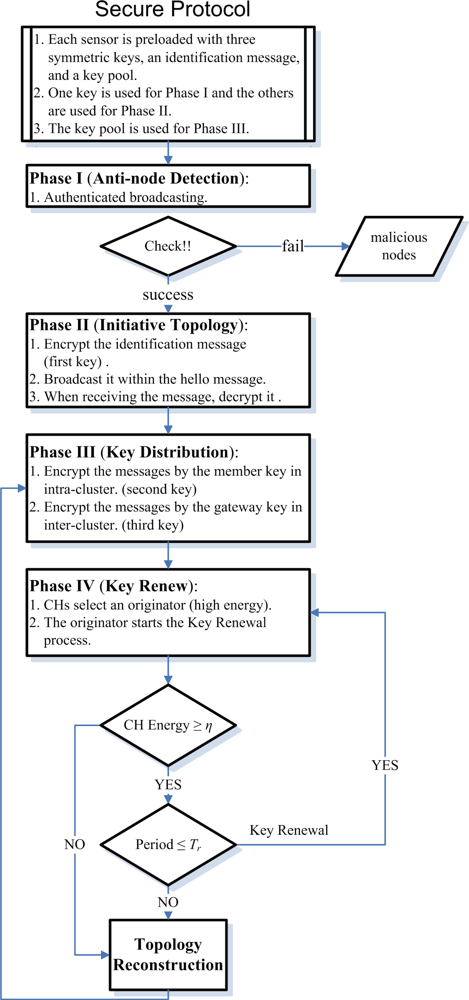
In most sensor network applications, the lifetime of sensor nodes is an important concern, which can shorten rapidly under spam attacks. Moreover, maintaining network connectivity is crucial to provide reliable communication in wireless ad-hoc networks. In order not to rely on a central controller, clustering is carried out by adaptive distributed control techniques. To this end, the Secure Adaptive Distributed Topology Control Algorithm (SADTCA) aims at topology control and performs secure self-organization in four phases: (I) Anti-node Detection, (II) Cluster Formation, (III) Key Distribution; and (IV) Key Renewal, to protect against spam attacks.
In Phase I, in order to strengthen the network against spam attacks, the secure control is embedded into the SADTCA. A challenge is made for all sensors in the field such that normal nodes and anti-nodes can be differentiated. In Phase II, based on the operation in Phase I, the normal sensors may apply the adaptive distributed topology control algorithm (ADTCA) from [
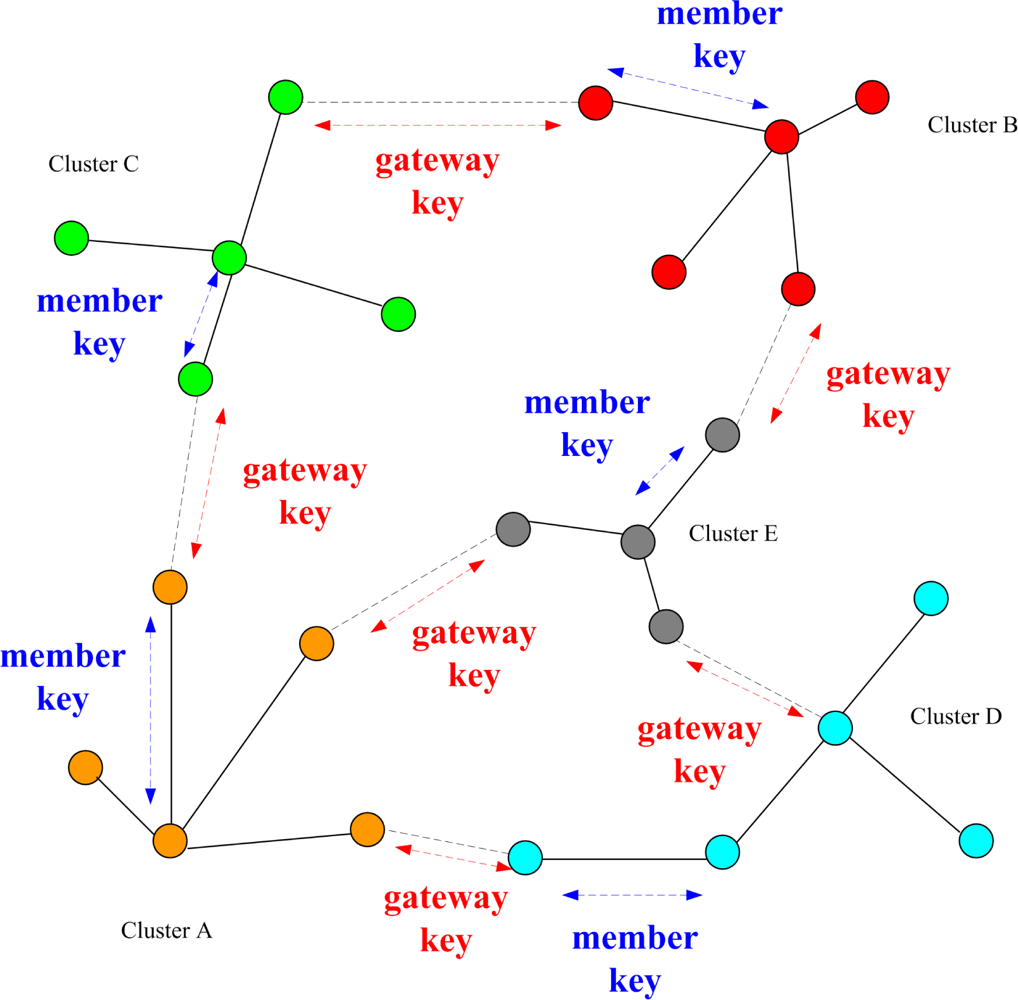
16] to partition the sensors into clusters. In Phase III, a simple and efficient key distribution scheme is used in the network. Two symmetric shared keys, a cluster key and a gateway key, are encrypted by the pre-distributed key and are distributed locally. A cluster key is a key shared by a clusterhead and all its cluster members, which is mainly used for securing locally broadcast messages. Moreover, in order to form a secure inter-cluster communication channel, a symmetric shared key may be used to encrypt the sending messages between the gateways of adjacent clusters. Since using the same encryption key for extended periods may incur a cryptanalysis risk, in Phase IV, key renewing may be necessary for protecting the sensor network and guarding against the adversary getting the keys.
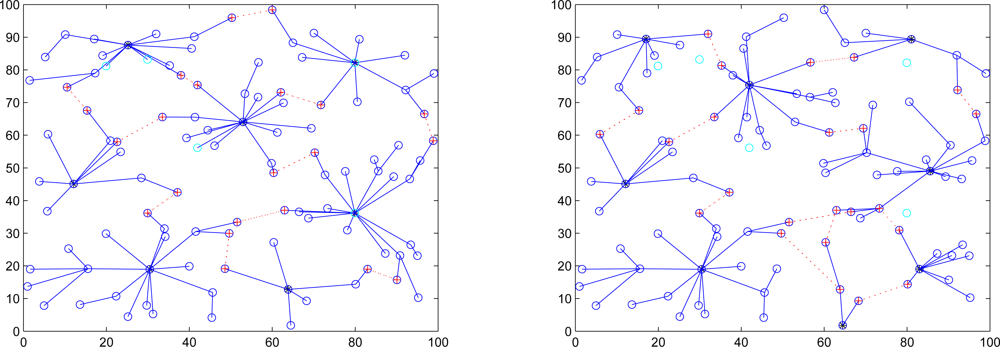
Built upon the cluster-based network topology, three quarantine methods, Method 1: quarantine for clusters, Method 2: quarantine for nodes, and Method 3: quarantine for infected areas, are proposed for dynamically determining the quarantine region. In order to explore the fundamental performance of the SADTCA scheme, an analytical discussion and experiments are presented to investigate the energy consumption, communication complexity, the increase of communication overheads for data dissemination, and the percentage of the quarantine region in the sensing field when facing the spam attack.
The organization of this paper is as follows: In Section 2., we briefly introduce the related work and summary of security issues for wireless sensor network environment. Section 3. describes the system model and algorithm for secure self-organization in a cluster-based network topology. Section 4. presents dynamic approaches for determining the quarantine region. In Section 5., we analyze the SADTCA and make comparisons with protocols in the flat-based topology. In Section 6., the simulation results are shown and discussed. Finally, Section 7. draws conclusions and shows future research directions.
2. Literature Review
There are many vulnerabilities and threats to wireless sensor networks. The broadcast nature of the transmission medium incurs various types of security attacks. Different schemes to detect and defend against the attacks are proposed in [
2–
15]. A number of anti-nodes deployed inside the sensing field can originate several attacks to interfere with message transmission and even paralyze the whole sensor network. Most network layer attacks against sensor networks fall into one of the following categories:
The spam attack, which is a kind of flooding Denial of Service (DoS) attack, can be carried out by the anti-node inside the sensor network. Such attack can retard the message transmission and exhaust the energy of a sensor node by generating spam messages frequently. In [
17] and [
18], the authors propose detect and defend spam (DADS) scheme and quarantine region scheme (QRS) to address the following issues: spam detection, quarantined nodes determination, messages authentication, and quarantine region cancelation. Two detection mechanisms against spam attacks on sensor networks are proposed in DADS [
17]. The first method is to filter incoming messages according to their contents and detect the nodes that send faulty messages frequently. The second method uses the frequencies of messages sent by the sensors in the same region. In DADS, the anti-node is detected by the sink, not by the sensor node. The packets of each sensor are counted by the sink. Such centralized detection architecture can be well suitable to a small-scale sensor network, but the total number of packets could be large in a large-scale sensor network. Based on the distributed strategy, the QRS makes each node to detect neighbor anti-node individually [
18]. By requesting authenticated messages, each sensor node decides whether there is an anti-node in its transmitting range or not. Comparing to the central detection architecture, the total packet number is reduced rapidly and the limitation of scalability is eliminated.
These schemes classify the transmission range of the anti-node as the “quarantine region”. The nodes in the quarantine region are called “quarantined nodes”. A message must be authenticated in the quarantine regions. Any unauthenticated messages from nodes in the quarantined region will not be replied and are discarded. The nodes outside the quarantine regions do not need authentication to transmit a message even if the message was an originally authenticated message coming from a quarantine region. By this partial authentication strategy, the cost of authentication is reduced effectively.
Notice that the overheads of authentication in [
17,
18] are dependent on the number of anti-nodes and the area of quarantine region. Moreover, when determining the quarantine region, the location information of the nodes is required for the approaches in [
17,
18]. In contrast, based on a cluster-based topology, the proposed SADTCA adaptively forms the quarantine region without using network location information. Therefore, a management scheme, such as hierarchical clustering, may be added to further enhance the formation, message transmission, and management of a quarantine region. Our previous works [
16,
19] propose the extensive research for distributed cluster-based topology control. In these algorithms, a cluster is suitable for a base unit of quarantine region such that the complexity of management of quarantine region can be reduced.
Accordingly, in this paper, the cluster-based architecture efficiently assists in forming and managing quarantine regions and effectively protects the network from attacks. Compared with [
17,
18], our protocol can be used to enhance the control of quarantine region, as well as to restrain the packet number of transmitting messages caused by the anti-node. The performance comparison of the SADTCA and DADS is further investigated in Sections 5. and 6.
3. Secure Adaptive Distributed Topology Control Algorithm
In this section we present a secure adaptive distributed topology control algorithm (SADTCA) for wireless sensor networks. The proposed algorithm organizes the sensors in four phases: Anti-node Detection, Cluster Formation, Key Distribution, and Key Renewal. The main keys used in the network are (a) Pre-distributed Key, (b) Cluster Key, and (c) Gateway Key. Each sensor is pre-distributed with three initial symmetric keys, an identification message, and a key pool. Pre-distributed key is established with key management schemes [
6,
7], and is used for anti-node detection and cluster formation in Phases I and II. The Cluster Key and Gateway Key are used for key distribution in Phase III. The key pool is used for key renewing in Phase IV. Note that since our research aims at network topology control, the pre-distributed key establishment is beyond the scope of this paper.
3.1. Phase I: Anti-node Detection
In order to strengthen the network against spam attacks, the secure control is embedded into the SADTCA. An authenticated broadcasting mechanism, such as the
μTESLA in SPINS [
20], may be applied in this phase. In the authenticated broadcasting mechanism, a challenge is made for all sensors in the field such that normal nodes and anti-nodes can be differentiated. The challenge is that when a sensor broadcasts a
Hello message to identify its neighbors, it encrypts the plaintext and then broadcasts; when receiving the
Hello message, the sensor decrypts it. If the sensor decrypts the received message successfully, the sender is considered normal. Otherwise, the sender is said to be an anti-node. Therefore, we keep on the network topology without anti-nodes in order to make the network safe.
If an anti-node is presented in the first deployment of a sensor network, its neighboring normal nodes will notice the existence of the anti-node, since the anti-node will fail in authentication. Thus, referring to the cluster-based topology formed in Phase II, the spam attacks can be handled by adaptively forming the quarantine region as detailed in Section 4..
Notice that an external attack can be prevented by the operation of Phase I. In this work, we do not have a lightweight countermeasure to defend against authenticated malicious nodes. If the authenticated node is compromised and perform malicious activities, a mechanism for evicting the compromised nodes is required [
7].
3.3. Phase III: Key Distribution
According to the cluster construction in Phase II, a simple and efficient key distribution scheme is applied in the network. In this phase, two symmetric shared keys, a cluster key and a gateway key, are encrypted by the pre-distributed key and are distributed locally. A cluster key is a key shared by a clusterhead and all its cluster members, which is mainly used for securing locally broadcast messages, e.g., routing control information, or securing sensor messages. Moreover, in order to form a secure communication channel between the gateways of adjacent clusters, a symmetric shared key may be used to encrypt the sending message. The process of key distribution is shown in
Figure 2. In this phase, another challenge may be made to guard against anti-nodes that have not been found out in Phase I. The challenge is that if any sensor cannot decrypt ciphertext encrypted by a cluster key or a gateway key, the node will be removed from the member or neighbor list. Therefore, the security of intra-cluster communication and inter-cluster communication are established upon a cluster key and a shared gateway key, respectively.
3.4. Phase IV: Key Renewal
Using the same encryption key for extended periods may incur a cryptanalysis risk. To protect the sensor network and prevent the the adversary from getting the keys, key renewing may be necessary. In the case of the revocation, in order to accomplish the renewal of the keys, the originator node generates a renewal index, and forwards the index to the gateways. The procedures of key renewal are detailed as follows.
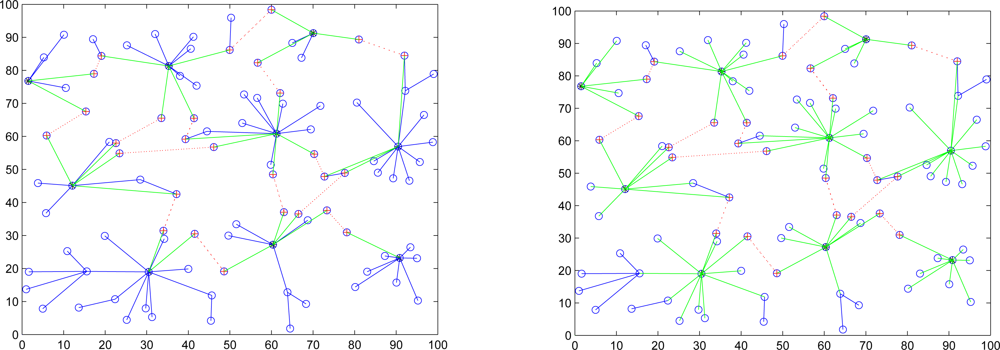
Initially all clusterheads (CHs) choose an originator to start the “key renewals”, and then it will send the index to all clusterheads in the network. There are many possible approaches for determining the originator. For instance, the clusterhead with the highest energy level or the clusterhead with the lowest cluster ID. After selecting the originator, it initializes the “Key renewal” process and sends the index to its neighboring clusters by gateways. Then the clusterhead refreshes the two keys from the key pool and broadcasts the two new keys to their cluster members locally. The operation repeats the way through to all clusters in the network. The key renewing process is depicted in
Figure 3. A period of time (
Tr) is set in order to avoid that the originator does not start the “key renewal” process. If the other clusters do not receive the index after
Tr, they will choose a new originator from themselves. The method helps to rescue when the previous originator is broken off. The focal procedures of the SADTCA are summarized in
Figure 4.
4. Determining the Quarantine Region
If the anti-nodes are scattered randomly in the first deployment of a sensor network, the anti-nodes can be detected by authentication in Phase I of the SADTCA. On the other hand, given the cluster-based topology formed in Phase II of the SADTCA, the clusterhead and cluster members may detect external attacks and check the unsolicited messages by observing the abnormal behaviors of the sending nodes. For instance, filtering the content of the incoming messages, detecting the frequency of the faulty messages, or checking the sending frequency of messages. Thus, these scenarios may imply a possible spam attack and then the clusterhead may broadcast a message throughout the whole cluster to announce the existence of anti-nodes. Therefore, in order to defend against spam attacks, three distributed methods, Method 1: quarantine for clusters, Method 2: quarantine for nodes, and Method 3: quarantine for infected areas, are proposed for dynamically determining the quarantine region.
4.1. Method 1: Quarantine for Clusters
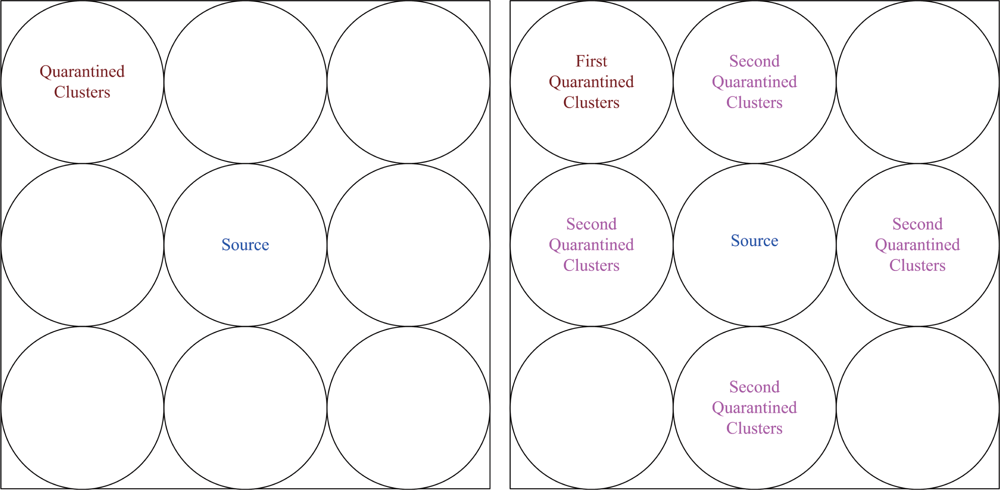
When the clusterhead finds out the occurrence of a spam attack, it broadcasts a message throughout the whole cluster. In this condition, the set of quarantine nodes is composed of the clusterhead and cluster members. Note that the performance of the SADTCA with Method 1 may be considered as a conservative approach for forming the quarantine region.
4.2. Method 2: Quarantine for Nodes
In this scheme, the quarantine region is the region where the transmission of the anti-node can be received. Thus, the transmission range of an anti-node may be denoted as the distance between the anti-node and the borderline of the quarantine region. The concept of this method is the same as the DASA scheme. However, if the quarantined node is a clusterhead, the whole cluster will be quarantined since clusterheads are important nodes for controlling the cluster operation. On the other hand, if the quarantined node is a cluster member, the whole cluster will not be quarantined.
4.3. Method 3: The Infected Areas
Here we introduce a way to determine the set of quarantine nodes and quarantine region with a threshold of the infected percentage of cluster coverage. Assuming the uniform distribution of the sensor nodes, the clusters may be located one by one from the coordinate of (0,0) in
X-Y plane as shown in
Figure 5 (left). Thus, a decision for quarantine region may be made with proper settings for the normal clusters and anti-nodes.
Since each cluster is responsible for sensing the scope in the network ℓ
2/NCH, the possible coverage range of a cluster is
where ℓ is the side length of the sensing square and
NCH is the number of clusters. Accordingly, the coordinates of the clusters yields
where
and
. Assume the coordinates and the transmission range of an anti-node are (
xe,
ye) and
re, respectively. As depicted in
Figure 5 (right), the infected region O between the coverage of a neighboring clusterhead and an anti-node is given by
where
is the length between two intersection points
A and
B. Therefore, given the infected region
O and a threshold of infected percentage of the cluster coverage
η, the decision of quarantine region may be determined. For instance, when
the infected cluster is quarantined.
Accordingly, when O/πr2 ≥ η, Method 1 may be applied; otherwise, Method 2 may be chosen to quarantine the whole cluster. Therefore, Method 3 achieves the operation balance of Methods 1 and 2 for establishing local quarantine regions.
6. Simulation
In this section, we study the performance of the proposed SADTCA scheme via simulation when executing the four cases: quarantine for clusters, quarantine for nodes, quarantine with
η ≥ 1/3, and quarantine with
η ≥ 1/5 (as detailed in Section 4.). Referring to [
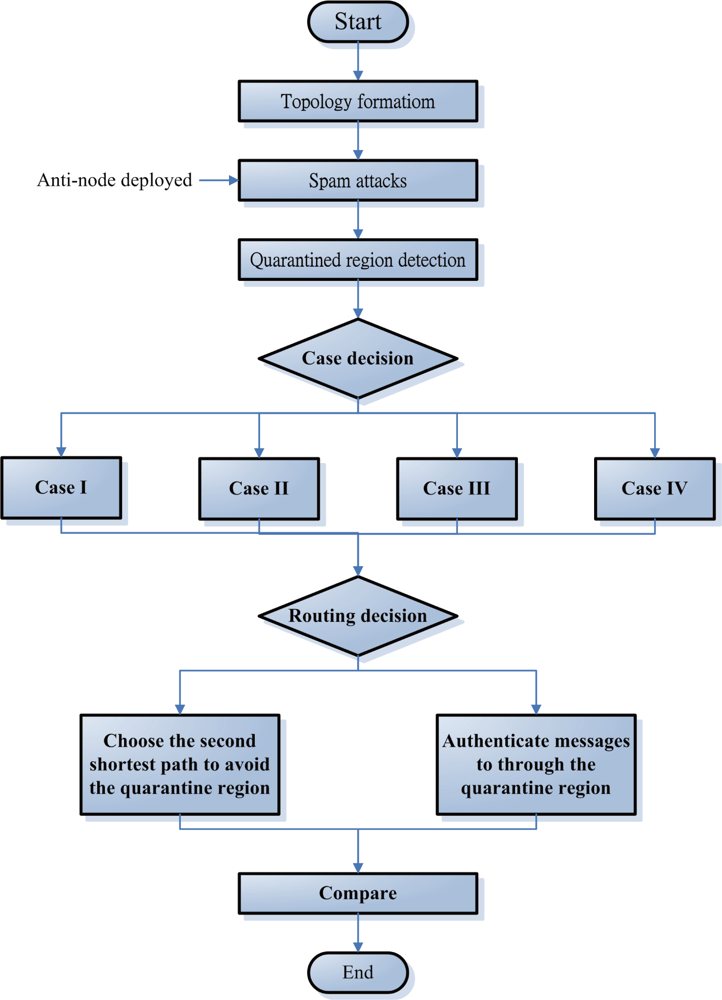
18], the simulation flow chart is shown in
Figure 11.
For the experiments, 100, 500, 1000 (
Figures 12) sensor nodes are randomly deployed in the sensor field 100×100 units in size. In order to maintain the network connectivity with high probability, the transmitting range
R of sensors may be given by [
21]:
where
n is the number of sensors and ℓ is the length of sides of a
d-dimensional cube.
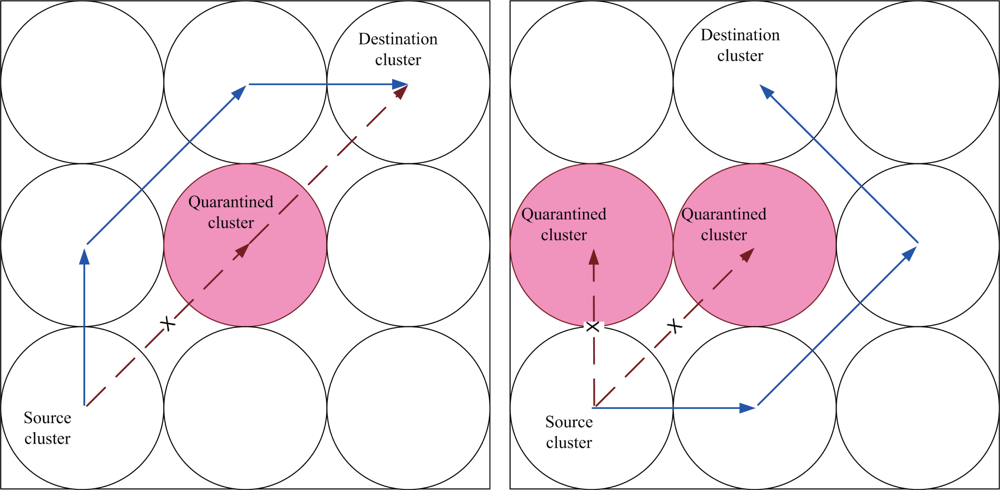
Here we focus on two kinds of variation. One is the hop difference between the shortest path through the quarantine region and the shortest path avoiding the quarantine region. The other is the number of hops with authenticated messages through the quarantine region. We assume that each cluster sends one message to other clusters, except the quarantined clusters, and then calculate the total number of hops.
6.1. Case I: Quarantine for Clusters
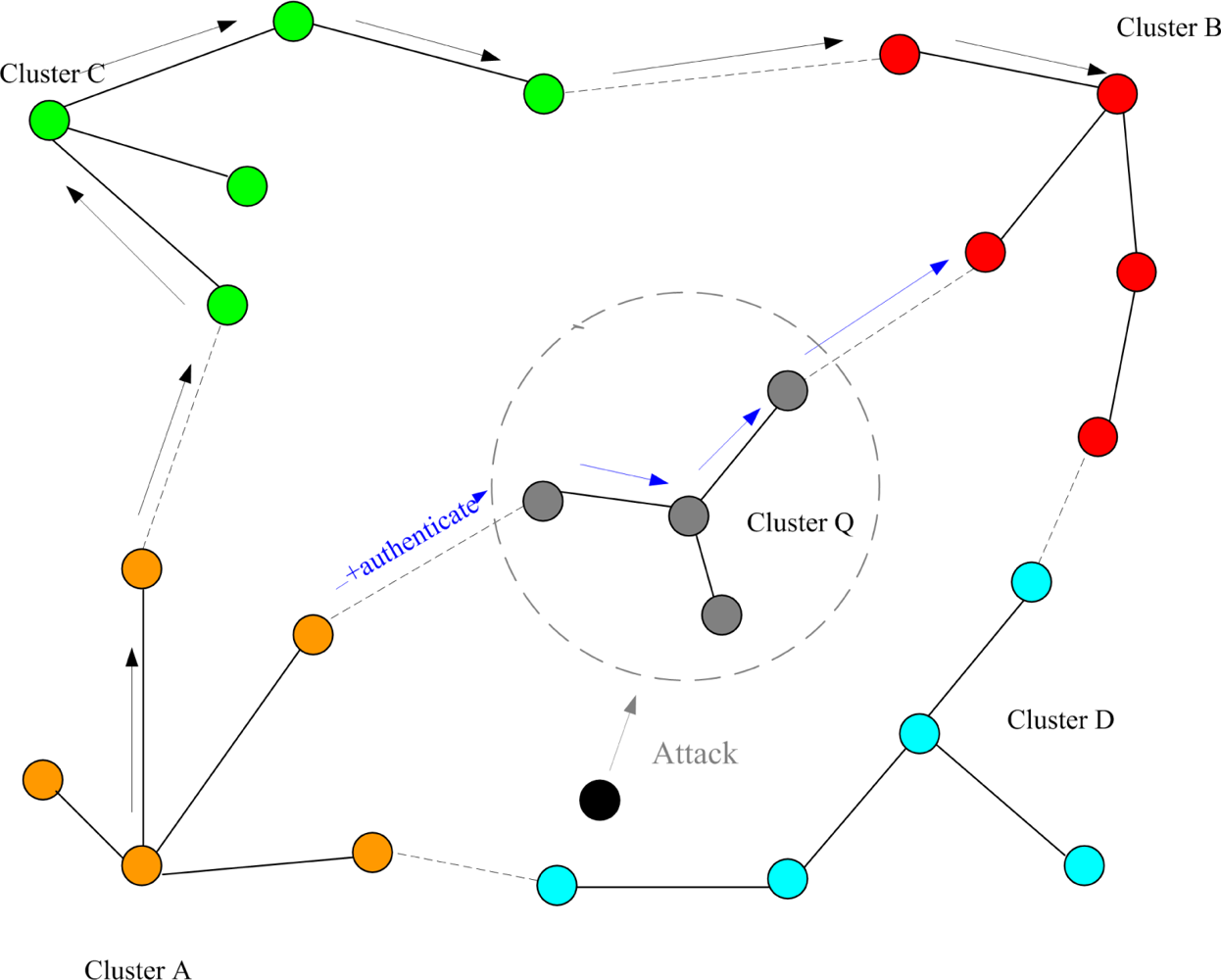
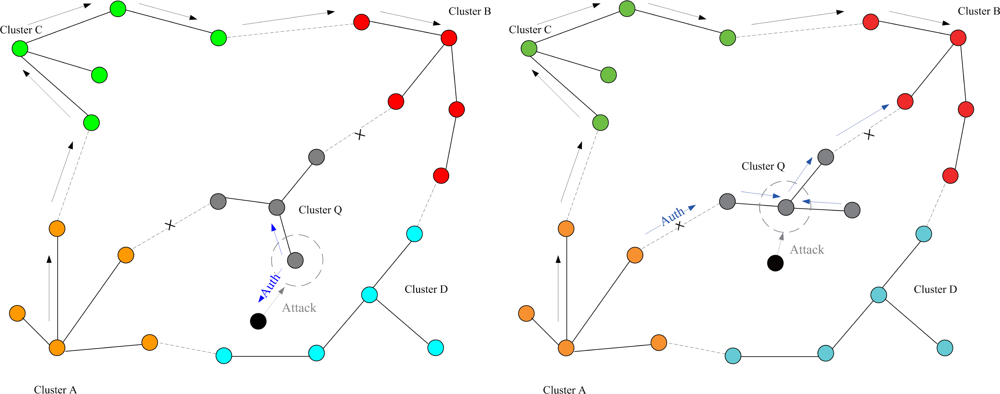
This set of experiments investigates the performance of the quarantine strategy for clusters with varying the number of anti-nodes ranging from 1 to 5. We assume that the attacker threatens different clusters. If the cluster is attacked, it will be quarantined. A description of quarantine process for clusters is illustrated in
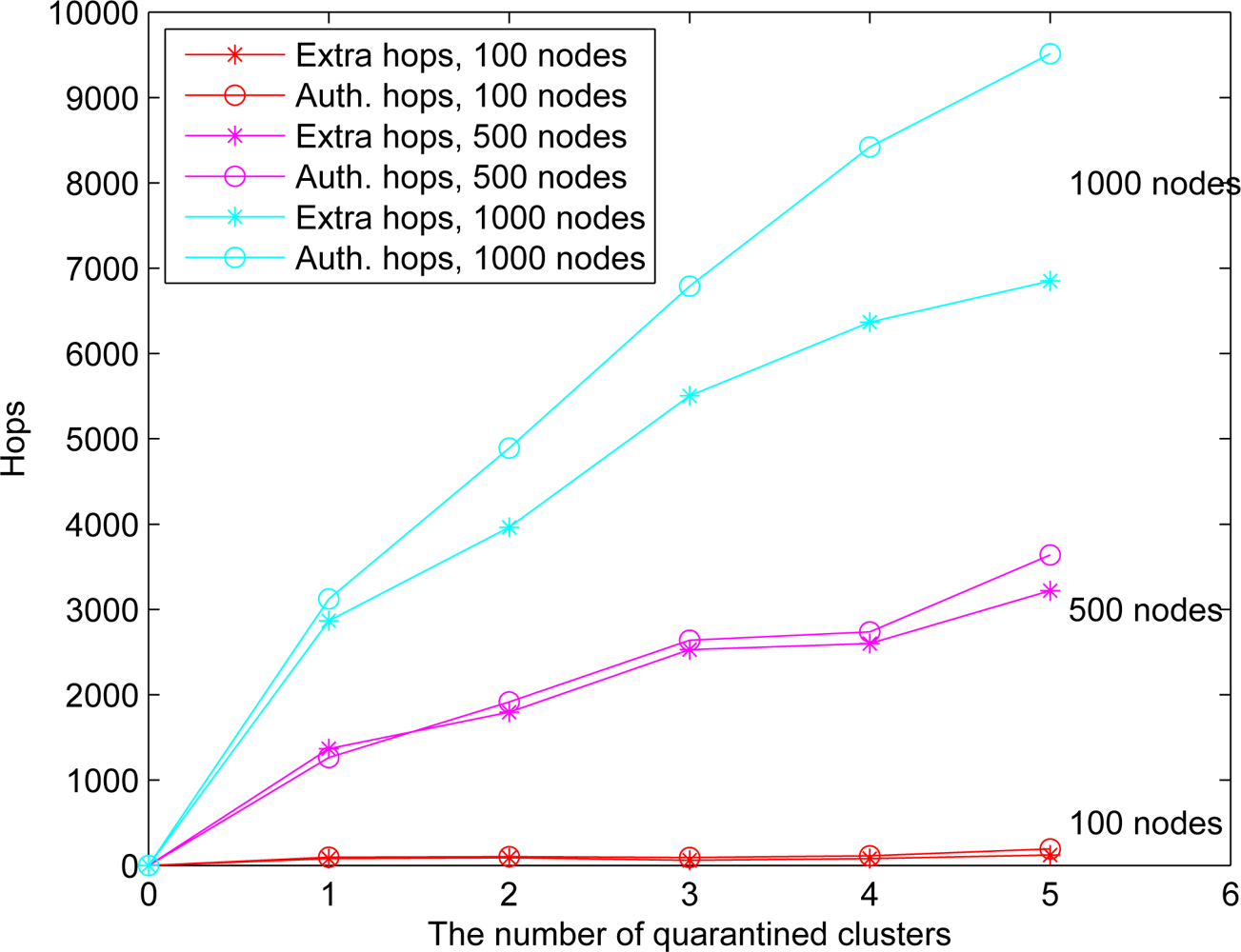
Figure 13. As depicted in
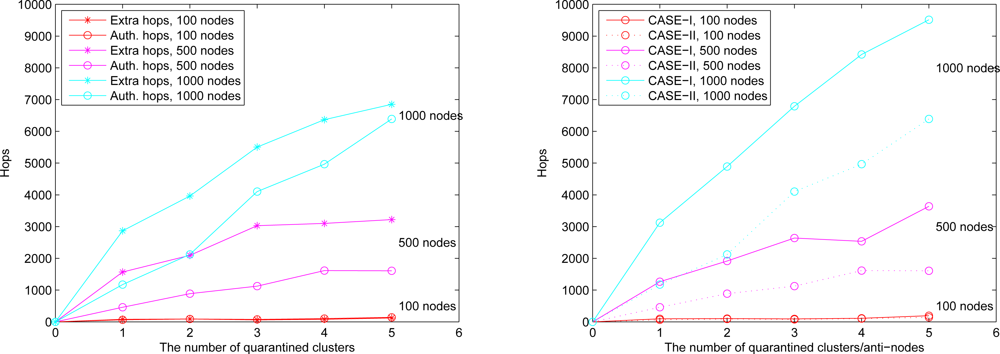
Figure 14, the number of extra hops for bypassing routing path is less than the number of authenticated hops for going through the quarantined clusters. Thus, a bypassing routing may be efficient in this case.
6.2. Case II: Quarantine for Nodes
In Case II, we assume that the attacker threatens the nodes. If the node is attacked, it will be quarantined. When the quarantined node is a member, the authentications are executed between the quarantined node and the clusterhead, and between the quarantined node and the attacker since it may prevent the threat from extending to the whole cluster. In this scenario, a message is allowed to pass through the cluster. A description of quarantine for nodes is shown in
Figure 15 and the result is depicted in
Figure 16, which compares the total number of hops with authenticated messages through the quarantine region for Case I and Case II, respectively.
Figure 16 shows that the number of authenticated hops for going through the infected clusters is less than the number of extra hops for bypassing the routing path. Hence, a bypass routing may not be efficient in this case. Observe that the number of hops in Case II is much less than that in Case I. Therefore, Case II may have a better energy control than Case I.
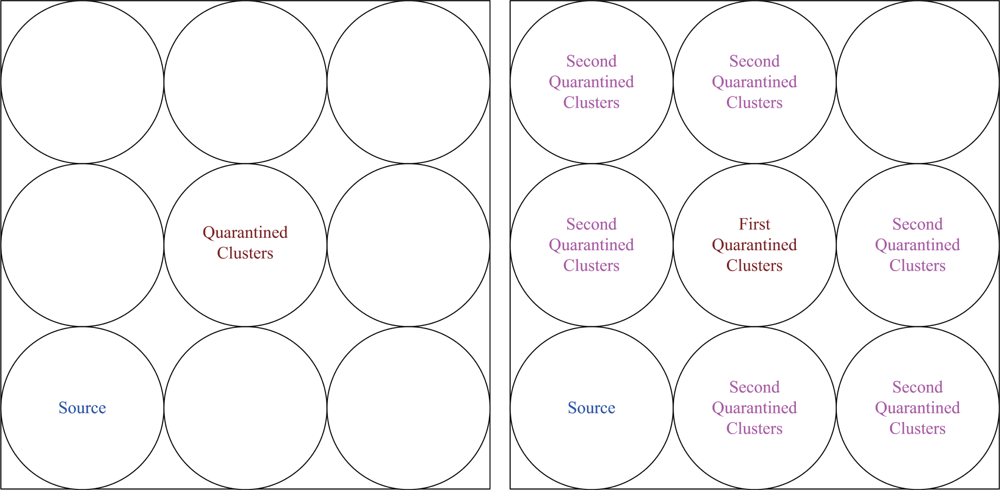
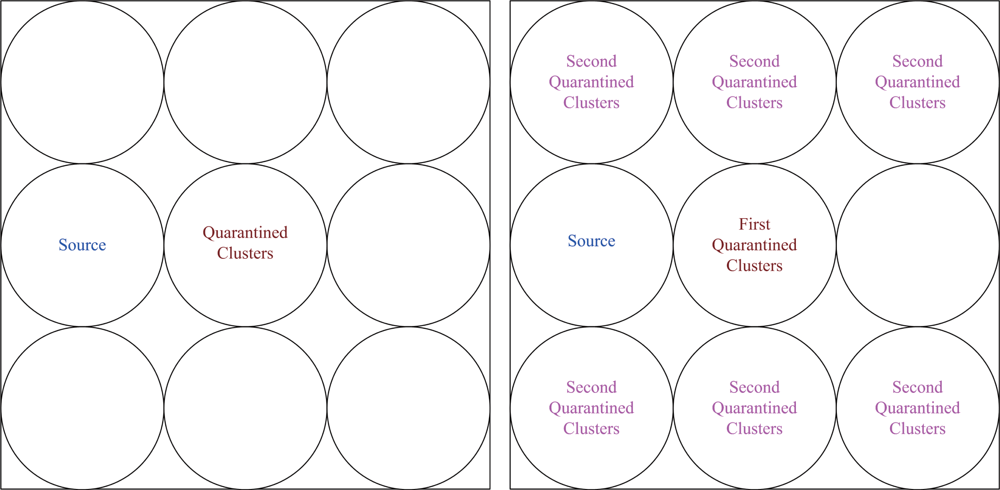
6.3. Quarantine for Infected Areas (Cases III and IV)
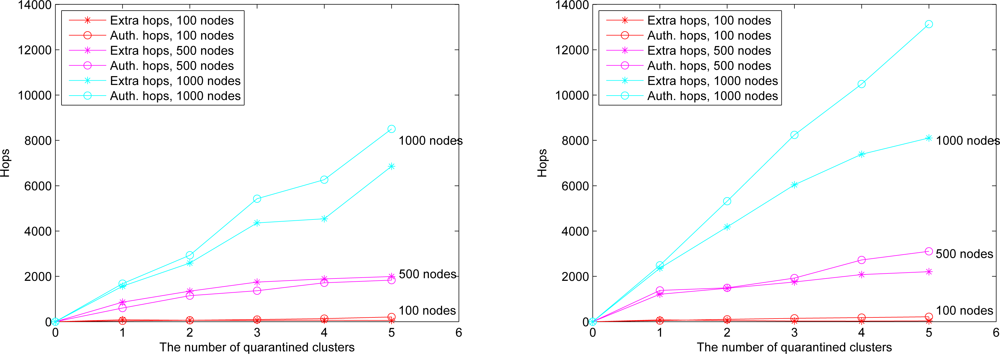
When anti-nodes start spam attacks, the quarantine region of the infected cluster can be determined based on the dimension of infected area (O) as detailed in Section 4. In Case III, if the dimension ratio of infected area (O) to the cluster coverage is over 1/3, the cluster will be quarantined. Similarly, in Case IV, if the dimension ratio of infected area (O) to the cluster coverage is over 1/5, the cluster will be quarantined. Assuming the sensors are uniformly distributed, instead of using the criterion in (5), the ratio of the number of nodes within the transmission range of an anti-node to the number of nodes within a cluster sensing scope (i.e., the number of infected cluster members) may be applied to determine the quarantine region. Experimental results show that this ratio can well represent the cover ratio in a random network with high network density.
We assume an anti-node’s transmission range is the same as normal nodes. The results of Case III and Case IV are depicted in
Figure 17 (left) and
Figure 17 (right), respectively.
Figure 17 shows that compared with the scheme in Case III, the mechanism in Case IV is more secure to defend against spam attacks, but with higher energy consumption.
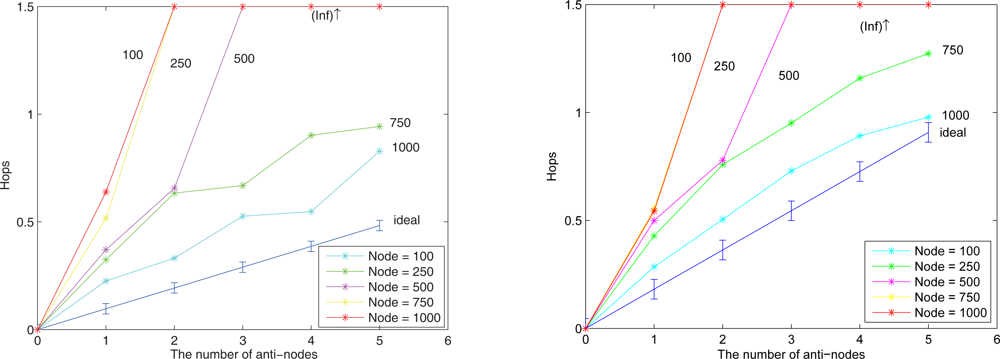
Figure 18 depicts that with a larger network scale, the performance of the proposed approach matches well with the derived ideal results. Note that the (Inf) in this figure indicates that a bypassing routing path is not reachable due to the low density of nodes.
6.4. Proportion of the Quarantine Region
The percentage of the quarantine region in the sensing field impacts two performance metrics of sensor networks: network lifetime and network connectivity. This is because the message authentication in quarantine region represents extra energy consumption of sensors, which may shorten the lifetime of sensor networks. Moreover, with a high percentage of quarantine region in the network, a sensing field might be partitioned due to the energy depletion of infected sensor nodes. Notice that the quarantine region proportion reflects the control of infected nodes within the neighborhood of an attack.
Referring to the transmission range of sensors given by (27),
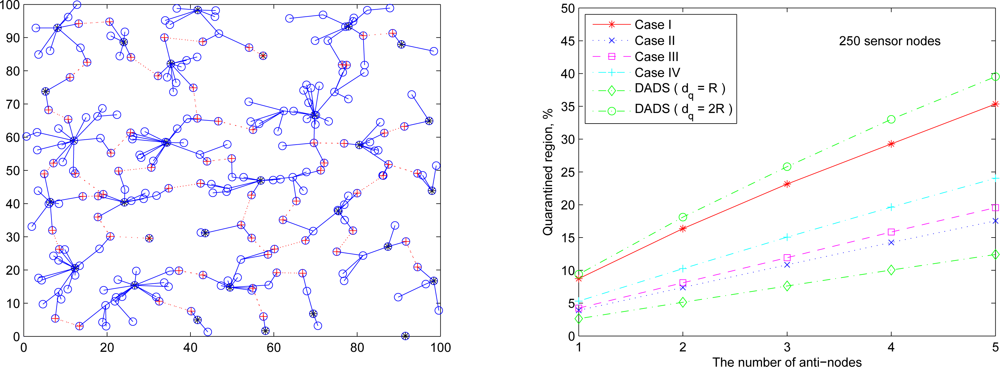
Figure 19 (left) and
Figure 19 (right) show the cluster topology and the average percentage of the quarantine region with 250 sensor nodes using different quarantine methods, respectively. The quarantine strategy for clusters (Case I) stands for the most strict quarantine condition and the quarantine strategy for nodes (Case II) stands for the loosest one. In the worst case (Case I), 5 anti-nodes cause about 35% of the entire network to be marked as the quarantine region. Thus, only about 35% of the network nodes need to authenticate the messages, which means the 65% of network nodes do not pay the cost for authentication. The quarantine region proportion of Case II is about half of the proportion of quarantine region in Case I (about 17%). The quarantine strategies for infected areas (Cases III and IV) can reduce the average percentage to 24% (Case IV) and even 19% (Case III).
Observe that, as shown in
Figure 19 (right), the performance of the DADS with
dq =
R may represent a lower bound for the performance of the SADTCA with the quarantine strategies. Due to the 2-hop cluster topology, the quarantine strategy for clusters (Case I) expands the quarantine region, which makes the average percentage of Case I close to that of the DADS with
dq = 2
R. Thus, the DASA scheme with
dq = 2
R may be used to benchmark the performance of the proposed SADTCA with Method 1 (
i.e., Case I: quarantine for clusters).
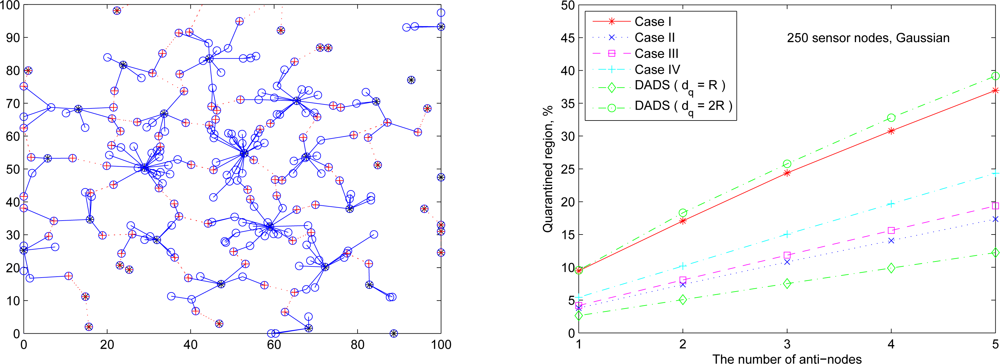
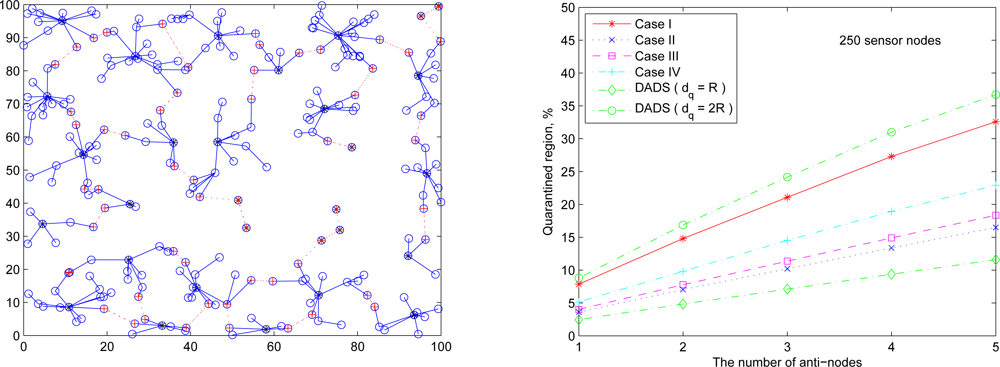
The following set of experiments investigates the influence of the distribution of sensor nodes on the proportion of quarantine region. Here two sensor deployment strategies are considered: (I) Making sensor density high at the center of the terrain, and (II) Making sensor density high at the border of the terrain. For deployment strategy I,
Figure 20 (right) shows the average percentage of the quarantine region assuming that the 250 sensors are deployed based on Gaussian distribution with the center (
x0,
y0) = (50, 50) and the spreads of the blob σ
x = σ
y = 0.25ℓ (
Figure 20 (left)). For deployment strategy II, assuming that 50 sensors are deployed within the center sensing field 80 × 80 units in size and the other 200 nodes are deployed outside the center square (
Figure 21 (left)),
Figure 21 (right) shows the proportion of the quarantine region in the sensing field. Observe that these performances are similar to the one with uniform distribution as shown in
Figure 19 (right). Thus, except under extreme conditions for specific topologies, the distribution of the sensor nodes may not have significant impact on the performance of the proposed quarantine strategies.
In a flat network topology, the DADS scheme considers the neighborhood control of an attack and provides a heuristic way to determine the quarantine region. On the other hand, in a hierarchical network topology, the SADTCA explores the cluster structure and applies distributed quarantine strategies to determine the set of infected nodes. Although the DADS has a less proportion of the quarantine region, by adjusting the threshold of infected percentage of the cluster coverage η, our schemes can dynamically coordinate the proportion of the quarantine region and adaptively achieve the cluster control and the neighborhood control of attacks.
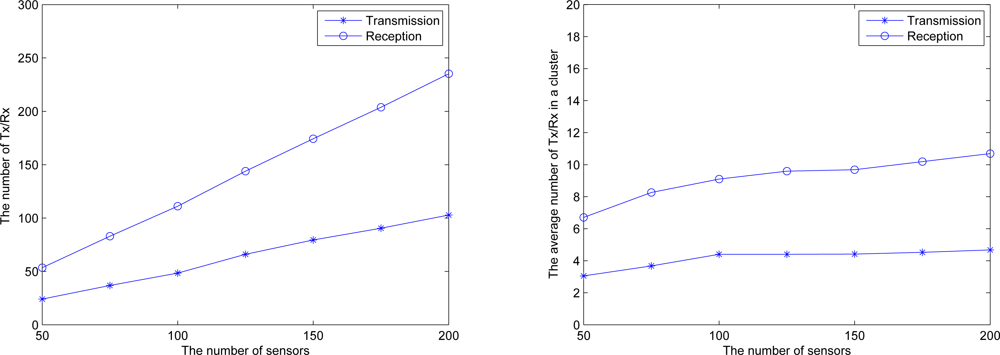
6.5. Energy Consumption
Figure 22 (left) illustrates the total number of transmission and reception in the network for executing key distribution, which increases with the increasing number of sensors.
Figure 22 (right) illustrates the average number of transmission and reception in a cluster for executing key distribution. Observe that with a sensible topology control in Phase II, the average number of transmission and reception in a cluster increases slightly when the number of sensors increases.
7. Conclusions
We describe a secure protocol for topology management in wireless sensor networks. By adaptively forming quarantine regions, the proposed secure protocol is demonstrated to reach a network security agreement and can effectively protect the network from energy-exhaustion attacks. Therefore, in a hierarchical network topology, the SADTCA scheme can adapt cluster control and neighborhood control in order to achieve dynamic topology management of the spam attacks. Compared with the DADS scheme, our protocol can be used to enhance the control of quarantine region, as well as to restrain the number of packet transmissions caused by anti-nodes.
Although the initial secure goals of the research have been achieved in this paper, further experimental and theoretical extensions are possible. In our future work, we plan to involve more mechanisms to make the protocol faultless and practical, such as developing a new algorithm to identity anti-network sensors and proposing efficient security mechanisms to make protocol suitable for adaptive topology management.