Reliability Testing Procedure for MEMS IMUs Applied to Vibrating Environments
Abstract
:1. Introduction
2. Analysis of Signal Components
3. Reliability Test Description
- 1—first static calibration and Allan variance (AV) calculation
- 2—dynamic excitation
- 3—second static calibration and AV calculation
3.1. Static Calibration
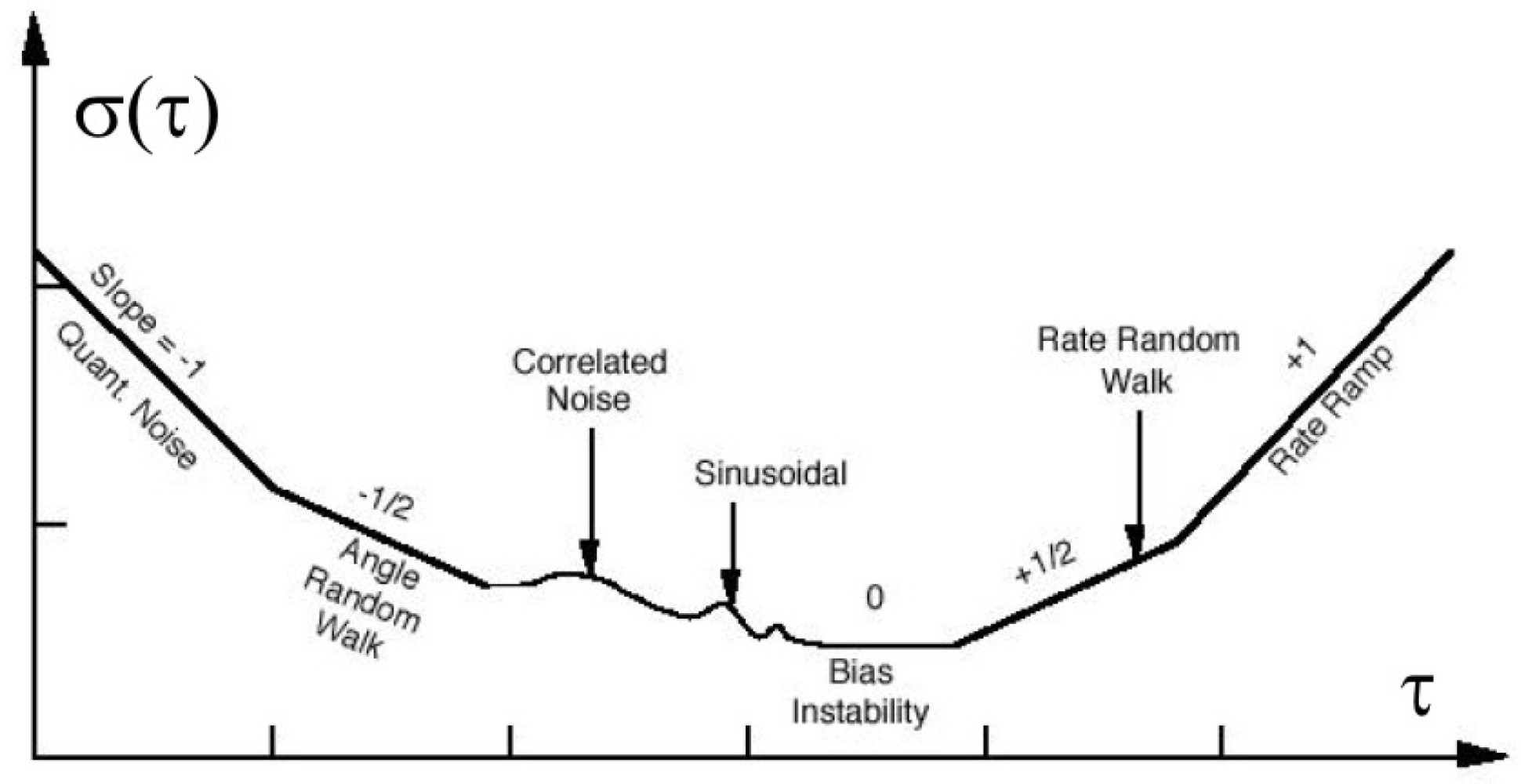
3.2. Allan Variance
3.3. Dynamic Excitation
4. Procedure Validation
4.1. Description of the IMU
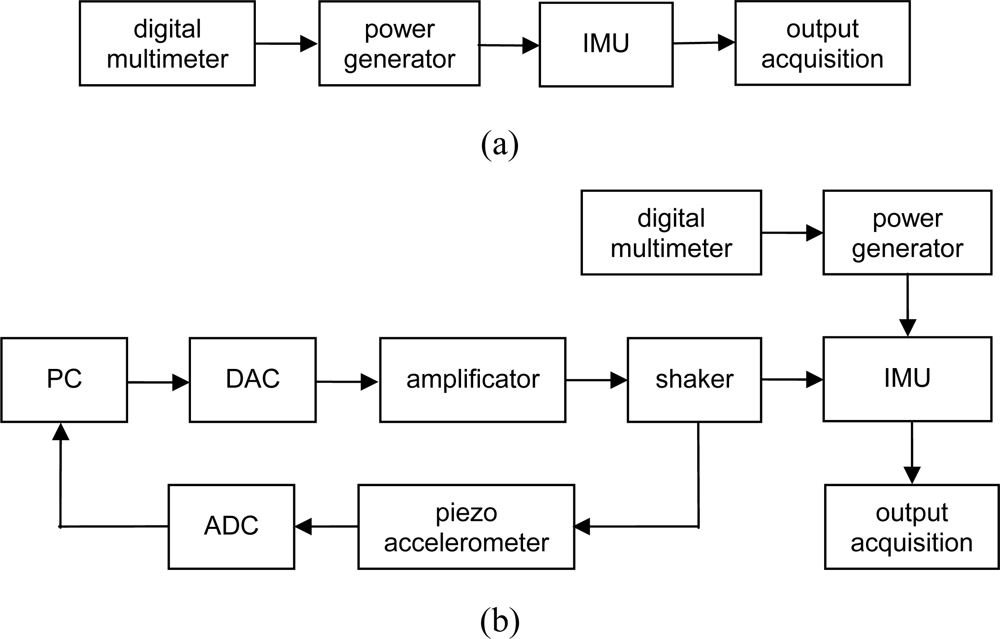
4.2. Experimental Setting
5. Reliability Test Results
5.1. Static Calibration
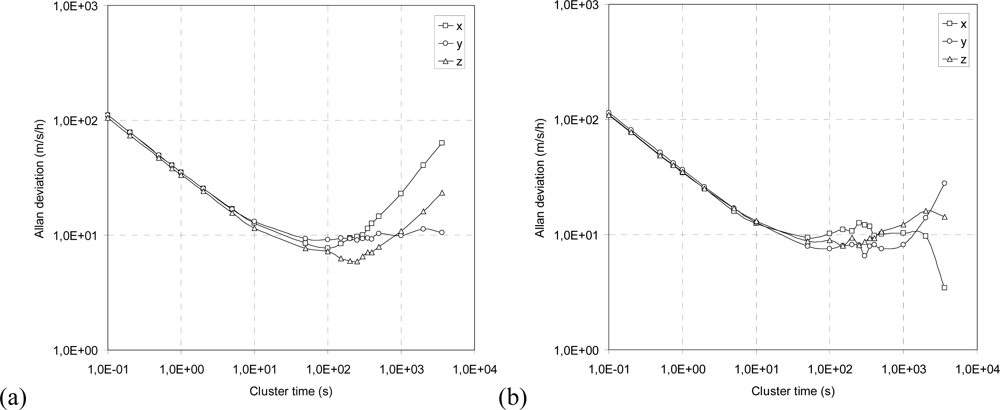
5.2. Allan Variance
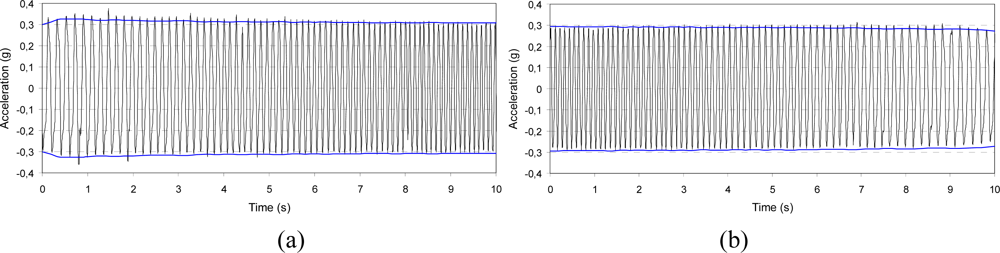
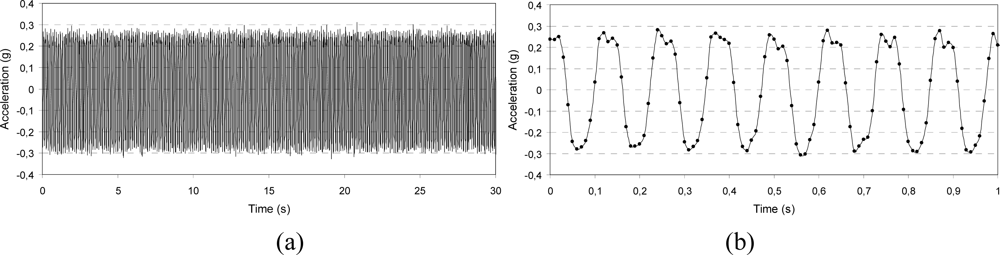
5.3. Signal Acquisition
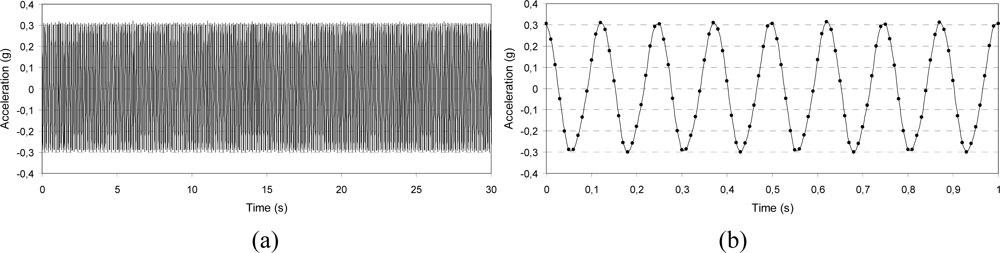
- □ Output stability over time: Two values of vibration level were selected (0.3 and 0.6 g), each at the frequency values of 6 and 8 Hz; the output signal was stored for 30 s and its amplitude stability and wave form were checked.
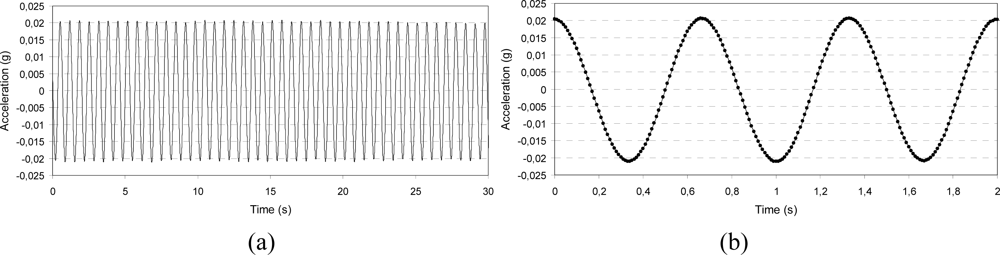
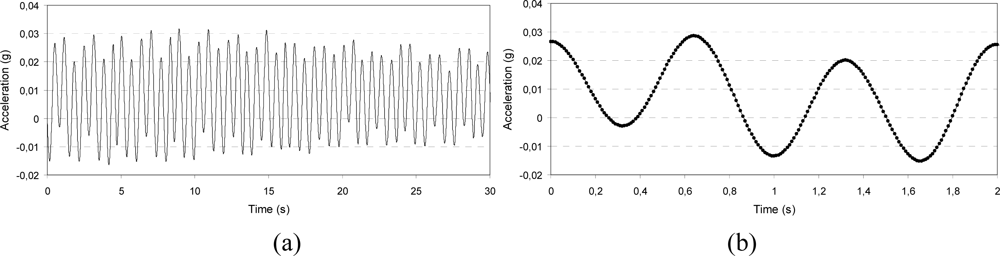
- □ Low frequency characterization: The vibration level was set to the value of 0.02 g at frequencies of 1.5 and 2 Hz; the signal was stored for 30 s and its amplitude stability and wave form were checked.
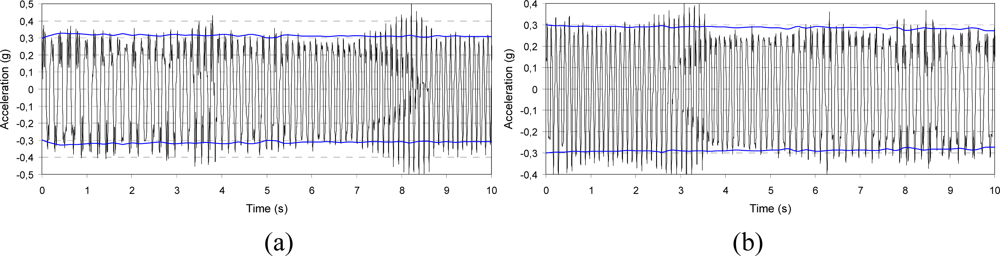
- □ Sine sweep: Two values of vibration level were selected (0.3 and 0.6 g) and the frequency was first linearly increased from 5 to 10 Hz and then decreased from 10 to 5 Hz at the sweep rate of 0.5 Hz/s (the test was 10-s long).
6. Discussion
7. Conclusions
List of symbols
| a | acceleration |
| ba | acceleration bias |
| bω | angular velocity bias |
| K | rate random walk coefficient |
| la | measured acceleration |
| lω | measured angular velocity |
| N | number of samples |
| R | drift rate ramp coefficient |
| S | power spectral density |
| Sa | acceleration scale factor (gain) |
| Sω | angular velocity scale factor (gain) |
| T | non-orthogonality factor |
| dγ | acceleration of gravity variation |
| εa | acceleration noise |
| εω | angular velocity noise |
| γ | acceleration of gravity |
| σ | Allan deviation |
| τ | cluster time |
| τ0 | sampling period |
| Ω | output signal |
| ω | angular velocity |
| ωe | earth angular velocity |
Acknowledgments
References
- van Heeren, H.; Bouchaud, J.; Dixon, R.; Salomon, P. Rewards and risks of moving into new applications: case study accelerometers. Mst. News 2007, 1, 35–39. [Google Scholar]
- Lüdtke, O.; Biefeld, V.; Buhrdorf, A.; Binder, J. Laterally driven accelerometer fabricated in single crystalline silicon. Sens. Actuat. A-Phys 2000, 82, 149–154. [Google Scholar]
- Liu, C.H.; Kenny, T.W. A high-precision, wide-bandwidth micromachined tunneling accelerometer. J. Microelectromech.l Syst 2001, 10, 425–433. [Google Scholar]
- Plaza, J.A.; Collado, A.; Cabruja, E.; Esteve, J. Piezoresistive accelerometers for MCM package. J. Microelectromech. Syst 2002, 11, 794–801. [Google Scholar]
- Chen, T.L.; Park, S. MEMS SoC: observer-based coplanar gyro-free inertial measurement unit. J. Micromechanic. Microengineer 2005, 15, 1664–1673. [Google Scholar]
- Eklund, E.J.; Shkel, A.M. Single-mask fabrication of high-G piezoresistive accelerometers with extended temperature range. J. Micromechanic. Microengineer 2007, 17, 730–736. [Google Scholar]
- Fan, K.; Che, L.; Xiong, B.; Wang, Y. A silicon micromachined high-shock accelerometer with a bonded hinge structure. J.Micromechanic. Microengineer 2007, 17, 1206–1210. [Google Scholar]
- Albarbar, A.; Mekid, S.; Starr, A.; Pietruszkiewicz, R. Suitability of MEMS accelerometers for conditioning monitoring: an experimental study. Sensors 2008, 8, 784–799. [Google Scholar]
- Lee, S.W.; Rhim, J.W.; Park, S.W.; Yang, S.S. A micro rate gyroscope based on the SAW gyroscopic effect. J. Micromechanic. Microengineer 2007, 17, 2272–2279. [Google Scholar]
- Liu, G.; Wang, A.; Jiang, T.; Jiao, J.; Jang, J.B. Effects of environmental temperature on the performance of a micromachined gyroscope. Microsyst. Technol 2008, 14, 199–204. [Google Scholar]
- Kealy, A.; Scott-Young, S.; Leahy, F.; Cross, P. Improving the performance of satellite navigation systems for land mobile applications through the integration of MEMS inertial sensors. Proceedings of the 14th Institute of Navigation International Technical Meeting (ION GPS), Salt Lake City, UT, USA, 2001.
- Brown, A.K. Test results of a GPS/inertial navigation system using a low cost MEMS IMU. Proceedings of the 11th International Conference on Integrated Navigation System, Saint Petersburg, Russia, 2004.
- Kingstone, D.B.; Beard, R.W. Real-time attitude and position estimation for small UAVs using low-cost sensors. Proceedings of the 3rd American Institute of Aeronautics and Astronautics (AIAA) Technical Conference, Chicago, IL, USA, 2004; pp. 20–23.
- Skog, I.; Händel, P. Calibration of a MEMS inertial measurement unit. Proceedings of the XVII Imeko World Congress, Rio de Janeiro, Brazil, 2006.
- Wendel, J.; Meister, O.; Schlaile, C.; Trommer, G.F. An integrated GPS/MEMS-IMU navigation system for an autonomous helicopter. Aerosp. Sci. Technology 2006, 10, 527–533. [Google Scholar]
- Syed, Z.F.; Aggarwal, P.; Goodall, C.; Niu, W.; El-Sheimi, N. A new multi-position calibration method for MEMS inertial navigation systems. Meas. Sci. Technol 2007, 18, 1897–1907. [Google Scholar]
- Leclerc, J. MEMs for aerospace navigation. IEEE A&E Syst. Mag 2007, 22, 31–36. [Google Scholar]
- Jang, J.S.; Liccardo, D. Small UAV automation using MEMS. IEEE A&E Syst. Mag 2007, 22, 30–34. [Google Scholar]
- Mohr, B.B.; Fitzpatrick, D.L. Micro air vehicle navigation systems. IEEE A&E Syst. Mag 2008, 23, 19–24. [Google Scholar]
- Jeerage, M.K. Reliability analysis of fault-tolerant IMU architectures with redundant inertial sensors. Proceedings of the IEEE Position Location and Navigation Symposium, Las Vegas, NV, USA, 1990; pp. 587–592.
- Reibman, A.; Veeraraghavan, M. Reliability modeling: an overview for system designers. IEEE Comput 1991, 24, 49–57. [Google Scholar]
- Yi, Y. On improving the accuracy and reliability of GPS/INS-based direct sensor georeferencing, Ph.D. Dissertation,; The Ohio State University: Columbus, OH, USA, 2007.
- Domíngues-García, A.D.; Kassakian, J.G.; Schindall, J.E.; Zinchuk, J.J. An integrated methodology for the dynamic performances and reliability evaluation of fault-tolerant systems. Rel. Engineer. Syst. Safety 2008, 93, 1628–1649. [Google Scholar]
- Szűcs, Z.; Rencz, M. A novel method for fatigue testing of MEMS devices containing movable elements. Proceedings of the Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS (DTIP), Stresa, Italy, 2007.
- De Pasquale, G.; Somà, A. Reliability in MEMS: Design of Gold Devices for Mechanical Fatigue Tests. Rom. J. Inf. Sci. Technol 2008, 11, 177–191. [Google Scholar]
- Somà, A.; De Pasquale, G. MEMS Mechanical Fatigue: Experimental Results on Gold Microbeams. J. Microelectromechanical Syst 2009, 18, 828–835. [Google Scholar]
- Evans, J.; Hodge, W.; Liebman, J.; Tomlin, C.J.; Parkinson, B. Flight tests of an unmanned air vehicle with integrated multi-antenna GPS receiver and IMU: towards a testbed for distributed control and formation flight. Proceedings of the ION-GPS Conference, Nashville, TN, USA, 1999.
- Godha, S.; Petovello, M.G.; Lachapelle, G. Performance analysis of MEMS IMU/HSGPS/ magnetic sensor integrated system in urban canyons. Proceedings of ION-GNSS Conference, Long Beach, CA, USA, 2005.
- Gu, D.; El-Sheimi, N. Heading accuracy improvement of MEMS IMU/DGPS integrated navigation system for land vehicle. Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 2008; pp. 1292–1296.
- Brown, A.K. GPS/INS uses Low-Cost MEMS IMU. IEEE Aerosp. Electron. Syst. Mag 2005, 20, 3–10. [Google Scholar]
- De Agostino, M. A multi-frequency filtering procedure for inertial navigation. Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 2008; pp. 1115–1121.
- Ferraris, F.; Grimaldi, U.; Parvis, M. Procedure for effortless in-field calibration of three-axis rate gyros and accelerometers. Sensor. Mater 1995, 7, 311–330. [Google Scholar]
- Titterton, D.H.; Weston, J.L. Strapdown Inertial Navigation Technology, 2nd ed; American Institute of Aeronautics and Astronautics: New York, NY, USA, 2004. [Google Scholar]
- Zhang, X.; Li, J.; Mumford, P.; Rizos, C. Allan variance analysis on error characters of MEMS inertial sensors for an FPGA-based GPS/INS system. Proceedings of the International Symposium on GPS / GNNS, Tokyo, Japan, 2008.
- El-Diasty, M.; El-Rabbany, A.; Pagiatakis, S. Temperature variation effects on stochastic characteristics for low-cost MEMS-based inertial sensor error. Meas. Sci. Technol 2007, 18, 3321–3328. [Google Scholar]
- IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Interferometric Fiber Optics Gyros; IEEE Aerospace and Electronic Systems Society, 1998.
- IEEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology. IEEE Std. 1139–1988. Proceedings of the 1997 IEEE International, Orlando, FL, USA, 1997.
- Fong, W.T.; Ong, S.K.; Nee, A.Y. Methods for in-field user calibration of an inertial measurement unit without external equipment. Meas. Sci. Technol 2008, 19, 085202. [Google Scholar]
- Tracewell Systems, Inc. Available online: www.tracewellsystems.com (accessed on June 2009).
- Military Standard, Environmental Test Methods and Engineering Guidelines. MIL-STD-810-E (1989); Aeronautical Systems Div. Wrigth-Patterson AFB OH Fuel and Hazards Branch.
- Axis Automation for Industrial Systems. Available online: www.axisautomazione.it (accessed on June 2009).
- Ghaffarian, R. Qualification and Reliability for MEMS and IC Packages; Jet Propulsion Laboratory, National Aeronautics and Space Administration: Pasadena, CA, USA, 2004. [Google Scholar]


| Tactical grade | Navigation grade | Strategic grade | |
|---|---|---|---|
| Error | >20 km/h | <1 km/h | <30 m/h |
| Gyro drift rate | 1–10 deg/h | 0.015 deg/h | 0.0001 deg/h |
| Accelerometers bias | 100–1000 μg | 50–100 μg | 1 μg |
| Costs of IMU | <10.000 $ | 10.000–70.000 $ | >200.000 $ |
| Functional section | Endurance section | |||
|---|---|---|---|---|
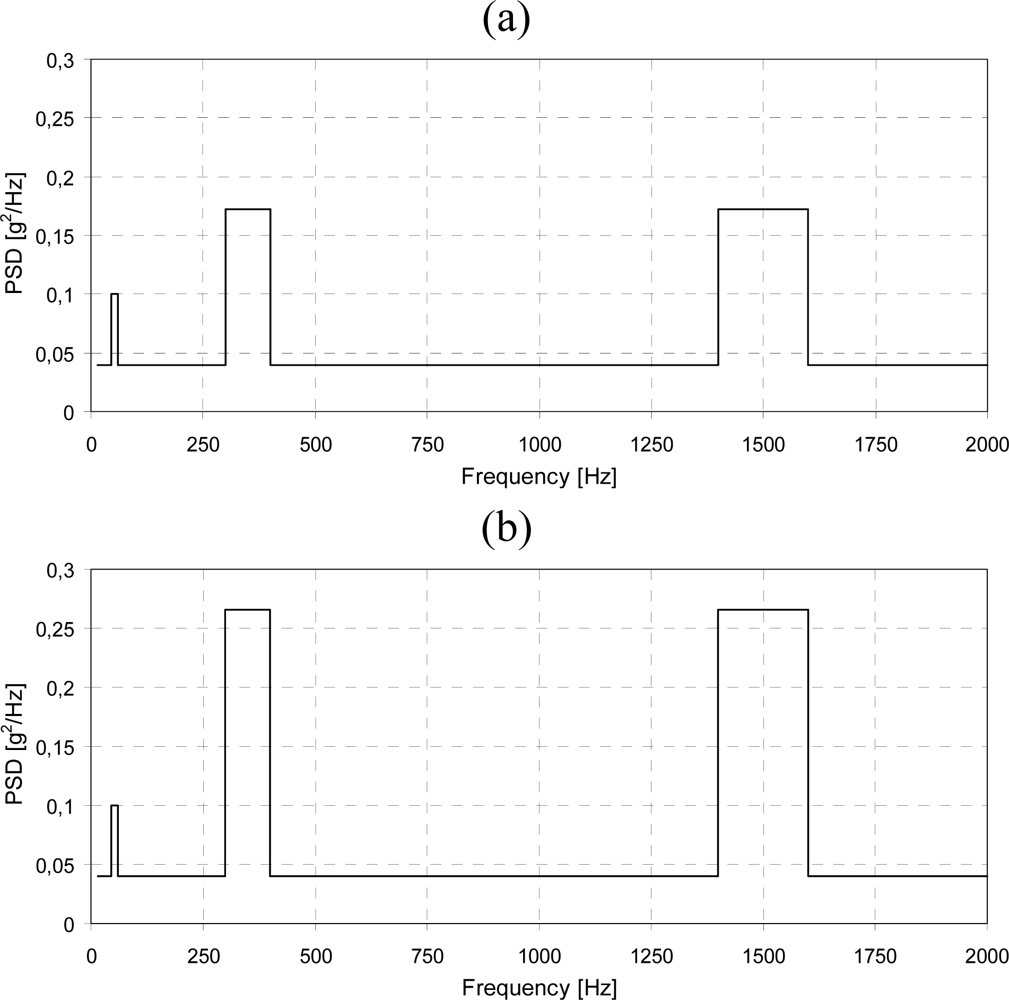
| Level [PSD] | Sweep rate [Hz/s] | Level [PSD] | Sweep rate [Hz/s] | |
| Broadband vibration | 0.040 | 3.684 | 0.040 | 0.100 |
| 45–60 Hz band | 0.100 | 0.067 | 0.100 | 0.067 |
| 300–400 Hz band | 0.172 | 0.445 | 0.266 | 0.445 |
| 1,400–1,600 Hz band | 0.172 | 0.890 | 0.266 | 0.890 |
| Functional section | Endurance section | Functional section | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Axis | x | y | z | x | y | z | x | y | z |
| Time | 30 min | 30 min | 30 min | 5 h | 5 h | 5 h | 30 min | 30 min | 30 min |
| Dimensions | 70 × 60 × 40 mm |
| Fixing flange dimensions | 78 × 66 mm |
| Weight | 230 g |
| Supply voltage | 9–30 V |
| Current | 175 mA at 9 V |
| Measurement field | Static precision | Dynamic precision | Resolution | Noise | Bandwidth | |
|---|---|---|---|---|---|---|
| Angular velocity | ±150°/s | ±0.5°/s | - | 0.07°/s | 0.07°/s | 5 Hz |
| Acceleration | ±2/±15 g | (±20/±100)·10−3 g | - | (1/9)·10−3 g | (1/12)·10−3 g | 5 Hz |
| Roll | ±180° | ±1.5° | ±4° | 0.025° | 0.15° | 5 Hz |
| Pitch | ±90° | ±1° | ±4° | 0.012° | 0.10° | 5Hz |
| Yaw/Heading | 0–360° | ±3° | ±4° | 0.025° | 0.5° | - |
| Velocity | ±1,200 km/h | ±0.2 m/s | - | 0.05 m/s | 0.2 m/s | - |
| Altitude | −0.6–8 km | 5 m | - | 1 m | 1 m | - |
| Positioning | - | 3 m | - | 0.01 m | 1 m | - |
| Before | After | |
|---|---|---|
| bx | −4.9 mg | −6.8 mg |
| by | −4.4 mg | −8.3 mg |
| bz | −4.7 mg | −2.6 mg |
| Sx | −0.02 % | −0.14 % |
| Sy | −0.07 % | 0.01 % |
| Sz | −0.05% | −0.14% |
©2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/)
Share and Cite
De Pasquale, G.; Somà, A. Reliability Testing Procedure for MEMS IMUs Applied to Vibrating Environments. Sensors 2010, 10, 456-474. https://doi.org/10.3390/s100100456
De Pasquale G, Somà A. Reliability Testing Procedure for MEMS IMUs Applied to Vibrating Environments. Sensors. 2010; 10(1):456-474. https://doi.org/10.3390/s100100456
Chicago/Turabian StyleDe Pasquale, Giorgio, and Aurelio Somà. 2010. "Reliability Testing Procedure for MEMS IMUs Applied to Vibrating Environments" Sensors 10, no. 1: 456-474. https://doi.org/10.3390/s100100456






