Tracking Control of Shape-Memory-Alloy Actuators Based on Self-Sensing Feedback and Inverse Hysteresis Compensation
Abstract
:1. Introduction
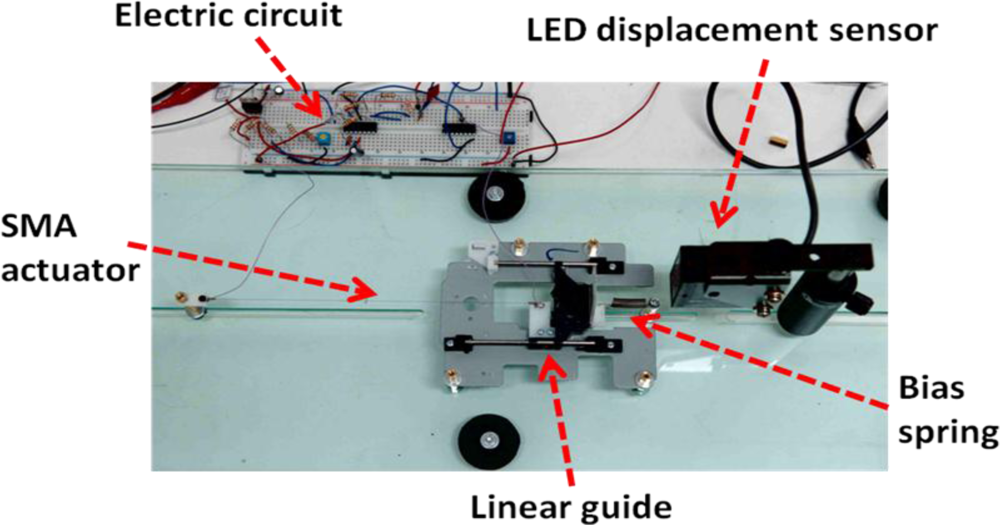
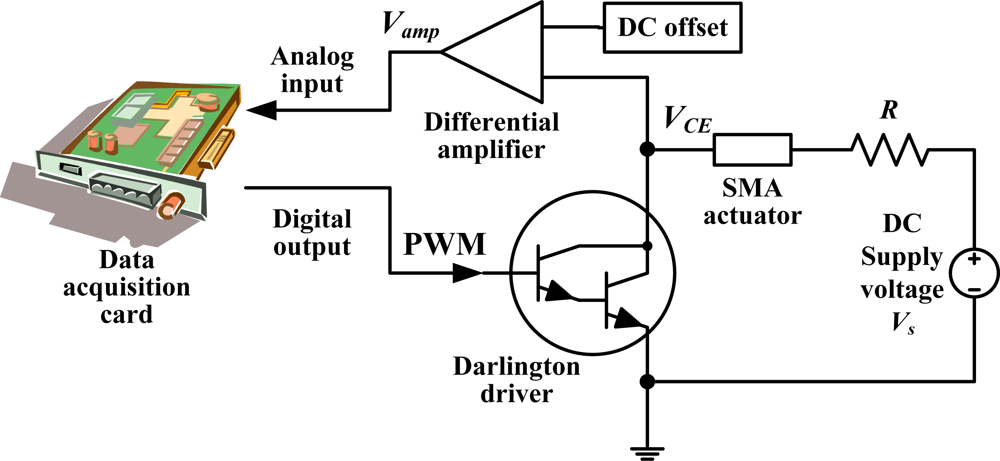
2. Experimental Setup
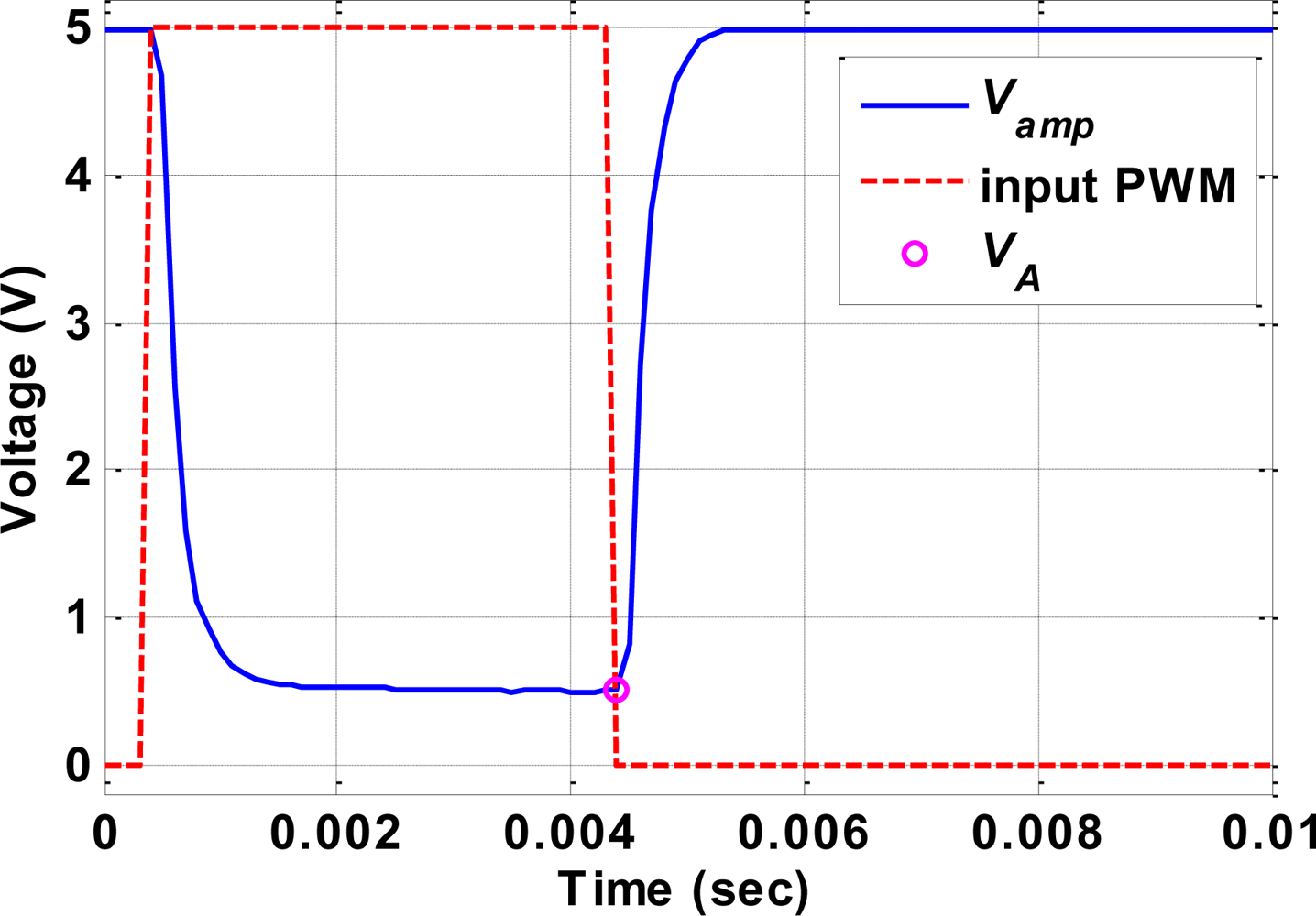
3. Self-Sensing Property of SMA Actuator
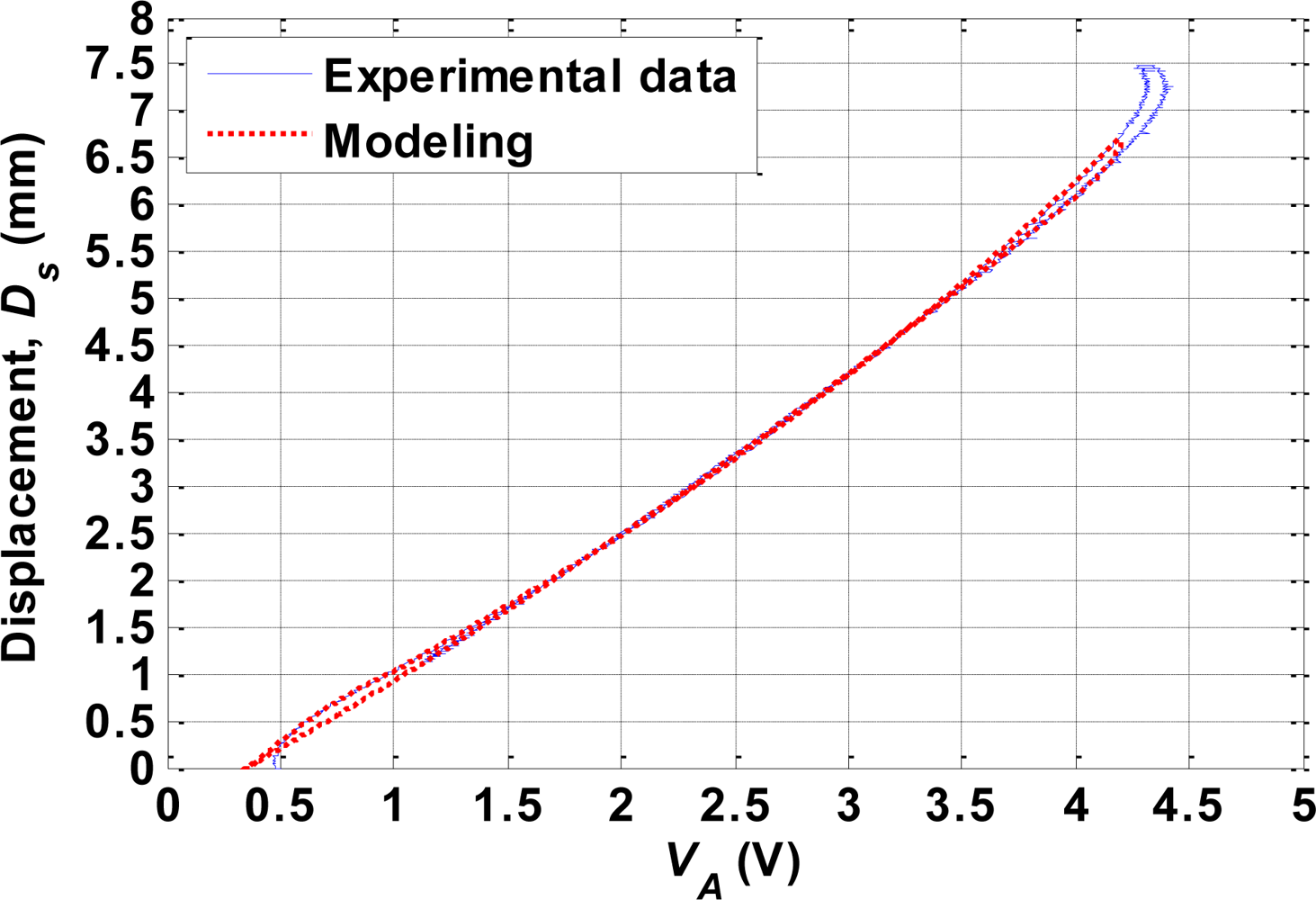
4. Modeling of SMA Actuator
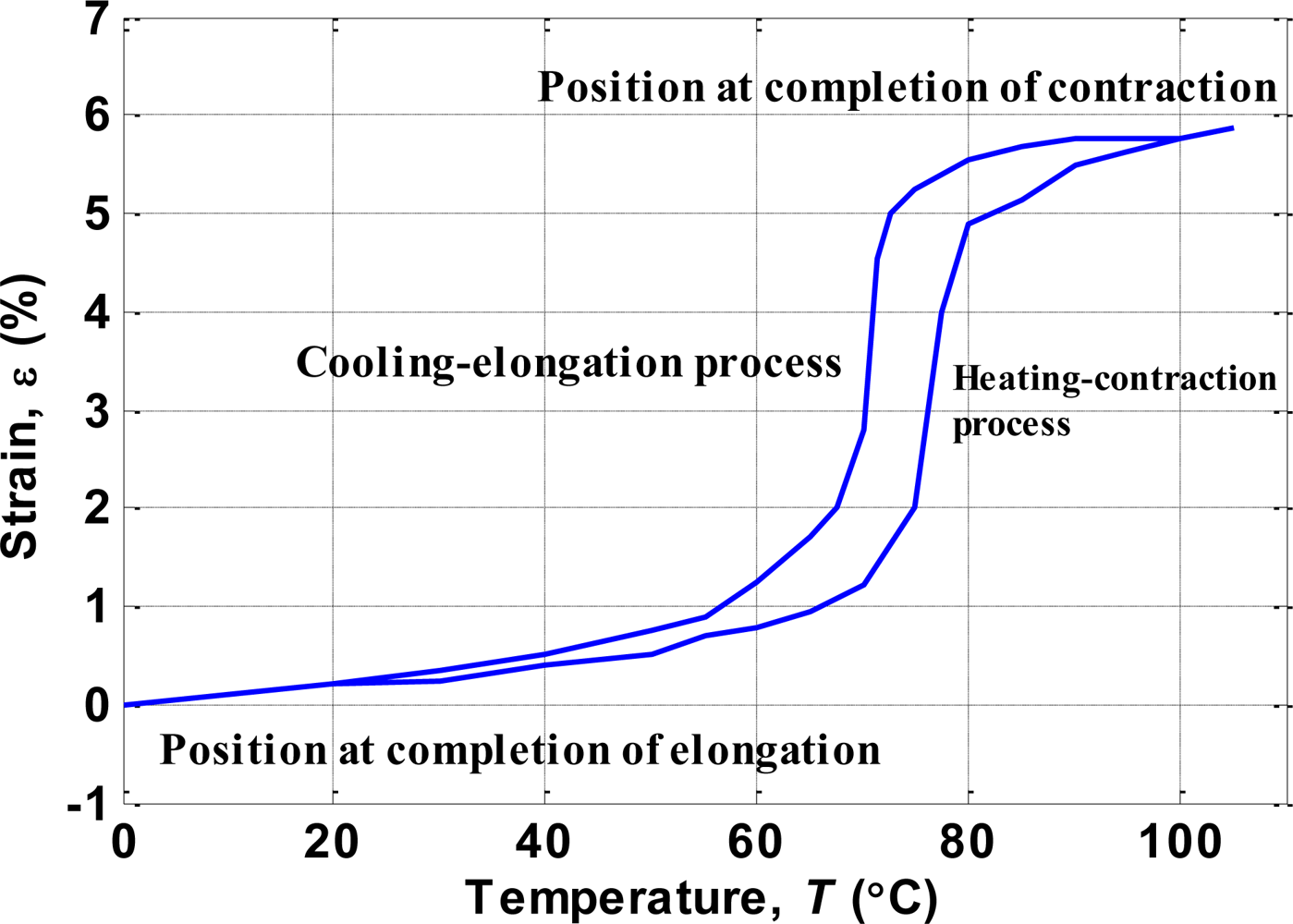
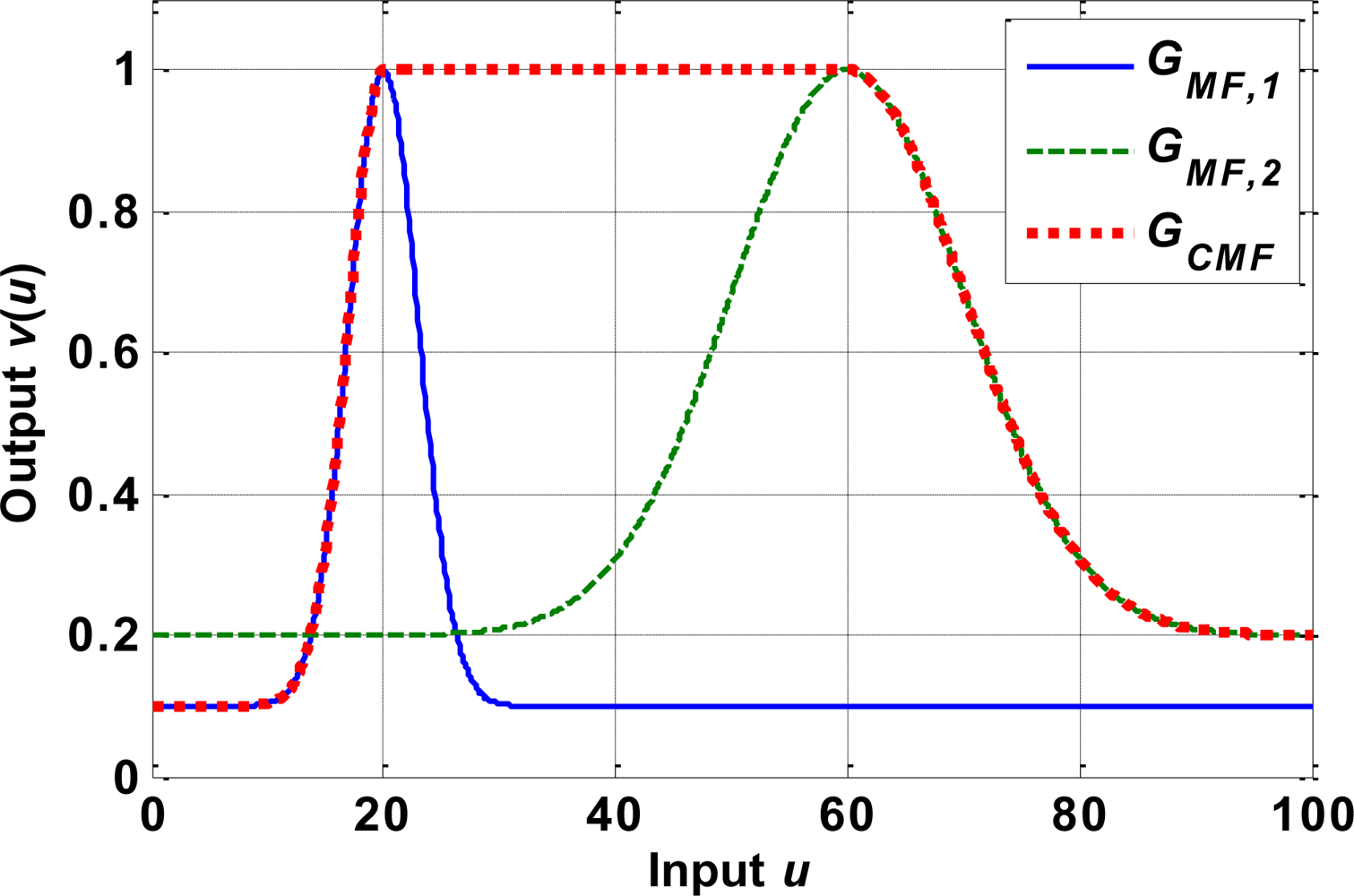
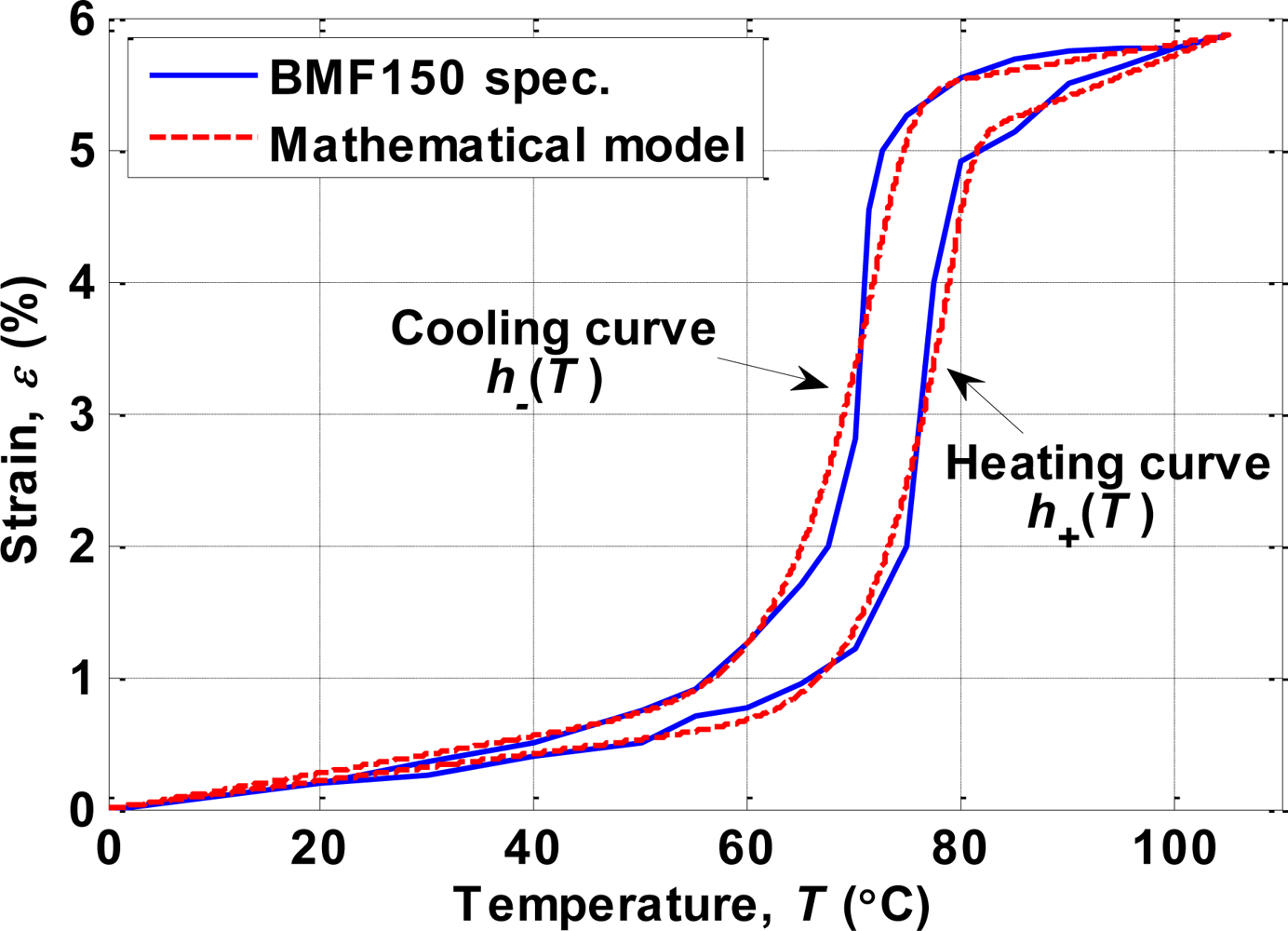
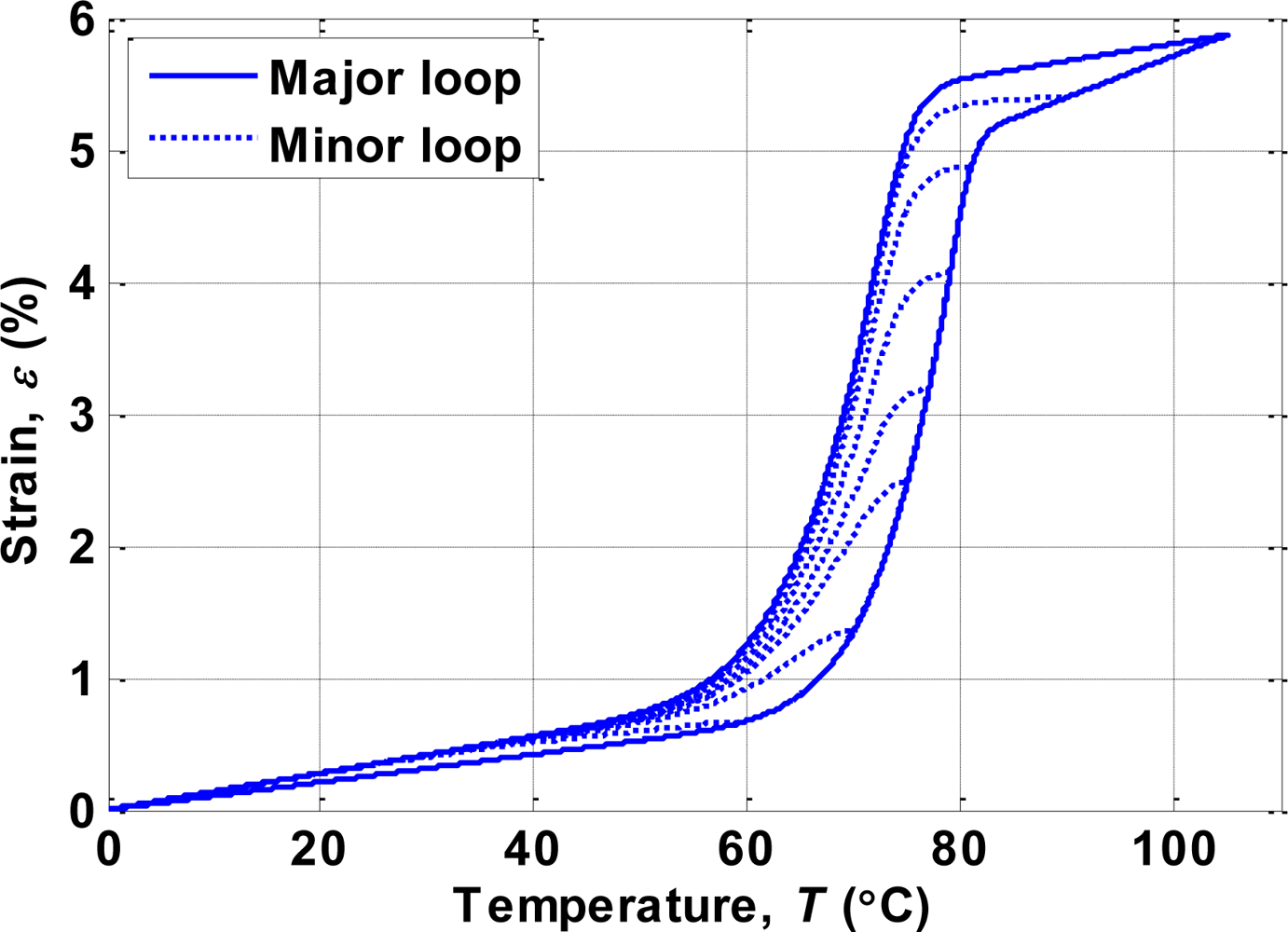
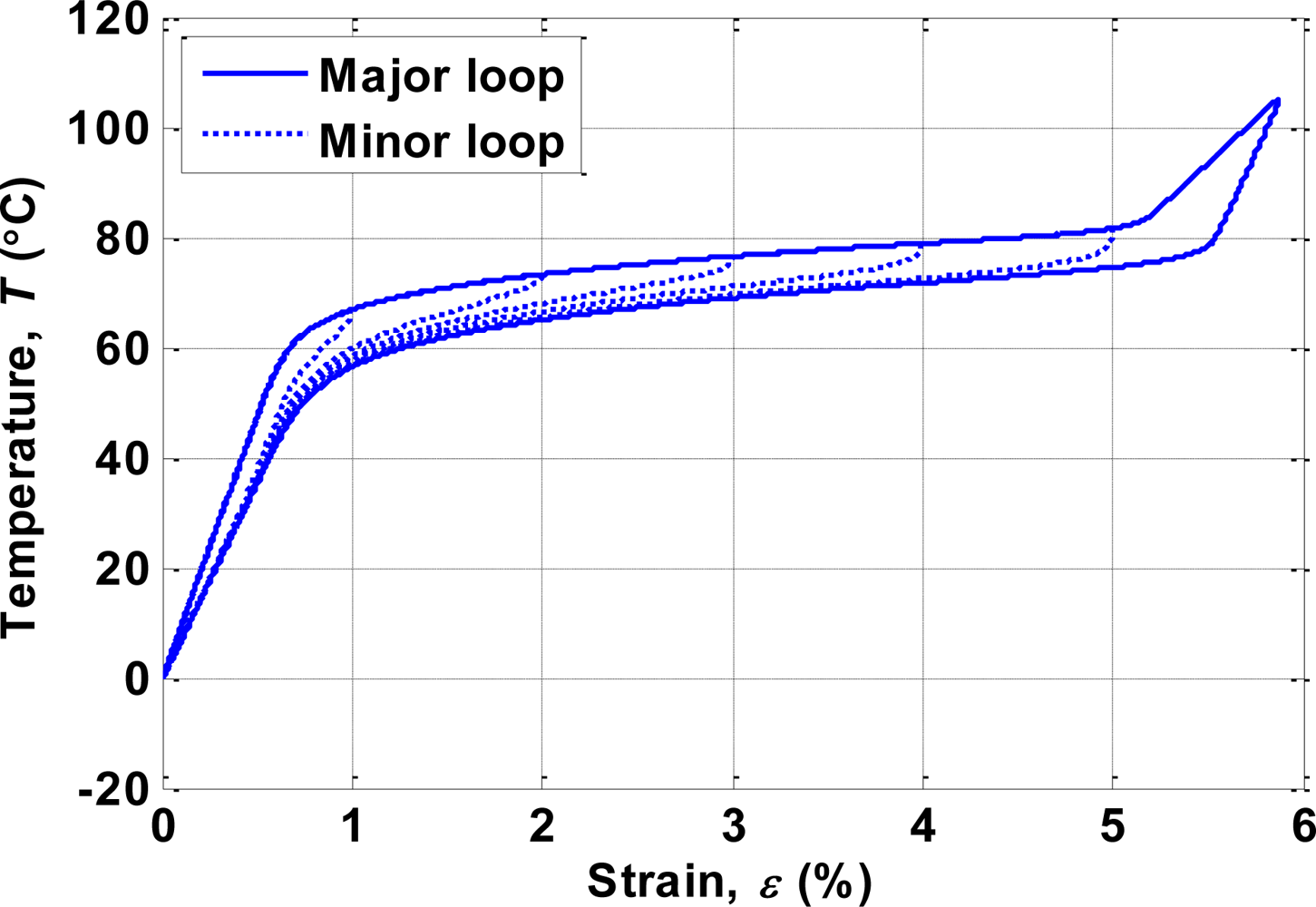
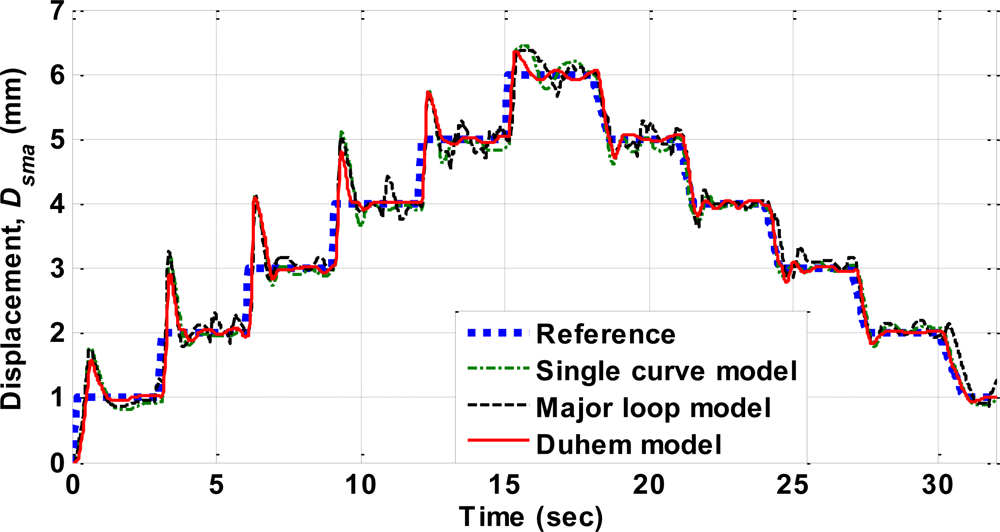
4.1. Modeling of Hysteresis
4.2. Modeling of Inverse Hysteresis
4.3. Modeling of Temperature Dynamics
4.4. Electric Power Calculation
4.5. Modeling of Self-Sensing Properties
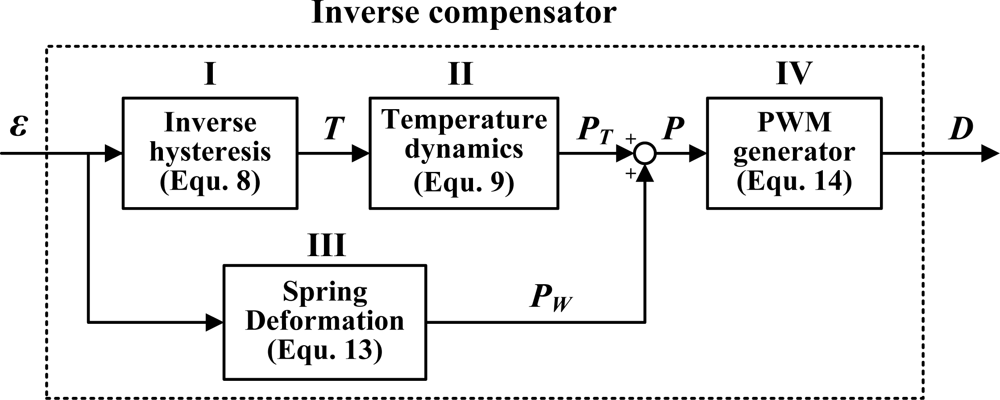
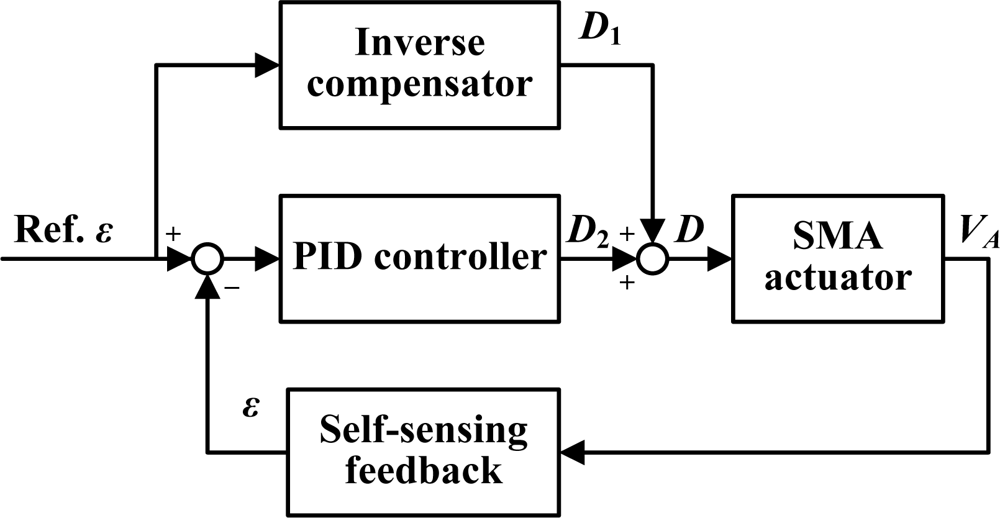
5. Tracking Control with Self-Sensing Feedback and Inverse Compensation
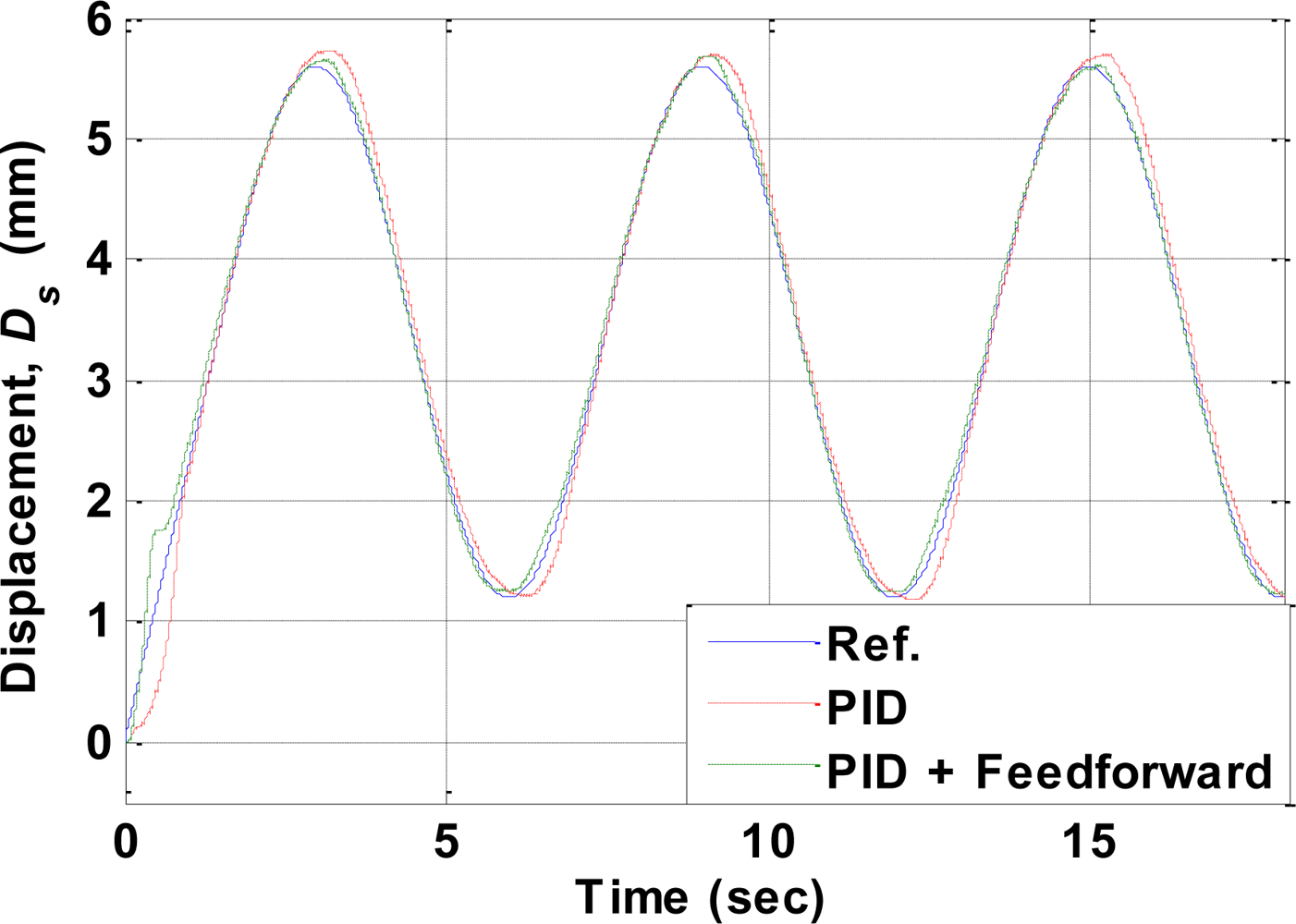
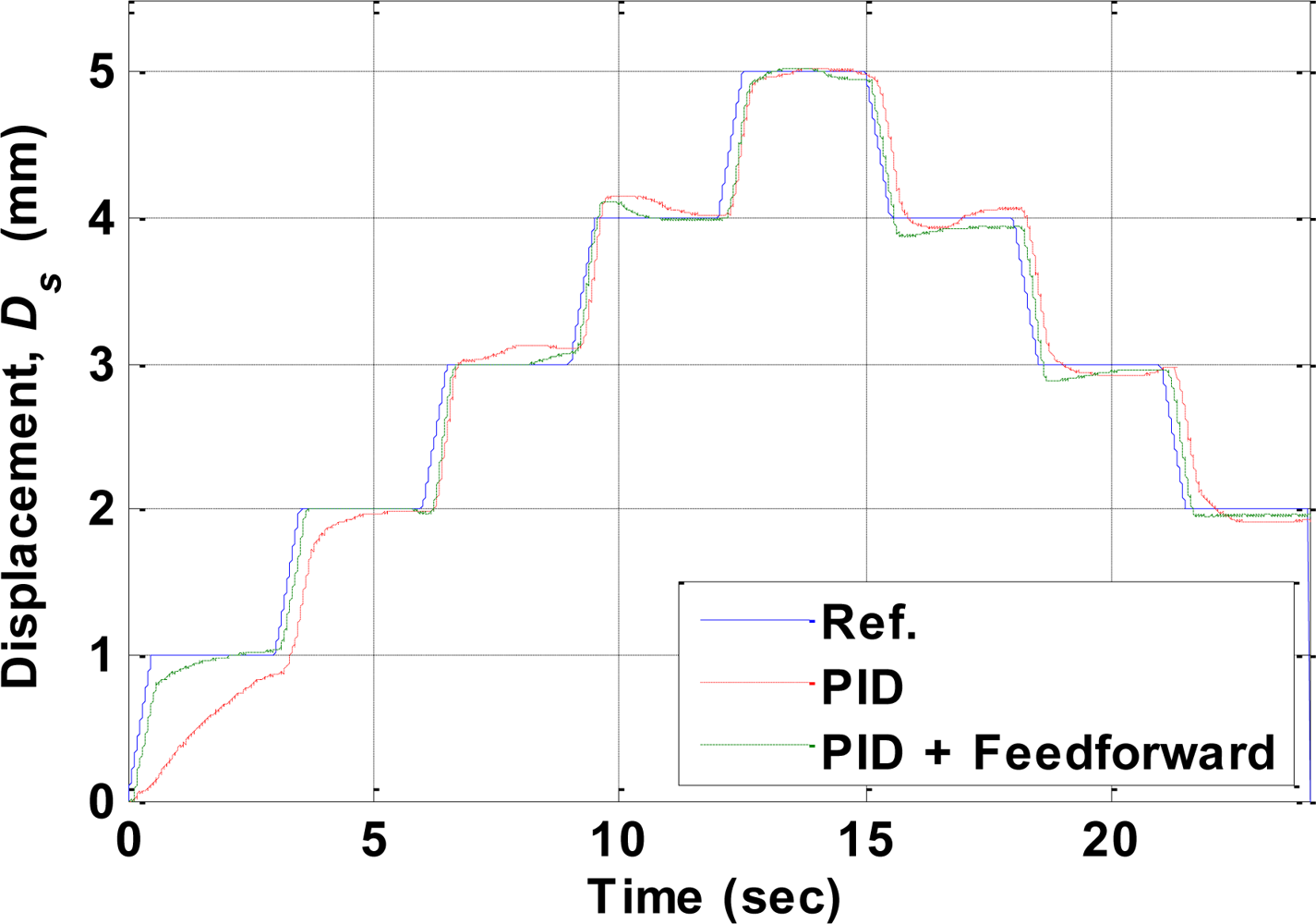
6. Experimental Results
7. Conclusions and Future Remarks
Acknowledgments
References
- Smith, R.C. Smart Material Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA; March 2005.
- Kudva, J.N.; Sanders, B.P.; Pinkerton-Florance, J.L.; Garcia, E. Overview of the DARPA/ AFRL/NASA smart wing phase II program. In Smart Structures and Materials 2001: Industrial and Commercial Applications of Smart Structures Technologies; SPIE-International Society for Optical Engine: Newport Beach, CA, USA, 2001; pp. 383–389. [Google Scholar]
- Song, G.B.; Ma, N. Robust control of a shape memory alloy wire actuated flap. Smart Mater. Struct 2007, 16, N51–N57. [Google Scholar]
- Yan, S.; Liu, X.; Xu, F.; Wang, J. A gripper actuated by a pair of differential SMA springs. J. Intel. Mat. Syst. Struct 2007, 18, 459–466. [Google Scholar]
- Zhang, H.; Bellouard, Y.; Burdet, E.; Clavel, R.; Poo, A.N.; Hutamacher, D.W. Shape memory alloy microgripper for robotic microassembly of tissue engineering scaffolds. Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, April 2004; pp. 4918–4924.
- Ashrafiuon, H.; Jala, V.R. Sliding mode control of mechanical systems actuated by shape memory alloy. J. Dyn. Syst., Meas. Contr 2009, 131, 011010–011016. [Google Scholar]
- Yang, K.; Gu, C.L. A novel robot hand with embedded shape memory alloy actuators. Proc. IME C J. Mech. Eng. Sci 2002, 216, 737–745. [Google Scholar]
- Williams, E.; Elahinia, M.H. An automotive SMA mirror actuator: modeling, design, and experimental evaluation. J. Intel. Mat. Syst. Struct 2008, 19, 1425–1434. [Google Scholar]
- Dhanalakshmi, K.; Umapathy, M. Active vibration control of SMA actuated structures using fast output sampling based sliding mode control. Instrum. Sci. Technol 2008, 36, 180–193. [Google Scholar]
- Ikuta, K.; Tsukamoto, M.; Hirose, S. Shape memory alloy servo actuator system with electric resistance feedback and application for active endoscope. Proceedings of IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, April 1988; pp. 427–430.
- Liu, S.H.; Yen, J.Y. A hexapod robot based on shape memory alloy actuators. Proceedings of the 4th IFAC-Symposium on Mechatronic Systems, Heidelberg, Germany, September 2006; pp. 689–693.
- Tu, K.Y.; Lee, T.T.; Wang, C.H.; Chang, C.A. Design of a fuzzy walking pattern (FWP) for a shape memory alloy (SMA) biped robot. Robotica 1999, 17, 373–382. [Google Scholar]
- Song, G.B.; Ma, N.; Lee, H.J. Position estimation and control of SMA actuators based on electrical resistance measurement. Smart Struct. Syst 2007, 3, 189–200. [Google Scholar]
- Jayender, J.; Patel, R.V.; Nikumb, S.; Ostojic, M. Modeling and control of shape memory alloy actuators. IEEE Trans. Control Syst. Technol 2008, 16, 279–287. [Google Scholar]
- Majima, S.; Kodama, K.; Hasegawa, T. Modeling of shape memory alloy actuator and tracking control system with the model. IEEE Trans. Control Syst. Technol 2001, 9, 54–59. [Google Scholar]
- Dutta, S.M.; Ghorbel, F.H. Differential hysteresis modeling of a shape memory alloy wire actuator. IEEE-ASME Trans. Mechatron 2005, 10, 189–197. [Google Scholar]
- Instruction Manual of Bio-Metal Fiber BMF150; Toki Corporation: Tokyo Japan, 2009.
- Visintin, A. Differential Models of Hysteresis; Springer-Verlag: New York, NY, USA, 1995. [Google Scholar]
- Dutta, S.M.; Ghorbel, F.H.; Dabney, J.B. Modeling and control of a shape memory alloy actuator. Proceedings of the 20th IEEE International Symposium on Intelligent Control, Limassol, Cyprus, June 2005; pp. 1007–1012.
- Elahinia, M.H.; Seigler, T.M.; Leo, D.J.; Ahmadian, M. Nonlinear stress-based control of a rotary SMA-actuated manipulator. J. Intel. Mat. Syst. Struct 2004, 15, 495–508. [Google Scholar]
- Holman, J.P. Heat Transfer, 8th ed; McGraw-Hill Companies: New York, NY, USA, 1997. [Google Scholar]
- Pons, J.L.; Reynaerts, D.; Peirs, J; Ceres, R.; VanBrussel, H. Comparison of different control approaches to drive SMA actuators. Proceedings of 8th International Conference on Advanced Robotics, Monterey, CA, USA, July 1997; pp. 819–824.

| 10 °C2 | 12 °C2 | ||
| μ1,+ | 88 °C | μ1,– | 84.6 °C |
| c1,+ | 0.015% | c1,– | 0.02% |
| 1.8 °C2 | 3 °C2 | ||
| μ2,+ | 78.65 °C | μ2,– | 71 °C |
| c2,+ | 0.045% | c2,– | 0.019% |
| kCMF,+ | 0.7 | kCMF,– | 0.7 |
| RMSE | Single curve model | Major loop model | Duhem model | Proposed model |
|---|---|---|---|---|
| (mm) | 0.2781 | 0.2890 | 0.2311 | 0.1223 |
©2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/)
Share and Cite
Liu, S.-H.; Huang, T.-S.; Yen, J.-Y. Tracking Control of Shape-Memory-Alloy Actuators Based on Self-Sensing Feedback and Inverse Hysteresis Compensation. Sensors 2010, 10, 112-127. https://doi.org/10.3390/s100100112
Liu S-H, Huang T-S, Yen J-Y. Tracking Control of Shape-Memory-Alloy Actuators Based on Self-Sensing Feedback and Inverse Hysteresis Compensation. Sensors. 2010; 10(1):112-127. https://doi.org/10.3390/s100100112
Chicago/Turabian StyleLiu, Shu-Hung, Tse-Shih Huang, and Jia-Yush Yen. 2010. "Tracking Control of Shape-Memory-Alloy Actuators Based on Self-Sensing Feedback and Inverse Hysteresis Compensation" Sensors 10, no. 1: 112-127. https://doi.org/10.3390/s100100112




