Base Flip in DNA Studied by Molecular Dynamics Simulationsof Differently-Oxidized Forms of Methyl-Cytosine
Abstract
:1. Introduction
2. Results
2.1. DNA Conformation

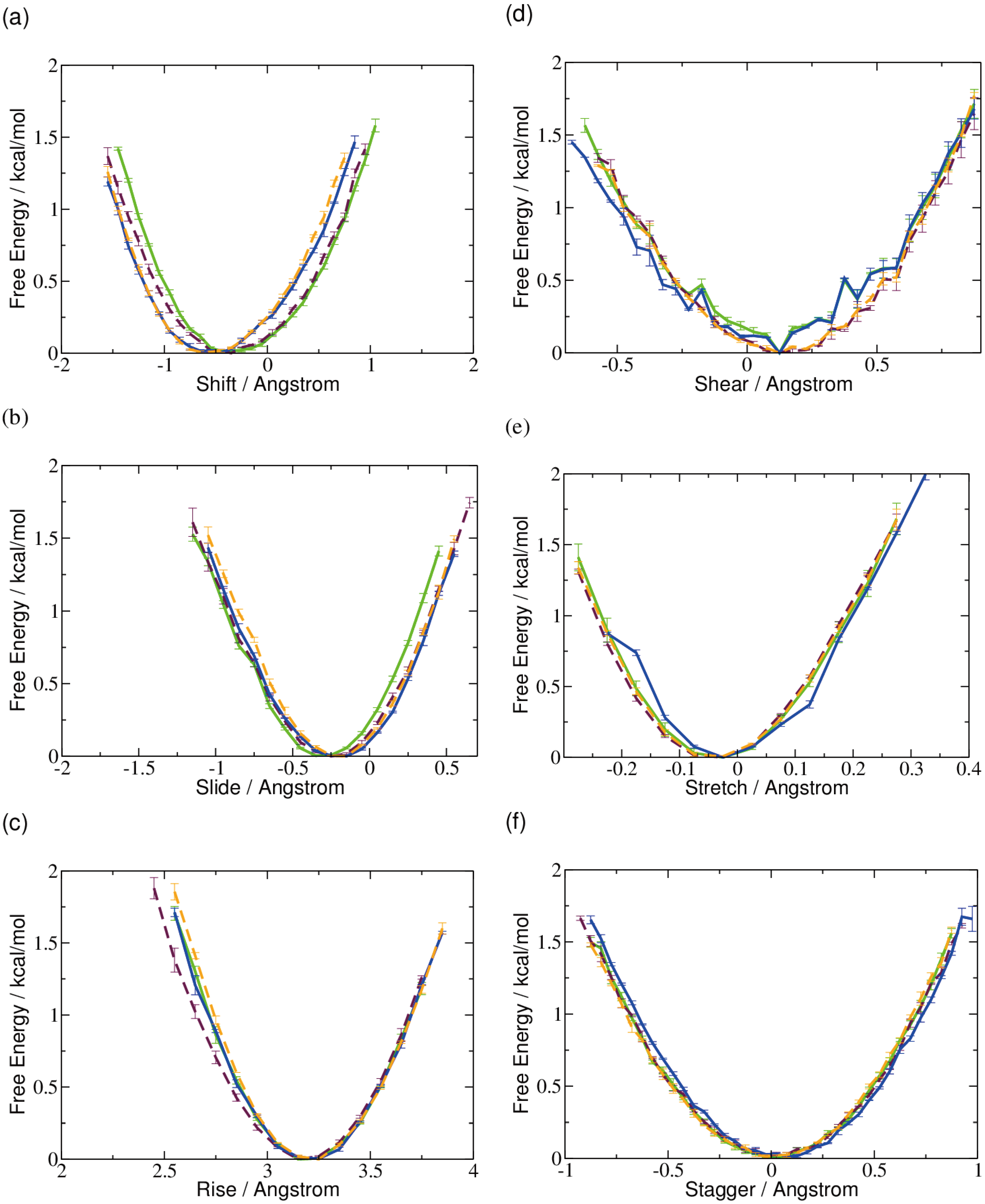
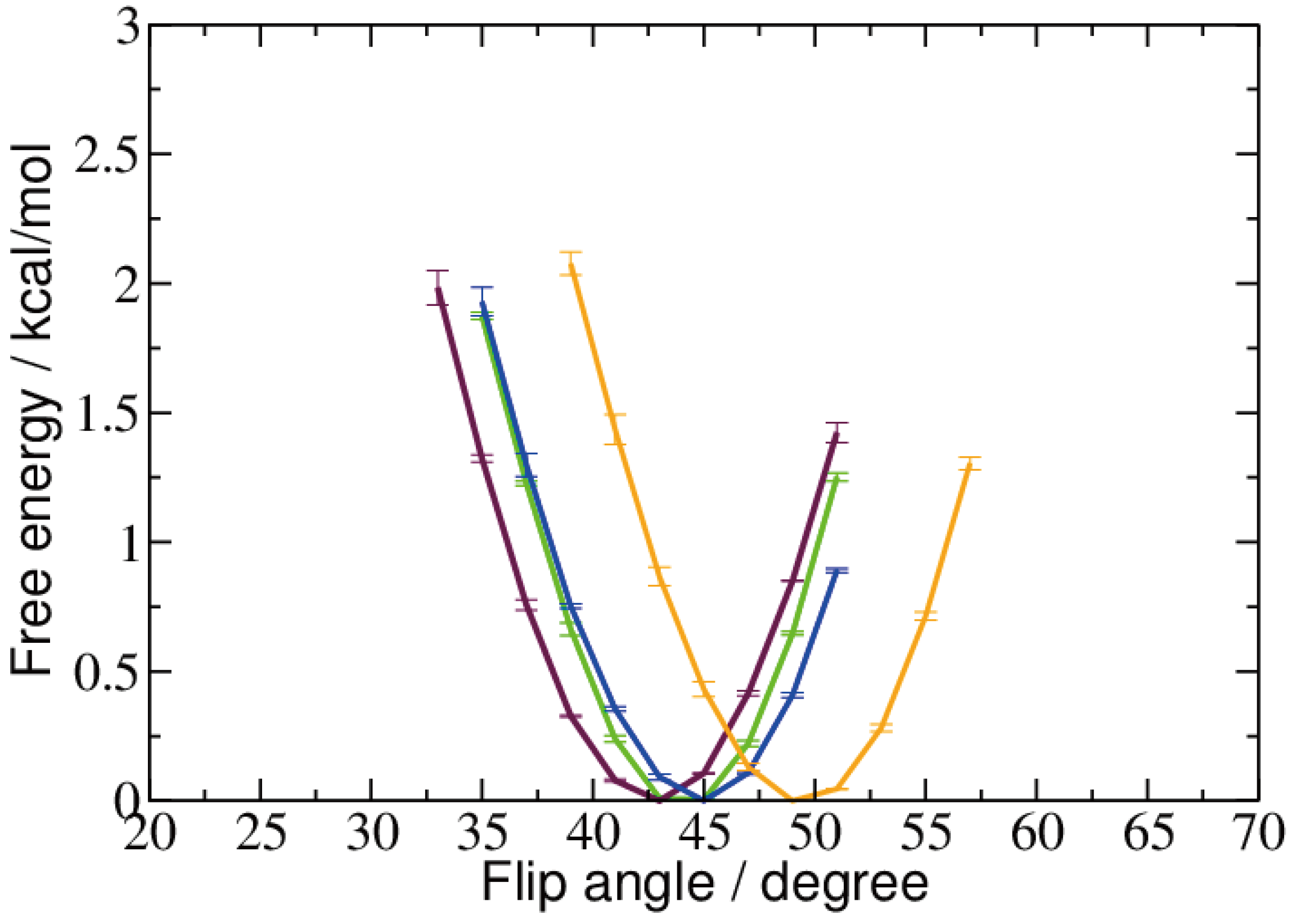
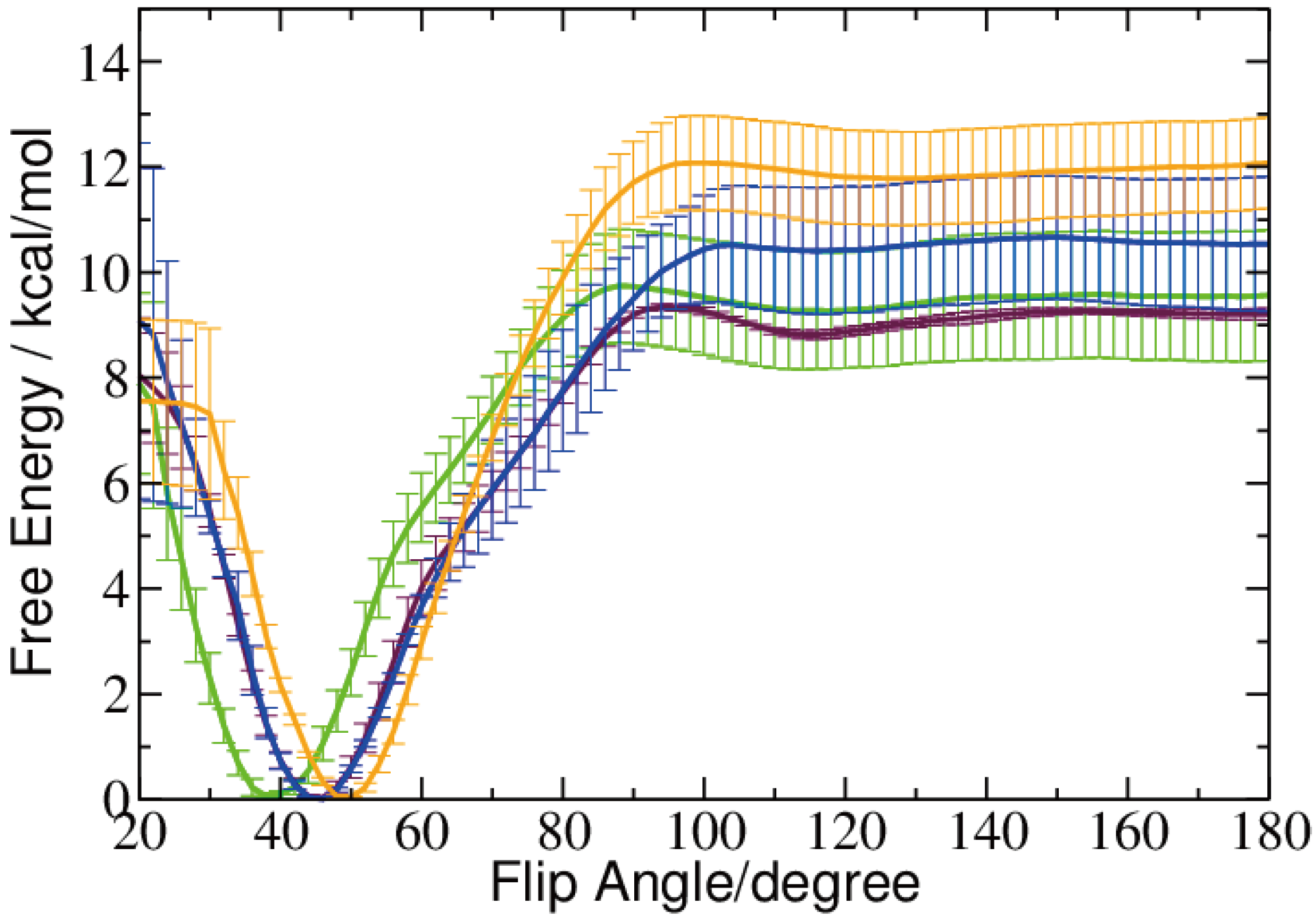
2.2. Base Flip
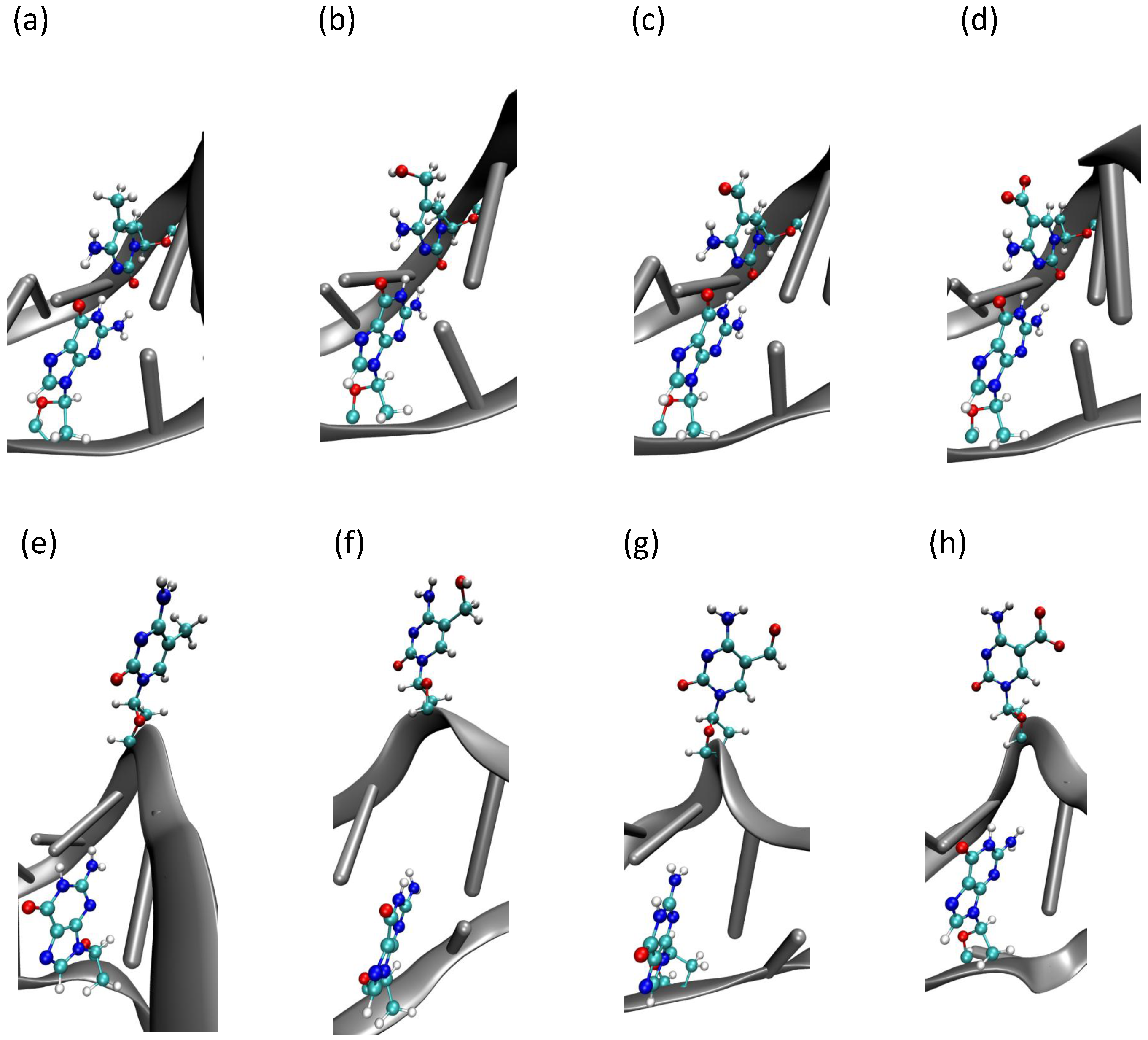
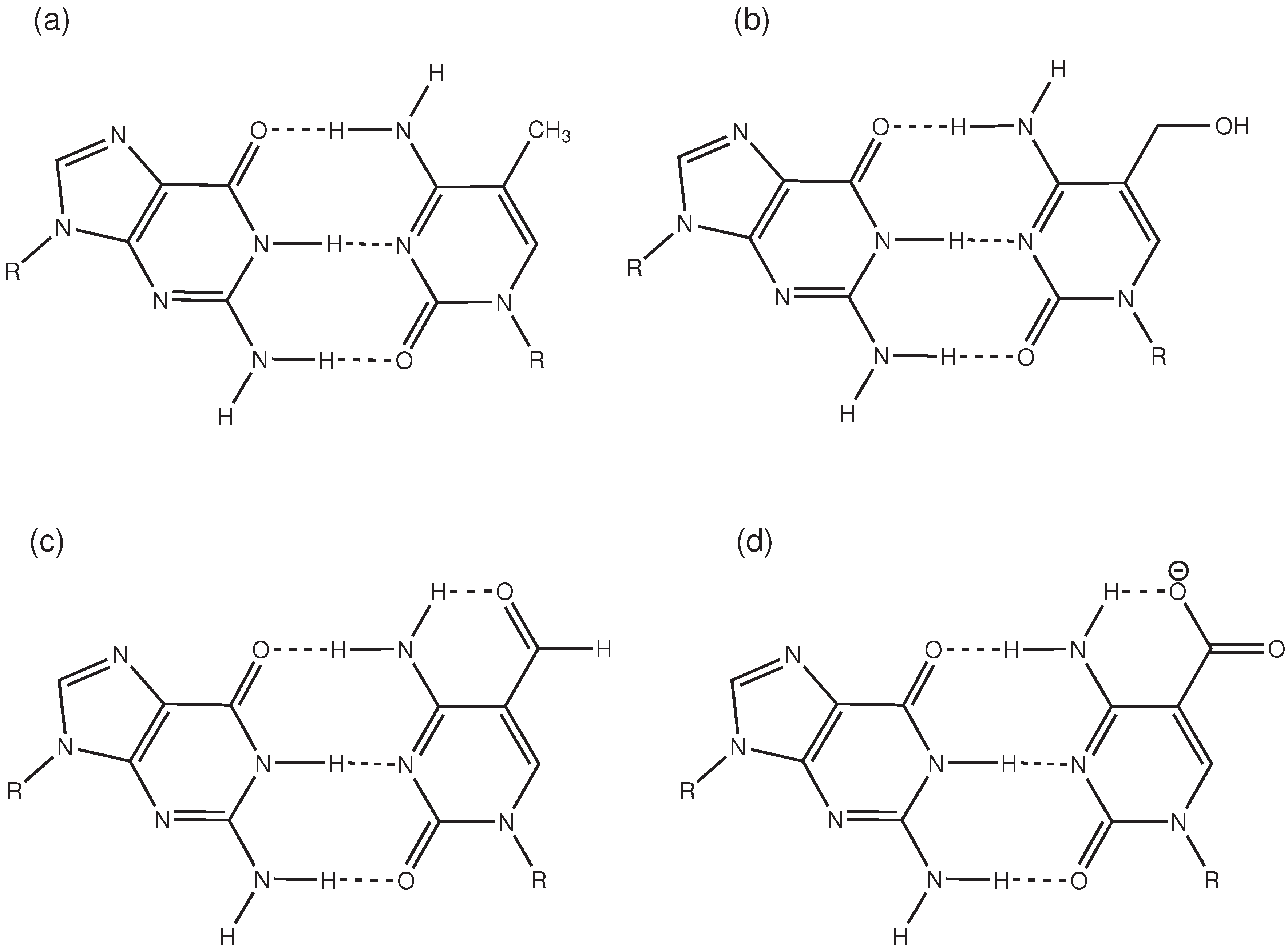
2.3. Hydrogen Bonds and Solvent Accessibility
| Donor | Acceptor | Occupancy/% | |||
|---|---|---|---|---|---|
| 5mC | 5hmC | 5fC | 5caC | ||
| GUA7-N2 | CYT7-O2 | 93.0 ± 1.1 | 92.2 ± 5.6 | 94.9 ± 1.2 | 95.8 ± 0.4 |
| CYT7-N4 | GUA7-O6 | 86.9 ± 0.7 | 88.8 ± 6.6 | 87.2 ± 0.4 | 88.1 ± 0.5 |
| GUA7-N1 | CYT7-N3 | 96.9 ± 0.9 | 94.7 ± 1.2 | 95.4 ± 1.0 | 95.8 ± 0.2 |
| Water | CYT7-O2 | 73.2 ± 2.8 | 70.7 ± 0.2 | 70.7 ± 0.2 | 73.4 ± 0.5 |
| CYT7-N4 | Water | 30.2 ± 1.6 | 32.2 ± 1.1 | 6.9 ± 0.1 | 9.4 ± 0.4 |
| OX1 | Water | 9.8 ± 0.2 | |||
| Water | OX1 | 51.4 ± 0.7 | 66.1 ± 3.3 | 95.8 ± 3.3 | |
| Water | OX2 | 88.0 ± 3.2 | |||
| Sasa/nm2 | ||||
|---|---|---|---|---|
| Group | 5mC | 5hmC | 5fC | 5caC |
| Base | 0.691 ± 0.002 | 0.696 ± 0.003 | 0.667 ± 0.001 | 0.709 ± 0.006 |
| Methyl group | 0.393 ± 0.002 | 0.485 ± 0.001 | 0.471 ± 0.002 | 0.529 ± 0.004 |
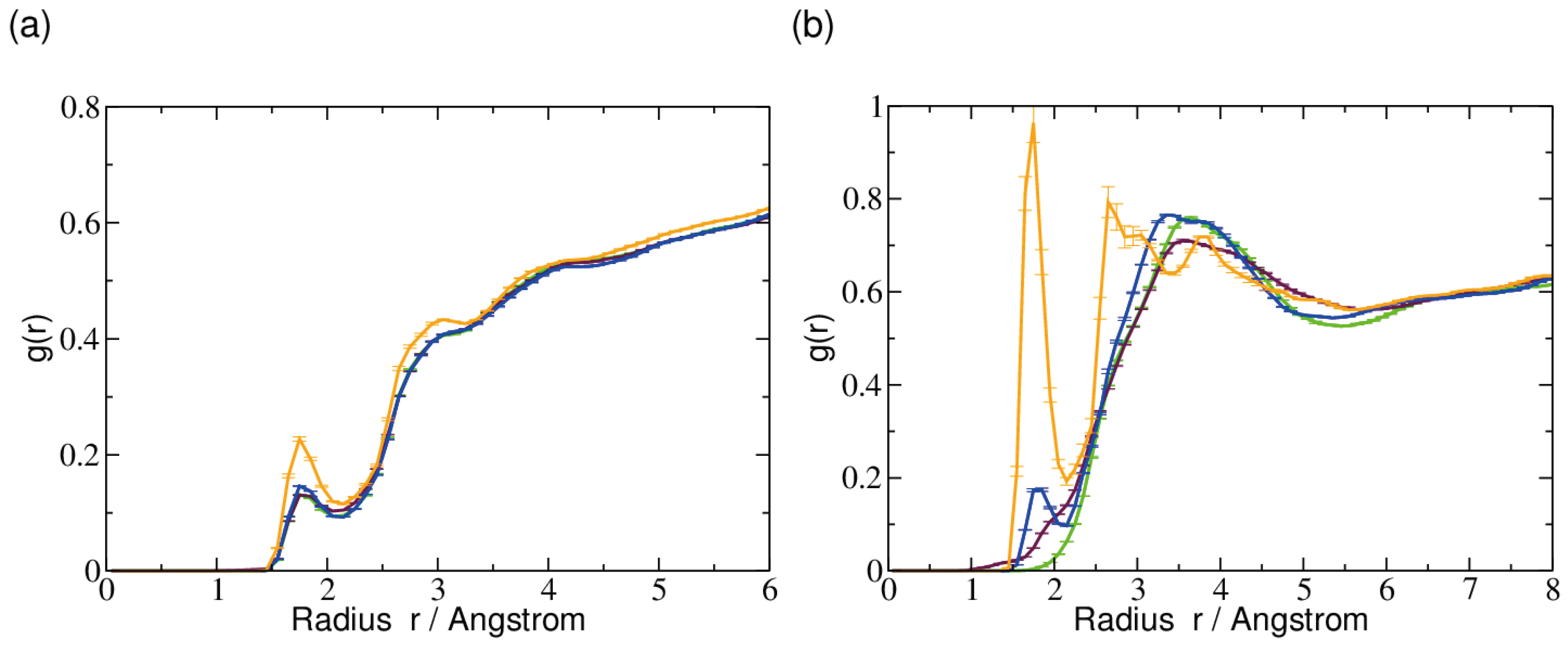
3. Discussion
4. Experimental Section
4.1. Model Setup
4.2. Molecular Dynamics (MD) Simulations
4.2.1. Unbiased MD Simulations
4.2.2. Adaptive Biasing Force (ABF) MD Simulations

4.2.3. Analysis
4.3. Force Field Parameter Development
4.4. Programs
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sidghat-Ullah, P.G.; Xu, Y.Z.; Goodman, M.F.; Bloom, L.B.; Jiricny, J.; Day, R.S., III. Base analog and neighboring base effects on substrate specificity of recombinant human G:T mismatch-specific thymine DNA glycosylase. Biochemistry 1996, 35, 12926–12932. [Google Scholar]
- Lindahl, T. DNA repair enzymes. Annu. Rev. Biochem. 1982, 51, 61–87. [Google Scholar] [CrossRef]
- Sancar, A.; Sancar, G. DNA repair enzymes. Annu. Rev. Biochem. 1988, 57, 29–67. [Google Scholar] [CrossRef]
- Stivers, J. Extrahelical damaged base recognition by DNA glycosylase enzymes. Chemistry 2008, 14, 786–793. [Google Scholar]
- Friedman, J.I.; Stivers, J.T. Detection of damaged DNA bases by DNAglycosylase enzymes. Biochemistry 2010, 49, 4957–4967. [Google Scholar] [CrossRef]
- He, Y.; Li, B.Z.; Liu, Z.L.P.; Wang, Y.; Tang, Q.; Ding, J.; Jia, Y.; Chen, Z.; Li, L.; Sun, Y.; et al. Tet-mediated formation of 5-carboxylcytosine and its excision by TDG in mammalian DNA. Science 2011, 333, 1303–1307. [Google Scholar] [CrossRef]
- Maiti, A.; Drohat, A.C. Thymine DNA glycosylase can rapidly excise 5-formylcytosine and 5-carboxylcytosine potential implications for active demethylation of CpG sites. J. Biol. Chem. 2011, 286, 35334–35338. [Google Scholar]
- Hashimoto, J.H.; Hong, S.; Bhagwat, A.S.; Zhang, X.; Cheng, X. Excision of 5-hydroxymethyluracil and 5-carboxylcytosine by the thymine DNA glycosylase domain: Its structural basis and implications for active DNA demethylation. Nucleic Acid. Res 2012, 40, 10203–10214. [Google Scholar] [CrossRef]
- Hashimoto, H.; Zhang, X.; Cheng, X. Activity and crystal structure of human thymine DNA glycosylase mutant N140A with 5-carboxylcytosine DNA at low pH. DNA Repair 2013, 12, 535–540. [Google Scholar] [CrossRef]
- Kamiya, H.; Tsuchiya, H.; Karino, N.; Ueno, Y.; Matsuda, A.; Harashima, H. Mutagenicity of 5-formylcytosine, an oxidation product of 5-methylcytosine, in DNA in mammalian cells. J. Biochem. 2002, 132, 551–555. [Google Scholar]
- Karino, N.; Ueno, Y.; Matsuda, A. Synthesis and properties of oligonucleotides containing 5-formyl-2’-deoxycytidine: In vitro DNA polymerase reactions on DNA templates containing 5-formyl-2’-deoxycytidine. Nucleic Acids Res. 2001, 29, 2456–2463. [Google Scholar] [CrossRef]
- Maiti, A.; Michelson, A.Z.; Armwood, C.J.; Lee, J.K.; Drohat, A.C. Divergent mechanisms for enzymatic excision of 5-formylcytosine and 5-carboxylcytosine from DNA. J. Am. Chem. Soc. 2013, 135, 15813–15822. [Google Scholar] [CrossRef]
- Maiti, A.; Drohat, A. Dependance of substrate binding and catalysis on pH, ionic strength, and temperature for thymine DNA glycosylase: Insights into recognition and provessing of G:T mispairs. DNA Repair 2011, 10, 545–553. [Google Scholar] [CrossRef]
- Imhof, P.; Zahran, M. The effect of a G:T mispair on the dynamics of DNA. PLoS One 2013, 8, e53305. [Google Scholar] [CrossRef]
- Cheatham, T.E. Simulation and modeling of nucleic acid structure, dynamics and interactions. Curr. Opin. Struct. Biol. 2004, 14, 360–367. [Google Scholar] [CrossRef]
- Zacharias, M. Minor groove deformability of DNA: A molecular dynamics free energy simulation study. Biophys. J. 2006, 91, 882–891. [Google Scholar] [CrossRef]
- Curuksu, J.; Zakrzewska, K.; Zacharias, M. Magnitude and direction of DNA bending induced by screw-axis orientation: Influence of sequence, mismatches and abasic sites. Nucleic Acids Res. 2008, 36, 2268–2283. [Google Scholar] [CrossRef]
- Chen, J.; Dupradeau, F.; Case, D.; Turner, C.; Stubbe, J. DNA oligonucleotides with A, T, G or C opposite an abasic site: Structure and dynamics. Nucleic Acids Res. 2008, 36, 253–262. [Google Scholar]
- Lavery, R.; Zakrzewska, K.; Beveridge, D.; Bishop, T.; Case, D.; Cheatham, T., III; Dixit, S.; Jayaram, B.; Lankas, F.; Laughton, C.; et al. A systematic molecular dynamics study of nearest-neighbor effects on base pair and base pair step conformations and fluctuations in B-DNA. Nucleic Acids Res. 2010, 38, 299–313. [Google Scholar] [CrossRef]
- Orozco, M.; Noy, A.; Pérez, A. Recent advances in the study of nucleic acid flexibility by molecular dynamics. Curr. Opin. Struct. Biol. 2008, 18, 185–193. [Google Scholar] [CrossRef]
- Banavali, N.K.; MacKerell, A.D., Jr. Free energy and structural pathways of base flipping in a DNA GCGC containing sequence. J. Mol. Biol. 2002, 319, 141–160. [Google Scholar] [CrossRef]
- Bouvier, B.; Grubmüller, H. A molecular dynamics study of slow base flipping in DNA using conformational flooding. Biophys. J. 2007, 93, 770–786. [Google Scholar] [CrossRef]
- Priyakumar, U.D.; MacKerell, A.D., Jr. Computational approaches for investigating base flipping in oligonucleotides. Chem. Rev. 2006, 106, 489–505. [Google Scholar] [CrossRef]
- Zheng, H.; Cai, Y.; Ding, S.; Tang, Y.; Kropachev, K.; Zhou, Y.; Wang, L.; Wang, S.; Geacintov, N.E.; Zhang, Y.; et al. Base flipping free energy profiles for damaged and undamaged DNA. Chem. Res. Toxicol. 2010, 23, 1868–1870. [Google Scholar] [CrossRef]
- Song, K.; Campbell, A.J.; Bergonzo, C.; de los Santos, C.; Grollman, A.P.; Simmerling, C. An improved reaction coordinate for nucleic acid base flipping studies. J. Chem. Theory Comput. 2009, 5, 3105–3113. [Google Scholar]
- Huang, N.; MacKerell, A.D. Atomistic view of base flipping in DNA. J. Philos. Trans. R. Soc. Lond. Ser. A 2004, 362, 1439–1460. [Google Scholar] [CrossRef]
- Daniels, D.S.; Woo, T.T.; Luu, K.X.; Noll, D.M.; Clarke, N.D.; Pegg, A.E.; Tainer, J.A. DNA binding and nucleotide flipping by the human DNA repair protein AGT. Nat. Struct. Mol. Biol. 2004, 11, 714–720. [Google Scholar] [CrossRef]
- Hu, J.; Ma, A.; Dinner, A.R. A two-step nucleotide-flipping mechanism enables kinetic discrimination of DNA lesions by AGT. Proc. Natl. Acad. Sci. USA 2008, 105, 4615–4620. [Google Scholar] [CrossRef]
- Szczepanowski, R.; Carpenter, M.; Czapinska, H.; Zaremba, M.; Tamulaitis, G.; Siksnys, V.; Bhagwat, A.; Bochtler, M. Central base pair flipping and discrimination by PspGI. Nucleic Acids Res. 2008, 36, 6109–6117. [Google Scholar] [CrossRef]
- Huang, N.; MacKerell, A.D. Protein-facilitated base-flipping in DNA by Cytosine-5-Methyltransferase. Proc. Natl. Acad. Sci. USA 2003, 100, 68–73. [Google Scholar] [CrossRef]
- Huang, N.; MacKerell, A.D. Specificity in protein–DNA interactions; energetic recognition by the (Cytosine-C5)-methyltransferase from HhaI. J. Mol. Biol. 2005, 345, 265–274. [Google Scholar] [CrossRef]
- Negureanu, L.; Salsbury, F.R., Jr. Non-specificity and synergy at the binding site of the carboplatin-induced DNA adduct via molecular dynamics simulations of the MutSα-DNA recognition complex. J. Biol. Mol. Struct. Dyn. 2014, 32, 969–992. [Google Scholar]
- Lu, X.J.; Olson, W.K. 3DNA: A software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003, 31, 5108–5121. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- Darden, T.; York, D.; Pedersen, L.G. Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comp. Phys. 1977, 23, 327–341. [Google Scholar]
- Darve, E.; Pohorille, A. Calculating free energies using average force. J. Chem. Phys. 2001, 115, 9169–9183. [Google Scholar]
- Chipot, C.; Hénin, J. Exploring the free-energy landscape of a short peptide using an average force. J. Chem. Phys. 2005, 123, 244906. [Google Scholar]
- Darve, E.; Rodríomez-Gómez, D.; Pohorille, A. Adaptive biasing force method for scalar and vector free energy calculations. J. Chem. Phys. 2008, 128, 144120. [Google Scholar]
- Huang, N.; MacKerell, A., Jr. Atomistic view of base flipping in DNA. Philos. Trans. R. Soc. Lond. Ser. A 2004, 362, 1439–1460. [Google Scholar] [CrossRef]
- Priyakumar, U.; MacKerell, A., Jr. Base flipping in a GCGC containing DNA dodecamer: A comparative study of the performance of the nucleic acid force fields, CHARMM, AMBER, and BMS. J. Chem. Theory Comput. 2006, 2, 187–200. [Google Scholar]
- Lavery, R.; Sklenar, H. The definition of generalized helicoidal parameters and of axis curvature for irregular nucleic acids. J. Biomol. Struct. Dyn. 1988, 6, 63–91. [Google Scholar] [CrossRef]
- Eisenhaber, F.; Lijnzaad, P.; Argos, P.; Sander, C.; Scharf, M. The double cube lattice method: Efficient approaches to numerical integration of surface area and volume and to dot surface contouring of molecular assemblies. J. Comp. Chem. 1995, 16, 273–284. [Google Scholar] [CrossRef]
- ParamChem. Available online: https://cgenff.paramchem.org (accessed on 30 January 2014).
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar]
- Vanommeslaeghe, K.; MacKerell, A.D. Automation of the CHARMM general force field (CGenFF) I: Bond perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell, A.D. Automation of the CHARMM general force Field (CGenFF) II: Assignment of bonded parameters and partial atomic charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D. Extension of the CHARMM general force field to sulfonyl-containing compounds and its utility in biomolecular simulations. J. Comput. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09; Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lavery, R.; Moakher, M.; Maddocks, J.H.; Petkeviciute, D.; Zakrzewskal, K. Conformational analysis of nucleic acids revisited: Curves+. Nucleic Acids Res. 2009, 37, 5917–5929. [Google Scholar] [CrossRef]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Helabad, M.B.; Kanaan, N.; Imhof, P. Base Flip in DNA Studied by Molecular Dynamics Simulationsof Differently-Oxidized Forms of Methyl-Cytosine. Int. J. Mol. Sci. 2014, 15, 11799-11816. https://doi.org/10.3390/ijms150711799
Helabad MB, Kanaan N, Imhof P. Base Flip in DNA Studied by Molecular Dynamics Simulationsof Differently-Oxidized Forms of Methyl-Cytosine. International Journal of Molecular Sciences. 2014; 15(7):11799-11816. https://doi.org/10.3390/ijms150711799
Chicago/Turabian StyleHelabad, Mahdi Bagherpoor, Natalia Kanaan, and Petra Imhof. 2014. "Base Flip in DNA Studied by Molecular Dynamics Simulationsof Differently-Oxidized Forms of Methyl-Cytosine" International Journal of Molecular Sciences 15, no. 7: 11799-11816. https://doi.org/10.3390/ijms150711799






