Comparisons of Non-Gaussian Statistical Models in DNA Methylation Analysis
Abstract
:1. Introduction
2. Results and Discussion
2.1. Data Description and Preprocessing
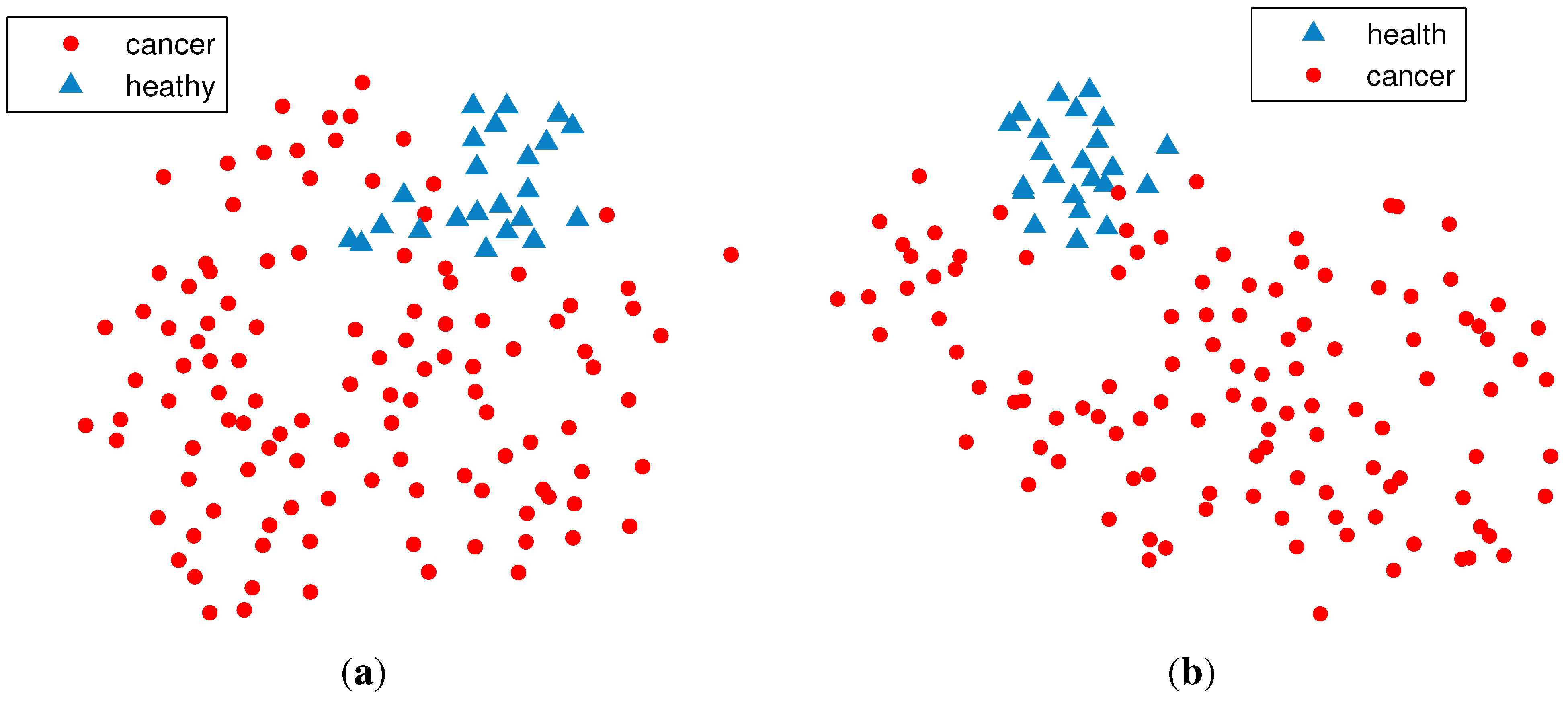
2.2. Unsupervised Clustering
2.2.1. PCA (Principal Component Analysis) + VBGMM (Variational Bayesian Gaussian Mixture Model)
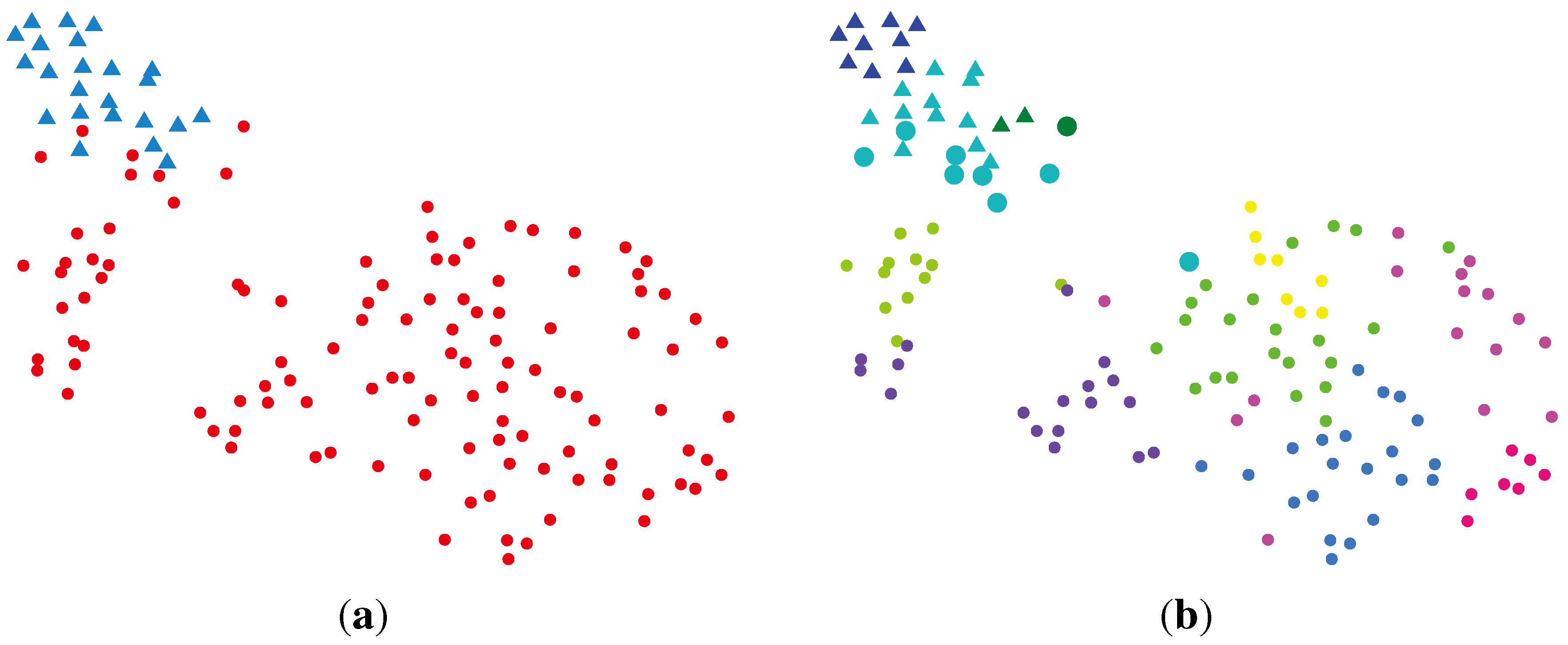
2.2.2. BG-NMF (Beta-Gamma-Nonnegative Matrix Factorization) + RPBMM (Recursive Partitioning Beta Mixture Model)
| Cluster | Normal | Cancer |
|---|---|---|
| rLLLL | 16 | 4 |
| rLLLR | 6 | 0 |
| rLLR | 1 | 32 |
| rLR | 0 | 31 |
| rRLLL | 0 | 4 |
| rRLLR | 0 | 3 |
| rRLRL | 0 | 10 |
| rRLRR | 0 | 5 |
| rRR | 0 | 34 |
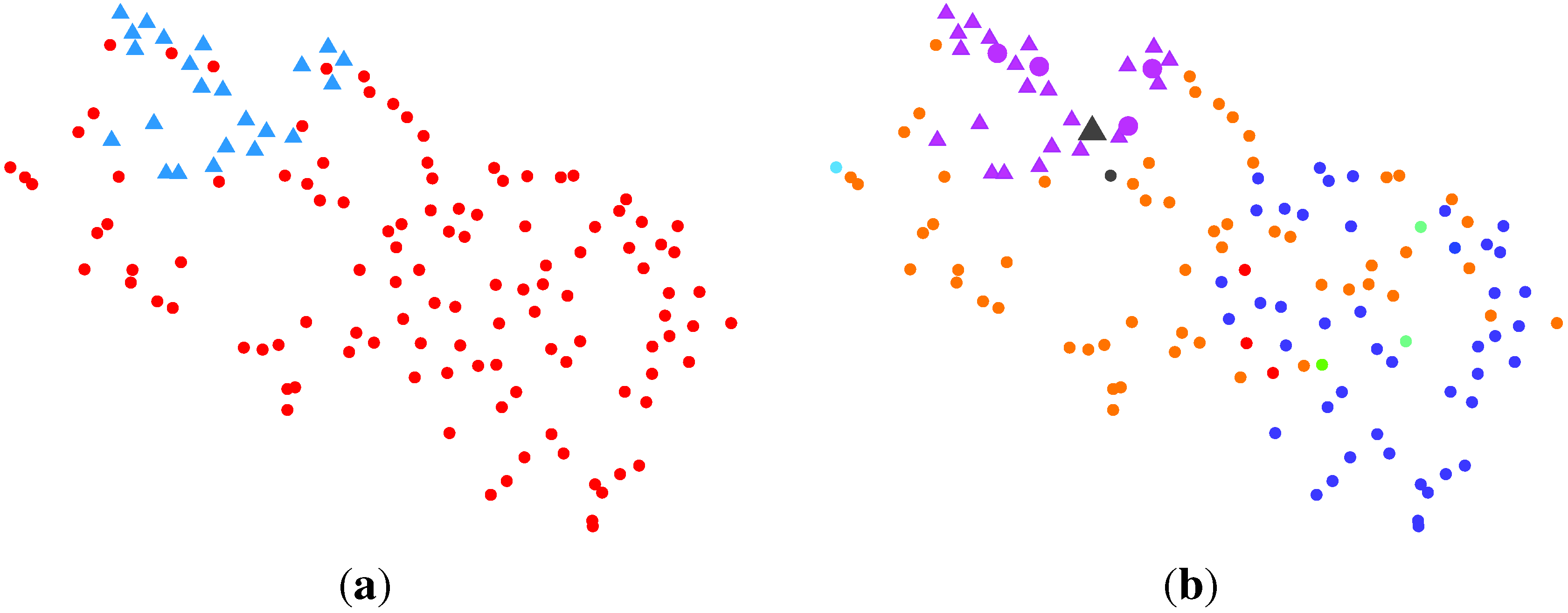
2.2.3. BG-NMF + VBBMM (Variational Bayesian Estimation Framework for BMM)
2.2.4. SC (Spectral Clustering) + VBvMM (Variational Inference Framework-based Bayesian Analysis of the vMF Mixture Model)
2.2.5. SC + VBWMM (Variational Bayesian Estimation of WMM)
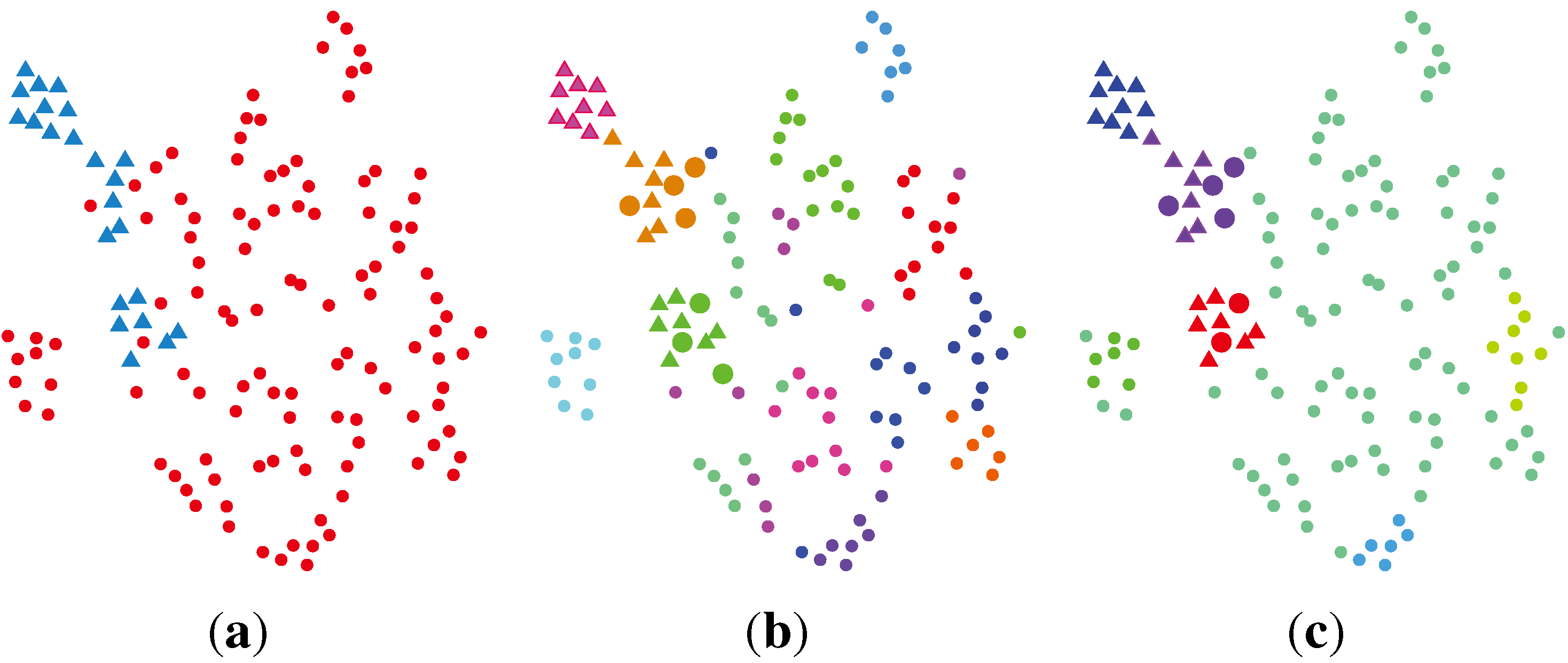
2.2.6. Discussion
| Method | Error Rate | Cancer→Normal | Normal→Cancer |
|---|---|---|---|
| PCA + VBGMM | 6.62% | 9 | 0 |
| BGNMF + RPBMM | 3.68% | 4 | 1 |
| BGNMF + VBBMM | 3.68% | 4 | 1 |
| SC + VBvMM | 5.15% | 7 | 0 |
| SC + VBWMM | 4.41% | 6 | 0 |
3. Experimental Section
3.1. Non-Gaussian Statistical Distributions
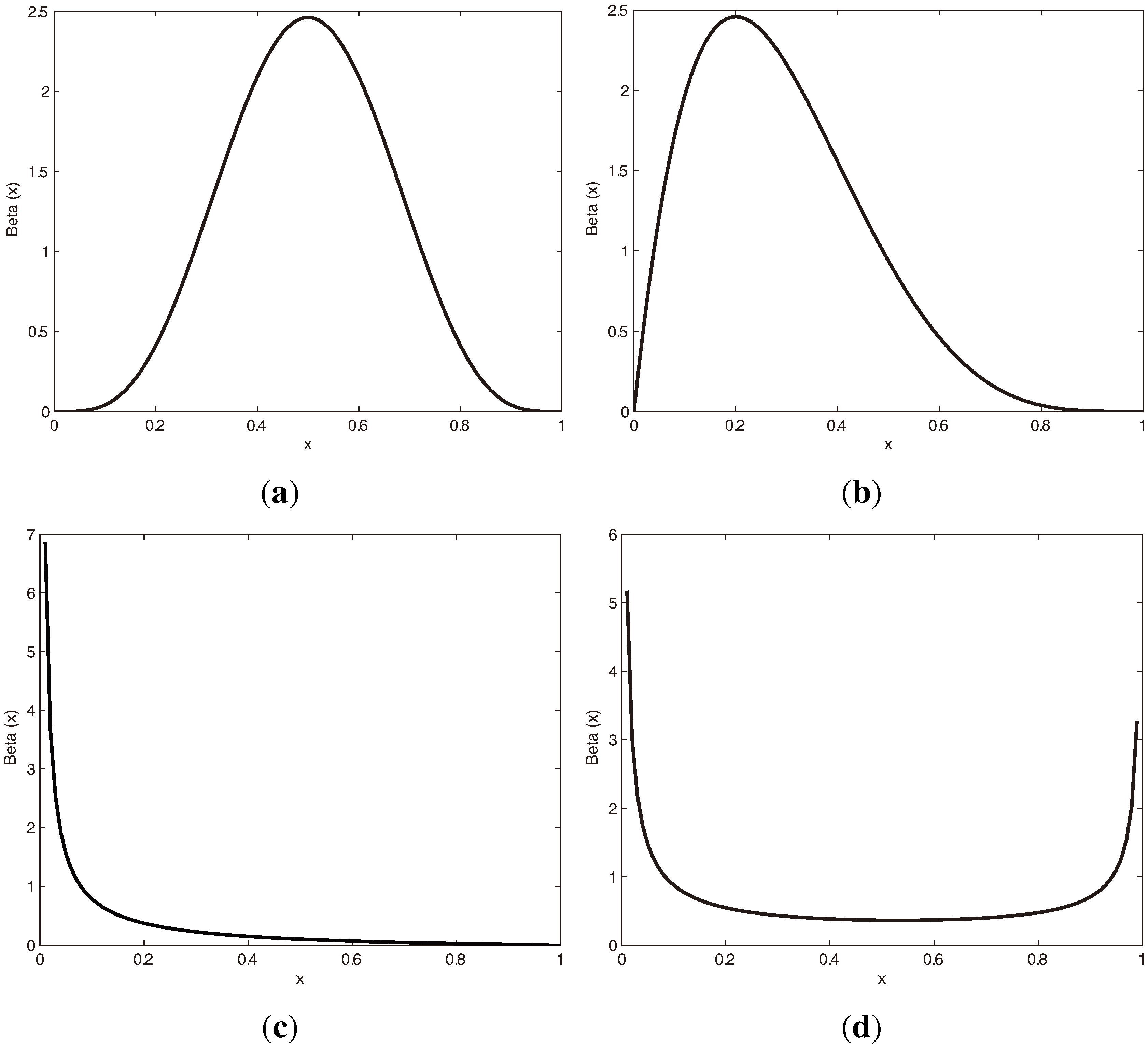
3.1.1. Beta Distribution
3.1.2. vMF (von Mises-Fisher) Distribution
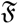 (μ, 400) (shown by green colors) are highly concentrated around the mean direction, while for samples generated from
(μ, 400) (shown by green colors) are highly concentrated around the mean direction, while for samples generated from
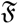 (μ, 4) (shown by blue colors), the distribution of samples on the sphere is more uniform around the mean direction.
(μ, 4) (shown by blue colors), the distribution of samples on the sphere is more uniform around the mean direction.
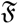 (μ, 400) (shown by green colors) are highly concentrated around the mean direction, while for samples generated from
(μ, 400) (shown by green colors) are highly concentrated around the mean direction, while for samples generated from
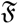 (μ, 4) (shown by blue colors), the distribution of samples on the sphere is more uniform around the mean direction.
(μ, 4) (shown by blue colors), the distribution of samples on the sphere is more uniform around the mean direction.
3.1.3. Watson Distribution
 which are axially symmetric, that is f(−x) = f(x). In such cases, the p-dimensional observation ±x can be regarded as being on the projective space ℙp−1, which is obtained by identifying opposite points on the sphere
which are axially symmetric, that is f(−x) = f(x). In such cases, the p-dimensional observation ±x can be regarded as being on the projective space ℙp−1, which is obtained by identifying opposite points on the sphere
 .
.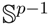 , has the (p − 1)-dimensional Watson distribution
Wp (μ, κ), with the mean direction μ and the concentration parameter κ, if its probability density function is:
, has the (p − 1)-dimensional Watson distribution
Wp (μ, κ), with the mean direction μ and the concentration parameter κ, if its probability density function is: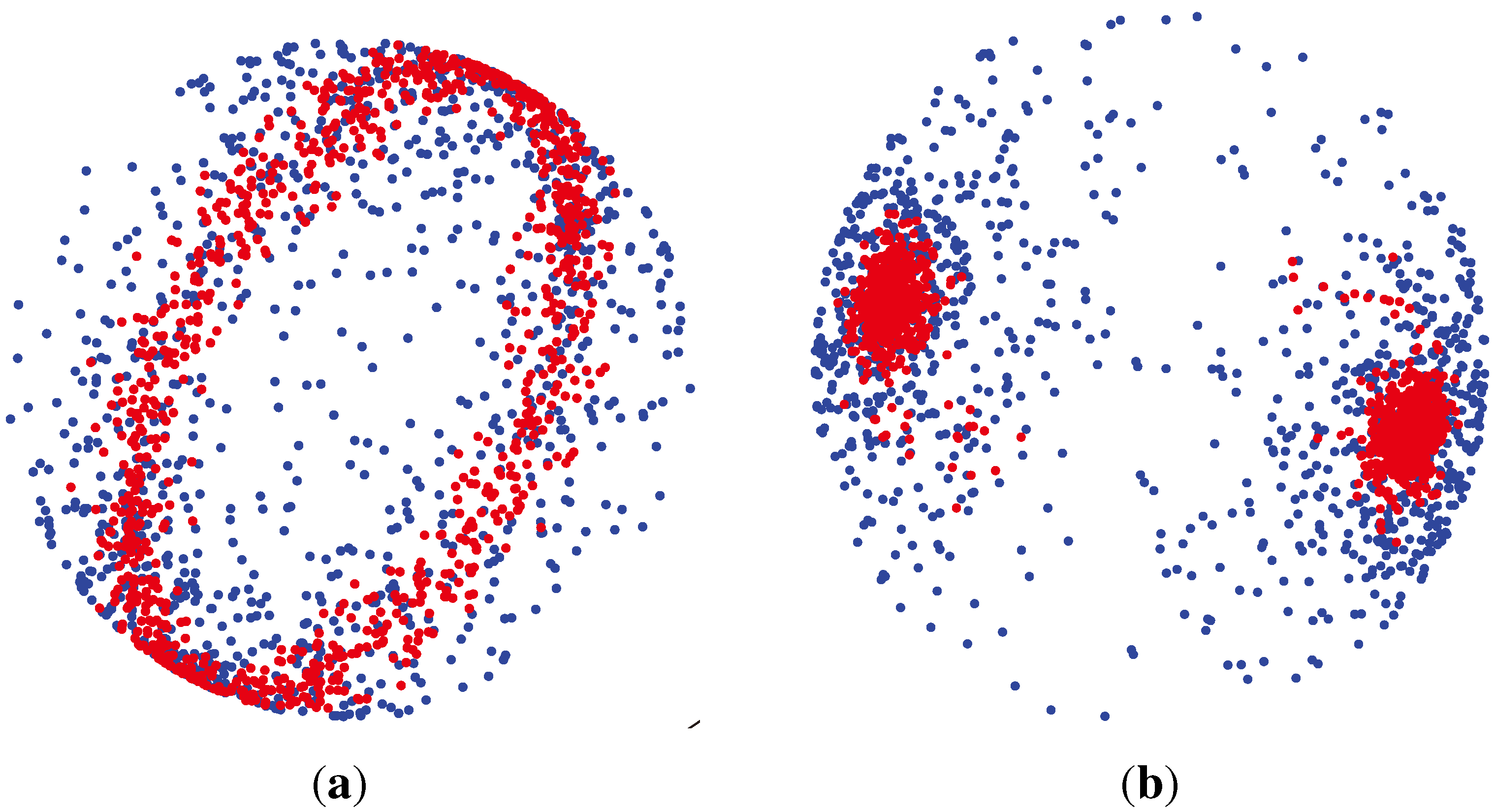
3.2. Non-Gaussian Dimension Reduction Methods
3.3. Nonnegative Matrix Factorization for Bounded Support Data
3.3.1. Spectral Clustering for Non-Gaussian Reduced Features
Input: Original data matrix X = {x1, x2, …, xN}, each column is a L-dimensional vector.
|
3.4. Non-Gaussian Statistical Models for Unsupervised Clustering
3.4.1. Recursive Partitioning Beta Mixture Model
3.4.2. Variational Beta Mixture Model
3.4.3. Variational von Mises-Fisher Mixture Model
3.4.4. Variational Watson Mixture Model
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deaton, A.M.; Bird, A. CpG islands and the regulation of transcription. Genes Dev 2011, 25, 1010–1022. [Google Scholar]
- Petronis, A. Epigenetics as a unifying principle in the aetiology of complex traits and diseases. Nature 2010, 465, 721–727. [Google Scholar]
- Sandoval, J.; Heyn, H.; Moran, S.; Serra-Musach, J.; Pujana, M.A.; Bibikova, M.; Esteller, M. Validation of a DNA methylation microarray for 450,000 CpG sites in the human genome. Epigenetics 2011, 6, 692–702. [Google Scholar]
- Du, P.; Zhang, X.; Huang, C.C.; Jafari, N.; Kibbe, W.A.; Hou, L.; Lin, S.M. Comparison of Beta-value and M-value methods for quantifying methylation levels by microarray analysis. BMC Bioinform 2010, 11. [Google Scholar] [CrossRef]
- Zhuang, J.; Widschwendter, M.; Teschendorff, A.E. A comparison of feature selection and classification methods in DNA methylation studies using the Illumina 27k platform. BMC Bioinform 2012, 13. [Google Scholar] [CrossRef]
- Barfield, R.T.; Kilaru, V.; Smith, A.K.; Conneely, K.N. CpGassoc: An R function for analysis of DNA methylation microarray data. Bioinformatics 2012, 28, 1280–1281. [Google Scholar]
- Kilaru, V.; Barfield, R.T.; Schroeder, J.W.; Smith, A.K.; Conneely, K.N. MethLAB: A graphical user interface package for the analysis of array-based DNA methylation data. Epigenetics 2012, 7, 225–229. [Google Scholar]
- Laurila, K.; Oster, B.; Andersen, C.; Lamy, P.; Orntoft, T.; Yli-Harja, O.; Wiuf, C. A beta-mixture model for dimensionality reduction, sample classification and analysis. BMC Bioinform 2011, 12. [Google Scholar] [CrossRef]
- Koestler, D.C.; Marsit, C.J.; Christensen, B.C.; Karagas, M.R.; Bueno, R.; Sugarbaker, D.J.; Kelsey, K.T.; Houseman, E.A. Semi-supervised recursively partitioned mixture models for identifying cancer subtypes. Bioinformatics 2010, 26, 2578–2585. [Google Scholar]
- Kuan, P.F.; Wang, S.; Zhou, X.; Chu, H. A statistical framework for Illumina DNA methylation arrays. Bioinformatics 2010, 26, 2849–2855. [Google Scholar]
- Houseman, E.A.; Christensen, B.C.; Karagas, M.R.; Wrensch, M.R.; Nelson, H.H.; Wiemels, J.L.; Zheng, S.; Wiencke, J.K.; Kelsey, K.T.; Marsit, C.J. Copy number variation has little impact on bead-array-based measures of DNA methylation. Bioinformatics 2009, 25, 1999–2005. [Google Scholar]
- Houseman, E.A.; Christensen, B.C.; Yeh, R.F.; Marsit, C.J.; Karagas, M.R.; Wrensch, M.; Nelson, H.H.; Wiemels, J.; Zheng, S.; Wiencke, J.K.; et al. Model-based clustering of DNA methylation array data: A recursive-partitioning algorithm for high-dimensional data arising as a mixture of beta distributions. BMC Bioinform 2008, 9. [Google Scholar] [CrossRef]
- Ji, Y.; Wu, C.; Liu, P.; Wang, J.; Coombes, K.R. Applications of beta-mixture models in bioinformatics. Bioinformatics 2005, 21, 2118–2122. [Google Scholar]
- Teschendorff, A.E.; Marabita, F.; Lechner, M.; Bartlett, T.; Tegner, J.; Gomez-Cabrero, D.; Beck, S. A beta-mixture quantile normalization method for correcting probe design bias in Illumina Infinium 450 k DNA methylation data. Bioinformatics 2013, 29, 189–196. [Google Scholar]
- Ma, Z.; Teschendorff, A.E. A variational Bayes beta Mixture Model for Feature Selection in DNA methylation Studies. J. Bioinform. Comput. Biol 2013, 11. [Google Scholar] [CrossRef]
- Teschendorff, A.E.; Zhuang, J.; Widschwendter, M. Independent surrogate variable analysis to deconvolve confounding factors in large-scale microarray profiling studies. Bioinformatics 2011, 27, 1496–1505. [Google Scholar]
- Zinovyev, A.; Kairov, U.; Karpenyuk, T.; Ramanculov, E. Blind source separation methods for deconvolution of complex signals in cancer biology. Biochem. Biophys. Res. Commun 2013, 430, 1182–1187. [Google Scholar]
- Teschendorff, A.E.; Journée, M.; Absil, P.A.; Sepulchre, R.; Caldas, C. Elucidating the altered transcriptional programs in breast cancer using independent component analysis. PLoS Comput. Biol 2007, 3, e161. [Google Scholar]
- Flusberg, B.A.; Webster, D.R.; Lee, J.H.; Travers, K.J.; Olivares, E.C.; Clark, T.A.; Korlach, J.; Turner, S.W. Direct detection of DNA methylation during single-molecule, real-time sequencing. Nat. Methods 2010, 7, 461–465. [Google Scholar]
- Wang, G.; Kossenkov, A.V.; Ochs, M.F. LS-NMF: A modified non-negative matrix factorization algorithm utilizing uncertainty estimates. BMC Bioinform 2006, 7, 175. [Google Scholar]
- Muller, F.J.; Schuldt, B.M.; Williams, R.; Mason, D.; Altun, G.; Papapetrou, E.P.; Danner, S.; Goldmann, J.E.; Herbst, A.; Schmidt, N.O.; et al. A bioinformatic assay for pluripotency in human cells. Nat. Methods 2011, 8, 315–317. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive computation and machine learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- DasGupta, A. Probability for Statistics and Machine Learning: Fundamentals and Advanced Topics; Springer Texts in Statistics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Wegman, E.; Schwartz, S.; Thomas, J. Topics in Non-Gaussian Signal Processing; Springer London, Limited: London, UK, 2011. [Google Scholar]
- Ma, Z. Non-Gaussian Statistical Models and Their Applications. Ph.D. Thesis, KTH - Royal Institute of Technology, Stockholm, Sweden, 2011. [Google Scholar]
- Ma, Z.; Leijon, A. Bayesian estimation of beta mixture models with variational inference. IEEE Trans. Pattern Anal. Mach. Intell 2011, 33, 2160–2173. [Google Scholar]
- Bouguila, N.; Ziou, D. High-dimensional unsupervised selection and estimation of a finite generalized dirichlet mixture model based on minimum message length. IEEE Trans. Pattern Anal. Mach. Intell 2007, 29, 1716–1731. [Google Scholar]
- Ma, Z.; Leijon, A.; Kleijn, W.B. Vector quantization of LSF parameters with a mixture of dirichlet distributions. IEEE Trans. Audio, Speech, Lang. Process 2013, 21, 1777–1790. [Google Scholar]
- Blei, D.M.Y.; N.A.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res 2003, 3, 993–1022. [Google Scholar]
- Kwon, H.J. Performance of Non-Gaussian Distribution Based Communication and Compressed Sensing Systems. Ph.D. Thesis, University of California, San Diego, CA, USA, 2013. [Google Scholar]
- Guo, J.; Guo, H.; Wang, Z. An activation force-based affinity measure for analyzing complex networks. Sci. Rep 2011. [Google Scholar] [CrossRef]
- Rodger, J.A. Toward reducing failure risk in an integrated vehicle health maintenance system: A fuzzy multi-sensor data fusion Kalman filter approach for IVHMS. Expert Syst. Appl 2012, 39, 9821–9836. [Google Scholar]
- Rodger, J.A. A fuzzy nearest neighbor neural network statistical model for predicting demand for natural gas and energy cost savings in public buildings. Expert Syst. Appl 2014, 41, 1813–1829. [Google Scholar]
- Ma, Z.; Tan, Z.H.; Prasad, S. EEG signal classification with super-Dirichlet mixture model. Proceedings of the IEEE Statistical Signal Processing Workshop (SSP), Ann Arbor, MI, USA, 5–8 Auguest 2012; pp. 440–443.
- Ma, Z.; Leijon, A.; Tan, Z.H.; Gao, S. Predictive distribution of the dirichlet mixture model by local variational inference. J. Signal Process. Syst 2014, 74, 1–16. [Google Scholar]
- Curtis, C.; Shah, S.P.; Chin, S.F.; Turashvili, G.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature 2012, 486, 346–352. [Google Scholar]
- GEO. Gene Expression Omnibus. Available online: http://www.ncbi.nlm.nih.gov/geo/ (accessed on 12 June 2014).
- Zhuang, J.; Jones, A.; Lee, S.H.; Ng, E.; Fiegl, H.; Zikan, M.; Cibula, D.; Sargent, A.; Salvesen, H.B.; Jacobs, I.J.; et al. The dynamics and prognostic potential of DNA methylation changes at stem cell gene loci in women’s cancer. PLoS Genet 2012, 8, e1002517. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res 2008, 9, 2579–2605. [Google Scholar]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.A.; Guhr, T.; Stanley, H.E. Random matrix approach to cross correlations in financial data. Phys. Rev. E Stat. Nonlinear Soft Matter Phys 2002, 65, 066126. [Google Scholar]
- Jones, P.A.; Baylin, S.B. The epigenomics of cancer. Cell 2007, 128, 683–692. [Google Scholar]
- Widschwendter, M.; Fiegl, H.; Egle, D.; Mueller-Holzner, E.; Spizzo, G.; Marth, C.; Weisenberger, D.J.; Campan, M.; Young, J.; Jacobs, I.; et al. Epigenetic stem cell signature in cancer. Nat. Genet 2007, 39, 157–158. [Google Scholar]
- Bouguila, N.; Ziou, D.; Monga, E. Practical Bayesian estimation of a finite Beta mixture through gibbs sampling and its applications. Stat. Comput 2006, 16, 215–225. [Google Scholar]
- Kotz, S.; Balakrishnan, N.; Johnson, N.L. Continuous Multivariate Distributions. Volume 1: Models and Applications; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Krishnamoorthy, K. Handbook of Statistical Distributions with Applications; Statistics: A Series of Textbooks and Monographs; Taylor & Francis: Boca Ration, FL, USA, 2010. [Google Scholar]
- Taghia, J.; Ma, Z.; Leijon, A. Bayesian estimation of the von-Mises Fisher mixture model with variational inference. IEEE Trans. Pattern Anal. Mach. Intell 2012. [Google Scholar] [CrossRef]
- Sra, S.; Karp, D. The multivariate Watson distribution: Maximum-likelihood estimation and other aspects. J. Multivar. Anal 2013, 114, 256–269. [Google Scholar]
- Ma, Z.; Leijon, A. Beta mixture models and the application to image classification. Proceedings of the IEEE International Conference on Image Processing, Cairo, Egypt, 7–10 November 2009; pp. 2045–2048.
- Regoes, R.R. The role of exposure history on HIV acquisition: Insights from repeated low-dose challenge studies. PLoS Comput. Biol 2012, 8. [Google Scholar] [CrossRef]
- Mardia, K.V.; Jupp, P.E. Directional Statistics; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Banerjee, A.; Dhillon, I.S.; Ghosh, J.; Sra, S. Clustering on the unit hypersphere using von Mises-Fisher distributions. J. Mach. Learn. Res 2005, 6, 1345–1382. [Google Scholar]
- López-Cruz, P.L.; Bielza, C.; Larrañaga, P. The von Mises Naive Bayes classifier for angular data. In Advances in Artificial Intelligence; Lozano, J.A., Gámez, J.A., Moreno, J.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7023, pp. 145–154. [Google Scholar]
- Dhillon, I.S.; Marcotte, E.M.; Roshan, U. Diametrical clustering for identifying anti-correlated gene clusters. Bioinformatics 2003, 19, 1612–1619. [Google Scholar]
- Bingham, C. An antipodally symmetric distribution on the sphere. Ann. Stat 1974, 2, 1201–1225. [Google Scholar]
- Andrews, G.; Askey, R.; Roy, R. Special Functions; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Daalhuis, A.B.O. The NIST Handbook of Mathematical Functions; Olver, F.W., Lozier, D.W., Boisvert, R.F., Clark, C.W., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 321–349. [Google Scholar]
- Mardia, K.V.; Jupp, P.E. Directional Statistics; John Wiley and Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Taghia, J.; Leijon, A. Variational inference for Watson mixture model. IEEE Trans. Pattern Recognit. Mach. Intell 2014, in press. [Google Scholar]
- Ochs, M.F.; Godwin, A.K. Microarrays in cancer: Research and applications. Biotechniques 2003, 34 Suppl, S4–S15. [Google Scholar]
- Liu, J.; Morgan, M.; Hutchison, K.; Calhoun, V.D. A study of the influence of sex on genome wide methylation. PLoS One 2010, 5, e10028. [Google Scholar]
- Jung, I.; Kim, D. LinkNMF: Identification of histone modification modules in the human genome using nonnegative matrix factorization. Gene 2013, 518, 215–221. [Google Scholar]
- Bell, C.; Teschendorff, A.E.; Rakyan, V.K.; Maxwell, A.P.; Beck, S.; Savage, D.A. Genome-wide DNA methylation analysis for diabetic nephropathy in type 1 diabetes mellitus. Med. Genomics 2010, 3. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Teschendorff, A.E.; Leijon, A. Variational bayesian matrix factorization for bounded support data. IEEE Trans. Pattern Anal. Mach. Intell 2014, in press. [Google Scholar]
- Attias, H. A variational bayesian framework for graphical models. In Advances in Neural Information Processing Systems 12; MIT Press: Cambridge, MA, USA, 2000; pp. 209–215. [Google Scholar]
- Luxburg, U. A tutorial on spectral clustering. Stat. Comput 2007, 17, 395–416. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2001; pp. 849–856. [Google Scholar]
- Sra, S. A short note on parameter approximation for von Mises-Fisher distributions and a fast implementation of Is(x). Comput. Stat 2012, 27, 177–190. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ma, Z.; Teschendorff, A.E.; Yu, H.; Taghia, J.; Guo, J. Comparisons of Non-Gaussian Statistical Models in DNA Methylation Analysis. Int. J. Mol. Sci. 2014, 15, 10835-10854. https://doi.org/10.3390/ijms150610835
Ma Z, Teschendorff AE, Yu H, Taghia J, Guo J. Comparisons of Non-Gaussian Statistical Models in DNA Methylation Analysis. International Journal of Molecular Sciences. 2014; 15(6):10835-10854. https://doi.org/10.3390/ijms150610835
Chicago/Turabian StyleMa, Zhanyu, Andrew E. Teschendorff, Hong Yu, Jalil Taghia, and Jun Guo. 2014. "Comparisons of Non-Gaussian Statistical Models in DNA Methylation Analysis" International Journal of Molecular Sciences 15, no. 6: 10835-10854. https://doi.org/10.3390/ijms150610835




