A Convolutional Code-Based Sequence Analysis Model and Its Application
Abstract
:1. Introduction
- (i)
- The work of Ponnala et al.[19] produced a better result using a block code model, but a convolutional code model is another model that provides better performance in many cases in a coding system of communication engineering. This observation indicates that a convolutional code model approach should be studied more extensively.
- (ii)
- Researchers have discovered the effect of codon context on the expression and efficiency of the translation of some codons [20,21], but the effect of the adjacent nucleotides is not considered sufficiently in these models. Thus, a convolutional code model, which contains the effect of adjacent symbols, should be more suitable for studying DNA encoding than a block code model, which only considers the effect of the present symbols.
- (iii)
- A nucleotide in a DNA sequence is usually treated as an independent informational unit in the traditional methods, but codon functions in the process of translation imply that a codon itself could be treated as an informational unit [22].
- (iv)
- In addition, the degeneracy of the codons is quite interesting, as the existence of degeneracy provides more stability in genetic processes, such that a gene mutation of one nucleotide may result in another codon of the same amino acid. Thus, this feature of codon should be an important feature or consideration in designing an analytical model.
2. Results and Discussion
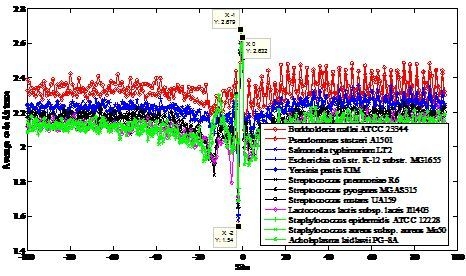
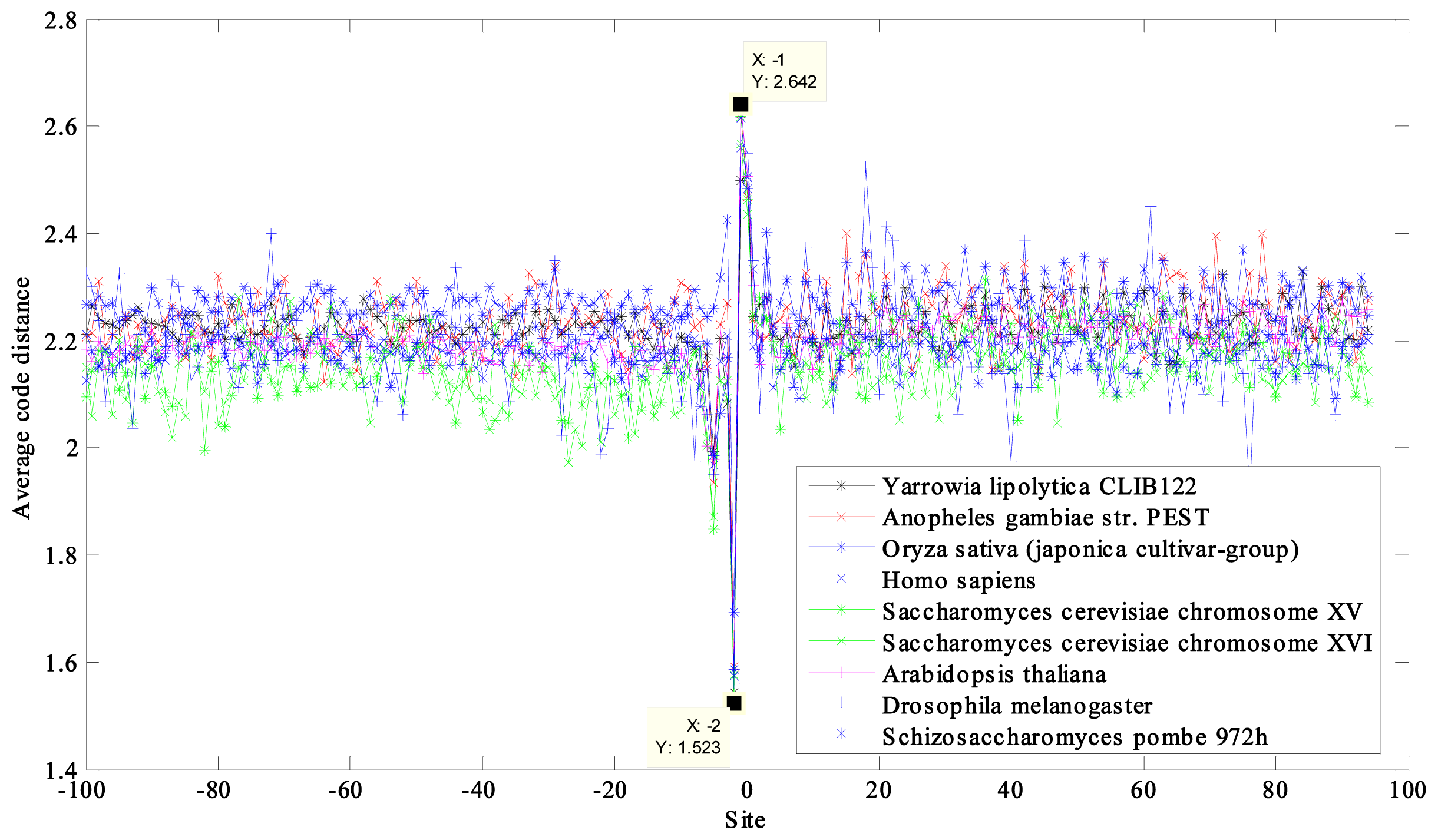
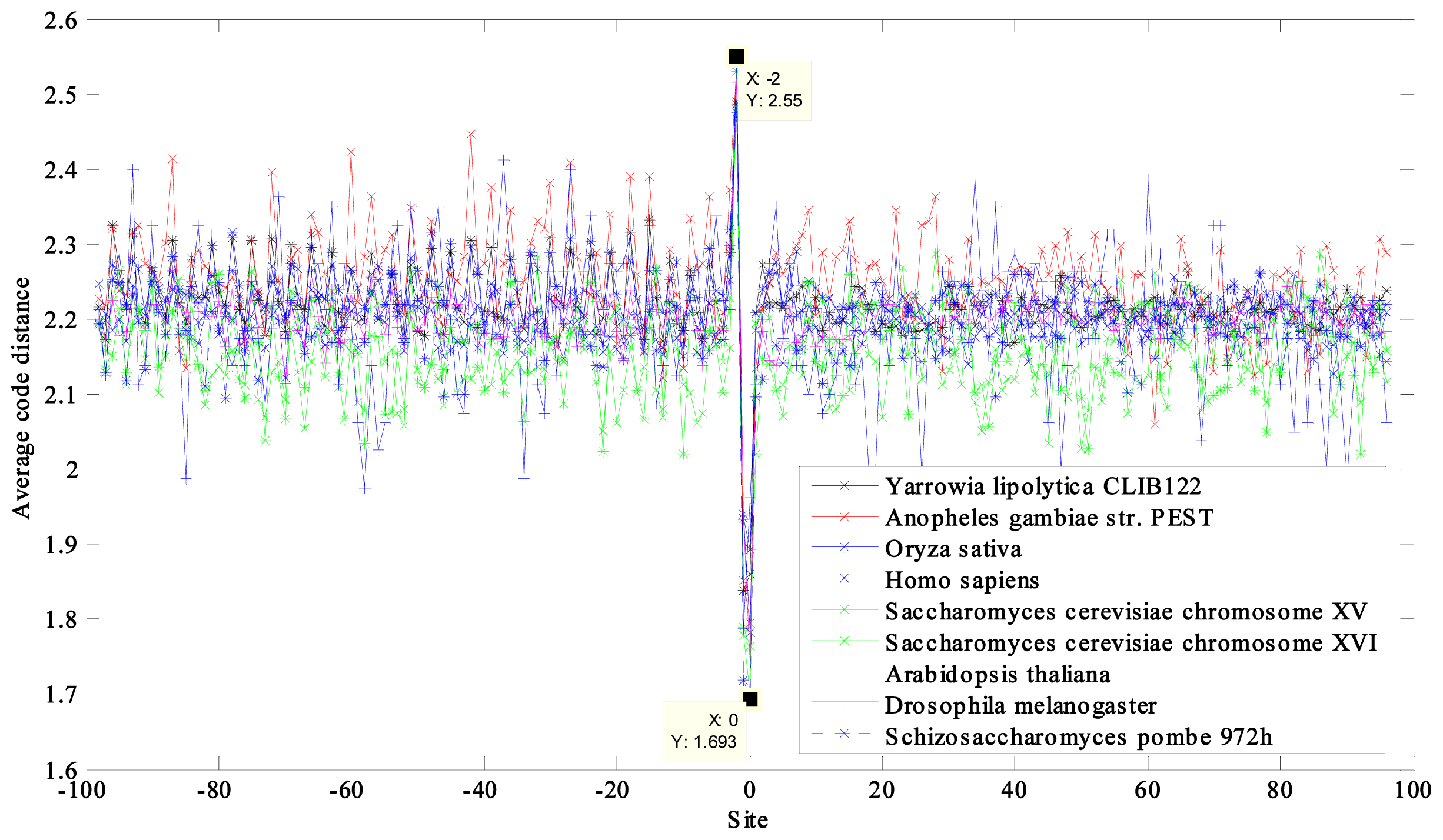
2.1. Region near the Initiation Site
2.2. Region near the Termination Site
2.3. Period-3 Feature in Coding Region
2.4. Separating the Derived Curves into Groups
3. Experimental Section
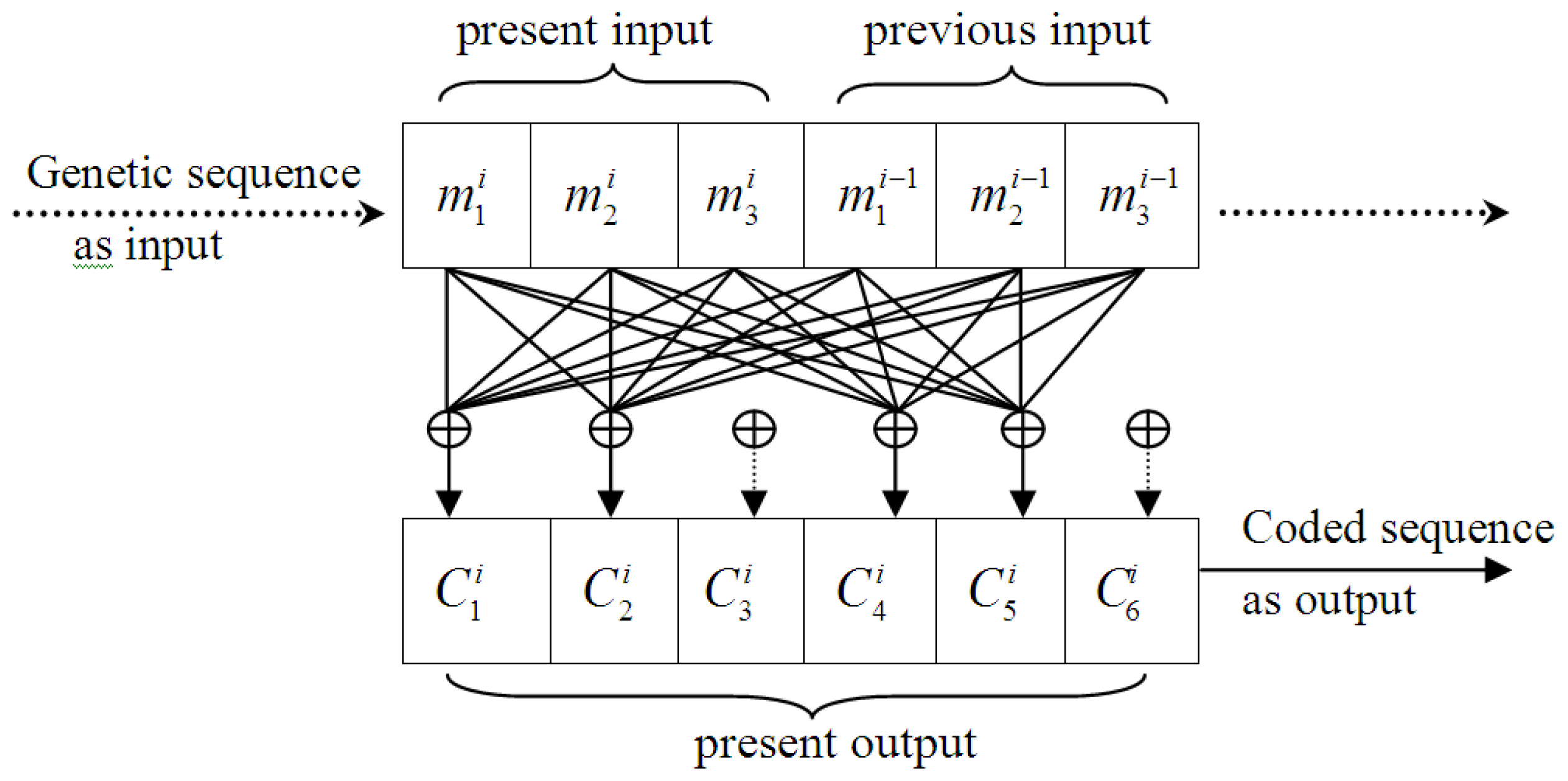
3.1. Designing the (6,3,2) Convolutional Code Model
- (i)
- A codon is treated as an informational unit, as a codon in the coding region is translated into an amino acid, which is different from using a single nucleotide. Thus, 3 or multiples of 3 should be used as the basic code length, and based on the short-range dominance of bases correlation [29], 2 was selected as the universal constraint length (i.e., L = 2), and the length of convolutional code was defined as 6. In other words, the encoder output depends on two contiguous codons, and the selected code is a (6,3,2) convolutional code. Every 3 nucleotides were used as a group of input and 6 symbols generated as outputs, which were simultaneously affected by both the present and previous inputs.
- (ii)
- The design of the coefficients in the generator matrix was based on codon degeneracy, i.e., the translated amino acid may be the same even for different codons (this is largely, but not entirely, confined to the third position of a codon, known as the wobble position). The wobble feature of synonymous codons reduces the influence of mutation on living systems, as a gene mutation of one nucleotide may result in another codon of the same amino acid. This phenomenon was considered an important feature in the design. We supposed that the first two codon nucleotides were affected by the original information directly and, therefore, a higher weight used; and the third nucleotide wobble feature was determined by certain natural choice mechanisms in evolutionary processes, indicating that this should be given a lower weight.
3.2. Analysis Method
- Step 1
- Digitizing the nucleotide sequences. The four nucleotides, A, G, C and T, were expressed as digital numbers, 0, 1, 2 and 3, respectively [7].
- Step 2
- Calculating the output of the convolutional code, using formula (2).
- Step 3
- Calculating the code distance. Code distance or Hamming distance, between two strings with equal length, is the number of positions for which the corresponding symbols are different. The first 3 numbers of the present convolutional output were compared with previous input data, m1, to calculate the code distance. The first code distance is remarked by d11.
- Step 4
- Calculating all ORFs of a DNA sequence. The same operation was performed for every ORF of an analyzed DNA sequence, and all code distance sequences of this DNA sequence were:where r is the total number of coding strands of the analyzed DNA sequence. Last, the average value of each site was calculated, described as:where dk average = (d1k + d2k +··· + drk)/r.
- Step 5
- Calculating the characteristic average code distance (CACD) of a DNA sequence. The new parameter, CACD, is defined to quantify the feature of code distance of a DNA sequence:
4. Conclusions
Acknowledgments
References and Notes
- Battail, G. Heredity as an encoded communication process. IEEE Trans. Inf. Theory 2010, 56, 678–687. [Google Scholar]
- Liebovitch, L.S.; Tao, Y.; Todorov, A.T.; Levine, L. Is there an error correcting code in the base sequence in DNA? Biophys. J 1996, 71, 1539–1544. [Google Scholar]
- May, E.E.; Vouk, M.A.; Bitzer, D.L.; Rosnick, D.I. The Ribosome as a Table-Driven Convolutional Decoder for the Escherichia coliK-12 Translation Initiation System. Proceedings of the 22nd Annual International Conference of the IEEE -Engineering-in-Medicineand- Biology-Society, Chicago, IL, USA, 23–28 July 2000; pp. 2466–2469.
- May, E.E.; Vouk, M.A.; Bitzer, D.L.; Rosnick, D.I. An error-correcting code framework for genetic sequence analysis. J. Frankl. Inst 2004, 341, 89–109. [Google Scholar]
- Milenkovic, O.; Vasic, B. Information theory and coding problems in genetics. Proceedings of the Information Theory Workshop, San Antonio, TX, USA, 24–29 October 2004; pp. 60–65.
- Roman-roldan, R.; Bernaola-galvan, P.; Oliver, J.L. Application of information theory to DNA sequence analysis: A review. Pattern Recognit 1996, 29, 1187–1194. [Google Scholar]
- Rosen, G.L. Examining coding structure and redundancy in DNA. IEEE Eng. Med. Biol. Mag 2006, 25, 62–68. [Google Scholar]
- Sibbald, P.R.; Banerjee, S.; Maze, J. Calculating higher order DNA sequence information measures. J. Theor. Biol 1989, 136, 475–483. [Google Scholar]
- Bataineh, M.A.; Huang, L.; Alonso, M.; Menhart, N.; Atkin, G.E. Analysis of gene translation using a communications theory approach. Adv. Exp. Med. Biol 2010, 680, 387–397. [Google Scholar]
- Dawy, Z; Morcos, F.; Weindl, J.; Mueller, JC. Translation initiation modeling and mutational analysis based on the 3′-end of the Escherichia coli16S rRNA sequence. Biosystems 2009, 96, 58–64. [Google Scholar]
- Bouaynaya, N.; Schonfeld, D. Protein communication system: Evolution and genomic structure. Algorithmica 2007, 48, 375–397. [Google Scholar]
- Barkai, N.; Leibler, S. Robustness in simple biochemical networks. Nature 1997, 387, 913–917. [Google Scholar]
- Rosen, G.L. Comparison of Autoregressive Measures for DNA Sequence Similarity. Proceedings of the IEEE International Workshop on Genomic Processing and Statistics, Tuusula, Finland, 10–12 June 2007. [CrossRef]
- Wang, X.H.; Istepanian, R.S.H.; Geake, T. Error control coding in microarray data analysis. Proceedings of the International Workshop on Genomic Signal Processing and Statistics, Baltimore MD, USA, 26–27 May 2004.
- Gupta, M.K. The quest for error correction in biology. IEEE Eng. Med. Biol. Mag 2006, 25, 46–53. [Google Scholar]
- May, E.E.; Lee, M.T.; Dolan, P.; Crozier, P.; Brozik, S.; Manginell, M. Computational sensing and in vitroclassification of GMOs and biomolecular events. Proceedings of the 26th Army Science Conference, 1–4 December 2008, Orlando, FL, USA.
- Yukinawa, N.; Oba, S.; Kato, K.; Ishii, S. Optimal Aggregation of Binary Classifiers for Multiclass Cancer Diagnosis Using Gene Expression Profiles. Proceedings of the 4th International Symposium on Bioinformatics Research and Applications, Georgia State University, Atlanta, GA, USA, 6–9 May 2008; pp. 333–343.
- Zheng, G.Y.; Qian, Z.L.; Yang, Q.; Wei, C.C.; Xie, L.; Zhu, Y.Y.; Li, Y.X. The combination approach of SVM and ECOC for powerful identification and classification of transcription factor. BMC Bioinforma 2008, 9, 282–289. [Google Scholar]
- Ponnala, L.; Bitzer, D.L.; Vouk, M.A. On Finding Convolutional Code Generators for Translation Initiation of Escherichia ColiK-12. Proceedings of the 25th Annual International Conference of the IEEE-Engineering-in-Medicine-and-Biology-Society, Cancun, Mexico, 17–21 September 2003; pp. 3854–3857.
- Shpaer, E.G. Constraints on codon context in Escherichia coli genes—Their possible role in modulating the effiency of translation. J. Mol. Biol 1986, 188, 555–564. [Google Scholar]
- Yarus, M.; Folley, L.S. Sense codons are found in specific contexts. J. Mol. Biol 1985, 182, 529–540. [Google Scholar]
- Jungck, J.R. Genetic Codes as Codes: Towards a Theoretical Basis for Bioinformatics. Proceedings of the International Symposium on Mathematical and Computational Biology, Campos do Jordao, Brazil, November 2008; pp. 300–337.
- Shine, J.; Dalgarno, L. Determinant of cistron specificity in bacterial ribosomes. Nature 1975, 254, 34–38. [Google Scholar]
- Marmur, J.; Falkow, S.; Mandel, M. New approaches to bacterial taxonomy. Annu. Rev. Microbiol 1963, 17, 329–372. [Google Scholar]
- Sneath, P.H.A. New Approaches to bacterial taxonomy-use of computers. Annu. Rev. Microbiol 1964, 18, 335–346. [Google Scholar]
- Yabuuchi, E.; Kosako, Y.; Oyaizu, H.; Yano, I.; Hotta, H.; Hashimoto, Y.; Ezaki, T.; Arakawa, M. Proposal of Burkholderia gen. nov. and transfer of seven species of the genus Pseudomonas homology group II to the new genus, with the type species Burkholderia cepacia (Palleroni and Holmes 1981) comb. nov. Microbiol. Immunol 1992, 36, 1251–1275. [Google Scholar]
- Lapeyre, B.; Michot, B.; Feliu, J.; Bachellerie, J.P. Nucleotide sequence of the Schizosaccharomyces pombe 25S ribosomal RNA and its phylogenetic implications. Nucleic Acids Res 1993, 21, 3322–3322. [Google Scholar]
- Proakis, J.G. Digital Communications, 3rd ed.; McGraw-Hill Inc: New York NY, USA, 1995; pp. 477–511. [Google Scholar]
- Luo, L.F.; Lee, W.J.; Jia, L.J.; Ji, F.M.; Tsai, L. Statistical correlation of nucleotides in a DNA sequence. Phys. Rev. E 1998, 58, 861–871. [Google Scholar]
- Cohen, B.A.; Mitra, R.D.; Hughes, J.D.; Church, G.M. A computational analysis of whole-genome expression data reveals chromosomal domains of gene expression. Nat. Genet 2000, 26, 183–186. [Google Scholar]
- Kruglyak, S.; Tang, H.X. Regulation of adjacent yeast genes. Trends Genet 2000, 16, 109–111. [Google Scholar]
- Marin, A.; Wang, M.N.; Gutierrez, G. Short-range compositional correlation in the yeast genome depends on transcriptional orientation. Gene 2004, 333, 151–155. [Google Scholar]
- Garrity, G.M.; Bell, J.A.; Lilburn, T.G. Taxonomic Outline of the Prokaryotes. Bergey’s Manual of Systematic Bacteriology, 2nd ed.; Springer: New York, NY, USA; p. 2004.
- Shifting by one for observing the detail of the process.
- Shen, P.; Chen, X.D. Microbiology, 2nd ed; Higher Education Press: Beijing, China, 2006; pp. 422–431. [Google Scholar]
- Liu, X.; Tian, F.C.; Wang, S.Y. Analysis of similarity/dissimilarity of dna sequences based on convolutional code model. Nucleosides, Nucleotides Nucleic Acids 2010, 29, 123–131. [Google Scholar]
- Richardson, A.O.; Palmer, J.D. Horizontal gene transfer in plants. J. Exp. Bot 2007, 58, 1–9. [Google Scholar]
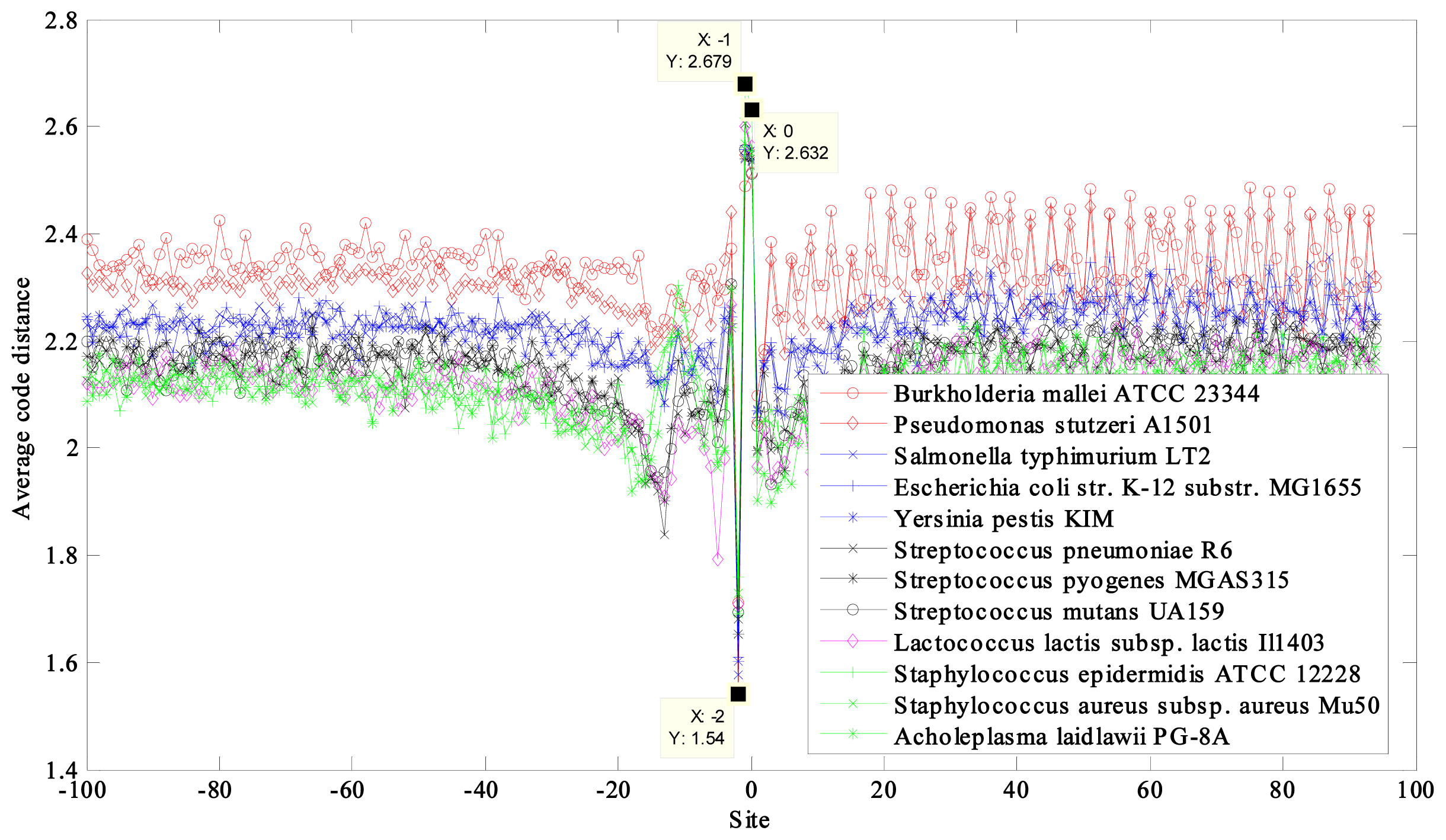
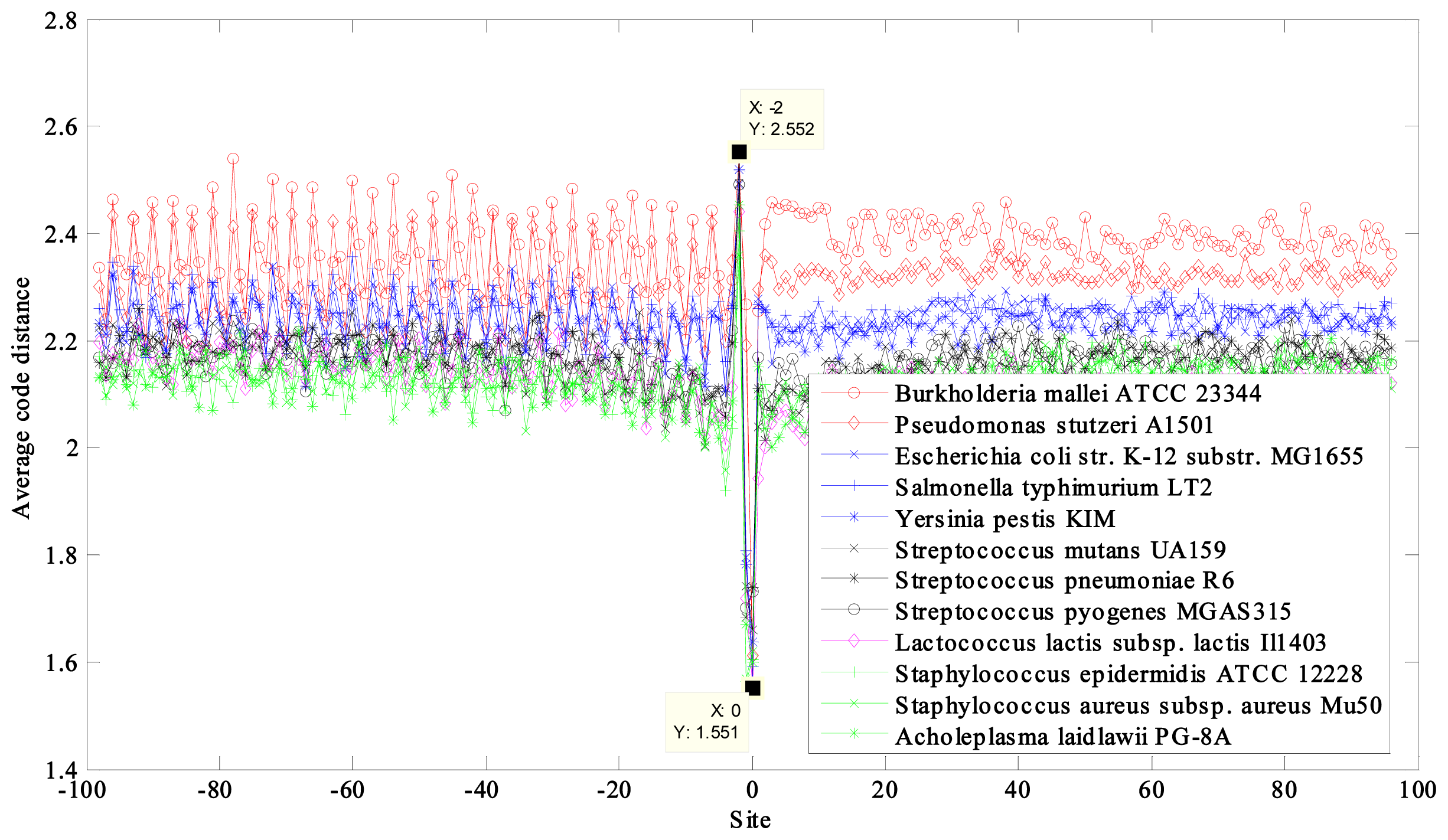
| NCBI Ref. Seq. Access Number | Selected Prokaryotes a | GC Content (%) | CACD b | CACD c |
|---|---|---|---|---|
| NC_006349 | Burkholderia mallei ATCC 23344 chromosome 2 | 68 | 2.3504 | 1.9076 |
| NC_009434 | Pseudomonas stutzeri A1501 | 63 | 2.3062 | 1.9455 |
| NC_003197 | Salmonella typhimurium LT2 | 52 | 2.2336 | 1.8721 |
| NC_000913 | Escherichia coli str. K-12 substr. MG1655 | 50 | 2.2330 | 1.8712 |
| NC_004088 | Yersinia pestis KIM | 47 | 2.2195 | 1.8624 |
| NC_003098 | Streptococcus pneumoniae R6 | 39 | 2.1547 | 1.7943 |
| NC_004070 | Streptococcus pyogenes MGAS315 | 38 | 2.1529 | 1.8028 |
| NC_004350 | Streptococcus mutans UA159 | 36 | 2.1524 | 1.7987 |
| NC_002662 | Lactococcus lactis subsp. lactis Il1403 | 35 | 2.1184 | 1.7827 |
| NC_004461 | Staphylococcus epidermidis ATCC 12228 | 32 | 2.1149 | 1.7699 |
| NC_002758 | Staphylococcus aureus subsp. aureus Mu50 | 32 | 2.1139 | 1.7658 |
| NC_010163 | Acholeplasma laidlawii PG-8A | 2.1135 | 1.7632 | |
| 31 | max − min = 0.2369 | max − min = 0.1823 |
| NCBI Ref. Seq. Access Number | Selected Eukaryotes a | GC Content (%) | CACD b | CACD c |
|---|---|---|---|---|
| NC_006070 | Yarrowia lipolytica CLIB122 chromosome D | 49 | 2.2267 | 1.9182 |
| NW_045720 | Anopheles gambiae str. PEST chromosome X | 45 | 2.2350 | 1.8954 |
| NC_008403 | Oryza sativa (japonica cultivar-group) genomic DNA, chromosome 10 | 44 | 2.2777 | 1.8945 |
| NT_011512 | Homo sapiens chromosome 21, reference assembly | 39 | 2.1900 | 1.8594 |
| NC_001147 | Saccharomyces cerevisiae chromosome XV | 38 | 2.1537 | 1.8303 |
| NC_001148 | Saccharomyces cerevisiae chromosome XVI | 38 | 2.1504 | 1.8347 |
| NC_003075 | Arabidopsis thaliana chromosome 4 | 36 | 2.2015 | 1.8409 |
| NC_004353 | Drosophila melanogaster chromosome 4 | 36 | 2.1966 | 1.8501 |
| NC_003421 | Schizosaccharomyces pombe 972h chromosome III | 36 | 2.1814 | 1.8328 |
| max − min = 0.1273 | max − min = 0.0879 |
| Addition Multiplication | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| + | 0 | 1 | 2 | 3 | × | 0 | 1 | 2 | 3 | |
| 0 | 0 | 1 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | |
| 2 | 2 | 3 | 0 | 1 | 2 | 0 | 2 | 3 | 1 | |
| 3 | 3 | 2 | 1 | 0 | 3 | 0 | 3 | 1 | 2 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, X.; Geng, X. A Convolutional Code-Based Sequence Analysis Model and Its Application. Int. J. Mol. Sci. 2013, 14, 8393-8405. https://doi.org/10.3390/ijms14048393
Liu X, Geng X. A Convolutional Code-Based Sequence Analysis Model and Its Application. International Journal of Molecular Sciences. 2013; 14(4):8393-8405. https://doi.org/10.3390/ijms14048393
Chicago/Turabian StyleLiu, Xiao, and Xiaoli Geng. 2013. "A Convolutional Code-Based Sequence Analysis Model and Its Application" International Journal of Molecular Sciences 14, no. 4: 8393-8405. https://doi.org/10.3390/ijms14048393