Use of Linear Free Energy Relationships (LFERs) to Elucidate the Mechanisms of Reaction of a γ-Methyl-β-alkynyl and an ortho-Substituted Aryl Chloroformate Ester
Abstract
:1. Introduction
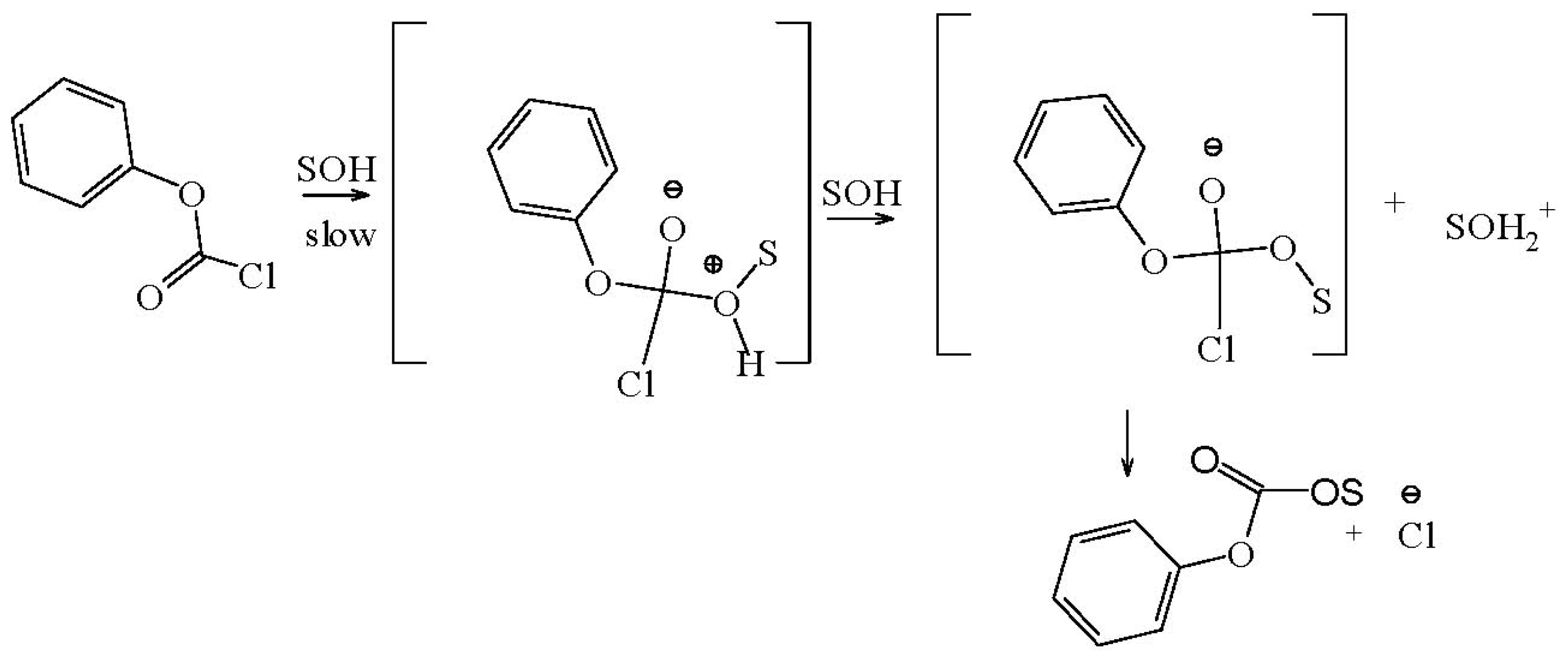
2. Results and Discussion
3. Experimental Section
4. Conclusions
Acknowledgments
References
- Rinehart, J.K. Symmetrical alkynyl ureas. U.S. Patent 4,066,440, 3 January 1978. [Google Scholar]
- Hirao, G.; Totani, Y.; Itou, T.; Nakatsuka, M.; Yamaguchi, T. Aromatic chloroformate compound. Jpn. Patent JP3394057, 31 January 2003. [Google Scholar]
- Wang, W.; Xu, B.; Hammond, G.B. Synthesis of functionalized α, α-disubstituted β-alkynyl esters from allenoates through an alkynylenolate intermediate. Org. Lett 2008, 10, 3713–3716. [Google Scholar]
- Lepore, S.D.; He, Y.; Damisse, P. Studies on the base-promoted conversion of conjugated alkynyl esters to α-substituted α-allenyl esters. J. Org. Chem 2004, 69, 9171–9175. [Google Scholar]
- Fathalla, O.A.; Zeid, I.F.; Haiba, M.E.; Soliman, A.M.; Abd-Elmoez, Sh.I.; El-Serwy, W.S. Synthesis, antibacterial and anticancer evaluation of some pyrimidine derivatives. World J. Chem 2009, 4, 127–132. [Google Scholar]
- Wells, P.R. Linear Free Energy Relationships; Academic Press: New York NY, USA, 1968; pp. 8–35. [Google Scholar]
- Roberts, I.; Johnson, C.D.; Taylor, P.G. Linear free energy and solvolysis reactions. Tetrahedron 1977, 33, 2123–2126. [Google Scholar]
- Shorter, J. Correlations Analysis of Organic Reactivity; with Particular Reference to Multiple Regression Analysis; John Wiley & Sons, Inc: Somerset, NJ, USA, 1982; pp. 1–235. [Google Scholar]
- Winstein, S.; Grunwald, E.; Jones, H.W. The correlation of solvolyses rates and the classification of solvolysis reactions into mechanistic categories. J. Am. Chem. Soc 1951, 73, 2700–2707, and references there in. [Google Scholar]
- Bentley, T.W.; Garley, M.S. Correlations and predictions of solvent effects on reactivity: some limitations of multi-parameter equations and comparisons with similarity models based on one solvent parameter. J. Phys. Org. Chem 2006, 19, 341–349. [Google Scholar]
- Bentley, T.W.; Harris, H.C.; Ryu, Z.-H.; Lim, G.T.; Sung, D.D.; Szajda, S.R. Mechanisms of solvolyses of acid chlorides and chloroformates. Chloroacetyl and phenylacetyl chloride as similarity models. J. Org. Chem 2005, 70, 8963–8970. [Google Scholar]
- Kevill, D.N.; D’Souza, M.J. Sixty years of the Grunwald-Winstein equation: development and recent applications. J. Chem. Res 2008, 2008, 61–66, and references therein. [Google Scholar]
- Bentley, T.W.; Carter, G.E. The SN2-SN1 spectrum. 4. Mechanism for solvolyses of tert-butyl chloride: A revised Y scale of solvent ionizing power based on solvolyses of 1-adamantyl chloride. J. Am. Chem. Soc 1982, 104, 5741–5747. [Google Scholar]
- Bentley, T.W.; Llewellyn, G. Yx scales of solvent ionizing power. Prog. Phys. Org. Chem 1990, 17, 121–158. [Google Scholar]
- Kevill, D.N.; D’Souza, M.J. Additional YCl values and correlation of the specific rates of solvolysis of tert-butyl chloride in terms of NT and YCl scales. J. Chem. Res. Synop 1993, 174–175. [Google Scholar]
- Lomas, J.S.; D’Souza, M.J.; Kevill, D.N. Extremely large acceleration of the solvolysis of 1-adamantyl chloride upon incorporation of a spiro adamantane substituent: Solvolysis of 1-chlorospiro[adamantane-2, 2′-adamantane]. J. Am. Chem. Soc 1995, 117, 5891–5892. [Google Scholar]
- Kevill, D.N.; Ryu, Z.H. Additional solvent ionizing power values for binary water-1,1,1,3,3,3,- hexafluoro-2-propanol solvents. Int. J. Mol. Sci 2006, 7, 451–455. [Google Scholar]
- Schadt, F.L.; Bentley, T.W.; Schleyer, P.v.R. The SN2-SN1 spectrum. 2. Quantitative treatments of nucleophilic solvent assistance. A scale of solvent nucleophilicities. J. Am. Chem. Soc 1976, 98, 7667–7674. [Google Scholar]
- Kevill, D.N.; Anderson, S.W. An improved scale of solvent nucleophilicity based on the solvolysis of the S-methyldibenzothiophenium Ion. J. Org. Chem 1991, 56, 1845–1850. [Google Scholar]
- Kevill, D.N. Development and Uses of Scales of Solvent Nucleophilicity. In Advances in Quantitative Structure-Property Relationships; Charton, M., Ed.; JAI Press: Greenwich, CT, USA, 1996; Volume 1, pp. 81–115. [Google Scholar]
- D’Souza, M.J.; Ryu, Z.-H.; Park, B.-C.; Kevill, D.N. Correlation of the rates of solvolysis of acetyl chloride and α-substituted derivatives. Can. J. Chem 2008, 86, 359–367. [Google Scholar]
- Bentley, T.W. Structural effects on the solvolytic reactivity of carboxylic and sulfonic acid chlorides. Comparisons with gas-phase data for cation formation. J. Org. Chem 2008, 73, 6251–6257. [Google Scholar]
- D’Souza, M.J.; Yaakoubd, L.; Mlynarski, S.L.; Kevill, D.N. Concerted solvent processes for common sulfonyl chloride precursors used in the synthesis of sulfonamide-based drugs. Int. J. Mol. Sci 2008, 9, 914–925. [Google Scholar]
- D’Souza, M.J.; Shuman, K.E.; Carter, S.E.; Kevill, D.N. Extended Grunwald-Winstein analysis-LFER used to gauge solvent effects in p-nitrophenyl chloroformate solvolysis. Int. J. Mol. Sci 2008, 9, 2231–2242. [Google Scholar]
- Ryu, Z.-H.; Lee, S.W.; D’Souza, M.J.; Yaakoubd, L.; Feld, S.E.; Kevill, D.N. Correlation of the rates of solvolysis of two arenesulfonyl chlorides and of trans-β-styrenesulfonyl chloride—Precursors in the development of new pharmaceuticals. Int. J. Mol. Sci 2008, 9, 2639–2657. [Google Scholar]
- D’Souza, M.J.; Reed, D.N.; Erdman, K.J.; Kyong, J.B.; Kevill, D.N. Grunwald-Winstein analysis—isopropyl chloroformate solvolysis revisited. Int. J. Mol. Sci 2009, 10, 862–879. [Google Scholar]
- Bentley, T.W.; Jones, R.O.; Kang, D.H.; Koo, I.S. The SN3-SN2 spectrum. Rate constants and product selectivities for solvolyses of benzenesulfonyl chlorides in aqueous alcohols. J. Phys. Org. Chem 2009, 22, 799–806. [Google Scholar]
- D’Souza, M.J.; Hailey, S.M.; Kevill, D.N. Use of empirical correlations to determine solvent effects in the solvolysis of S-methyl chlorothioformate. Int. J. Mol. Sci 2010, 11, 2253–2266. [Google Scholar]
- D’Souza, M.J.; Mahon, B.P.; Kevill, D.N. Analysis of the nucleophilic solvation effects in isopropyl chlorothioformate solvolysis. Int. J. Mol. Sci 2010, 11, 2507–2611. [Google Scholar]
- Koh, H.J.; Kang, S.J.; Kevill, D.N. Kinetic studies of the solvolyses of 2,2,2-trichloro-1,1-dimethylethyl chloroformate. Bull. Korean Chem. Soc 2010, 31, 835–839. [Google Scholar]
- Koh, H.J.; Kang, S.J. Kinetic studies of the solvolyses of isopropenyl chloroformate. Bull. Korean Chem. Soc 2010, 31, 1793–1796. [Google Scholar]
- D’Souza, M.J.; Darrington, A.M.; Kevill, D.N. On the importance of the aromatic ring parameter in studies of the solvolyses of cinnamyl and cinnamoyl halides. Org. Chem. Int 2010, (2010). [Google Scholar] [CrossRef]
- Moon, D.H.; Seong, M.H.; Kyong, J.B.; Lee, Y.; Lee, Y.-W. Correlation of the rates of solvolysis of 1- and 2-naphthyl chloroformates using the extended Grunwald-Winstein equation. Bull. Korean Chem. Soc 2011, 32, 2413–2417. [Google Scholar]
- D’Souza, M.J.; Carter, S.E.; Kevill, D.N. Correlation of the rates of solvolysis of neopentyl chloroformate—A recommended protecting agent. Int. J. Mol. Sci 2011, 12, 1161–1174. [Google Scholar]
- D’Souza, M.J.; Darrington, A.M.; Kevill, D.N. A study of solvent effects in the solvolysis of propargyl chloroformate. ISRN Org. Chem 2011, 2011, 767141:1–767141:6. [Google Scholar]
- D’Souza, M.J.; McAneny, M.J.; Kevill, D.N.; Kyong, J.B.; Choi, S.H. Kinetic evaluation of the solvolysis of isobutyl chloro- and chlorothioformate esters. Beilstein J. Org. Chem 2011, 7, 543–552. [Google Scholar]
- D’Souza, M.J.; Shuman, K.E.; Omondi, A.O.; Kevill, D.N. Detailed analysis for the solvolysis of isopropenyl chloroformate. Eur. J. Chem 2011, 2, 130–135. [Google Scholar]
- D’Souza, M.J.; Hailey, S.M.; Mahon, B.P.; Kevill, D.N. Understanding solvent effects in the solvolyses of 4-fluorophenyl chlorothionoformate. 2011, 1–9. [Google Scholar]
- Koh, H.J.; Kang, S.J. A kinetic study on solvolysis of 9-fluorenylmethyl chloroformate. Bull. Korean Chem. Soc 2011, 32, 3799–3801. [Google Scholar]
- Ruff, F.; Farkas, Ö. Concerted SN2 mechanism for the hydrolysis of acid chlorides: Comparisons of reactivities calculated by the density functional theory with experimental data. J. Phys. Org. Chem 2011, 24, 480–491. [Google Scholar]
- Park, K.-H.; Kevill, D.N. Influence of the ortho effect in the solvolyses of dichlorobenzoyl chlorides. J. Phys. Org. Chem 2011. [Google Scholar] [CrossRef]
- Park, K.-H.; Kevill, D.N. The importance of the ortho effect in the solvolyses of 2,6-difluorobenzoyl chloride. J. Phys. Org. Chem 2011. [Google Scholar] [CrossRef]
- Bentley, T.W.; Harris, H.C. Solvolyses of benzoyl chlorides in weakly nucleophilic media. Int. J. Mol. Sci 2011, 12, 4805–4818. [Google Scholar]
- Kevill, D.N.; Ismail, N.H.J.; D’Souza, M.J. Solvolysis of the (p-methoxybenzyl)dimethylsulfonium Ion. Development and use of a scale to correct for dispersion in Grunwald-Winstein plots. J. Org. Chem 1994, 59, 6303–6312. [Google Scholar]
- Kevill, D.N.; D’Souza, M.J. Use of the simple and extended Grunwald-Winstein equations in the correlation of the rates of solvolysis of highly hindered tertiary alkyl derivatives. Cur. Org. Chem 2010, 14, 1037–1049. [Google Scholar]
- Queen, A. Kinetics of the hydrolysis of acyl chlorides in pure water. Can. J. Chem 1967, 45, 1619–1629. [Google Scholar]
- Butler, A.R.; Robertson, I.H.; Bacaloglu, R. Kinetics and mechanism of the base-catalysed hydrolysis of some substituted phenyl chloroformates. J. Chem. Soc. Perkin Trans 2 1974, 1733–1736. [Google Scholar]
- Yew, K.H.; Koh, H.J.; Lee, H.W.; Lee, I. Nucleophilic substitution reactions of phenyl chloroformate. J. Chem. Soc. Perkin Trans. 2 1995, 2263–2268. [Google Scholar]
- Koo, I.S.; Yang, K.; Kang, K.; Oh, H.K.; Lee, I. Stoichiometric solvation effects. Product-rate correlation for the solvolyses of phenyl chloroformate in alcohol-water mixtures. Bull. Korean Chem. Soc 1996, 17, 520–524. [Google Scholar]
- Kevill, D.N.; D’Souza, M.J. Correlation of the rates of solvolysis of phenyl chloroformate. J. Chem. Soc. Perkin Trans. 2 1997, 1721–1724. [Google Scholar]
- Koo, I.S.; Yang, K.; Koo, J.C.; Park, J.-K.; Lee, I. Stoichiometric solvation effects. Part 4. Product—Rate correlations for solvolyses of p-methoxyphenyl chloroformate in alcohol-water mixtures. Bull. Korean Chem. Soc 1997, 18, 1017–1021. [Google Scholar]
- Koo, I.S.; Yang, K.; Kang, K.; Lee, I.; Bentley, T.W. Stoichiometric solvation effects. Part 3. Product—Rate correlations for solvolyses of p-nitrophenyl chloroformate in alcohol-water mixtures. J. Chem. Soc. Perkin Trans 2 1998, 1179–1183. [Google Scholar]
- Koo, I.S.; Yang, K.; Kang, K.; Lee, I. Transition-state variation in the solvolyses of para-substituted phenyl chloroformates in alcohol-water mixtures. Bull. Korean Chem. Soc 1998, 19, 968–973. [Google Scholar]
- Kevill, D.N.; Koyoshi, F.; D’Souza, M.J. Correlation of the specific rates of solvolysis of aromatic carbamoyl chlorides, chloroformates, chlorothionoformates, and chlorodithioformates revisited. Int. J. Mol. Sci 2007, 8, 346–352. [Google Scholar]
- D’Souza, M.J.; Reed, D.; Koyoshi, F.; Kevill, D.N. Consideration of the factors influencing the specific rates of solvolysis of p-methoxyphenyl chloroformate. Int. J. Mol. Sci 2007, 8, 788–796. [Google Scholar]
- Castro, E.A.; Ruiz, M.G.; Salinas, S.; Santos, J.G. Kinetics and mechanism of the aminolysis of phenyl and 4-nitrophenyl chloroformates in aqueous solution. J. Org. Chem 1999, 64, 4817–4820. [Google Scholar]
- Castro, E.A.; Ruiz, M.G.; Santos, J.G. Structure-reactivity correlations in the aminolysis of aryl chloroformates. Int. J. Chem. Kinetics 2001, 281–287. [Google Scholar]
- Crugerias, J.; Leis, J.R.; Ríos, A. Micellar effects on the spontaneous hydrolysis of phenyl chloroformate. J. Chem. Educ 2001, 78, 1538–1540. [Google Scholar]
- Muňoz, M.; Rodríguez, A.; Graciani, M.d.M.; Moyá, M.L. Micellar medium effects on the hydrolysis of phenyl chloroformate in ionic, zwitterionic, nonionic, and mixed micellar solutions. Int. J. Chem. Kinetics 2002, 34, 445–451. [Google Scholar]
- Graciani, M.d.M.; Rodríguez, A.; Muňoz, M.; Moyá, M. Water-ethylene glycol alkyltrimethylammonium bromide micellar solutions as reaction media: Study of spontaneous hydrolysis of phenyl chloroformate. Langmuir 2003, 19, 8685–8691. [Google Scholar]
- McManus, S.P.; Safavy, A. Solvolysis in mixed solvents with complementary electrophilic and nucleophilic properties. Hexafluoro-2-propanol and 1,3-propanedithiol. J. Org. Chem 1986, 51, 3532–3535. [Google Scholar]
- Doherty, R.M.; Abraham, M.H.; Harris, J.M.; Taft, R.W.; Kamlet, M.J. Linear solvation energy relationships. 39. A double-difference method for estimating electrophilic solvent assistance effects in solvolysis reactions. J. Org. Chem 1986, 51, 4872–4875. [Google Scholar]
- Koo, I.S.; Lee, J.S.; Yang, K.; Kang, K.; Lee, I. The studies on substituent and kinetic solvent isotope effect in solvolyses of phenyl chloroformates. Bull. Korean Chem. Soc 1999, 20, 573–576. [Google Scholar]
- Kim, R.; Ali, D.; Lee, J.P.; Yang, K.; Koo, I.S. Correlation of the rates of solvolysis of 4-morpholinecarbonyl chloride using the extended Grunwald-Winstein equation. Bull. Korean Chem. Soc 2010, 31, 1963–1967. [Google Scholar]
- Choi, H.; Ali, D.; Lee, J.P.; Yang, K.; Park, J.K.; Koo, I.S. Correlation of the rates of solvolysis of 1-piperidincarbonyl chloride using the extended Grunwald-Winstein equation. Bull. Korean Chem. Soc 2011, 32, 3941–3946. [Google Scholar]
- Kevill, D.N.; Casamassa, A.J.; D’Souza, M.J. Rates and product selectivities for the solvolyses of 4-(chloroformyl)morpholine. J. Chem. Res. S 1996, 472–473. [Google Scholar]
- Chemical Compounds Database. Available online: http://www.chembase.com/cbid_84810.htm accessed on 8 October 2010.
- Kevill, D.N.; D’Souza, M.J. Concerning the two reaction channels for the solvolyses of ethyl chloroformate and ethyl chlorothioformate. J. Org. Chem 1998, 63, 2120–2124. [Google Scholar]
- Kyong, J.B.; Won, H.; Kevill, D.N. Application of the extended Grunwald-Winstein equation to solvolyses of n-propyl chloroformate. Int. J. Mol. Sci 2005, 6, 87–96. [Google Scholar]
- Kevill, D.N.; Kim, J.C.; Kyong, J.B. Correlation of the rates of solvolysis of methyl chloroformate and solvent properties. J. Chem. Res. S 1999, 150–151. [Google Scholar]
- Frost, A.A.; Pearson, R.G. Kinetics and Mechanism-a Study of Homogeneous Chemical Reactions, 2nd Ed ed; Wiley: New York, NY, USA, 1961; pp. 49–50. [Google Scholar]
- Kevill, D.N.; Abduljaber, M.H. Correlation of the rates of solvolysis of cyclopropylcarbinyl and cyclobutyl bromides using the extended Grunwald-Winstein equation. J. Org. Chem 2000, 65, 2548–2554. [Google Scholar]
- Microsoft Office, Excel 2010; Microsoft Corporation: Redmond, WA, USA, 2010.
- SigmaPlot, version 9.0; SYSTAT Software Inc.: San Jose, CA, USA, 2005.
- KnowItAll® Informatics System, ADME/Tox 2008; BioRad Laboratories: Philadelphia, PA, USA, 2008.
- D’Souza, M.J.; Dwyer, P.; Allison, B.E.; Miller, J.M.; Drohan, J. Wesley College ignites potential with undergraduate student research program. CUR Quart 2011, 32, 41–45. [Google Scholar]
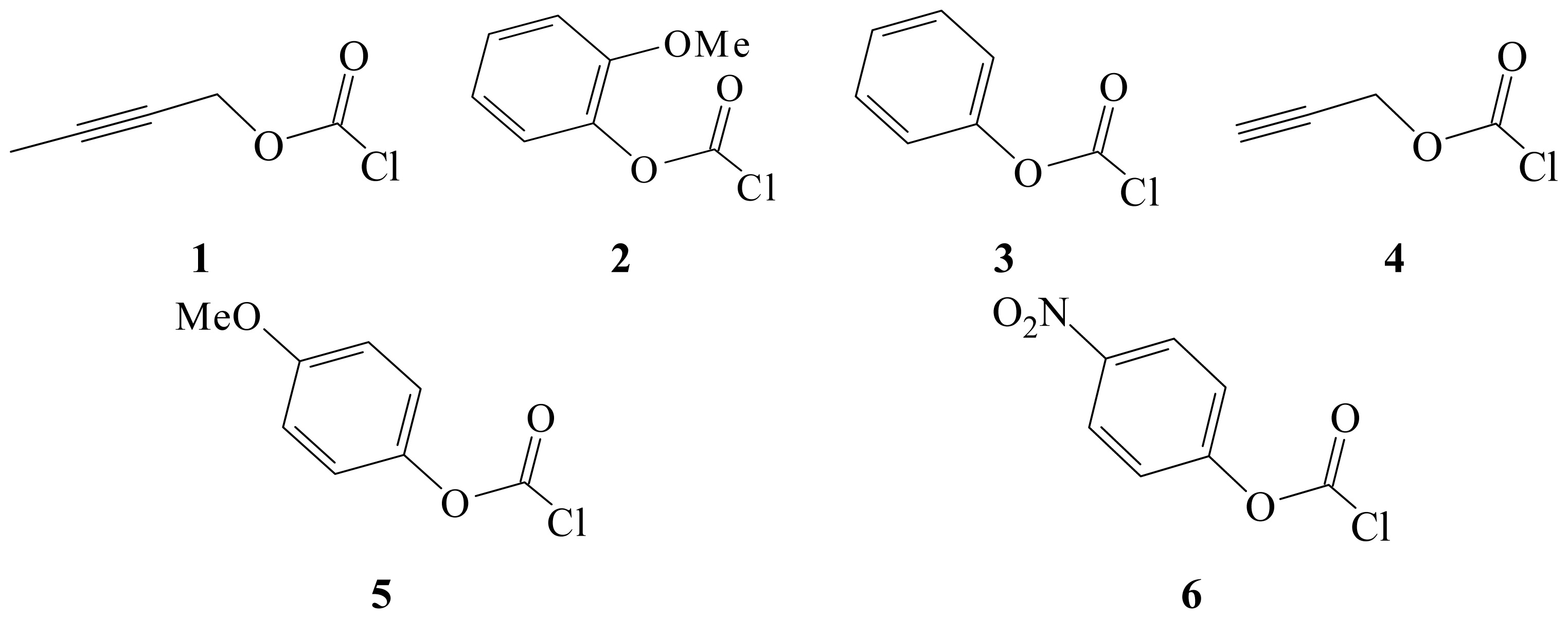

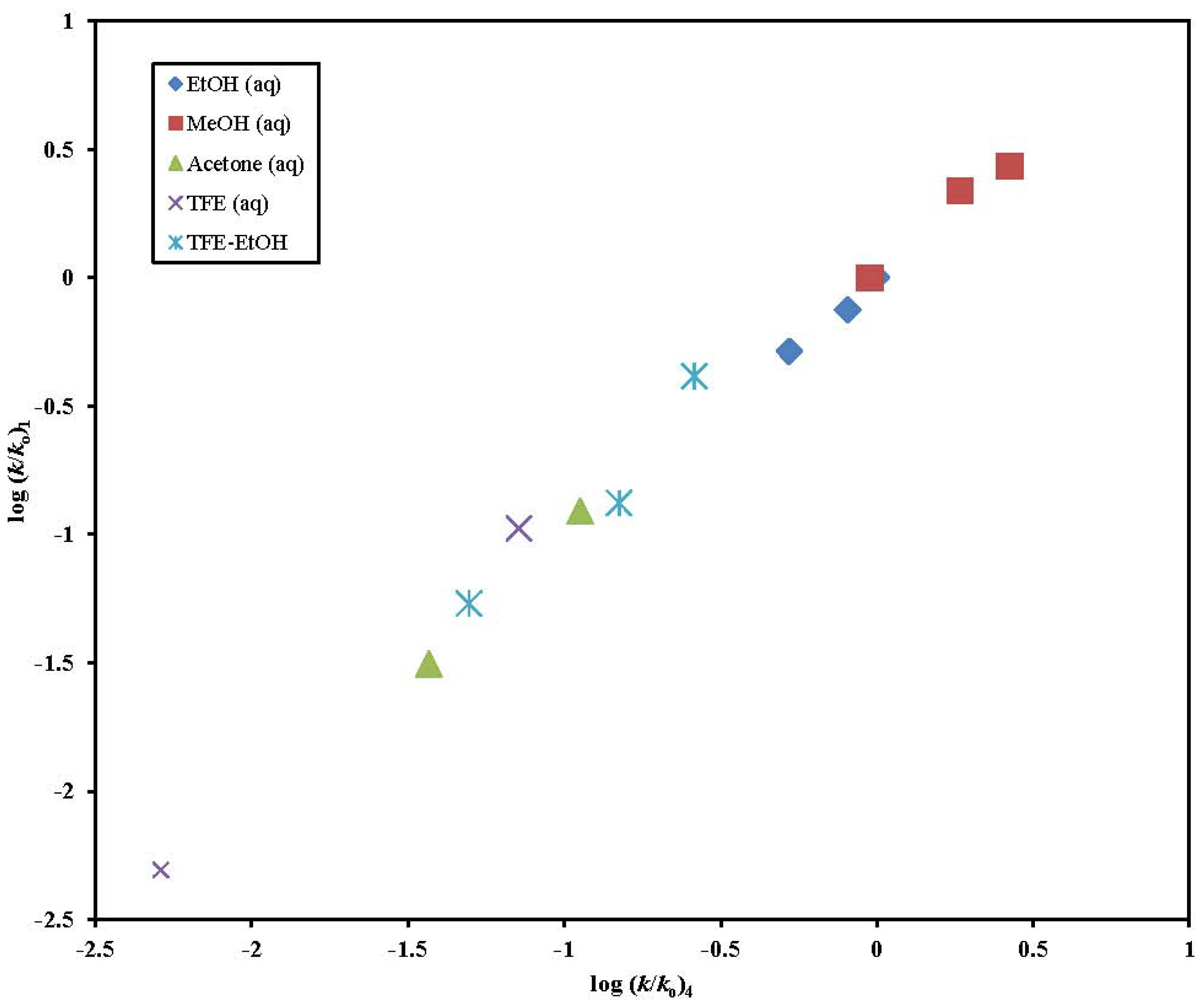

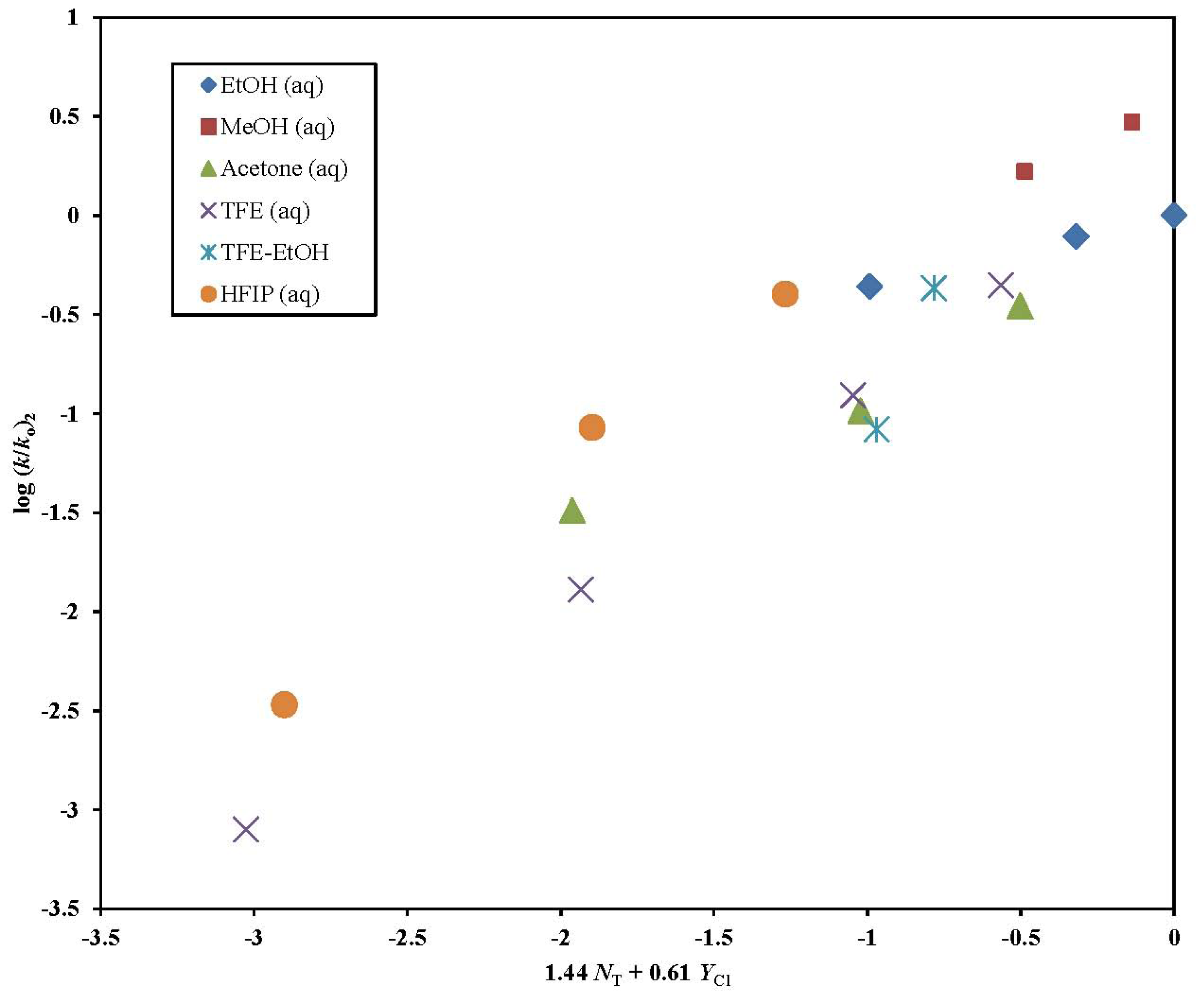
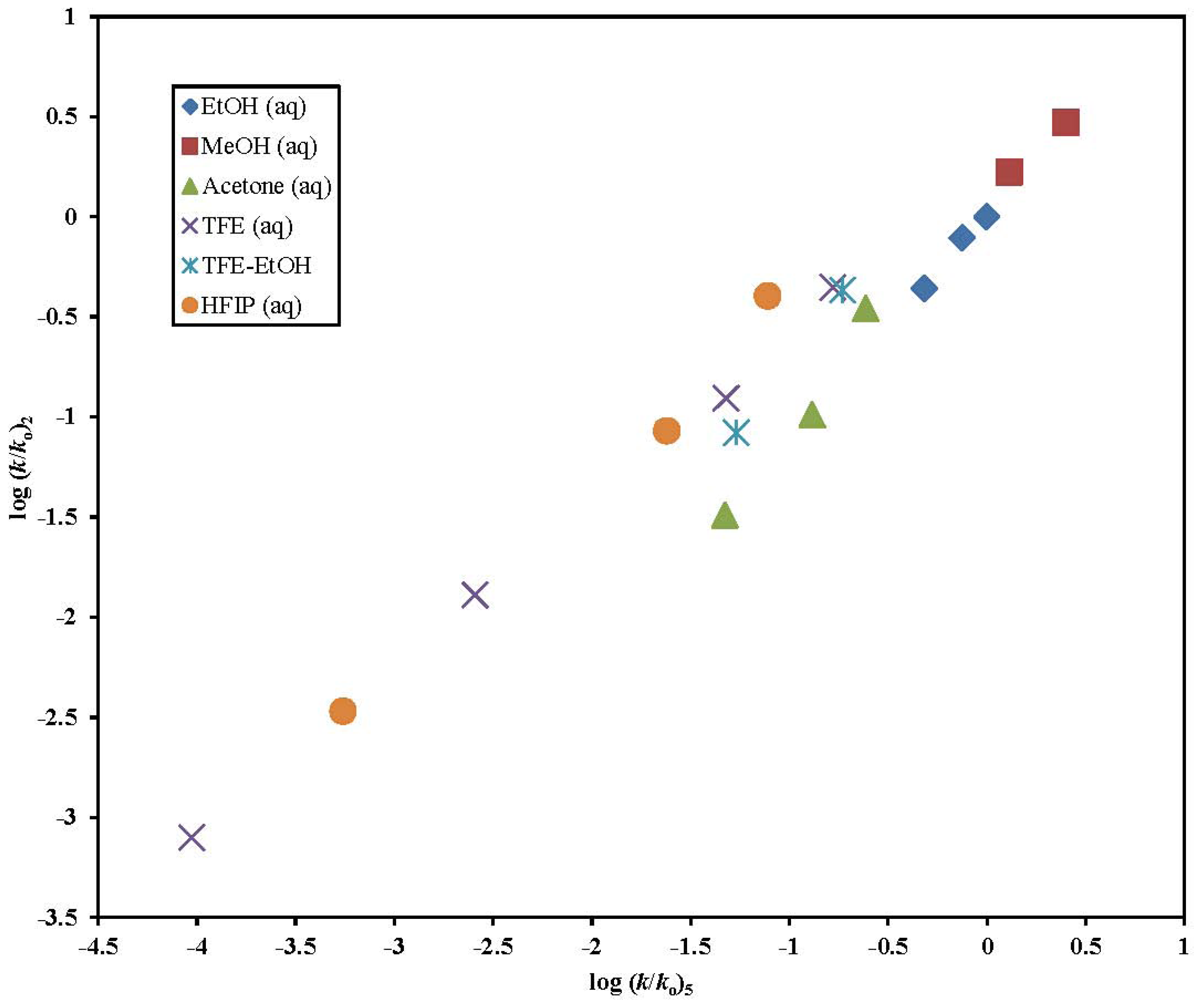
| Solvent (%) a | 1 @ 25.0 °C; 105 k, s−1b | 4 @ 25.0 °C; 105 k, s−1b,c | k1/k4 | NT d | YCl e |
|---|---|---|---|---|---|
| 100% MeOH | 34.0 ± 1.2 | 63.4 ± 1.2 | 0.536 | 0.17 | −1.2 |
| 90% MeOH | 74.2 ± 2.5 | 123 ± 3 | 0.603 | −0.01 | −0.20 |
| 80% MeOH | 92.9 ± 3.7 | 178 ± 10 | 0.522 | −0.06 | 0.67 |
| 100% EtOH | 17.6 ± 0.9 | 35.0 ± 0.8 | 0.503 | 0.37 | −2.50 |
| 90% EtOH | 25.6 ± 1.9 | 53.9 ± 1.2 | 0.474 | 0.16 | −0.90 |
| 80% EtOH | 34.2 ± 1.6 | 66.7 ± 1.6 | 0.513 | 0.00 | 0.00 |
| 90% Acetone | 1.07 ± 0.04 | 2.46 ± 0.10 | 0.435 | −0.35 | −2.39 |
| 80% Acetone | 4.21 ± 0.20 | 7.52 ± 0.22 | 0.560 | −0.37 | −0.80 |
| 70 % Acetone | 6.77 ± 0.24 | −0.42 | 0.17 | ||
| 90% TFE (w/w) | 0.168 ± 0.020 | 0.342 ± 0.007 | 0.491 | −2.55 | 2.85 |
| 70% TFE (w/w) | 3.62 ± 0.17 | 4.78 ± 0.07 | 0.757 | −1.98 | 2.96 |
| 60T-40E | 1.84 ± 0.12 | 3.31 ± 0.01 | 0.556 | −0.94 | 0.63 |
| 40T-60E | 4.52 ± 0.21 | 10.0 ± 0.2 | 0.452 | −0.34 | −0.48 |
| 20T-80E | 14.1 ± 1.4 | 17.4 ± 1.0 | 0.810 | 0.08 | −1.42 |
| 97%HFIP (w/w) | 0.413 ± 0.027 | 0.00116 ± 0.00009 | 356 | −5.26 | 5.17 |
| 90%HFIP (w/w) | 0.625 ± 0.029 | 0.0426 ± 0.0020 | 14.7 | −3.84 | 4.41 |
| 70%HFIP (w/w) | 1.47 ± 0.13 | 3.52 ± 0.18 f | 0.417 | −2.94 | 3.83 |
| 50%HFIP (w/w) | 5.61 ± 0.25 | −2.49 | 3.80 |
| Solvent (%)a | 2 @ 25.0 °C; 105 k, s−1b | 3 @ 25.0 °C; 105 k, s−1b,c | 5 @ 25.0 °C; 105 k, s−1b,d | k5/k2 | 6 @ 25.0 °C; 105 k, s−1b,e |
|---|---|---|---|---|---|
| 100% MeOH | 127 ± 17 | 695 ± 9 | 414 g | 3.25 | 13500 h |
| 90% MeOH | 226 ± 14 | 1290 f | 800 g | 3.54 | 22700 h |
| 100% EtOH | 33.3 ± 2.7 | 260 ± 3 | 153 ± 4 | 4.59 | 5570 h |
| 90% EtOH | 59.7 ± 2.4 | 389 ± 6 | 239 g | 4.00 | 11800 h |
| 80% EtOH | 76.3 ± 1.9 | 503 ± 11 | 318 g | 4.17 | 13900 h |
| 90% Acetone | 2.47 ± 0.13 | 23.8 ± 1.4 | 15.0 ± 0.6 | 6.07 | |
| 80% Acetone | 7.83 ± 0.17 | 68.8 ± 0.8 | 41.5 g | 5.30 | 2050 h |
| 70 % Acetone | 26.6 ± 0.82 | 125 f | 77.4 g | 2.91 | 3190 h |
| 97% TFE (w/w) | 0.0605 ± 0.0021 | 0.0570 ± 0.0030 | 0.0300 ± 0.0013 | 0.492 | 0.113 ± 0.008 |
| 90% TFE (w/w) | 0.976 ± 0.019 | 1.15 ± 0.08 | 0.825 ± 0.032 | 0.845 | 8.87 ± 0.28 |
| 70% TFE (w/w) | 9.43 ± 0.24 | 17.4 ± 1.3 | 15.2 ± 0.6 | 1.61 | 153 ± 1.5 |
| 50% TFE (w/w) | 33.7 ± 1.1 | 63.5 ± 3.0 | 52.6 ± 2.8 | 1.56 | 438 ± 44 |
| 60T-40E | 6.39 ± 0.22 | 19.9 ± 0.5 | 17.0 ± 0.5 | 2.66 | |
| 40T-60E | 32.7 ± 1.2 | 57.7 ± 1.9 | 59.2 ± 2.3 | 1.81 | |
| 90%HFIP (w/w) | 0.258 ± 0.018 | 0.166 ± 0.004 | 0.175 ± 0.007 | 0.678 | 1.20 ± 0.06 |
| 70%HFIP (w/w) | 6.48 ± 0.20 | 10.5 ± 0.3 | 7.58 ± 0.22 | 1.17 | 83.8 ± 0.9 |
| 50%HFIP (w/w) | 30.5 ± 0.18 | 31.6 ± 0.6 | 24.9 ± 0.5 | 0.816 | 277 ± 2 |
| Substrate | n a | l b | m b | l/m | c c | R d | F e |
|---|---|---|---|---|---|---|---|
| 1 | 18 | 0.78 ± 0.18 | 0.31 ± 0.12 | 2.52 | −0.15 ± 0.17 | 0.832 | 17 |
| 14 f | 1.50 ± 0.15 | 0.49 ± 0.08 | 3.06 | 0.15 ± 0.10 | 0.956 | 58 | |
| 13 f,g | 1.52 ± 0.14 | 0.51 ± 0.07 | 2.98 | 0.18 ± 0.10 | 0.963 | 63 | |
| 2 | 17 | 1.44 ± 0.16 | 0.61 ± 0.10 | 2.36 | 0.32 ± 0.14 | 0.941 | 54 |
| 3 | 49 h | 1.66 ± 0.05 | 0.56 ± 0.03 | 2.96 | 0.15 ± 0.07 | 0.980 | 568 |
| 17 i | 1.58 ± 0.17 | 0.54 ± 0.10 | 2.93 | 0.21 ± 0.15 | 0.958 | 79 | |
| 4 | 22 | 1.37 ± 0.10 | 0.47 ± 0.07 | 2.91 | 0.11± 0.11 | 0.970 | 152 |
| 13 f,g | 1.49 ± 0.13 | 0.48± 0.07 | 3.10 | 0.14 ± 0.09 | 0.969 | 77 | |
| 5 | 44 j | 1.60 ± 0.05 | 0.57 ± 0.05 | 2.81 | 0.18 ± 0.06 | 0.981 | 517 |
| 17 i | 1.60 ± 0.17 | 0.57 ± 0.10 | 2.81 | 0.26 ± 0.15 | 0.958 | 78 | |
| 6 | 39 k | 1.68 ± 0.06 | 0.46 ± 0.04 | 3.65 | 0.074 ± 0.08 | 0.976 | 363 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
D’Souza, M.J.; Knapp, J.A.; Fernandez-Bueno, G.A.; Kevill, D.N. Use of Linear Free Energy Relationships (LFERs) to Elucidate the Mechanisms of Reaction of a γ-Methyl-β-alkynyl and an ortho-Substituted Aryl Chloroformate Ester. Int. J. Mol. Sci. 2012, 13, 665-682. https://doi.org/10.3390/ijms13010665
D’Souza MJ, Knapp JA, Fernandez-Bueno GA, Kevill DN. Use of Linear Free Energy Relationships (LFERs) to Elucidate the Mechanisms of Reaction of a γ-Methyl-β-alkynyl and an ortho-Substituted Aryl Chloroformate Ester. International Journal of Molecular Sciences. 2012; 13(1):665-682. https://doi.org/10.3390/ijms13010665
Chicago/Turabian StyleD’Souza, Malcolm J., Jaci A. Knapp, Gabriel A. Fernandez-Bueno, and Dennis N. Kevill. 2012. "Use of Linear Free Energy Relationships (LFERs) to Elucidate the Mechanisms of Reaction of a γ-Methyl-β-alkynyl and an ortho-Substituted Aryl Chloroformate Ester" International Journal of Molecular Sciences 13, no. 1: 665-682. https://doi.org/10.3390/ijms13010665
APA StyleD’Souza, M. J., Knapp, J. A., Fernandez-Bueno, G. A., & Kevill, D. N. (2012). Use of Linear Free Energy Relationships (LFERs) to Elucidate the Mechanisms of Reaction of a γ-Methyl-β-alkynyl and an ortho-Substituted Aryl Chloroformate Ester. International Journal of Molecular Sciences, 13(1), 665-682. https://doi.org/10.3390/ijms13010665




