Nucleated Polymerisation in the Presence of Pre-Formed Seed Filaments
Abstract
:1. Introduction
2. Results and Discussion
2.1. Derivation of the Rate Laws for the Polymer Number and Mass Concentrations
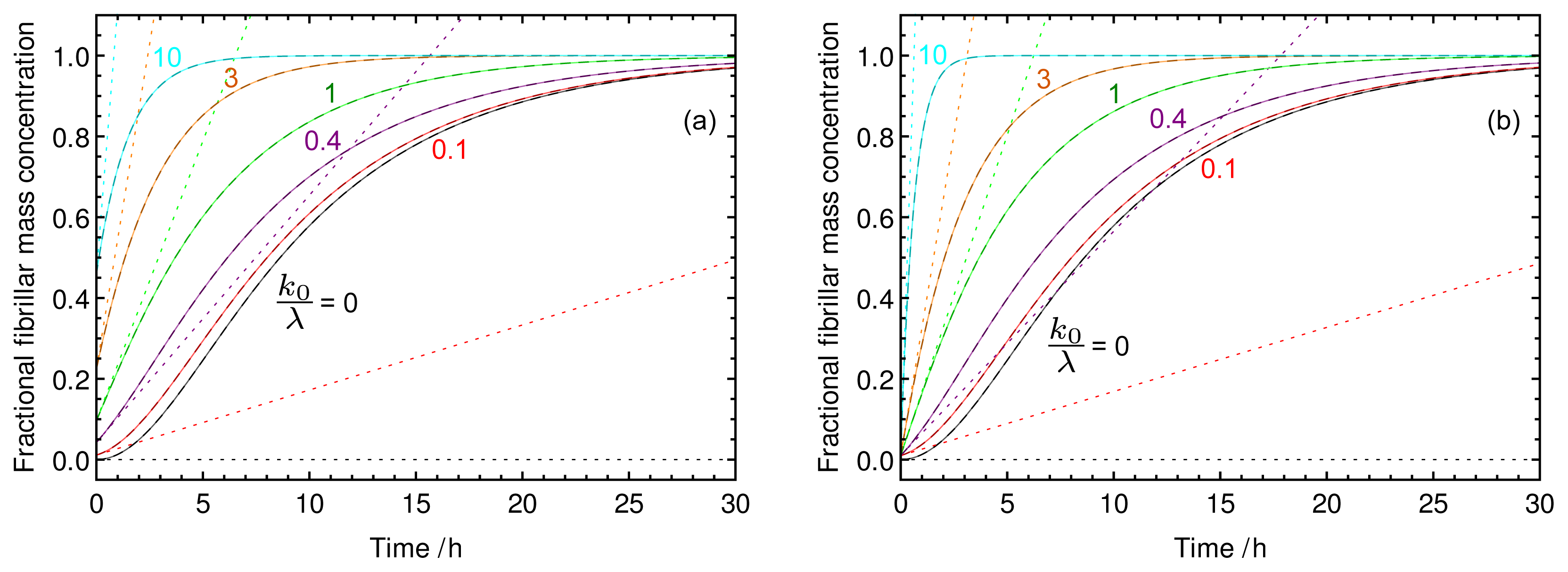
2.2. Characteristic Features of Growth Involving Pre-Formed Seed Material
2.3. Comparison between Nucleated Polymerisation in the Presence and Absence of Secondary Pathways
3. Conclusions
Acknowledgements
References
- Oosawa, F; Asakura, S. Thermodynamics of the Polymerization of Protein; Academic Press: Waltham, MA, USA, 1975. [Google Scholar]
- Gibbs, JW. On the equilibrium of heterogeneous substances. Trans Conn Acad Arts Sci 1878, 3, 108–343. [Google Scholar]
- Volmer, M; Weber, A. Keimbildung in übersättigten Gebilden. Z Phys Chem 1926, 119, 277. [Google Scholar]
- Kaischew, R; Stranski, IN. The theory of the linear rate of crystallisation. Z Phys Chem 1934, A170, 295. [Google Scholar]
- Stranski, IN; Kaischew, R. Crystal growth and crystal nucleation. Z Phys 1935, 36, 393. [Google Scholar]
- Becker, R; Döring, W. Kinetische Behandlung der Keimbildung in übersättigten Dämpfen. Ann Phys 1935, 24, 719–752. [Google Scholar]
- Avrami, M. Kinetics of phase change. I General theory. J Chem Phys 1939, 7, 1103–1112. [Google Scholar]
- Oosawa, F; Kasai, M. A theory of linear and helical aggregations of macromolecules. J Mol Biol 1962, 4, 10–21. [Google Scholar]
- Ferrone, FA; Hofrichter, J; Sunshine, HR; Eaton, WA. Kinetic studies on photolysis-induced gelation of sickle cell hemoglobin suggest a new mechanism. Biophys J 1980, 32, 361–380. [Google Scholar]
- Bishop, MF; Ferrone, FA. Kinetics of nucleation-controlled polymerization. A perturbation treatment for use with a secondary pathway. Biophys J 1984, 46, 631–644. [Google Scholar]
- Ferrone, FA; Hofrichter, J; Eaton, WA. Kinetics of sickle hemoglobin polymerization. II. A double nucleation mechanism. J Mol Biol 1985, 183, 611–631. [Google Scholar]
- Wegner, A; Savko, P. Fragmentation of actin filaments. Biochemistry 1982, 21, 1909–1913. [Google Scholar]
- Wegner, A. Spontaneous fragmentation of actin filaments in physiological conditions. Nature 1982, 296, 266–267. [Google Scholar]
- Hofrichter, J; Ross, PD; Eaton, WA. Kinetics and mechanism of deoxyhemoglobin S gelation: A new approach to understanding sickle cell disease. Proc Natl Acad Sci USA 1974, 71, 4864–4868. [Google Scholar]
- Firestone, MP; De Levie, R; Rangarajan, SK. On one-dimensional nucleation and growth of ”living” polymers. I. Homogeneous nucleation. J Theor Biol 1983, 104, 535–552. [Google Scholar]
- Goldstein, RF; Stryer, L. Cooperative polymerization reactions. Analytical approximations, numerical examples, and experimental strategy. Biophys J 1986, 50, 583–599. [Google Scholar]
- Ataka, M; Ogawa, T. Nucleation and growth of oxide precipitates in CZ-Si wafers. J Mater Res 1993, 11, 2889–2992. [Google Scholar]
- Bessho, Y; Ataka, M; Asai, M; Katsura, T. Analysis of the crystallization kintics of lysozyme using a model with polynuclear growth mechanism. Biophys J 1994, 66, 310–313. [Google Scholar]
- Flyvbjerg, H; Jobs, E; Leibler, S. Kinetics of self-assembling microtubules: An “inverse problem” in biochemistry. Proc Natl Acad Sci USA 1996, 93, 5975–5979. [Google Scholar]
- Lomakin, A; Teplow, DB; Kirschner, DA; Benedek, GB. Kinetic theory of fibrillogenesis of amyloid beta-protein. Proc Natl Acad Sci USA 1997, 94, 7942–7947. [Google Scholar]
- Ferrone, F. Analysis of protein aggregation kinetics. Methods Enzymol 1999, 309, 256–274. [Google Scholar]
- Murphy, RM; Pallitto, MM. Probing the kinetics of beta-amyloid self-association. J Struct Biol 2000, 130, 109–122. [Google Scholar]
- Serio, TR; Cashikar, AG; Kowal, AS; Sawicki, GJ; Moslehi, JJ; Serpell, L; Arnsdorf, MF; Lindquist, SL. Nucleated conformational conversion and the replication of conformational information by a prion determinant. Science 2000, 289, 1317–1321. [Google Scholar]
- Chen, S; Ferrone, FA; Wetzel, R. Huntington’s disease age-of-onset linked to polyglutamine aggregation nucleation. Proc Natl Acad Sci USA 2002, 99, 11884–11889. [Google Scholar]
- Andrews, JM; Roberts, CJ. A Lumry-Eyring nucleated polymerization model of protein aggregation kinetics: 1. Aggregation with pre-equilibrated unfolding. J Phys Chem B 2007, 111, 7897–7913. [Google Scholar]
- Cohen, SIA; Vendruscolo, M; Welland, ME; Dobson, CM; Terentjev, EM; Knowles, TPJ. Nucleated polymerization with secondary pathways. I. Time evolution of the principal moments. J Chem Phys 2011, 135, 065105:1–065105:16. [Google Scholar]
- Cohen, SIA; Vendruscolo, M; Dobson, CM; Knowles, TPJ. Nucleated polymerization with secondary pathways. II. Determination of self-consistent solutions to growth processes described by non-linear master equations. J Chem Phys 2011, 135, 065106:1–065106:18. [Google Scholar]
- Cohen, SIA; Vendruscolo, M; Dobson, CM; Knowles, TPJ. Nucleated polymerization with secondary pathways. III. Equilibrium behavior and oligomer populations. J Chem Phys 2011, 135, 065107:1–065107:10. [Google Scholar]
- Knowles, TPJ; Waudby, CA; Devlin, GL; Cohen, SIA; Aguzzi, A; Vendruscolo, M; Terentjev, EM; Welland, ME; Dobson, CM. An analytical solution to the kinetics of breakable filament assembly. Science 2009, 326, 1533–1537. [Google Scholar]
- Fändrich, M. Absolute correlation between lag time and growth rate in the spontaneous formation of several amyloid-like aggregates and fibrils. J Mol Biol 2007, 365, 1266–1270. [Google Scholar]
- Hellstrand, E; Boland, B; Walsh, DM; Linse, S. Amyloid β-protein aggregation produces highly reproducible kinetic data and occurs by a two-phase process. ACS Chem Neurosci 2010, 1, 13–18. [Google Scholar]
- Wegner, A. Kinetic analysis of actin assembly suggests that tropomyosin inhibits spontaneous fragmentation of actin filaments. J Mol Biol 1982, 161, 217–227. [Google Scholar]
- Andersen, CB; Yagi, H; Manno, M; Martorana, V; Ban, T; Christiansen, G; Otzen, DE; Goto, Y; Rischel, C. Branching in amyloid fibril growth. Biophys J 2009, 96, 1529–1536. [Google Scholar]
- Collins, SR; Douglass, A; Vale, RD; Weissman, JS. Mechanism of prion propagation: Amyloid growth occurs by monomer addition. PLoS Biol 2004, 2, e321. [Google Scholar]
- Meinhardt, J; Tartaglia, GG; Pawar, A; Christopeit, T; Hortschansky, P; Schroeckh, V; Dobson, CM; Vendruscolo, M; Fändrich, M. Similarities in the thermodynamics and kinetics of aggregation of disease-related Abeta (1–40) peptides. Protein Sci 2007, 16, 1214–1222. [Google Scholar]
- Auer, S; Kashchiev, D. Insight into the correlation between lag time and aggregation rate in the kinetics of protein aggregation. Proteins 2010, 78, 2412–2416. [Google Scholar]
| Primary nucleation | Fragmentation | Monomer-dependent secondary nucleation | |
|---|---|---|---|
| Kinetic parameters | λ, k+ | λ, κ−, k+ | λ, κ2, k+ |
| Early time growth | Polynomial | Exponential | Exponential |
| Scaling behaviour (lag time, max growth rate) | Yes with λ | Yes with κ− | Yes with κ2 |
| Positive feedback | No | Yes | Yes |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cohen, S.I.A.; Vendruscolo, M.; Dobson, C.M.; Knowles, T.P.J. Nucleated Polymerisation in the Presence of Pre-Formed Seed Filaments. Int. J. Mol. Sci. 2011, 12, 5844-5852. https://doi.org/10.3390/ijms12095844
Cohen SIA, Vendruscolo M, Dobson CM, Knowles TPJ. Nucleated Polymerisation in the Presence of Pre-Formed Seed Filaments. International Journal of Molecular Sciences. 2011; 12(9):5844-5852. https://doi.org/10.3390/ijms12095844
Chicago/Turabian StyleCohen, Samuel I. A., Michele Vendruscolo, Christopher M. Dobson, and Tuomas P. J. Knowles. 2011. "Nucleated Polymerisation in the Presence of Pre-Formed Seed Filaments" International Journal of Molecular Sciences 12, no. 9: 5844-5852. https://doi.org/10.3390/ijms12095844




