Prediction of Lysine Ubiquitylation with Ensemble Classifier and Feature Selection
Abstract
:1. Introduction
2. Materials and Methods
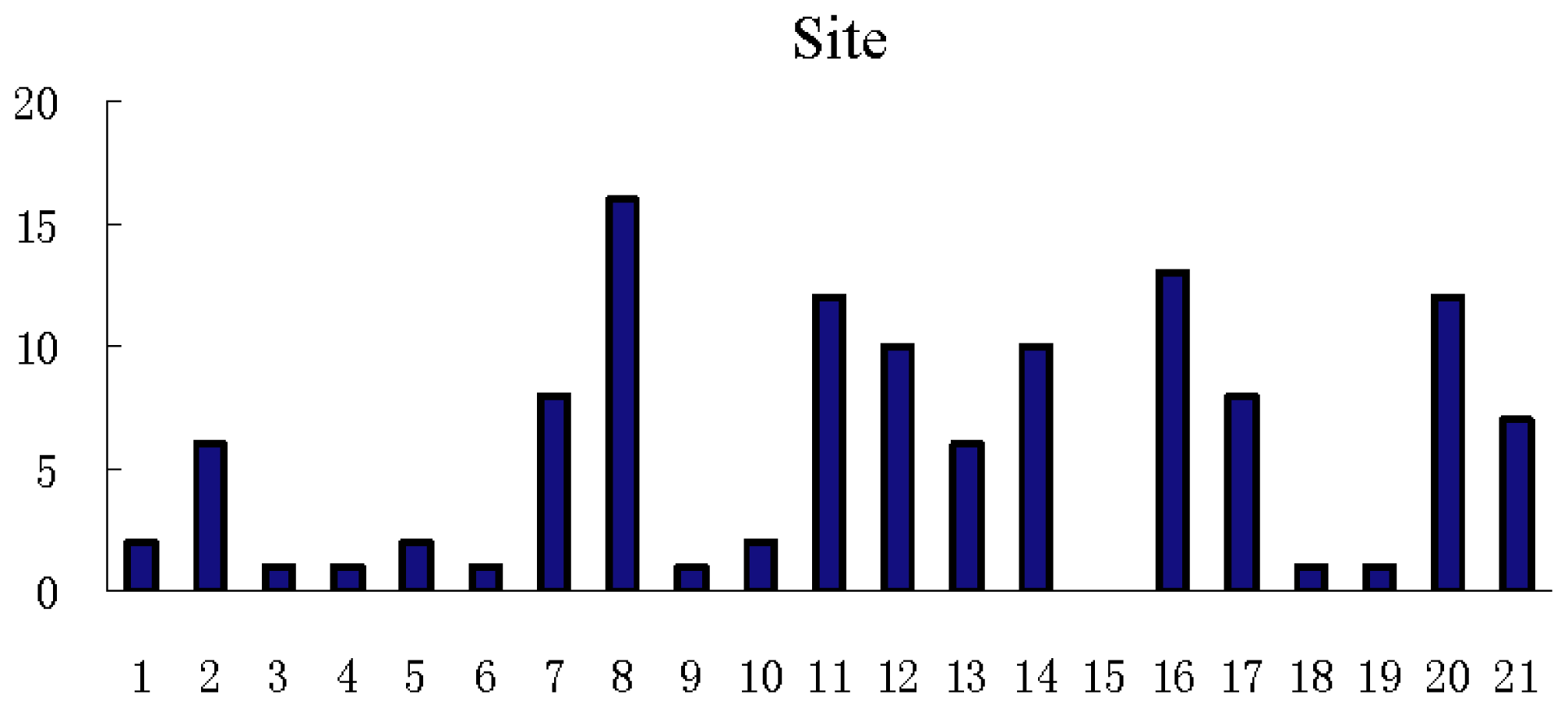
2.1. Data Sets
2.2. Representation of Peptides
2.2.1. Amino Acid Compositions
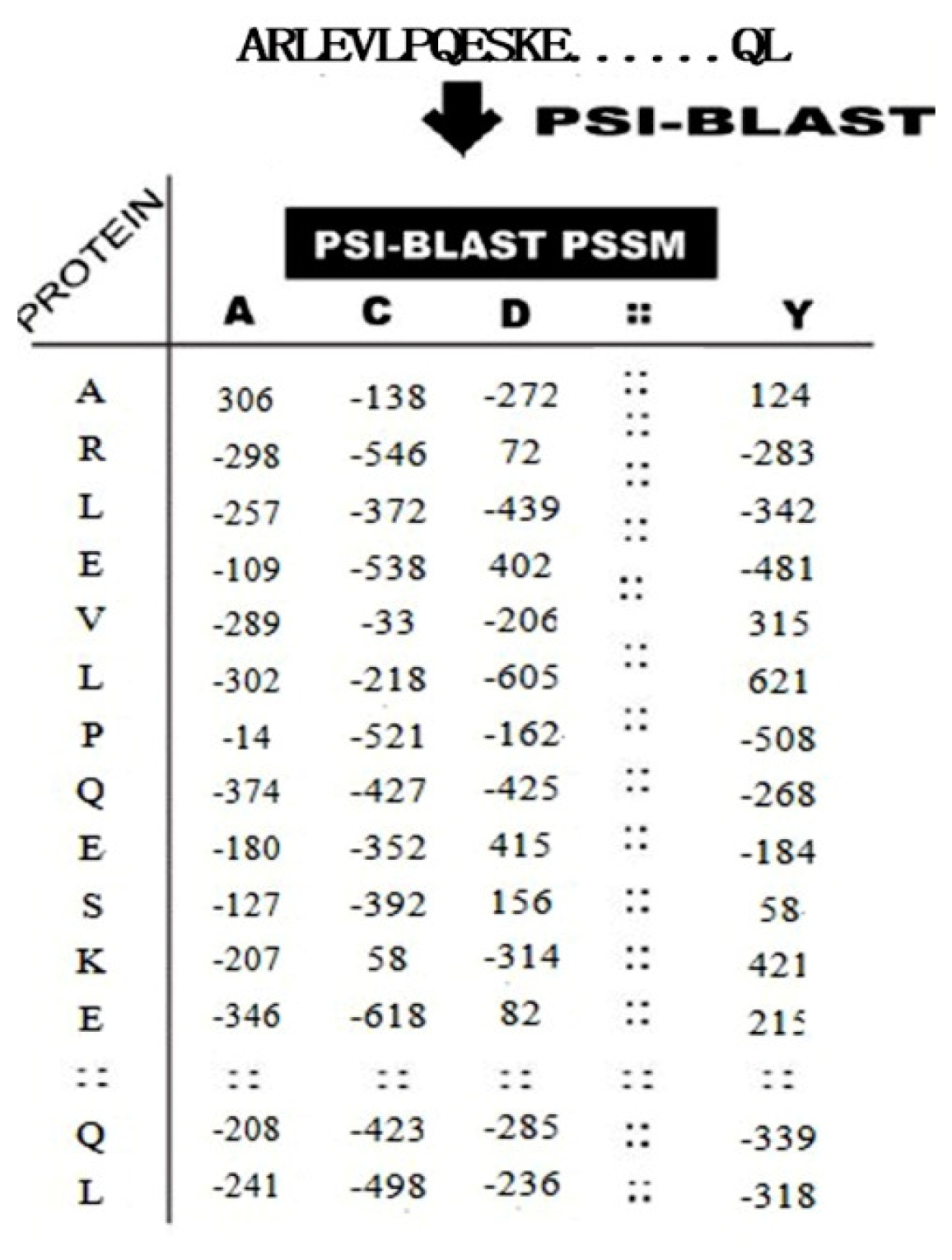
2.2.2. PSSM Conservation Scores
2.2.3. Disorder Scores
2.2.4. Amino Acid Factors
2.2.5. Feature Space
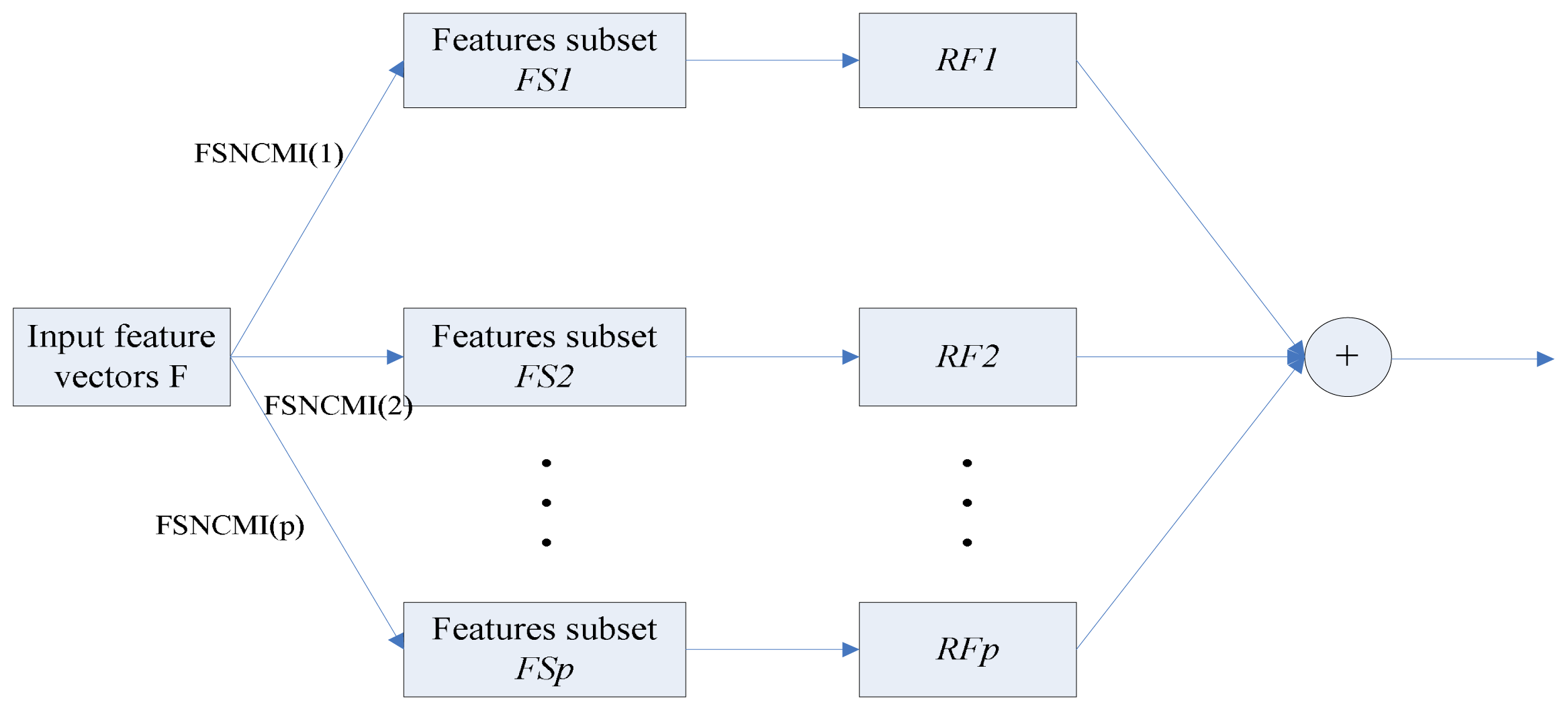
2.3. Feature Selection Based on Normalized Conditional Mutual Information
| (1) | Initialize related parameters, FSi =Ø, F = F, t = 0; |
| (2) | For each feature f ε F do |
| (3) | calculate its mutual information with the target classes C; |
| (4) | Sort them in a descending order; |
| (5) | FSi = {ft}, F = F − {ft}, where ft is the starting point; |
| (6) | While |FSi| < k do |
| (7) | For each feature f ε F do |
| (8) | Calculate its criterion J(f) according to Equation.(4); |
| (9) | If J(f) = 0 then F = F − {f}; |
| (10) | Select the gene with the largest J(f); |
| (11) | FSi = FSi ∪{f}, F = F − {f}; |
| (12) | End |
2.4. Random Forests Classification
2.5. Model Building
2.6. Evaluation
3. Results and Discussion
3.1. Prediction Performance of Our Method
3.2. Comparison with Existing Methods
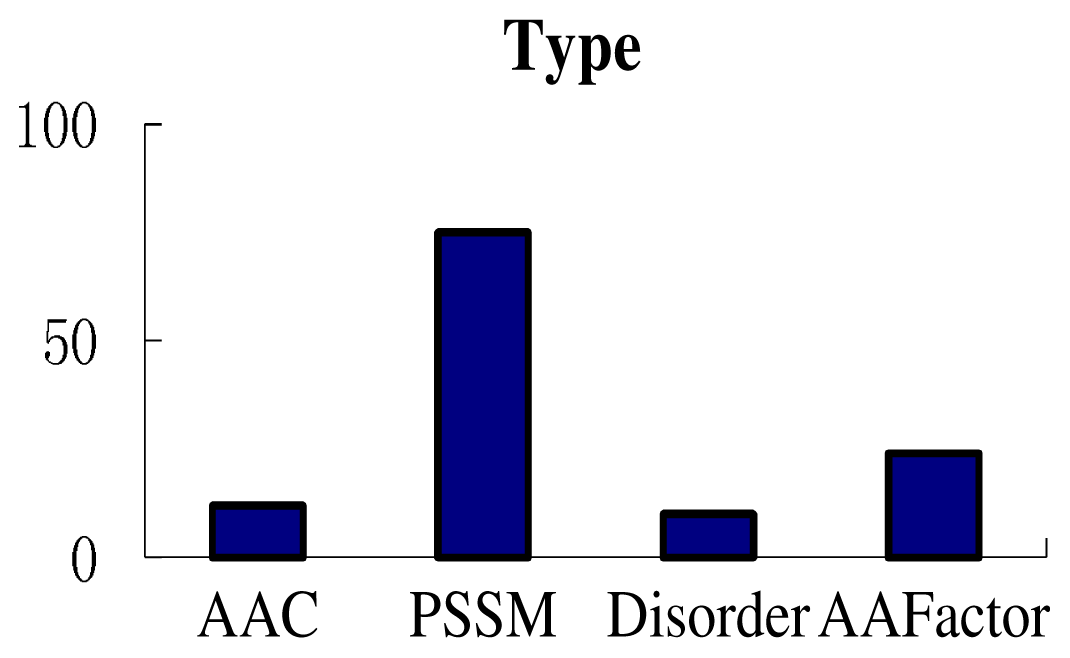
3.3. Feature Analysis
4. Conclusions
Acknowledgments
References
- Pickart, C.M. Ubiquitin enters the new millennium. Mol. Cell 2001, 8, 499–504. [Google Scholar]
- Aguilar, R.C.; Wendland, B. Ubiquitin: Not just for proteasomes anymore. Curr. Opin. Cell Biol 2003, 15, 184–190. [Google Scholar]
- Saghatelian, A.; Cravatt, B.F. Assignment of protein function in the postgenomic era. Nat. Chem. Biol 2005, 1, 130–142. [Google Scholar]
- Herrmann, J.; Lerman, L.O.; Lerman, A. Ubiquitin and ubiquitin-like proteins in protein regulation. Circ. Res 2007, 100, 1276–1291. [Google Scholar]
- Hicke, L.; Dunn, R. Regulation of membrane protein transport by ubiquitin and ubiquiti-binding proteins. Annu. Rev. Cell Dev. Biol 2003, 19, 141–172. [Google Scholar]
- Welchman, R.L.; Gordon, C.; Mayer, R.J. Ubiquitin and ubiquitin-like proteins as multifunctional signals. Nat. Rev. Mol. Cell Biol 2005, 6, 599–609. [Google Scholar]
- Hershko, A.; Ciechanover, A. The ubiquitin system. Annu. Rev. Biochem 1998, 67, 425–479. [Google Scholar]
- Hicke, L. Protein regulation by monoubiquitin. Nat. Rev. Mol. Cell Biol 2001, 2, 195–201. [Google Scholar]
- Denis, N.J.; Vasilescu, J.; Lambert, J.P.; Smith, J.C.; Figeys, D. Tryptic digestion of ubiquitin standards reveals an improved strategy for identifying ubiquitinated proteins by mass spectrometry. Proteomics 2007, 7, 868–874. [Google Scholar]
- Hitchcock, A.L.; Auld, K.; Gygi, S.P.; Silver, P.A. A subset of membrane-associated proteins is ubiquitinated in response to mutations in the endoplasmic reticulum degradation machinery. Proc. Natl. Acad. Sci. USA 2003, 100, 12735–12740. [Google Scholar]
- Jeon, H.B.; Choi, E.S.; Yoon, J.F.; Hwang, J.H.; Chang, J.W.; Lee, E.K.; Choi, H.W.; Park, Z.Y.; Yoo, Y.J. A proteomics approach to identify the ubiquitinated proteins in mouse heart. Biochem. Biophys. Res. Commun 2007, 357, 731–736. [Google Scholar]
- Kirkpatrick, D.S.; Weldon, S.F.; Tsaprailis, G.; Liebler, D.C.; Gandolfi, A.J. Proteomic identification of ubiquitinated proteins from human cells expressing His-tagged ubiquitin. Proteomics 2005, 5, 2104–2111. [Google Scholar]
- Tung, C.W.; Ho, S.Y. Computational identification of ubiquitylation sites from protein sequences. BMC Bioinf 2008, 9, 310–324. [Google Scholar]
- Radivojac, P.; Vacic, V.; Haynes, C.; Cocklin, R.R.; Mohan, A.; Heyen, J.W.; Goebl, M.G.; Iakoucheva, L.M. Identification, analysis, and prediction of protein ubiquitination sites. Proteins 2010, 78, 365–380. [Google Scholar]
- Cai, Y.; Huang, T.; Hu, L.; Shi, X.; Xie, L.; Li, Y. Prediction of lysine ubiquitination with mRMR feature selection and analysis. Amino Acids 2011, 17, 273–281. [Google Scholar]
- Roy, S.; Martinez, A.D.; Platero, H.; Lane, T.; Werner-Washburne, M. Exploiting amino acid composition for predicting protein-protein interactions. PLoS One 2009, 4. [Google Scholar] [CrossRef]
- Jones, D.T. Improving the accuracy of transmembrane protein topology prediction using evolutionary information. Bioinformatics 2007, 23, 538–544. [Google Scholar]
- Kaur, H.; Raghava, G.P. A neural network method for prediction of beta-turn types in proteins using evolutionary information. Bioinformatics 2004, 20, 2751–2758. [Google Scholar]
- Atchey, W.R.; Zhao, J.; Fernandes, A.D.; Druke, T. Solving the protein sequence metric problem. Proc. Natl. Acad. Sci. USA 2005, 102, 6395–6400. [Google Scholar]
- Peng, K.; Radivojac, P.; Vucetic, S.; Dunker, A.K.; Obradovic, Z. Length-dependent prediction of protein intrinsic disorder. BMC Bioinf 2006, 7, 208–216. [Google Scholar]
- Boeckmann, B.; Bairoch, A.; Apweiler, R.; Blatter, M.C.; Estreicher, A.; Gasteiger, E.; Martin, M.J.; Michoud, K.; O’Donovan, C.; Phan, I.; Pilbout, S.; Schneider, M. The SWISS-PROT protein knowledgebase and its supplement TrEMBL. Nucleic Acids Res 2003, 31, 365–370. [Google Scholar]
- UniProt database. Available online: http://www.uniprot.org/ Accessed on 26 May 2010.
- Li, W.; Godzik, A. Cd-hit: A fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics 2006, 22, 1658–1659. [Google Scholar]
- Anand, A.; Pugalenthi, G.; Suganthan, P.N. Predicting Protein Structural Class by SVM with Class-wise Optimized Features and Decision Probabilities. J. Theor. Biol 2008, 253, 375–380. [Google Scholar]
- Xiao, X.; Wang, P.; Chou, K.C. Predicting protein structural classes with pseudo amino acid composition: An approach using geometric moments of cellular automaton image. J. Theor. Biol 2008, 254, 691–696. [Google Scholar]
- Pugalenthi, G.; Tang, K.; Suganthan, P.N.; Archunan, G.; Sowdhamini, R. A machine learning approach for the identification of odorant binding proteins from sequence-derived properties. BMC Bioinf 2007, 19, 351–362. [Google Scholar]
- NR database. Available online: ftp://ftp.ncbi.nih.gov/blast/db/nr Accessed on 23 June 2011.
- Altschul, S.F.; Madden, T.L.; Schaffer, A.A.; Zhang, J.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res 1997, 25, 3389–3402. [Google Scholar]
- Wright, P.E.; Dyson, H.J. Intrinsically unstructured proteins: Reassessing the protein structure-function paradigm. J. Mol. Biol 1999, 293, 321–331. [Google Scholar]
- Dunker, A.K.; Brown, C.J.; Lawson, J.D.; Iakoucheva, L.M.; Obradovic, Z. Intrinsic disorder and protein function. Biochemistry 2002, 41, 6573–6582. [Google Scholar]
- Liu, J.; Tan, H.; Rost, B. Loopy proteins appear conserved in evolution. J. Mol. Biol 2002, 322, 53–64. [Google Scholar]
- Tompa, P. Intrinsically unstructured proteins. Trends Biochem. Sci 2002, 27, 527–533. [Google Scholar]
- Peng, K.; Radivojac, P.; Vucetic, S.; Dunker, A.K.; Obradovuc, Z. Length-dependent prediction of protein intrinsic disorder. BMC Bioinf 2006, 7, 208–217. [Google Scholar]
- Bordoli, L.; Kiefer, F.; Schwede, T. Assessment of disorder predictions in CASP7. Proteins 2007, 69, 129–136. [Google Scholar]
- He, B.; Wang, K.; Liu, Y.; Xue, B.; Uversky, V.N.; Dunker, A.K. Predicting intrinsic disorder in proteins: an overview. Cell Res 2009, 19, 929–949. [Google Scholar]
- Matsumoto, M.; Hatakeyama, S.; Oyamada, K.; Oda, Y.; Nishimura, T.; Nakayama, K.I. Large-scale analysis of the human ubiquitin-related proteome. Proteomics 2005, 5, 4145–4151. [Google Scholar]
- Peng, J.; Schwartz, D.; Elias, J.E.; Thoreen, C.C.; Cheng, D.; Marsischky, G.; Roelofs, J.; Finley, D.; Gygi, S.P. A proteomics approach to understanding protein ubiquitination. Nat. Biotechnol 2003, 21, 921–926. [Google Scholar]
- Kawashima, S.; Pokarowski, P.; Pokarowska, M.; Kolinski, A.; Katayama, T.; Kanehisa, M. AAindex: amino acid index database, progress report. Nucleic Acids Res 2008, 36, 202–205. [Google Scholar]
- Levi, D.; Ullman, S. Learning to classify by ongoing feature selection. Image Vis. Comput 2010, 28, 715–723. [Google Scholar]
- Liu, H.W.; Liu, L.; Zhang, H.J. Ensemble gene selection for cancer classification. Pattern Recognit 2010, 43, 2763–2772. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Fleuret, F. Fast binary feature selection with conditional mutual information. J. Mach. Learn. Res 2004, 5, 1531–1555. [Google Scholar]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res 2004, 5, 1205–1224. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
- Sikic, M.; Tomic, S.; Vlahovicek, K. Prediction of protein-protein interaction sites in sequences and 3D structures by random forests. PLoS Comput. Biol 2009, 5, e1000278:1–e1000278:9. [Google Scholar]
- Wu, J.; Liu, H.; Duan, X.; Ding, Y.; Wu, H.; Bai, Y.; Sun, X. Prediction of DNA-binding residues in proteins from amino acid sequences using a random forest model with a hybrid feature. Bioinformatics 2009, 25, 30–35. [Google Scholar]
- Ma, X.; Guo, J.; Wu, J.; Liu, H.; Yu, J.; Xie, J.; Sun, X. Prediction of RNA-binding residues in proteins from primary sequence using an enriched random forest model with a novel hybrid feature. Proteins 2011, 79, 1230–1239. [Google Scholar]
- Skurichina, M.; Kuncheva, L.I.; Duin, R.P.W. Bagging, Boosting, and the Random Subspace Method for Linear Classifier. Pattern Anal. Appl 2002, 5, 102–112. [Google Scholar]
- Breiman, L.; Cutler, A. Random Forests. Available online: http://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm Accessed on 12 June 2011.
- Randomforest-matlab. Available online: http://code.google.com/p/randomforest-matlab/ Accessed on 12 June 2011.
- Liu, T.L.; Zheng, X.Q.; Wang, J. Prediction of protein structural class for low-similarity sequences using support vector machine and PSI-BLAST profile. Biochime 2010, 92, 1330–1334. [Google Scholar]
- Chou, K.C.; Zhang, C.T. Prediction of protein structural classes. Mol. Biol 1999, 30, 275–349. [Google Scholar]
- Chou, K.C.; Shen, H.B. Recent progress in protein subcellular location prediction. Anal. Biochem 2007, 370, 1–16. [Google Scholar]
- Zheng, X.; Liu, T.; Wang, J. A complexity-based method for predicting protein subcellular location. Amino Acids 2009, 37, 427–433. [Google Scholar]
- Shen, H.B.; Chou, K.C. Predicting protein subnuclear location with optimized evidence-theoretic K-nearest classifier and pseudo amino acid composition. Biochem. Biophys. Res. Commun 2005, 337, 752–756. [Google Scholar]
- Chou, K.C.; Shen, H.B. Cell-PLoc: A package of web-servers for predicting subcellular localization of proteins in various organisms. Nat. Protoc 2008, 3, 153–162. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell 2005, 27, 1226–1238. [Google Scholar]
- Wagner, S.A.; Beli, P.; Weinert, B.T.; Nielsen, M.L.; Cox, J.; Mann, M.; Choudhary, C. A proteome-wide, quantitative survey of in vivo ubiquitylation sites reveals widespread regulatory roles. Mol. Cell. Proteomics 2011. [Google Scholar] [CrossRef]
- Kim, W.; Bennett, E.J.; Huttlin, E.L.; Guo, A.; Li, J.; Possemato, A.; Sowa, M.E.; Rad, R.; Rush, J.; Comb, M.J.; et al. Systematic and quantitative assessment of the Ubiquitin-modified proteome. Mol. Cell 2011, 44, 325–340. [Google Scholar]
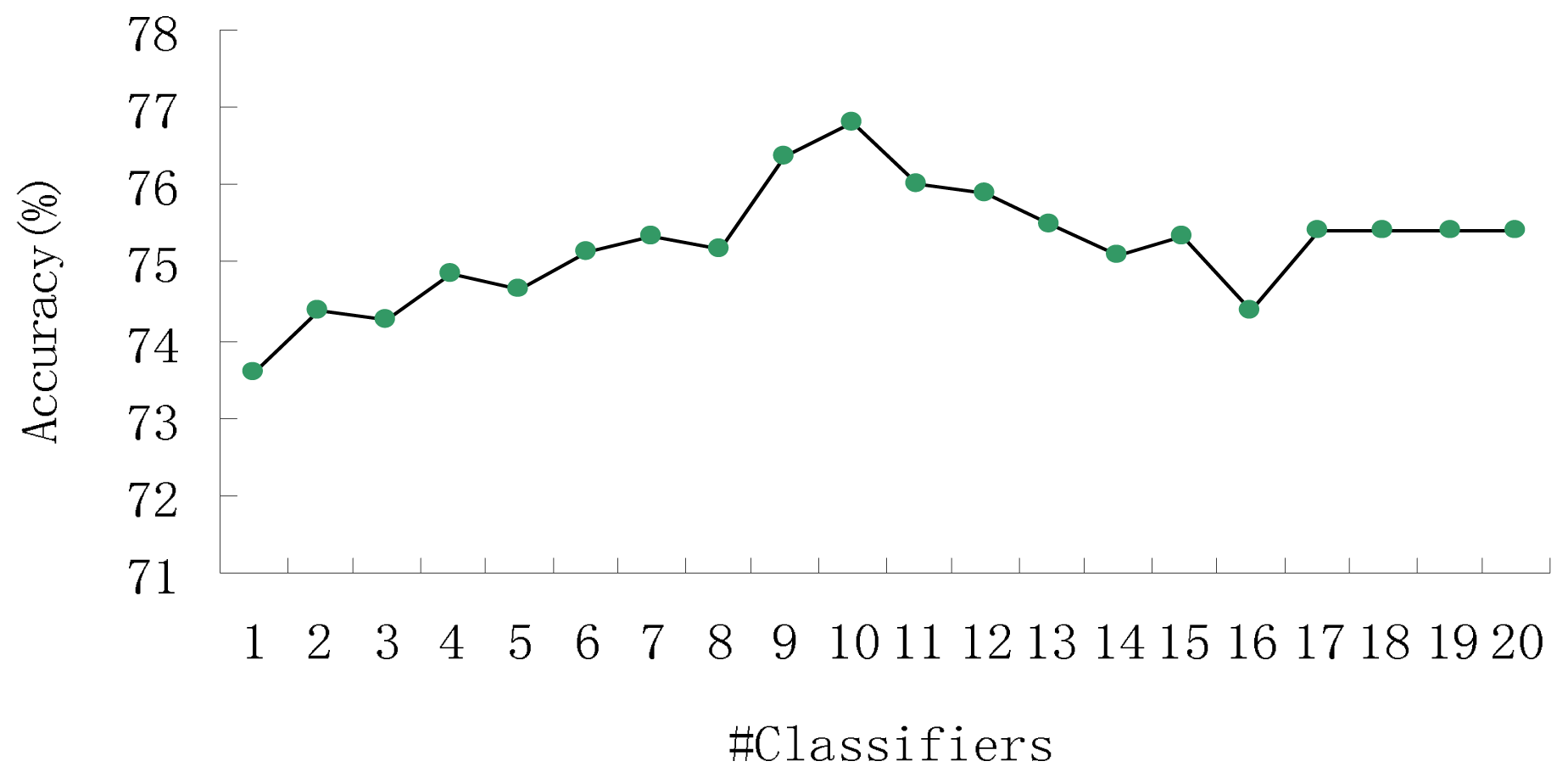

| Dataset | No of ubiquitylation sites | No of non-ubiquitylation sites |
|---|---|---|
| Training dataset | 298 | 563 |
| Test dataset | 170 | 357 |
| Independent dataset | 14 | 267 |
| Method | Sn (%) | Sp (%) | AC (%) | MCC |
|---|---|---|---|---|
| mRMR [57] | 64.76 ± 2.12 | 68.21 ± 3.52 | 67.42 ± 1.37 | 0.282 ± 0.13 |
| This paper | 76.85 ± 1.84 | 76.91 ± 2.09 | 76.82 ± 1.03 | 0.519 ± 0.08 |
| Method | Sn (%) | Sp (%) | AC (%) | MCC |
|---|---|---|---|---|
| mRMR [57] | 51.68 ± 1.35 | 74.22 ± 0.92 | 69.20 ± 1.06 | 0.229 ± 0.09 |
| This paper | 72.61 ± 2.34 | 81.27 ± 0.76 | 79.16 ± 0.98 | 0.503 ± 0.07 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhao, X.; Li, X.; Ma, Z.; Yin, M. Prediction of Lysine Ubiquitylation with Ensemble Classifier and Feature Selection. Int. J. Mol. Sci. 2011, 12, 8347-8361. https://doi.org/10.3390/ijms12128347
Zhao X, Li X, Ma Z, Yin M. Prediction of Lysine Ubiquitylation with Ensemble Classifier and Feature Selection. International Journal of Molecular Sciences. 2011; 12(12):8347-8361. https://doi.org/10.3390/ijms12128347
Chicago/Turabian StyleZhao, Xiaowei, Xiangtao Li, Zhiqiang Ma, and Minghao Yin. 2011. "Prediction of Lysine Ubiquitylation with Ensemble Classifier and Feature Selection" International Journal of Molecular Sciences 12, no. 12: 8347-8361. https://doi.org/10.3390/ijms12128347




