Computational Docking of Antibody-Antigen Complexes, Opportunities and Pitfalls Illustrated by Influenza Hemagglutinin
Abstract
:1. Introduction
1.1. Computational Docking
- “Bound”, if it originates from an experimental structure of the complex that needs to be docked. This is interesting when developing docking procedures but it is generally not biologically attractive, because computational docking is unlikely to add relevant information if an experimental structure is already available.
- “Unbound”, if it originates from an experimental structure of the molecule not bound to the partner that needs to be docked, i.e., either free or bound to a different partner. This is the most common scenario for antigens, especially since the number of available protein structures is increasing thanks to several structural genomics efforts. Structures of free antibodies, instead, are usually not available, nor they would be particularly useful since Abs are known to drastically change conformation upon binding [4].
- “Modeled”, if it has been predicted by homology modeling and/or other computational techniques like ab initio predictions or molecular dynamics. A thorough description of homology modeling for protein antigens is beyond the scope of this manuscript. Suffice to say that the results are remarkably accurate if the target protein has sequence similarity to a protein with known structure and that even ab initio predictions are starting to produce accurate results, albeit much less than homology modeling [5–7]. Antibody structures can be predicted with remarkable accuracy and precision as well; the process is relatively different from standard protein modeling and is covered in the next sections.
1.2. Antibody Structure, Implications for Modeling
1.3. Antibody Modeling Based on Canonical Structures, the PIGS Server
- Best heavy and light chains. Use the chains with highest sequence identity as templates. Since they come from different antibodies, the two chains need to be packed together by a least-squares fit of the residues conserved at the interface. This may introduce errors in the relative orientation of the two chains, with adverse consequences for the accurate modeling of the antigen binding site.
- Same canonical structures. Use a template whose CDR loops have the same canonical structures as the target even if a template with higher sequence identity exists for one or both chains. If framework and loops are taken from different templates, then the loops need to be grafted in, possibly introducing errors: the residues adjacent to the loop are superimposed to the framework by a weighted least-square fit of the main chain.
- Same antibody. Use the same antibody as template for both heavy and light chain, even if templates with higher sequence identity exist. This does not require optimization of the relative orientation of the two chains and thus avoids the errors illustrated earlier.
- Same antibody and canonical structures. The template is an antibody with the same canonical structures as the target and it is used to model both framework and the CDR loops. This option does not require optimization of framework orientation nor loop grafting and may offer more accurate results even if templates with higher sequence identity are available for one of the chains. The approach tends to fail, however, if the identity is too low.
1.4. Antibody Modeling by Rosetta Antibody
1.5. Other Procedures for Antibody Modeling
1.6. The Docking Calculation
1.7. Exploiting the Peculiarities of Antibodies to Simplify the Docking Search
2. Results and Discussion
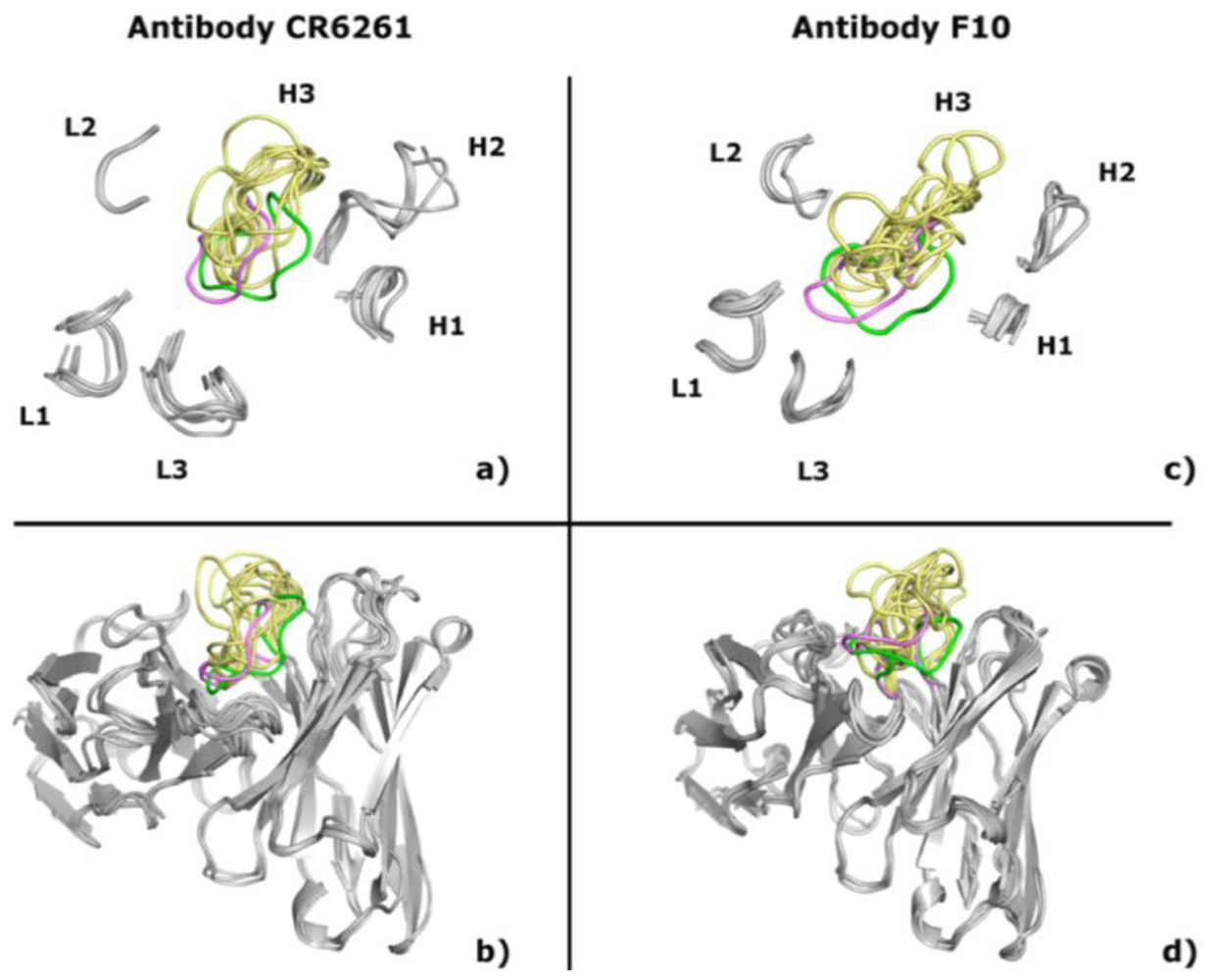
2.1. Modeling Antibodies against Influenza Virus Hemagglutinin
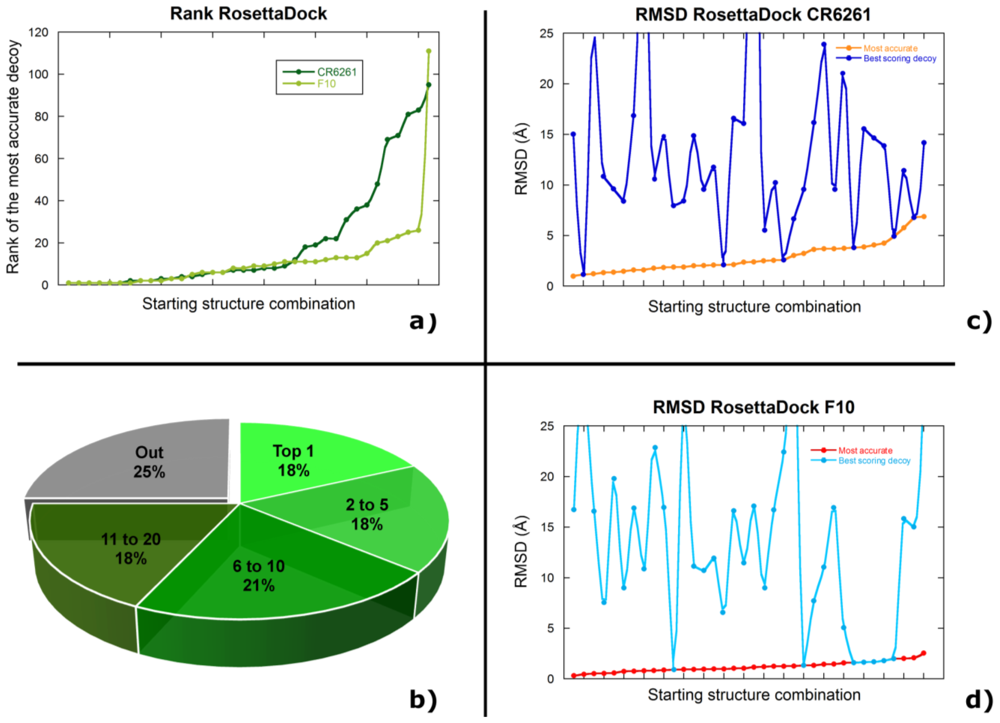
2.2. Docking Antibodies against Influenza Virus Hemagglutinin
2.3. Selecting the Most Accurate Solution: the Scoring Problem
2.4. Discussion
3. Experimental Section
3.1. Antibody Modeling
3.2. Docking
3.3. RMSD Calculations
4. Conclusions
Acknowledgements
References
- Edelman, GM; Benacerraf, B; Ovary, Z; Poulik, MD. Structural differences among antibodies of different specificities. Proc. Natl. Acad. Sci USA 1961, 47, 1751–1758. [Google Scholar]
- Edelman, GM; Poulik, MD. Studies on structural units of the gamma-globulins. J. Exp. Med 1961, 113, 861–884. [Google Scholar]
- Janin, J; Henrick, K; Moult, J; Eyck, LT; Sternberg, MJ; Vajda, S; Vakser, I; Wodak, SJ. CAPRI: a Critical Assessment of PRedicted Interactions. Proteins 2003, 52, 2–9. [Google Scholar]
- Rini, JM; Schulze-Gahmen, U; Wilson, IA. Structural evidence for induced fit as a mechanism for antibody-antigen recognition. Science 1992, 255, 959–965. [Google Scholar]
- Al-Lazikani, B; Lesk, AM; Chothia, C. Standard conformations for the canonical structures of immunoglobulins. J. Mol. Biol 1997, 273, 927–948. [Google Scholar]
- Chothia, C; Lesk, AM. Canonical structures for the hypervariable regions of immunoglobulins. J. Mol. Biol 1987, 196, 901–917. [Google Scholar]
- Tramontano, A; Chothia, C; Lesk, AM. Framework residue 71 is a major determinant of the position and conformation of the second hypervariable region in the VH domains of immunoglobulins. J. Mol. Biol 1990, 215, 175–182. [Google Scholar]
- Chothia, C; Lesk, AM; Levitt, M; Amit, AG; Mariuzza, RA; Phillips, SE; Poljak, RJ. The predicted structure of immunoglobulin D1.3 and its comparison with the crystal structure. Science 1986, 233, 755–758. [Google Scholar]
- Chothia, C; Lesk, AM; Tramontano, A; Levitt, M; Smith-Gill, SJ; Air, G; Sheriff, S; Padlan, EA; Davies, D; Tulip, WR; et al. Conformations of immunoglobulin hypervariable regions. Nature 1989, 342, 877–883. [Google Scholar]
- Chothia, C; Novotny, J; Bruccoleri, R; Karplus, M. Domain association in immunoglobulin molecules. The packing of variable domains. J. Mol. Biol 1985, 186, 651–663. [Google Scholar]
- PIGS, Prediction of ImmunoGlobulin Structure. Available online: http://www.biocomputing.it/pigs (accessed on 4 January 2011).
- Marcatili, P; Rosi, A; Tramontano, A. PIGS: automatic prediction of antibody structures. Bioinformatics 2008, 24, 1953–1954. [Google Scholar]
- Morea, V. Antibody Modeling: Implications for Engineering and Design. Methods 2000, 20, 267–279. [Google Scholar]
- Whitelegg, NR; Rees, AR. WAM: an improved algorithm for modelling antibodies on the WEB. Protein Eng 2000, 13, 819–824. [Google Scholar]
- Altschul, SF; Gish, W; Miller, W; Myers, EW; Lipman, DJ. Basic local alignment search tool. J. Mol. Biol 1990, 215, 403–410. [Google Scholar]
- Thompson, JD; Higgins, DG; Gibson, TJ. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res 1994, 22, 4673–4680. [Google Scholar]
- Morea, V; Tramontano, A; Rustici, M; Chothia, C; Lesk, AM. Antibody structure, prediction and redesign. Biophys. Chem 1997, 68, 9–16. [Google Scholar]
- Morea, V; Tramontano, A; Rustici, M; Chothia, C; Lesk, AM. Conformations of the third hypervariable region in the VH domain of immunoglobulins. J. Mol. Biol 1998, 275, 269–294. [Google Scholar]
- Shirai, H; Kidera, A; Nakamura, H. Structural classification of CDR-H3 in antibodies. FEBS Lett 1996, 399, 1–8. [Google Scholar]
- Ponder, JW; Richards, FM. Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes. J. Mol. Biol 1987, 193, 775–791. [Google Scholar]
- Sivasubramanian, A; Sircar, A; Chaudhury, S; Gray, JJ. Toward high-resolution homology modeling of antibody FV regions and application to antibody-antigen docking. Proteins 2009, 74, 497–514. [Google Scholar]
- Sircar, A; Kim, ET; Gray, JJ. RosettaAntibody: antibody variable region homology modeling server. Nucleic Acids Res 2009, 37, W474–W479. [Google Scholar]
- RosettaAntibody: FV Homology Modeling Server. Available online: http://antibody.graylab.jhu.edu/ (accessed on 4 January 2011).
- Canutescu, AA; Dunbrack, RL, Jr. Cyclic coordinate descent: A robotics algorithm for protein loop closure. Protein Sci 2003, 12, 963–972. [Google Scholar]
- Wang, C; Schueler-Furman, O; Baker, D. Improved side-chain modeling for protein-protein docking. Protein Sci 2005, 14, 1328–1339. [Google Scholar]
- Kortemme, T; Morozov, AV; Baker, D. An orientation-dependent hydrogen bonding potential improves prediction of specificity and structure for proteins and protein-protein complexes. J. Mol. Biol 2003, 326, 1239–1259. [Google Scholar]
- Lazaridis, T; Karplus, M. Effective energy function for proteins in solution. Proteins 1999, 35, 133–152. [Google Scholar]
- Dunbrack, RL, Jr; Cohen, FE. Bayesian statistical analysis of protein side-chain rotamer preferences. Protein Sci 1997, 6, 1661–1681. [Google Scholar]
- Warshel, A; Russell, ST; Churg, AK. Macroscopic models for studies of electrostatic interactions in proteins: limitations and applicability. Proc. Natl. Acad. Sci USA 1984, 81, 4785–4789. [Google Scholar]
- Davies, DR; Sheriff, S; Padlan, EA. Antibody-antigen complexes. J. Biol. Chem 1988, 263, 10541–10544. [Google Scholar]
- de la Paz, P; Sutton, BJ; Darsley, MJ; Rees, AR. Modelling of the combining sites of three anti-lysozyme monoclonal antibodies and of the complex between one of the antibodies and its epitope. EMBO J 1986, 5, 415–425. [Google Scholar]
- Jones, TA; Thirup, S. Using known substructures in protein model building and crystallography. EMBO J 1986, 5, 819–822. [Google Scholar]
- Coutre, SE; Stanford, JM; Hovis, JG; Stevens, PW; Wu, TT. Possible three-dimensional backbone folding around antibody combining site of immunoglobulin MOPC167. J. Theor. Biol 1981, 92, 417–434. [Google Scholar]
- Moult, J; James, MN. An algorithm for determining the conformation of polypeptide segments in proteins by systematic search. Proteins 1986, 1, 146–163. [Google Scholar]
- Bruccoleri, RE; Haber, E; Novotny, J. Structure of antibody hypervariable loops reproduced by a conformational search algorithm. Nature 1988, 335, 564–568. [Google Scholar]
- Bruccoleri, RE; Karplus, M. Prediction of the folding of short polypeptide segments by uniform conformational sampling. Biopolymers 1987, 26, 137–168. [Google Scholar]
- Fine, RM; Wang, H; Shenkin, PS; Yarmush, DL; Levinthal, C. Predicting antibody hypervariable loop conformations. II: Minimization and molecular dynamics studies of MCPC603 from many randomly generated loop conformations. Proteins 1986, 1, 342–362. [Google Scholar]
- Stanford, JM; Wu, TT. A predictive method for determining possible three-dimensional foldings of immunoglobulin backbones around antibody combining sites. J. Theor. Biol 1981, 88, 421–439. [Google Scholar]
- Halperin, I; Ma, B; Wolfson, H; Nussinov, R. Principles of docking: An overview of search algorithms and a guide to scoring functions. Proteins 2002, 47, 409–443. [Google Scholar]
- Camacho, CJ; Gatchell, DW; Kimura, SR; Vajda, S. Scoring docked conformations generated by rigid-body protein-protein docking. Proteins 2000, 40, 525–537. [Google Scholar]
- Cheng, TM; Blundell, TL; Fernandez-Recio, J. pyDock: electrostatics and desolvation for effective scoring of rigid-body protein-protein docking. Proteins 2007, 68, 503–515. [Google Scholar]
- Fernandez-Recio, J; Abagyan, R; Totrov, M. Improving CAPRI predictions: optimized desolvation for rigid-body docking. Proteins 2005, 60, 308–313. [Google Scholar]
- Heifetz, A; Eisenstein, M. Effect of local shape modifications of molecular surfaces on rigid-body protein-protein docking. Protein Eng 2003, 16, 179–185. [Google Scholar]
- Lorenzen, S; Zhang, Y. Monte Carlo refinement of rigid-body protein docking structures with backbone displacement and side-chain optimization. Protein Sci 2007, 16, 2716–2725. [Google Scholar]
- Meng, EC; Gschwend, DA; Blaney, JM; Kuntz, ID. Orientational sampling and rigid-body minimization in molecular docking. Proteins 1993, 17, 266–278. [Google Scholar]
- Cheng, TM; Blundell, TL; Fernandez-Recio, J. Structural assembly of two-domain proteins by rigid-body docking. BMC Bioinformatics 2008, 9, 441. [Google Scholar]
- Cherfils, J; Bizebard, T; Knossow, M; Janin, J. Rigid-body docking with mutant constraints of influenza hemagglutinin with antibody HC19. Proteins 1994, 18, 8–18. [Google Scholar]
- Clore, GM. Accurate and rapid docking of protein-protein complexes on the basis of intermolecular nuclear overhauser enhancement data and dipolar couplings by rigid body minimization. Proc. Natl. Acad. Sci USA 2000, 97, 9021–9025. [Google Scholar]
- Dell’Orco, D; Seeber, M; de Benedetti, PG; Fanelli, F. Probing fragment complementation by rigid-body docking: in silico reconstitution of calbindin D9k. J. Chem. Inf. Model 2005, 45, 1429–1438. [Google Scholar]
- Fanelli, F; Ferrari, S. Prediction of MEF2A-DNA interface by rigid body docking: a tool for fast estimation of protein mutational effects on DNA binding. J. Struct. Biol 2006, 153, 278–283. [Google Scholar]
- Gray, JJ; Moughon, S; Wang, C; Schueler-Furman, O; Kuhlman, B; Rohl, CA; Baker, D. Protein-protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J. Mol. Biol 2003, 331, 281–299. [Google Scholar]
- Segal, D; Eisenstein, M. The effect of resolution-dependent global shape modifications on rigid-body protein-protein docking. Proteins 2005, 59, 580–591. [Google Scholar]
- Chen, R; Li, L; Weng, Z. ZDOCK: an initial-stage protein-docking algorithm. Proteins 2003, 52, 80–87. [Google Scholar]
- Gray, JJ; Moughon, SE; Kortemme, T; Schueler-Furman, O; Misura, KM; Morozov, AV; Baker, D. Protein-protein docking predictions for the CAPRI experiment. Proteins 2003, 52, 118–122. [Google Scholar]
- Hwang, H; Vreven, T; Pierce, BG; Hung, JH; Weng, Z. Performance of ZDOCK and ZRANK in CAPRI rounds 13–19. Proteins 2010, 78, 3104–3110. [Google Scholar]
- Wiehe, K; Pierce, B; Mintseris, J; Tong, WW; Anderson, R; Chen, R; Weng, Z. ZDOCK and RDOCK performance in CAPRI rounds 3, 4, and 5. Proteins 2005, 60, 207–213. [Google Scholar]
- Wiehe, K; Pierce, B; Tong, WW; Hwang, H; Mintseris, J; Weng, Z. The performance of ZDOCK and ZRANK in rounds 6–11 of CAPRI. Proteins 2007, 69, 719–725. [Google Scholar]
- Chaudhury, S; Gray, JJ. Conformer selection and induced fit in flexible backbone protein-protein docking using computational and NMR ensembles. J. Mol. Biol 2008, 381, 1068–1087. [Google Scholar]
- Lyskov, S; Gray, JJ. The RosettaDock server for local protein-protein docking. Nucleic Acids Res 2008, 36, W233–W238. [Google Scholar]
- Schueler-Furman, O; Wang, C; Baker, D. Progress in protein-protein docking: atomic resolution predictions in the CAPRI experiment using RosettaDock with an improved treatment of side-chain flexibility. Proteins 2005, 60, 187–194. [Google Scholar]
- Wang, C; Schueler-Furman, O; Andre, I; London, N; Fleishman, SJ; Bradley, P; Qian, B; Baker, D. RosettaDock in CAPRI rounds 6–12. Proteins 2007, 69, 758–763. [Google Scholar]
- Ma, XH; Li, CH; Shen, LZ; Gong, XQ; Chen, WZ; Wang, CX. Biologically enhanced sampling geometric docking and backbone flexibility treatment with multiconformational superposition. Proteins 2005, 60, 319–323. [Google Scholar]
- Wang, C; Bradley, P; Baker, D. Protein-protein docking with backbone flexibility. J. Mol. Biol 2007, 373, 503–519. [Google Scholar]
- Moal, IH; Bates, PA. SwarmDock and the Use of Normal Modes in Protein-Protein Docking. Int. J. Mol. Sci 2010, 11, 3623–3648. [Google Scholar]
- de Vries, SJ; van Dijk, M; Bonvin, AM. The HADDOCK web server for data-driven biomolecular docking. Nat. Protoc 2010, 5, 883–897. [Google Scholar]
- Dominguez, C; Boelens, R; Bonvin, AM. HADDOCK: a protein-protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc 2003, 125, 1731–1737. [Google Scholar]
- Colwell, NS; Blinder, MA; Tsiang, M; Gibbs, CS; Bock, PE; Tollefsen, DM. Allosteric effects of a monoclonal antibody against thrombin exosite II. Biochemistry 1999, 38, 2610. [Google Scholar]
- Huang, SY; Zou, X. Ensemble docking of multiple protein structures: considering protein structural variations in molecular docking. Proteins 2007, 66, 399–421. [Google Scholar]
- Sircar, A; Chaudhury, S; Kilambi, KP; Berrondo, M; Gray, JJ. A generalized approach to sampling backbone conformations with RosettaDock for CAPRI rounds 13–19. Proteins 2010, 78, 3115–3123. [Google Scholar]
- Sircar, A; Gray, JJ. SnugDock: paratope structural optimization during antibody-antigen docking compensates for errors in antibody homology models. PLoS Comput. Biol 2010, 6, e1000644. [Google Scholar]
- Monto, AS; Ohmit, SE. Seasonal influenza vaccines: evolutions and future trends. Expert Rev Vaccines 2009, 8, 383–389. [Google Scholar]
- Ivanova, VT; Burtseva, EI; Slepushkin, AN; Oskerko, TA; Varmanian, RV. Variability of hemagglutinin from strains of influenza virus A (H3N2), isolated in Russian from 1989 to 1999. Vopr. Virusol 2000, 45, 28–31. [Google Scholar]
- Klimov, AI; Schrader, C; Herrmann, B; Seidel, W; Dohner, L; Ghendon Yu, Z. The variability of genes of influenza A (H3N2) virus strains isolated in the G.D.R. during the 1970–1978 epidemic seasons. Acta Virol 1985, 29, 466–474. [Google Scholar]
- Lopez-Galindez, C; Lopez, JA; Melero, JA; de la Fuente, L; Martinez, C; Ortin, J; Perucho, M. Analysis of genetic variability and mapping of point mutations in influenza virus by the RNase A mismatch cleavage method. Proc. Natl. Acad. Sci USA 1988, 85, 3522–3526. [Google Scholar]
- Sui, J; Hwang, WC; Perez, S; Wei, G; Aird, D; Chen, LM; Santelli, E; Stec, B; Cadwell, G; Ali, M; Wan, H; Murakami, A; Yammanuru, A; Han, T; Cox, NJ; Bankston, LA; Donis, RO; Liddington, RC; Marasco, WA. Structural and functional bases for broad-spectrum neutralization of avian and human influenza A viruses. Nat. Struct. Mol. Biol 2009, 16, 265–273. [Google Scholar]
- Ekiert, DC; Bhabha, G; Elsliger, MA; Friesen, RH; Jongeneelen, M; Throsby, M; Goudsmit, J; Wilson, IA. Antibody recognition of a highly conserved influenza virus epitope. Science 2009, 324, 246–251. [Google Scholar]
- Roy, A; Kucukural, A; Zhang, Y. I-TASSER: a unified platform for automated protein structure and function prediction. Nat. Protoc 2010, 5, 725–738. [Google Scholar]
- I-Tasser Online. Protein Structure and Function Predictions. Available online: http://zhanglab.ccmb.med.umich.edu/I-TASSER/ (accessed on 4 January 2011).
- London, N; Schueler-Furman, O. Assessing the energy landscape of CAPRI targets by FunHunt. Proteins 2007, 69, 809–815. [Google Scholar]
- London, N; Schueler-Furman, O. FunHunt: model selection based on energy landscape characteristics. Biochem. Soc. Trans 2008, 36, 1418–1421. [Google Scholar]
- Ponomarenko, JV; Bourne, PE. Antibody-protein interactions: benchmark datasets and prediction tools evaluation. BMC Struct. Biol 2007, 7, 64. [Google Scholar]
- Simonelli, L; Beltramello, M; Yudina, Z; Macagno, A; Calzolai, L; Varani, L. Rapid structural characterization of human antibody-antigen complexes through experimentally validated computational docking. J. Mol. Biol 2010, 396, 1491–1507. [Google Scholar]
- Johansson, BE; Kilbourne, ED. Immunization with purified N1 and N2 influenza virus neuraminidases demonstrates cross-reactivity without antigenic competition. Proc. Natl. Acad. Sci USA 1994, 91, 2358–2361. [Google Scholar]
- Mazurkova, NA; Isaeva, EI; Podcherniaeva, R. Peptide mapping of the monoclonal antibodies against the heavy chain hemagglutinin from influenza virus H3N2. Mol. Gen. Mikrobiol. Virusol 2006, 4, 19–23. [Google Scholar]
- Andrew, CR. Martin’s Group. ProFit. Available online: http://www.bioinf.org.uk/software/profit/ (accessed on 4 January 2011).

| RMSD (Å) C Only | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CR6261 | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | PIGS same Ab | PIGS same CanSt | PIGS Best HcLc |
| Hc + Lc | 1.2 | 1.1 | 1.4 | 1.3 | 1.1 | 1.9 | 1.5 | 1.1 | 1.5 | 1.6 | 1.0 | 2.1 | 1.7 |
| Lc | 1.0 | 0.9 | 1.2 | 1.1 | 0.9 | 1.6 | 1.3 | 0.9 | 1.2 | 1.3 | 0.9 | 1.9 | 1.7 |
| Hc | 1.4 | 1.2 | 1.6 | 1.5 | 1.3 | 2.2 | 1.7 | 1.2 | 1.7 | 1.8 | 1.1 | 2.5 | 1.7 |
| CDR (all) | 1.5 | 1.3 | 1.6 | 2.0 | 1.3 | 2.3 | 2.8 | 1.8 | 1.7 | 1.9 | 1.1 | 2.3 | 1.8 |
| CDR (Lc) | 1.2 | 1.0 | 1.3 | 1.8 | 1.1 | 1.8 | 1.4 | 1.7 | 1.4 | 1.5 | 1.0 | 2.0 | 1.7 |
| CDR (Hc) | 1.5 | 1.3 | 1.7 | 1.6 | 1.4 | 2.4 | 1.9 | 1.3 | 1.8 | 2.0 | 1.2 | 2.4 | 1.8 |
| L1 (12) | 1.2 | 1.0 | 1.3 | 1.5 | 1.1 | 1.9 | 1.5 | 1.4 | 1.4 | 1.5 | 1.0 | 2.0 | 1.7 |
| L2 (4) | 1.2 | 1.1 | 1.4 | 1.4 | 1.1 | 1.9 | 1.5 | 1.3 | 1.4 | 1.6 | 1.0 | 2.1 | 1.7 |
| L3 (8) | 1.2 | 1.1 | 1.3 | 1.5 | 1.1 | 1.9 | 1.5 | 1.3 | 1.4 | 1.5 | 1.0 | 2.0 | 1.7 |
| H1 (9) | 1.3 | 1.2 | 1.5 | 1.4 | 1.2 | 1.9 | 1.6 | 1.2 | 1.5 | 1.6 | 1.1 | 2.1 | 1.8 |
| H2 (5) | 1.2 | 1.1 | 1.4 | 1.3 | 1.1 | 1.9 | 1.5 | 1.1 | 1.4 | 1.6 | 1.0 | 2.4 | 2.1 |
| H3 (9) | 1.5 | 1.3 | 1.7 | 1.6 | 1.3 | 2.5 | 1.9 | 1.3 | 1.8 | 2.0 | 1.1 | 2.4 | 1.7 |
| F10 | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | PIGS same Ab | PIGS same CanSt | PIGS Best HcLc |
| Hc + Lc | 2.1 | 1.9 | 1.8 | 1.7 | 2.0 | 1.9 | 2.0 | 2.6 | 2.1 | 2.3 | 1.3 | - | - |
| Lc | 2.1 | 1.9 | 1.7 | 1.7 | 2.0 | 1.9 | 2.0 | 2.6 | 2.1 | 2.3 | 1.3 | - | - |
| Hc | 2.5 | 2.1 | 1.9 | 1.8 | 2.3 | 2.1 | 2.2 | 3.1 | 2.3 | 2.7 | 1.2 | - | - |
| CDR (all) | 2.5 | 2.5 | 2.0 | 1.9 | 2.4 | 2.3 | 2.3 | 3.1 | 2.5 | 2.8 | 1.5 | - | - |
| CDR (Lc) | 2.1 | 2.2 | 1.7 | 1.6 | 2.0 | 1.9 | 1.9 | 2.5 | 2.0 | 2.3 | 1.3 | - | - |
| CDR (Hc) | 2.6 | 2.3 | 2.1 | 2.0 | 2.5 | 2.4 | 2.4 | 3.2 | 2.5 | 2.9 | 1.5 | - | - |
| L1 (11) | 2.1 | 2.1 | 1.7 | 1.7 | 2.0 | 1.9 | 1.9 | 2.6 | 2.1 | 2.3 | 1.3 | - | - |
| L2 (4) | 2.1 | 2.0 | 1.7 | 1.7 | 2.0 | 1.9 | 1.9 | 2.6 | 2.1 | 2.3 | 1.3 | - | - |
| L3 (7) | 2.1 | 2.0 | 1.7 | 1.6 | 2.0 | 1.9 | 1.9 | 2.6 | 2.1 | 2.3 | 1.3 | - | - |
| H1 (8) | 2.1 | 1.9 | 1.8 | 1.7 | 2.0 | 1.9 | 1.9 | 2.6 | 2.1 | 2.3 | 1.3 | - | - |
| H2 (4) | 2.1 | 1.9 | 1.7 | 1.7 | 2.0 | 1.9 | 1.9 | 2.6 | 2.1 | 2.3 | 1.3 | - | - |
| H3 (12) | 2.7 | 2.3 | 2.1 | 2.0 | 2.6 | 2.4 | 2.4 | 3.4 | 2.6 | 3.0 | 1.4 | - | - |
| Bound R6261 | Bound F10 | Unbound | Model CR6261 | Model F10 | |
|---|---|---|---|---|---|
| Bound CR6261 | 0.6 | 1.0 | 1.4 | 0.9 | |
| Bound F10 | 0.6 | 1.1 | 1.3 | 1.6 | |
| Unbound | 1.0 | 1.1 | 1.0 | 1.1 | |
| Model CR6261 | 1.4 | 1.3 | 1.0 | 0.6 | |
| Model F10 | 0.9 | 1.6 | 1.1 | 0.6 |
| Bound | Unbound | Model | |
|---|---|---|---|
| R1 | 1.9 | 4.9 | 2.0 |
| R2 | 3.0 | 4.2 | 1.3 |
| R3 | 2.5 | 3.7 | 1.4 |
| R4 | 2.4 | 3.7 | 2.1 |
| R5 | 2.1 | 3.2 | 1.8 |
| R6 | 1.6 | 3.8 | 1.5 |
| R7 | 1.0 | 3.9 | 1.8 |
| R8 | 2.6 | 3.6 | 2.6 |
| R9 | 2.4 | 3.7 | 1.2 |
| R10 | 2.1 | 4.1 | 1.6 |
| PIGS | 5.8 | 6.9 | 6.8 |
| Bound | 2.0 | 1.9 | 1.1 |
| Bound | Unbound | Model | |
|---|---|---|---|
| R1 | 0.9 | 0.8 | 1.3 |
| R2 | 1.3 | 1.2 | 1.6 |
| R3 | 1.0 | 1.0 | 1.7 |
| R4 | 0.8 | 1.8 | 1.6 |
| R5 | 1.0 | 1.2 | 0.9 |
| R6 | 0.6 | 1.3 | 2.0 |
| R7 | 1.3 | 0.9 | 0.9 |
| R8 | 1.6 | 0.5 | 0.8 |
| R9 | 1.0 | 2.0 | 0.5 |
| R10 | 0.9 | 1.4 | 2.5 |
| PIGS | 0.7 | 1.2 | 0.4 |
| Bound | 0.3 | 2.1 | 1.5 |
© 2011 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Pedotti, M.; Simonelli, L.; Livoti, E.; Varani, L. Computational Docking of Antibody-Antigen Complexes, Opportunities and Pitfalls Illustrated by Influenza Hemagglutinin. Int. J. Mol. Sci. 2011, 12, 226-251. https://doi.org/10.3390/ijms12010226
Pedotti M, Simonelli L, Livoti E, Varani L. Computational Docking of Antibody-Antigen Complexes, Opportunities and Pitfalls Illustrated by Influenza Hemagglutinin. International Journal of Molecular Sciences. 2011; 12(1):226-251. https://doi.org/10.3390/ijms12010226
Chicago/Turabian StylePedotti, Mattia, Luca Simonelli, Elsa Livoti, and Luca Varani. 2011. "Computational Docking of Antibody-Antigen Complexes, Opportunities and Pitfalls Illustrated by Influenza Hemagglutinin" International Journal of Molecular Sciences 12, no. 1: 226-251. https://doi.org/10.3390/ijms12010226