Advances and Challenges in Protein-Ligand Docking
Abstract
:1. Introduction
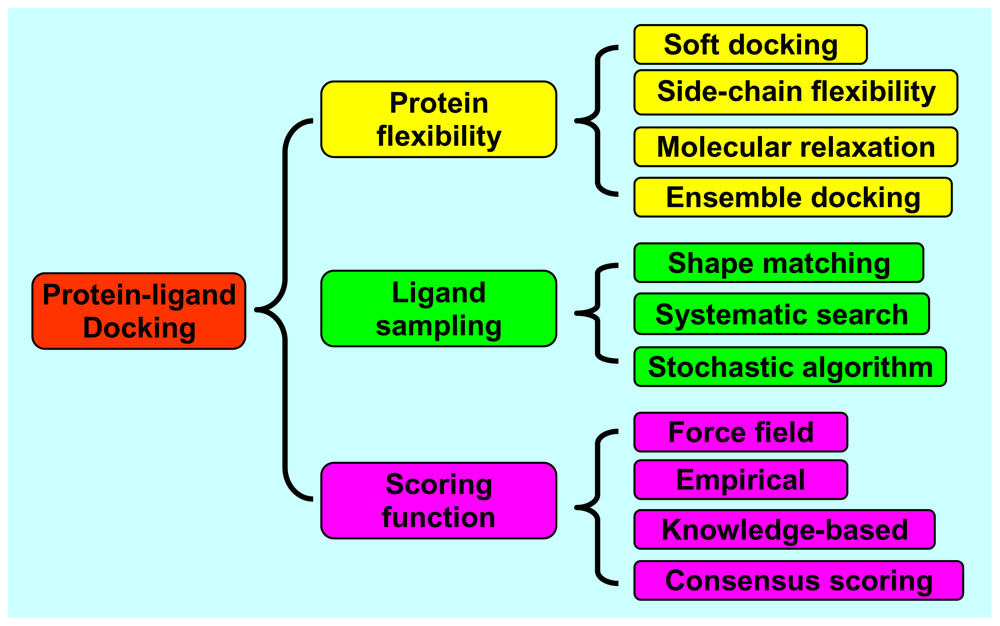
2. Protein Flexibility
2.1. Soft Docking
2.2. Side-Chain Flexibility
2.3. Molecular Relaxation
2.4. Docking of Multiple Protein Structures
3. Ligand Sampling
3.1. Shape Matching
3.2. Systematic Search
3.3. Stochastic Algorithms
4. Scoring Functions
4.1. Force Field Scoring Functions
4.2. Empirical Scoring Functions
4.3. Knowledge-Based Scoring Functions
4.4. Consensus Scoring
4.5. Clustering and Entropy-Based Scoring Methods
5. Conclusion and Discussions
Acknowledgments
References
- Kuntz, ID; Blaney, JM; Oatley, SJ; Langridge, R; Ferrin, TE. A geometric approach to macromolecule-ligand interactions. J. Mol. Biol 1982, 161, 269–288. [Google Scholar]
- Brooijmans, N; Kuntz, ID. Molecular recognition and docking algorithms. Annu. Rev. Biophys. Biomol. Struct 2003, 32, 335–373. [Google Scholar]
- Halperin, I; Ma, B; Wolfson, H; Nussinov, R. Principles of docking: An overviewof search algorithms and a guide to scoring functions. Proteins 2002, 47, 409–443. [Google Scholar]
- Shoichet, BK; McGovern, SL; Wei, B; Irwin, JJ. Lead discovery using molecular docking. Curr. Opin. Chem. Biol 2002, 6, 439–446. [Google Scholar]
- Kitchen, DB; Decornez, H; Furr, JR; Bajorath, J. Docking and scoring in virtual screening for drug discovery: Methods and applications. Nat. Rev. Drug Discov 2004, 3, 935–948. [Google Scholar]
- Muegge, I; Rarey, M. Small molecule docking and scoring. Rev. Comput. Chem 2001, 17, 1–60. [Google Scholar]
- Sousa, SF; Fernandes, PA; Ramos, MJ. Protein-ligand docking: Current status and future challenges. Proteins 2006, 65, 15–26. [Google Scholar]
- Kolb, P; Ferreira, RS; Irwin, JJ; Shoichet, BK. Docking and chemoinformatic screens for new ligands and targets. Curr. Opin. Biotech 2009, 20, 429–436. [Google Scholar]
- Carlson, HA. Protein flexibility is an important component of structure-based drug discovery. Curr. Pharm. Des 2002, 8, 1571–1578. [Google Scholar]
- Carlson, HA; McCammon, JA. Accommodating protein flexibility in computational drug design. Mol. Pharmacol 2000, 57, 213–218. [Google Scholar]
- Teodoro, ML; Kavraki, LE. Conformational flexibility models for the receptor in structure based drug design. Curr. Pharm. Des 2003, 9, 1635–1648. [Google Scholar]
- Teague, SJ. Implications of protein flexibility for drug discovery. Nat. Rev. Drug Discov 2003, 2, 527–541. [Google Scholar]
- Cozzini, P; Kellogg, GE; Spyrakis, F; Abraham, DJ; Costantino, G; Emerson, A; Fanelli, F; Gohlke, H; Kuhn, LA; Morris, GM; et al. Target flexibility: An emerging consideration in drug discovery and design. J. Med. Chem 2008, 51, 6237–6255. [Google Scholar]
- Totrov, M; Abagyan, R. Flexible ligand docking to multiple receptor conformations: A practical alternative. Curr. Opin. Struct. Biol 2008, 18, 178–184. [Google Scholar]
- Jiang, F; Kim, SH. Soft docking: Matching of molecular surface cubes. J. Mol. Biol 1991, 219, 79–102. [Google Scholar]
- Ferrari, AM; Wei, BQ; Costantino, L; Shoichet, BK. Soft docking and multiple receptor conformations in virtual screening. J. Med. Chem 2004, 47, 5076–5084. [Google Scholar]
- Leach, AR. Ligand docking to proteins with discrete side-chain flexibility. J. Mol. Biol 1994, 235, 345–356. [Google Scholar]
- Abagyan, R; Totrov, M; Kuznetzov, D. ICM – a new method for protein modeling and design: Applications to docking and structure prediction from the distorted native conformation. J. Comput. Chem 1994, 15, 488–506. [Google Scholar]
- Desmet, J; Wilson, IA; Joniau, M; De Maeyer, M; Lasters, I. Computation of the binding of fully flexible peptides to proteins with flexible side-chains. FASEB J 1997, 11, 164–172. [Google Scholar]
- Schaffer, L; Verkhivker, GM. Predicting structural effects in HIV-1 protease mutant complexes with flexible ligand docking and protein side-chain optimization. Proteins 1998, 33, 295–310. [Google Scholar]
- Schnecke, V; Kuhn, LA. Virtual screening with solvation and ligand-induced complementarity. Perspect. Drug Discov. Des 2000, 20, 171–190. [Google Scholar]
- Frimurer, TM; Peters, GH; Iversen, LF; Andersen, HS; Moller, NP; Olsen, OH. Ligand-induced conformational changes: Improved predictions of ligand binding conformations and affinities. Biophys. J 2003, 84, 2273–2281. [Google Scholar]
- Meiler, J; Baker, D. ROSETTALIGAND: Protein-small molecule docking with full side-chain flexibility. Proteins 2006, 65, 538–584. [Google Scholar]
- Nabuurs, SB; Wagener, M; de Vlieg, J. A flexible approach to induced fit docking. J. Med. Chem 2007, 50, 6507–6518. [Google Scholar]
- Apostolakis, J; Pluckthun, A; Caflisch, A. Docking small ligands in flexible binding sites. J. Comput. Chem 1998, 19, 21–37. [Google Scholar]
- Davis, IW; Baker, D. ROSETTALIGAND docking with full ligand and receptor flxibility. J. Mol. Biol 2009, 385, 381–392. [Google Scholar]
- Knegtel, RM; Kuntz, ID; Oshiro, CM. Molecular docking to ensembles of protein structures. J. Mol. Biol 1997, 266, 424–440. [Google Scholar]
- Morris, GM; Goodsell, DS; Halliday, RS; Huey, R; Hart, WE; Belew, RK; Olson, AJ. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem 1998, 19, 1639–1662. [Google Scholar]
- Osterberg, F; Morris, GM; Sanner, MF; Olson, AJ; Goodsell, DS. Automated docking to multiple target structures: Incorporation of protein mobility and structural water heterogeneity in AutoDock. Proteins 2002, 46, 34–40. [Google Scholar]
- Claussen, H; Buning, C; Rarey, M; Lengauer, T. FlexE: Efficient molecular docking considering protein structure variations. J. Mol. Biol 2001, 308, 377–395. [Google Scholar]
- Wei, BQ; Weaver, LH; Ferrari, AM; Matthews, BW; Shoichet, BK. Testing a flexible-receptor docking algorithm in a model binding site. J. Mol. Biol 2004, 337, 1161–1182. [Google Scholar]
- Huang, S-Y; Zou, X. Ensemble docking of multiple protein structures: Considering protein structural variations in molecular docking. Proteins 2007, 66, 399–421. [Google Scholar]
- Huang, S-Y; Zou, X. Efficient molecular docking of NMR structures: Application to HIV-1 protease. Protein Sci 2007, 16, 43–51. [Google Scholar]
- Bottegoni, G; Kufareva, I; Totrov, M; Abagyan, R. Four-dimensional docking: A fast and accurate account of discrete receptor flexibility in ligand docking. J. Med. Chem 2009, 52, 397–406. [Google Scholar]
- Broughton, HB. A method for including protein flexibility in protein-ligand docking: Improving tools for database mining and virtual screening. J. Mol. Graph. Model 2000, 18, 247–257. [Google Scholar]
- Carlson, HA; Masukawa, KM; Rubins, K; Bushman, FD; Jorgensen, WL; Lins, RD; Briggs, JM; McCammon, JA. Developing a dynamic pharmacophore model for HIV-1 integrase. J. Med. Chem 2000, 43, 2100–2114. [Google Scholar]
- Meagher, KL; Carlson, HA. Incorporating protein flexibility in structure-based drug discovery: Using HIV-1 protease as test case. J. Am. Chem. Soc 2004, 126, 13276–13281. [Google Scholar]
- Lin, JH; Perryman, AL; Schames, JR; McCammon, JA. Computational drug design accommodating receptor flexibility: The relaxed complex scheme. J. Am. Chem. Soc 2002, 124, 5632–5633. [Google Scholar]
- Zavodszky, MI; Lei, M; Thorpe, MF; Day, AR; Kuhn, LA. Modeling correlated main-chain motions in proteins for flexible molecular recognition. Proteins 2004, 57, 243–261. [Google Scholar]
- Cavasotto, CN; Abagyan, RA. Protein flexibility in ligand docking and virtual screening to protein kinases. J. Mol. Biol 2004, 337, 209–225. [Google Scholar]
- Sherman, W; Day, T; Jacobson, MP; Friesner, RA; Farid, R. Novel procedure for modeling ligand/receptor induced fit effects. J. Med. Chem 2006, 49, 534–553. [Google Scholar]
- Zhao, Y; Sanner, MF. FLIPDock: Docking flexible ligands into flexible receptors. Proteins 2007, 68, 726–737. [Google Scholar]
- May, A; Zacharias, M. Protein-ligand docking accounting for receptor side chain and global flexibility in normal modes: Evaluation on kinase inhibitor cross docking. J. Med. Chem 2008, 51, 3499–3506. [Google Scholar]
- McGann, MR; Almond, HR; Nicholls, A; Grant, JA; Brown, FK. Gaussian docking functions. Biopolymers 2003, 68, 76–90. [Google Scholar]
- Miller, MD; Kearsley, SK; Underwood, DJ; Sheridan, RP. FLOG: A system to select quasi-flexible ligands complementary to a receptor of known three-dimensional structure. J. Comput. Aided Mol. Des 1994, 8, 153–174. [Google Scholar]
- Pang, YP; Perola, E; Xu, K; Prendergast, FG. EUDOC: A computer program for identification of drug interaction sites in macromolecules and drug leads from chemical databases. J. Comput. Chem 2001, 22, 1750–1771. [Google Scholar]
- Venkatachalam, CM; Jiang, X; Oldfield, T; Waldan, M. LigandFit: A novel method for the shape-directed rapid docking of ligands to protein active sites. J. Mol. Graph. Model 2003, 21, 289–307. [Google Scholar]
- Jain, AN. Surflex: Fully automatic molecular docking using a molecular similarity-based search engine. J. Med. Chem 2003, 46, 499–511. [Google Scholar]
- Sauton, N; Lagorce, D; Villoutreix, B; Miteva, M. MS-DOCK: Accurate multiple conformation generator and rigid docking protocol for multi-step virtual ligand screening. BMC Bioinformatics 2008, 9, 184. [Google Scholar]
- Lorber, DM; Shoichet, BK. Hierarchical docking of databases of multiple ligand conformations. Curr. Top. Med. Chem 2005, 5, 739–749. [Google Scholar]
- Friesner, RA; Banks, JL; Murphy, RB; Halgren, TA; Klicic, JJ; Mainz, DT; Repasky, MP; Knoll, EH; Shelley, M; Perry, JK; Shaw, DE; Francis, P; Shenkin, PS. Glide: A new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Med. Chem 2004, 47, 1739–1749. [Google Scholar]
- Halgren, TA; Murphy, RB; Friesner, RA; Beard, HS; Frye, LL; Pollard, WT; Banks, JL. Glide: A new approach for rapid, accurate docking and scoring. 2. Enrichment factors in database screening. J. Med. Chem 2004, 47, 1750–1759. [Google Scholar]
- Ewing, TJA; Kuntz, ID. Critical evaluation of search algorithms for automated molecular docking and database screening. J. Comput. Chem 1997, 18, 1175–1189. [Google Scholar]
- Bohm, HJ. The computer program LUDI: A new method for the de novo design of enzyme inhibitors. J. Comput. Aided Mol. Des 1992, 6, 61–78. [Google Scholar]
- Rarey, M; Kramer, B; Lengauer, T; Klebe, G. A fast flexible docking method using an incremental construction algorithm. J. Mol. Biol 1996, 261, 470–489. [Google Scholar]
- Mizutani, MY; Tomioka, N; Itai, A. Rational automatic search method for stable docking models of protein and ligand. J. Mol. Biol 1994, 243, 310–326. [Google Scholar]
- Zsoldos, Z; Reid, D; Simon, A; Sadjad, BS; Johnson, AP. eHiTS: An innovative approach to the docking and scoring function problems. Curr. Protein Pept. Sci 2006, 7, 421–435. [Google Scholar]
- Lorber, DM; Shoichet, BK. Flexible ligand docking using conformational ensembles. Protein Sci 1998, 7, 938–950. [Google Scholar]
- Joseph-McCarthy, D; Thomas, BEIV; Belmarsh, M; Moustakas, D; Alvarez, JC. Pharmacophore-based molecular docking to account for ligand flexibility. Proteins 2003, 51, 172–188. [Google Scholar]
- Brylinski, M; Skolnick, J. Q-Dock: Low-resolution flexible ligand docking with pocket-specific threading restraints. J. Comput. Chem 2008, 29, 1574–1588. [Google Scholar]
- Hart, TN; Read, RJ. A multiple-start Monte Carlo docking method. Proteins 1992, 13, 206–222. [Google Scholar]
- McMartin, C; Bohacek, RS. QXP: Powerful, rapid computer algorithms for structure-based drug design. J. Comput. Aided Mol. Des 1997, 11, 333–344. [Google Scholar]
- Trosset, JY; Scheraga, HA. Prodock: Software package for protein modeling and docking. J. Comput. Chem 1999, 20, 412–427. [Google Scholar]
- Liu, M; Wang, S. MCDOCK: A Monte Carlo simulation approach to the molecular docking problem. J. Comput. Aided Mol. Des 1999, 13, 435–451. [Google Scholar]
- Jones, G; Willett, P; Glen, RC. Molecular recognition of receptor sites using a genetic algorithm with a description of desolvation. J. Mol. Biol 1995, 245, 43–53. [Google Scholar]
- Jones, G; Willett, P; Glen, RC; Leach, AR; Taylor, R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol 1997, 267, 727–748. [Google Scholar]
- Clark, KP. Flexible ligand docking without parameter adjust-ment across four ligand-receptor complexes. J. Comput. Chem 1995, 16, 1210–1226. [Google Scholar]
- Taylor, JS; Burnett, RM. DARWIN: A program for docking flexible molecules. Proteins 2000, 41, 173–191. [Google Scholar]
- Thomsen, R; Christensen, MH. MolDock: A new technique for highaccuracy molecular docking. J. Med. Chem 2006, 49, 3315–3321. [Google Scholar]
- Pei, J; Wang, Q; Liu, Z; Li, Q; Yang, KL; Lai, L. PSI-DOCK: Towards highly efficient and accurate flexible ligand docking. Proteins 2006, 62, 934–946. [Google Scholar]
- Stroganov, OV; Novikov, FN; Stroylov, VS; Kulkov, V; Chilov, GG. Lead finder: An approach to improve accuracy of protein-ligand docking, binding energy estimation, and virtual screening. J. Chem. Inf. Model 2008, 48, 2371–2385. [Google Scholar]
- Grosdidier, A; Zoete, V; Michielin, O. EADock: Docking of small molecules into protein active sites with a multiobjective evolutionary optimization. Proteins 2007, 67, 1010–1025. [Google Scholar]
- Baxter, CA; Murray, CW; Clark, DE; Westhead, DR; Eldridge, MD. Flexible docking using Tabu search and an empirical estimate of binding affinity. Proteins 1998, 33, 367–382. [Google Scholar]
- Chen, H-M; Liu, B-F; Huang, H-L; Hwang, S-F; Ho, S-Y. SODOCK: Swarm optimization for highly flexible protein-ligand docking. J. Comput. Chem 2007, 28, 612–623. [Google Scholar]
- Chen, K; Li, T; Cao, T. Tribe-PSO: A novel global optimization algorithm and its application in molecular docking. Chemom. Intell. Lab. Syst 2006, 82, 248–259. [Google Scholar]
- Namasivayam, V; Gunther, R. PSO@Autodock: A fast flexible molecular docking program based on swarm intelligence. Chem. Biol. Drug. Des 2007, 70, 475–484. [Google Scholar]
- Korb, O; Stutzle, T; Exner, TE. PLANTS: Application of ant colony optimization to structure-based drug design. Ant Colony Optimization and Swarm Intelligence, 5th International Workshop, Brussels, Belgium, 4–7 September, 2006; pp. 247–258.
- Gohlke, H; Klebe, G. Statistical potentials and scoring functions applied to protein-ligand binding. Curr. Opin. Struct. Biol 2001, 11, 231–235. [Google Scholar]
- Schulz-Gasch, T; Stahl, M. Scoring functions for protein-ligand interactions: A critical perspective. Drug Discov. Today: Tech 2004, 1, 231–239. [Google Scholar]
- Jain, AN. Scoring functions for protein-ligand docking. Curr. Protein Pept. Sci 2006, 7, 407–420. [Google Scholar]
- Rajamani, R; Good, AC. Ranking poses in structure-based lead discovery and optimization: Current trends in scoring function development. Curr. Opin. Drug. Discov. Devel 2007, 10, 308–315. [Google Scholar]
- Gilson, MK; Zhou, HX. Calculation of protein-ligand binding affinities. Annu. Rev. Biophys. Biomol. Struct 2007, 36, 21–42. [Google Scholar]
- Huang, N; Kalyanaraman, C; Irwin, JJ; Jacobson, MP. Molecular mechanics methods for predicting protein-ligand binding. J. Chem. Inf. Model 2006, 46, 243–253. [Google Scholar]
- Meng, EC; Shoichet, BK; Kuntz, ID. Automated docking with grid-based energy approach to macromolecule-ligand interactions. J. Comput. Chem 1992, 13, 505–524. [Google Scholar]
- Weiner, PK; Kollman, PA. AMBER – assisted model building with energy refinementla general program for modeling molecules and their interactions. J. Comput. Chem 1981, 2, 287–303. [Google Scholar]
- Nilsson, L; Karplus, M. Empirical energy functions for energy minimization and dynamics of nucleic acids. J. Comput. Chem 1986, 7, 591–616. [Google Scholar]
- Brooks, BR; Bruccoleri, RE; Olafson, BD; States, DJ; Swaminathan, S; Karplus, M. CHARMM – a programm for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem 1983, 4, 187–217. [Google Scholar]
- Wang, W; Donini, O; Reyes, CM; Kollman, PA. Biomolecular simulations: Recent developments in force fields, simulations of enzyme catalysis, protein-ligand, protein-protein, and protein-nucleic acid noncovalent interactions. Annu. Rev. Biophys. Biomol. Struct 2001, 30, 211–243. [Google Scholar]
- Rocchia, W; Sridharan, S; Nicholls, A; Alexov, E; Chiabrera, A; Honig, B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects. J. Comput. Chem 2002, 23, 128–137. [Google Scholar]
- Grant, JA; Pickup, BT; Nicholls, A. A smooth permittivity function for Poisson-Boltzmann solvation methods. J. Comput. Chem 2001, 22, 608–640. [Google Scholar]
- Baker, NA; Sept, D; Joseph, S; Holst, MJ; McCammon, JA. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA 2001, 98, 10037–10041. [Google Scholar]
- Wei, BQ; Baase, WA; Weaver, LH; Matthews, BW; Shoichet, BK. A model binding site for testing scoring functions in molecular docking. J. Mol. Biol 2002, 322, 339–355. [Google Scholar]
- Wang, J; Morin, P; Wang, W; Kollman, PA. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J. Am. Chem. Soc 2001, 123, 5221–5230. [Google Scholar]
- Kuhn, B; Gerber, P; Schulz-Gasch, T; Stahl, M. Validation and use of the MM-PBSA approach for drug discovery. J. Med. Chem 2005, 48, 4040–4048. [Google Scholar]
- Kuhn, B; Kollman, PA. Binding of a diverse set of ligands to avidin and strepavidin: An accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models. J. Med. Chem 2000, 43, 3786–3791. [Google Scholar]
- Pearlman, DA. Evaluating the molecular mechanics poisson-boltzmann surface area free energy method using a congeneric series of ligands to p38 MAP kinase. J. Med. Chem 2005, 48, 7796–7807. [Google Scholar]
- Sims, PA; Wong, CF; McCammon, JA. A computational model of binding thermodynamics: The deisgn of cyclin-dependent kinase 2 inhibitors. J. Med. Chem 2003, 46, 3314–3325. [Google Scholar]
- Huang, D; Caflisch, A. Efficient evaluation of binding free energy using continuum electrostatics solvation. J. Med. Chem 2004, 47, 5791–5797. [Google Scholar]
- Thompson, DC; Humblet, C; Joseph-McCarthy, D. Investigation of MM-PBSA rescoring of docking poses. J. Chem. Inf. Model 2008, 48, 1081–1091. [Google Scholar]
- Still, WC; Tempczyk, A; Hawley, RC; Hendrickson, T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc 1990, 112, 6127–6129. [Google Scholar]
- Zou, X; Sun, Y; Kuntz, ID. Inclusion of solvation in ligand binding free energy calculations using the generalized-Born model. J. Am. Chem. Soc 1999, 121, 8033–8043. [Google Scholar]
- Liu, H-Y; Kuntz, ID; Zou, X. Pairwise GB/SA scoring function for structure-based drug design. J. Phys. Chem. B 2004, 108, 5453–5462. [Google Scholar]
- Liu, H-Y; Zou, X. Electrostatics of ligand binding: Parametrization of the generalized born model and comparison with the Poisson-Boltzmann approach. J. Phys. Chem. B 2006, 110, 9304–9313. [Google Scholar]
- Liu, H-Y; Grinter, SZ; Zou, X. Multiscale generalized born modeling of ligand binding energies for virtual database screening. J. Phys. Chem. B 2009, 113, 11793–11799. [Google Scholar]
- Majeux, N; Scarsi, M; Apostolakis, J; Ehrhardt, C; Caflisch, A. Exhaustive docking of molecular fragments with electrostatic solvation. Proteins 1999, 37, 88–105. [Google Scholar]
- Cecchini, M; Kolb, P; Majeux, N; Caflisch, A. Automated docking of highly flexible ligands by genetic algorithms: A critical assessment. J. Comput. Chem 2004, 25, 412–422. [Google Scholar]
- Huang, D; Luthi, U; Kolb, P; Edler, K; Cecchini, M; Audetat, S; Barberis, A; Caflisch, A. Discovery of cell-permeable non-peptide inhibitors of beta-secretase by high-throughput docking and continuum electrostatics calculations. J. Med. Chem 2005, 48, 5108–5111. [Google Scholar]
- Cho, AE; Wendel, JA; Vaidehi, N; Kekenes-Huskey, PM; Floriano, WB; Maiti, PK; Goddard, WA, II. The MPSim-Dock hierarchical docking algorithm: Application to the eight trypsin inhibitor cocrystals. J. Comput. Chem 2005, 26, 48–71. [Google Scholar]
- Ghosh, A; Rapp, CS; Friesner, RA. Generalized Born model based on a surface integral formulation. J. Phys. Chem. B 1998, 102, 10983–10990. [Google Scholar]
- Lyne, PD; Lamb, ML; Saeh, JC. Accurate prediction of the relative potencies of members of a series of kinase inhibitors using molecular docking and MM-GBSA scoring. J. Med. Chem 2006, 49, 4805–4808. [Google Scholar]
- Guimaraes, CRW; Cardozo, M. MM-GB/SA rescoring of docking poses in structure-based lead optimization. J. Chem. Inf. Model 2008, 48, 958–970. [Google Scholar]
- Jain, AN. Scoring noncovalent protein-ligand interactions: A continuous differentiable function tuned to compute binding affinities. J. Comput.-Aided Mol. Des 1996, 10, 427–440. [Google Scholar]
- Head, RD; Smythe, ML; Oprea, TI; Waller, CL; Green, SM; Marshall, GR. Validate a new method for the receptor-based prediction of binding affinities of novel ligands. J. Am. Chem. Soc 1996, 118, 3959–3969. [Google Scholar]
- Eldridge, MD; Murray, CW; Auton, TR; Paolini, GV; Mee, RP. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Comput.-Aided Mol. Des 1997, 11, 425–445. [Google Scholar]
- Böhm, HJ. The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure. J. Comput.-Aided Mol. Des 1994, 8, 243–256. [Google Scholar]
- Wang, R; Liu, L; Lai, L; Tang, Y. SCORE: A new empirical method for estimating the binding affinity of a protein-ligand complex. J. Mol. Model 1998, 4, 379–394. [Google Scholar]
- Böhm, HJ. Prediction of binding constants of ptotein ligands: A fast method for the polarization of hits obtained from de novo design or 3D database search programs. J. Comput.-Aided Mol. Des 1998, 12, 309–323. [Google Scholar]
- Krammer, A; Kirchhoff, PD; Jiang, X; Venkatachalam, CM; Waldman, M. LigScore: A novel scoring function for predicting binding affinities. J. Mol. Graph. Model 2005, 23, 395–407. [Google Scholar]
- Gehlhaar, DK; Verkhivker, GM; Rejto, PA; Sherman, CJ; Fogel, DB; Freer, ST. Molecular recognition of the inhibitor AG-1343 by HIV-1 Protease: Conformationally flexible docking by evolutionary programming. Chem. Biol 1995, 2, 317–324. [Google Scholar]
- Gehlhaar, DK; Bouzida, D; Rejto, PA. Parrill, L, Reddy, MR, Eds.; Rational Drug Design: Novel Methodology and Practical Applications; American Chemical Society: Washington, DC, USA, 1999; Volume 719, pp. 292–311. [Google Scholar]
- Wang, R; Lai, L; Wang, S. Further development and validation of empirical scoring functions for structure-based binding affinity prediction. J. Comput.-Aided Mol. Des 2002, 16, 11–26. [Google Scholar]
- Yin, S; Biedermannova, L; Vondrasek, J; Dokholyan, NV. MedusaScore: An accurate force-field based scoring function for virtual drug screening. J. Chem. Inf. Model 2008, 48, 1656–1662. [Google Scholar]
- Raub, S; Steffen, A; Kämper, A; Marian, CM. AIScore – Chemically diverse empirical scoring function employing quantum chemical binding energies of hydrogen-bonded complexes. J. Chem. Inf. Model 2008, 48, 1492–1510. [Google Scholar]
- Sotriffer, CA; Sanschagrin, P; Matter, H; Klebe, G. SFCscore: Scoring functions for affinity prediction of protein-ligand complexes. Proteins 2008, 73, 395–419. [Google Scholar]
- Tanaka, S; Scheraga, HA. Medium- and long-range interaction parameters between amino acids for predicting three-dimensional structures of proteins. Macromolecules 1976, 9, 945–950. [Google Scholar]
- Miyazawa, S; Jernigan, RL. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 1985, 18, 534–552. [Google Scholar]
- Sippl, MJ. Calculation of conformational ensembles from potentials of mean force. J. Mol. Biol 1990, 213, 859–883. [Google Scholar]
- Verkhivker, G; Appelt, K; Freer, ST; Villafranca, JE. Empirical free energy calculations of ligand-protein crystallographic complexes. I. Knowledge-based ligand-protein interaction potentials applied to the prediction of human immunodeficiency virus 1 protease binding affinity. Protein Eng 1995, 8, 677–691. [Google Scholar]
- Huang, S-Y; Zou, X. Mean-force scoring functions for protein-ligand binding. Annu. Rep. Comput. Chem 2010, 6, 281–296. [Google Scholar]
- Thomas, PD; Dill, KA. An iterative method for extracting energy-like quantities from protein structures. Proc. Natl. Acad. Sci. USA 1996, 93, 11628–11633. [Google Scholar]
- Koppensteiner, WA; Sippl, MJ. Knowledge-based potentials – Back to the roots. Biochemistry (Moscow) 1998, 63, 247–252. [Google Scholar]
- Thomas, PD; Dill, KA. Statistical potentials extracted from protein structures: How accurate are they? J. Mol. Biol 1996, 257, 457–469. [Google Scholar]
- McQuarrie, DA. Statistical Mechanics; Harper Collins Publishers: New York, NY, USA, 1976. [Google Scholar]
- Muegge, I; Martin, YC. A general and fast scoring function for protein-ligand interactions: A simplified potential approach. J. Med. Chem 1999, 42, 791–804. [Google Scholar]
- Muegge, I. PMF scoring revisited. J. Med. Chem 2006, 49, 5895–5902. [Google Scholar]
- Huang, S-Y; Zou, X. An iterative knowledge-based scoring function to predict protein-ligand interactions: I. Derivation of interaction potentials. J. Comput. Chem 2006, 27, 1866–1875. [Google Scholar]
- Huang, S-Y; Zou, X. An iterative knowledge-based scoring function to predict protein-ligand interactions: II. Validation of the scoring function. J. Comput. Chem 2006, 27, 1876–1882. [Google Scholar]
- Gohlke, H; Hendlich, M; Klebe, G. Knowledge-based scoring function to predict protein-ligand interactions. J. Mol. Biol 2000, 295, 337–356. [Google Scholar]
- Velec, HFG; Gohlke, H; Klebe, G. DrugScoreCSD-knowledge-based scoring function derived from small molecule crystal data with superior recognition rate of near-native ligand poses and better affinity prediction. J. Med. Chem 2005, 48, 6296–6303. [Google Scholar]
- DeWitte, RS; Shakhnovich, EI. SMoG: de Novo design method based on simple, fast, and accutate free energy estimate. 1. Methodology and supporting evidence. J. Am. Chem. Soc 1996, 118, 11733–11744. [Google Scholar]
- Ishchenko, AV; Shakhnovich, EI. Small molecule growth 2001 (SMoG2001): An improved knowledge-based scoring function for protein-ligand interactions. J. Med. Chem 2002, 45, 2770–2780. [Google Scholar]
- Mitchell, JBO; Laskowski, RA; Alex, A; Thornton, JM. BLEEP – Potential of mean force describing protein-ligand interactions: I. Generating potential. J. Comput. Chem 1999, 20, 1165–1176. [Google Scholar]
- Mitchell, JBO; Laskowski, RA; Alex, A; Forster, MJ; Thornton, JM. BLEEP – Potential of mean force describing protein-ligand interactions: II. Calculation of binding energies and comparison with experimental data. J. Comput. Chem 1999, 20, 1177–1185. [Google Scholar]
- Mooij, WT; Verdonk, ML. General and targeted statistical potentials for protein-ligand interactions. Proteins 2005, 61, 272–287. [Google Scholar]
- Yang, CY; Wang, RX; Wang, SM. M-score: A knowledge-based potential scoring function accounting for protein atom mobility. J. Med. Chem 2006, 49, 5903–5911. [Google Scholar]
- Zhao, X; Liu, X; Wang, Y; Chen, Z; Kang, L; Zhang, H; Luo, X; Zhu, W; Chen, K; Li, H; Wang, X; Jiang, H. An improved PMF scoring function for universally predicting the interactions of a ligand with protein, DNA, and RNA. J. Chem. Inf. Model 2008, 48, 1438–1447. [Google Scholar]
- Zhang, C; Liu, S; Zhu, Q; Zhou, Y. A knowledge-based energy function for protein-ligand, protein-protein, and protein-DNA complexes. J. Med. Chem 2005, 48, 2325–2335. [Google Scholar]
- Huang, S-Y; Zou, X. Inclusion of solvation and entropy in the knowledge-based scoring function for protein-ligand interactions. J. Chem. Inf. Model 2010, 50, 262–273. [Google Scholar]
- Charifson, PS; Corkery, JJ; Murcko, MA; Walters, WP. Consensus scoring: A method for obtaining improved hit rates from docking databases of three-dimensional structures into proteins. J. Med. Chem 1999, 42, 5100–5109. [Google Scholar]
- Wang, R; Wang, S. How does consensus scoring work for virtual library screening? An idealized computer experiment. J. Chem. Inf. Comput. Sci 2001, 41, 1422–1426. [Google Scholar]
- Clark, RD; Strizhev, A; Leonard, JM; Blake, JF; Matthew, JB. Consensus scoring for ligand/protein interactions. J. Mol. Graph. Model 2002, 20, 281–295. [Google Scholar]
- Terp, GE; Johansen, BE; Christensen, IT; Jorgensen, FS. A new concept for multidimensional selection of ligand conformations (MultiSelect) and multidimensional scoring (MultiScore) of protein-ligand binding affinities. J. Med. Chem 2001, 44, 2333–2343. [Google Scholar]
- Cole, JC; Murray, CW; Nissink, JWM; Taylor, RD; Taylor, R. Comparing protein-ligand docking programs is difficult. Proteins 2005, 60, 325–332. [Google Scholar]
- Chen, H; Lyne, PD; Giordanetto, F; Lovell, T; Li, J. On evaluating molecular-docking methods for pose prediction and enrichment factors. J. Chem. Inf. Model 2006, 46, 401–415. [Google Scholar]
- Jain, AN; Nicholls, A. Recommendations for evaluation of computational methods. J. Comput.-Aided Mol. Des 2008, 22, 133–139. [Google Scholar]
- Hawkins, PCD; Warren, GL; Skillman, AG; Nicholls, A. How to do an evaluation: Pitfalls and traps. J. Comput.-Aided Mol. Des 2008, 22, 179–190. [Google Scholar]
- Kirchmair, J; Markt, P; Distinto, S; Wolber, G; Langer, T. Evaluation of the performance of 3D virtual screening protocols: RMSD comparisons, enrichment assessments, and decoy selectionsWhat can we learn from earlier mistakes. J. Comput.-Aided Mol. Des 2008, 22, 213–228. [Google Scholar]
- Wang, R; Lu, Y; Wang, S. Comparative evaluation of 11 scoring functions for molecular docking. J. Med. Chem 2003, 46, 2287–2303. [Google Scholar]
- Stahl, M; Rarey, M. Detailed analysis of scoring functions for virtual screening. J. Med. Chem 2001, 44, 1035–1042. [Google Scholar]
- Ferrara, P; Gohlke, H; Price, DJ; Klebe, G; Brooks, CL, III. Assessing scoring functions for protein-ligand interactions. J. Med. Chem 2004, 47, 3032–3047. [Google Scholar]
- Bissantz, C; Folkers, G; Rognan, D. Protein-based virtual screening of chemical databases 1. Evaluation of different docking/scoring combinations. J. Med. Chem 2000, 43, 4759–4767. [Google Scholar]
- Perola, E; Walters, WP; Charifson, PS. A detailed comparison of current docking and scoring methods on systems of pharmaceutical relevance. Proteins 2004, 56, 235–249. [Google Scholar]
- Warren, GL; Andrews, CW; Capelli, A-M; Clarke, B; LaLonde, J; Lambert, MH; Lindvall, M; Nevins, N; Semus, SF; Senger, S; Tedesco, G; Wall, ID; Woolven, JM; Peishoff, CE; Head, MS. A critical assessment of docking programs and scoring functions. J. Med. Chem 2006, 49, 5912–5931. [Google Scholar]
- Kellenberger, E; Rodrigo, J; Muller, P; Rognan, D. Comparative evaluation of eight docking tools for docking and virtual screening accuracy. Proteins 2004, 57, 225–242. [Google Scholar]
- Bursulaya, BD; Totrov, M; Abagyan, R; Brooks, CL, III. Comparative study of several algorithms for flexible ligand docking. J. Comput. Aided Mol. Des 2003, 17, 755–763. [Google Scholar]
- Kim, R; Skolnick, J. Assessment of programs for ligand binding affinity prediction. J. Comput. Chem 2008, 29, 1316–1331. [Google Scholar]
- Huang, N; Shoichet, BK; Irwin, JJ. Benchmarking sets for molecular docking. J. Med. Chem 2006, 49, 6789–6801. [Google Scholar]
- Irwin, JJ; Shoichet, BK; Mysinger, MM; Huang, N; Colizzi, F; Wassam, P; Cao, Y. Automated docking screens: A feasibility study. J. Med. Chem 2009, 52, 5712–5720. [Google Scholar]
- Ruvinsky, AM. Calculations of protein-ligand binding entropy of relative and overall molecular motions. J. Comput.-Aided Mol. Des 2007, 21, 361–370. [Google Scholar]
- Chang, MW; Belew, RK; Carroll, KS; Olson, AJ; Goodsell, DS. Empirical entropic contributions in computational docking: Evaluation in APS reductase complexes. J. Comput. Chem 2008, 29, 1753–1761. [Google Scholar]
- Lee, J; Seok, C. A statistical rescoring scheme for protein-ligand docking: Consideration of entropic effect. Proteins 2008, 70, 1074–1083. [Google Scholar]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huang, S.-Y.; Zou, X. Advances and Challenges in Protein-Ligand Docking. Int. J. Mol. Sci. 2010, 11, 3016-3034. https://doi.org/10.3390/ijms11083016
Huang S-Y, Zou X. Advances and Challenges in Protein-Ligand Docking. International Journal of Molecular Sciences. 2010; 11(8):3016-3034. https://doi.org/10.3390/ijms11083016
Chicago/Turabian StyleHuang, Sheng-You, and Xiaoqin Zou. 2010. "Advances and Challenges in Protein-Ligand Docking" International Journal of Molecular Sciences 11, no. 8: 3016-3034. https://doi.org/10.3390/ijms11083016