Use of Empirical Correlations to Determine Solvent Effects in the Solvolysis of S-Methyl Chlorothioformate
Abstract
:1. Introduction
2. Results and Discussion
3. Conclusions
4. Experimental Section
Acknowledgments
References and Notes
- Grunwald, E; Winstein, S. The Correlation of Solvolysis Rates. J. Am. Chem. Soc 1948, 70, 846–854. [Google Scholar]
- Schleyer, PvR; Nicholas, RD. The Reactivity of Bridgehead Compounds of Adamantane. J. Am. Chem. Soc 1961, 83, 2700–2707. [Google Scholar]
- Bentley, TW; Schleyer, PvR. Medium Effects on the Rates and Mechanisms of Solvolytic Reactions. Adv. Phys. Org. Chem 1977, 14, 32–40. [Google Scholar]
- Bentley, TW; Llewellyn, G. Yx Scales of Solvent Ionizing Power. Prog Phys Org Chem 1990, 17, 121–158. [Google Scholar]
- Winstein, S; Grunwald, E; Jones, HW. The Correlation of Solvolyses Rates and the Classification of Solvolysis Reactions into Mechanistic Categories. J. Am. Chem. Soc 1951, 73, 2700–2707. [Google Scholar]
- Schadt, FL; Bentley, TW; Schleyer, PvR. The SN2-SN1 Spectrum. 2. Quantitative Treatments of Nucleophilic Solvent Assistance. A Scale of Solvent Nucleophilicities. J. Am. Chem. Soc 1976, 98, 7667–7674. [Google Scholar]
- Kevill, DN; Anderson, SW. An Improved Scale of Solvent Nucleophilicity Based on the Solvolysis of the S-Methyldibenzothiophenium Ion. J. Org. Chem 1991, 56, 1845–1850. [Google Scholar]
- Kevill, DN. Development and Uses of Scales of Solvent Nucleophilicity. In Advances in Quantitative Structure-Property Relationships; Charton, M, Ed.; JAI Press: Greenwich, CT, USA, 1996; Volume 1, pp. 81–115. [Google Scholar]
- Bentley, TW; Garley, MS. Correlations and Predictions of Solvent Effects on Reactivity: Some Limitations of Multi-Parameter Equations and Comparisons with Similarity Models Based on One Solvent Parameter. J. Phys. Org. Chem 2006, 19, 341–349. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Sixty Years of the Grunwald-Winstein Equation: Development and Recent Applications. J Chem Res 2008, 61–66. [Google Scholar]
- Bentley, TW; Koo, IS; Norman, SJ. Distinguishing Between Solvation Effects and Mechanistic Changes. Effects Due to Differences in Solvation of Aromatic Rings and Alkyl Groups. J. Org. Chem 1991, 56, 1604–1609. [Google Scholar]
- Liu, KT; Sheu, HC. Solvolysis of 2-Aryl-2-Chloroadamantanes. A New Y scale for Benzylic Chlorides. J. Org. Chem 1991, 56, 3021–3025. [Google Scholar]
- Fujio, M; Saeki, Y; Nakamoto, K; Yatsugi, K; Goto, N; Kim, SH; Tsuji, Y; Rappoport, Z; Tsuno, Y. Solvent Effects on Anchimerically Assisted Solvolyses. II. Solvent Effects in Solvolyses of threo-2-Aryl-1-methylpropyl-p-toluenesulfonates. Bull. Chem. Soc. Jpn 1995, 68, 2603–2617. [Google Scholar]
- Kevill, DN; Ismail, NHJ; D’Souza, MJ. Solvolysis of the (p-Methoxybenzyl)dimethyl Sulfonium Ion. Development and Use of a Scale to Correct for Dispersion in Grunwald-Winstein Plots. J. Org. Chem 1994, 59, 6303–6312. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Application of the Aromatic Ring Parameter (I) to the Grunwald-Winstein Treatment of the Specific Rates of Solvolysis of Substituted Naphthylmethyl and Anthrylmethyl Sufonates. Org. React. (Tartu) 1995, 29, 55. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Considerably Improved Grunwald-Winstein Correlations for Solvolyses of Several Secondary and Tertiary Benzylic Derivatives upon Inclusion of a Term Governed by the Aromatic Ring Parameter (I). J Chem Soc, Perkin Trans 1995, 2, 973–980. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Incorporation of a Term Governed by the Aromatic Ring Parameter (I) into Grunwald-Winstein Correlations of the Solvolyses of Diarylmethyl, Naphthylmethyl and Arylmethyl Bromides. J Chem Res Synop 1996, 286–287. [Google Scholar]
- Kevill, DN; Anderson, SW; Ismail, NHJ. Correlation of the Rates of Solvolyses of the Benzhydryldimethylsulfonium Ion. Application of the Aromatic Ring Parameter. J. Org. Chem 1996, 61, 7256–7262. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Application of the Aromatic Ring Parameter (I) to Solvolyses of β-Arylalkyl Toluene-p-sulfonates. J Chem Soc Perkin Trans 1997, 2, 257–263. [Google Scholar]
- Kevill, DN; D’Souza, MJ; Ren, H. Correlation of the Rates of Solvolysis of Arylmethyl p-Toluenesulfonates: Application of the Aromatic Ring Parameter and a Discussion of Similarity Models. Can. J. Chem 1998, 76, 751–757. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Application of the Aromatic Ring Parameter (I) to Solvolyses of Extremely Crowded Alkyl Derivatives. Tett. Lett 1998, 39, 3973–3976. [Google Scholar]
- Kevill, DN; Ismail, NHJ. Correlation of the Rates of Solvolysis of (Arylmethyl)methylphenyl-Sulfonium Ions. J Chem Soc Perkin Trans 1998, 2, 1865–1868. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Concerning the Extents of Nucleophilic Participation in Solvolyses of p-Methoxybenzyl Halides. J Chem Res (S) 1999, 336–337. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolyses of Benzoyl Chloride and Derivatives Using Extended Forms of the Grunwald-Winstein Equation. J. Phys. Org. Chem 2002, 15, 881–888. [Google Scholar]
- D’Souza, MJ; Boggs, ME; Kevill, DN. Correlation of the Rates of Solvolysis of 2-Furancarbonyl Chloride and Three Napthoyl Chlorides. J. Phys. Org. Chem 2006, 19, 173–178. [Google Scholar]
- Reis, MC; Elvas-Leitão, R; Martins, F. The Influence of Carbon-Carbon Multiple Bonds on the Solvolyses of Tertiary Alkyl Halides: A Grunwald-Winstein Analysis. Int. J. Mol. Sci 2008, 9, 1704–1716. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Use of the Simple and Extended Grunwald-Winstein Equations in the Correlation of the Rates of Solvolysis of Highly Hindered Tertiary Alkyl Derivatives. Cur. Org. Chem 2010, 14, 1037–1049. [Google Scholar]
- D’Souza, MJ; Darington, AM; Kevill, DN. On the Importance of the Aromatic Ring Parameter in Studies of the Solvolyses of Cinnamyl and Cinnamoyl Halides. Org Chem Int 2010, 2, 130506:1–130506:16. [Google Scholar]
- Wong, SS. Chemistry of Protein Conjugation and Cross-Linking; CRC-Press: Boca Raton, FL, USA, 1991; pp. 7–51. [Google Scholar]
- Khan, JA; Gijs, L; Berger, C; Martin, N; Piraprez, G; Spinnler, HE; Vulfson, EN; Collin, S. Combinatorial Approach to Flavor Analysis. 1. Preparation and Characterization of a S-Methyl Thioester Library. J. Agric. Food Chem 1999, 47, 3269–3273. [Google Scholar]
- Berger, C; Martin, N; Collin, S; Gijs, L; Khan, JA; Piraprez, G; Spinnler, HE; Vulfson, EN. Combinatorial Approach to Flavor Analysis. 2. Olfactory Investigation of a Library of S-Methyl Thioesters and Sensory Evaluation of Selected Components. J. Agric. Food Chem 1999, 47, 3274–3279. [Google Scholar]
- Queen, A; Nour, TA; Bock, E. Electric Moments, Sulfur Bonding, and Conformations of Substituted Thiochloroformate Esters in Benzene. Can. J. Chem 1969, 47, 343–348. [Google Scholar]
- Lee, I. Nucleophilic Substitution at a Carbonyl Carbon. Part II. CNDO/2 Studies on Conformation and Reactivity of the Thio-Analogues of Methyl Chloroformate. J. Korean Chem. Soc 1972, 16, 334–340. [Google Scholar]
- Silvia, CJ; True, NS; Bohn, RK. Low Resolution Microwave Spectroscopy. 13. Conformations of S-n-Propyl Thioesters. J. Phys. Chem 1978, 82, 483–488. [Google Scholar]
- Shen, Q; Krisak, R; Hagen, K. The Molecular Structure of Methyl Chlorothioformate by Gas-Phase Electron Diffraction and Microwave Spectroscopy Data. J. Mol. Struc 1995, 346, 13–19. [Google Scholar]
- Gobbato, KI; Della Védova, CO; Mack, H–G; Oberhammer, H. Structures and Conformations of (Trifluoromethyl)thioacetic Acid, CF3C(O)SH, and Derivatives CF3C(O)SCH3 and CF3C(O)SCl. Inorg. Chem 1996, 35, 6152–6157. [Google Scholar]
- So, SP. Structures, Relative Stabilities and Barriers to Internal Rotation of Chloroformyl Hypochlorite and Thiohypochlorite. J. Mol. Struc. Theochem 1998, 168, 217–225. [Google Scholar]
- Ulic, SE; Coyanis, EM; Romano, RM; Della Védova, CO. S-Ethyl Thiochloroformate, ClC(O)CH2CH3: Unusual Conformational Properties? Spectrochim. Acta Part A: Mol. Biomol. Spec 1998, 54, 695–705. [Google Scholar]
- Romano, RM; Della Védova, CO; Downs, AJ; Parsons, S; Smith, S. Structural and Vibrational Properties of ClC(O)SY Compounds with Y = Cl and CH3. New J. Chem 2003, 27, 514–519. [Google Scholar]
- Erben, MF; Della Védova, CO; Boese, R; Willner, H; Oberhammer, H. Trifluoromethyl Chloroformate: ClC(O)OCF3: Structure, Conformation, and Vibrational Analysis Studied by Experimental and Theoretical Methods. J. Phys. Chem. A 2004, 108, 699–706. [Google Scholar]
- Bentley, TW. Structural Effects on the Solvolytic Reactivity of Carboxylic and Sulfonic Acid Chlorides. Comparisons with Gas-Phase Data for Cation Formation. J. Org. Chem 2008, 73, 6251–6257. [Google Scholar]
- Crunden, EW; Hudson, RF. The Mechanism of Hydrolysis of Acid Chlorides. Part VII. Alkyl Chloroformates. J Chem Soc 1961, 3748–3755. [Google Scholar]
- Queen, A. Kinetics of the Hydrolysis of Acyl Chlorides in Pure Water. Can. J. Chem 1967, 45, 1619–1629. [Google Scholar]
- Queen, A; Nour, TA; Paddon-Row, MN; Preston, K. Kinetics and Hydrolysis of Thiochloroformate Esters in Pure Water. Can. J. Chem 1970, 48, 522–527. [Google Scholar]
- McKinnon, DM; Queen, A. Kinetics and Mechanism for the Hydrolysis of Chlorothionoformate and Chlorodithioformate Esters in Water and Aqueous Acetone. Can. J. Chem 1972, 50, 1401–1406. [Google Scholar]
- Kevill, DN. Choloroformate Esters and Related Compounds. Patai, S, Ed.; In The Chemistry of the Functional Groups: The Chemistry of Acyl Halides; Wiley: New York, NY, USA, 1972; Chapter 12, pp. 381–453. [Google Scholar]
- Bentley, TW; Harris, HC; Zoon, H-R; Gui, TL; Dae, DS; Szajda, SR. Mechanisms of Solvolyses of Acid Chlorides and Chloroformates. Chloroacetyl and Phenylacetyl Chloride as Similarity Models. J. Org. Chem 2005, 70, 8963–8970. [Google Scholar]
- La, S; Koh, KS; Lee, I. Nucleophilic Substitution at a Carbonyl Carbon Atom (XI). Solvolysis of Methyl Chloroformate and Its Thioanalogues in Methanol, Ethanol and Ethanol-Water Mixtures. J. Korean Chem. Soc 1980, 24, 1–7. [Google Scholar]
- La, S; Koh, KS; Lee, I. Nucleophilic Substitution at a Carbonyl Carbon Atom (XII). Solvolysis of Methyl Chloroformate and Its Thioanalogues in CH3CN-H2O and CH3COCH3-H2O Mixtures. J. Korean Chem. Soc 1980, 24, 8–14. [Google Scholar]
- Oh, HK; Ha, JS; Sung, DD; Lee, I. Aminolysis of Aryl Chlorothionoformates with Anilines in Acetonitrile: Effects of Amine Nature and Solvent on the Mechanism. J. Org. Chem 2004, 69, 8219–8223. [Google Scholar]
- Castro, EA. Kinetics and Mechanisms of Reactions of Thiol, Thiono, and Dithio Analogues of Carboxylic Esters with Nucleophilies. Chem. Rev 1999, 99, 3505–3524. [Google Scholar]
- Castro, EA; Cubillos, M; Santos, JG. Kinetics and Mechanisms of the Pyridinolysis of Phenyl and 4-Nitrophenyl Chlorothionoformates. Formation and Hydrolysis of 1-(Aryloxythiocarbonyl)pyridinum Cations. J. Org. Chem 2004, 69, 4802–4807. [Google Scholar]
- Castro, EA; Aliaga, M; Gazitúa, M; Santos, JG. Kinetics and Mechanism of the Reactions of S-Methyl Chlorothioformate with Pyridines and Secondary Alicyclic Amines. Tetrahedron 2006, 62, 4863–4869. [Google Scholar]
- Castro, EA. Kinetics and Mechanisms of Reactions of Thiol, Thiono, and Dithio Analogues of Carboxylic Esters with Nucleophilies. An Update. J. Sulf. Chem 2007, 28, 401–429. [Google Scholar]
- Castro, EA; Aliaga, M; Campodonico, PR; Leis, JR; García-Río, L; Santos, JG. Reactions of Aryl Chlorothionoformates with Quinuclidines. A Kinetic Study. J. Phys. Org. Chem 2008, 21, 102–107. [Google Scholar]
- Castro, EA; Gazitúa, M; Santos, JG. Kinetics and Mechanism of the Reactions of Aryl Chlorodithioformates with Pyridines and Secondary Alicyclic Amines. J Phys Org Chem 2009, 22, 1030–1037. [Google Scholar]
- D’Souza, MJ; Ryu, ZH; Park, B-C; Kevill, DN. Correlation of the Rates of Solvolysis of Acetyl Chloride and α-Substituted Derivatives. Can. J. Chem 2008, 86, 359–367. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Concerning the Two Reaction Channels for the Solvolyses of Ethyl Chloroformate and Ethyl Chlorothioformate. J. Org. Chem 1998, 63, 2120–2124. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Dual Pathways in the Solvolyses of Phenyl Chlorothioformate. J. Org. Chem 1997, 62, 7869–7871. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolysis of Phenyl Chlorothionoformate and Phenyl Chlorodithioformate. Can. J. Chem 1999, 77, 1118–1122. [Google Scholar]
- Kevill, DN; Koyoshi, F; D’Souza, MJ. Correlation of the Specific Rates of Solvolysis of Aromatic Carbamoyl Chlorides, Chloroformates, Chlorothionoformates, and Chlorodithioformates Revisited. Int. J. Mol. Sci 2007, 8, 346–352. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolysis of Phenyl Chloroformate. J Chem Soc Perkin Trans 1997, 2, 1721–1724. [Google Scholar]
- Koo, IS; Yang, K; Kang, DH; Park, HJ; Kang, K; Lee, I. Transition-State Variation in the Solvolyses of Phenyl Chlorothionoformate in Alcohol-Water Mixtures. Bull. Korean Chem. Soc 1999, 20, 577–580. [Google Scholar]
- An, SK; Yang, JS; Cho, JM; Yang, K; Lee, PL; Bentley, TW; Lee, I; Koo, IS. Correlation of the Rates of Solvolysis of Phenyl Chlorodithioformate. Bull. Korean Chem. Soc 2002, 23, 1445–1450. [Google Scholar]
- Kevill, DN; Kim, JC; Kyong, JB. Correlation of the Rates of Methyl Chloroformate with Solvent Properties. J Chem Res Synop 1999, 150–151. [Google Scholar]
- D’Souza, MJ; Stant-Boggs, ME; White, R; Kevill, DN. Correlation of the Rates of Solvolysis of 2-Thiophenecarbonyl Chloride. J. Chem. Res. (S) 2003, 12, 775–777. [Google Scholar]
- D’Souza, MJ; Bogg, ME; Kevill, DN. Correlation of the Rates of Solvolysis of 2-Furancarbonyl Chloride and Three Naphthoyl Chlorides. J. Phys. Org. Chem 2006, 19, 173–178. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Additional YCl Values and Correlation of the Specific Rates of Solvolysis of tert-Butyl Chloride in Terms of NT and YCl Scales. J Chem Res Synop 1993, 174–175. [Google Scholar]
- Seong, MH; Choi, SH; Lee, Y-W; Kyong, JB; Kim, DK; Kevill, DN. Correlation of the Rates of Solvolysis of Methyl Fluoroformate Using the Extended Grunwald-Winstein Equation. Bull. Korean Chem. Soc 2009, 30, 2408–2412. [Google Scholar]
- Bentley, TW; Llewellyn, G; McAlister, JA. SN2 Mechanism for the Alcoholysis, Aminolysis, and Hydrolysis of Acetyl Chloride. J. Org. Chem 1996, 61, 7927–7932. [Google Scholar]
- Romano, RM; Della Védova, CO; Downs, AJ. Matrix Photochemistry of the Chlorocarbonyl Sulfenyl Compounds ClC(O)SY, with Y = Cl or CH3. J. Phys. Chem. A 2004, 108, 7179–7187. [Google Scholar]
- Kevill, DN; Park, B-C; Park, K-H; D’Souza, MJ; Yaakoubd, L; Mlynarski, SL; Kyong, JB. Rate and Product Studies in the Solvolyses of N,N-Dimethylsulfamoyl and 2-Propanesulfonyl Chlorides. Org. Biomol. Chem 2006, 4, 1580–1586. [Google Scholar]
- Frost, AA; Pearson, RG. Kinetics and Mechanism-a Study of Homogeneous Chemical Reactions, 2nd ed; Wiley: New York, NY, USA, 1961; pp. 49–50. [Google Scholar]
- Kevill, DN; Abduljaber, MH. Correlation of the Rates of Solvolysis of Cyclopropylcarbinyl and Cyclobutyl Bromides Using the Extended Grunwald-Winstein Equation. J. Org. Chem 2000, 65, 2548–2554. [Google Scholar]

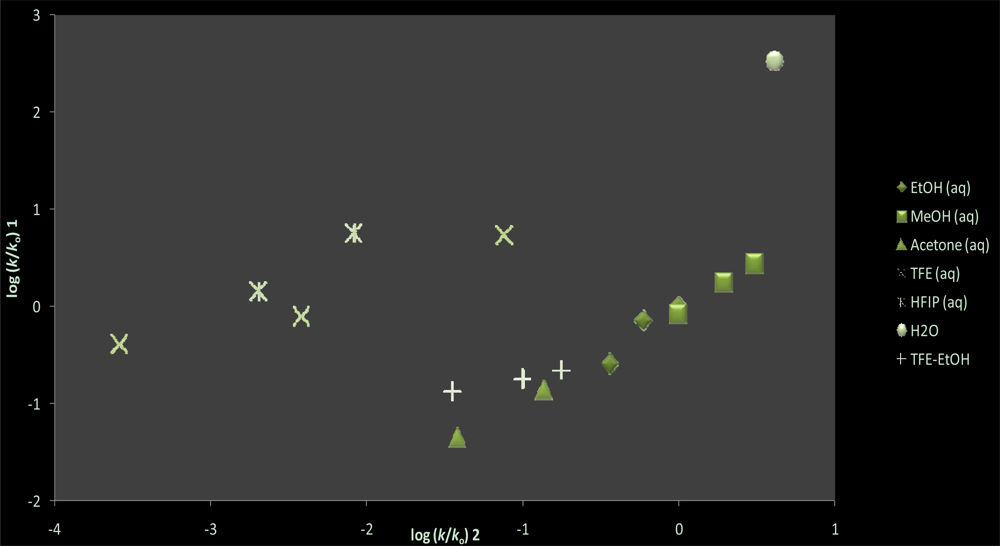
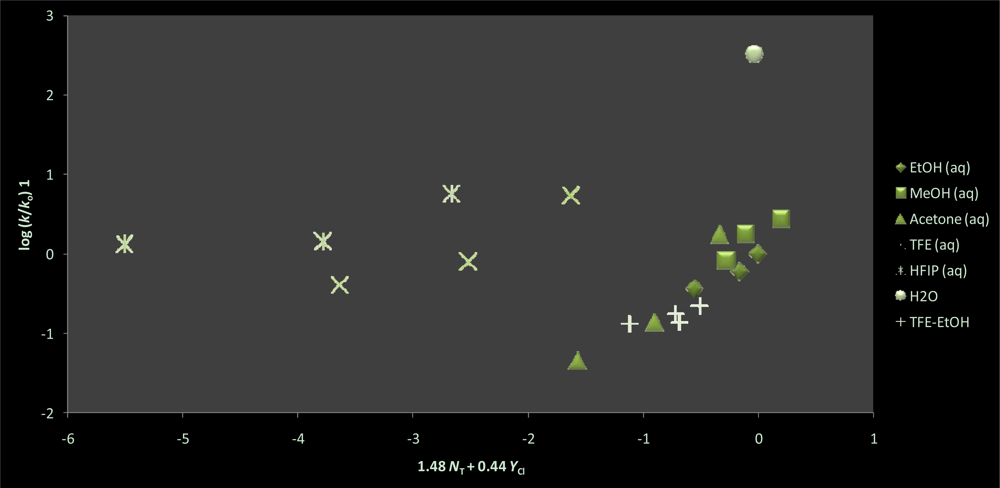
| Solvent (%)a | 1 @ 25.0 °C; 105k, s−1b | NTc | YCld |
|---|---|---|---|
| 100% MeOH | 2.00 ± 0.07e | 0.17 | −1.2 |
| 90% MeOH | 4.29 ± 0.15 | −0.01 | −0.20 |
| 80% MeOH | 6.75 ± 0.27f | −0.06 | 0.67 |
| 100% EtOH | 0.884 ± 0.021g | 0.37 | −2.50 |
| 90% EtOH | 1.45 ± 0.15 | 0.16 | −0.90 |
| 80% EtOH | 2.44 ± 0.12h | 0.00 | 0.00 |
| 90% Acetone | 0.107 ± 0.007 | −0.35 | −2.39 |
| 80% Acetone | 0.334 ± 0.013 | −0.37 | −0.80 |
| 60% Acetone | 4.30 ± 0.20 | −0.52 | 1.00 |
| 97% TFE (w/w) | 0.986 ± 0.030 | −3.30 | 2.83 |
| 90% TFE (w/w) | 1.92 ± 0.13 | −2.55 | 2.85 |
| 70% TFE (w/w) | 13.2 ± 1.5 | −1.98 | 2.96 |
| 60T-40E | 0.321 ± 0.015 | −0.94 | 0.63 |
| 50T-50E | 0.333 ± 0.017 | −0.64 | 0.60 |
| 40T-60E | 0.431 ± 0.013 | −0.34 | −0.48 |
| 20T-80E | 0.537 ± 0.016 | 0.08 | −1.42 |
| 100% H2O | 820i | −1.38 | 4.57 |
| 97%HFIP (w/w) | 3.21 ± 0.15 | −5.26 | 5.17 |
| 90%HFIP (w/w) | 3.48 ± 0.092j | −3.84 | 4.41 |
| 70%HFIP (w/w) | 13.9 ± 0.78 | −2.94 | 3.83 |
| Substrate | na | lb | mb | cc | Rd | Fe |
|---|---|---|---|---|---|---|
| 1 | 20f | 0.23 ± 0.06 | −0.29 ± 0.16 | 0.637 | 12 | |
| 0.64 ± 0.12 | 0.60 ± 0.08 | 0.10 ± 0.13 | 0.879 | 29 | ||
| 13g | 0.21 ± 0.13 | −0.29 ± 0.16 | 0.435 | 3 | ||
| 1.47 ± 0.21 | 0.49 ± 0.07 | 0.14 ± 0.09 | 0.927 | 30 | ||
| 12h | 0.17 ± 0.15 | −0.34 ± 0.18 | 0.341 | 1 | ||
| 1.48 ± 0.18 | 0.44 ± 0.06 | 0.08 ± 0.08 | 0.949 | 40 | ||
| 8i | 0.24 ± 0.26 | −0.30 ± 0.97 | 0.341 | 1 | ||
| 0.79 ± 0.06 | 0.85 ± 0.07 | −0.27 ± 0.18 | 0.987 | 95 |
| Substrate | na | lb | mb | l/m | cc | Rd | Fe |
|---|---|---|---|---|---|---|---|
| EtOCOClf | 28 | 1.56 ± 0.09 | 0.55 ± 0.03 | 2.84 | 0.19 ± 0.24 | 0.967 | 179 |
| 7 | 0.69 ± 0.13 | 0.82 ± 0.16 | 0.84 | −2.40 ± 0.27 | 0.946 | 17 | |
| MeOCOClg | 19 | 1.59 ± 0.09 | 0.58 ± 0.05 | 2.74 | 0.16 ± 0.07 | 0.977 | |
| PhOCOClh | 49 | 1.66 ± 0.05 | 0.56 ± 0.03 | 2.96 | 0.15 ± 0.07 | 0.980 | 568 |
| PhSCSCli | 31 | 0.69 ± 0.05 | 0.95 ± 0.03 | 0.73 | 0.18 ± 0.05 | 0.987 | 521 |
| PhOCSClj | 9 | 1.88 ± 0.28 | 0.56 ± 0.15 | 3.36 | 0.38 ± 0.15 | 0.950 | 28 |
| 18 | 0.34 ± 0.05 | 0.93 ± 0.09 | 0.37 | −2.54 ± 0.34 | 0.955 | 77 | |
| PhSCOClk | 16 | 1.74 ± 0.17 | 0.48 ± 0.07 | 3.63 | 0.19 ± 0.23 | 0.946 | 55 |
| 6 | 0.62 ± 0.08 | 0.92 ± 0.11 | 0.67 | −2.29 ± 0.13 | 0.983 | 44 | |
| EtSCOCll | 19 | 0.66 ± 0.08 | 0.93 ± 0.07 | 0.71 | −0.16 ± 0.31 | 0.961 | 96 |
| MeOCOFm | 14 | 1.33 ± 0.09 | 0.73 ± 0.06 | 1.82 | −0.08 ± 0.08 | 0.972 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
D’Souza, M.J.; Hailey, S.M.; Kevill, D.N. Use of Empirical Correlations to Determine Solvent Effects in the Solvolysis of S-Methyl Chlorothioformate. Int. J. Mol. Sci. 2010, 11, 2253-2266. https://doi.org/10.3390/ijms11052253
D’Souza MJ, Hailey SM, Kevill DN. Use of Empirical Correlations to Determine Solvent Effects in the Solvolysis of S-Methyl Chlorothioformate. International Journal of Molecular Sciences. 2010; 11(5):2253-2266. https://doi.org/10.3390/ijms11052253
Chicago/Turabian StyleD’Souza, Malcolm J., Stefan M. Hailey, and Dennis N. Kevill. 2010. "Use of Empirical Correlations to Determine Solvent Effects in the Solvolysis of S-Methyl Chlorothioformate" International Journal of Molecular Sciences 11, no. 5: 2253-2266. https://doi.org/10.3390/ijms11052253




