Combined Molecular Algorithms for the Generation, Equilibration and Topological Analysis of Entangled Polymers: Methodology and Performance
Abstract
:1. Introduction
2. Monte Carlo Scheme for the Generation and Relaxation of Athermal Polymer Models
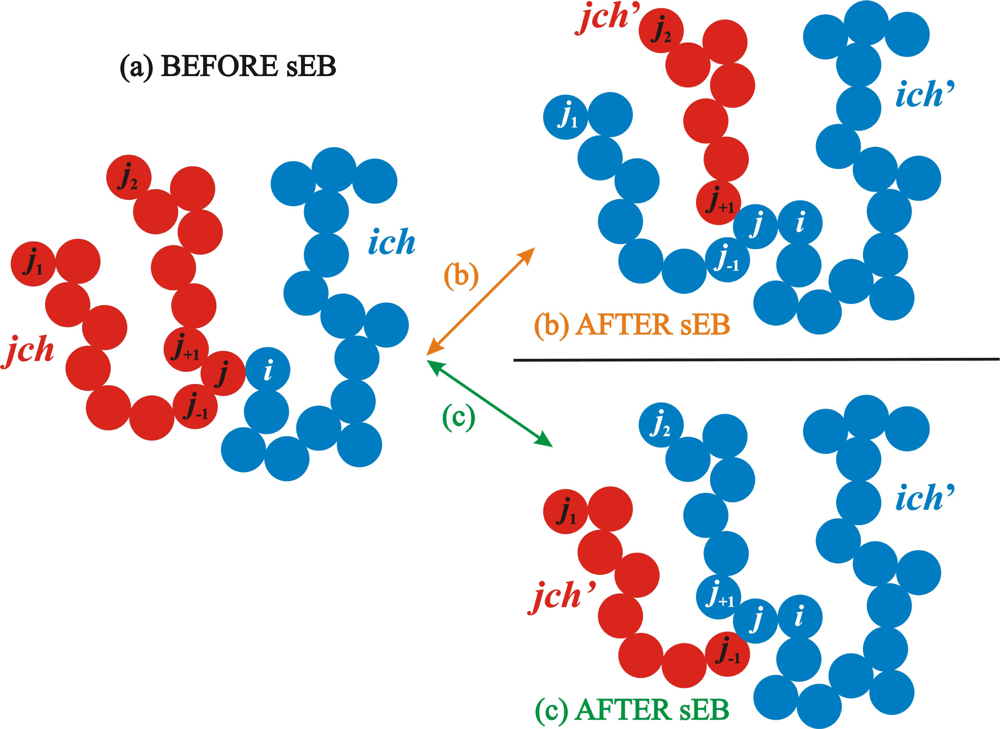
2.1. Simplified End-Bridging
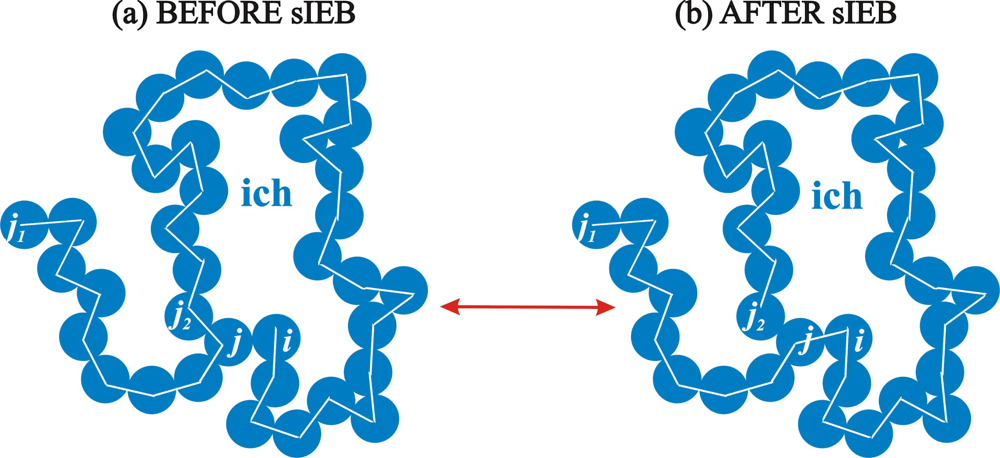
2.2. Simplified Intramolecular End-Bridging
2.3. Algorithmic Implementation of the sEB and sIEB Algorithms
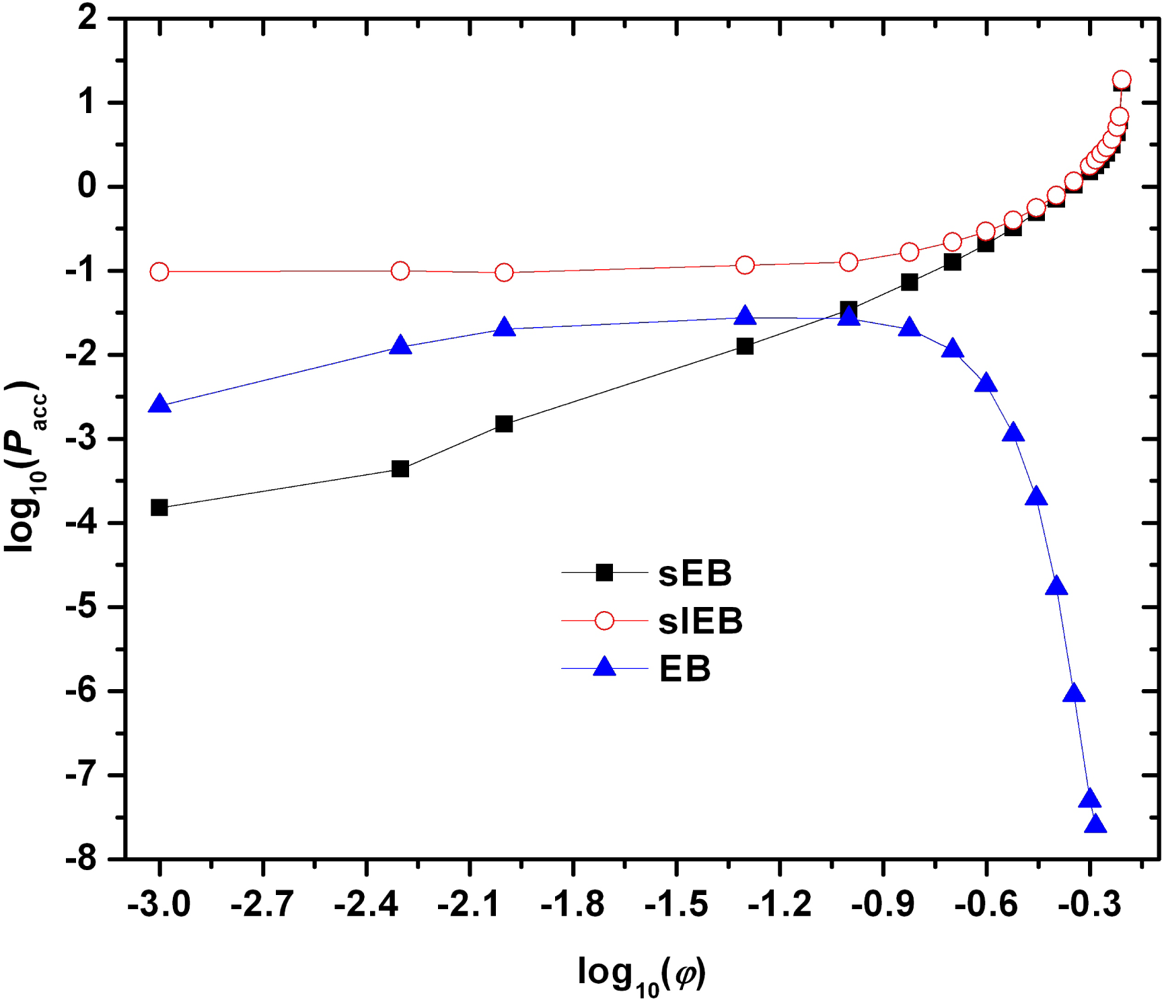
2.4. Monte Carlo Scheme Based on sEB and sIEB
3. Results from Monte Carlo Simulations on Hard-Sphere Chains
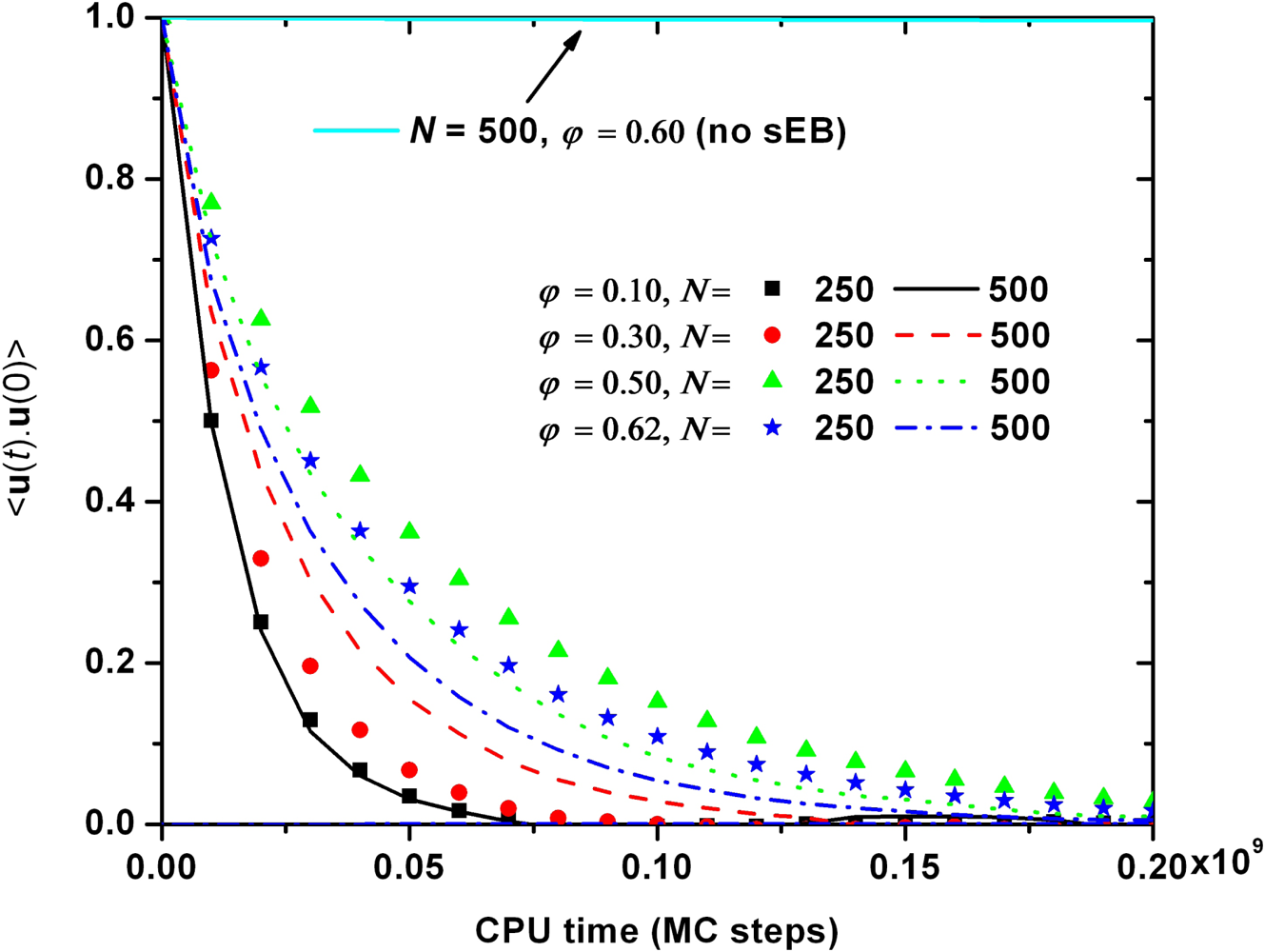
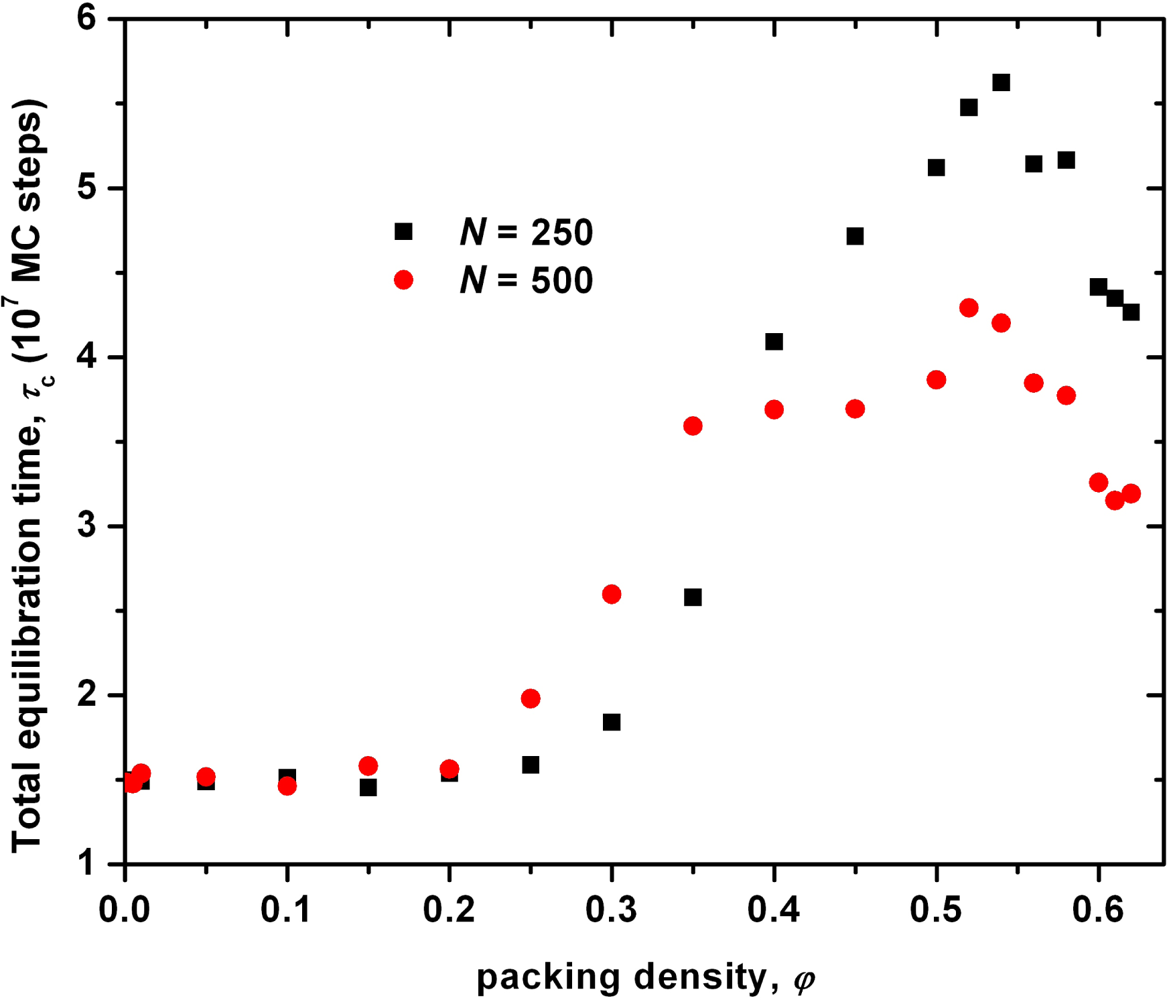
3.1. Analysis of the Effect of System Size on Chain Dimensions in MC Simulations
4. Direct Topological Analysis of Entanglements and Primitive Paths in Polymeric Systems
4.1. Calculation of the Primitive Path
4.2. Algorithmic Details of the Z1 Code
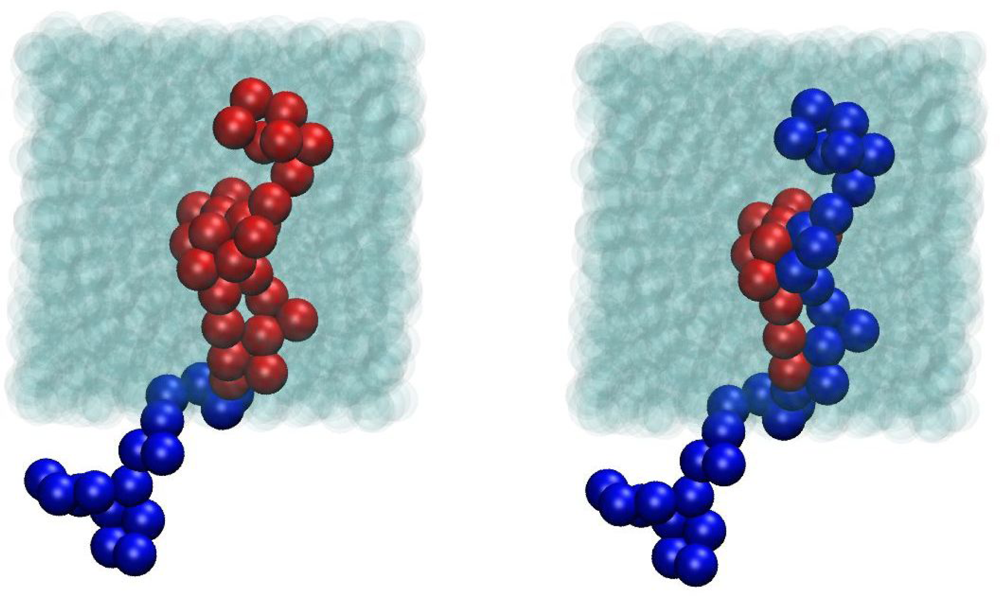
4.3. Comment about Self-Entanglements
4.4. Estimating the Entanglement Molecular Weight
5. Conclusions
Acknowledgments
References
- Sperling, LH. Introduction to Physical Polymer Science; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Debye, P. The Intrinsic Viscosity of Polymer Solutions. J. Chem. Phys 1946, 14, 636–639. [Google Scholar]
- Flory, PG. Statistical Mechanics of Chain Molecules; Hanser Verlag: Munich, Germany, 1989. [Google Scholar]
- Horton, JC; Squires, GL; Boothroyd, AT; Fetters, LJ; Rennie, AR; Glinka, CJ; Robinson, RA. Small-Angle Neutron-Scattering from Star-Branched Polymers in the Molten State. Macromolecules 1989, 22, 681–686. [Google Scholar]
- Takeuchi, H; Roe, RJ. Molecular-Dynamics Simulation of Local Chain Motion in Bulk Amorphous Polymers. I. Dynamics above the Glass-Transition. J. Chem. Phys 1991, 94, 7446–7457. [Google Scholar]
- Takeuchi, H; Roe, RJ. Molecular-Dynamics Simulation of Local Chain Motion in Bulk Amorphous Polymers. II. Dynamics at Glass-Transition. J. Chem. Phys 1991, 94, 7458–7465. [Google Scholar]
- Rouse, PE. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys 1953, 21, 1272–1280. [Google Scholar]
- de Gennes, PG. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Doi, M; Edwards, SF. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Lodge, TP. Reconciliation of the Molecular Weight Dependence of Diffusion and Viscosity in Entangled Polymers. Phys. Rev. Lett 1999, 83, 3218–3221. [Google Scholar]
- Wang, SQ. Chain Dynamics in Entangled Polymers: Diffusion versus Rheology and Their Comparison. J. Polym. Sci., Polym. Phys 2003, 41, 1589–1604. [Google Scholar]
- Milner, ST; McLeish, TCB. Parameter-Free Theory for Stress Relaxation in Star Polymer Melts. Macromolecules 1997, 30, 2159–2166. [Google Scholar]
- Juliani, J; Archer, LA. Relaxation Dynamics of Entangled and Unentangled Multiarm Polymer Solutions: Experiment. Macromolecules 2002, 35, 6953–6960. [Google Scholar]
- Kapnistos, M; Vlassopoulos, D; Roovers, J; Leal, LG. Linear Rheology of Architecturally Complex Macromolecules: Comb Polymers with Linear Backbones. Macromolecules 2005, 38, 7852–7862. [Google Scholar]
- Lee, JH; Orfanou, J; Driva, P; Iatrou, H; Hadjichristidis, N; Lohse, DJ. Linear and Nonlinear Rheology of Dendritic Star Polymers: Experiment. Macromolecules 2008, 41, 9165–9178. [Google Scholar]
- Kapnistos, M; Lang, M; Vlassopoulos, D; Pyckhout-Hintzen, W; Richter, D; Cho, D; Chang, T; Rubinstein, M. Unexpected Power-Law Stress Relaxation of Entangled Ring Polymers. Nature Mater 2008, 7, 997–1002. [Google Scholar]
- De Gennes, PG. Reptation of a Polymer Chain in Presence of Fixed Obstacles. J. Chem. Phys 1971, 55, 572. [Google Scholar]
- De Gennes, PG. Dynamics of Entangled Polymer-Solutions. 2 Inclusion of Hydrodynamic Interactions. Macromolecules 1976, 9, 594–598. [Google Scholar]
- McLeish, TCB. Molecular Rheology of H-Polymers. Macromolecules 1988, 21, 1062–1070. [Google Scholar]
- Kröger, M; Hess, S. Viscoelasticity of Polymeric Melts and Concentrated-Solutions—The Effect of Flow-Induced Alignment of Chain Ends. Physica A 1993, 195, 336–353. [Google Scholar]
- Marrucci, G. Dynamics of Entanglements: A Nonlinear Model Consistent with the Cox-Merz Rule. J. Non-Newtonian Fluid Mech 1996, 62, 279–289. [Google Scholar]
- Bishko, G; McLeish, TCB; Harlen, OG; Larson, RG. Theoretical Molecular Rheology of Branched Polymers in Simple and Complex Flows: The Pom-Pom Model. Phys. Rev. Lett 1997, 79, 2352–2355. [Google Scholar]
- McLeish, TCB; Larson, RG. Molecular Constitutive Equations for a Class of Branched Polymers: The Pom-Pom Polymer. J. Rheol 1998, 42, 81–110. [Google Scholar]
- McLeish, TCB; Allgaier, J; Bick, DK; Bishko, G; Biswas, P; Blackwell, R; Blottiere, B; Clarke, N; Gibbs, B; Groves, DJ; Hakiki, A; Heenan, RK; Johnson, JM; Kant, R; Read, DJ; Young, RN. Dynamics of Entangled H-Polymers: Theory, Rheology, and Neutron-Scattering. Macromolecules 1999, 32, 6734–6758. [Google Scholar]
- Fang, JN; Kröoger, M; Öttinger, HC. A Thermodynamically Admissible Reptation Model for Fast Flows of Entangled Polymers. II Model Predictions for Shear and Extensional Flows. J. Rheol 2000, 44, 1293–1317. [Google Scholar]
- Ianniruberto, G; Marrucci, G. Convective Orientational Renewal in Entangled Polymers. J. Non-Newtonian Fluid Mech 2000, 95, 363–374. [Google Scholar]
- Likhtman, AE; McLeish, TCB. Quantitative Theory for Linear Dynamics of Linear Entangled Polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar]
- Marrucci, G; Ianniruberto, G. Interchain Pressure Effect in Extensional Flows of Entangled Polymer Melts. Macromolecules 2004, 37, 3934–3942. [Google Scholar]
- Greco, F. Entangled Polymeric Liquids: Nonstandard Statistical Thermodynamics of a Subchain Between Entanglement Points and a New Calculation of the Strain Measure Tensor. Macromolecules 2004, 37, 10079–10088. [Google Scholar]
- Liu, CY; Keunings, R; Bailly, C. Do Deviations from Reptation Scaling of Entangled Polymer Melts Result from Single- or Many-Chain Effects? Phys. Rev. Lett 2006, 97, 246001. [Google Scholar]
- Schieber, JD; Nair, DM; Kitkrailard, T. Comprehensive Comparisons with Nonlinear Flow Data of a Consistently Unconstrained Brownian Slip-Link Model. J. Rheol 2007, 51, 1111–1141. [Google Scholar]
- Yaoita, T; Isaki, T; Masubushi, Y; Watanabe, H; Ianniruberto, G; Greco, F; Marruci, G. Statics, Linear, and Nonlinear Dynamics of Entangled Polystyrene Melts Simulated through The Primitive Chain Network Model. J. Chem. Phys 2008, 128, 154901. [Google Scholar]
- Zamponi, M; Wischnewski, A; Monkenbusch, M; Willner, L; Richter, D; Falus, P; Farago, B; Guenza, MG. Cooperative Dynamics in Homopolymer Melts: A Comparison of Theoretical Predictions with Neutron Spin Echo Experiments. J. Phys. Chem. B 2008, 112, 16220–16229. [Google Scholar]
- Greco, F. Equilibrium Statistical Distributions for Subchains in an Entangled Polymer Melt. Eur. Phys. J. E 2008, 25, 175–180. [Google Scholar]
- Kremer, K. Computer Simulations for Macromolecular Science. Macromol. Chem. Phys 2003, 204, 257. [Google Scholar]
- Theodorou, DN. Understanding and Predicting Structure-Property Relations in Polymeric Materials through Molecular Simulations. Mol. Phys 2004, 102, 147–166. [Google Scholar]
- Aleman, C; Karayiannis, NC; Curco, D; Foteinopoulou, K; Laso, M. Computer Simulations of Amorphous Polymers: From Quantum Mechanical Calculations to Mesoscopic Models. J. Mol. Struct. (THEOCHEM) 2009, 898, 62–72. [Google Scholar]
- Nielaba, P; Mareschal, M; Ciccotti, G (Eds.) Bridging Time Scales: Molecular Simulations for the Next Decade; Springer: Berlin, Germany, 2002.
- Laso, M; Perpete, EA (Eds.) Multiscale Modelling of Polymer Properties (Computer-Aided Chemical Engineering 22); Elsevier: Amsterdam, The Netherlands, 2006.
- Ilg, P; Öttinger, HC; Kröger, M. Systematic Time-Scale-Bridging Molecular Dynamics Applied to Flowing Polymer Melts. Phys. Rev. E 2009, 79, 011802. [Google Scholar]
- Allen, MP; Tildesley, DJ. Computer Simulation of Liquids; Clarendon: Oxford, 1987. [Google Scholar]
- Binder, K (Ed.) Monte Carlo and Molecular Dynamics Simulations in Polymer Science; Clarendon: Oxford, 1995.
- Frenkel, D; Smit, B. Understanding Molecular Simulation; Academic: London, 2001. [Google Scholar]
- Plimpton, SJ. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys 1995, 117, 1–19. [Google Scholar]
- van der Spoel, D; Lindahl, E; Hess, B; Groenhof, G; Mark, AE; Berendsen, HJC. GRO-MACS: Fast, Flexible and Free. J. Comp. Chem 2005, 26, 1701–1718. [Google Scholar]
- Tschop, W; Kremer, K; Batoulis, J; Burger, T; Hahn, O. Simulation of Polymer Melts. I. Coarse-Graining Procedure for Polycarbonates. Acta Polym 1998, 49, 61–74. [Google Scholar]
- Müller-Plathe, F. Coarse-Graining in Polymer Simulation: From the Atomistic to the Mesoscopic Scale and Back. Chem. Phys. Chem 2002, 124, 754–769. [Google Scholar]
- Aoyagi, T; Sawa, F; Shoji, T; Fukunaga, H; Takimoto, J; Doi, M. A General-Purpose Coarse-Grained Molecular Dynamics Program. Comput. Phys. Commun 2002, 145, 267–279. [Google Scholar]
- Padding, JT; Briels, WJ. Time and Length Scales of Polymer Melts Studied by Coarse-Grained Molecular Dynamics Simulations. J. Chem. Phys 2002, 117, 925–943. [Google Scholar]
- Hess, B; Leon, S; van der Vegt, N; Kremer, K. Long Time Atomistic Polymer Trajectories from Coarse Grained Simulations: Bisphenol-A Polycarbonate. Soft Matter 2006, 2, 409–414. [Google Scholar]
- Harmandaris, VA; Adhikari, NP; van der Vegt, NFA; Kremer, K. Hierarchical Modeling of Polystyrene: From Atomistic to Coarse-Grained Simulations. Macromolecules 2006, 39, 6708–6719. [Google Scholar]
- Kamio, K; Moorthi, K; Theodorou, DN. Coarse Grained End Bridging Monte Carlo Simulations of Poly(ethylene terephthalate) Melt. Macromolecules 2007, 40, 710–722. [Google Scholar]
- Spyriouni, T; Tzoumanekas, C; Theodorou, D; M¨ller-Plathe, F; Milano, G. Coarse-Grained and Reverse-Mapped United-Atom Simulations of Long-Chain Atactic Polystyrenr Melts: Structure, Thermodynamic Properties, Chain Conformation, and Entanglements. Macromolecules 2007, 40, 3876–3885. [Google Scholar]
- Curco, D; Aleman, C. Coarse-Graining: A Procedure to Generate Equilibrated and Relaxed Models of Amorphous Polymers. J. Comput. Chem 2007, 28, 1929–1935. [Google Scholar]
- Carbone, P; Karimi-Varzaneh, HA; Müller-Plathe, F. Fine-Graining Without Coarse-Graining: An Easy and Fast Way to Equilibrate Dense Polymer Melts. Faraday Discuss 2010, 144, 25–42. [Google Scholar]
- Vacatello, M; Avitabile, G; Corradini, P; Tuzi, A. A Computer-Model of Molecular Arrangement in a n-Paraffinic Liquid. J. Chem. Phys 1980, 73, 548–552. [Google Scholar]
- Siepmann, JI; Frenkel, D. Configurational Bias Monte-Carlo—A New Sampling Scheme for Flexible Chains. Mol. Phys 1992, 75, 59–70. [Google Scholar]
- de Pablo, JJ; Laso, M; Suter, UW. Simulation of Polyethylene Above and Below the Melting-Point. J. Chem. Phys 1992, 96, 2395–2403. [Google Scholar]
- Laso, M; de Pablo, JJ; Suter, UW. Simulation of Phase-Equilibria for Chain Molecules. J. Chem. Phys 1992, 97, 2817–2819. [Google Scholar]
- Dodd, LR; Boone, TD; Theodorou, DN. A Concerted Rotation Algorithm for Atomistic Monte-Carlo Simulation of Polymer Melts and Glasses. Mol. Phys 1993, 78, 961–996. [Google Scholar]
- Santos, S; Suter, UW; Müller, M; Nievergelt, J. A Novel Parallel-Rotation Algorithm for Atomistic Monte Carlo Simulation of Dense Polymer Systems. J. Chem. Phys 2001, 114, 9772–9779. [Google Scholar]
- Pant, PVK; Theodorou, DN. Variable Connectivity Method for the Atomistic Monte Carlo Simulation of Polydisperse Polymer Melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar]
- Mavrantzas, VG; Boone, TD; Zervopoulou, E; Theodorou, DN. End-Bridging Monte Carlo: A Fast Algorithm for Atomistic Simulation of Condensed Phases of Long Polymer Chains. Macromolecules 1999, 32, 5072–5096. [Google Scholar]
- Karayiannis, NC; Mavrantzas, VG; Theodorou, DN. A Novel Monte Carlo Scheme for the Rapid Equilibration of Atomistic Model Polymer Systems of Precisely Defined Molecular Architecture. Phys. Rev. Lett 2002, 88, 105503. [Google Scholar]
- Karayiannis, NC; Giannousaki, AE; Mavrantzas, VG; Theodorou, DN. Atomistic Monte Carlo Simulation of Strictly Monodisperse Long Polyethylene Melts through a Generalized Chain Bridging Algorithm. J. Chem. Phys 2002, 117, 5465–5479. [Google Scholar]
- Uhlherr, A; Mavrantzas, VG; Doxastakis, M; Theodorou, DN. Directed Bridging Methods for Fast Atomistic Monte Carlo Simulations of Bulk Polymers. Macromolecules 2001, 34, 8554–8568. [Google Scholar]
- Balijepalli, S; Rutledge, GC. Molecular Simulation of the Intercrystalline Phase of Chain Molecules. J. Chem. Phys 1998, 1998, 6523–6526. [Google Scholar]
- Bunker, A; Dünweg, B. Parallel Excluded Volume Tempering for Polymer Melts. Phys. Rev. E 2000, 63, 016701. [Google Scholar]
- Auhl, R; Everaers, R; Grest, GS; Kremer, K; Plimpton, SJ. Equilibration of Long Chain Polymer Melts in Computer Simulations. J. Chem. Phys 2003, 119, 12718–12728. [Google Scholar]
- Banaszak, BJ; de Pablo, JJ. A New Double-Rebridging Technique for Linear Polyethylene. J. Chem. Phys 2003, 119, 2456–2462. [Google Scholar]
- Ulhlerr, A; Doxastakis, M; Mavrantas, VG; Theodorou, DN; Leak, SJ; Adam, NE; Nyberg, PE. Atomistic Structure of a High Polymer Melt. Europhys. Lett 2002, 57, 506–511. [Google Scholar]
- Karayiannis, NC; Giannousaki, AE; Mavrantzas, VG. An Advanced Monte Carlo Method for the Equilibration of Model Long-Chain Branched Polymers with a Well-Defined Molecular Architecture: Detailed Atomistic Simulation of an H-Shaped Polyethylene Melt. J. Chem. Phys 2003, 118, 2451–2454. [Google Scholar]
- Ramos, J; Peristeras, LD; Theodorou, DN. Monte Carlo Simulation of Short Chain Branched Polyolefins in the Molten State. Macromolecules 2007, 40, 9640–9650. [Google Scholar]
- Peristeras, LD; Economou, IG; Theodorou, DN. Structure and Volumetric Properties of Linear and Triarm Star Polyethylenes from Atomistic Monte Carlo Simulation Using New Internal Rearrangement Moves. Macromolecules 2005, 38, 386–397. [Google Scholar]
- Doxastakis, M; Mavrantzas, VG; Theodorou, DN. Atomistic Monte Carlo Simulation of Cis-1,4 Polyisoprene Melts. I Single Temperature End-Bridging Monte Carlo Simulations. Macromolecules 2001, 115, 11339–11351. [Google Scholar]
- Gestoso, P; Nicol, E; Doxastakis, M; Theodorou, DN. Atomistic Monte Carlo Simulation of Polybutadiene Isomers: Cis- 1,4-Polybutadiene and 1,2-Polybutadiene. Macromolecules 2003, 36, 6925–6938. [Google Scholar]
- Wick, CD; Theodorou, DN. Connectivity-altering Monte Carlo Simulations of the End Group Effects of Volumetric Properties for Poly(ethylene oxide). Macromolecules 2004, 37, 7026–7033. [Google Scholar]
- Harmandaris, VA; Mavrantzas, VG; Theodorou, DN; Kröger, M; Ramirej, J; Öttinger, HC; Vlassopoulos, D. Crossover from the Rouse to the Entangled Polymer Melt Regime: Signals from Long, Detailed Atomistic Molecular Dynamics Simulations, Supported by Rheological Experiments. Macromolecules 2003, 36, 1376–1387. [Google Scholar]
- Karayiannis, NC; Mavrantzas, VG. Hierarchical Modeling of the Dynamics of Polymers with a Nonlinear Molecular Architecture: Calculation of Branch Point Friction and Chain Reptation Time of H-Shaped Polyethylene Melts from Long Molecular Dynamics Simulations. Macromolecules 2005, 38, 8583–8596. [Google Scholar]
- Ramos, J; Vega, JF; Theodorou, DN; Martinez-Salazar, J. Entanglement Relaxation Time in Polyethylene: Simulation Versus Experimental Data. Macromolecules 2008, 41, 2959–2962. [Google Scholar]
- Gestoso, P; Karayiannis, NC. Molecular Simulation of the Effect of Temperature and Architecture on Polyehtylene Barrier Properties. J. Chem. Phys. B 2008, 112, 5646–5660. [Google Scholar]
- Leontidis, E; de Pablo, JJ; Laso, M; Suter, UW. A Critical Evaluation of Novel Algorithms for the Off-Lattice Monte-Carlo Simulation of Condensed Polymer Phases. Adv. Polym. Sci 1994, 116, 283–318. [Google Scholar]
- Laso, M; Karayiannis, NC; Müller, M. Min-Map Bias Monte Carlo for Chain Molecules: Biased Monte Carlo Sampling Based on Bijective Minimum-to-Minimum Mapping. J. Chem. Phys 2006, 125, 164108. [Google Scholar]
- Theodorou, DN. A Reversible Minimum-to-Minimum Mapping Method for the Calculation of Free-Energy Differences. J. Chem. Phys 2006, 124, 034109. [Google Scholar]
- Uhlherr, A; Theodorou, DN. Accelerating Molecular Simulations by Reversible Mapping Between Local Minima. J. Chem. Phys 2006, 125, 084107. [Google Scholar]
- Voigt, H; Kröger, M. On a Cuantity Describing the Degree of Entanglement in Linear Polymer Systems. Macromol. Theory Simul 1994, 3, 639–647. [Google Scholar]
- Everaers, R; Sukumaran, SK; Grest, GS; Svaneborg, C; Sivasubramanian, A; Kremer, K. Rheology and Microscopic Topology of Entangled Polymeric Liquids. Science 2004, 303, 823–826. [Google Scholar]
- Sukumaran, SK; Grest, GS; Kremer, K; Everaers, R. Identifying the Primitive Path Mesh in Entangled Polymer Liquids. J. Polym. Sci., Part B: Polym. Phys 2005, 43, 917–933. [Google Scholar]
- Kremer, K; Sukumaran, SK; Everaers, R; Grest, GS. Entangled Polymer Systems. Comput. Phys. Commun 2005, 169, 75–81. [Google Scholar]
- Leon, S; van der Vegt, N; Delle Site, L; Kremer, K. Bisphenol a Polycarbonate: Entanglement Analysis from Coarse-Grained MD Simulations. Macromolecules 2005, 38, 8078–8092. [Google Scholar]
- Uchida, N; Grest, GS; Everaers, R. Viscoelasticity and Primitive Path Analysis of Entangled Polymer Liquids: From F-actin to Polyethylene. J. Chem. Phys 2008, 128, 044902. [Google Scholar]
- Shanbhang, S; Larson, RG. Chain Retraction Potential in a Fixed Entanglement Network. Phys. Rev. Lett 2005, 94, 076001. [Google Scholar]
- Zhou, Q; Larson, RG. Primitive Path Identification and Statistics in Molecular Dynamics Simulations of Entangled Polymer Melts. Macromolecules 2005, 38, 5761–5765. [Google Scholar]
- Shanbhag, S; Larson, RG. Identification of Topological Constraints in Entangled Polymer Melts Using the Bond-Fluctuation Model. Macromolecules 2006, 39, 2413–2417. [Google Scholar]
- Larson, RG; Zhou, Q; Shanbhag, S; Park, SJ. Advances in Modeling of Polymer Melt Rheology. AIChE J 2007, 53, 542–548. [Google Scholar]
- Larson, RG. Looking inside the Entanglement “Tube” Using Molecular Dynamics Simulations. J. Polym. Sci., Part B: Polym. Phys 2007, 45, 3240–3248. [Google Scholar]
- Hoy, RS; Robbins, MO. Effect of Equilibration on Primitive Path Analyses of Entangled Polymers. Phys. Rev. E 2005, 72, 061802. [Google Scholar]
- Hoy, RS; Robbins, MO. Strain Hardening of Polymer Glasses: Effect of Entanglement Density, Temperature and Rate. J. Polym. Sci., Part B: Polym. Phys 2006, 44, 3487–3500. [Google Scholar]
- Hoy, RS; Grest, GS. Entanglements of an End-Grafted Polymer Brush in a Polymeric Matrix. Macromolecules 2007, 40, 8389–8395. [Google Scholar]
- Vladkov, M; Barrat, JL. Local Dynamics and Primitive Path Analysis for a Model Polymer Melt near a Surface. Macromolecules 2007, 40, 3797–3804. [Google Scholar]
- Kröger, M. Shortest Multiple Disconnected Path for the Analysis of Entanglements in Two- and Three-Dimensional Polymeric Systems. Comput. Phys. Commun 2005, 168, 209–232. [Google Scholar]
- Kröger, M. Models for Polymeric and Anisotropic Liquids; Lecture Notes in Physics 675; Springer: Berlin, Germany, 2005. [Google Scholar]
- Tzoumanekas, C; Theodorou, DN. Topological Analysis of Linear Polymer Melts: A Statistical Approach. Macromolecules 2006, 39, 4592–4604. [Google Scholar]
- Tzoumanekas, C; Theodorou, DN. From Atomistic Simulations to Slip-Link Models of Entangled Polymer Melts: Hierarchical Strategies for the Prediction of Rheological Properties. Curr. Opin. Solid State Mater 2006, 10, 61–72. [Google Scholar]
- Foteinopoulou, K; Karayiannis, NC; Mavrantzas, VG; Kröger, M. Primitive Path Identification and Entanglement Statistics in Polymer Melts: Results from Direct Topological Analysis on Atomistic Polyethylene Models. Macromolecules 2006, 39, 4207–4216. [Google Scholar]
- Shanbhag, S; Kröger, M. Primitive Path Networks Generated by Annealing and Geometrical Methods: Insights into Differences. Macromolecules 2007, 40, 2897–2903. [Google Scholar]
- Kim, JM; Keffer, DJ; Kröger, M; Edwards, BJ. Rheological and Entanglement Characteristics of Linear Chain Polyethylene Liquids in Planar Couette and Planar Elongational Flows. J. Non-Newtonian Fluid Mech 2008, 152, 168–183. [Google Scholar]
- Foteinopoulou, K; Karayiannis, NC; Laso, M; Kröger, M. Structure, Dimensions and Entanglement Statistics of Long Polyethylene Chains. J. Phys. Chem. B 2009, 113, 442–455. [Google Scholar]
- Hoy, RS; Foteinopoulou, K; Kröger, M. Topological Analysis of Polymeric Melts: Chain Length Effects and Fast-Converging Estimators for Entanglement Length. Phys. Rev. E 2009, 80, 031803. [Google Scholar]
- Riggleman, RA; Toepperwein, G; Papakonstantopoulos, GJ; Barrat, JL; de Pablo, JJ. Entanglement network in nanoparticle reinforced polymers. J. Chem. Phys 2009, 130, 244903. [Google Scholar]
- Tzoumanekas, C; Lahmar, F; Rousseau, B; Theodorou, DN. Onset of Entanglements Revisited. Toplogical Analysis. Macromolecules 2009, 42, 7474–7484. [Google Scholar]
- Lahmar, F; Tzoumanekas, C; Theodorou, DN; Rousseau, B. Onset of Entanglements Revisited. Dynamical Analysis. Macromolecules 2009, 42, 7485–7494. [Google Scholar]
- Schieber, JD. Fluctuations in Entanglements of Polymer Liquids. J. Chem. Phys 2003, 118, 5162–5166. [Google Scholar]
- Khaliullin, RN; Schieber, JD. Analytic Expressions for the Statistics of the Primitive-Path Length in Entangled Polymers. Phys. Rev. Lett 2008, 100, 188302. [Google Scholar]
- Karayiannis, NC; Laso, M. Monte Carlo Scheme for Generation and Relaxation of Dense and Nearly Jammed Random Structures of Freely Jointed Hard-Sphere Chains. Macromolecules 2008, 41, 1537–1551. [Google Scholar]
- Karayiannis, NC; Mavrantzas, VG. Multiscale Modelling of Polymer Properties; Computer Aided Chemical Engineering 22; Laso, M, Perpet, E, Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 22, , Chapter 2, pp. 201–240. [Google Scholar]
- Wu, MG; Deem, MW. Efficient Monte Carlo Methods for Cyclic Peptides. Mol. Phys 1999, 97, 559–580. [Google Scholar]
- Karayiannis, NC; Laso, M. Dense and Nearly Jammed Random Packings of Freely Jointed Chains of Tangent Hard Spheres. Phys. Rev. Lett 2008, 100, 050602. [Google Scholar]
- Karayiannis, NC; Foteinopoulou, K; Laso, M. The Structure of Random Packings of Freely Jointed Chains of Tangent Hard Spheres. J. Chem. Phys 2009, 130, 164908. [Google Scholar]
- Karayiannis, NC; Foteinopoulou, K; Laso, M. Contact Network in Nearly Jammed Disordered Packings of Hard-Sphere Chains. Phys. Rev. E 2009, 80, 011307. [Google Scholar]
- Mavrantzas, VG; Theodorou, DN. Atomistic Simulation of Polymer Melt Elasticity: Calculation of the Free Energy of an Oriented Polymer Melt. Macromolecules 1998, 31, 6310–6332. [Google Scholar]
- de Pablo, JJ; Laso, M; Suter, UW. Estimation of the Chemical Potential of Chain Molecules by Simulation. J. Chem. Phys 1992, 96, 6157. [Google Scholar]
- Jodrey, WS; Tory, EM. Computer Simulation of Close Random Packing of Equal Spheres. Phys. Rev. A 1985, 32, 2347–2351. [Google Scholar]
- Tobochnik, J; Chapin, PM. Monte Carlo Simulation of Hard Spheres Near Random Closest Packing Using Spherical Boundary Conditions. J. Chem. Phys 1988, 88, 5824–5830. [Google Scholar]
- Lubachevsky, BD; Stillinger, FH. Geometric Properties of Random Disk Packings. J. Stat. Phys 1990, 60, 561–583. [Google Scholar]
- Bernal, JD. Geometry of the Structureof Monatomic Liquids. Nature 1960, 185, 68–70. [Google Scholar]
- Bernal, JD; Mason, J; Knight, KR. Radial Distribution of the Random Close Packing of Equal Spheres. Nature 1962, 194, 957–958. [Google Scholar]
- Finney, JL. Random Packings and the Structure of Simple Liquids. I. The Geometry of Random Close Packing. Proc. Roy. Soc. Lond. A 1970, 319, 479–493. [Google Scholar]
- Torquato, S; Truskett, TM; Debenedetti, PG. Is Random Close Packing of Spheres Well Defined? Phys. Rev. Lett 2000, 84, 2064–2067. [Google Scholar]
- Donev, A; Torquato, S; Stillinger, FH. Pair Correlation Function Characteristics of Nearly Jammed Disordered and Ordered Hard-Sphere Packings. Phys. Rev. E 2005, 71, 011105. [Google Scholar]
- Donev, A; Stillinger, FH; Torquato, S. Unexpected Density Fluctuations in Jammed Disordered Sphere Packings. Phys. Rev. Lett 2005, 95, 090604. [Google Scholar]
- Anikeenko, AV; Medvedev, NN; Aste, T. Structural and Entropic Insights into the Nature of the Random-Close-Packing Limit. Phys. Rev. E 2008, 77, 031101. [Google Scholar]
- Hopkins, AB; Stillinger, FH; Torquato, S. Dense Sphere Packings from Optimized Correlation Functions. Phys. Rev. E 2009, 79, 031123. [Google Scholar]
- Yethiraj, A; Hall, CK. Monte Carlo Simulations and Integral Equation Theory for Microscopic Correlations in Polymeric Fluids. J. Chem. Phys 1992, 96, 797–807. [Google Scholar]
- Yethiraj, A; Dickman, R. Local Structure of Model Polymeric Fluids: Hard-Sphere Chains and the Three-Dimensional Fluctuating Bond Model. J. Chem. Phys 1992, 97, 4468–4475. [Google Scholar]
- Escobedo, FA; de Pablo, JJ. Extended Continuum Configurational Bias Monte Carlo Methods for Simulation of Flexible Molecules. J. Chem. Phys 1995, 102, 2636–2652. [Google Scholar]
- Malanoski, AP; Monson, PA. The High Density Equation of State and Solid-Fluid Equilibrium in Systems of Freely Jointed Chains of Tangent Hard Spheres. J. Chem. Phys 1997, 107, 6899–6907. [Google Scholar]
- Haslam, AJ; Jackson, G; McLeish, TCB. Monte Carlo Simulation Study of the Induced Deformation of Polymer Chains Dissolved in Stretched Networks. Macromolecules 1999, 32, 7289–7298. [Google Scholar]
- Kröger, M. Efficient Hybrid Algorithm for the Dynamic Creation of Wormlike Chains in Solutions, Brushes, Melts and Glasses. Comput. Phys. Commun 1999, 118, 278–298. [Google Scholar]
- Kröger, M; Müller, M; Nievergelt, JA. Geometric Embedding Algorithm for Efficiently Generating Semiflexible Chains in the Molten State. CMES-Comput. Model. Eng. Sci 2003, 4, 559–570. [Google Scholar]
- Hoover, WG; Ree, FH. Melting Transition and Communal Entropy for Hard Spheres. J. Chem. Phys 1968, 49, 3609–3617. [Google Scholar]
- Humphrey, W; Dalke, A; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [Google Scholar]
- Chang, R; Yethiraj, A. Dynamics of Chain Molecules in Disordered Materials. Phys. Rev. Lett 2006, 96, 107802. [Google Scholar]
- Denlinger, MA; Hall, CK. Molecular-Dynamics Simulation Results for the Pressure of Hard-Chain Fluids. Mol. Phys 1990, 71, 541–559. [Google Scholar]
- Laso, M; Karayiannis, NC. Flexible Chain Molecules in the Marginal and Concentrated Regimes: Universal Static Scaling Laws and Cross-Over Predictions. J. Chem. Phys 2008, 128, 174901. [Google Scholar]
- Laso, M; Karayiannis, NC; Foteinopoulou, F; Mansfield, ML; Kröger, M. Random Packing of Model Polymers: Local Structure, Topological Hindrance and Universal Scaling. Soft Matter 2009, 5, 1762–1770. [Google Scholar]
- Foteinopoulou, K; Karayiannis, NC; Laso, M; Kröger, M; Mansfield, ML. Universal Scaling, Entanglements, and Knots of Model Chain Molecules. Phys. Rev. Lett 2008, 101, 265702. [Google Scholar]
- .
- Rubinstein, M; Colby, RH. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Harmandaris, VA; Kremer, K. Dynamics of Polystyrene Melts through Hierarchical Multiscale Simulations. Macromolecules 2009, 42, 791–802. [Google Scholar]
- Svaneborg, C; Everaers, R; Grest, GS; Curro, JG. Connectivity and Entanglement Stress Contributions in Strained Polymer Networks. Macromolecules 2008, 41, 4920–4928. [Google Scholar]
- Larson, RG. Looking inside the Entanglement “Tube” Using Molecular Dynamics Simulations. J. Polym. Sci. Part B 2007, 45, 3240–3248. [Google Scholar]
- Hess, S; Kröger, M; Hoover, WG. Shear Modulus of Fluids and Solids. Physica A 1997, 239, 449–466. [Google Scholar]
- Karayiannis, NC; Foteinopoulou, K; Laso, M. The Characteristic Crystallographic Element Norm: A Descriptor of Local Structure in Atomistic and Particulate Systems. J. Chem. Phys 2009, 130, 074704. [Google Scholar]
- Karayiannis, NC; Foteinopoulou, K; Laso, M. Entropy-Driven Crystallization in Dense Systems of Athermal Chain Molecules. Phys. Rev. Lett 2009, 103, 045703. [Google Scholar]
- Edwards, SF. The Theory of Polymer Solutions at Intermediate Concentration. Proc. Phys. Soc. London 1966, 88, 265–280. [Google Scholar]
- Daoud, M; Cotton, JP; Farnoux, B; Jannink, G; Sarma, G; Benoit, H; Duplessix, R; Picot, C; de Gennes, PG. Solutions of Flexible Polymers. Neutron Experiments and Interpretation. Macromolecules 1975, 8, 804–818. [Google Scholar]
- Mansfield, ML. Efficient Knot Group Identification as a Tool for Studying Entanglements of Polymers. J. Chem. Phys 2007, 127, 244901. [Google Scholar]
- Mansfield, ML. Development of Knotting during the Collapse Transition of Polymers. J. Chem. Phys 2007, 127, 244902. [Google Scholar]
- Kivotides, D; Wilkin, SL; Theofanous, TG. Entangled Chain Dynamics of Polymer Knots in Extensional Flow. Phys. Rev. E 2009, 80, 041808. [Google Scholar]
- Ottinger, HC. Beyond Equilibrium Thermodynamics; Wiley & Sons: Hoboken, NJ, 2005. [Google Scholar]
- Öttinger, HC. Systematic Coarse Graining: “Four Lessons and A Caveat” from Nonequilibrium Statistical Mechanics. MRS Bull 2007, 32, 936–940. [Google Scholar]
- Kröger, M; Öttinger, HC. Beyond-Equilibrium Molecular Dynamics of a Rarefied Gas Subjected to Shear Flow. J. Non-Newtonian Fluid Mech 2004, 120, 175–187. [Google Scholar]
- Ilg, O; Karlin, IV; Kröger, M; Öttinger, HC. Canonical Distribution Functions in Polymer Dynamics: II Liquid-Crystalline Polymers. Physica A 2003, 319, 134–150. [Google Scholar]
- Kröger, M; Ramirez, J; Öttinger, HC. Projection from an Atomistic Chain Contour to Its Primitive Path. Polymer 2002, 43, 477–487. [Google Scholar]
- Öttinger, HC. Coarse-Graining of Wormlike Polymer Chains for Substantiating Reptation. J. Non-Newtonian Fluid Mech 2004, 120, 207–213. [Google Scholar]

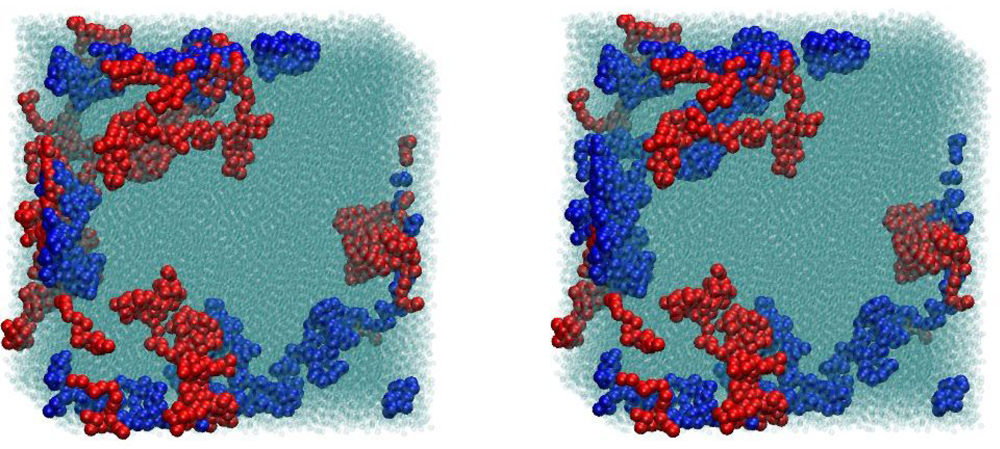
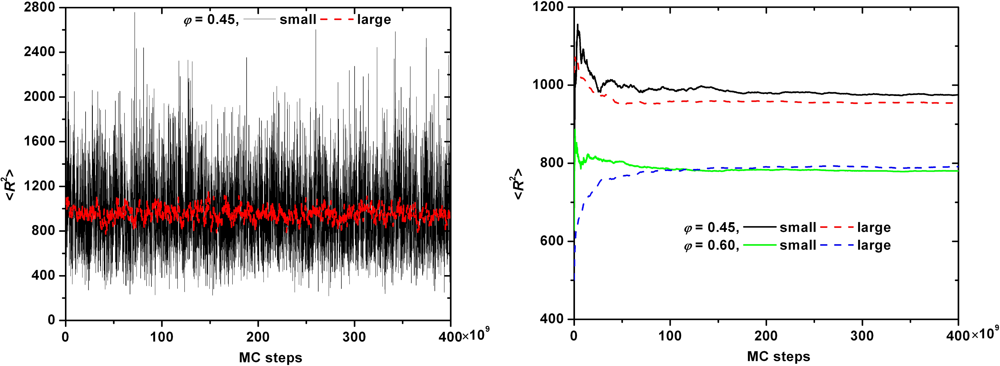
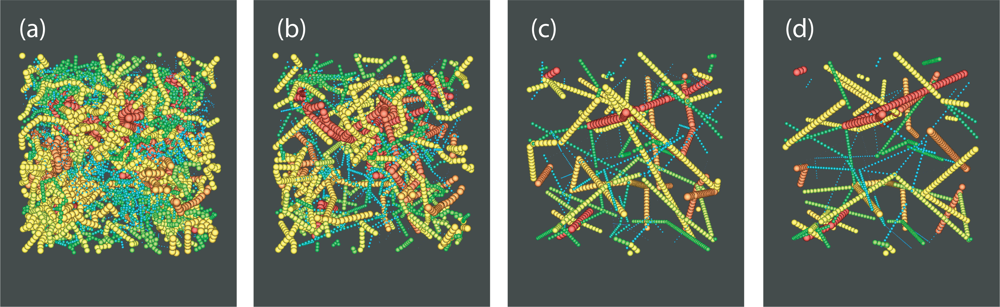
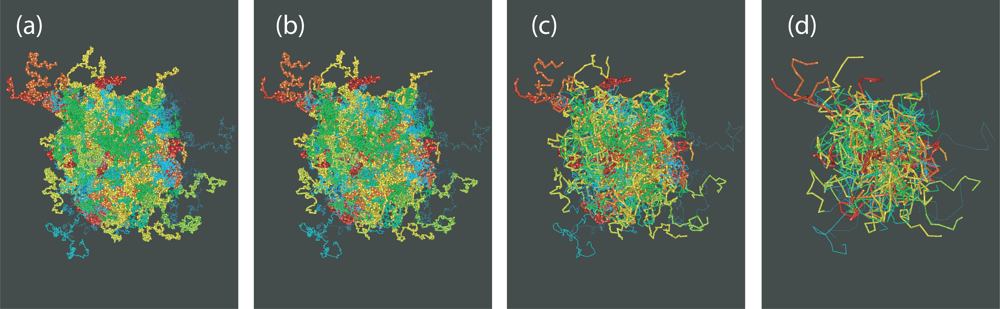
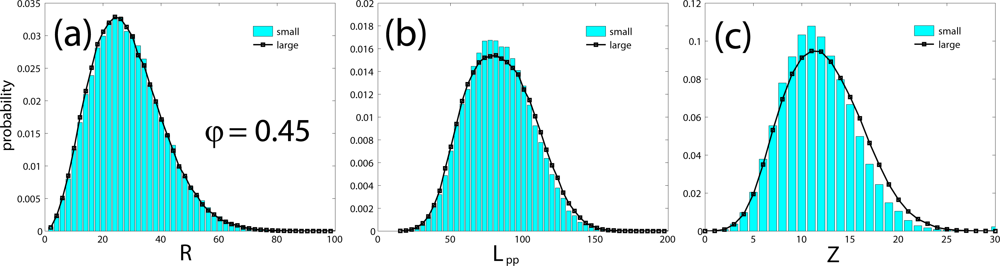
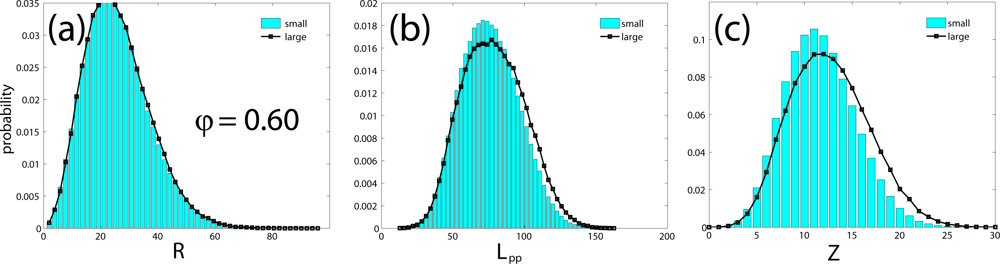

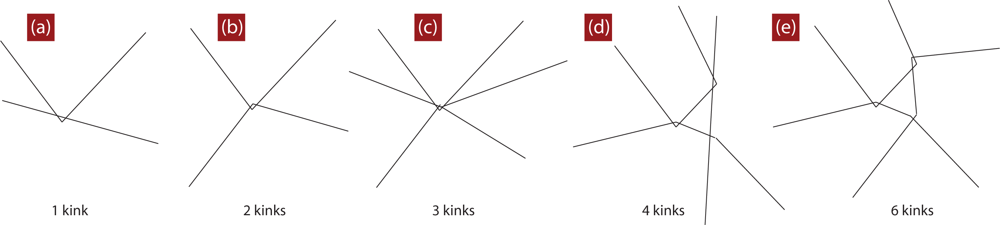
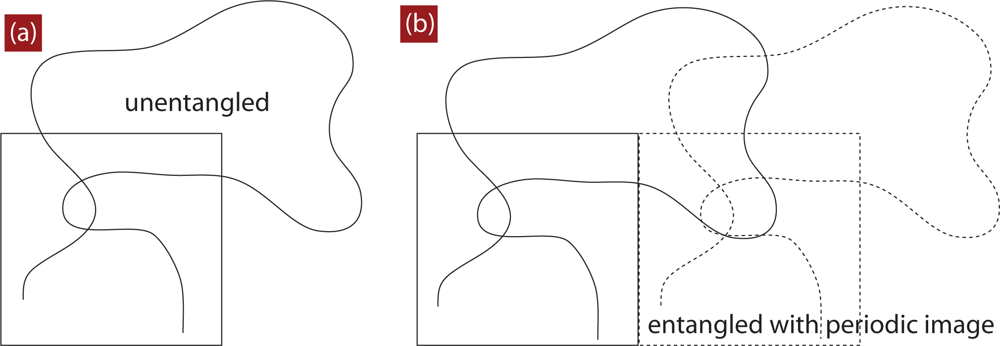
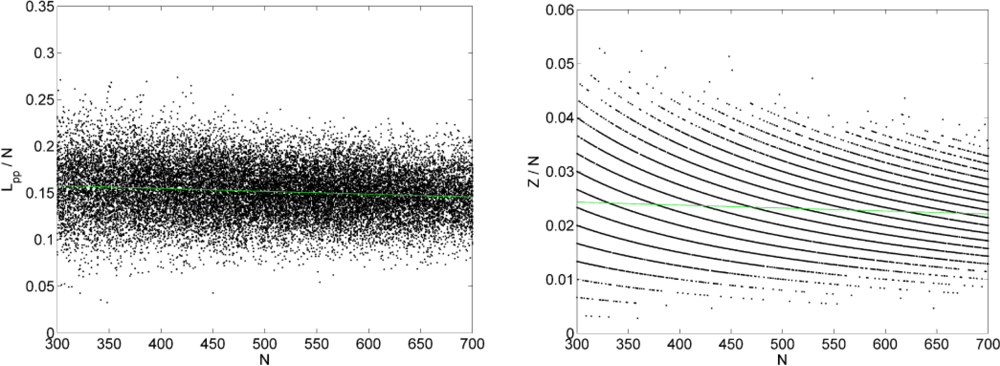
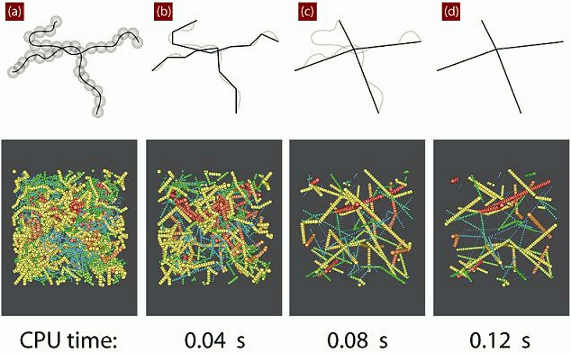
| system | chains | 〈N〉 | 〈R2〉1/2 | CPU time | 〈Lpp〉 | 〈Z〉 | Z* | Ne | |
|---|---|---|---|---|---|---|---|---|---|
| φ = 0.45 | |||||||||
| small | 6 | 500 | 31.1 | 0.12 s | 83.5 | 11.8 | 13.2 | 42.4 | 37.9 |
| large | 162 | 500 | 30.8 | 7.93 s | 84.0 | 12.2 | 12.2 | 40.9 | 40.9 |
| φ = 0.60 | |||||||||
| small | 6 | 500 | 27.9 | 0.16 s | 75.5 | 11.6 | 13.0 | 43.1 | 38.5 |
| large | 162 | 500 | 28.1 | 8.34 s | 78.3 | 12.6 | 12.6 | 39.7 | 39.7 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Karayiannis, N.C.; Kröger, M. Combined Molecular Algorithms for the Generation, Equilibration and Topological Analysis of Entangled Polymers: Methodology and Performance. Int. J. Mol. Sci. 2009, 10, 5054-5089. https://doi.org/10.3390/ijms10115054
Karayiannis NC, Kröger M. Combined Molecular Algorithms for the Generation, Equilibration and Topological Analysis of Entangled Polymers: Methodology and Performance. International Journal of Molecular Sciences. 2009; 10(11):5054-5089. https://doi.org/10.3390/ijms10115054
Chicago/Turabian StyleKarayiannis, Nikos Ch., and Martin Kröger. 2009. "Combined Molecular Algorithms for the Generation, Equilibration and Topological Analysis of Entangled Polymers: Methodology and Performance" International Journal of Molecular Sciences 10, no. 11: 5054-5089. https://doi.org/10.3390/ijms10115054