EPuL: An Enhanced Positive-Unlabeled Learning Algorithm for the Prediction of Pupylation Sites
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Development of EPuL
| Algorithm 1. An enhanced positive-unlabeled learning algorithm. | |
| Input | P—Positive training set; U—Unlabeled training set; —The distance coefficient; —Sequence in P and U; |
| Model1,2,3,4,5 —Five models trained by five subsets with P respectively; | |
| N1,2,3,4,5 —Five negative sets predicted by Model1,2,3,4,5 on the remaining unlabeled training set respectively; cs—Common sequences of five negative sets N1,2,3,4,5 —Negative support vectors of five Model1,2,3,4,5 | |
| Output | F—Final classifier. |
| Stage 0: | Initialization |
| l0; Avg_dist = 0; LN = ∅; RN = ∅; i | |
| Stage 1: | Select the reliably negative initial set |
| pr = ; | |
| Avg_dist + = ; | |
| FOR i from 1 to |U| | |
| IF dist(pr,) > Avg_dist * | |
| LN = LN∪{Si}; | |
| END IF | |
| END FOR | |
| Randomly divide the LN into five subsets D1, D2, D3, D4, D5. | |
| FOR i from 1 to 5 | |
| Modeli = SVM(P, Di); Ni = Modeli(U − LN); | |
| END FOR | |
| The common sequence are represented to reliably negative initial set cs = N1 ∩ N2 ∩ N3 ∩ N4 ∩ N5; RN0 = RN0 ∪ cs; then the negative support vectors of five models are included in = . | |
| Stage 2 | Expand the reliably negative set |
| WHILE TRUE | |
| IF Ul > 5∗|P| | |
| = −; | |
| = ; | |
| ELSE IF Ul < 5 ∗ |P| | |
| Go to Stage 3 | |
| END IF | |
| Train a SVM classifier fl+1 on the PRNl+1 with optimal parameter C and γ. | |
| Each sequence xi in Ul+1 would have a decision value f(xi) through the obtained fl+1, use the threshold T to get the reliably negative set. | |
| l l + 1 | |
| Stage 3 | Return the final classifier |
| Return F = (P, RN) | |
2.2. The Performance of EPuL on the Training Dataset
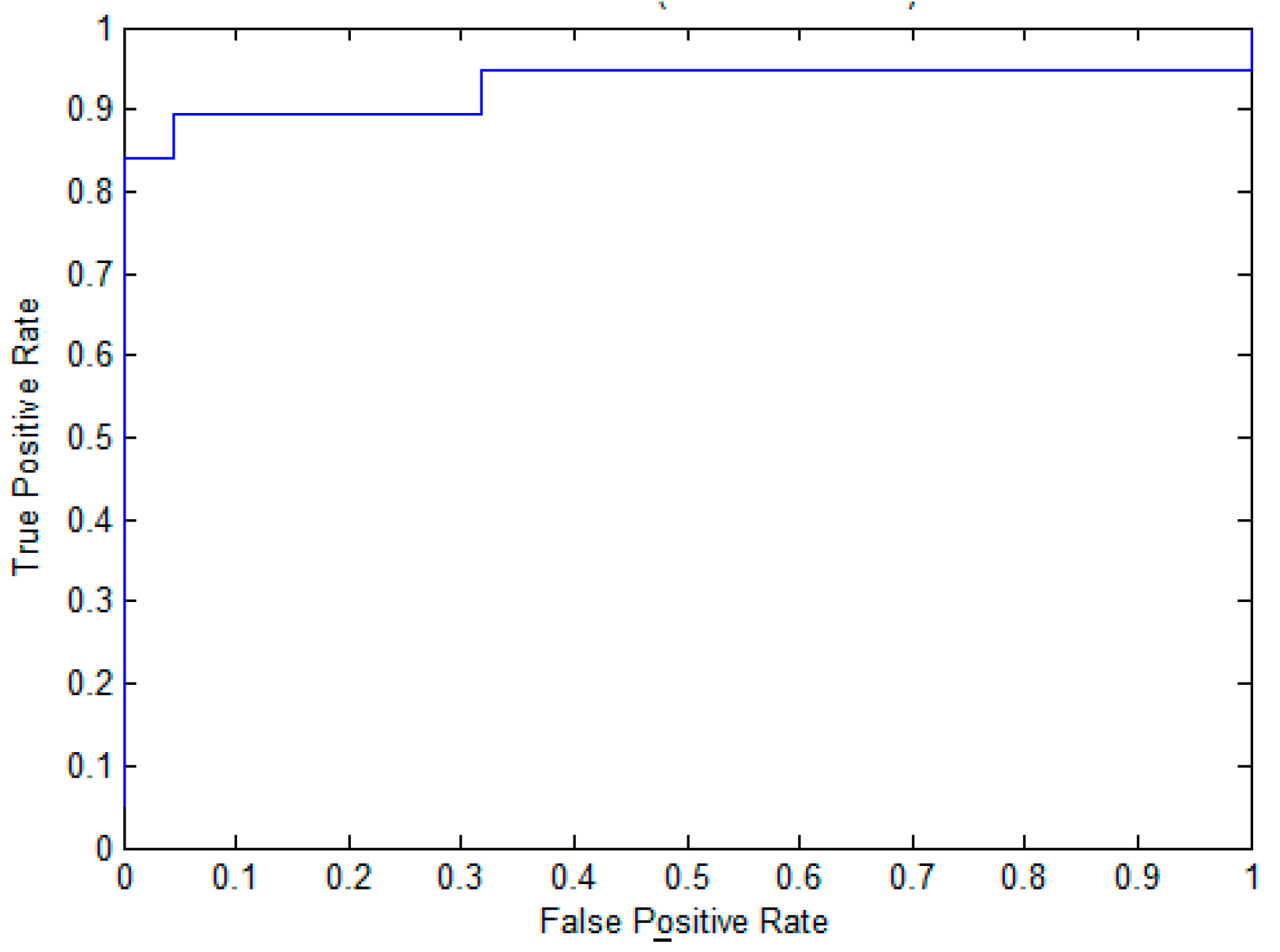
2.3. The Performance Evaluation on the Independent Testing Dataset
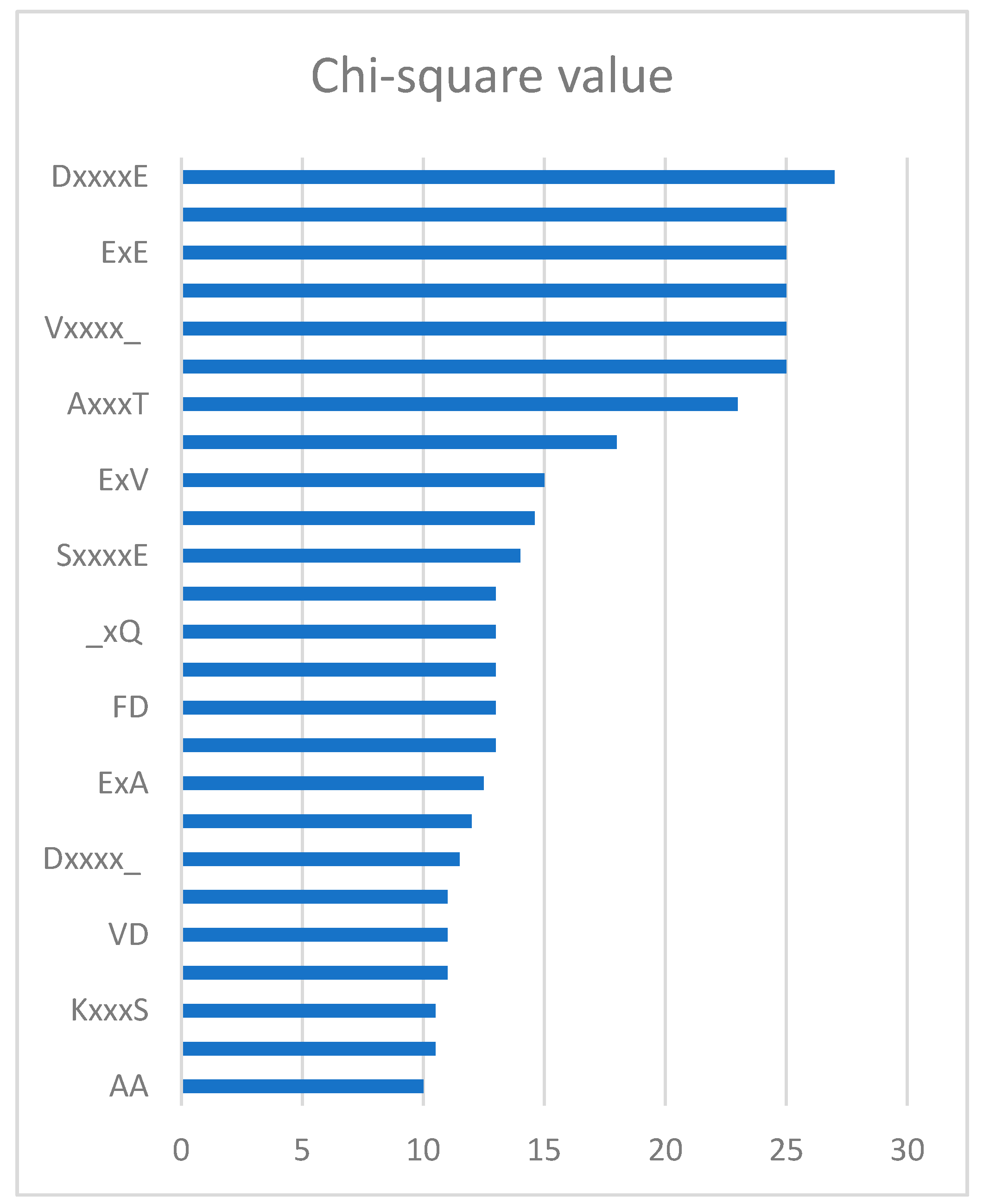
2.4. Feature Analysis
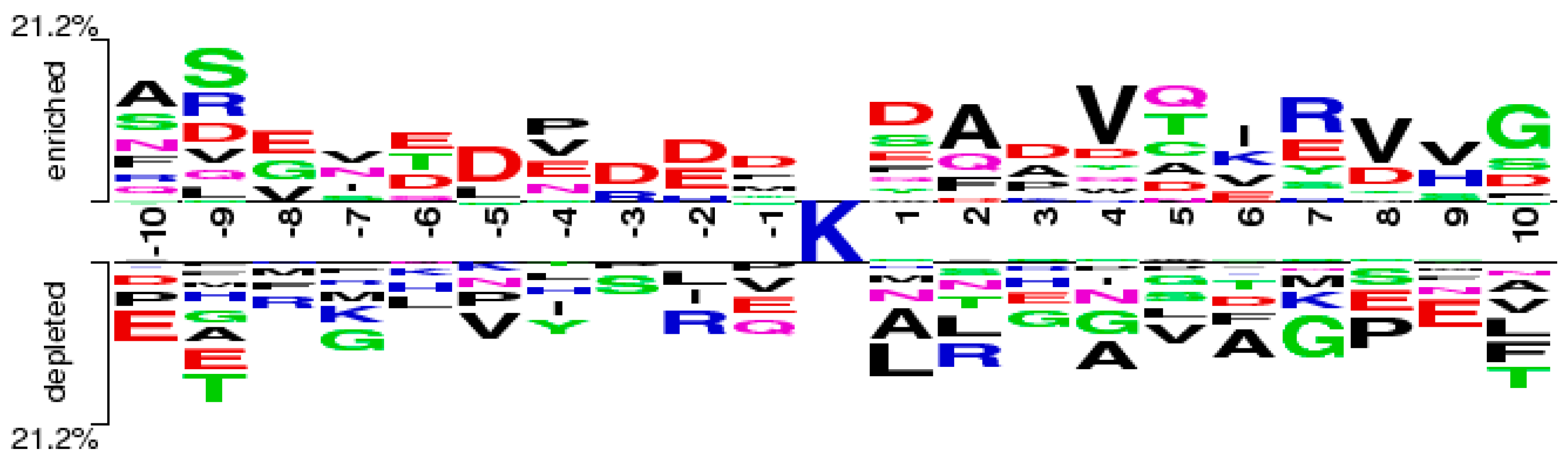
2.5. Case Study
3. Materials and Methods
3.1. Datasets
3.2. Construction of Feature Vectors
3.3. Feature Selection
3.4. Support Vector Machine
3.5. Performance Evaluation of EPuL
4. Conclusions
Reference
Supplementary Materials
Acknowledgment
Author Contributions
References
- Pearce, M.J.; Mintseris, J.; Ferreyra, J.; Gygi, S.P.; Darwin, K.H. Ubiquitin-like protein involved in the proteasome pathway of Mycobacterium tuberculosis. Science 2008, 322, 1104–1107. [Google Scholar] [CrossRef] [PubMed]
- Burns, K.E.; Liu, W.T.; Boshoff, H.I.; Dorrestein, P.C.; Barry, C.E. Proteasomal protein degradation in mycobacteria is dependent upon a prokaryotic ubiquitin-like protein. J. Biol. Chem. 2009, 284, 3069–3075. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Solomon, W.C.; Kang, Y.; Cerda-Maira, F.; Darwin, K.H.; Walters, K.J. Prokaryotic ubiquitin-like protein pup is intrinsically disordered. J. Mol. Biol. 2009, 392, 208–217. [Google Scholar] [CrossRef] [PubMed]
- Tung, C.W. PupDB: A database of pupylated proteins. BMC Bioinf. 2012, 13, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Striebel, F.; Imkamp, F.; Sutter, M.; Steiner, M.; Mamedov, A.; Weber-Ban, E. Bacterial ubiquitin-like modifier Pup is deamidated and conjugated to substrates by distinct but homologous enzymes. Nat. Struct. Mol. Biol. 2009, 16, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Poulsen, C.; Akhter, Y.; Jeon, A.H.-W.; Schmitt-Ulms, G.; Meyer, H.E.; Stefanski, A.; Stühler, K.; Wilmanns, M.; Song, Y.H. Proteome-wide identification of mycobacterial pupylation targets. Mol. Syst. Biol. 2010, 6, 386–392. [Google Scholar] [CrossRef] [PubMed]
- Georgiou, D.N.; Karakasidis, T.E.; Megaritis, A.C. A short survey on genetic sequences, chou’s pseudo amino acid composition and its combination with fuzzy set theory. Open Bioinf. J. 2013, 7, 41–48. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, Q.; Cao, J.; Gao, X.; Ren, J.; Xue, Y. GPS-PUP: Computational prediction of pupylation sites in prokaryotic proteins. Mol. Biosyst. 2011, 7, 2737–2740. [Google Scholar] [CrossRef] [PubMed]
- Tung, C.W. Prediction of pupylation sites using the composition of k-spaced amino acid pairs. J. Theor. Biol. 2013, 336, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Dai, J.; Ning, Q.; Ma, Z.; Yin, M.; Sun, P. Position-specific analysis and prediction of protein pupylation sites based on multiple features. BioMed. Res. Int. 2013, 12, 109549. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Qiu, J.D.; Shi, S.P.; Suo, S.B.; Liang, R.P. Systematic analysis and prediction of pupylation sites in prokaryotic proteins. PLoS ONE 2013, 8, 130. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.M.; Zhou, Y.; Lu, X.; Li, J.; Song, J.; Zhang, Z. Computational identification of protein pupylation sites by using profile-based composition of k-spaced amino acid pairs. PLoS ONE 2015, 10, e0129635. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ding, C.; Meraz, R.F.; Holbrook, S.R. PSoL: A positive sample only learning algorithm for finding non-coding RNA genes. Bioinformatics 2006, 22, 2590. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Cao, J.Z. Positive-Unlabeled learning for pupylation sites prediction. Biomed. Res. Int. 2016, 16, 1–5. [Google Scholar] [CrossRef] [PubMed]
- EPuL: An Enhanced Positive-Unlabeled Learning Algorithm for the Prediction of Pupylation Sites. Available online: http://59.73.198.144:8080/EPuL (accessed on 30 August 2017).
- Zeng, X.; Liao, Y.; Liu, Y.; Zou, Q. Prediction and validation of disease genes using HeteSim Scores. IEEE/ACM Trans. Comput. Biol. Bioinf. 2016, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Liao, M.; Gao, Y.; Ji, R.; He, Z.; Zou, Q. Improved and promising identification of human microRNAs by incorporating a high-quality negative set. IEEE/ACM Trans. Comput. Biol. Bioinf. 2013, 11, 192–201. [Google Scholar] [CrossRef] [PubMed]
- Zou, Q.; Zeng, J.; Cao, L.; Ji, R. A novel features ranking metric with application to scalable visual and bioinformatic sdata classification. Neurocomputing 2016, 173, 346–354. [Google Scholar] [CrossRef]
- Cerda-Maira, F.A.; McAllsiter, F.; Bode, N.J.; Burns, K.E.; Gygi, S.P.; Darwin, K.H. Reconstitution of the Mycobackterium tuberculosis pupylation pathway in Escherichia coli. EMBO Rep. 2011, 12, 863–870. [Google Scholar] [CrossRef] [PubMed]
- Zhe, J.; Cao, J.Z.; Gu, H. ILM-2L: A two-level predictor for identifying protein lysine methylation sites and their methylation degrees by incorporating K-gap amino acid pairs into Chou’s general PseAAC. J. Theor. Biol. 2015, 385, 50–57. [Google Scholar]
- Zhe, J.; Cao, J.Z.; Gu, H. Predicting lysine phosphoglycerylation with fuzzy SVM by incorporating k-spaced amino acid pairs into Chou’s general PseAAC. J. Theor. Biol. 2016, 397, 145–150. [Google Scholar]
- Ju, Z.; Gu, H. Predicting pupylation sites in prokaryotic proteins using semi-supervised self-training support vector machine algorithm. Anal. Biochem. 2016, 507, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 389–396. [Google Scholar] [CrossRef]
- Yan, R.X.; Si, J.N.; Wang, C.; Zhang, Z. DescFold: A web server for protein fold recognition. BMC Bioinf. 2008, 10, 1949. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Tan, H.; Shen, H.; Mahmood, K.; Boyd, S.E.; Webb, G.I.; Akutsu, T.; Whisstock, J.C. Cascleave: towards more accurate prediction of caspase substrate cleavage sites. Bioinformatics 2010, 26, 752–760. [Google Scholar] [CrossRef] [PubMed]
- Si, J.N.; Yan, R.X.; Wang, C.; Zhang, Z.; Su, X.D. TIM-Finder: A new method for identifying TIM-barrel proteins. BMC Struct. Biol. 2009, 9, 73. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.G.; Deb, S.; Cui, Z. Monarch Butterfly Optimization. Neural Comput. Appl. 2015, 1–20. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Coelho, L.D.S. Earthworm optimization algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Int. J. Bio-Inspired Comput. 2015. [Google Scholar] [CrossRef]
- Wang, G.G.; Coelho, L.D.S.; Gao, X.Z.; Coelho, L.D.S. A new metaheuristic optimization algorithm motivated by elephant herding behaviour. Int. J. Bio-Inspired Comput. 2016, 8, 394. [Google Scholar] [CrossRef]
- Wang, G.G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memet. Comput. 2016, 1–14. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.; Wang, H.; Duan, H.; Liu, L.; Li, J. Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Comput. Appl. 2014, 24, 1231. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. Stud krill herd algorithm. Neorucomputing 2014, 128, 363–370. [Google Scholar] [CrossRef]
- Wang, G.G.; Guo, L.; Gandomi, A.H.; Hao, G.S.; Wang, H. Chaotic Krill Herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Wang, G.G.; Gandomi, A.H.; Alavi, A.H.; Gong, D. A comprehensive review of krill herd algorithm: variants, hybrids and applications. Artif. Intell. Rev. 2017, 1–30. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |
| Method | Sn (%) | Sp (%) | ACC (%) | MCC | AUC |
|---|---|---|---|---|---|
| EPuL | 84.21 | 95.45 | 90.24 | 0.81 | 0.93 |
| PUL-PUP | 82.24 | 91.57 | 88.92 | 0.74 | 0.92 |
| PSoL | 67.50 | 73.60 | 70.55 | 0.42 | 0.80 |
| SVM_balance | 76.71 | 63.65 | 69.88 | 0.40 | 0.77 |
| Method | Sn (%) | Sp (%) | ACC (%) | MCC | AUC |
|---|---|---|---|---|---|
| EPuL | 72.41 | 71.57 | 71.63 | 0.24 | 0.78 |
| PUL-PUP | 68.97 | 70.83 | 70.71 | 0.22 | 0.77 |
| PSoL | 51.72 | 73.14 | 71.62 | 0.13 | 0.74 |
| SVM-balance | 62.07 | 67.4 | 67.05 | 0.15 | 0.7 |
| Predictors | Thresholds | Sn (%) | Sp (%) | ACC (%) | MCC | AUC |
|---|---|---|---|---|---|---|
| GPS-PUP | High | 31.03 | 89.46 | 85.62 | 0.16 | |
| Medium | 34.48 | 85.54 | 82.19 | 0.14 | 0.6 | |
| Low | 41.38 | 76.72 | 74.43 | 0.1 | ||
| iPUP | High | 48.28 | 82.84 | 80.55 | 0.2 | |
| Medium | 51.72 | 76.47 | 74.83 | 0.16 | 0.66 | |
| Low | 55.17 | 72.06 | 70.94 | 0.15 | ||
| pbPUP | High | 17.24 | 88.48 | 83.75 | 0.04 | |
| Medium | 31.03 | 80.15 | 76.89 | 0.07 | 0.6 | |
| Low | 41.38 | 69.85 | 67.96 | 0.07 | ||
| PUL-PUP | High | 51.72 | 83.33 | 81.24 | 0.22 | |
| Medium | 65.52 | 76.72 | 75.97 | 0.24 | 0.77 | |
| Low | 68.97 | 72.79 | 72.54 | 0.23 | ||
| EPuL | High | 37.93 | 89.46 | 86.04 | 0.21 | |
| Medium | 58.62 | 79.90 | 78.49 | 0.23 | 0.78 | |
| Low | 68.97 | 74.02 | 73.68 | 0.24 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, X.; Bao, L.; Zhao, X.; Zhao, X.; Sangaiah, A.K.; Wang, G.-G.; Ma, Z. EPuL: An Enhanced Positive-Unlabeled Learning Algorithm for the Prediction of Pupylation Sites. Molecules 2017, 22, 1463. https://doi.org/10.3390/molecules22091463
Nan X, Bao L, Zhao X, Zhao X, Sangaiah AK, Wang G-G, Ma Z. EPuL: An Enhanced Positive-Unlabeled Learning Algorithm for the Prediction of Pupylation Sites. Molecules. 2017; 22(9):1463. https://doi.org/10.3390/molecules22091463
Chicago/Turabian StyleNan, Xuanguo, Lingling Bao, Xiaosa Zhao, Xiaowei Zhao, Arun Kumar Sangaiah, Gai-Ge Wang, and Zhiqiang Ma. 2017. "EPuL: An Enhanced Positive-Unlabeled Learning Algorithm for the Prediction of Pupylation Sites" Molecules 22, no. 9: 1463. https://doi.org/10.3390/molecules22091463







