Single Actin Bundle Rheology
Abstract
:1. Introduction
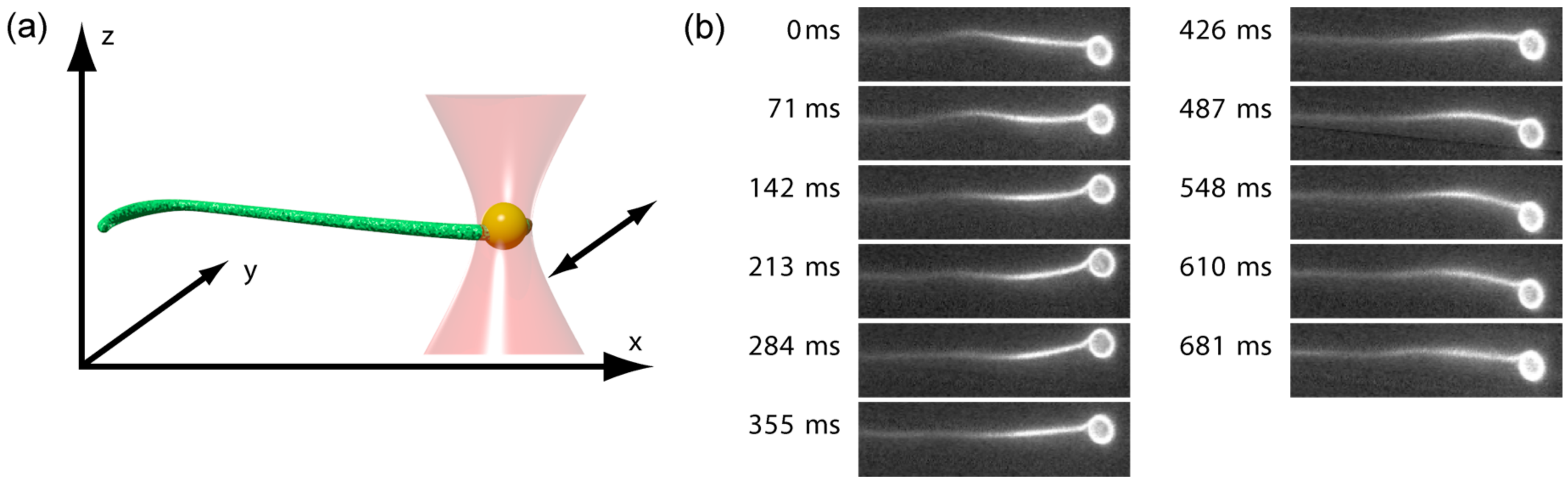
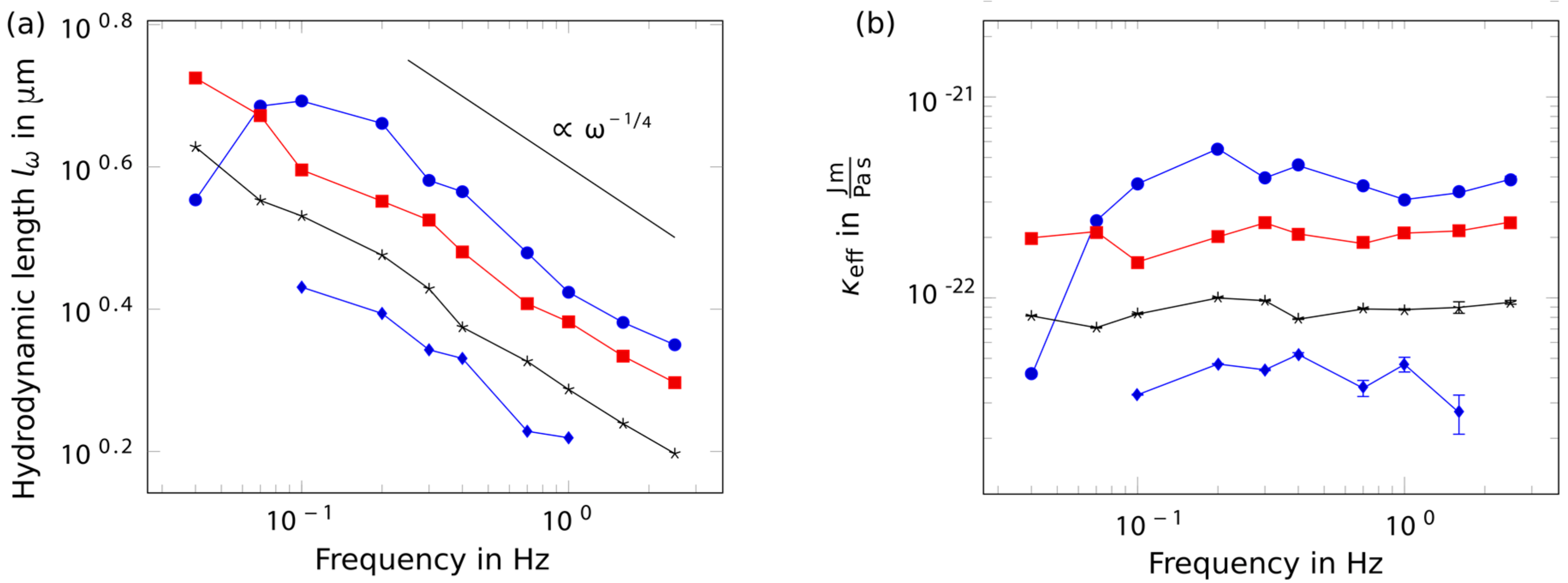
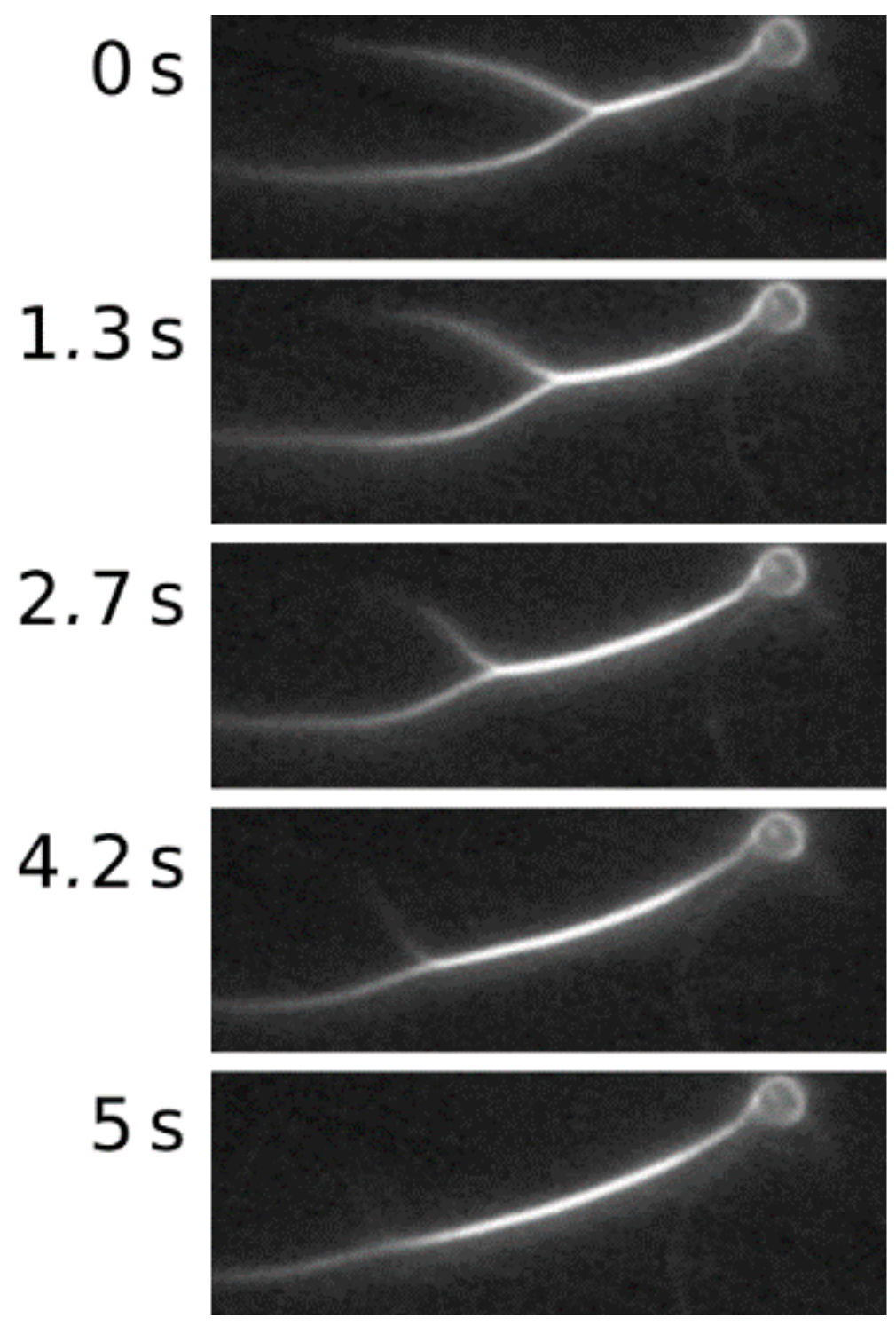
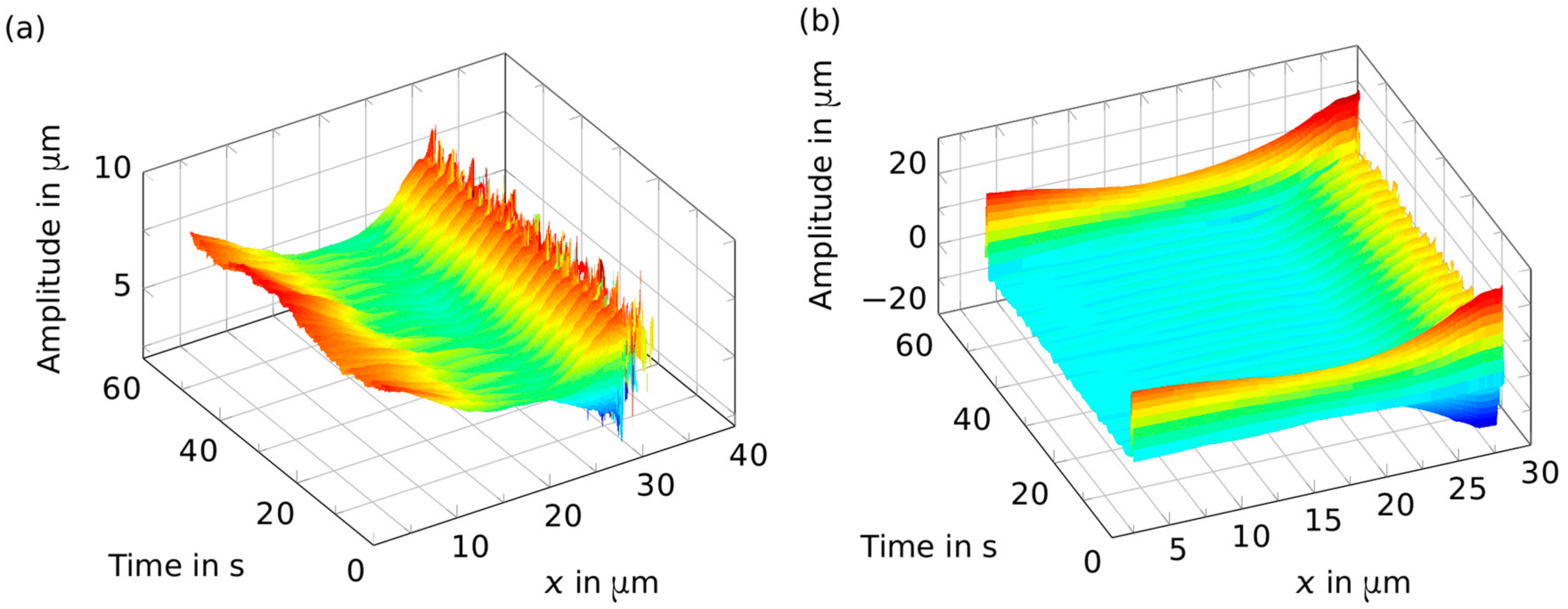
2. Results
3. Discussion
4. Materials and Methods
4.1. Protein Preparation, Bead Functionalization, and Bundle Formation
4.2. Optical Tweezers Setup and Fluorescence Microscopy
4.3. Experimental Procedure
4.4. Analytical Tools
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huber, F.; Schnauß, J.; Rönicke, S.; Rauch, P.; Müller, K.; Fütterer, C.; Käs, J. Emergent complexity of the cytoskeleton: From single filaments to tissue. Adv. Phys. 2013, 62, 1–112. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Gentry, B.; Stuhrmann, B.; Huber, F.; Strehle, D.; Brunner, C.; Koch, D.; Steinbeck, M.; Betz, T.; Käs, J. The cytoskeleton: An active polymer-based scaffold. Biophys. Rev. Lett. 2009. [Google Scholar] [CrossRef]
- Lodish, H.F. Molecular Cell Biology, 6th ed.; W.H. Freeman: New York, NY, USA, 2008. [Google Scholar]
- MacKintosh, F.C.; Kas, J.; Janmey, P.A. Elasticity of Semiflexible Biopolymer Networks. Phys. Rev. Lett. 1995, 75, 4425–4428. [Google Scholar] [CrossRef] [PubMed]
- Backouche, F.; Haviv, L.; Groswasser, D.; Bernheim-Groswasser, A. Active gels: Dynamics of patterning and self-organization. Phys. Biol. 2006, 3, 264–273. [Google Scholar] [CrossRef] [PubMed]
- Hotulainen, P.; Lappalainen, P. Stress fibers are generated by two distinct actin assembly mechanisms in motile cells. J. Cell Biol. 2006, 173, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Schnauß, J.; Golde, T.; Schuldt, C.; Schmidt, B.U.S.; Glaser, M.; Strehle, D.; Händler, T.; Heussinger, C.; Käs, J.A. Transition from a Linear to a Harmonic Potential in Collective Dynamics of a Multifilament Actin Bundle. Phys. Rev. Lett. 2016, 116, 108102. [Google Scholar] [CrossRef] [PubMed]
- Wachsstock, D.H.; Schwartz, W.H.; Pollard, T.D. Affinity of alpha-actinin for actin determines the structure and mechanical properties of actin filament gels. Biophys. J. 1993, 65, 205–214. [Google Scholar] [CrossRef]
- Hinner, B.; Tempel, M.; Sackmann, E.; Kroy, K.; Frey, E. Entanglement, Elasticity, and Viscous Relaxation of Actin Solutions. Phys. Rev. Lett. 1998, 81, 2614–2617. [Google Scholar] [CrossRef]
- Semmrich, C.; Storz, T.; Glaser, J.; Merkel, R.; Bausch, A.R.; Kroy, K. Glass transition and rheological redundancy in F-actin solutions. Proc. Natl. Acad. Sci. USA 2007, 104, 20199–20203. [Google Scholar] [CrossRef] [PubMed]
- Gardel, M.L.; Shin, J.H.; MacKintosh, F.C.; Mahadevan, L.; Matsudaira, P.; Weitz, D.A. Elastic Behavior of Cross-Linked and Bundled Actin. Science 2004, 304, 1301–1305. [Google Scholar] [CrossRef] [PubMed]
- Isambert, H.; Maggs, A.C. Dynamics and Rheology of Actin Solutions. Macromolecules 1996, 29, 1036–1040. [Google Scholar] [CrossRef]
- Käs, J.; Strey, H.; Tang, J.X.; Finger, D.; Ezzell, R.; Sackmann, E.; Janmey, P.A. F-actin, a model polymer for semiflexible chains in dilute, semidilute, and liquid crystalline solutions. Biophys. J. 1996, 70, 609–625. [Google Scholar] [CrossRef]
- Morse, D.C. Tube diameter in tightly entangled solutions of semiflexible polymers. Phys. Rev. E 2001, 63, 31502. [Google Scholar] [CrossRef] [PubMed]
- Heussinger, C.; Bathe, M.; Frey, E. Statistical mechanics of semiflexible bundles of wormlike polymer chains. Phys. Rev. Lett. 2007, 99, 48101. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, G.H.; Dogic, Z.; Nakamura, F.; Bendix, P.M.; MacKintosh, F.C.; Hartwig, J.H.; Stossel, T.P.; Weitz, D.A. An active biopolymer network controlled by molecular motors. Proc. Natl. Acad. Sci. USA 2009, 106, 15192–15197. [Google Scholar] [CrossRef] [PubMed]
- Fabry, B.; Maksym, G.N.; Butler, J.P.; Glogauer, M.; Navajas, D.; Fredberg, J.J. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001, 87, 148102. [Google Scholar] [CrossRef] [PubMed]
- Falzone, T.T.; Blair, S.; Robertson-Anderson, R.M. Entangled F-actin displays a unique crossover to microscale nonlinearity dominated by entanglement segment dynamics. Soft Matter 2015, 11, 4418–4423. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.X.; Janmey, P. The Polyelectrolyte Nature of F-actin and the Mechanism of actin bundle formation. J. Biol. Chem. 1996, 271, 8556–8563. [Google Scholar] [CrossRef] [PubMed]
- Strehle, D.; Schnauss, J.; Heussinger, C.; Alvarado, J.; Bathe, M.; Käs, J.; Gentry, B. Transiently crosslinked F-actin bundles. Eur. Biophys. J. EBJ 2011, 40, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Claessens, M.M.A.E.; Bathe, M.; Frey, E.; Bausch, A.R. Actin-binding proteins sensitively mediate F-actin bundle stiffness. Nat. Mater. 2006, 5, 748–753. [Google Scholar] [CrossRef] [PubMed]
- Rückerl, F.; Lenz, M.; Betz, T.; Manzi, J.; Martiel, J.-L.; Safouane, M.; Paterski-Boujemaa, R.; Blanchoin, L.; Sykes, C. Adaptive Response of Actin Bundles under Mechanical Stress. Biophys. J. 2017, 113, 1072–1079. [Google Scholar] [CrossRef] [PubMed]
- Riveline, D.; Wiggins, C.H.; Goldstein, R.E.; Ott, A. Elastohydrodynamic study of actin filaments using fluorescence microscopy. Phys. Rev. E 1997, 56, R1330–R1333. [Google Scholar] [CrossRef]
- Wiggins, C.H.; Riveline, D.; Ott, A.; Goldstein, R.E. Trapping and Wiggling: Elastohydrodynamics of Driven Microfilaments. Biophys. J. 1998, 74, 1043–1060. [Google Scholar] [CrossRef]
- Aragon, S.R.; Pecora, R. Dynamics of wormlike chains. Macromolecules 1985, 18, 1868–1875. [Google Scholar] [CrossRef]
- Bathe, M.; Heussinger, C.; Claessens, M.M.A.E.; Bausch, A.R.; Frey, E. Cytoskeletal bundle mechanics. Biophys. J. 2008, 94, 2955–2964. [Google Scholar] [CrossRef] [PubMed]
- Ward, A.; Hilitski, F.; Schwenger, W.; Welch, D.; Lau, A.W.C.; Vitelli, V.; Mahadevan, L.; Dogic, Z. Solid friction between soft filaments. Nat. Mater. 2015, 14, 583–588. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.H.; Mahadevan, L.; So, P.T.; Matsudaira, P. Bending stiffness of a crystalline actin bundle. J. Mol. Biol. 2004, 337, 255–261. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, J.; Frey, E. Radial Distribution Function of Semiflexible Polymers. Phys. Rev. Lett. 1996, 77, 2581–2584. [Google Scholar] [CrossRef] [PubMed]
- Claessens, M.M.A.E.; Tharmann, R.; Kroy, K.; Bausch, A.R. Microstructure and viscoelasticity of confined semiflexible polymer networks. Nat. Phys. 2006, 2, 186–189. [Google Scholar] [CrossRef]
- Janmey, P.A.; Euteneuer, U.; Traub, P.; Schliwa, M. Viscoelastic Properties of Vimentin Compared with Other Filamentous Biopolymer Networks. J. Cell Biol. 1991, 113, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Heussinger, C.; Schüller, F.; Frey, E. Statics and dynamics of the wormlike bundle model. Phys. Rev. E 2010, 81, 21904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lieleg, O.; Claessens, M.M.A.E.; Heussinger, C.; Frey, E.; Bausch, A.R. Mechanics of bundled semiflexible polymer networks. Phys. Rev. Lett. 2007, 99, 88102. [Google Scholar] [CrossRef] [PubMed]
- Taute, K.M.; Pampaloni, F.; Frey, E.; Florin, E.-L. Microtubule dynamics depart from the wormlike chain model. Phy. Rev. Lett. 2008, 100, 28102. [Google Scholar] [CrossRef] [PubMed]
- Pampaloni, F.; Lattanzi, G.; Jonás, A.; Surrey, T.; Frey, E.; Florin, E.-L. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc. Natl. Acad. Sci. USA 2006, 103, 10248–10253. [Google Scholar] [CrossRef] [PubMed]
- Kononova, O.; Kholodov, Y.; Theisen, K.E.; Marx, K.A.; Dima, R.I.; Ataullakhanov, F.I.; Grishchuk, E.L.; Barsegov, V. Tubulin bond energies and microtubule biomechanics determined from nanoindentation in silico. J. Am. Chem. Soc. 2014, 136, 17036–17045. [Google Scholar] [CrossRef] [PubMed]
- Broedersz, C.P.; MacKintosh, F.C. Modeling semiflexible polymer networks. Rev. Mod. Phys. 2014, 86, 995–1036. [Google Scholar] [CrossRef]
- Schnauß, J.; Händler, T.; Käs, J. Semiflexible Biopolymers in Bundled Arrangements. Polymers 2016, 8, 274. [Google Scholar] [CrossRef]
- Bullerjahn, J.T.; Kroy, K. Analytical catch-slip bond model for arbitrary forces and loading rates. Phys. Rev. E 2016, 93, 12404. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Ziebert, F.; Humphrey, D.; Duggan, C.; Steinbeck, M.; Zimmermann, W.; Käs, J. Molecular motor-induced instabilities and cross linkers determine biopolymer organization. Biophys. J. 2007, 93, 4445–4452. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, D.; Duggan, C.; Saha, D.; Smith, D.; Käs, J. Active fluidization of polymer networks through molecular motors. Nature 2002, 416, 413–416. [Google Scholar] [CrossRef] [PubMed]
- Cooper, J.A. Effects of Cytochalasin and Phalloidin on Actin. J. Cell Biol. 1987, 105, 1473–1478. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Taylor, D.W.; Taylor, K.A. A 3-D reconstruction of smooth muscle alpha-actinin by CryoEm reveals two different conformations at the actin-binding region. J. Mol. Biol. 2004, 338, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Asakura, S.; Oosawa, F. On Interaction between Two Bodies Immersed in a Solution of Macromolecules. J. Chem. Phys. 1954, 22, 1255–1256. [Google Scholar] [CrossRef]
- Hosek, M.; Tang, J.X. Polymer-induced bundling of F actin and the depletion force. Phys. Rev. E 2004, 69, 51907. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are not available from the authors. |


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strehle, D.; Mollenkopf, P.; Glaser, M.; Golde, T.; Schuldt, C.; Käs, J.A.; Schnauß, J. Single Actin Bundle Rheology. Molecules 2017, 22, 1804. https://doi.org/10.3390/molecules22101804
Strehle D, Mollenkopf P, Glaser M, Golde T, Schuldt C, Käs JA, Schnauß J. Single Actin Bundle Rheology. Molecules. 2017; 22(10):1804. https://doi.org/10.3390/molecules22101804
Chicago/Turabian StyleStrehle, Dan, Paul Mollenkopf, Martin Glaser, Tom Golde, Carsten Schuldt, Josef A. Käs, and Jörg Schnauß. 2017. "Single Actin Bundle Rheology" Molecules 22, no. 10: 1804. https://doi.org/10.3390/molecules22101804




