1. Introduction
The best known, earliest identified non-covalent interaction is the hydrogen bond, although the halogen bond was discovered (but not so called) as long ago as 1869 through the reaction of iodine with ammonia [
1]. The pioneering experiments of Hassel and co-workers in the late 1950s and early 1960s [
2] led to the recognition of the halogen bridge (the term used by Hassel for the halogen bond). This was followed by a lull in experimental work until the mid-1990s when there was a very rapid growth of interest [
3,
4] in what then became known as the halogen bond. In the last 10 years, several new types of non-covalent interaction have been named, including the tetrel bond [
5], the pnictogen bond [
6] and the chalcogen bond [
7], although it has been pointed out [
8,
9] that these types of interaction were known for at least 30 years before they were assigned their current names.
Each non-covalent bond can be described [
9,
10] in terms of the interaction of an electrophilic region of one molecule with a nucleophilic region of another molecule (or even the same molecule). In this article, we shall concentrate on the pairwise interaction B⋯A of a Lewis base molecule B (the provider of the nucleophilic site, usually a non-bonding (n) or a π-bonding electron pair) and a Lewis acid A molecule (the provider of the electrophilic site). The electrophilic site in A can be identified variously as associated with a hydrogen atom (Group 1 of the Periodic Table), a tetrel atom (Group 14), a pnictogen atom (Group 15), a chalcogen atom (Group 16) or a halogen atom (Group 17); hence, the names assigned to the different types of non-covalent interaction. The electrophilic regions associated with halogen atoms in Lewis acids A were identified as positive regions on the molecular electrostatic surface potentials (MESP) by Clark, Murray and Politzer [
11], who named the regions as σ-holes. Subsequently, σ-holes were similarly identified at or near Group 16 [
12], 15 [
13] and 14 [
14] atoms in various Lewis acid molecules A.
An important aim in attempting to obtain a deeper understanding of non-covalent interactions in complexes B⋯A is to be able to predict the strength of the interaction in terms of the properties of the individual molecules B and A. Two measures of interaction strength have been recognized, namely the intermolecular stretching force constant
and the dissociation energy
for the process B⋯A = B + A. The former is a measure of the energy
required for a unit infinitesimal extension of the intermolecular bond from its equilibrium length, while the latter is the energy required for infinite extension of that bond. It was recognized some time ago [
15] that experimental
. values (determined, for example, by rotational spectroscopy [
16] from centrifugal distortion constants) of weak hydrogen-bonded complexes B⋯HX (X = F, Cl, Br, CCH or CN) could be described by the following expression:
in which
c = 2.5 N m
−1 (a conveniently chosen constant) and
and
are the numerical nucleophilicity and electrophilicity of the Lewis base B and the Lewis acid A, respectively. It was shown later [
3,
17] that Equation 1 also applied to halogen-bonded complexes B⋯XY, where XY is a homo- or hetero-dihalogen molecule. A subsequent analysis [
18] established that, for many hydrogen-bonded and halogen-bonded complexes B⋯HX and B⋯XY, the property
(not generally available from experiment, but readily calculated
ab initio) is directly proportional to the property
to a good level of accuracy and therefore that Equation 1 can be rewritten as
where
is another constant.
If the various types of non-covalent interaction referred to earlier can all be described through the interaction of a nucleophilic region of B with an electrophilic region of A, it should be possible to use Equation (2) to define a scale of nucleophilicities and electrophilicities for a wide range of Lewis bases B and Lewis acids A, whether held together in the complex B⋯A by a hydrogen bond, a tetrel bond, a pnictogen bond, a chalcogen bond or a halogen bond. In this article, we test this hypothesis for 11 Lewis bases and 23 Lewis acids. Thus, the values of for 250 complexes B⋯A covering the whole range of interaction types have been calculated ab initio at a high level of theory and fitted to Equation (2) (with the convenient choice kJ mol−1) to yield and values for the individual molecules. It is concluded that Equation (2) does indeed lead to a reliable scale of nucleophilicities and electrophilicities for the specified Lewis bases and acids.
2. Computational Methods
The geometries of the isolated monomers and complexes have been optimized at the MP2/aug-cc-pVTZ computational level [
19,
20,
21] with the Gaussian-09 program [
22]. Frequency calculations at the same level have been carried out to confirm that the resulting geometry corresponds to an energy minimum. Using these geometries, a series of calculations have been performed to derive the complete basis set (CBS) extrapolation at MP2 level. In addition, CCSD(T)/aug-cc-pVTZ calculations [
23] have been carried out with the MOLPRO program [
24] to derive the CCSD(T)/CBS energy. The extrapolation scheme is divided in the three parts. The first one corresponds to the Hartree–Fock (HF) contribution that is obtained using the aug-cc-pVTZ (AVTZ, X = 3) in Equations (3)–(6), aug-cc-pVQZ (AVQZ, X = 4) and aug-ccV5Z (AV5Z, X = 5) and Equations 1,2 [
25]. In the second part, the MP2 correlation contribution is derived from the results obtained with MP2/aug-cc-pVTZ and MP2/aug-cc-pVQZ calculations and applying Equations (5)–(7) [
26]. In the third part, higher order contributions are obtained as the difference of the CCSD(T)/aug-cc-pVTZ and MP2/aug-cc-pVTZ energies (Equation (6)) [
27,
28]. Finally, a CCSD(T)/CBS quality energy is generated by adding the
,
and
(Equation (9)). The latter energy has been obtained for all systems and used to calculate the dissociation energy,
De, of the complexes as the difference of the energy of the complex and the sum of the isolated monomers in their minimum geometry.
The
De energies of all the complexes have been used to fit simultaneously the nucleophilicities and electrophilicities of the Lewis bases and Lewis acids studied by means of Equation (10).
The values of
xi and
xj are 1.0 when the corresponding Lewis base or Lewis acid is present in the complex, and 0.0 if it is absent.
The molecular electrostatic surface potentials (MESP) of the isolated Lewis bases and Lewis acids in their minimum-energy configurations have been calculated at the MP2/aug-cc-pVTZ computational level and analyzed with the Multiwfn [
29,
30] and DAMQT [
31] programs. In the Lewis acids, the maximum value on the 0.001 au electron density isosurface associated with the interaction,
VS,max, has been characterized. For the Lewis bases, two different values have been obtained. The first one, in analogy with the Lewis acids, is the minimum on the 0.001 au electron density isosurface,
VS,min. The second value avoids the arbitrariness of the isosurface value by evaluation of the real minimum,
Vmin.
3. Results
Table 1 displays values of
for 11 Lewis bases and
for 23 Lewis acids obtained from a least-squares fit of
values calculated
ab initio for 250 binary complexes B⋯A by using Equation (10). We actually carried out calculations of
for the all of the 264 possible complexes that can be formed from the following 11 molecules B acting as Lewis bases: N
2, CO, HC≡CH, CH
2=CH
2, C
3H
6 (cyclopropane), PH
3, H
2S, HCN, H
2O, H
2CO and NH
3; and the following 24 molecules acting as Lewis acids: HF, HCl, HBr, HC≡CH, HCN, and H
2O (constituting the hydrogen-bonded group); F
2, Cl
2, Br
2, ClF, and BrCl (the halogen-bonded group); H
3SiF, H
3GeF, F
2CO, and CO
2 (the tetrel-bonded group); N
2O, NO
2F, PH
2F, and AsH
2F (the pnictogen-bonded group); and SO
2, SO
3, SeO
2, SF
2, and SeF
2 (the chalcogen-bonded group). The resulting
values are given in
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6, respectively, for these various classes of non-covalent interaction. The reasons that 14 values were excluded from the global fit were as follows: (1) The complex H
3P⋯ClF is known [
32] to have significant ion-pair character [H
3PCl]
+⋯Cl
− with an enhanced
as a consequence and was excluded. (2) It was clear that several of the 11 complexes containing SO
3 as a Lewis acid considerably worsened the fit. We noted that each B⋯SO
3 complex had much a larger
value than any of its B⋯A counterparts, possibly a sign of significant ionic character and accordingly these too were excluded from the fit. (3) The complexes H
3P⋯AsH
2F and H
3P⋯PH
2F were significant outliers when included in the fit, perhaps because in these complexes each molecule can act simultaneously as a Lewis acid and a Lewis base [
6,
33], in contrast to the rest of the complexes where each molecule has only a single role. The values in
Table 1 indicate that the order of nucleophilicities of the Lewis bases is:
N2 < CO < HC≡CH ~ PH3 < CH2=CH2 ~ C3H6 ~ H2S < HCN < H2O < H2CO < NH3
For the hydrogen-bonded complexes, the order of the electrophilicities of the Lewis acids is:
HF < HBr ~ HCl < HCN ~ H2O < HC≡CH
The order among the halogen-bonded systems is:
ClF > BrCl ~ Br2 > Cl2 > F2
The electrophilicity of the molecules forming chalcogen bonds via Se atoms are significantly larger than those involving S. Likewise, the AsH2F molecule has a larger electrophilicity and forms stronger pnictogen bonds than its P analogue, and the same order obtains for the propensity to form of tetrel bonds in H3GeF and H3SiF containing complexes.
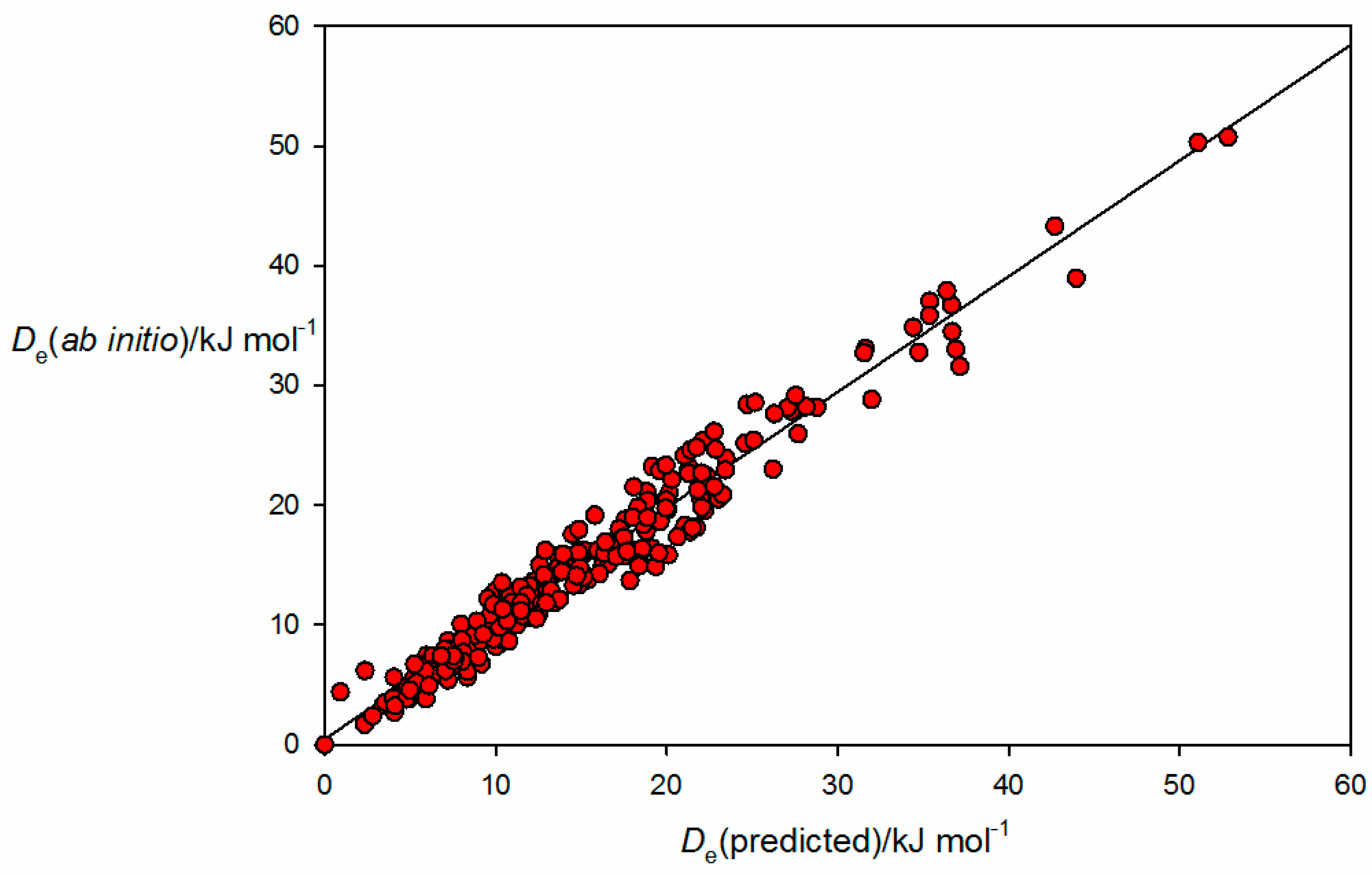
A plot of
from the
ab initio calculations for the 250 complexes versus
values generated from Equation (10) by using the
and
values given in
Table 1 is shown in
Figure 1. The correlation coefficient is 0.959 and indicates strongly that Equation (10) represents a good approximation for the 250 complexes included in the fit, a group that includes the sub-classes of complex in which the non-covalent interaction is a hydrogen bond, a halogen bond, a tetrel bond, a pnictogen bond and a chalcogen bond. Thus, it appears that Equation (2) (and therefore Equation (10)) provides a method of assigning nucleophilicities and electrophilicities to Lewis bases and Lewis acids, respectively, when involved in a wide range of non-covalent interactions. Conversely, the
NB and
EA values provide a method of predicting
De for a given complex B⋯A.
It is instructive to discuss the behavior of the
ab initio calculated
values of the B⋯A within a given non-covalent interaction type with the
NB values determined by the least-squares fit (see
Table 1). This discussion will refer to the
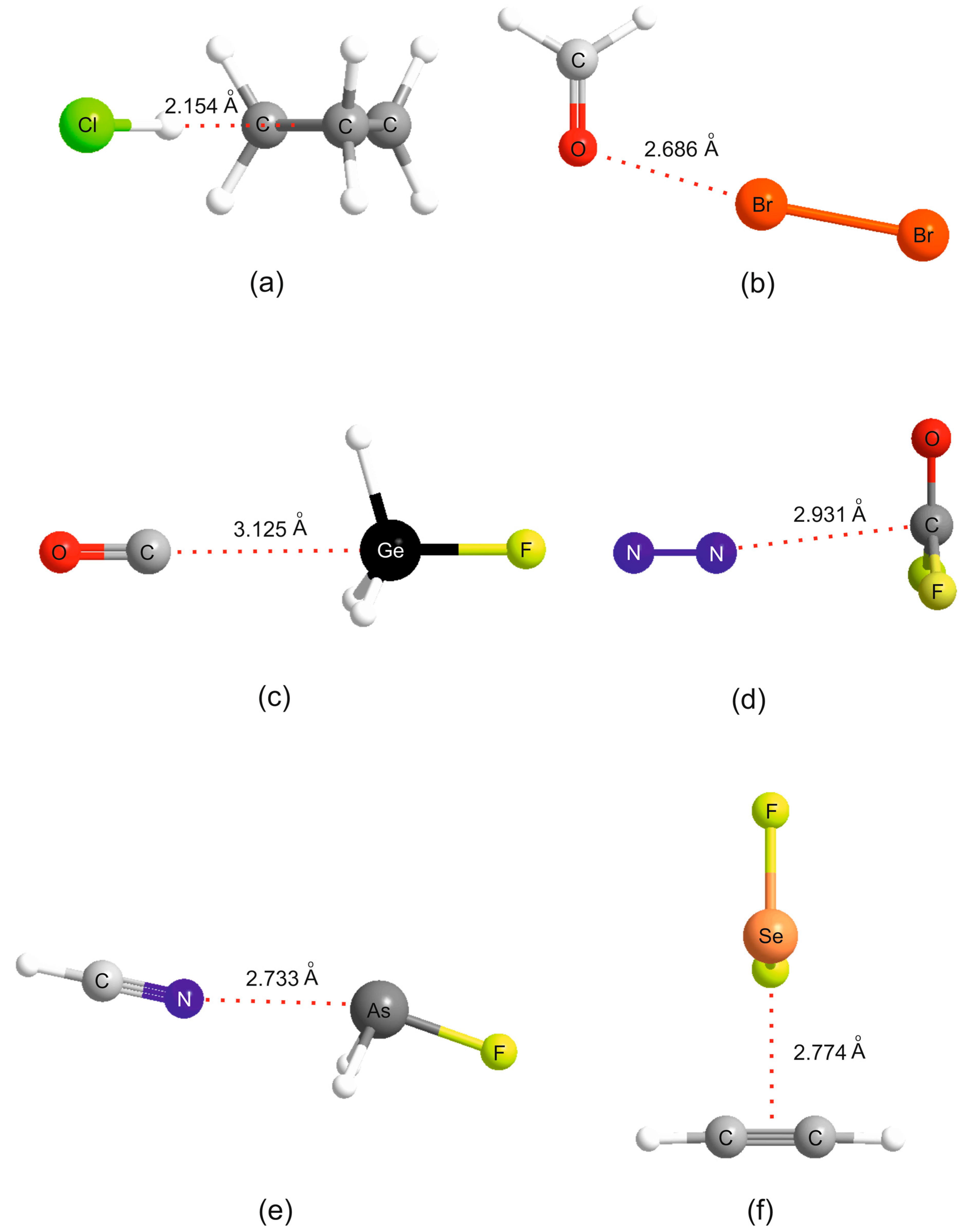
ab initio geometries of the six selected complexes shown in
Figure 2.
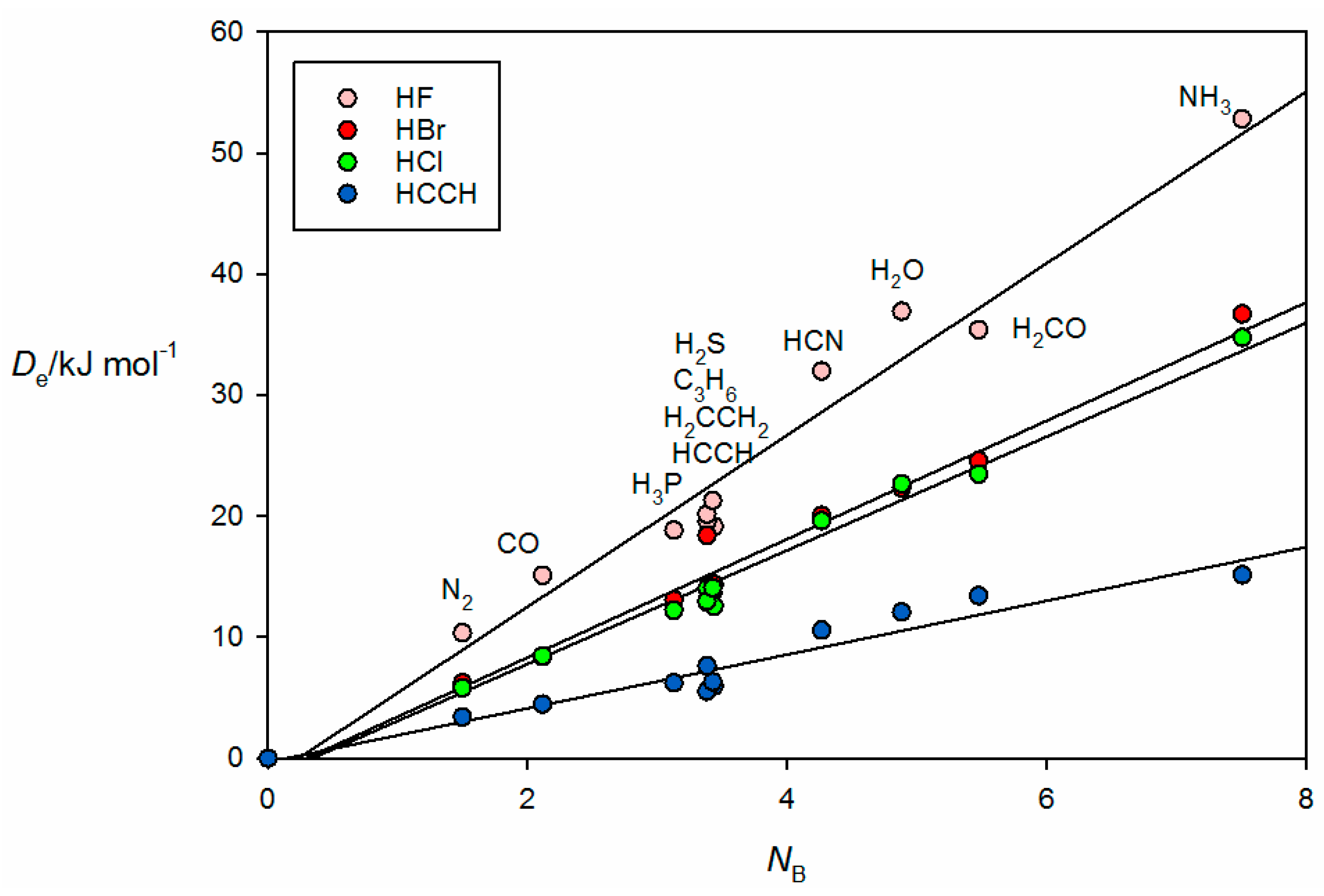
Figure 3 shows the plot of
versus
NA for 44 hydrogen bonded complexes B⋯HX formed from the 11 Lewis bases with HF, HCl, HBr and HC≡CH. The geometry determined for cyclopropane⋯HCl is shown in
Figure 2a, where it is seen that the HCl molecules lies along a median of the cyclopropane equilateral triangle and therefore the electrophilic H atom of HCl samples one of the pseudo-π bonds of cyclopropane, in agreement with experiment [
34]. Complexes involving HCN and H
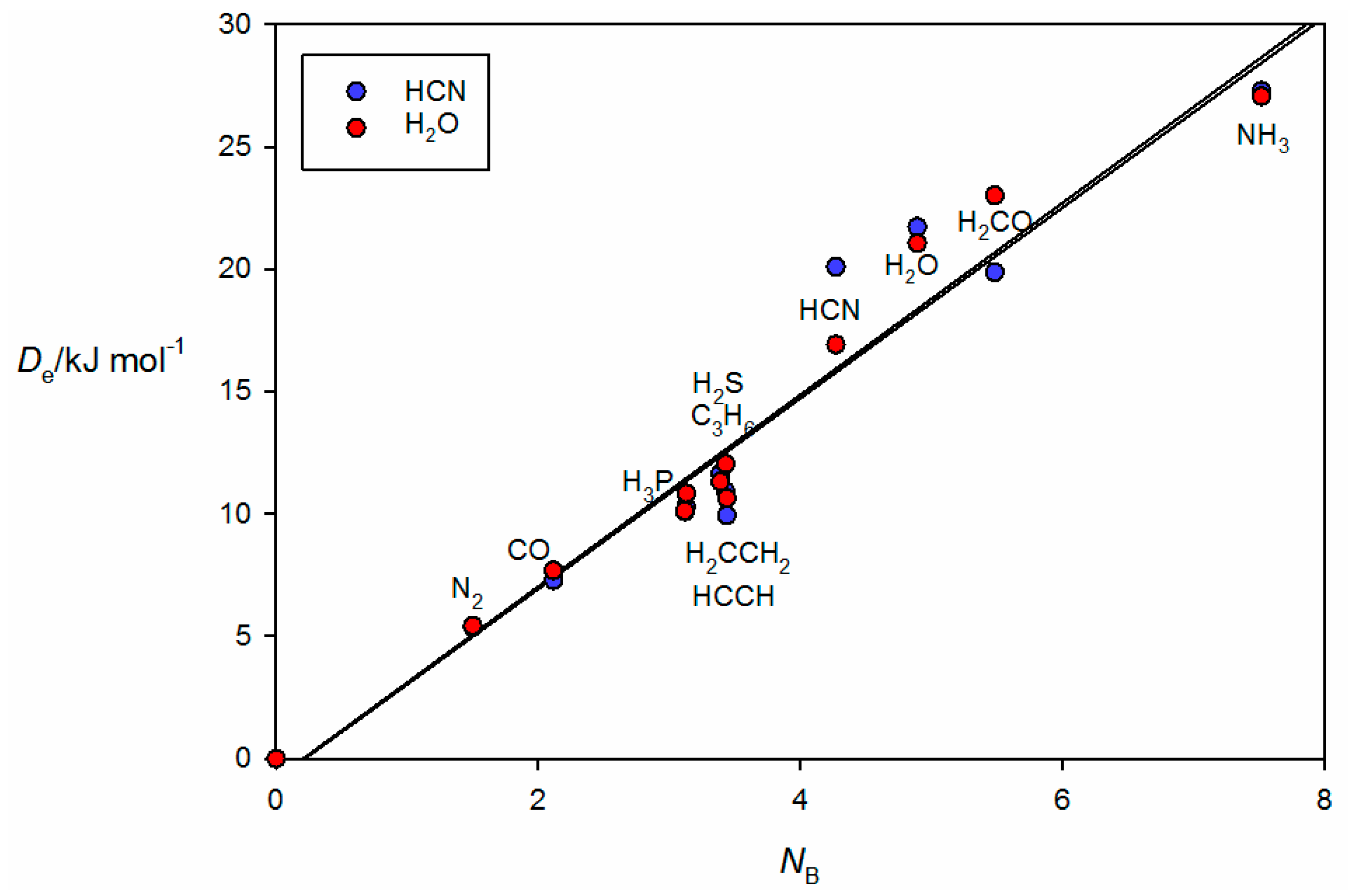
2O as the hydrogen donors are treated separately in
Figure 4 because the points for the B⋯HCN and B⋯HOH complexes would be almost coincident with those associated with B⋯HCl and B⋯HBr if they were included in
Figure 3. The individual straight lines represent the least-squares fit of the points for each B⋯HX series. The slope of each straight line is a measure of the electrophilicity of the given HX and corresponds approximately to the
EA value obtained in the global fit shown in
Figure 1, as seen in
Table 1.
We note that, in
Figure 3 and
Figure 4, there is a bunching of the points for B⋯HX, when B = PH
3, H
2S, HC≡CH, C
3H
6 and CH
2=CH
2 for each HX. The bunching is clearly systematic and independent of the HX molecule. Further, it is clear that the scatter of points from the appropriate straight line increases with the electrophilicity of HX.
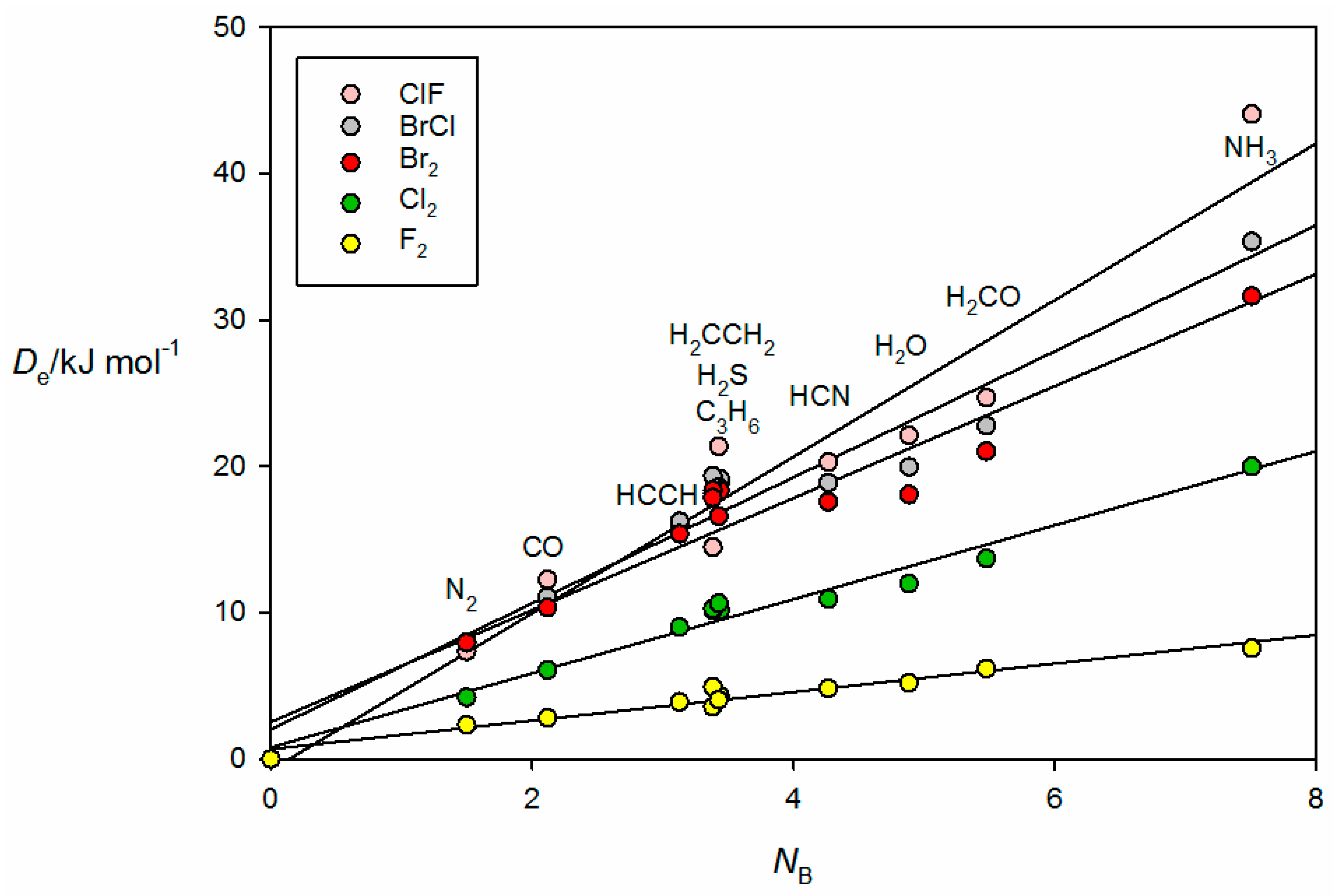
The corresponding graph for the halogen-bonded complexes B⋯ClF, B⋯BrCl, B⋯Br
2, B⋯Cl
2 and B⋯F
2 is displayed in
Figure 5. Note that, for reasons already given, the result for H
3P⋯ClF is omitted. The systematic bunching of complexes involving B = PH
3, H
2S, HC≡CH, C
3H
6 and CH
2=CH
2 for each XY and the increased scatter as the electrophilicity of the Lewis acid increases are again apparent for the B⋯XY. The geometry determined for H
2CO⋯Br
2 (see
Figure 2b) suggests that the axial σ hole at each Br atom in the Br
2 molecule lies along the direction of a nonbonding electron pair (n pair) on O, as conventionally envisaged. A similar geometry has been determined experimentally for H
2CO⋯ClF [
35]. Such interpretations led to sets of simple rules for predicting the geometries of hydrogen- and halogen-bonded complexes [
3,
36].
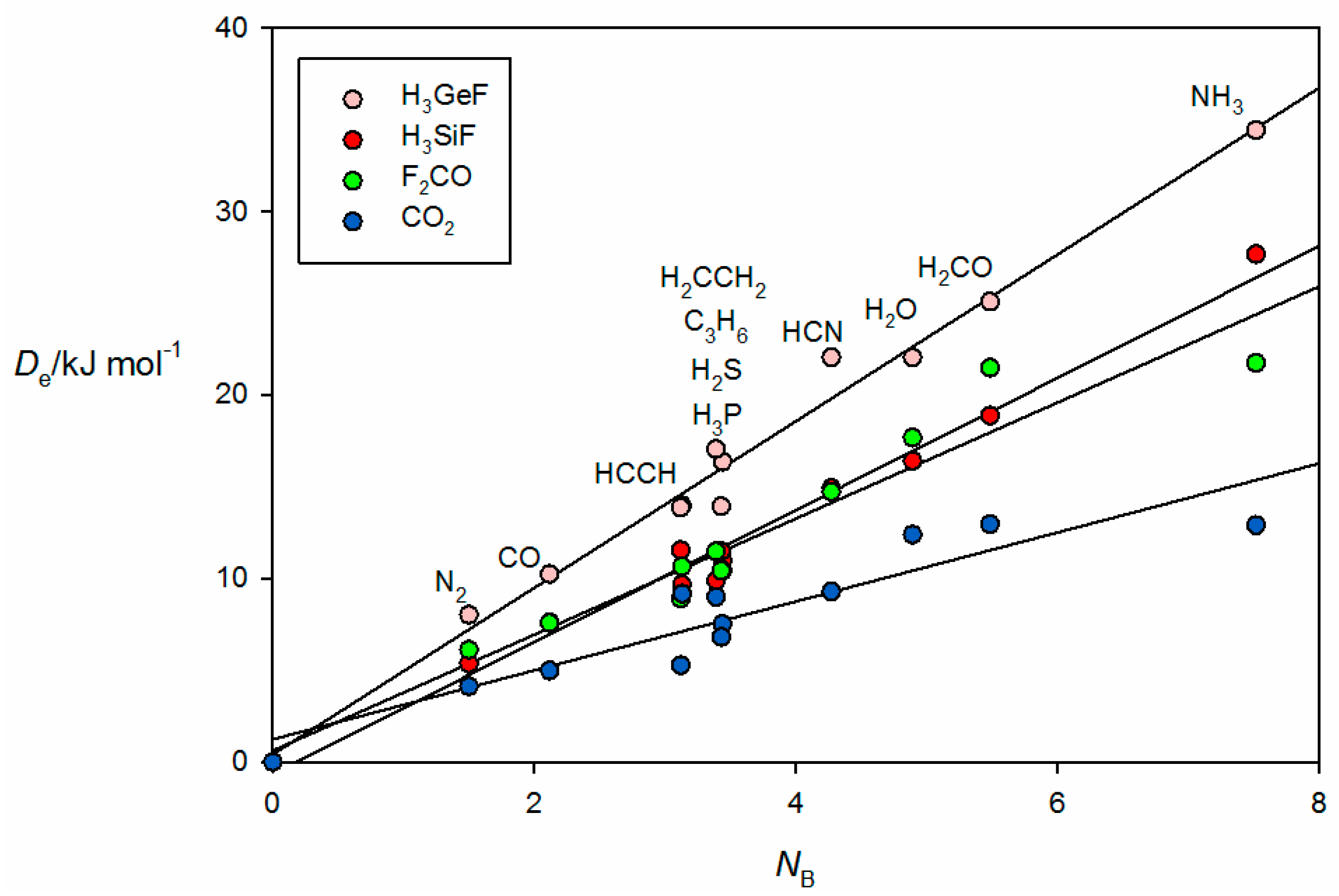
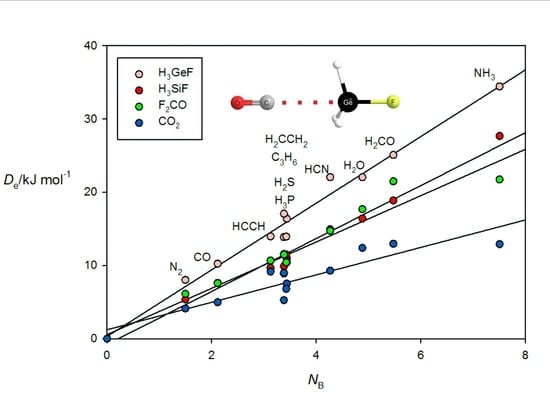
Figure 6 gives the results for tetrel-bonded complexes B⋯CO
2, B⋯H
3SiF, B⋯H
3GeF and B⋯F
2C=O when their
ab initio values of
are plotted against
NB of the 11 Lewis bases B. For the B⋯H
3SiF and B⋯H
3GeF complexes, the tetrel bond involves the n- or π-electron pairs of the Lewis base interacting with a σ hole that lies near the Si or Ge atom on the
C3 axis, as can be clearly seen in the
ab initio geometry determined for OC⋯H
3GeF.shown in
Figure 2c. The n-pair on the C atom of OC clearly interacts with the σ hole at Ge. F
2CO forms tetrel bonds of a different type. This planar molecule has a π-hole at the carbon atom which is perpendicular to the molecular plane and the n- or π-pair of electrons of a Lewis base can interact with this, as is evident from the geometry determined for the N
2⋯F
2CO complex displayed in
Figure 2d. A π-hole at C is also involved in the tetrel bond in B⋯CO
2. The systematic features identified for hydrogen- and halogen-bonded complexes in
Figure 3,
Figure 4 and
Figure 5 may also be seen in
Figure 6.
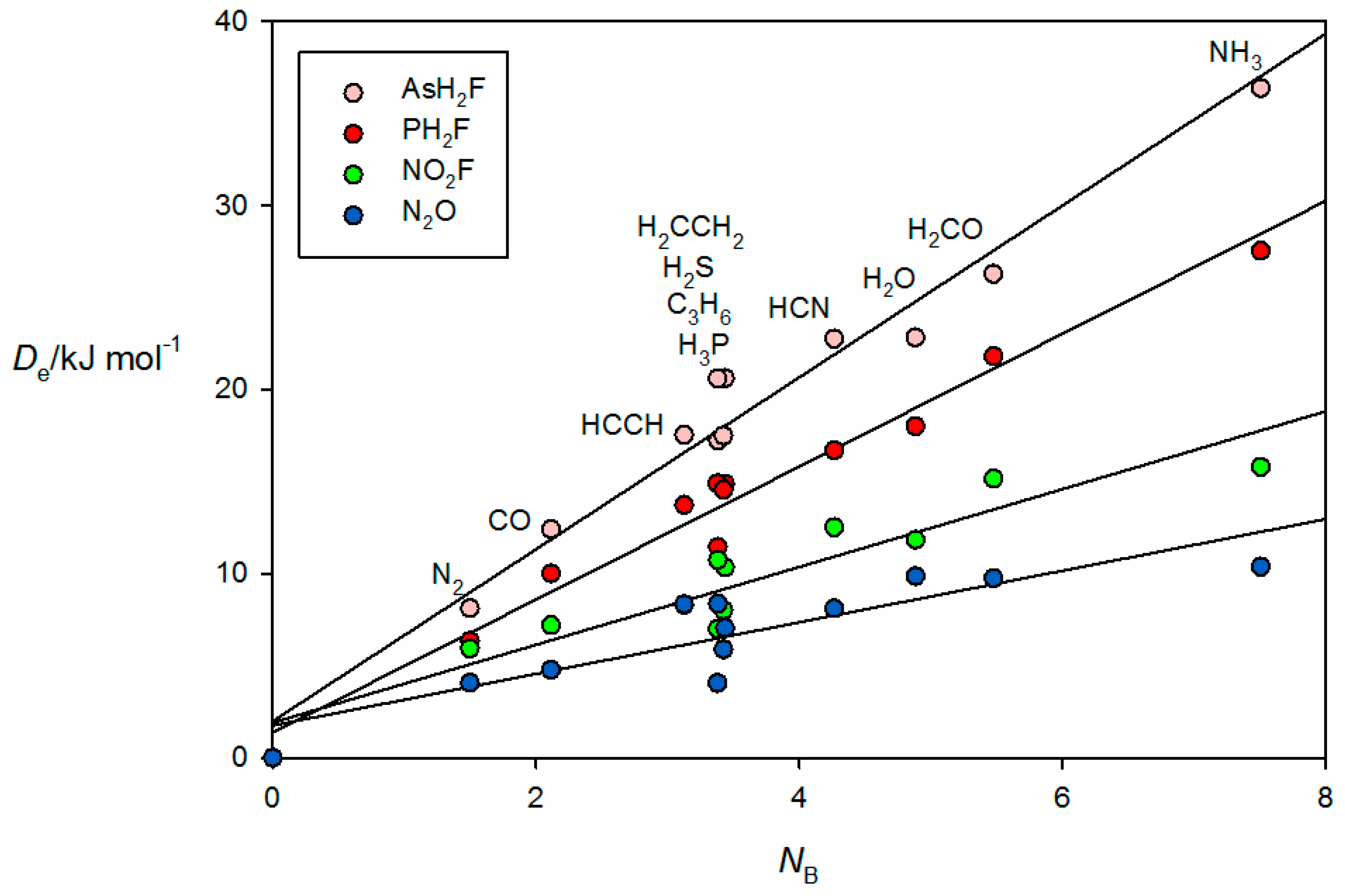
The corresponding plots of
against
NB for the pnictogen-bonded complexes B⋯PFH
2, B⋯AsFH
2, B⋯NO
2F and B⋯N
2O are given in
Figure 7. The first two groups of pnictogen-bonded complexes utilize a σ hole near P or As along the P–F or As–F bond direction to form the non-covalent bond, while for the last two groups a π hole at the central N atom fulfills the role. The
ab initio geometry of HCN⋯AsH
2F in
Figure 2e provides evidence of the σ-hole type of interaction. The pattern displayed by the
De values of the pnictogen-bonded complexes in
Figure 7 is similar to that seen in
Figure 6 for the tetrel-bonded systems and again involves the characteristic bunching of points for the complexes in which B = PH
3, H
2S, HC≡CH, C
3H
6 and CH
2=CH
2. Recall that, for reasons given earlier, complexes H
3P⋯PFH
2 and H
3P⋯AsFH
2 were excluded from the global fit in
Figure 1 and therefore from
Figure 7.
The familiar bunching pattern is again observed in
Figure 8, in which the
ab initio calculated values of
for complexes of the 11 Lewis bases B with each of the four Lewis acids SF
2, SeF
2, SO
2 and SeO
2 are plotted as a function of the
NB values of the various B. The complexes here all involve chalcogen bonds. In the B⋯SO
2 and B⋯SeO
2, the chalcogen bond is between a π hole at S or Se that is perpendicular to the plane containing the SO
2 or SeO
2 nuclei, but for B⋯SF
2 and B⋯SeF
2 a σ hole near S or Se at the termination of a S–F or Se–F bond is involved, as seen from the
ab initio geometry of the complex formed by the interaction of π electrons of acetylene with the Se atom of SeF
2 shown in
Figure 2f.
It is of interest to ask whether there exists a linear relationship between the calculated
Devalues and the intermolecular distances in the various complexes B⋯A investigated. For this purpose, the intermolecular distances of the hydrogen-bonded complexes have been gathered in
Table 7 while the intermolecular distances for the rest of the complexes are given in
Tables S1–S4 (Supplementary Materials). (The full optimized geometries of all the systems are gathered in
Table S5 of the Supplementary Materials). When seeking a linear relationship between the calculated
De values (given in
Table 2) and the intermolecular distances of all complexes a poor
R2 value of 0.68 results. A more detailed analysis considering the individual hydrogen-bonded donors with all the bases (
n = 11 for each correlation) reveals values of
R2 between 0.80 and 0.53 (
Table S6). Alternatively, looking to the correlation for a given base with the different HB donors (
n = 5 for each correlation), leads to
R2 values between 0.94 and 0.53. Similar results are obtained for the rest of the interactions considered here (
Table S6). Thus, it is clear that the
De values and the intermolecular distances are poorly correlated for the systems considered and consequently cannot be used to predict each other.
Parameters used in the literature to rationalize the
De values are the molecular electrostatic potential values of the isolated bases (
VS,min and
Vmin) or acids (
VS,max) (see
Section 2. for the definitions of the various quantities
V). The corresponding values have been gathered in
Table S7. The comparison of the
De values of the complexes of each Lewis acids with the
VS,min or
Vmin of the Lewis bases (
n = 11 for each correlation) provide
R2 values between 0.95 and 0.37 and between 0.97 and 0.43, respectively. Alternatively, the relationship of the V
S,max of the Lewis acids with the corresponding
De values for a single Lewis base (
n = 24) show
R2 values between 0.75 and 0.25 (
Table S8). Attempts to use simultaneously
VS,min of the Lewis bases and
VS,max of the Lewis acids in conjunction with the intermolecular distances for all the systems provide
R2 values smaller than 0.56. As in the case of the intermolecular distances, these parameters do not seem to be useful as predictive tool, save in closely related systems.