Analysis of Genetic Diversity and Structure Pattern of Indigofera Pseudotinctoria in Karst Habitats of the Wushan Mountains Using AFLP Markers
Abstract
:1. Introduction
2. Results
2.1. Gene Diversity of I. Pseudotinctoria
2.2. Structure Pattern of I. Pseudotinctoria
2.3. Genetic Differentiation and Gene Flow
2.4. Genetic Diversity Associated with Environmental Factors
3. Discussion
3.1. Genetic Diversity Across all Accessions
3.2. Genetic Diversity Related to Geographic and Climate Parameters
3.3. Structure Pattern and Gene Flow
4. Materials and Methods
4.1. Study Sites and Sampling
4.2. DNA Isolation
4.3. AFLP Procedure
4.4. Data Analysis
4.4.1. Band Statistics
4.4.2. Gene Diversity
4.4.3. Genetic Structure
4.4.4. Differentiation and Gene Flow
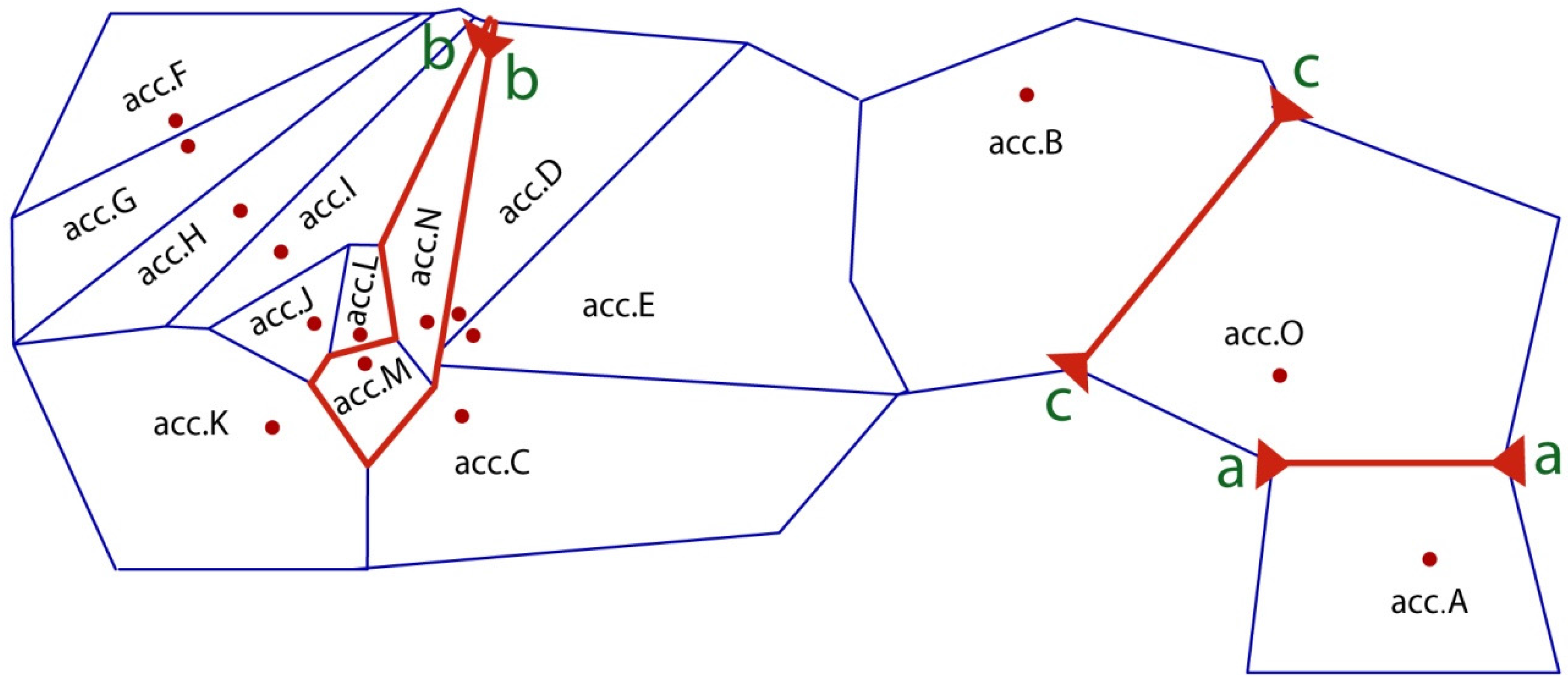
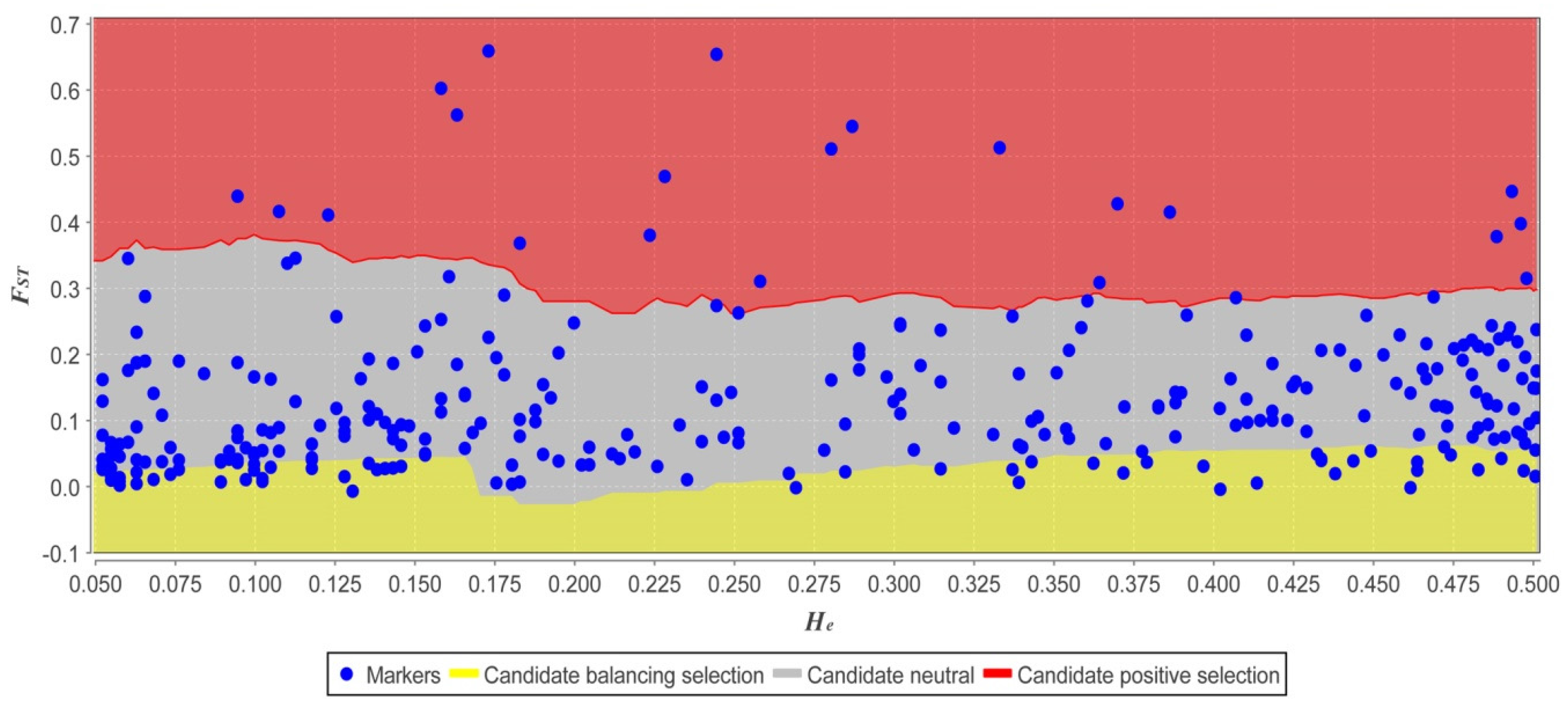
4.4.5. Genetic Barriers and Divergence Outlier Analysis
4.4.6. Correlation Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hewitt, G.M. Genetic consequences of climatic oscillations in the Quaternary. Philos. Trans. R. Soc. Lond. 2004, 359, 183–195. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, D.G.; Carey, M.; Czerniewska, J.; Fletcher, J.; Hether, T.; Jones, A.; Knight, S.; Knox, J.; Long, T.; Mannino, M.; et al. A meta-analysis of isolation by distance: Relic or reference standard for landscape genetics? Ecography 2010, 33, 315–320. [Google Scholar] [CrossRef]
- Coppi, A.; Mengoni, A.; Selvi, F. AFLP fingerprinting of Anchusa (Boraginaceae) in the Corso-Sardinian system: Genetic diversity, population differentiation and conservation priorities in an insular endemic group threatened with extinction. Biol. Conserv. 2008, 141, 2000–2011. [Google Scholar] [CrossRef]
- Parisod, C.; Bonvin, G. Fine-scale genetic structure and marginal processes in an expanding population of Biscutella laevigata L. (Brassicaceae). Heredity 2008, 101, 536–542. [Google Scholar] [CrossRef] [PubMed]
- Last, L.; Widmer, F.; Fjellstad, W.; Stoyanova, S.; Kölliker, R. Genetic diversity of natural orchardgrass (Dactylis glomerata L.) populations in three regions in Europe. BMC Genet. 2013, 14, 102. [Google Scholar] [CrossRef] [PubMed]
- Ndiade-Bourobou, D.; Hardy, O.J.; Favreau, B.; Moussavou, H.; Nzengue, E.; Mignot, A.; Bouvet, J.M. Long-distance seed and pollen dispersal inferred from spatial genetic structure in the very low-density rainforest tree, Baillonella toxisperma Pierre, in Central Africa. Mol. Ecol. 2010, 19, 4949–4962. [Google Scholar] [CrossRef] [PubMed]
- Bennett, A.F. Habitat fragmentation. Semin. Immunol. 2003, 22, 48. [Google Scholar]
- Young, A.; Boyle, T.; Brown, T. The population genetic consequences of habitat fragmentation for plants. Trends Ecol. Evol. 1996, 11, 413–418. [Google Scholar] [CrossRef]
- Gentry, A.H. Changes in plant community diversity and floristic composition on environmental and geographical gradients. Ann. Mo. Bot. Gard. 1988, 75, 1–34. [Google Scholar] [CrossRef]
- Grubb, P.J.; Whitmore, T.C. A comparison of montane and lowland rain forest in Ecuador: II. The Climate and its Effects on the Distribution and Physiognomy of the Forests. J. Ecol. 1966, 54, 303–333. [Google Scholar] [CrossRef]
- Mpaula, Q.; Andreac, P. Genetic patterns in Podocarpus parlatorei reveal the long-term persistence of cold-tolerant elements in the southern Yungas. J. Biogeogr. 2007, 34, 447–455. [Google Scholar]
- Schluter, D. Evidence for ecological speciation and its alternative. Science 2009, 323, 737–741. [Google Scholar] [CrossRef] [PubMed]
- Crow, J.F. The genetic basis of evolutionary change. Am. J. Hum. Genet. 1975, 27, 249–251. [Google Scholar]
- Mcewen, J.R.; Vamosi, J.C.; Rogers, S.M. Natural selection and neutral evolution jointly drive population divergence between alpine and lowland ecotypes of the allopolyploid plant Anemone multifida (Ranunculaceae). PLoS ONE 2013, 8, 68889. [Google Scholar] [CrossRef] [PubMed]
- Bierne, N.; Welch, J.; Loire, E.; Bonhomme, F.; David, P. The coupling hypothesis: Why genome scans may fail to map local adaptation genes. Mol. Ecol. 2011, 20, 2044–2072. [Google Scholar] [CrossRef] [PubMed]
- Chung, K.F.; Leong, W.C.; Rubite, R.R.; Repin, R.; Kiew, R.; Liu, Y.; Peng, C.I. Phylogenetic analyses of Begoniasect. Coelocentrumand allied limestone species of China shed light on the evolution of Sino-Vietnamese karst flora. Bot. Stud. 2014, 55, 1. [Google Scholar] [CrossRef] [PubMed]
- Clements, R.; Sodhi, N.S.; Schilthuizen, M.; Ng, P.K.L. Limestone karsts of southeast Asia: Imperiled Arks of Biodiversity. Bioscience 2006, 56, 733–742. [Google Scholar] [CrossRef]
- Zhu, H. The karst ecoystem of southern China and its biodiversity. Trop. For. 2007, 5, 44–47. [Google Scholar]
- Wang, J.; Kang, M.; Huang, H. Long-distance pollen dispersal ensures genetic connectivity of the low-density tree species, Eurycorymbus cavaleriei, in a fragmented karst forest landscape. Conserv. Genet. 2014, 15, 1163–1172. [Google Scholar] [CrossRef]
- Hu, X.Q.; Shi, Z.J.; Tian, Y.M.; Wang, C.C. The restoration of karst ancient landform of the Maokou Formation in southeastern Sichuan basin. Geol. Bull. China 2014, 33, 874–882. [Google Scholar]
- Ren, G.; Mateo, R.G.; Liu, J.; Suchan, T.; Alvarez, N.; Guisan, A.; Conti, E.; Salamin, N. Genetic consequences of Quaternary climatic oscillations in the Himalayas: Primula tibetica as a case study based on restriction site-associated DNA sequencing. New Phytol. 2017, 213, 1500–1512. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Pei, J.; Xie, Y.; Cao, J.; Wang, L. Impact of land use covers upon karst processes in a typical Fengcong depression system of Nongla, Guangxi, China. Environ. Geol. 2008, 55, 1621. [Google Scholar] [CrossRef]
- Yue, Y.M.; Wang, K.L.; Zhang, B.; Jiao, Q.J.; Liu, B.; Zhang, M.Y. Remote sensing of fractional cover of vegetation and exposed bedrock for karst rocky desertification assessment. Procedia Environ. Sci. 2012, 13, 847–853. [Google Scholar] [CrossRef]
- Fantz, P.R. Vascular Flora of the Southeastern United States, Volume 3, Part 2: Leguminosae (Fabaceae) by Duane Isely. Syst. Bot. 1991, 16, 756. [Google Scholar] [CrossRef]
- Woods, M.; Leverett, L. The genus Indigofera (Fabaceae) in Alabama. Ala. Acad. Sci. 2010, 1, 81. [Google Scholar]
- Kodama, A. Karyotype analyses of chromosomes in eighteen species belonging to nine tribes in leguminosae. Bull. Hiroshima Agric. Coll. 1989, 8, 691–706. [Google Scholar]
- Otao, T.; Kobayashi, T.; Uehara, K. Development and characterization of 14 microsatellite markers for Indigofera pseudotinctoria (Fabaceae). Appl. Plant Sci. 2013, 4, 1500110. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.L.; Zhang, H.; Sun, Q.Y. Effect of artifical vegetation on the soil and water consevation and the control of phosphorus loss on the slope. J. Soil Water Conserv. 2011, 3, 25–32. [Google Scholar]
- Yu, J.H.; Bai, M.; Fang, W.; Hong, L.X. Physiological and biochemical substances of four shrubs with drought stress. J. Zhejiang For. Coll. 2009, 26, 485–489. [Google Scholar]
- Smith, L.M.; Case, J.L.; Smith, H.M.; Harwell, L.C.; Summers, J.K. Relating ecoystem services to domains of human well-being: Foundation for a U.S. index. Ecol. Indic. 2013, 28, 79–90. [Google Scholar] [CrossRef]
- Yu, L.F.; Zhu, S.Q.; Ye, J.Z.; Wei, L.M.; Chen, Z.R. A study on the evaluation of natural restoration for degraded karst forest. Sci. Silvae Sin. 2000, 36, 12–19. [Google Scholar]
- Vuylsteke, M.; Peleman, J.D.; van Eijk, M.J. AFLP technology for DNA fingerprinting. Nat. Protoc. 2007, 2, 1387–1398. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, J.; Fan, Y.; Sun, M.; Wu, W.; Zhao, W.; Yang, X.; Huang, L.; Peng, Y.; Ma, X.; et al. Genetic structure and eco-geographical differentiation of wild sheep Fescue (Festuca ovina L.) in Xinjiang, Northwest China. Molecules 2017, 22, 1316. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.R.; Mitchellolds, T. Quantifying effects of environmental and geographical factors on patterns of genetic differentiation. Mol. Ecol. 2011, 20, 4631–4642. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Zhang, X.Q.; Zhou, Y.H.; Bai, S.Q.; Liu, W. Assessing genetic diversity of Elymus sibiricus (Poaceae: Triticeae) populations from Qinghai-Tibet Plateau by ISSR markers. Biochem. Syst. Ecol. 2008, 36, 514–522. [Google Scholar] [CrossRef]
- Ersoz, E.S.; Yu, J.; Buckler, E.S. Applications of linkage disequilibrium and association mapping in Maize. Biotechnol Agric. For. 2009, 63, 97–119. [Google Scholar]
- Mcvean, G.A. A genealogical interpretation of linkage disequilibrium. Genetics 2002, 162, 987–991. [Google Scholar] [PubMed]
- Jones, C.J.; Edwards, K.J.; Castaglione, S.; Winfield, M.O.; Sala, F.; Van de Wiel, C.; Bredemeijer, G.; Vosman, B.; Matthes, M.; Daly, A.; et al. Reproducibility testing of RAPD, AFLP and SSR markers in plants by a network of European laboratories. Mol. Breed. 1997, 3, 381–390. [Google Scholar] [CrossRef]
- Kölliker, R.; Jones, E.S.; Jahufer, M.Z.Z.; Forster, J.W. Bulked AFLP analysis for the assessment of genetic diversity in white clover (Trifolium repens L.). Euphytica 2001, 121, 305–315. [Google Scholar] [CrossRef]
- Thoquet, P.; Ghérardi, M.; Journet, E.P.; Kereszt, A.; Ané, J.M.; Prosperi, J.M.; Huguet, T. The molecular genetic linkage map of the model legume Medicago truncatula: An essential tool for comparative legume genomics and the isolation of agronomically important genes. BMC Plant Biol. 2002, 2, 1. [Google Scholar] [CrossRef] [Green Version]
- Larson, S.R.; Jones, T.A.; Mccracken, C.L.; Jensen, K.B. Amplified fragment length polymorphism in Elymus elymoides, other Elymus taxa. Can. J. Bot. 2003, 81, 789–804. [Google Scholar] [CrossRef]
- Ouborg, N.J.; Treuren, R.V.; Damme, J.M.M.V. The significance of genetic erosion in the process of extinction. Oecologia 1991, 86, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Hamrick, J.L.; Godt, M.J.W. Effects of life history traits on genetic diversity in plant species. Philos. Trans. R. Soc. Lond. Ser. Biol. Sci. 1996, 351, 1291–1298. [Google Scholar] [CrossRef]
- Gitzendanner, M.A.; Soltis, P.S. Patterns of genetic variation in rare and widespread plant congeners. Am. J. Bot. 2000, 87, 783–792. [Google Scholar] [CrossRef] [PubMed]
- Stern, D.L.; Orgogozo, V. Is genetic evolution predictable? Science 2009, 323, 746–751. [Google Scholar] [CrossRef] [PubMed]
- Heywood, J.S. Spatial analysis of genetic variation in plant populations. Annu. Rev. Ecol. Syst. 1991, 22, 335–355. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Ohsawa, T.; Ide, Y. Global patterns of genetic variation in plant species along vertical and horizontal gradients on mountains. Glob. Ecol. Biogeogr. 2008, 17, 152–163. [Google Scholar] [CrossRef]
- Warren, S.D.; Harper, K.T. Booth GM Elevational distribution of insect pollinators. Am. Midl. Nat. 1988, 120, 325–330. [Google Scholar] [CrossRef]
- Linhartyan, B.; Grant, M.C. Evolutionary significane of local genetic differentiation in plants. Annu. Rev. Ecol. Syst. 1996, 27, 237–277. [Google Scholar] [CrossRef]
- Hayes, P.; Barker, G.L.A.; Walsby, A. The genetic structure of populations. Br. Med. J. 1997, 2, 36. [Google Scholar]
- And, M.D.L.; Hamrick, J.L. Ecological determinants of genetic structure in plant populations. Annu Rev. Ecol. Syst. 1984, 15, 65–95. [Google Scholar]
- Hutchison, D.W.; Templeton, A.R. Correlation of pairwise genetic and geographic distance measures: Inferring the relative influences of gene flow and drift on the distribution of genetic variability. Evolution 1999, 53, 1898–1914. [Google Scholar] [CrossRef] [PubMed]
- Garant, D.; Forde, S.E.; Hendry, A.P. The multifarious effects of dispersal and gene flow on contemporary adaptation. Funct. Ecol. 2007, 21, 434–443. [Google Scholar] [CrossRef]
- Räsänen, K.; Hendry, A.P. Disentangling interactions between adaptive divergence and gene flow when ecology drives diversification. Ecol. Lett. 2008, 11, 624–636. [Google Scholar] [CrossRef] [PubMed]
- Dhuyvetter, H.; Gaublomme, E.; Desender, K. Bottlenecks, drift and differentiation: The fragmented population structureof the saltmarsh beetle Pogonus chalceus. Genetica 2005, 124, 167–177. [Google Scholar] [CrossRef] [PubMed]
- Manni, F.; Heyer, E. Geographic patterns of (genetic, morphologic, linguistic) variation: How barriers can be detected by using Monmonier's Algorithm. Hum. Biol. 2004, 76, 173–190. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.W. Spermatophyte flora of Wulipo Nature Reserve, Wushan County, Chongqing City. J. Huazhong Agric. Univ. 2012, 31, 303–312. [Google Scholar]
- Pirttilä, A.M.; Hirsikorpi, M.; Kämäräinen, T.; Jaakola, L.; Hohtola, A. DNA isolation methods for medicinal and aromatic plants. Plant Mol. Biol. Report. 2001, 19, 273. [Google Scholar] [CrossRef]
- Laurent, E.; Guillaume, L.; Stefan, S. Arlequin (version 3.0): An integrated software package for population genetics data analysis. Evol. Bioinform. Online 2007, 1, 47. [Google Scholar]
- Hou, Y.; Lou, A. Population genetic diversity and structure of a naturally isolated plant species, Rhodiola dumulosa (Crassulaceae). PLoS ONE 2011, 6, 24497. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.; Milligan, B.G. Analysis of population genetic structure with RAPD markers. Mol. Ecol. 1994, 3, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Holsinger, K.E.; Lewis, P.O.; Dey, D.K. A Bayesian approach to inferring population structure from dominant markers. Mol. Ecol. 2002, 11, 1157–1164. [Google Scholar] [CrossRef] [PubMed]
- Felsenstein, J. PHYLIP: Phylogeny inference package. Cladistics Int. J. Willi Hennig Soc. 1989, 5, 164–166. [Google Scholar]
- Dessau, R.B.; Pipper, C.B. The R project for statistical computing. Ugeskr. Laeger 2008, 170, 328–330. [Google Scholar] [PubMed]
- Daniel, F.; Matthew, S.; Pritchard, J.K. Inference of population structure using multilocus genotype data: Dominant markers and null alleles. Genetics 2003, 164, 1567. [Google Scholar]
- Jakobsson, M.; Rosenberg, N.A. CLUMPP: A cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics 2007, 23, 1801–1806. [Google Scholar] [CrossRef] [PubMed]
- Ramasamy, R.K.; Ramasamy, S.; Bindroo, B.B.; Naik, V.G. STRUCTURE PLOT: A program for drawing elegant STRUCTURE bar plots in user friendly interface. Springerplus 2014, 3, 431. [Google Scholar] [CrossRef] [PubMed]
- Ilves, A.; Lanno, K.; Sammul, M.; Tali, K. Genetic variability, population size and reproduction potential in Ligularia sibirica (L.) populations in Estonia. Conserv. Genet. 2013, 14, 661–669. [Google Scholar] [CrossRef]
- Slatkin, M.; Barton, N.H. A comparisonof three indirect methods for estimating average average levels of gene flow. Evolution 1989, 43, 1349–1368. [Google Scholar] [CrossRef] [PubMed]
- Antao, T.; Beaumont, M.A. Mcheza: A workbench to detect selection using dominant markers. Bioinformatics 2011, 27, 1717–1718. [Google Scholar] [CrossRef] [PubMed]
- Luebert, F.; Jacobs, P.; Hilger, H.H.; Muller, L.A.H. Evidence for nonallopatric speciation among closely related sympatric Heliotropium species in the Atacama Desert. Ecolo. Evol. 2014, 4, 266–275. [Google Scholar] [CrossRef] [PubMed]
- Ivetic, V.; Isajev, V.; Stavretović, N. Implementation of Monmonier’s algorithm of maximum differences for the regionalization of forest tree populations as a basis for the selection of seed sources. Arch. Biol. Sci. 2010, 62, 425–430. [Google Scholar] [CrossRef]
- Dray, S.; Dufour, A. The ade4 package: Implementing the duality diagram for ecologists. J. Stat. Softw. 2007, 22, 1–20. [Google Scholar] [CrossRef]
Sample Availability: Not Availability. |


| Primer | TNB | NPB | PPB(%) | PIC | Hj | Ho |
|---|---|---|---|---|---|---|
| E53M55 | 102 | 56 | 54.90% | 0.1690 | 0.2308 | 0.3189 |
| E59M55 | 80 | 49 | 61.25% | 0.3029 | 0.2773 | 0.1998 |
| E76M85 | 81 | 57 | 70.37% | 0.2481 | 0.3980 | 0.2635 |
| E78M85 | 80 | 54 | 67.50% | 0.2341 | 0.3863 | 0.2829 |
| E85M60 | 84 | 57 | 67.86% | 0.2211 | 0.3308 | 0.2826 |
| E86M85 | 88 | 51 | 57.95% | 0.1708 | 0.2949 | 0.3165 |
| Total | 515 | 324 | 62.91% | 0.2243 | 0.4023 | 0.3764 |
| Mean | 85.83 | 54 | 62.91% | 0.2243 | 0.3197 | 0.2774 |
| Acc. | Np | PLP(%) | LD(%) | Na | Ne | Hj | Ho | HB |
|---|---|---|---|---|---|---|---|---|
| A | 253 | 78.09 | 10.65 | 1.7809 | 1.4478 | 0.2985 ± 0.0097 | 0.3907 ± 0.0205 | 0.2869 ± 0.0032 |
| B | 282 | 80.74 | 9.01 | 1.8704 | 1.4491 | 0.2992 ± 0.0090 | 0.4130 ± 0.0217 | 0.2816 ± 0.0031 |
| C | 286 | 88.27 | 12.41 | 1.8827 | 1.4036 | 0.2779 ± 0.0092 | 0.3788 ± 0.0199 | 0.2580 ± 0.0032 |
| D | 293 | 90.43 | 5.74 | 1.8889 | 1.4304 | 0.2805 ± 0.0097 | 0.3966 ± 0.0208 | 0.2605 ± 0.0027 |
| E | 296 | 91.36 | 12.52 | 1.9136 | 1.4086 | 0.2563 ± 0.0100 | 0.3818 ± 0.0200 | 0.2482 ± 0.0026 |
| F | 202 | 62.35 | 12.72 | 1.6235 | 1.2874 | 0.2020 ± 0.0102 | 0.2708 ± 0.0142 | 0.1993 ± 0.0031 |
| G | 228 | 70.37 | 14.16 | 1.7037 | 1.3105 | 0.2131 ± 0.0101 | 0.2969 ± 0.0156 | 0.2068 ± 0.0031 |
| H | 235 | 72.53 | 9.70 | 1.7253 | 1.2971 | 0.2039 ± 0.0099 | 0.2899 ± 0.0152 | 0.1997 ± 0.0029 |
| I | 283 | 87.35 | 9.10 | 1.8735 | 1.3707 | 0.2474 ± 0.0097 | 0.3571 ± 0.0187 | 0.2330 ± 0.0030 |
| J | 224 | 69.14 | 10.67 | 1.6914 | 1.3384 | 0.2396 ± 0.0100 | 0.3140 ± 0.0165 | 0.2271 ± 0.0033 |
| K | 239 | 73.77 | 9.17 | 1.7377 | 1.3588 | 0.2360 ± 0.0103 | 0.3282 ± 0.0172 | 0.2278 ± 0.0028 |
| L | 244 | 75.31 | 11.14 | 1.7531 | 1.3622 | 0.2501 ± 0.0099 | 0.3393 ± 0.0178 | 0.2404 ± 0.0031 |
| M | 266 | 82.1 | 9.72 | 1.8210 | 1.3731 | 0.2558 ± 0.0094 | 0.3592 ± 0.0188 | 0.2407 ± 0.0031 |
| N | 237 | 73.15 | 12.01 | 1.7315 | 1.3378 | 0.2288 ± 0.0101 | 0.3188 ± 0.0167 | 0.2250 ± 0.0029 |
| O | 202 | 62.35 | 12.22 | 1.6235 | 1.3037 | 0.2079 ± 0.0105 | 0.2757 ± 0.0145 | 0.2095 ± 0.0031 |
| Total | 324 | 100.00 | 10.73 | 2.0000 | 1.4433 | 0.2986 ± 0.0097 | 0.4291 ± 0.0100 | 0.2895 ± 0.0008 |
| Mean | 251 | 77.15 | 10.73 | 1.7747 | 1.3653 | 0.2465 ± 0.0099 | 0.3407 ± 0.0179 | 0.2362 ± 0.0030 |
| Group | Source of Variance | D.f. | Sum of Squares | Variance Components | Percentage of Variance (%) | FST |
|---|---|---|---|---|---|---|
| Two clusters (lowland vs. highland) | Between Clusters | 1 | 1120.049 | 11.1906 | 8.98 | FCT = 0.0898 |
| Among acc. within Cluster | 13 | 3269.13 | 8.74707 | 16.44 | FSC = 0.1801 | |
| Within accessions | 349 | 13844.89 | 39.67018 | 74.57 | FST = 0.2543 | |
| Total | 363 | 18234.07 | 53.19614 | |||
| All accessions | Among accessions | 14 | 4389.178 | 11.29686 | 22.17 | FST = 0.2217 |
| Within accessions | 349 | 13,844.89 | 39.67018 | 77.83 | ||
| Total | 363 | 18,234.07 | 50.96705 |
| Variable | All Accessions | Lowland Cluster | Highland Cluster |
|---|---|---|---|
| HT | 0.2986 | 0.3020 | 0.2384 |
| HS | 0.2465 | 0.2641a | 0.2142b |
| GST | 0.1746 | 0.1255 | 0.1015 |
| Isp | 0.4291 | 0.4406 | 0.3796 |
| Ipop | 0.3407 | 0.3618a | 0.3223b |
| G'ST | 0.2060 | 0.1789 | 0.1511 |
| FST | 0.2217 | 0.2124 | 0.1491 |
| Nm | 1.1819 | 1.7421 | 2.2128 |
| Model | θB | f | DIC | ||||
|---|---|---|---|---|---|---|---|
| Mean ± SD | 2.50% | 97.50% | Mean ± SD | 2.50% | 97.50% | ||
| full model | 0.1899 ± 0.0040 | 0.1397 | 0.2094 | 0.0169 ± 0.0250 | 0.0140 | 0.1279 | 19,432.7 |
| f = 0 model | 0.1844 ± 0.0022 | 0.1388 | 0.1941 | 0 | - | - | 19,375.6 |
| θB = 0 model | 0 | - | - | 0.3587 ± 0.2889 | 0.0316 | 0.2821 | 39,248.4 |
| free model | 0.1997 ± 0.0123 | 0.1645 | 0.2103 | 0.3987 ± 0.2889 | 0.0254 | 0.9721 | 20,836.1 |
| Accession | acc.A | acc.B | acc.C | acc.D | acc.E | acc.F | acc.G | acc.H | acc.I | acc.J | acc.K | acc.L | acc.M | acc.N | acc.O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| acc.A | - | 3.0701 | 2.0691 | 1.5629 | 0.9053 | 0.6658 | 0.6973 | 0.6995 | 1.0474 | 0.9761 | 1.0126 | 1.0353 | 1.1259 | 0.8398 | 0.8989 |
| acc.B | 0.0753 | - | 3.9659 | 2.4152 | 1.3125 | 0.9144 | 1.0294 | 1.0742 | 1.5964 | 1.4335 | 1.4507 | 1.4909 | 1.5294 | 1.0714 | 1.0777 |
| acc.C | 0.1078 | 0.0593 | - | 9.4025 | 1.9430 | 1.3734 | 1.5460 | 1.5682 | 2.6981 | 2.5749 | 2.4852 | 2.4942 | 2.3705 | 1.3154 | 1.2120 |
| acc.D | 0.1379 | 0.0938 | 0.0259 | - | 3.2319 | 1.5909 | 1.8868 | 1.8633 | 3.3784 | 2.1355 | 1.9742 | 2.0104 | 3.4050 | 1.7580 | 1.4484 |
| acc.E | 0.2164 | 0.1600 | 0.1140 | 0.0718 | - | 4.1670 | 4.4316 | 2.1562 | 3.0833 | 1.7792 | 1.6790 | 1.4837 | 1.9108 | 1.1312 | 1.0190 |
| acc.F | 0.2730 | 0.2147 | 0.154 | 0.1358 | 0.0566 | - | 8.3411 | 2.2550 | 2.4067 | 1.6746 | 1.4438 | 1.2077 | 1.2524 | 0.7835 | 0.7472 |
| acc.G | 0.2639 | 0.1954 | 0.1392 | 0.1170 | 0.0534 | 0.0291 | - | 7.6364 | 4.6138 | 2.0289 | 1.8579 | 1.5306 | 1.5815 | 0.9037 | 0.8116 |
| acc.H | 0.2633 | 0.1888 | 0.1375 | 0.1183 | 0.1039 | 0.0998 | 0.0317 | - | 7.1029 | 1.9683 | 1.7629 | 1.4013 | 1.5499 | 0.8916 | 0.8125 |
| acc.I | 0.1927 | 0.1354 | 0.0848 | 0.0689 | 0.075 | 0.0941 | 0.0514 | 0.0340 | - | 5.5370 | 4.4316 | 2.8828 | 2.9842 | 1.3713 | 1.2232 |
| acc.J | 0.2039 | 0.1485 | 0.0885 | 0.1048 | 0.1232 | 0.1299 | 0.1097 | 0.1127 | 0.0432 | - | 33.5338 | 8.2246 | 2.0563 | 1.0700 | 0.9938 |
| acc.K | 0.1980 | 0.1470 | 0.0914 | 0.1124 | 0.1296 | 0.1476 | 0.1186 | 0.1242 | 0.0534 | 0.0074 | - | 11.7117 | 1.9565 | 1.0353 | 0.9416 |
| acc.L | 0.1945 | 0.1436 | 0.0911 | 0.1106 | 0.1442 | 0.1715 | 0.1404 | 0.1514 | 0.0798 | 0.0295 | 0.0209 | - | 1.8941 | 1.0321 | 0.9166 |
| acc.M | 0.1817 | 0.1405 | 0.0954 | 0.0684 | 0.1157 | 0.1664 | 0.1365 | 0.1389 | 0.0773 | 0.1084 | 0.1133 | 0.1166 | - | 8.7106 | 3.5321 |
| acc.N | 0.2294 | 0.1892 | 0.1597 | 0.1245 | 0.1810 | 0.2419 | 0.2167 | 0.2190 | 0.1542 | 0.1894 | 0.1945 | 0.1950 | 0.0279 | - | 4.6520 |
| acc.O | 0.2176 | 0.1883 | 0.1710 | 0.1472 | 0.1970 | 0.2507 | 0.2355 | 0.2353 | 0.1697 | 0.2010 | 0.2098 | 0.2143 | 0.0661 | 0.0510 | - |
| Acc. | Ind. | Elev. | Longitude | Latitude | Tmean (°C) | P (mm) | pH | Soil Type | OM (g/kg) |
|---|---|---|---|---|---|---|---|---|---|
| A | 23 | 379 | 109°51’21.97” | 31°06’55.85” | 16.042 | 1041 | 7.40 | loess soil | 6.2 |
| B | 26 | 552 | 109°55’40.15” | 31°03’16.74” | 16.142 | 1029 | 7.64 | loess soil | 21.3 |
| C | 23 | 600 | 109°53’20.59” | 30°56’32.75” | 14.733 | 1150 | 7.65 | purple soil | 9.4 |
| D | 24 | 640 | 109°53’49.32” | 30°56’34.47” | 14.733 | 1150 | 7.72 | purple soil | 18.1 |
| E | 30 | 1002 | 109°53’49.30” | 30°56’34.47” | 14.733 | 1150 | 7.30 | purple soil | 14.4 |
| F | 21 | 1612 | 109°55’2.82” | 30°54’50.84” | 14.429 | 1169 | 5.85 | purple soil | 66.3 |
| G | 21 | 1533 | 109°55’0.68” | 30°54’51.78” | 14.429 | 1169 | 7.50 | purple soil | 9.9 |
| H | 24 | 1444 | 109°54’32.72” | 30°55’11.86” | 14.733 | 1150 | 7.91 | purple soil | 45.0 |
| I | 25 | 1336 | 109°54’17.56” | 30°55’27.16” | 14.733 | 1150 | 5.83 | purple soil | 13.9 |
| J | 19 | 1212 | 109°53’50.89” | 30°55’39.22” | 14.733 | 1150 | 7.66 | purple soil | 15.6 |
| K | 29 | 1071 | 109°53’17.98” | 30°55’23.87” | 14.733 | 1150 | 7.85 | purple soil | 10.5 |
| L | 26 | 1018 | 109°53’45.56” | 30°55’56.45” | 14.733 | 1150 | 7.16 | purple soil | 10.6 |
| M | 25 | 913 | 109°53’38.58” | 30°55’57.98” | 14.733 | 1150 | 7.57 | purple soil | 10.6 |
| N | 27 | 778 | 109°53’51.79” | 30°56’21.01” | 14.733 | 1150 | 7.53 | purple soil | 13.4 |
| O | 21 | 311 | 109°51’13.92” | 31°07’3.41” | 17.442 | 960 | 7.20 | loess soil | 15.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Zhang, C.; Wu, W.; He, W.; Zhang, L.; Ma, X. Analysis of Genetic Diversity and Structure Pattern of Indigofera Pseudotinctoria in Karst Habitats of the Wushan Mountains Using AFLP Markers. Molecules 2017, 22, 1734. https://doi.org/10.3390/molecules22101734
Fan Y, Zhang C, Wu W, He W, Zhang L, Ma X. Analysis of Genetic Diversity and Structure Pattern of Indigofera Pseudotinctoria in Karst Habitats of the Wushan Mountains Using AFLP Markers. Molecules. 2017; 22(10):1734. https://doi.org/10.3390/molecules22101734
Chicago/Turabian StyleFan, Yan, Chenglin Zhang, Wendan Wu, Wei He, Li Zhang, and Xiao Ma. 2017. "Analysis of Genetic Diversity and Structure Pattern of Indigofera Pseudotinctoria in Karst Habitats of the Wushan Mountains Using AFLP Markers" Molecules 22, no. 10: 1734. https://doi.org/10.3390/molecules22101734





