Optimal Energy Transfer in Light-Harvesting Systems
Abstract
:1. Introduction
2. Efficient Energy Transfer in Natural Light-Harvesting Systems
2.1. State of the Art Theoretical Treatment of Energy Transfer in Light Harvesting Systems
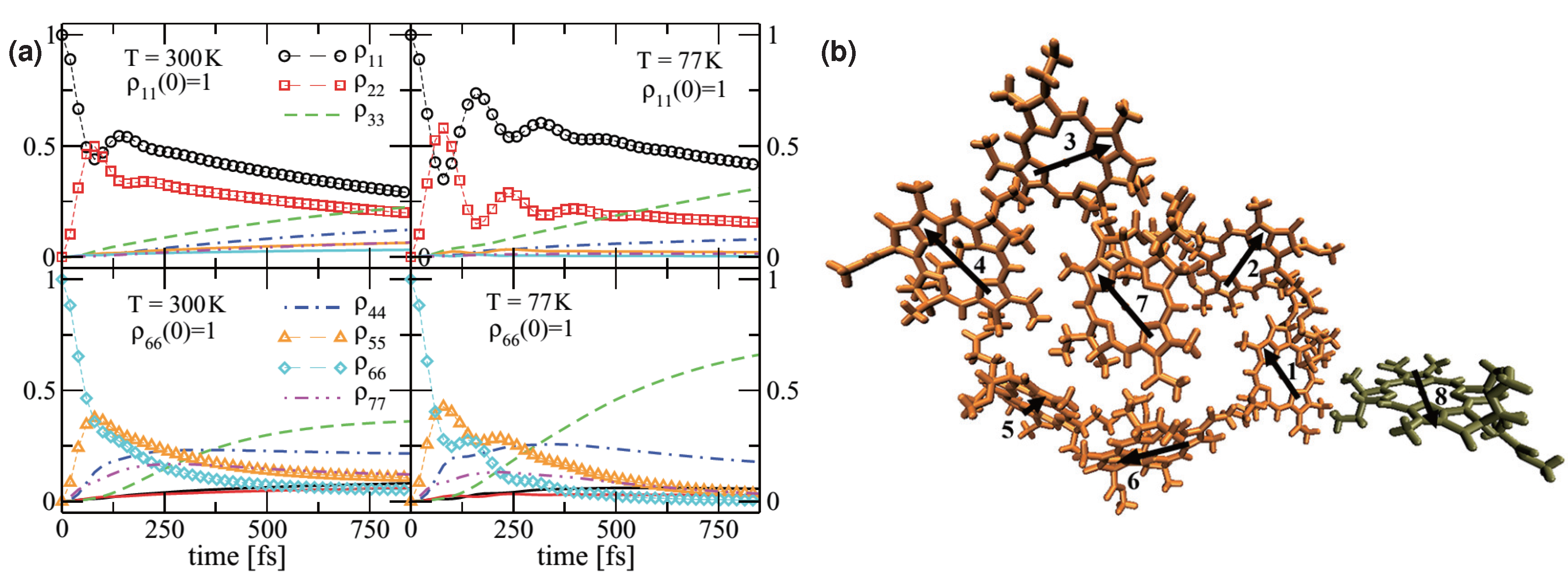


2.2. Quantum Efficiency and Average Trapping Time
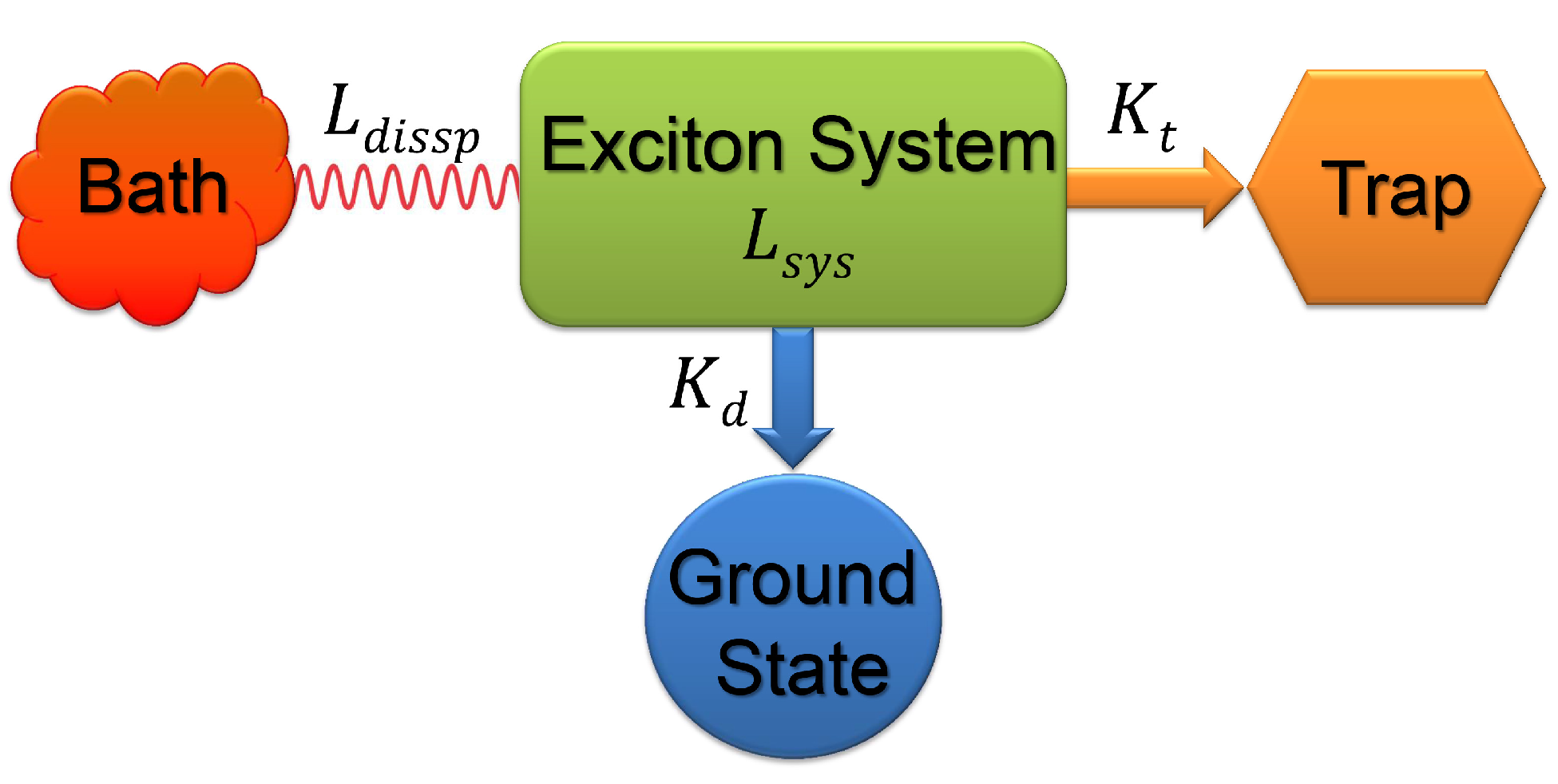
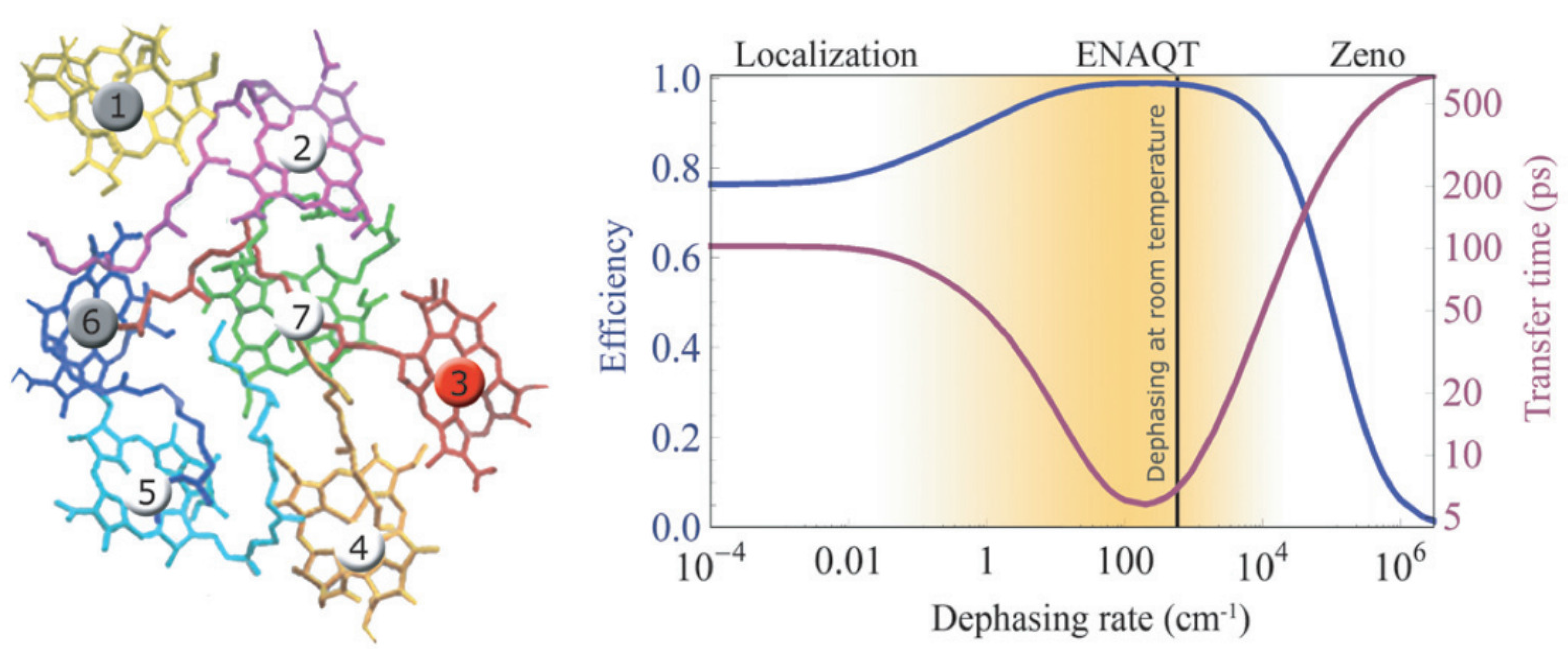
2.3. Quantum Coherence and Its Interplay with Protein Environments

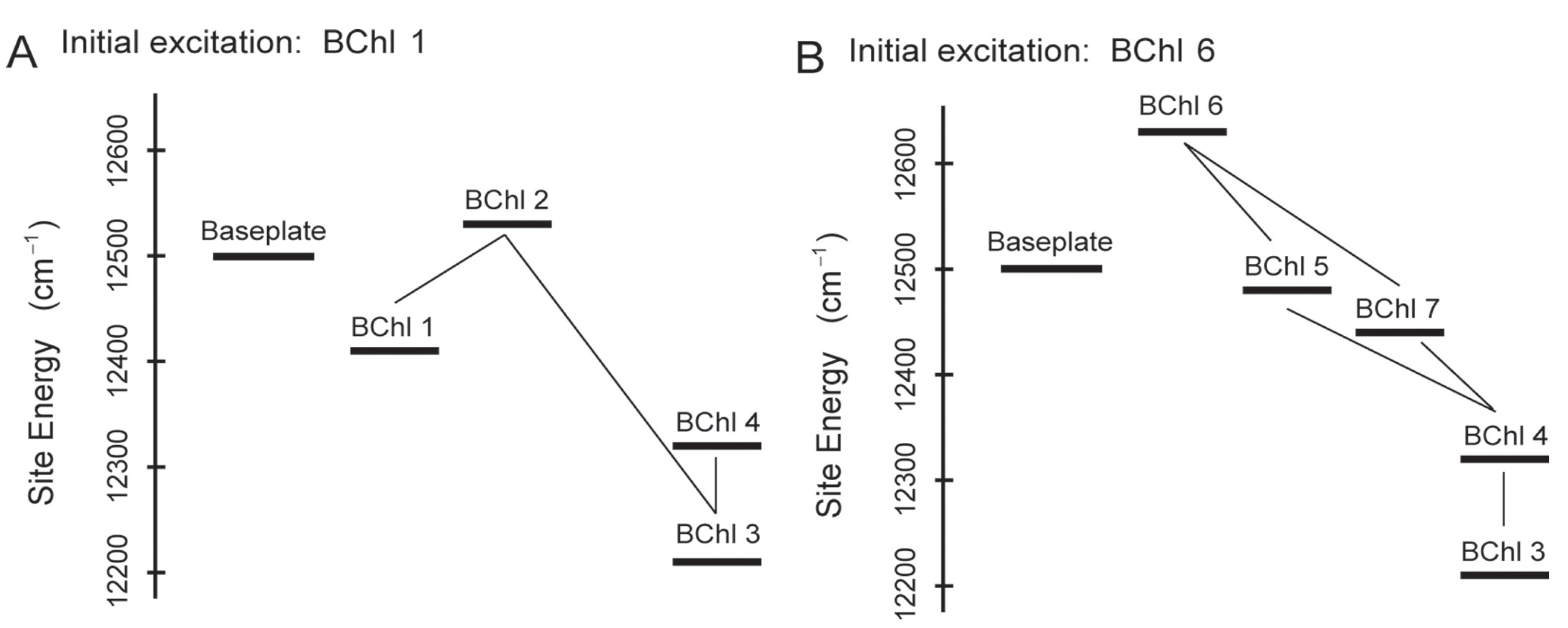
2.4. Non-Photochemical Quenching

2.5. Charge Separation in the Reaction Center
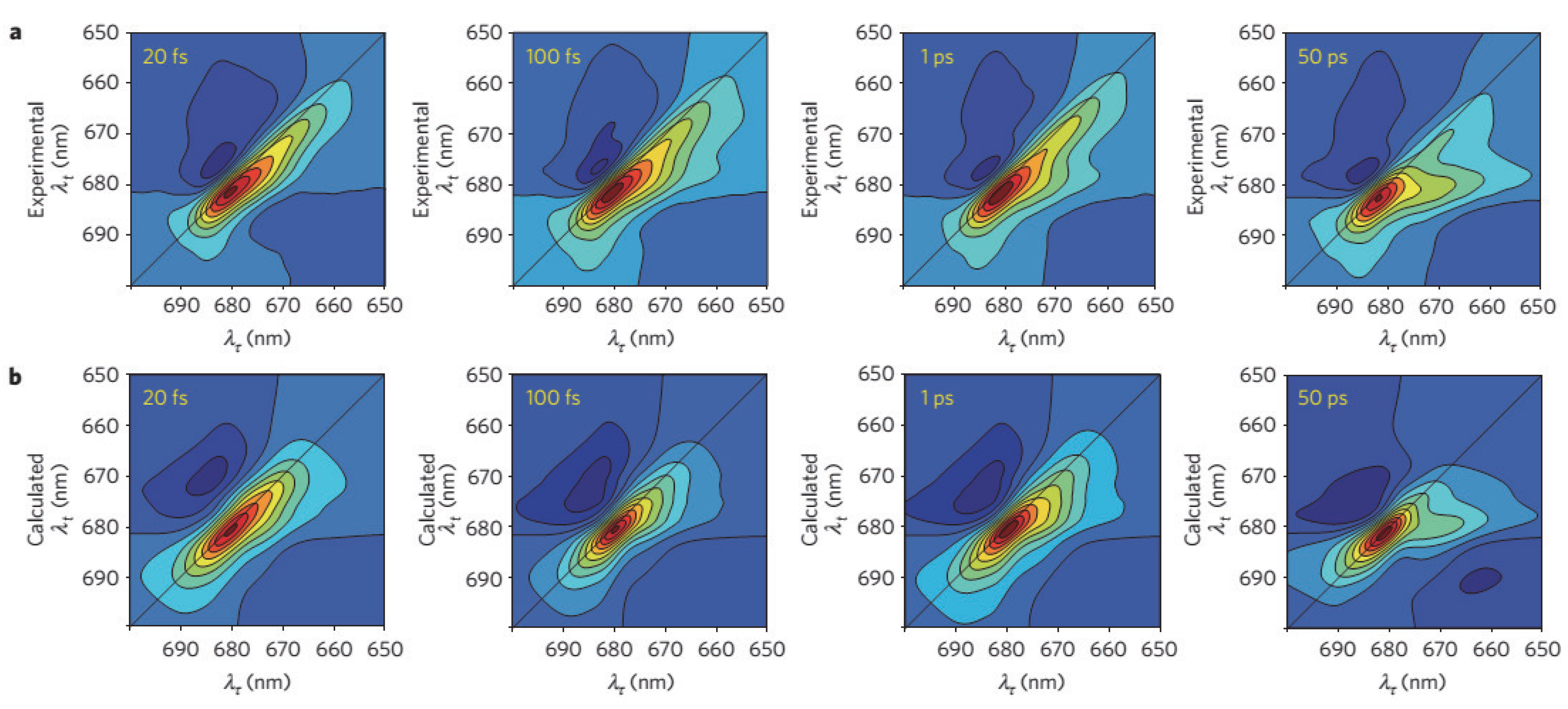
3. Energy and Charge Transport in Organic Molecules for Solar Cells
3.1. Organic Solar Cells

3.2. Charge Transport in Organic Semiconductors
3.2.1. Theoretical Models
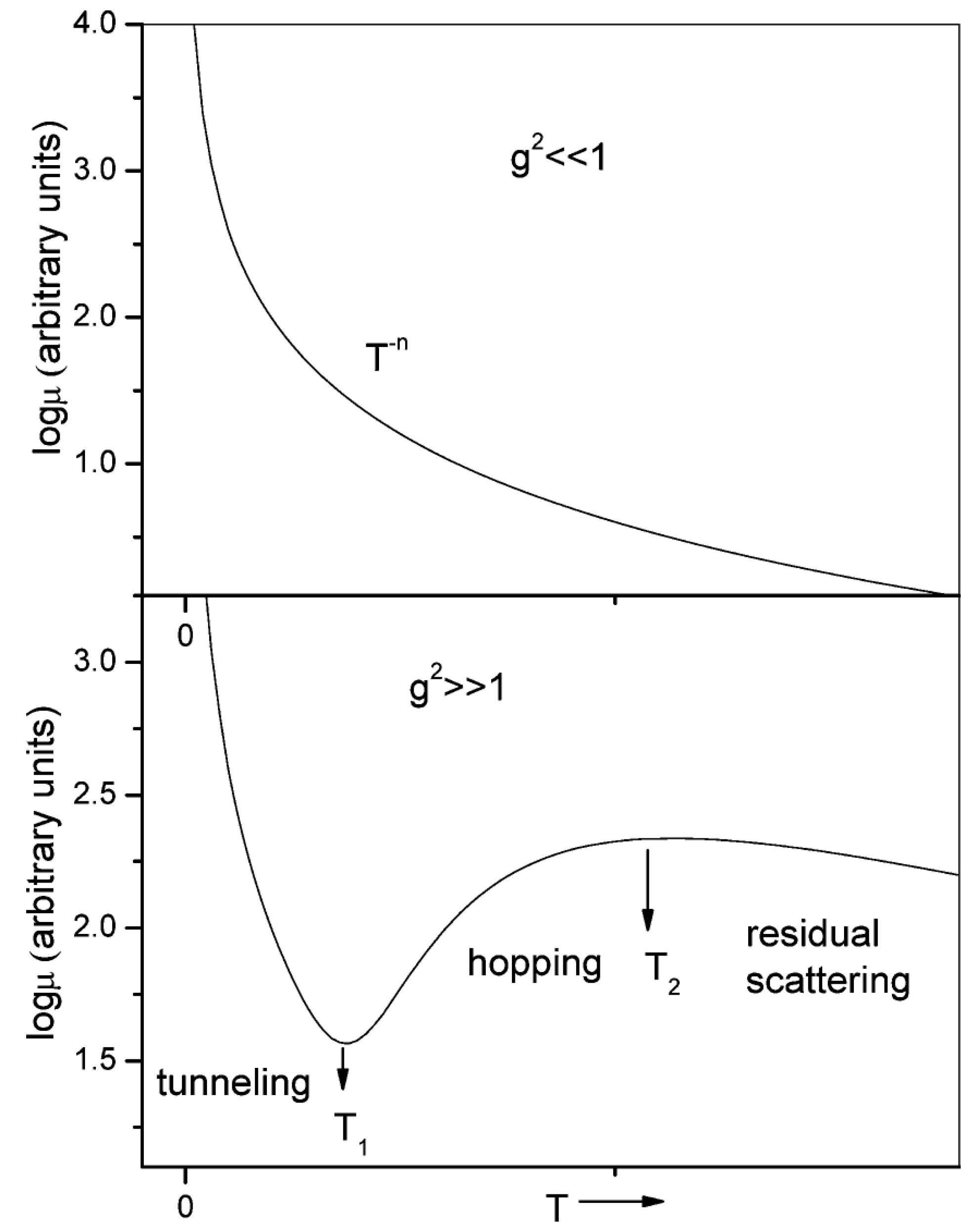
3.2.2. Charge Transport in Organic Molecules

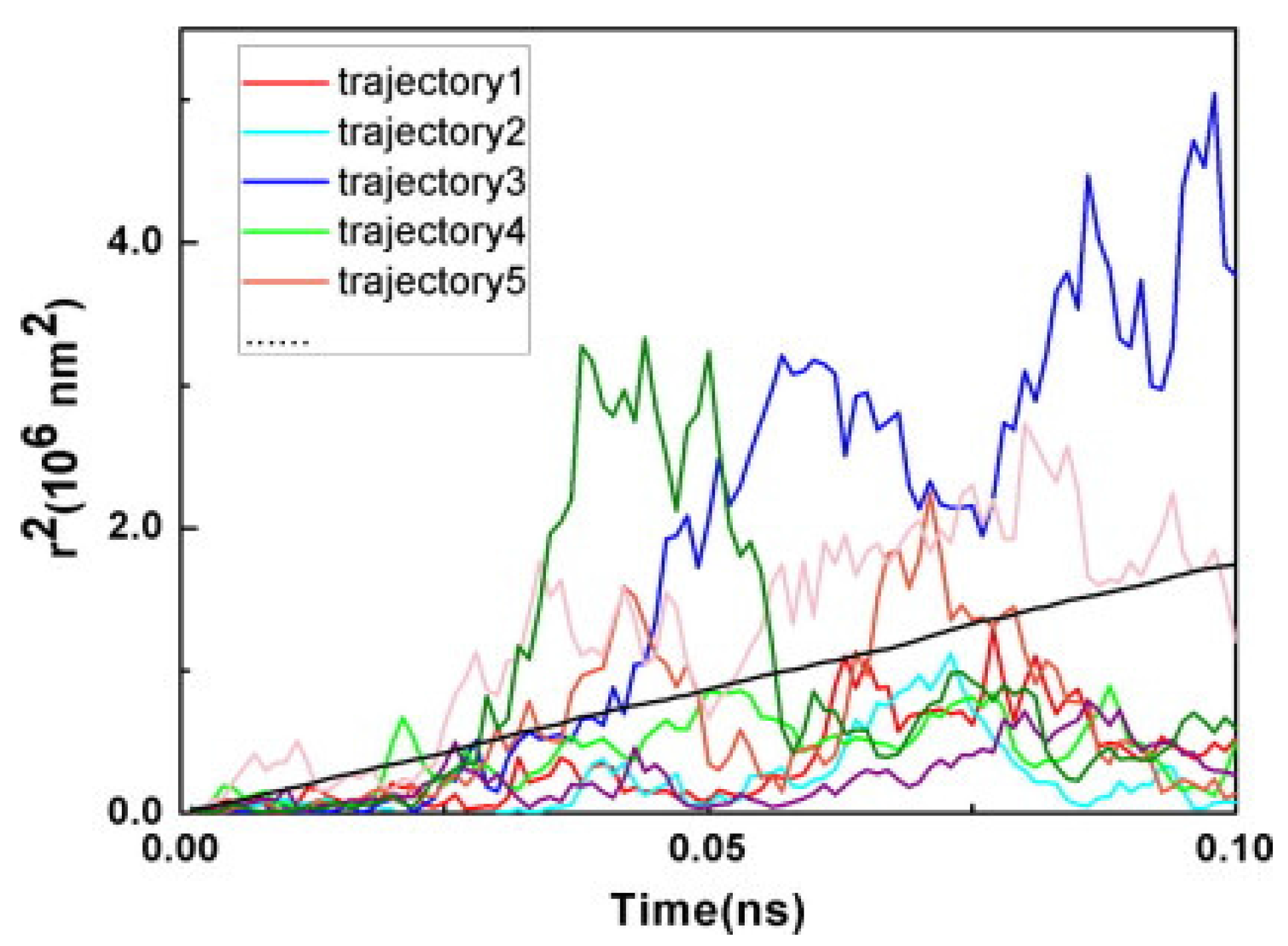
3.3. Photoinduced Charge Separation in Organic Solar Cells

4. Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blankenship, R.E. Molecular Mechanisms of Photosynthesis; World Scientific: London, UK, 2002. [Google Scholar]
- Niyogi, K.K. Photoprotection Revisited: Genetic and Molecular Approaches. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1999, 50, 333–359. [Google Scholar] [CrossRef] [PubMed]
- Ruban, A.V.; Johnson, M.P.; Duffy, C.D. The photoprotective molecular switch in the photosystem II antenna. Biochim. Biophys. Acta 2002, 1817, 167–181. [Google Scholar] [CrossRef] [PubMed]
- Jonas, D.M. Two-Dimensional femtosecond spectroscopy. Annu. Rev. Phys. Chem. 2003, 54, 425–463. [Google Scholar] [CrossRef] [PubMed]
- Brixner, T.; Mancal, T.; Stiopkin, I.V.; Fleming, G.R. Phase-stabilized two-dimensional electronic spectroscopy. J. Chem. Phys. 2004, 121, 4221–4236. [Google Scholar] [CrossRef] [PubMed]
- Brixner, T.; Stenger, J.; Vaswani, H.M.; Cho, M.; Blankenship, R.E.; Fleming, G.R. Two-dimensional spectroscopy of electronic couplings in photosynthesis. Nature 2005, 434, 625–628. [Google Scholar] [CrossRef] [PubMed]
- Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.K.; Mancal, T.; Chung, Y.C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786. [Google Scholar] [CrossRef] [PubMed]
- Collini, E.; Wong, C.Y.; Wilk, K.E.; Curmi, P.M.G.; Brumer, P.; Scholes, G.D. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 2010, 463, 644–647. [Google Scholar] [CrossRef] [PubMed]
- Panitchayangkoon, G.; Hayes, D.; Fransted, K.A.; Caram, J.R.; Harel, E.; Wen, J.Z.; Blankenship, R.E.; Engel, G.S. Long lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl. Acad. Sci. USA 2010, 107, 12766–12770. [Google Scholar] [CrossRef] [PubMed]
- Nagy, A.; Prokhorenko, V.; Miller, R.J. Do we live in a quantum world? Advances in multidimensional coherent spectroscopies refine our understanding of quantum coherences and structural dynamics of biological systems. Curr. Opin. Struct. Biol. 2006, 16, 654–663. [Google Scholar] [PubMed]
- Prezhdo, O.V.; Rossky, P.J. Relationship between quantum docoherence times and solvation dynamics in condensed phase chemical systems. Phys. Rev. Lett. 1998, 81, 5294–5297. [Google Scholar] [CrossRef]
- Calhoun, T.R.; Ginsberg, N.S.; Schlau-Cohen, G.S.; Cheng, Y.C.; Ballottari, M.; Bassi, R.; Fleming, G.R. Quantum coherence enabled determination of the energy landscape in light harvesting complex II. J. Phys. Chem. B 2009, 113, 16291–16295. [Google Scholar] [CrossRef] [PubMed]
- Collini, E.; Scholes, G.D. Electronic and vibrational coherences in resonance energy transfer along MEH-PPV chains at room temperature. J. Phys. Chem. A 2009, 113, 4223–4241. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.S.; Silbey, R.J. Optimization of exciton trapping in energy transfer processes. J. Phys. Chem. A 2009, 113, 13825–13838. [Google Scholar] [CrossRef] [PubMed]
- Leegwater, J.A.; Durrant, J.R.; King, D.R. Exciton equilibrium induced by phonons: Theory and application to PS II reaction centers. J. Phys. Chem. B 1997, 101, 7205–7210. [Google Scholar] [CrossRef]
- Tretiak, S.; Middleton, C.; Chernyak, V.Y.; Mukamel, S. Bacteriochlorophyll and carotenoid excitonic coupling in the LH2 system of purple bacteria. J. Phys. Chem. B 2000, 104, 9540–9553. [Google Scholar] [CrossRef]
- Abramavicius, D.; Palmieri, B.; Voronine, D.V.; Sanda, F.; Mukamel, S. Coherent multidimensional optimal spectroscopy of excitons in molecular aggregates: Quasiparticle versus supermolecule perspectives. Chem. Rev. 2009, 109, 2350–2408. [Google Scholar] [CrossRef] [PubMed]
- Cho, M.; Vaswani, H.M.; Brixner, T.; Stenger, J.; Fleming, G.R. Exciton analysis in 2D electronic spectroscopy. J. Phys. Chem. B 2005, 109, 10542–10556. [Google Scholar] [CrossRef] [PubMed]
- Adolphs, J.; Renger, T. How proteins trigger excitation energy transfer in the FMO complex of green sulfur bacteria. Biophys. J. 2006, 91, 2778–2797. [Google Scholar] [CrossRef] [PubMed]
- Sener, M.K.; Park, S.; Lu, D.; Damjanovic, A.; Ritz, T.; Fromme, P.; Schulten, K. Excitation migration in trimeric cyanobacterial photosystem I. J. Chem. Phys. 2004, 120, 11183–11195. [Google Scholar] [CrossRef] [PubMed]
- Cogdell, R.J.; Gall, A.; Köhler, J. The architecture and function of the light-harvesting apparatus of purple bacteria: From single molecules to in vivo membranes. Q. Rev. Biophys. 2006, 39, 227–324. [Google Scholar] [CrossRef] [PubMed]
- Hohmann-Marriott, M.F.; Blankenship, R.E. Evolution of photosynthesis. Annu. Rev. Plant Biol. 2011, 62, 515–548. [Google Scholar] [CrossRef] [PubMed]
- Strümpfer, J.; Sener, M.; Schulten, K. How Quantum Coherence Assists Photosynthetic Light Harvesting. J. Phys. Chem. Lett. 2012, 3, 536–542. [Google Scholar] [CrossRef] [PubMed]
- Mar, T.; Govindjee; Singhal, G.S.; Merkelo, H. Lifetime of the Excited State in vivo. Biophys. J. 1972, 12, 797–808. [Google Scholar] [CrossRef]
- Tanimura, Y. Stochastic Liouville, Langevin, Fokker–Planck, and Master Equation Approaches to Quantum Dissipative Systems. J. Phys. Soc. Jpn. 2006, 75. [Google Scholar] [CrossRef]
- Ishizaki, A.; Fleming, G.R. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 17255–17260. [Google Scholar] [CrossRef] [PubMed]
- Strumpfer, J.; Schulten, K. Light harvesting complex II B850 excitation dynamics. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef] [PubMed]
- Strumpfer, J.; Schulten, K. The effect of correlated bath fluctuations on exciton transfer. J. Chem. Phys. 2011, 134. [Google Scholar] [CrossRef] [PubMed]
- Strumpfer, J.; Schulten, K. Open Quantum Dynamics Calculations with the Hierarchy Equations of Motion on Parallel Computers. J. Chem. Theory Comput. 2012, 8, 2808–2816. [Google Scholar] [CrossRef] [PubMed]
- Strumpfer, J.; Schulten, K. Excited state dynamics in photosynthetic reaction center and light harvesting complex 1. J. Chem. Phys. 2012, 137. [Google Scholar] [CrossRef] [PubMed]
- Kreisbeck, C.; Kramer, T.; Rodríguez, M.; Hein, B. HighPerformance Solution of Hierarchical Equations of Motion for Studying Energy Transfer in Light-Harvesting Complexes. J. Chem. Theory Comput. 2011, 7, 2166–2174. [Google Scholar] [CrossRef] [Green Version]
- Kreisbeck, C.; Kramer, T. Long-Lived Electronic Coherence in Dissipative Exciton Dynamics of Light-Harvesting Complexes. J. Phys. Chem. Lett. 2012, 3, 2828–2833. [Google Scholar] [CrossRef]
- Kreisbeck, C.; Kramer, T.; Aspuru-Guzik, A. Scalable High-Performance Algorithm for the Simulation of Exciton Dynamics. Application to the Light-Harvesting Complex II in the Presence of Resonant Vibrational Modes. J. Chem. Theory Comput. 2014, 10, 4045–4054. [Google Scholar]
- Shi, Q.; Chen, L.; Nan, G.; Xu, R.; Yan, Y. Efficient hierarchical Liouville space propagator to quantum dissipative dynamics. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef]
- Yeh, S.-H.; Zhu, J.; Kais, S. Population and coherence dynamics in light harvesting complex II (LH2). J. Chem. Phys. 2012, 137. [Google Scholar] [CrossRef] [PubMed]
- Smyth, C.; Oblinskyb, D.G.; Scholes, G.D. B800-B850 coherence correlates with energy transfer rates in the LH2 complex of photosynthetic purple bacteria. Phys. Chem. Chem. Phys. 2015. [Google Scholar] [CrossRef] [PubMed]
- Yeh, S.-H.; Kais, S. Simulated two-dimensional electronic spectroscopy of the eight-bacteriochlorophyll FMO complex. J. Chem. Phys. 2014, 141. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Xu, R.X.; Yan, Y.J. Communication: Pade´ spectrum decomposition of Fermi function and Bose function. J. Chem. Phys. 2010, 133. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Luo, M.; Jiang, F.; Xu, R.X.; Yan, Y.J. Pade´ spectrum decompositions of quantum distribution functions and optimal hierarchical equations of motion construction for quantum open systems. J. Chem. Phys. 2011, 134. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.J.; Xu, J.; Hu, J.; Xu, R.X.; Yan, Y.J. Optimized hierarchical equations of motion theory for Drude dissipation and efficient implementation to nonlinear spectroscopies. J. Chem. Phys. 2011, 135. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.J.; Xu, R.X.; Yan, Y.J. Optimizing hierarchical equations of motion for quantum dissipation and quantifying quantum bath effects on quantum transfer mechanisms. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.A.; Yang, F.; Liu, Y.; Shao, J.S. Hierarchical approach based on stochastic decoupling to dissipative systems. Chem. Phys. Lett. 2004, 395, 216–221. [Google Scholar] [CrossRef]
- Zhou, Y.; Yan, Y.; Shao, J.S. Stochastic simulation of quantum dissipative dynamics. Europhys. Lett. 2005, 72, 334–340. [Google Scholar] [CrossRef]
- Moix, J.M.; Cao, J. A hybrid stochastic hierarchy equations of motion approach to treat the low temperature dynamics of non-Markovian open quantum systems. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef] [PubMed]
- Nalbach, P.; Braun, D.; Thorwart, M. Exciton transfer dynamics and quantumness of energy transfer in the Fenna-Matthews-Olson complex. Phys. Rev. E 2011, 84. [Google Scholar] [CrossRef]
- Nalbach, P.; Mujica-Martinez, C.A.; Thorwart, M. Vibronically coherent speed-up of the excitation energy transfer in the Fenna-Matthews-Olson complex. Phys. Rev. E 2015, 91. [Google Scholar] [CrossRef]
- Ye, J.; Sun, K.; Zhao, Y.; Yu, Y.; Lee, C.K.; Cao, J. Excitonic energy transfer in light-harvesting complexes in purple bacteria. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Ye, J.; Zhao, Y. Path induced coherent energy transfer in light-harvesting complexes in purple bacteria. J. Chem. Phys. 2014, 141. [Google Scholar] [CrossRef] [PubMed]
- Huynh, T.D.; Sun, K.; Gelin, M.F.; Zhao, Y. Polaron dynamics in two-dimensional photon-echo spectroscopy of molecular rings. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Gelin, M.F.; Chernyak, V.Y.; Zhao, Y. Davydov ansatz as an efficient tool for the simulation of nonlinear optical response of molecular aggregates. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Gelin, M.F.; Domcke, W.; Zhao, Y. Theory of femtosecond coherent double-pump single-molecule spectroscopy: Application to light harvesting complexes. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Shi, W.; Ye, J.; Wang, X.; Hirao, H.; Zhao, Y. QM/MM Modeling of Environmental Effects on Electronic Transitions of the FMO Complex. J. Phys. Chem. B 2013, 117, 3488–3495. [Google Scholar] [PubMed]
- Olson, J.M.; Ormerod, J.G.; Amesz, J.; Stackebrandt, E.; Trüper, H.G. Green Photosynthetic Bacteria; Plenum Press: New York, NY, USA, 1987. [Google Scholar]
- Blankenship, R.E.; Michael, T.M.; Carl, E.B. Anoxygenic Photosynthetic Bacteria; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Kovacs, S.; Bricker, W.P.; Niedzwiedzki, D.M.; Colletti, P.F.; Lo, C.S. Computational determination of the pigment binding motif in the chlorosome protein of green sulfur bacteria. Photosynth. Res. 2013, 118, 231–247. [Google Scholar] [CrossRef] [PubMed]
- Psencík, J.; Ikonen, T.P.; Laurinmäki, P.; Merckel, M.C.; Butcher, S.J.; Serimaa, R.E.; Tuma, R. Lamellar organization of pigments in chlorosomes, the light harvesting complexes of green photosynthetic bacteria. Biophys. J. 2004, 87, 1165–1172. [Google Scholar]
- Ganapathy, S.; Oostergetel, G.T.; Wawrzyniak, P.K.; Reus, M.; Chew, A.G.M.; Buda, F.; Boekema, E.J.; Bryant, D.A.; Holzwarth, A.R.; de-Groot, H.J.M. Alternating syn-anti bacteriochlorophylls form concentric helical nanotubes in chlorosomes. Proc. Natl. Acad. Sci. USA 2009, 106, 8525–8530. [Google Scholar]
- Tian, Y.X.; Camacho, R.; Thomsson, D.; Reus, M.; Holzwarth, A.R.; Scheblykin, I.G. Organization of bacteriochlorophylls in individual chlorosomes from Chlorobaculum tepidum studied by 2-dimensional polarization fluorescence microscopy. J. Am. Chem. Soc. 2011, 133, 17192–17199. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.C.; Khin, Y.; Huang, S.J.; Yang, Y.S.; Hou, T.Y.; Cheng, Y.C.; Chen, H.M.; Chin, Y.Y.; Chen, C.T.; Lin, H.J.; et al. Probing Spatial Organization of Bacteriochlorophyll c by Solid-State Nuclear Magnetic Resonance. Biochemistry 2014, 54, 5515–5525. [Google Scholar] [CrossRef] [PubMed]
- Klugkist, J.A.; Knoester, J. Optical Properties of Helical Cylindrical Molecular Aggregates: The Homogeneous Limit. J. Phys. Chem. B 2002, 106, 11474–11486. [Google Scholar]
- Didraga, C.; Knoester, J. Absorption and dichroism spectra of cylindrical J aggregates and chlorosomes of green bacteria. J. Lumin. 2003, 102, 60–66. [Google Scholar] [CrossRef]
- Didraga, C.; Knoester, J. Optical spectra and localization of excitons in inhomogeneous helical cylindrical aggregates. J. Chem. Phys. 2004, 121. [Google Scholar] [CrossRef] [PubMed]
- Furumaki, S.; Vacha, F.; Habuchi, S.; Tsukatani, Y.; Bryant, D.A.; Vacha, M. Absorption linear dichroism measured directly on a single light-harvesting system: The role of disorder in chlorosomes of green photosynthetic bacteria. J. Am. Chem. Soc. 2011, 133, 6703–6710. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenko, V.I.; Steensgaard, D.B.; Holzwarth, A.R. Exciton dynamics in the chlorosomal antennae of the green bacteria Chloroflexus aurantiacus and Chlorobium tepidum. Biophys. J. 2000, 79, 2105–2120. [Google Scholar] [CrossRef]
- Prokhorenko, V.I.; Steensgaard, D.B.; Holzwarth, A.R. Exciton theory for supramolecular chlorosomal aggregates: 1. Aggregate size dependence of the linear spectra. Biophys. J. 2003, 85, 3173–3186. [Google Scholar]
- Martiskainen, J.; Linnanto, J.M.; Kananavičius, R.; Lehtovuori, V.; Tommola, J.K. Excitation energy transfer in isolated chlorosomes from Chloroflexus aurantiacus. Chem. Phys. Lett. 2009, 477, 216–220. [Google Scholar] [CrossRef]
- Martiskainen, J.; Linnanto, J.M.; Aumanen, V.; Myllyperkiö, P.; Tommola, J.K. Excitation energy transfer in isolated chlorosomes from Chlorobaculum tepidum and Prosthecochloris aestuarii. Photochem. Photobiol. 2012, 88, 675–683. [Google Scholar] [CrossRef] [PubMed]
- Linnanto, J.M.; Korppi-Tommola, J.E.I. Exciton description of chlorosome to baseplate excitation energy transfer in filamentous anoxygenic phototrophs and green sulfur bacteria. J. Phys. Chem. B 2013, 117, 11144–11161. [Google Scholar] [CrossRef] [PubMed]
- Diers, J.R.; Zhu, Y.; Blankenship, R.E.; Bocian, D.F. Qy-excitation resonance Raman spectra of chlorophyll a and bacteriochlorophyll c/d aggregates. Effects of peripheral substituents on the low-frequency vibrational characteristics. J. Phys. Chem. 1996, 100, 8573–8579. [Google Scholar] [PubMed]
- Nerine, J.C.; Mei, D.; Holzwarth, A.R.; Richard, A.M. Near-Infrared Resonance Raman Spectra of Chlorosomes: Probing Nuclear Coupling in Electronic Energy Transfer. J. Phys. Chem. 1996, 100, 4662–4671. [Google Scholar]
- Banchi, L.; Costagliola, G.; Ishizaki, A.; Giorda, P. An analytical continuation approach for evaluating emission lineshapes of molecular aggregates and the adequacy of multichromophoric Förster theory. J. Chem. Phys. 2013, 138. [Google Scholar] [CrossRef]
- Ma, J.; Cao, J. Förster resonance energy transfer, absorption and emission spectra in multichromophoric systems. I. Full cumulant expansions and system-bath entanglement. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef]
- Ma, J.; Moix, J.; Cao, J. Förster resonance energy transfer, absorption and emission spectra in multichromophoric systems. II. Hybrid cumulant expansion. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef]
- Moix, J.; Ma, J.; Cao, J. Förster resonance energy transfer, absorption and emission spectra in multichromophoric systems. III. Exact stochastic path integral evaluation. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef]
- Abramavicius, V.; Abramavicius, D. Excitation transfer pathways in excitonic aggregates revealed by the stochastic Schrödinger equation. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Cheng, Y.-C. On the accuracy of coherent modified Redfield theory in simulating excitation energy transfer dynamics. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef] [PubMed]
- Hwang-Fu, Y.-H.; Chen, W.; Cheng, Y.-C. A coherent modified Redfield theory for excitation energy transfer in molecular aggregates. Chem. Phys. 2015, 447, 46–53. [Google Scholar] [CrossRef]
- Mančal, T.; Balevičius, V., Jr.; Valkunas, L. Decoherence in Weakly Coupled Excitonic Complexes. J. Phys. Chem. A 2011, 115, 3845–3858. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Liu, H.; Shi, Q. A new method to account for the difference between classical and quantum baths in quantum dissipative dynamics. New J. Phys. 2013, 15. [Google Scholar] [CrossRef]
- Kosztin, I.; Kleinekatho, U.; Schulten, K.; Damjanović, A. Excitons in a photosynthetic light-harvesting system: A combined molecular dynamics, quantum chemistry, and polaron model study. Phys. Rev. E 2002, 65. [Google Scholar] [CrossRef]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Nitzan, A. Chemical Dynamics in Condensed Phases: Relaxation, Transfer, and Reactions in Condensed Molecular Systems; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- May, V.; Oliver, K. Charge and Energy Transfer Dynamics in Molecular Systems; Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar]
- Haken, H.; Strobl, G. An exactly solvable model for coherent and incoherent exciton motion. Z. Phys. 1973, 262, 135–148. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Guzik, A.A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003–033014. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Guzik, A.A. Role of quantum coherence and environmental fluctuations in chromophoric energy transport. J. Phys. Chem. B 2009, 113, 9942–9947. [Google Scholar] [CrossRef] [PubMed]
- Ritz, T.; Park, S.; Schulten, K. Kinetics of excitation migration and trapping in the photosynthetic unit of purple bacteria. J. Phys. Chem. B 2001, 105, 8259–8267. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F. Dephasing-assisted transport: Quantum networks and biomolecules. New J. Phys. 2008, 10, 113019–113032. [Google Scholar] [CrossRef]
- Cao, J.; Silbey, R.J. Generic schemes for singlemolecule kinetics. 1: Self-consistent pathway solutions for renewal processes. J. Phys. Chem. B 2008, 112, 12867–12880. [Google Scholar] [PubMed]
- Moerner, W.E. A dozen years of single-molecule spectroscopy in physics, chemistry, and biophysics. J. Phys. Chem. B 2002, 106, 910–927. [Google Scholar] [CrossRef]
- Brinks, D.; Hildner, R.; van Dijk, E.M.H.P.; Stefani, F.D.; Nieder, J.B.; Hernando, J.; van Hulst, N.F. Ultrafast dynamics of single molecules. Chem. Soc. Rev. 2014, 43, 2476–2491. [Google Scholar] [CrossRef] [PubMed]
- Orrit, M.; Ha, T.; Sandoghdar, V. Single-molecule optical spectroscopy. Chem. Soc. Rev. 2014, 43. [Google Scholar] [CrossRef] [PubMed]
- Schleifenbaum, F.; Blum, C.; Brecht, M.; Meixner, A.J. Single-Molecule Spectroscopy. In Handbook of Spectroscopy, 2nd ed.; Gauglitz, G., Moore, D.S., Eds.; Wiley-VCH: Weinheim, Germany, 2014; Volume 4, pp. 823–875. [Google Scholar]
- Moerner, W.; Kador, L. Optical detection and spectroscopy of single molecules in a solid. Phys. Rev. Lett. 1989, 62, 2535–2538. [Google Scholar] [CrossRef] [PubMed]
- Moerner, W.E.; Ambrose, W.P. Comment on “Single pentacene molecules detected by fluorescence excitation in a p-terphenyl crystal”. Phys. Rev. Lett. 1991, 66, 1376. [Google Scholar] [CrossRef]
- Van Oijen, A.M. Unraveling the Electronic Structure of Individual Photosynthetic Pigment-Protein Complexes. Science 1999, 285, 400–402. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.; Silbey, R.J. Theory of single molecule line shapes of multichromophoric macromolecules. J. Chem. Phys. 2003, 118, 9312–9323. [Google Scholar] [CrossRef]
- Jang, S.; Silbey, R.J. Single complex line shapes of the B850 band of LH2. J. Chem. Phys. 2003, 118, 9324–9336. [Google Scholar] [CrossRef]
- Pieper, J.; Voigt, J.; Renger, G.; Small, G. Analysis of phonon structure in line-narrowed optical spectra. Chem. Phys. Lett. 1999, 310, 296–302. [Google Scholar] [CrossRef]
- Brecht, M.; Studier, H.; Radics, V.; Nieder, J.B.; Bittl, R. Spectral diffusion induced by proton dynamics in pigment-protein complexes. J. Am. Chem. Soc. 2008, 130, 17487–17493. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, C.; Aartsma, T.; Michel, H.; Köhler, J. Direct observation of tiers in the energy landscape of a chromoprotein: A single-molecule study. Proc. Natl. Acad. Sci. USA 2003, 100, 15534–15538. [Google Scholar] [CrossRef] [PubMed]
- Ha, T.; Enderle, T.; Chemla, D.; Selvin, P.; Weiss, S. Single Molecule Dynamics Studied by Polarization Modulation. Phys. Rev. Lett. 1996, 77, 3979–3982. [Google Scholar] [CrossRef] [PubMed]
- Jares-Erijman, E.A.; Jovin, T.M. FRET imaging. Nat. Biotechnol. 2003, 21, 1387–1395. [Google Scholar] [CrossRef] [PubMed]
- Meixner, A.J.; Weber, M.A. Single molecule spectral dynamics at room temperature. J. Lumin. 2000, 86, 181–187. [Google Scholar] [CrossRef]
- Vosgröne, T.; Meixner, A.J. Surface- and resonance-enhanced micro-raman spectroscopy of xanthene dyes: From the ensemble to single molecules. ChemPhysChem 2005, 6, 154–163. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Tabaei, S.R.; Thomsson, D.; Mirzov, O.; Larsson, P.O.; Scheblykin, I.G. Fluorescence blinking, exciton dynamics, and energy transfer domains in single conjugated polymer chains. J. Am. Chem. Soc. 2008, 130, 7042–7051. [Google Scholar] [CrossRef] [PubMed]
- Brinks, D.; Stefani, F.D.; Kulzer, F.; Hildner, R.; Taminiau, T.H.; Avlasevich, Y.; Müllen, K.; van Hulst, N.F. Visualizing and controlling vibrational wave packets of single molecules. Nature 2010, 465, 905–908. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Cheng, Y.C.; Fleming, G.R. Coherence dynamics in photosynthesis: Protein protection of excitonic coherence. Science 2007, 316, 1462–1465. [Google Scholar] [CrossRef] [PubMed]
- Collini, E.; Scholes, G.D. Coherent interchain energy migration in a conjugated polymer at room temperature. Science 2009, 323, 369–373. [Google Scholar] [CrossRef] [PubMed]
- Gaab, K.; Bardeen, C. The effects of connectivity, coherence, and trapping on energy transfer in simple light-harvesting systems studied using the Haken-Strobl model with diagonal disorder. J. Chem. Phys. 2004, 121, 7813–7820. [Google Scholar] [CrossRef] [PubMed]
- Olaya, C.A.; Lee, C.F.; Olsen, F.F.; Johnson, N.F. Efficiency of energy transfer in a light harvesting system under quantum coherence. Phys. Rev. B 2008, 78, 085115–085121. [Google Scholar] [CrossRef]
- Mohseni, M.; Rebentrosi, P.; Lloyd, S.; Guzik, A.A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 2008, 129, 174106–174114. [Google Scholar] [CrossRef] [PubMed]
- Caruso, F.; Chin, A.W.; Datta, A.; Huelga, S.F.; Plenio, M.B. Highly efficient energy excitation transfer in light harvesting complexes: The fundamental role of noise-assisted transport. J. Chem. Phys. 2009, 131, 105106–105120. [Google Scholar] [CrossRef] [Green Version]
- Xiong, S.J.; Chen, L.P.; Zhao, Y. Dephasing and dissipation in a source drain model of light harveting systems. Chem. Phys. Chem. 2014, 13. [Google Scholar] [CrossRef]
- Misra, B.; Sudarshan, E.C.G. The Zeno’s paradox in quantum theory. J. Math. Phys. 1977, 18, 756–763. [Google Scholar] [CrossRef]
- Wu, J.L.; Liu, F.; Shen, Y.; Cao, J.S.; Silbey, R.J. Efficient energy transfer in light-harvesting systems, I: Optimal temperature, reorganization energy and spatial-temperal correlations. New J. Phys. 2010, 12, 105012–105028. [Google Scholar] [CrossRef]
- Ishizaki, A.; Fleming, G.R. Unified treatement of quantum coherent and incoherent hopping dynamics in electronic energy transfer: Reduced hierarchy equation approach. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef]
- Ben-Shem, A.; Frolow, F.; Nelson, N. Evolution of photosystem I from symmetry through pseudosymmetry to asymmetry. FEBS. Lett. 2004, 564, 274–280. [Google Scholar] [CrossRef]
- Tronrud, D.E.; Wen, J.; Gay, L.; Blankenship, R.E. The structural basis for the difference in absorbance spectra for the FMO antenna protein from various green sulfur bacteria. Photosynth. Res. 2009, 100, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Moix, J.; Wu, J.L.; Huo, P.F.; Coker, D.; Cao, J.S. Efficient energy transfer in light-harvesting systems, III: The influence of the eighth bacteriochlorophyll on the dynamics and efficiency in FMO. J. Phys. Chem. Lett. 2011, 2, 3045–3052. [Google Scholar] [CrossRef]
- Huelga, S.F.; Plenio, M.B. Vibrations, quanta and biology. Contemp. Phys. 2013, 54, 181–207. [Google Scholar] [CrossRef]
- Van Amerongen, H.; Valkunas, L.; van Grondelle, R. Photosynthetic Excitons; World Science: Singapore, Singapore, 2000. [Google Scholar]
- Womick, J.M.; Moran, A.M. Exciton coherence and energy transport in the light-harvesting dimers of allophycocyanin. J. Phys. Chem. B 2009, 113, 15747–15759. [Google Scholar] [CrossRef] [PubMed]
- Womick, J.M.; Moran, A.M. Nature of excited states and relaxation mechanisms in Cphycocyanin. J. Phys. Chem. B 2009, 113, 15771–15782. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, A.; Fleming, G.R. On the adequacy of the Redfield equation and related approaches to the study of quantum dynamics in electronic energy transfer. J. Chem. Phys. 2009, 130, 234110–234117. [Google Scholar] [CrossRef] [PubMed]
- Palmieri, B.; Abramavicius, D.; Mukamel, S. Lindblad equations for strongly coupled populations and coherences in photosynthetic complexes. J. Chem. Phys. 2009, 130, 204512–204521. [Google Scholar] [CrossRef] [PubMed]
- Fassioli, F.; Nazir, A.; Olaya-Castro, A. Quantum state tuning of energy transfer in a correlated environment. J. Phys. Chem. Lett. 2010, 1, 2139–2143. [Google Scholar] [CrossRef]
- Sarovar, M.; Ishizaki, A.; Fleming, G.R.; Whaley, K.B. Quantum entanglment in photosynthetic light-harveting complexes. Nat. Phys. 2010, 6, 462–467. [Google Scholar] [CrossRef]
- Jackson, J.A.; Lin, S.; Taguchi, A.K.W.; Williams, J.C.; Allen, J.P.; Woodbury, N.W. Energy transfer in Rhodobacter sphaeroides reaction centers with the initial electron donor oxidized or missing. J. Phys. Chem. B 1997, 101, 5747–5754. [Google Scholar] [CrossRef]
- Liu, Z.F.; Yan, H.C.; Wang, K.B.; Kuang, T.Y.; Zhang, J.P.; Gui, L.L.; An, X.M.; Chang, W.R. Crystal structure ofspinach major light-harvesting complex at 2.72 resolution. Nature 2004, 428, 287–292. [Google Scholar] [PubMed]
- Cheng, Y.C.; Fleming, G.R. Coherence quantum beats in two-dimensional electronic spectroscopy. J. Phys. Chem. A 2008, 112, 4254–4260. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, A.; Calhoun, T.R.; Schlau-Cohen, G.S.; Fleming, G.R. Quantum coherence and its interplay with protein environments in photosynthetic electronic energy transfer. Phys. Chem. Chem. Phys. 2010, 12, 7319–7337. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, A.; Fleming, G.R. Quantum coherence in photosynthetic light harvesting. Annu. Rev. Condens. Matter. Phys. 2012, 3, 333–361. [Google Scholar] [CrossRef]
- Förster, T. Zwischenmolekulare energiewanderungund fluoreszenz. Ann. Phys. 1948, 2, 55–75. [Google Scholar] [CrossRef]
- Redfield, A.G. On the Theory of Relaxation Processes. IBM J. Res. Dev. 1957, 1, 19–31. [Google Scholar] [CrossRef]
- Kimura, A.; Kakitani, T.; Yamato, T. Theory of excitation energy transfer in the intermediate coupling case. II. criterion for intermediate coupling excitation energy transfer mechanism and application to the photosynthetic antenna system. J. Phys. Chem. B 2000, 104, 9276–9287. [Google Scholar] [CrossRef]
- Jang, S.; Cheng, Y.C.; Reichman, D.R.; Eaves, J.D. Theory of coherent resonance energy transfer. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef] [PubMed]
- Kolli, A.; Nazir, A.; Olaya-Castro, A. Electronic excitation dynamics in multichromophoric systems described via a polaron-representation master equation. J. Chem. Phys. 2011, 135. [Google Scholar] [CrossRef] [PubMed]
- Nalbach, P.; Thorwart, M. Multiphonon transitions in the biomolecular energy transfer dynamics. J. Chem. Phys. 2010, 132. [Google Scholar] [CrossRef] [PubMed]
- Huo, P.; Coker, D.F. Iterative linearized density matrix propagation for modeling coherent excitation energy transfer in photosynthetic light harvesting. J. Chem. Phys. 2010, 133. [Google Scholar] [CrossRef] [PubMed]
- Tao, G.; Miller, W.H. Semiclassical description of electronic excitation population transfer in a model photosynthetic system. J. Phys. Chem. Lett. 2010, 1, 891–894. [Google Scholar] [CrossRef]
- Prior, J.; Chin, A.W.; Huelga, S.F.; Plenio, M.B. Efficient simulation of strong system-environment interactions. Phys. Rev. Lett. 2010, 105, 050404–050407. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Luo, B.; Zhao, Y. Dynamics of a one dimensional Holstein polaron with the Davydov Ansatze. Phys. Rev. B 2010, 82. [Google Scholar] [CrossRef]
- Luo, B.; Ye, J.; Guan, C.B.; Zhao, Y. Validity of time dependent trial states for the Holstein polaron. Phys. Chem. Chem. Phys. 2010, 12. [Google Scholar] [CrossRef] [PubMed]
- Grover, L.K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 1997, 79, 325–328. [Google Scholar] [CrossRef]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Hoyer, S.; Sarovar, M.; Whaley, K.B. Limits of quantum speedup in photosynthetic light harvesting. New. J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Dostál, J.; Vácha, F.; Pšenčík, J.; Zigmantas, D. 2D Electronic Spectroscopy Reveals Excitonic Structure in the Baseplate of a Chlorosome. J. Phys. Chem. Lett. 2014, 5, 1743–1747. [Google Scholar] [CrossRef] [PubMed]
- Scholes, G.D.; Fleming, G.R.; Olaya-Castro, A.; van Grondelle, R. Lessons from nature about solar light harvesting. Nat. Chem. 2011, 3, 763–774. [Google Scholar] [CrossRef] [PubMed]
- Demmig, B.; Winter, K.; Kruger, A.; Czygan, F.C. Photoinhibition and Zeaxanthin formation in intact leaves: A possible role of the Xanthophyll cycle in the dissipation of excess light energy. Plant Physiol. 1987, 84, 218–224. [Google Scholar] [CrossRef] [PubMed]
- Demmig, B.; Winter, K.; Kruger, A.; Czygan, F.C. Light response of CO2 assimilation, dissipation of excess excitation energy, and Zeaxanthin content of sun and shade leaves. Plant. Physiol. 1989, 90, 881–886. [Google Scholar] [CrossRef]
- Horton, P.; Ruban, A.V.; Rees, D.; Pascal, A.A.; Noctor, G.; Young, A.J. Control of the light harvesting function of chloroplast membranes by aggregation of the LHCII chlorophyll-protein complex. FEBS Lett. 1991, 292, 1–4. [Google Scholar]
- Ruban, A.V.; Phillip, D.; Young, A.J.; Horton, P. Carotenoid dependent oligomerization of the major chlorophyll a/b light harvesting complex of photosystem II or plants. Biochemistry 1997, 36, 7855–7859. [Google Scholar] [CrossRef] [PubMed]
- Holzwarth, A.R.; Miloslavina, Y.; Nilkens, M.; Jahns, P. Identification of two quenching sites active in the regulation of photosynthetic light harvesting studied by time resolved fluorescence. Chem. Phys. Lett. 2009, 483, 262–267. [Google Scholar] [CrossRef]
- Moya, I.; Silvestri, M.; Vallon, O.; Cinque, G.; Bassi, R. Time-resolved fluorescence analysis of the photosystem II antenna proteins in detergent micelles and liposomes. Biochemistry 2001, 40, 12552–12561. [Google Scholar] [CrossRef] [PubMed]
- Pascal, A.A.; Liu, Z.F.; Broess, K.; van Oort, B.; van Amerongen, H.; Wang, C.; Horton, P.; Robert, B.; Chang, W.; Ruban, A. Molecular basis of photoprotection and control of photosynthetic light harvesting. Nature 2005, 436, 134–137. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.J.; Barber, J.; Zhao, Y. Role of formation of statistical aggregates in chlorophyll fluorescence concentration quenching. J. Phys. Chem. B 2013, 117, 3976–3982. [Google Scholar] [CrossRef] [PubMed]
- Beddard, G.S.; Porter, G. Concentration quenching in chlorophyll. Nature 1976, 260, 366–367. [Google Scholar] [CrossRef]
- Knox, R.S. Spectral effects of exciton splitting in statistical pairs. J. Phys. Chem. 1994, 98, 7270–7273. [Google Scholar] [CrossRef]
- Miloslavina, Y.; Wehner, A.; Wientjes, E.; Reus, M.; Lambrev, P.; Garab, G.; Groce, R.; Holzwarth, A.R. Far-red fluorescence a direct spectroscopic marker for LHCII oligomer formation in non-photochemical quenching. FEBS Lett. 2008, 582, 3625–3631. [Google Scholar] [CrossRef] [PubMed]
- Muller, M.G.; Lambrev, P.; Reus, M.; Wientjes, E.; Croce, R.; Holzwarth, A.R. Singlet energy dissipation in the photosystem II light harvesting complex does not involve enrgy transfer to carotenoids. Chem. Phys. Chem. 2010, 11, 1289–1296. [Google Scholar] [PubMed]
- Holt, N.E.; Zigmantas, D.; Valkunas, L.; Li, X.P.; Niyogi, K.K.; Fleming, G. Carotenoid cation formation and the regulation of photosynthetic light harvesting. Science 2005, 307, 433–436. [Google Scholar] [CrossRef] [PubMed]
- Ahn, T.K.; Avenson, T.J.; Ballottari, M.; Cheng, Y.C.; Niyogi, K.K.; Bassi, R.; Fleming, G.R. Architecture of a charge transfer state regulating light harvesting in a plant antenna protein. Science 2008, 320, 794–797. [Google Scholar] [CrossRef] [PubMed]
- Krüger, T.P.J.; Ilioaia, C.; Johnson, M.P.; Ruban, A.V.; Papagiannakis, E.; Horton, P.; van Grondelle, R. Controlled disorder in plant light harvesting complex II explains its photoprotective role. Biophys. J. 2012, 102, 2669–2676. [Google Scholar] [CrossRef] [PubMed]
- Pandit, A.; Reus, M.; Morosinotto, T.; Bassi, R.; Holzwarth, A.R.; de Groot, H.J.M. An NMR comparison of the light harvesting complex II (LHCII) in active and photoprotective states reveals subtle changes in the chlorophyll a ground state electronic structures. Biochim. Biophys. Acta 2013, 1827, 738–744. [Google Scholar] [CrossRef] [PubMed]
- Nelson, T.; Fernandez-Alberti, S.; Chernyak, V.; Roitberg, A.E.; Tretiak, S. Nonadiabatic excited-state molecular dynamics modeling of photoinduced dynamics in conjugated molecules. J. Phys. Chem. B 2011, 115, 5402–5414. [Google Scholar] [CrossRef] [PubMed]
- Nelson, T.; Fernandez-Alberti, S.; Roitberg, A.; Tretiak, S. Nonadiabatic excited-state molecular dynamics: Modeling photophysics in organic conjugated materials. Acc. Chem. Res. 2014, 47, 1155–1164. [Google Scholar] [CrossRef] [PubMed]
- Bricker, W.P.; Shenai, P.M.; Ghosh, A.; Liu, Z.; Enriquez, M.G.M.; Lambrev, P.H.; Tan, H.S.; Lo, C.S.; Tretiak, S.; Fernandez-Alberti, S.; Zhao, Y. Non-radiative relaxation of photoexcited chlorophylls: Theoretical and experimental study. Sci. Rep. 2015, in press. [Google Scholar]
- Broess, K.; Trinkunas, G.; van der Wejj-de Wit, C.D.; Dekker, J.P.; van Amerongen, H.; van Hoek, A. Excitation energy transfer and charge separation in photosystem II membranes revisited. Biophys. J. 2006, 91, 3776–3786. [Google Scholar] [CrossRef] [PubMed]
- Caffarri, S.; Broess, K.; Groce, R.; van Amerongen, H. Excitation energy transfer and trapping in higher plant photosystem II complexes with different antenna sizes. Biophys. J. 2011, 100, 2094–2103. [Google Scholar] [CrossRef] [PubMed]
- Valkunas, L.; Trinkunas, G.; Chmeliov, J.; Ruban, A.V. Modeling of exciton quenching in photosystem II. Phys. Chem. Chem. Phys. 2009, 11, 7576–7584. [Google Scholar]
- Valkunas, L.; Chmeliov, J.; Trinkunas, G.; Duffy, C.D.P.; van Grondelle, R.; Ruban, A.V. Excitation migration, quenching, and regulation of photosynthetic light harvesting in photosystem II. J. Phys. Chem. B 2011, 115, 9252–9260. [Google Scholar] [CrossRef] [PubMed]
- Zaks, J.; Amarnathb, K.; Kramer, D.M.; Niyogi, K.K.; Fleming, G.R. A kinetic model of rapidly reversible nonphotochemical quenching. Proc. Natl. Acad. Sci. USA 2012, 109, 15757–15762. [Google Scholar] [CrossRef] [PubMed]
- Deisenhofer, J.; Epp, O.; Miki, K.; Huber, R.; Michel, H. Structure of the protein subunits in the photosynthetic reaction centre of Rhodopseudomonas viridis at 3 Å resolution. Nature 1985, 318, 618–624. [Google Scholar] [CrossRef] [PubMed]
- Jordan, P.; Fromme, P.; Witt, H.T.; Klukas, O.; Saenger, W.; Krauss, N. Three-dimensional structure of cyanobacterial photosystem I at 2.5 Å resolution. Nature 2001, 411, 909–917. [Google Scholar] [CrossRef] [PubMed]
- Ben-Shem, A.; Frolow, F.; Nelson, N. Crystal structure of plant photosystem I. Nature 2003, 426, 630–635. [Google Scholar] [CrossRef] [PubMed]
- Amunts, A.; Drory, O.; Nelson, N. The structure of a plant photosystem I supercomplex at 3.4 Å resolution. Nature 2007, 447, 58–63. [Google Scholar] [PubMed]
- Zouni, A.; Witt, H.; Kern, J.; Fromme, P.; Krauss, N.; Saenger, W.; Orth, P. Crystal structure of photosystem II from Synechococcus elongatus at 3.8 angstrom resolution. Nature 2001, 409, 739–743. [Google Scholar]
- Kamiya, N.; Shen, J.R. Crystal structure of oxygen-evolving photosystem II from Thermosynechococcus vulcanus at 3.7-angstrom resolution. Proc. Natl. Acad. Sci. USA 2003, 100, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, K.N.; Iverson, T.M.; Maghlaoui, K.; Barber, J.; Iwata, S. Architecture of the photosynthetic oxygen-evolving center. Science 2004, 303, 1831–1838. [Google Scholar] [CrossRef] [PubMed]
- Loll, B.; Kern, J.; Saenger, W.; Zouni, A.; Biesiadka, J. Towards complete cofactor arrangement in the 3.0 angstrom resolution structure of photosystem II. Nature 2005, 438, 1040–1044. [Google Scholar]
- Guskov, A.; Kern, J.; Gabdulkhakov, A.; Broser, M.; Zouni, A.; Saenger, W. Cyanobacterial photosystem II at 2.9-angstrom resolution and the role of quinones, lipids, channels and chloride. Nat. Struct. Mol. Biol. 2009, 16, 334–342. [Google Scholar]
- Umena, Y.; Kawakami, K.; Shen, J.R.; Kamiya, N. Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9 angstrom. Nature 2011, 473, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.P.; Feher, G.; Yeates, T.O.; Komiya, H.; Rees, D.C. Structure of the reaction center from Rhodobacter sphaeroides R-26: The protein subunits. Proc. Natl. Acad. Sci. USA 1987, 84, 6162–6166. [Google Scholar] [CrossRef] [PubMed]
- Nogi, T.; Fathir, I.; Kobayashi, M.; Nozawa, T.; Miki, K. Crystal structures of photosynthetic reaction center and high-potential iron-sulfur protein from Thermochromatium tepidum: Thermostability and electron transfer. Proc. Natl. Acad. Sci. USA 2000, 97, 13561–13566. [Google Scholar] [CrossRef] [PubMed]
- Van Brederode, M.E.; van Mourik, F.; van Stokkum, I.H.M.; Jones, M.R.; van Grondelle, R. Multiple pathways for ultrafast transduction of light energy in the photosynthetic reaction center of Rhodobacter sphaeroides. Proc. Natl. Acad. Sci. USA 1999, 96, 2054–2059. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, P.N.; Himmelstoss, M.; Michelmann, J.; Lehner, F.T.; Gardiner, A.T.; Cogdell, R.J.; Zinth, W. Primary reactions in photosynthetic reaction centers of Rhodobacter sphaeroides-Time constants of the initial electron transfer. Chem. Phys. Lett. 2014, 601, 103–109. [Google Scholar] [CrossRef]
- Dominguez, P.N.; Himmelstoss, M.; Michelmann, J.; Lehner, F.T.; Gardiner, A.T.; Cogdell, R.J.; Zinth, W. The Primary Photosynthetic Energy Conversion in Bacterial Reaction Centers-Stepwise Electron Transfer and the Effect of Elevated Exposure Levels. In Ultrafast Phenomena XIX; Yamanouchi, K., et al., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 162, pp. 580–583. [Google Scholar]
- Prokhorenko, V.I.; Holzwarth, A.R. Primary processes and structure of the photosystem II reaction center. A. Photon echo study. J. Phys. Chem. B 2000, 104, 11563–11578. [Google Scholar] [CrossRef]
- Holzwarth, A.R.; Mueller, M.G.; Reus, M.; Nowaczyk, M.; Sander, J.; Roegner, M. Kinetics and mechanism of electron transfer in intact photosystem II and in the isolated reaction center: Pheophytin is the primary electron acceptor. Proc. Natl. Acad. Sci. USA 2006, 103, 6895–6900. [Google Scholar] [CrossRef] [PubMed]
- Myers, J.A.; Lewis, K.L.M.; Fuller, F.D.; Tekavec, P.F.; Yocum, C.F.; Ogilvie, J.P. Two-dimensional electronic spectroscopy of the D1-D2-cyt b559 photosystem II reaction center complex. J. Phys. Chem. Lett. 2010, 1, 2774–2780. [Google Scholar] [CrossRef]
- Lewis, K.L.M.; Ogilvie, J.P. Probing Photosynthetic Energy and Charge Transfer with Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. Lett. 2012, 3, 503–510. [Google Scholar] [CrossRef]
- Romero, E.; Augulis, R.; Novoderezhkin, V.I.; Ferretti, M.; Thieme, J.; Zigmantas, D.; van Grondelle, R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676–682. [Google Scholar] [CrossRef]
- Durrant, J.R.; Klug, D.R.; Kwa, S.L.S.; van Grondelle, R.; Porter, G.; Dekker, J.P. A multimer model for P680, the primary electron donor of photosystem II. Proc. Natl. Acad. Sci. USA 1995, 92, 4798–4802. [Google Scholar] [CrossRef] [PubMed]
- Barter, L.M.C.; Durrant, J.R.; Klug, D.R. A quantitative structure-function relationship for the photosystem II reaction center: Supermolecular behavior in natural photosynthesis. Proc. Natl. Acad. Sci. USA 2003, 100, 946–951. [Google Scholar] [CrossRef] [PubMed]
- Renger, T.; Marcus, R. Photophysical properties of PS-2 reaction centers and a discrepancy in exciton relaxation times. J. Phys. Chem. B 2002, 106, 1809–1819. [Google Scholar] [CrossRef]
- Renger, T.; Schlodder, E. Optical properties, excitation energy and primary charge transfer in photosystem II: Theory meets experiment. J. Photochem. Photobiol. B 2011, 104, 126–141. [Google Scholar] [CrossRef] [PubMed]
- Raszewski, G.; Saenger, W.; Renger, T. Theory of optical spectra of photosystem II reaction centers: Location of the triplet state and the identity of the primary electron donor. Biophys. J. 2005, 88, 986–998. [Google Scholar] [CrossRef] [PubMed]
- Raszewski, G.; Diner, B.A.; Schlodder, E.; Renger, T. Spectroscopic Properties of Reaction Center Pigments in Photosystem II Core Complexes: Revision of the Multimer Model. Biophys. J. 2008, 95, 105–119. [Google Scholar] [CrossRef] [PubMed]
- Novoderezhkin, V.I.; Andrizhiyevskaya, E.G.; Dekker, J.P.; van Grondelle, R. Pathways and timescales of primary charge separation in the photosystem II reaction center as revealed by a simultaneous fit of time-resolved fluorescence and transient absorption. Biophys. J. 2005, 89, 1464–1481. [Google Scholar] [CrossRef] [PubMed]
- Novoderezhkin, V.I.; Dekker, J.P.; van Grondelle, R. Mixing of exciton and charge-transfer states in Photosystem II reaction centers: Modeling of Stark spectra with modified Redfield theory. Biophys. J. 2007, 93, 1293–1311. [Google Scholar] [CrossRef] [PubMed]
- Romero, E.; van Stokkum, I.H.M.; Novoderezhkin, V.I.; Dekker, J.P.; van Grondelle, R. Two different charge separation pathways in photosystem II. Biochemistry 2010, 49, 4300–4307. [Google Scholar] [CrossRef] [PubMed]
- Romero, E.; Diner, B.A.; Nixon, P.J.; Coleman, W.J.; Dekker, J.P.; van Grondelle, R. Mixed exciton-charge-transfer states in photosystem II: Stark spectroscopy on site-directed mutants. Biophys. J. 2012, 103, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Fuller, F.D.; Pan, J.; Gelzinis, A.; Butkus, V.; Senlik, S.S.; Wilcox, D.E.; Yocum, C.F.; Valkunas, L.; Abramavicius, D.; Ogilvie, J.P. Vibronic Coherence in Oxygenic Photosynthesis. Nat. Chem. 2014, 6, 706–711. [Google Scholar] [CrossRef] [PubMed]
- Lewis, K.L.M.; Fuller, F.D.; Myers, J.A.; Yocum, C.F.; Mukamel, S.; Abramavicius, D.; Ogilvie, J.P. Simulations of the Two-Dimensional Electronic Spectroscopy of the Photosystem II. J. Phys. Chem. A 2013, 117, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Abramavicius, D.; Mukamel, S. Energy-transfer and charge-separation pathways in the reaction center of photosystem II revealed by coherent two-dimensional optical spectroscopy. J. Chem. Phys. 2010, 133, 184501. [Google Scholar] [CrossRef] [PubMed]
- Gelzinis, A.; Valkunas, L.; Fuller, F.D.; Ogilvie, J.P.; Mukamel, S.; Abramavicius, D. Tight-Binding Model of the Photosystem II Reaction Center: Application to Two-Dimensional Electronic Spectroscopy. New J. Phys. 2013, 15, 075013. [Google Scholar] [CrossRef]
- Günes, S.; Neugebauer, H.; Sariciftci, N.S. Conjugate Polymer-Based Organic Solar Cells. Chem. Rev. 2007, 107, 1324–1338. [Google Scholar] [CrossRef] [PubMed]
- Brédas, J.L.; Norton, J.E.; Cornil, J.; Coropceanu, V. Molecular understanding of organic solar cells: The challenges. Acc. Chem. Res. 2009, 42, 1691–1699. [Google Scholar] [CrossRef] [PubMed]
- Hoppe, H.; Sariciftci, N.S. Organic solar cells: An overview. J. Mater. Res. 2004, 19, 1924–1945. [Google Scholar] [CrossRef]
- Clarke, T.M.; Durrant, J.R. Charge photogeneration in organic solar cells. Chem. Rev. 2010, 110, 6736–6767. [Google Scholar] [CrossRef] [PubMed]
- Chamberlain, G.A. Organic solar cells: A review. Sol. Cells 1983, 8, 47–83. [Google Scholar] [CrossRef]
- Wöhrle, W.D. Organic solar cells. Adv. Mater. 1991, 3, 129–138. [Google Scholar] [CrossRef]
- Karg, S.; Riess, W.; Dyakonov, V.; Schwoerer, M. Electrical and optical characterization of poly(phenylene-vinylene) light emitting diodes. Synth. Met. 1993, 54, 427–433. [Google Scholar] [CrossRef]
- Tang, C.W. Two-layer organic photovoltaic cell. Appl. Phys. Lett. 1986, 48, 183. [Google Scholar] [CrossRef]
- Winder, C.; Sariciftci, N.S. Low bandgap polymer for photon harvesting in bulk heterojunction solar cells. J. Mater. Chem. 2004, 14, 1077–1086. [Google Scholar] [CrossRef]
- Sariciftci, N.S.; Smilowitz, L.; Heeger, A.J.; Wudl, F. Photoinduced electron transfer from a conducting polymer to buck-minsterfullerene. Science 1992, 258, 1474–1476. [Google Scholar] [CrossRef] [PubMed]
- Smilowitz, L.; Sariciftci, N.S.; Wu, R.; Gettinger, C.; Heeger, A.J.; Wudl, F. Photoexcitation spectroscopy of conducting polymer-C60 composites: Photoinduced electron transfer. Phys. Rev. B 1993, 47, 13835. [Google Scholar] [CrossRef]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudl, F.; Heeger, A.J. Polymer photovoltaic cells: Enhanced efficiencies via a network of internal donor-acceptor heterojunctions. Science 1995, 270, 1789–1791. [Google Scholar]
- Yang, C.Y.; Heeger, A.J. Morphology of composites of semiconducting polymers mixed with C60. Synth. Met. 1996, 83, 85–88. [Google Scholar] [CrossRef]
- Brabec, C.J.; Durrant, J.R. Solution-processed organic solar cells. MRS Bull. 2008, 33, 670–675. [Google Scholar] [CrossRef]
- Nunzi, J.M. Organic photovoltaic materials and devices. C. R. Phys. 2002, 3, 523–542. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, K.; Coates, N.E.; Moses, D.; Nguyen, T.Q.; Dante, M.; Heeger, A.J. Efficient tandem polymer solar cells fabricated by all-solution processing. Science 2007, 317, 222–225. [Google Scholar] [CrossRef] [PubMed]
- Holstein, T. Studies of polaron motion: Part I. The molecular-crystal model. Ann. Phys. 1959, 8, 325–342. [Google Scholar]
- Holstein, T. Studies of polaron motion: Part II. The small polaron. Ann. Phys. 1959, 8, 343–389. [Google Scholar]
- Munn, R.W.; Silbey, R. Theory of electronic transport in molecular crystals. II. Zeroth order states incorporating nonlocal linear electron phonon coupling. J. Chem. Phys. 1985, 83, 1843. [Google Scholar] [CrossRef]
- Munn, R.W.; Silbey, R. Theory of electronic transport in molecular crystals. III. Diffusion coefficient incorporating nonlocal linear electron phonon coupling. J. Chem. Phys. 1985, 83, 1854. [Google Scholar] [CrossRef]
- Zhao, Y.; Brown, D.W.; Lindenberg, K. On the Munn-Silbey approach to nonlocal exciton-phonon coupling. J. Chem. Phys. 1994, 100, 2335. [Google Scholar] [CrossRef]
- Zhao, Y.; Brown, D.W.; Lindenberg, K. A variational approach to nonlocal exciton phonon coupling. J. Chem. Phys. 1997, 106, 2728. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, G.; Sun, J.; Wang, W. An Improved Variational Approach to Off-Diagonal Exciton-Phonon Coupling, J. Chem. Phys. 2008, 129, 124114. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Zhao, Y.; Wang, W.; Kato, T. Global-Local Ansatz and Dynamical Coherent Potential Approximation Study of Off-Diagonal Exciton-Phonon Coupling. Phys. Rev. B 2009, 79, 165105. [Google Scholar] [CrossRef]
- Zhao, Y.; Brown, D.W.; Lindenberg, K. Variational energy band theory for polarons: Mapping polaron structure with the merrifield method. J. Chem. Phys. 1997, 106, 5622–5630. [Google Scholar] [CrossRef]
- Zhao, Y.; Brown, D.W.; Lindenberg, K. Variational energy band theory for polarons: Mapping polaron structure with the Global-Local method. J. Chem. Phys. 1997, 107, 3179–3195. [Google Scholar] [CrossRef]
- Zhao, Y.; Brown, D.W.; Lindenberg, K. Variational energy band theory for polarons: Mapping polaron structure with the Toyozawa method. J. Chem. Phys. 1997, 107, 3159–3178. [Google Scholar] [CrossRef]
- Hannewald, K.; Stojanovic, V.M.; Schellekens, J.M.T.; Bobbert, P.A.; Kresse, G.; Hafner, J. Theory of polaron bandwidth narrowing in organic molecular crystals. Phys. Rev. B 2004, 69. [Google Scholar] [CrossRef]
- Hannewald, K.; Bobbert, P.A. Ab initio theory of charge-carrier conduction in ultrapure organic crystals. Appl. Phys. Lett. 2004, 85, 1535–1537. [Google Scholar] [CrossRef]
- Hultell, M.; Stafstrom, S. Polaron dynamics in highly ordered molecular crystals. Chem. Phys. Lett. 2006, 428, 446–450. [Google Scholar] [CrossRef]
- Troisi, A.; Orlandi, G. Charge-Transport Regime of Crystalline Organic Semiconductors: Diffusion Limited by Thermal Off-Diagonal Electronic Disorder. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef]
- Marcus, R.A.; Sutin, N. Electron transfers in chemistry and biology. Biochim. Biophys. Acta 1985, 811, 265–322. [Google Scholar] [CrossRef]
- Brédas, J.L.; Calbert, J.P.; da Silva Filho, D.A.; Cornil, J. Organic semiconductors: A theoretical characterization of the basic parameters governing charge transport. Proc. Natl. Acad. Sci. USA 2002, 99, 5804–5809. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, D.A.; Kim, E.G.; Brédas, J.L. Transport Properties in the Rubrene Crystal: Electronic Coupling and Vibrational Reorganization Energy. Adv. Mater. 2005, 17, 1072–1076. [Google Scholar] [CrossRef]
- Zhao, Y.; Liang, W.Z. Charge transfer in organic molecules for solar cells. Chem. Soc. Rev. 2012, 41, 1075–1087. [Google Scholar] [CrossRef] [PubMed]
- Georgievskii, Y.; Burshtein, A.I.; Chernobrod, B.M. Electron transfer in the inverted region: Adiabatic suppression and relaxation hindrance of the reaction rate. J. Chem. Phys. 1996, 105, 3108–3120. [Google Scholar] [CrossRef]
- Zhao, Y.; Milnikov, G.; Nakamura, H. Evaluation of canonical and microcanonical nonadiabatic reaction rate constants by using the Zhu-Nakamura formulas. J. Chem. Phys. 2004, 121, 8854–8860. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liang, W.Z. Quantum Kramers-like theory of the electron-transfer rate from weak-to-strong electronic coupling regions. Phys. Rev. A 2006, 74. [Google Scholar] [CrossRef]
- Zhu, W.J.; Zhao, Y. Quantum effect of intramolecular high-frequency vibrational modes on diffusion-controlled electron transfer rate: From the weak to the strong electronic coupling regions. J. Chem. Phys. 2007, 126, 184105. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liang, W.Z. Non-Condon nature of fluctuating bridges on nonadiabatic electron transfer: Analytical interpretation. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef] [PubMed]
- Coropceanu, V.; Cornil, J.; da Silva Filho, D.A.; Olivier, Y.; Silbey, R.; Brédas, J.L. Charge transport in organic semiconductors. Chem. Rev. 2007, 107, 926–952. [Google Scholar] [CrossRef] [PubMed]
- Pope, M.; Swenberg, C.E. Electronic Processes in Organic Crystals and Polymers; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Silbey, S.; Munn, R.W. General theory of electronic transport in molecular crystals. 1. Local linear electron-phonon coupling. J. Chem. Phys. 1980, 72, 2763–2773. [Google Scholar]
- Cheng, Y.C.; Silbey, R.J. A unified theory for charge carrier transport in organic crystals. J. Chem. Phys. 2008, 128. [Google Scholar] [CrossRef] [PubMed]
- Ortmann, F.; Bechstedt, F.; Hannewald, K. Charge transport in organic crystals: Interplay of band transport, hopping and electron phonon scattering. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Ortmann, F.; Bechstedt, F.; Hannewald, K. Characteristics of small- and large-polaron motion in organic crystals. J. Phys. Condens. Matter. 2010, 22. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.M.; Ye, J.; Zhang, H.J.; Zhao, Y. On the Munn-Silbey approach to polaron transport with off-diagonal coupling and temperature-dependent canonical transformations. J. Phys. Chem. B 2011, 115, 5312–5321. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.J.; Nan, G.J.; Yang, X.D.; Peng, Q.; Li, Q.K.; Shuai, Z.G. Computational methods for design of organic materials with high charge mobility. Chem. Soc. Rev. 2010, 39, 423–434. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.D.; Wang, L.J.; Wang, C.L.; Long, W.; Shuai, Z.G. Influences of Crystal Structures and Molecular Sizes on the Charge Mobility of Organic Semiconductors: Oligothiophenes. Chem. Mater. 2008, 20, 3205–3211. [Google Scholar] [CrossRef]
- Tan, L.; Zhang, L.; Jiang, X.; Yang, X.D.; Wang, L.J.; Wang, Z.H.; Li, L.Q.; Hu, W.P.; Shuai, Z.G.; Li, L.; et al. A Densely and Uniformly Packed Organic Semiconductor Based on Annelated Trithiophenes for High-Performance Thin Film Transistors. Adv. Funct. Mater. 2009, 19, 272–276. [Google Scholar] [CrossRef]
- Bixon, M.; Jortner, J. Non-Arrhenius temperature dependence of electron-transfer rates. J. Phys. Chem. 1991, 95, 1941–1944. [Google Scholar] [CrossRef]
- Nan, G.J.; Wang, L.J.; Yang, X.D.; Shuai, Z.G.; Zhao, Y. Charge transfer rates in organic semiconductors beyond first-order perturbation: From weak to strong coupling regimes. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.Y.; Nakamura, H. Theory of nonadiabatic transition for general two-state curve crossing problems. I. Nonadiabatic tunneling case. J. Chem. Phys. 1994, 101, 10630–10647. [Google Scholar]
- Warta, W.; Karl, N. Hot holes in naphthalene: High electric-field-dependent mobilities. Phys. Rev. B 1985, 32. [Google Scholar] [CrossRef]
- Ostroverkhova, O.; Cooke, D.G.; Shcherbyna, S.; Egerton, R.F.; Hegmann, F.A.; Tykwinski, R.R.; Anthony, J.E. Bandlike transport in pentacene and functionalized pentacene thin films revealed by subpicosecond transient photoconductivity measurements. Phys. Rev. B 2005, 71, 035204. [Google Scholar] [CrossRef]
- Jurchescu, O.D.; Baas, J.; Palstra, T.T.M. Effect of impurities on the mobility of single crystal pentacene. Appl. Phys. Lett. 2004, 84, 3061–3063. [Google Scholar] [CrossRef]
- Podzorov, V.; Menard, E.; Borissov, A.; Kiryukhin, V.; Rogers, J.A.; Gershenson, M.E. Intrisic charge transport on the surface of organic semiconductors. Phys. Rev. Lett. 2004, 93, 086602. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Silbey, R.J.; da Silva Filho, D.A.; Calbert, J.P.; Cornil, J.; Brédas, J.L. Three-dimensional band structure and bandlike mobility in oligoacene single crystals: A theoretical invesitagtion. J. Chem. Phys. 2003, 118, 3764–3774. [Google Scholar] [CrossRef]
- Brédas, J.L.; Beljonne, D.; Coropceanu, V.; Cornil, J. Charge transfer and energy transfer processs in π-conjugated oligomers and polymers: A molecular Picture. Chem. Rev. 2004, 104, 4971–5003. [Google Scholar] [CrossRef] [PubMed]
- Paulson, B.; Curtiss, L.; Bal, B.; Closs, G.; Miller, J. Investigation of through-bond coupling dependence on spacer structure. J. Am. Chem. Soc. 1996, 118, 378–387. [Google Scholar] [CrossRef]
- Senthikumar, K.; Grozema, F.; Bickelhaupt, F.; Siebbeles, L. Charge transport in columnar stacked triphenylenes: Effects of conformational fluctuations on charge transfer integrals and site energy. J. Chem. Phys. 2003, 119. [Google Scholar] [CrossRef]
- Troisi, A.; Orlandi, G. Hole migration in DNA: A theoretical analysis of the role of structural fluctuations. J. Phys. Chem. B 2002, 106, 2093–2101. [Google Scholar] [CrossRef]
- Reimers, J. A practical method for the use of curvilinear coordinates in calculations of normal-mode-projected displacements and duschinsky rotation matrices for large molecules. J. Chem. Phys. 2001, 115, 9103–9109. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, H.; Tang, Q.; He, Y.; Hu, W. Mobility dependence on the conducting channel dimension of organic field-effect transistors based on single crystalline nanoribbons. J. Mater. Chem. 2010, 20, 7029–7033. [Google Scholar] [CrossRef]
- Lin, L.L.; Geng, H.; Shuai, Z.G.; Luo, Y. Theoretical insights into the charge transport in perylene diimides based n-type organic semiconductors. Org. Electron. 2012, 13, 2763–2772. [Google Scholar] [CrossRef]
- Geng, H.; Peng, Q.; Wang, L.J.; Li, H.J.; Liao, Y.; Ma, Z.Y.; Shuai, Z.G. Toward quantitative prediction of charge mobility in organic semicondcutors: Tunneling enabled hopping model. Adv. Mater. 2012, 24, 3568–3572. [Google Scholar] [CrossRef] [PubMed]
- Gledhill, S.E.; Scott, B.; Gregg, B.A. Organic and nano-structured composite photovoltaics: An overview. J. Mater. Res. 2005, 20, 3167–3179. [Google Scholar] [CrossRef]
- Morteani, A.C.; Sreearunothai, P.; Herz, L.M.; Friend, R.H.; Silva, C. Exciton regeneration at polymeric semiconductor heterojunctions. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef]
- Ohkita, H.; Cook, S.; Astuti, Y.; Duffy, W.; Tierney, S.; Zhang, W.; Heeney, M.; McCulloch, I.; Nelson, J.; Bradley, D.D.C.; et al. Charge carrier formation in polythiophene/fullerene blend films studied by transient absorption spectroscopy. J. Am. Chem. Soc. 2008, 130, 3030–3042. [Google Scholar] [CrossRef] [PubMed]
- Veldman, D.; Ipek, O.; Meskers, S.C.J.; Sweelssen, J.; Koetse, M.M.; Veenstra, S.C.; Kroon, J.M.; van Bavel, S.S.; Loos, J.; Janssen, R.A.J. Compositional and electric field dependence of the dissociation of charge transfer excitons in alternating polyfluorene copolymer/fullerene blends. J. Am. Chem. Soc. 2008, 130, 7721–7735. [Google Scholar] [CrossRef] [PubMed]
- Drori, T.; Sheng, C.X.; Ndobe, A.; Singh, S.; Holt, J.; Vardeny, Z.V. Below gap excitation of π-conjugated polymer-fullerene blends: Implications for bulk organic heterojunction solar cells. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef]
- Dimitrov, S.D.; Durrant, J.R. Materials design considerations for charge generation in organic solar cells. Chem. Mater 2014, 26, 616–630. [Google Scholar] [CrossRef]
- Bakulin, A.A.; Rao, A.; Pavelyev, V.G.; van Loosdrecht, P.H.M.; Pshenichnikov, M.S.; Niedzialek, D.; Cornil, J.; Beljonne, D.; Friend, R.H. The role of driving energy and delocalized states for charge separation in organic semiconductors. Science 2012, 335, 1340–1344. [Google Scholar] [CrossRef] [PubMed]
- Jailaubekov, A.E.; Willard, A.P.; Tritsch, J.R.; Chan, W.L.; Sai, N.; Gearba, R.; Kaake, L.G.; Williams, K.J.; Leung, K.; Rossky, P.J.; et al. Hot charge-transfer excitons set the time limit for charge separation at donor/acceptor interfacs in organic photovoltaics. Nat. Mater. 2013, 12, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Grancini, G.; Maiuri, M.; Fazzi, D.; Petrozza, A.; Egelhaaf, H.J.; Brida, D.; Cerullo, G.; Lanzani, G. Hot exciton dissociation in polymer solar cells. Nat. Mater. 2013, 12, 29–33. [Google Scholar] [CrossRef] [PubMed]
- Vandewal, K.; Albrecht, S.; Hoke, E.T.; Graham, K.R.; Widmer, J.; Douglas, J.D.; Schubert, M.; Mateker, W.R.; Bloking, J.T.; Burkhard, G.F.; et al. Efficient charge generation by relaxed charge transfer states at organic interfaces. Nat. Mater. 2014, 13, 63–68. [Google Scholar] [CrossRef] [PubMed]
- Brumer, P.; Shapiro, M. Molecular response in one-photon absorption via natural thermal light vs. pulsed laser excitation. Proc. Natl. Acad. Sci. USA 2012, 109, 19575–19578. [Google Scholar] [CrossRef] [PubMed]
- Fassioli, F.; Olaya-Castro, A.; Scholes, G.D. Coherent energy transfer under incoherent light conditions. J. Phys. Chem. Lett. 2012, 3, 3136–3142. [Google Scholar] [CrossRef]
- Kassal, I.; Yuen-Zhou, J.; Rahimi-Keshari, S. Does coherence enhance transport in photosynthesis? J. Phys. Chem. Lett. 2013, 4, 362–367. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.B.; Howey, D.J.; Sutor, E.J.; Hendrickson, R.A.; Gealy, M.W.; Ulness, D.J. Two dimensional electronic spectroscopy using incoherent light: Theoretical analysis. J. Phys. Chem. A 2013, 117, 5926–5954. [Google Scholar] [CrossRef] [PubMed]
- Hildner, R.; Brinks, D.; van Hulst, N.F. Femtosecond coherence and quantum control of single molecules at room temperature. Nat. Phys. 2010, 7, 172–177. [Google Scholar] [CrossRef]
- Hildner, R.; Brinks, D.; Nieder, J.B.; Gogdell, R.J.; van Hulst, N.F. Quantum coherent energy transfer over varying pathways in single light harvesting complexes. Science 2013, 340, 1448–1451. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Yang, W.C.; Zhao, Y. Exciton dissociation in the presence of phonons: A reduced hierarchy equations of motion approach. J. Chem. Phys. 2014, 140, 104113. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Shenai, P.; Zheng, F.; Somoza, A.; Zhao, Y. Optimal Energy Transfer in Light-Harvesting Systems. Molecules 2015, 20, 15224-15272. https://doi.org/10.3390/molecules200815224
Chen L, Shenai P, Zheng F, Somoza A, Zhao Y. Optimal Energy Transfer in Light-Harvesting Systems. Molecules. 2015; 20(8):15224-15272. https://doi.org/10.3390/molecules200815224
Chicago/Turabian StyleChen, Lipeng, Prathamesh Shenai, Fulu Zheng, Alejandro Somoza, and Yang Zhao. 2015. "Optimal Energy Transfer in Light-Harvesting Systems" Molecules 20, no. 8: 15224-15272. https://doi.org/10.3390/molecules200815224




