Solving Molecular Docking Problems with Multi-Objective Metaheuristics
Abstract
:1. Introduction
2. Multi-Objective Molecular Docking
2.1. Multi-Objective Optimization
Definition 1 (MOP)
Definition 2 (Pareto optimality).
Definition 3 (Pareto dominance).
Definition 4 (Pareto optimal set).
Definition 5 (Pareto front).
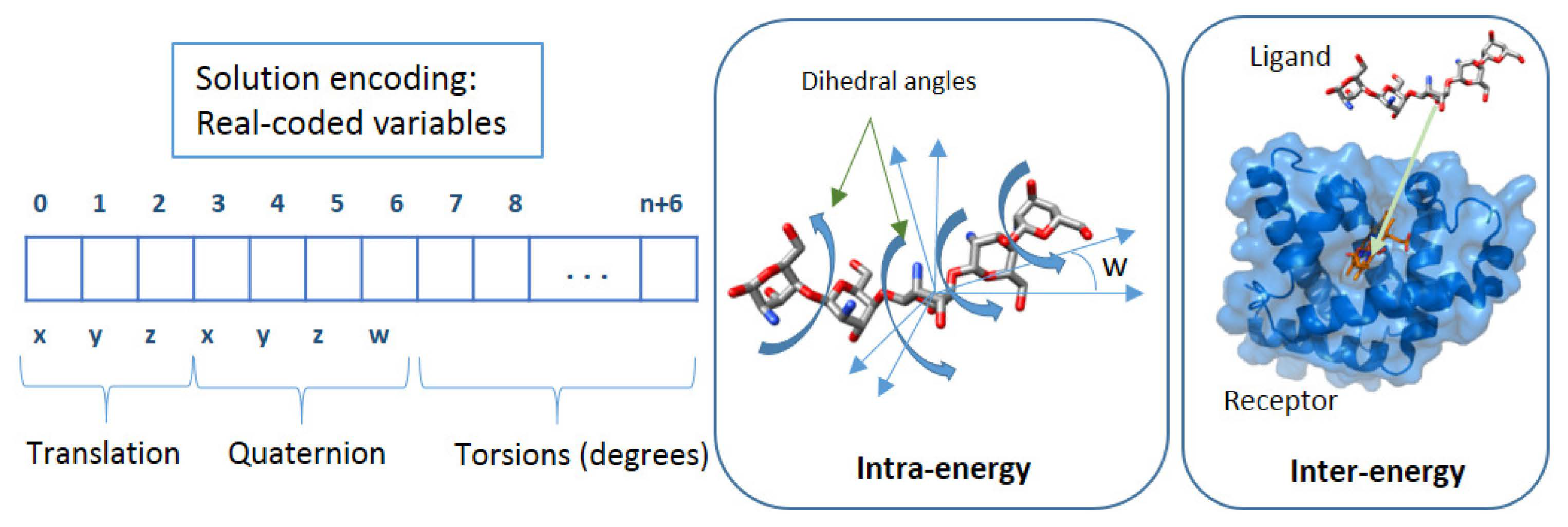
2.2. Molecular Docking Optimization Strategy
Definition 6 (Docking optimization).
Decision space
Objective space
- Objective 1: the Eintra energy (Equation (2)) of the ligand and receptor is estimated by the difference between the bound and unbound states of the ligand and receptor.
- Objective 2: the Einter energy (Equation (3)) is estimated by the difference of the bound and unbound states of the ligand-macromolecule complex.
3. Metrics and Algorithms
3.1. Metrics
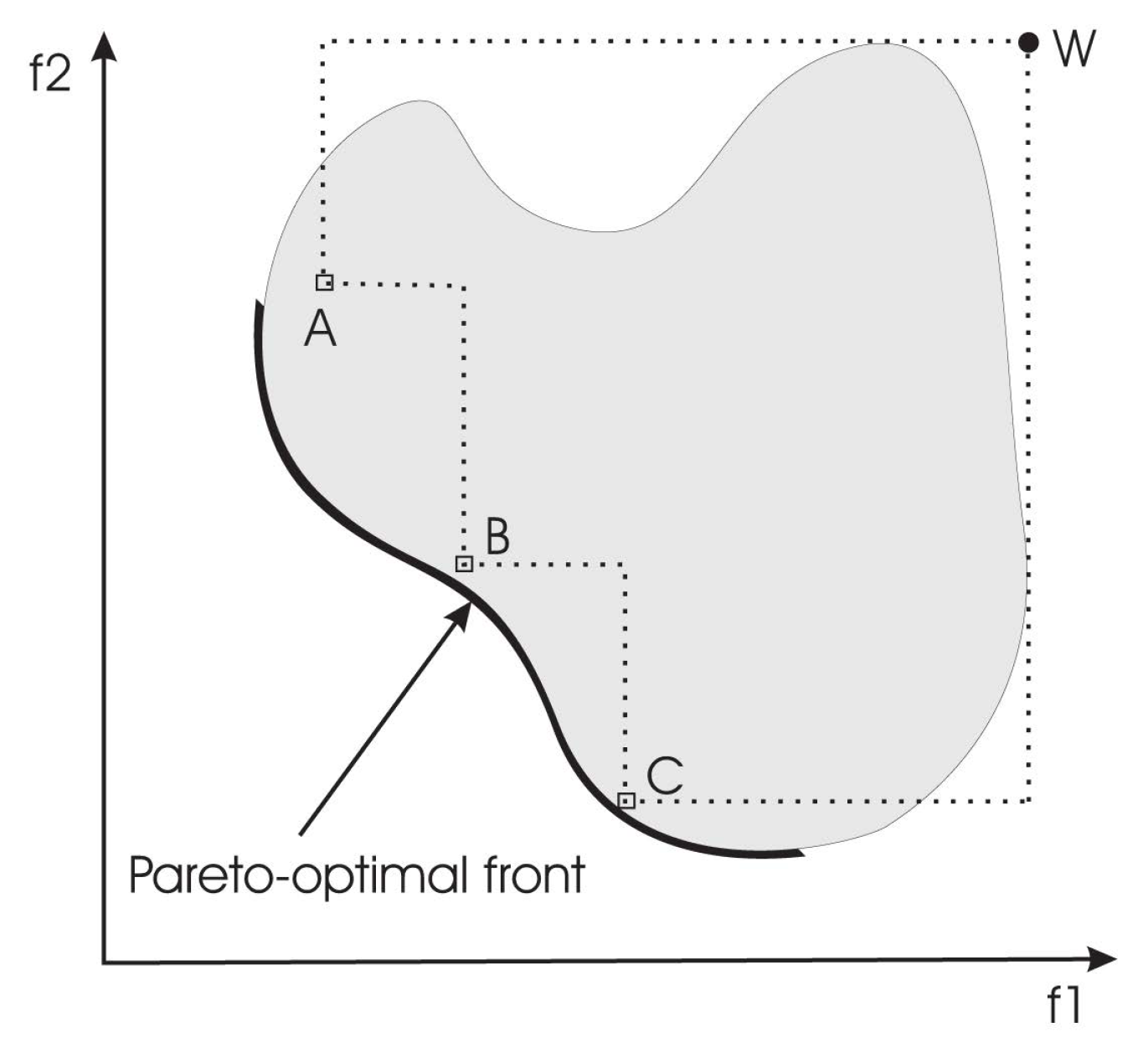
- IHV : This indicator calculates the n-dimensional space covered by members of a non-dominated set of solutions Q, e.g., the region enclosed by the discontinuous line in Figure 2, Q = {A,B,C}, for problems where all objectives are to be minimized. Mathematically, for each solution i ∈ Q, a hypercube vi is constructed with a reference point W and the solution i as the diagonal corners of the hypercube. The reference point can simply be found by constructing a vector of worst objective function values. Thereafter, a union of all hypercubes is found, and its hyper-volume (IHV ) is calculated:Solution fronts with larger values of IHV are desirable.
- Iɛ+: Given a computed front for a problem, A, this indicator is a measure of the smallest distance one would need to translate every solution in A, so that it dominates the optimal Pareto front of this problem. More formally, given and , where n is the number of objectives:where if and only if . In this case, solution fronts with lower values of Iɛ+ are desirable.
3.2. Algorithms
- NSGA-II: NSGA-II [10] is the most widely-used multi-objective optimization algorithm. It is a genetic algorithm based on obtaining a new individual from the original population by applying the typical genetic operators (selection, crossover and mutation). A ranking procedure is applied to promote convergence, while a density estimator (the crowding distance) is used to enhance the diversity of the set of found solutions.
- ssNSGA-II: The steady-state version of the NSGA-II was presented in [11]. This study showed that ssNSGA-II outperformed NSGA-II in a set of benchmark problems, although at the cost of increasing the running time with respect to the original algorithm.
- SMPSO: SMPSO [12] is a multi-objective particle swarm optimization algorithm whose main characteristic is the use of a strategy to limit the velocity of the particles, in order to allow new effective particle positions to be produced in those cases where the velocity becomes too high. Furthermore, SMPSO includes the polynomial mutation as the turbulence factor and an external archive that stores the non-dominated solutions found during the search.
- GDE3: The generalized differential evolution (GDE) algorithm [13] is based on NSGA-II, but the crossover and mutation variation operators are changed to use the differential evolution operator; concretely, it uses the rand/1/bin variant. Another difference is that GDE3 modifies the crowding distance of NSGA-II to generate a better distributed set of solutions.
- MOEA/D: MOEA/D [14] is based on decomposing a multi-objective optimization problem into a number of scalar optimization subproblems, which are optimized simultaneously, only using information from their neighboring subproblems. We have used the variant MOEA/D-DE [24], which applies differential evolution instead of the genetic crossover and mutation operators used in the original algorithm. This algorithm also applies a mutation operator to the solutions.
- SMS-EMOA: When comparing the results of evolutionary multi-objective optimization algorithms (EMOA), the hyper-volume measure quality (also called the S-metric) can be applied. The S-metric selection steady-state EMOA [15] uses a selection operator based on the hyper-volume measure combined with the concept of non-dominated sorting. Its main feature lies in making its population evolve to a well-distributed set of solutions, in order to focus on interesting regions of the Pareto front, at the cost of the high computing time of computing the hyper-volume. To cope with this issue, we have incorporated the WFG hyper-volume [25] into SMS-EMOA, which is very efficient in the case of bi-objective problems, as the one we are solving. In this approach, the reference point to measure the hyper-volume contribution is based on adding a constant offset to the maximum value of each objective.
4. Results and Discussion
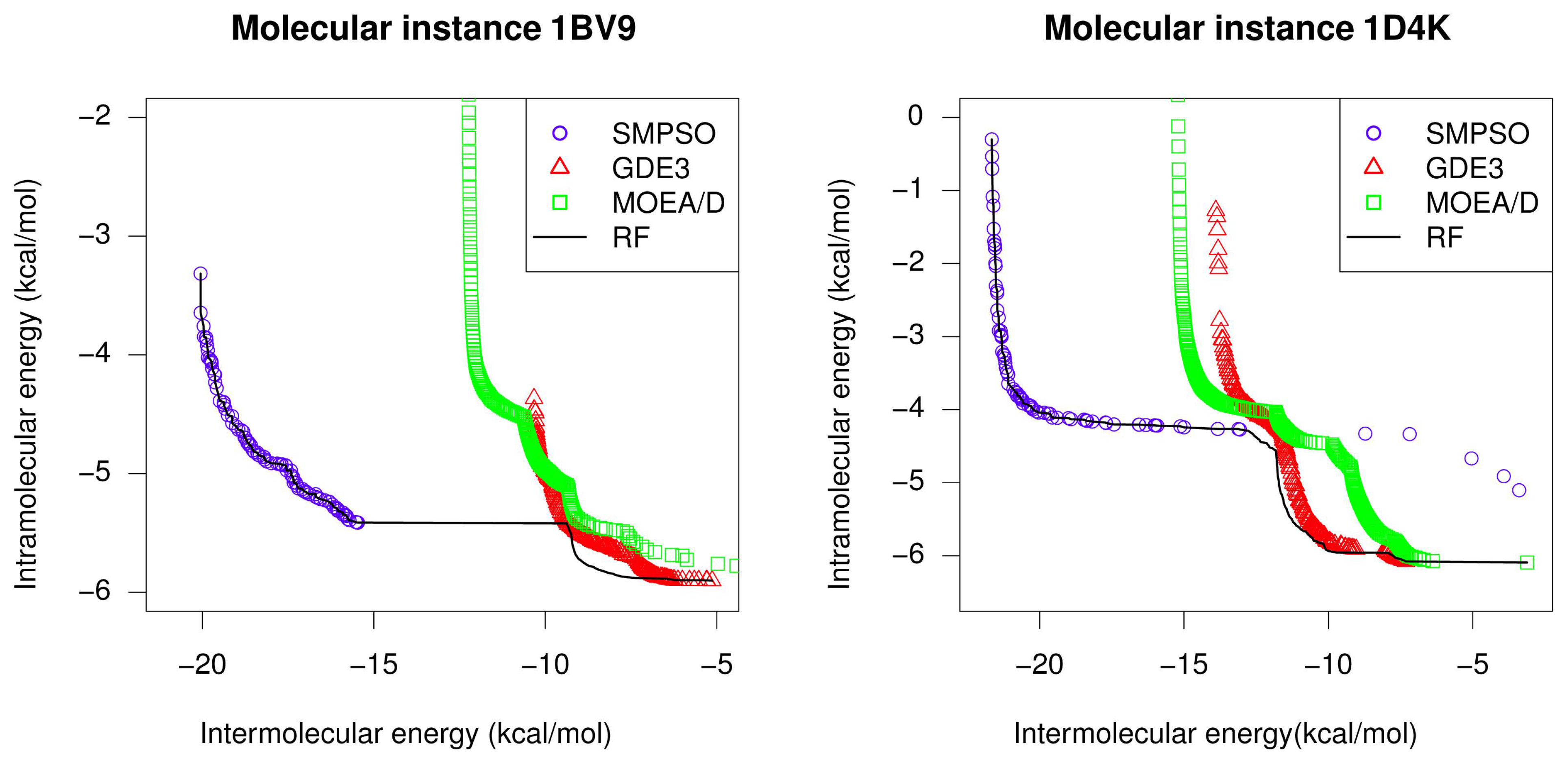
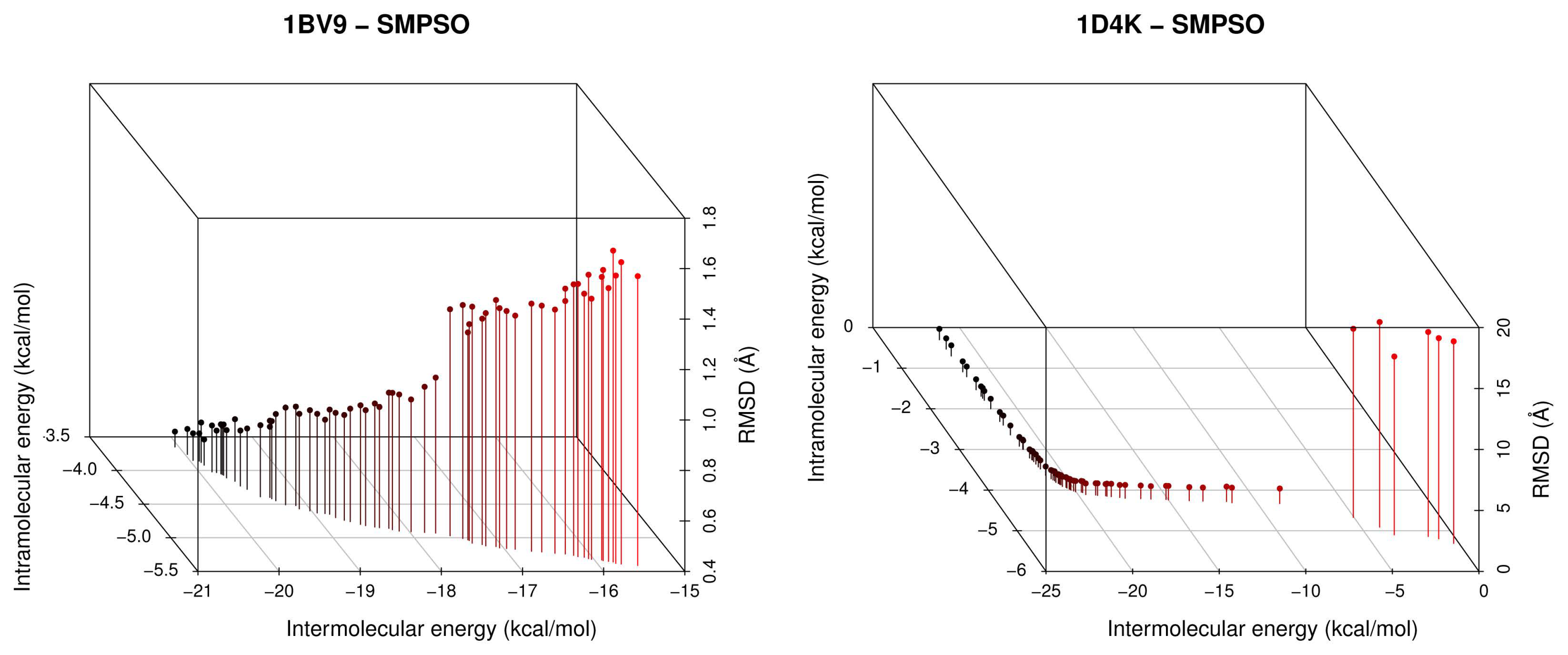
4.1. Performance Comparisons
4.2. Comparison with a Mono-Objective Approach
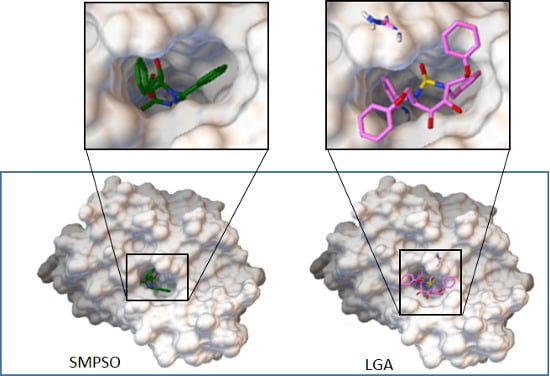
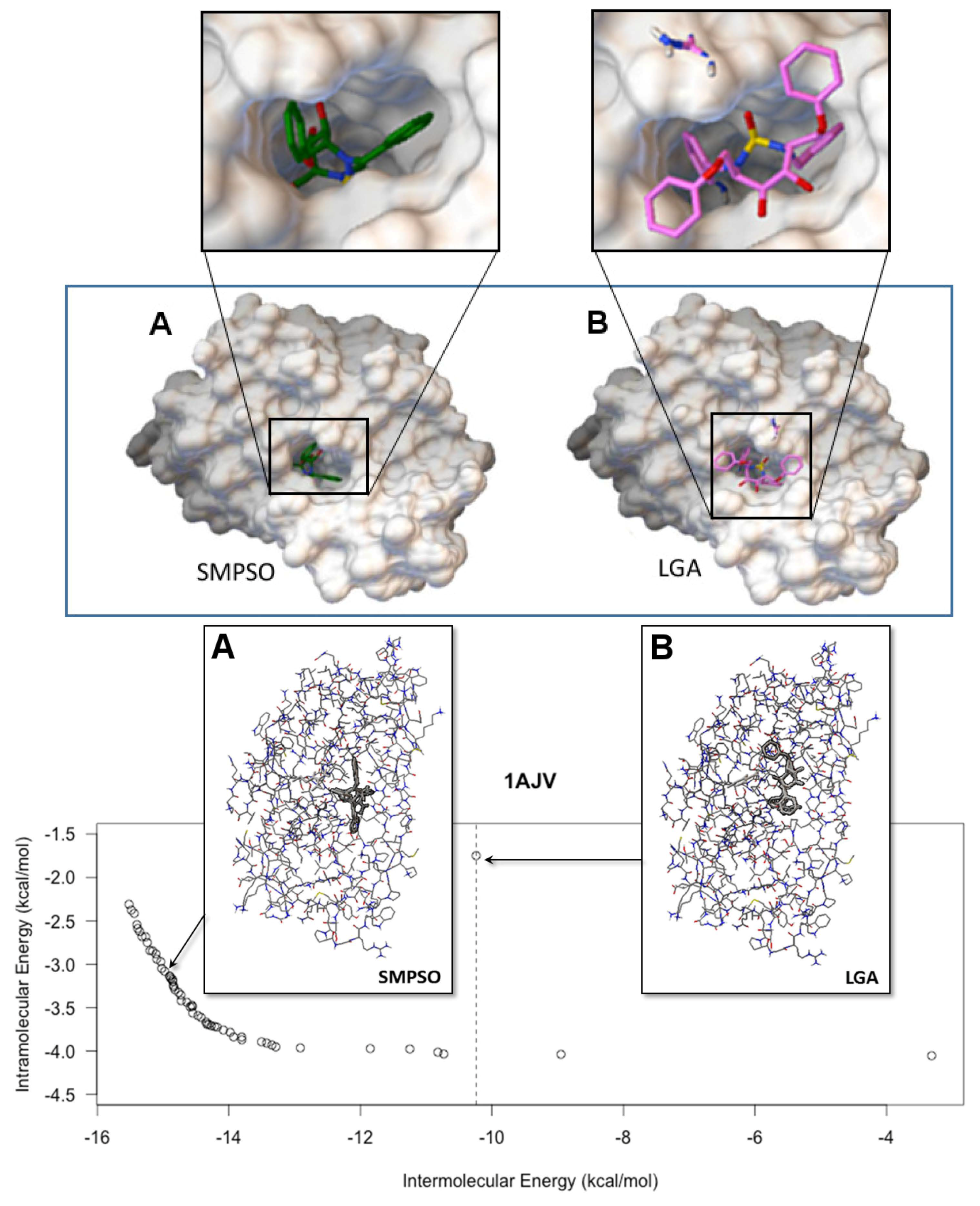
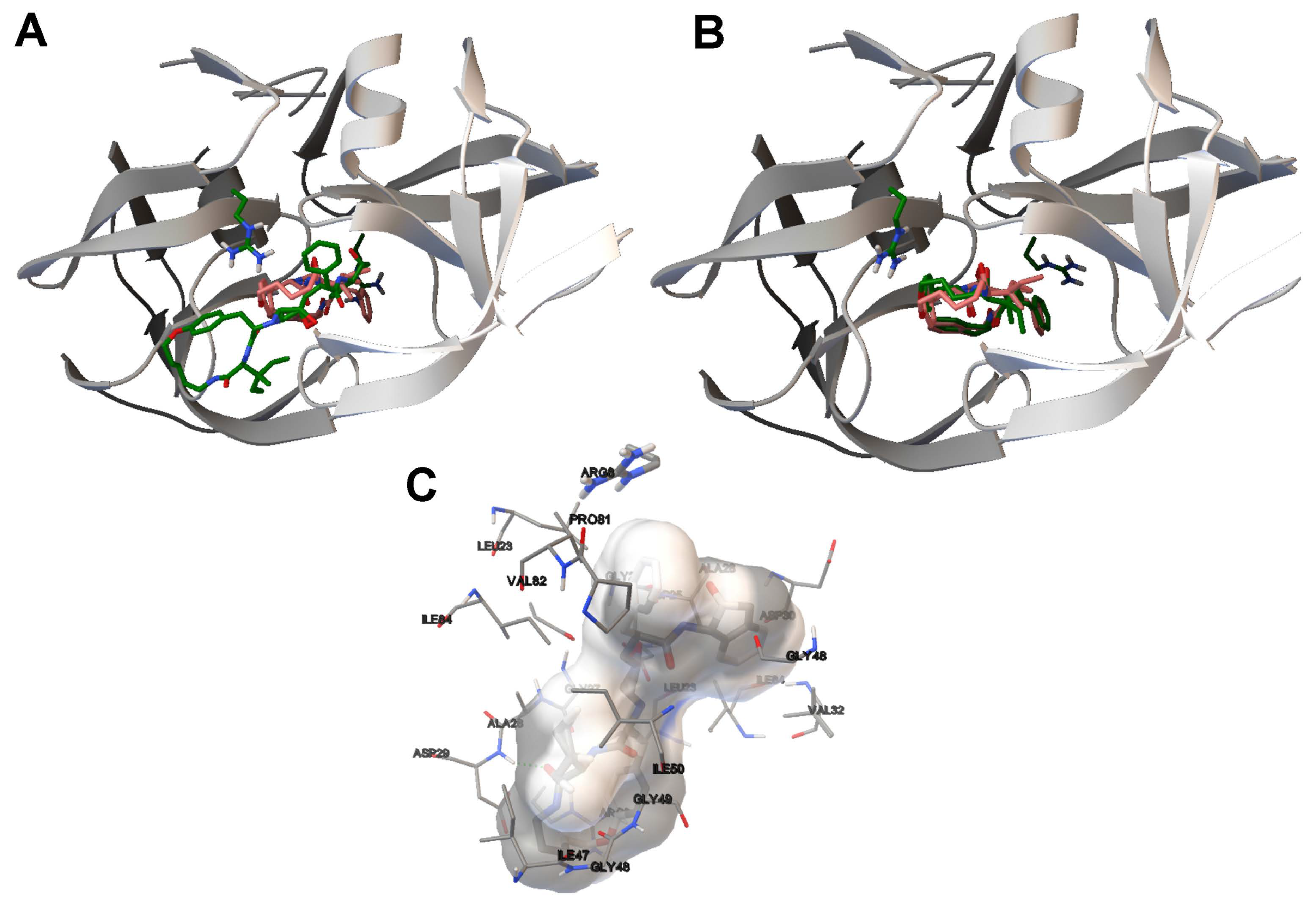
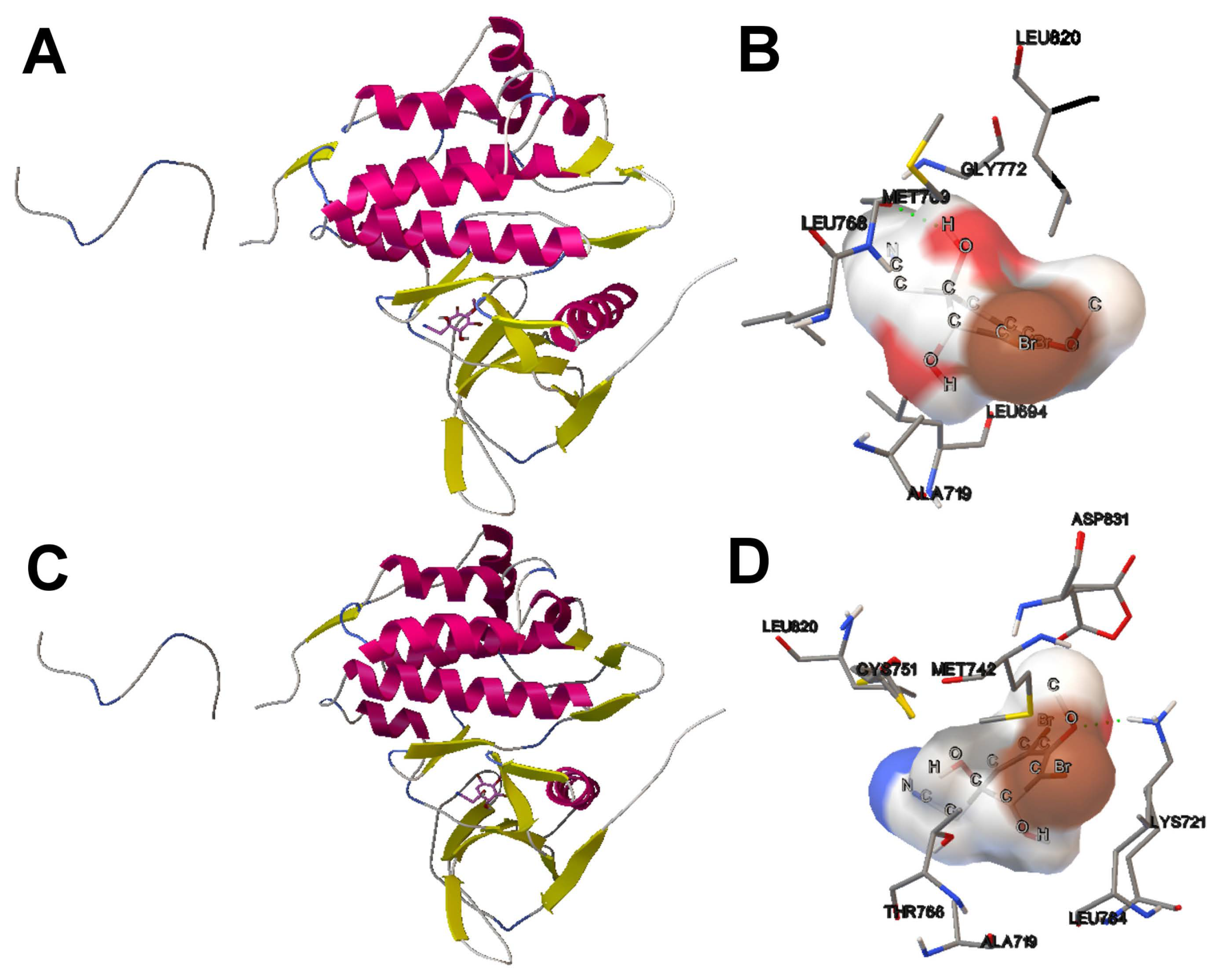
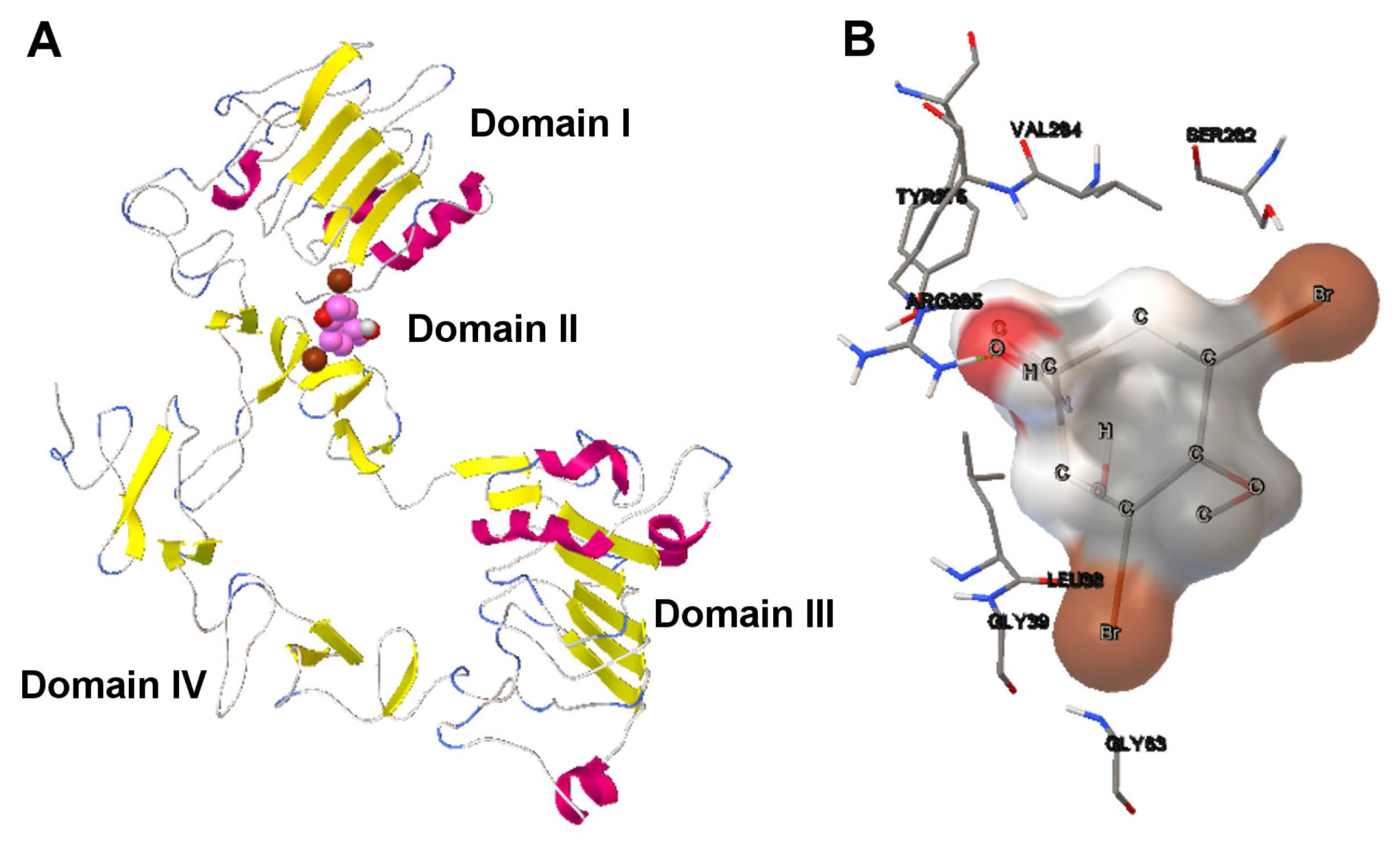
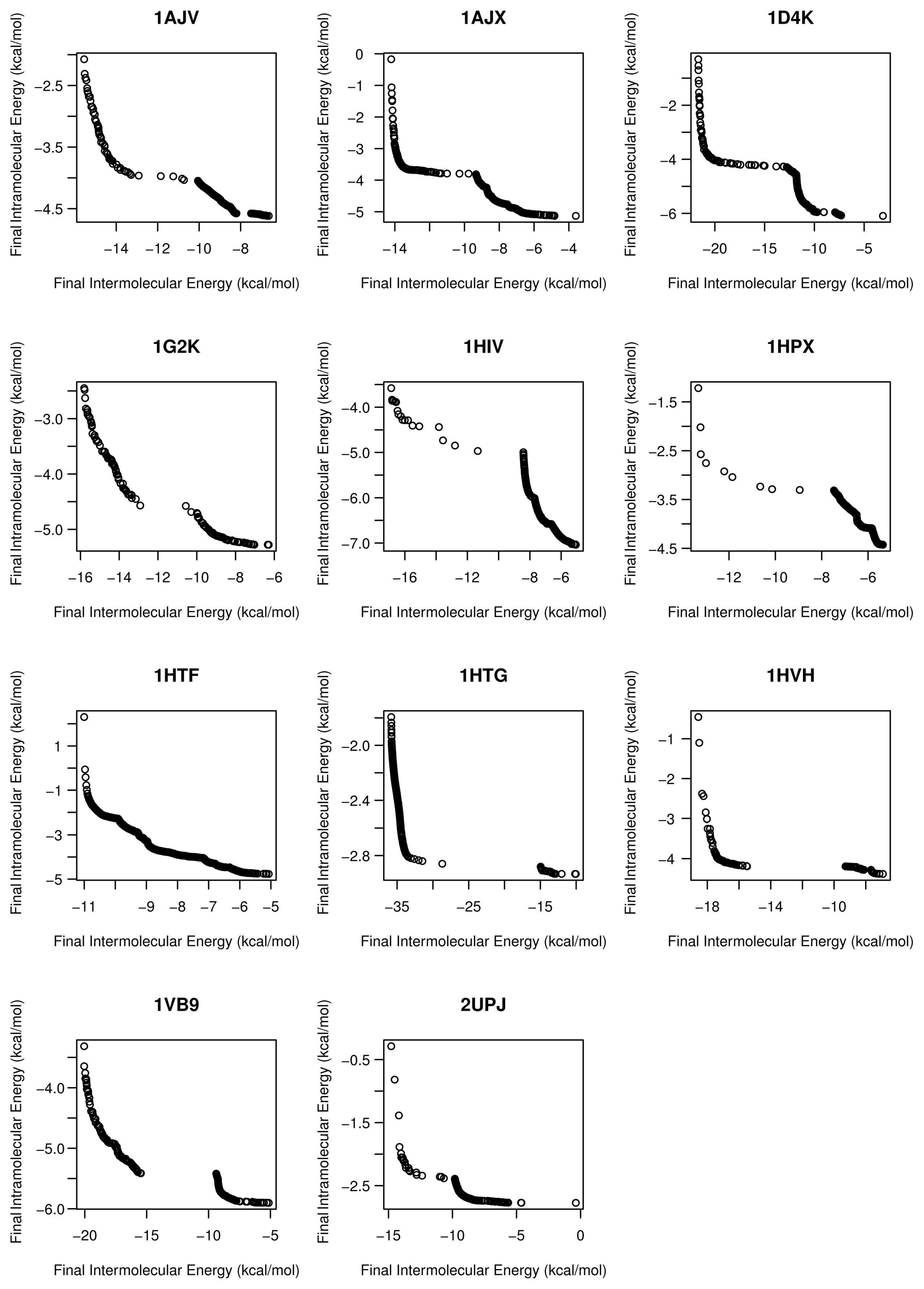
4.3. Analysis on Ligand Binding Site and Molecular Interactions
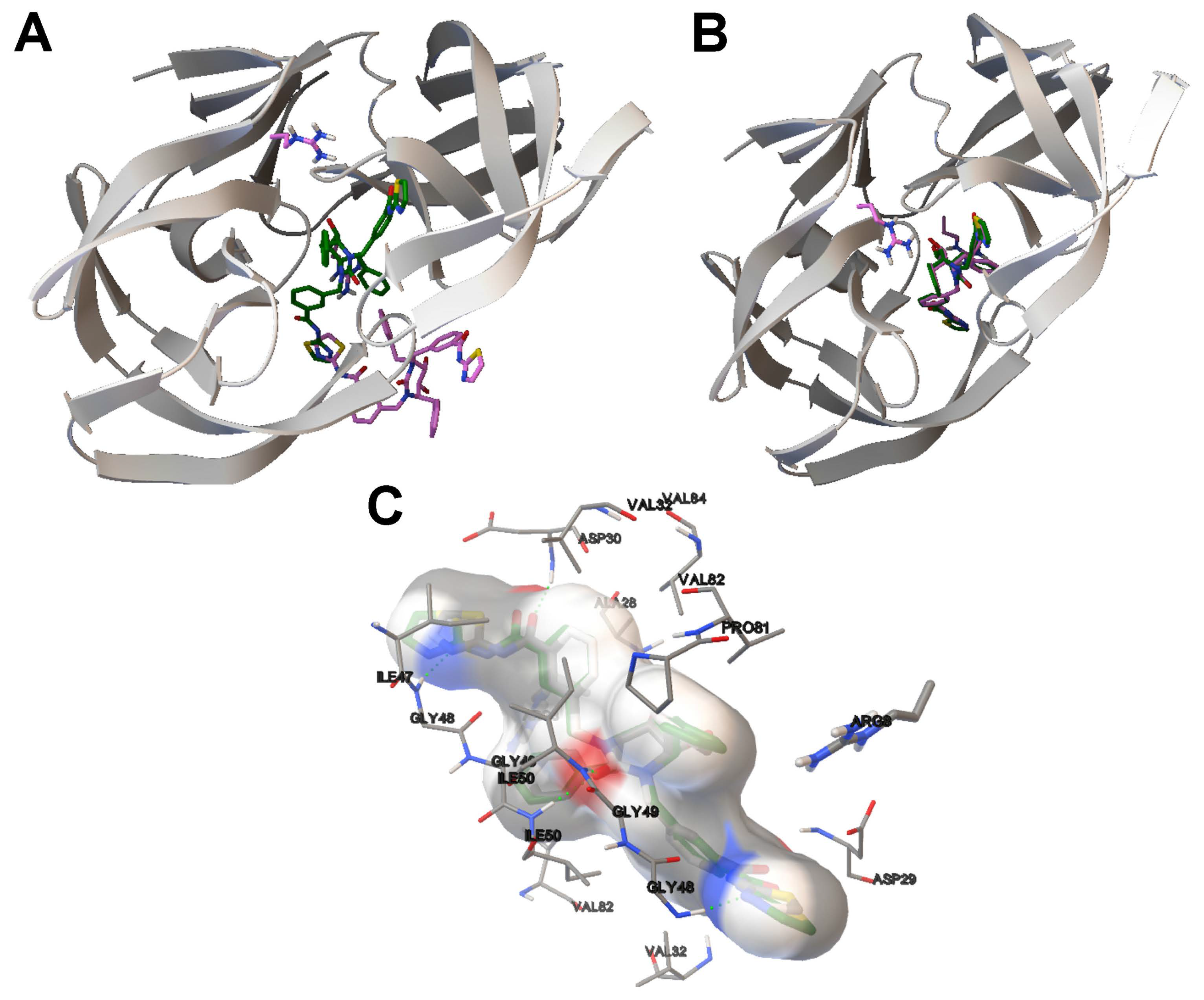
4.4. Application of Multi-Objective Docking in Drug Discovery: A Use Case Based on the Aeroplysinin-1 Compound and EGFR
5. Experimental Section
- Preparation of the ligand and macromolecule: Chimera UCSF software [44] was used to separate the macromolecule and the ligand into two PDB files and to remove small molecules, such as solvent molecules, non-interacting ions, etc., from the crystal structure. The AutoDockTools (ADT) graphical interface suite [45] was used to prepare the macromolecule and ligand PDBQT (Protein Data Bank with partial chages and atom type) files. For the preparation of the ligand, partial atomic charges and AutoDock atom types are computed and assigned. For the macromolecule, atom partial charges and hydrogens were added by using the Gasteiger and Babel methods [45]. The rigid and flexible portions of the macromolecule were separately saved as PDBQT files.
- For running AutoDock, calculation of the grid maps beforehand is necessary in order to reduce the acting area for ligand-macromolecule movements. These maps are calculated by Autogrid, once the coordinates have been established (120 Å ×120 Å ×120 Å) with 0.375 Å of grid spacing. Once Autogrid is executed and the output files obtained, a docking parameter file is configured to run AutoDock.
- For running AutoDock + jMetal, calculation of the grid maps beforehand is necessary in order to reduce the acting area for ligand-macromolecule movements. These maps are calculated by Autogrid, once the coordinates have been established (120 Å ×120 Å ×120 Å) with 0.375 Å of grid spacing. Once Autogrid is executed and the output files obtained, a docking parameter file is configured to run AutoDock + jMetal.
- Using the output files created in the previous steps, we have carried out a thorough experimentation consisting of 30 independent runs for each algorithm evaluated (see Section 3) and molecular instance. From the results of these executions, we have calculated the median and interquartile range (IQR) as measures of location (or central tendency) and statistical dispersion, respectively.
5.1. Parameter Setup
6. Conclusions
- Using a multi-objective approach to solve the molecular docking problem could lead to a broad set of solutions, which can be selected according to the weight of the Einter and Eintra energies, instead of only getting one solution from AutoDock.
- SMPSO provides the best overall performance according to the two quality indicators used and for the studied molecular instances.
- GDE3 and MOEA/D also show a successful performance in terms of convergence and diversity.
- For all studied molecular instances, SMPSO converges to the region biased towards the Einter objective, whereas GDE3 and MOEA/D generate their fronts of non-dominated solutions in a different region to the ones of SMPSO, thereby giving a clue to intramolecular energy optimization.
- According to the mono-objective AutoDock 4.2 fitness function, the SMPSO algorithm found, in most of the cases, better solutions than the ones obtained by the LGA algorithm. This is a noticeable result, since SMPSO is a general purpose optimization technique in addition to having to distribute its resources to different parts of the Pareto front, whereas LGA is specifically adapted to deal with the molecular docking problem.
- The analysis of the ligand binding site and the molecular interactions shows a better position for the ligand conformation computed by the SMPSO than the best energy binding solution returned by the LGA according to the obtained RMSD values. Furthermore, the molecular interactions between the ligand conformation obtained by the SMPSO are in accordance with the reference ligand interactions reported in the literature.
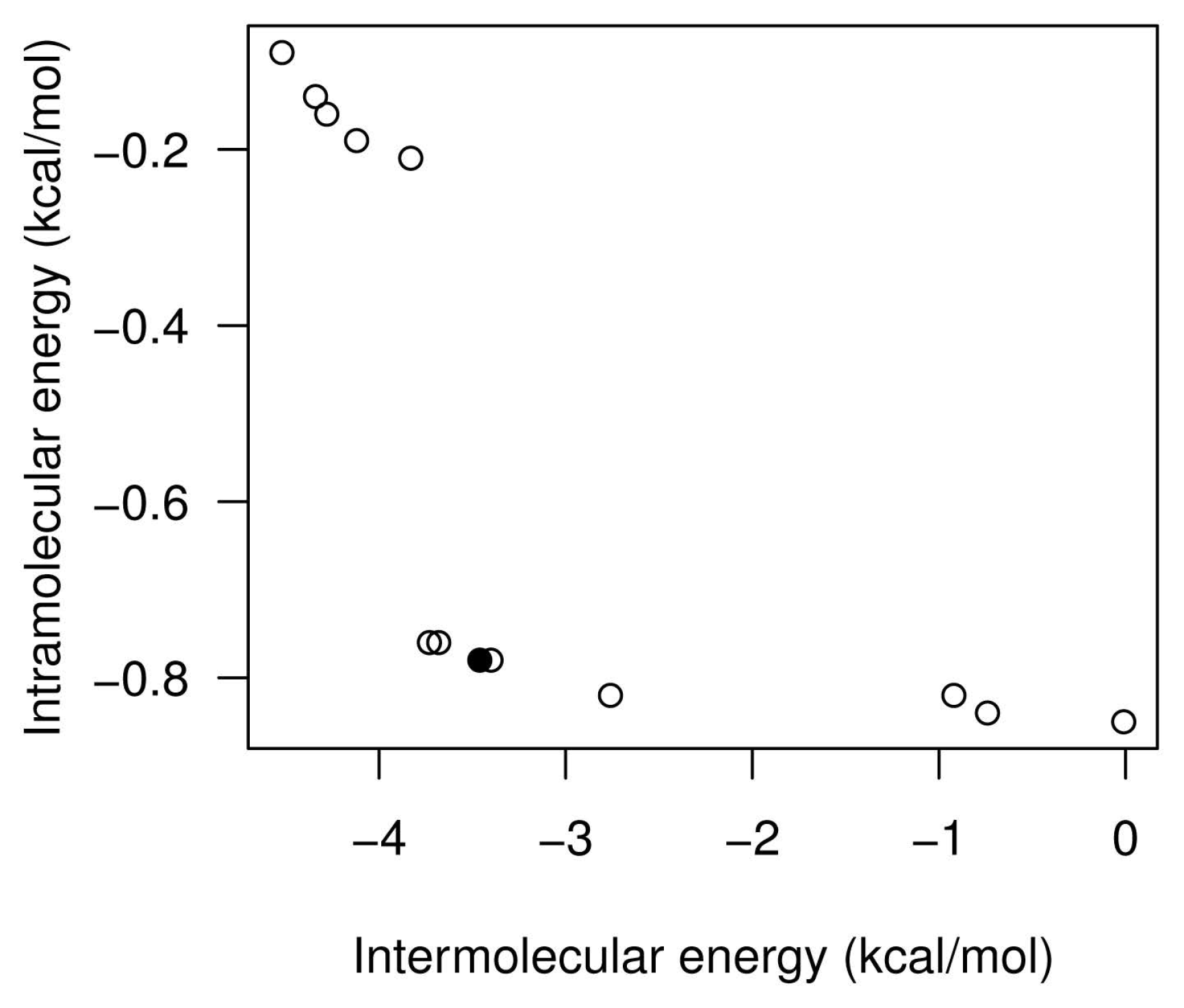
- We have also provided a use case of drug discovery that involves the aeroplysinin-1 compound and the EGFR. The results have demonstrated that according to the use cases presented, it can be more interesting to select a specific docking solution with a balanced tradeoff between Einter and Eintra values. This approach can improve the way in which the expert can select a solution and contributes to the current methods of drug discovery.
Acknowledgments
Author Contributions
Conflicts of Interest
- Sample Availability: Not available
References
- Morris, G.M.; Goodsell, D.S.; Halliday, R.S.; Huey, R.; Hart, W.E.; Belew, R.K.; Olson, A.J. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J Comput Chem 1998, 19, 1639–1662. [Google Scholar]
- Oduguwa, A.; Tiwari, A.; Fiorentino, S.; Roy, R. Multi-objective optimisation of the protein-ligand docking problem in drug discovery. Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 1793–1800.
- Grosdidier, A.; Zoete, V.; Michielin, O. EADock: Docking of small molecules into protein active sites with a multi-objective evolutionary optimization. Proteins 2007, 67, 1010–1025. [Google Scholar]
- Janson, S.; Merkle, D.; Middendorf, M. Molecular docking with multi-objective Particle Swarm Optimization. Appl Soft Comput 2008, 8, 666–675. [Google Scholar]
- Boisson, J.C.; Jourdan, L.; Talbi, E.; Horvath, D. Parallel Multi-objective Algorithms for the Molecular Docking Problem. Proceedings of the 2008 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB ’08), Sun Valley, ID, USA, 15–17 September 2008; pp. 187–194.
- Sandoval-Perez, A.; Becerra, D.; Vanegas, D.; Restrepo-Montoya, D.; Niño, F. A Multi-Objective Optimization Energy Approach to Predict the Ligand Conformation in a Docking Process; EuroGP: Vienna, Austria, 2013; pp. 181–192. [Google Scholar]
- Durillo, J.J.; Nebro, A.J. jMetal: A Java framework for multi-objective optimization. Adv Eng Softw 2011, 42, 760–771. [Google Scholar]
- Sanchez-Faddeev, H.; Emmerich, M.; Verbeek, F.; Henry, A.; Grimshaw, S.; Spaink, H.; van Vlijmen, H.; Bender, A. Using Multiobjective Optimization and Energy Minimization to Design an Isoform-Selective Ligand of the 14-3-3 Protein. Lect Notes Comput Sci 2012, 7610, 12–24. [Google Scholar]
- Van der Horst, E.; Marqués-Gallego, P.; Mulder-Krieger, T.; van Veldhoven, J.; Kruisselbrink, J.; Aleman, A.; Emmerich, M.T.M.; Brussee, J.; Bender, A.; Ijzerman, A.P. Multi-Objective Evolutionary Design of Adenosine Receptor Ligands. J Chem Inf Model 2012, 52, 1713–1721. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A. Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans Evol Comput 2002, 6, 182–197. [Google Scholar]
- Durillo, J.J.; Nebro, A.J.; Luna, F.; Alba, E. On the Effect of the Steady-State Selection Scheme in Multi-Objective Genetic Algorithms. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5467, pp. 183–197. [Google Scholar]
- Nebro, A.J.; Durillo, J.J.; García-Nieto, J.; Coello Coello, C.A.; Luna, F.; Alba, E. SMPSO: A New PSO-based Metaheuristic for Multi-objective Optimization. Proceedings of the IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making, Nashville, TN, USA, 30 March–2 April 2009; pp. 66–73.
- Kukkonen, S.; Lampinen, J. GDE3: The Third Evolution Step of Generalized Differential Evolution. Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 5 September 2005; 1, pp. 443–450.
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans Evol Comput 2007, 11, 712–731. [Google Scholar]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur J Oper Res 2007, 181, 1653–1669. [Google Scholar]
- Coello, C.; Lamont, G.B.; van Veldhuizen, D.A. Multi-Objective Optimization Using Evolutionary Algorithms, 2nd Ed ed; John Wiley & Sons, Inc: New York, NY, USA, 2007. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Inc: New York, NY, USA, 2001. [Google Scholar]
- López-Camacho, E.; García-Godoy, M.J.; Nebro, A.J.; Aldana-Montes, J.F. jMetalCpp: Optimizing molecular docking problems with a C++ metaheuristic framework. Bioinformatics 2014, 30, 437–438. [Google Scholar]
- Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J Comput Chem 2009, 30, 2785–2791. [Google Scholar]
- Rastelli, G. Emerging Topics in Structure-Based Virtual Screening. Pharm Res 2013, 30, 1458–1463. [Google Scholar]
- Dallakyan, S.; Pique, M.E.; Huey, R. Autodock, version 4.2. Available online: http://autodock.scripps.edu/ (accessed on 25 May 2015).
- Thomsen, R. Flexible ligand docking using evolutionary algorithms: Investigating the effects of variation operators and local search hybrids. Biosystems 2009, 72, 57–73. [Google Scholar]
- Huey, R.; Morris, G.M.; Olson, A.J.; Goodsell, D.S. A semiempirical free energy force field with charge-based desolvation. J Comput Chem 2007, 28, 1145–1152. [Google Scholar]
- Li, H.; Zhang, Q. Multiobjective Optimization Problems With Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans Evol Comput 2009, 13, 229–242. [Google Scholar]
- While, L.; Bradstreet, L.; Barone, L. A. Fast Way of Calculating Exact Hypervolumes. Evol Comput IEEE Trans 2012, 16, 86–95. [Google Scholar]
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behavior: A case study on the CEC’2005 Special Session on Real Parameter Optimization. J Heuristics 2009, 15, 617–644. [Google Scholar]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf Sci 2010, 180, 2044–2064. [Google Scholar]
- López-Camacho, E.; Godoy, M.J.G.; García-Nieto, J.; Nebro, A.J.; Aldana-Montes, J.F. Solving molecular flexible docking problems with metaheuristics: A comparative study. Appl Soft Comput 2015, 28, 379–393. [Google Scholar]
- Backbro, K.; Lowgren, S.; Osterlund, K.; Atepo, J.; Unge, T.; Hulten, J.; Bonham, N.M.; Schaal, W.; Karlen, A.; Hallberg, A. Unexpected binding mode of a cyclic sulfamide HIV-1 protease inhibitor. J Med Chem 1997, 40, 898–902. [Google Scholar]
- Ala, P.J.; Huston, E.E.; Klabe, R.M.; Jadhav, P.K.; Lam, P.Y.S.; Chang, C.H. Counteracting HIV-1 Protease Drug Resistance:? Structural Analysis of Mutant Proteases Complexed with XV638 and SD146, Cyclic Urea Amides with Broad Specificities. Biochemistry 1998, 37, 15042–15049. [Google Scholar]
- Fattorusso, E.; Minale, L.; Sodano, G. Aeroplysinin-1, an antibacterial bromo-compound from the sponge Verongia aerophoba. J Chem Soc Perkin Trans 1 1972, 1, 16–18. [Google Scholar]
- Thoms, C.; Ebel, R.; Proksch, P. Activated Chemical Defense in Aplysina Sponges Revisited. J Chem Ecol 2006, 32, 97–123. [Google Scholar]
- Nieder, M.; Hager, L. Conversion of alpha-amino acids and peptides to nitriles and aldehydes by bromoperoxidase. Arch Biochem Biophys 1985, 240, 121–127. [Google Scholar]
- Hinterding, K.; Knebel, A.; Herrlich, P.; Waldmann, H. Synthesis and biological evaluation of aeroplysinin analogues: A new class of receptor tyrosine kinase inhibitors. Bioorg Med Chem 1998, 6, 1153–1162. [Google Scholar]
- Ebel, R.; Brenzinger, M.; Kunze, A.; Gross, H.; Proksch, P. Wound Activation of Protoxins in Marine Sponge Aplysina aerophoba. J Chem Ecol 1997, 23, 1451–1462. [Google Scholar]
- Senthilkumar, K.; Venkatesan, J.; Manivasagan, P.; Kim, S.K. Antiangiogenic effects of marine sponge derived compounds on cancer. Environ Toxicol Pharmacol 2013, 36, 1097–1108. [Google Scholar]
- Kreuter, M.; Leake, R.; Rinaldi, F.; Muller-Klieser, W.; Maidhof, A.; Muller, W.; Schroder, H. Inhibition of intrinsic protein tyrosine kinase activity of EGF-receptor kinase complex from human breast cancer cells by the marine sponge metabolite (+)-aeroplysinin-1. Comp Biochem Physiol B Comp Biochem 1990, 97, 151–158. [Google Scholar]
- Chemsketch for Academics and Personal Usage. Available online: http://www.acdlabs.com/resources/freeware/chemsketch/ (accessed on 25 May 2015).
- Stamos, J.; Sliwkowski, M.X.; Eigenbrot, C. Structure of the Epidermal Growth Factor Receptor Kinase Domain Alone and in Complex with a 4-Anilinoquinazoline Inhibitor. J Biol Chem 2002, 227, 46265–46272. [Google Scholar]
- Gorshkov, B.; Gorshkova, I.; Makarieva, T. Inhibitory characteristics of 3,5-dibromo-1-acetoxy-4-oxo-2,5-cyclohexadien-1-acetonitrile, a semisynthetic derivative of aeroplysinin-1 from sponges (Aplysinidae), on Na+ - K+-ATPase. Toxicon 1984, 22, 441–449. [Google Scholar]
- Li, S.; Schmitz, K.R.; Jeffrey, P.D.; Wiltzius, J.J.; Kussie, P.; Ferguson, K.M. Structural basis for inhibition of the epidermal growth factor receptor by cetuximab. Cancer Cell 2005, 7, 301–311. [Google Scholar]
- Protein Data Bank Database. Available online: http://www.rcsb.org/pdb/home/home.do (accessed on 25 May 2015).
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J Comput Chem 2004, 25, 1605–1612. [Google Scholar]
- AutoDockTools. Available online: http://autodock.scripps.edu/resources/adt (accessed on 29 May 2015).
- AutoDock-jMetal Framework. Available online: http://khaos.uma.es/autodockjmetal/ (accessed on 25 May 2015).
- HTCONDOR Software. Available online: http://research.cs.wisc.edu/htcondor/ (accessed on 25 May 2015).
- Norgan, A.P.; Coffman, P.K.; Kocher, J.P.A.; Katzmann, D.J.; Sosa, C.P. Multilevel Parallelization of AutoDock 4.2. J Cheminform 2011, 3, 12. [Google Scholar] [CrossRef]
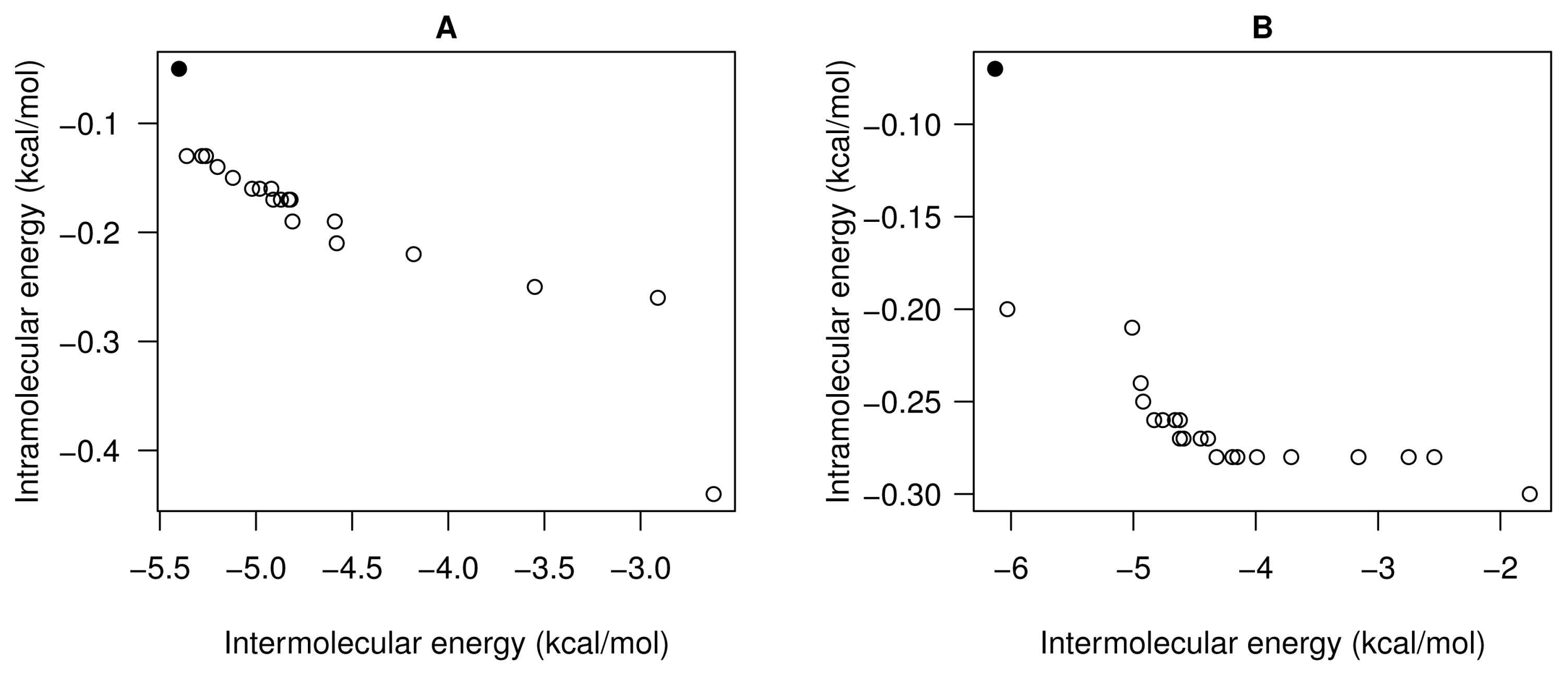
| IHV | Hyper-Volume | |||||
|---|---|---|---|---|---|---|
| NSGA-II | ssNSGA-II | SMPSO | GDE3 | MOEA/D | SMS-EMOA | |
| 1AJV | 4.75×10−21.1×10−1 | 7.47×10−43.1×10−2 | 2.65×10−19.5×10−2 | 1.23×10−19.2×10−2 | 7.39×10−21.3×10−1 | 1.33×10−21.4×10−1 |
| 1AJX | 2.91×10−11.2×10−1 | 2.96×10−11.3×10−1 | 5.69×10−11.1×10−1 | 3.44×10−110−2 | 3.22×10−11.2×10−1 | 3.07×10−11.6×10−1 |
| 1BV9 | 1.33×10−11.3×10−1 | 1.17×10−11.1×10−1 | 5.41×10−13.7×10−1 | 1.79×10−11.9×10−2 | 1.81×10−11.2×10−1 | 1.34×10−11.1×10−1 |
| 1D4K | 2.38×10−11.3×10−1 | 2.54×10−11.2×10−1 | 5.09×10−11.5×10−1 | 3.79×10−110−2 | 2.76×10−17.8×10−2 | 2.62×10−19.6×10−2 |
| 1G2K | 8.06×10−21.5×10−1 | 6.11×10−21.0×10−1 | 5.74×10−12.0×10−1 | 1.62×10−16.4×10−2 | 1.13×10−11.2×10−1 | 5.69×10−21.0×10−1 |
| 1HIV | 7.12×10−29.0×10−2 | 5.39×10−28.0×10−2 | 7.61×10−28.5×10−2 | 1.10×10−17.8×10−2 | 7.78×10−28.8×10−2 | 5.80×10−29.5×10−2 |
| 1HPX | 5.77×10−21.3×10−1 | 2.09×10−26.8×10−2 | 3.06×10−13.8×10−1 | 9.50×10−24.2×10−2 | 8.69×10−29.7×10−2 | 4.93×10−21.1×10−1 |
| 1HTF | 2.80×10−12.8×10−1 | 2.85×10−12.0×10−1 | 5.29×10−21.3×10−1 | 4.03×10−11.3×10−1 | 4.98×10−11.8×10−1 | 2.95×10−12.1×10−1 |
| 1HTG | 9.20×10−21.0×10−1 | 9.08×10−28.5×10−2 | 3.68×10−32.7×10−2 | 1.80×10−11.6×10−2 | 1.62×10−13.3×10−2 | 1.47×10−18.8×10−2 |
| 1HVH | 2.10×10−11.5×10−1 | 9.27×10−21.1×10−1 | 5.04×10−12.9×10−1 | 3.28×10−11.0×10−1 | 1.78×10−11.9×10−1 | 9.22×10−22.2×10−1 |
| 2UPJ | 3.65×10−17.2×10−2 | 3.75×10−19.5×10−2 | 4.23×10−11.1×10−1 | 5.20×10−11.6×10−1 | 4.05×10−19.3×10−2 | 3.75×10−11.1×10−1 |
| Iɛ+ | Epsilon | |||||
| NSGA-II | ssNSGA-II | SMPSO | GDE3 | MOEA/D | SMS-EMOA | |
| 1AJV | 7.74×10+02.2×10+0 | 8.64×10+01.7×10+0 | 1.48×10+03.2×10−1 | 6.55×10+08.3×10−1 | 6.84×10+01.7×10+0 | 8.21×10+02.4×10+0 |
| 1AJX | 6.65×10+01.5×10+0 | 7.04×10+01.4×10+0 | 1.64×10+02.6×10−1 | 6.44×10+03.9×10−1 | 6.18×10+09.5×10−1 | 6.51×10+02.0×10+0 |
| 1BV9 | 1.11×10+11.8×10+0 | 1.15×10+12.0×10+0 | 1.09×10+08.7×10−1 | 1.15×10+13.7×10−1 | 1.03×10+11.6×10+0 | 1.15×10+12.0×10+0 |
| 1D4K | 1.15×10+12.5×10+0 | 1.17×10+12.4×10+0 | 2.45×10+06.7×10−1 | 1.06×10+11.3×10+0 | 1.11×10+11.7×10+0 | 1.14×10+12.5×10+0 |
| 1G2K | 7.55×10+02.4×10+0 | 7.81×10+01.7×10+0 | 9.30×10+05.1×10−1 | 6.13×10+01.0×10+0 | 6.99×10+01.7×10+0 | 7.88×10+01.8×10+0 |
| 1HIV | 8.85×10+01.7×10+0 | 9.49×10+01.5×10+0 | 3.11×10+03.4×10+0 | 8.75×10+01.2×10+0 | 7.88×10+01.8×10+0 | 9.36×10+02.0×10+0 |
| 1HPX | 6.98×10+01.7×10+0 | 7.28×10+01.2×10+0 | 2.60×10+06.0×10+0 | 6.93×10+03.6×10−1 | 6.04×10+01.4×10+0 | 7.18×10+01.2×10+0 |
| 1HTF | 5.26×10+02.0×10+0 | 5.23×10+01.5×10+0 | 6.93×10+01.4×10+0 | 4.37×10+09.4×10−1 | 3.65×10+01.3×10+0 | 5.16×10+01.6×10+0 |
| 1HTG | 2.23×10+12.9×10+0 | 2.23×10+12.3×10+0 | 3.57×10+03.8×10+0 | 1.97×10+18.8×10−1 | 1.86×10+11.2×10+0 | 2.09×10+12.6×10+0 |
| 1HVH | 8.56×10+02.5×10+0 | 9.92×10+02.1×10+0 | 3.08×10+02.2×10+0 | 7.54×10+01.2×10+0 | 7.53×10+02.2×10+0 | 1.01×10+13.3×10+0 |
| 2UPJ | 8.05×10+01.6×10+0 | 7.74×10+02.2×10+0 | 1.60×10+02.2×10−1 | 5.82×10+02.7×10+0 | 6.45×10+01.0×10+0 | 7.59×10+01.8×10+0 |
| Hyper-Volume (IHV ) | Epsilon (Iɛ+) | Metrics’ Hits | |||||
|---|---|---|---|---|---|---|---|
| Algorithm | FriRank | HolmAp | Algorithm | FriRank | HolmAp | Algorithm | Ranking |
| GDE3 * | 1.81 | - | SMPSO * | 1.45 | - | SMPSO | (2 + 1 = 3) |
| SMPSO | 2.18 | 6.48×10−1 | MOEA/D | 2.27 | 3.05×10−1 | GDE3 | (1 + 3 = 4) |
| MOEA/D | 2.63 | 6.10×10−1 | GDE3 | 2.72 | 2.21×10−1 | MOEA/D | (3 + 2 = 5) |
| SMS-EMOA | 4.50 | 2.32×10−3 | NSGA-II | 4.50 | 4.04×10−4 | NSGA-II | (5 + 4 = 9) |
| NSGA-II | 4.63 | 1.64×10−3 | SMS-EMOA | 4.63 | 2.65×10−4 | SMS-EMOA | (6 + 5 = 11) |
| ssNSGA-II | 5.22 | 9.62×10−5 | ssNSGA-II | 5.40 | 3.57×10−5 | ssNSGA-II | (6 + 6 = 12) |
| Algorithms/Instance | 1AJV | 1AJX | 1BV9 | 1D4K | 1G2K | 1HIV | 1HPX | 1HTF | 1HTG | 1HVH | 2UPJ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SMPSO | −12.56 | −11.22 | −17.07 | −18.67 | −12.83 | −13.89 | −10.34 | −6.83 | −31.66 | −15.59 | −10.91 |
| LGA | −7.26 | −6.20 | −7.62 | −11.25 | −7.19 | −9.06 | −5.70 | −7.30 | −31.79 | −9.39 | −5.90 |
| Protein-Ligand Complexes | PDB Code | Resolution (Å) |
|---|---|---|
| HIV-1 protease/AHA006 | 1AJV | 2 |
| HIV-1 protease/AHA001 | 1AJX | 2 |
| HIV-1 protease/α-D-glucose | 1BV9 | 2.20 |
| HIV-1 protease/macrocyclic peptidomimetic inhibitor 8 | 1D4K | 1.85 |
| HIV-1 protease/AHA047 | 1G2K | 1.95 |
| HIV-1 protease/U75875 | 1HIV | 2 |
| HIV-1 protease/KNI-272 | 1HPX | 2 |
| HIV-1 protease/GR126045 | 1HTF | 2.20 |
| HIV-1 protease/GR137615 | 1HTG | 2 |
| HIV-1 protease/Q8261 | 1HVH | 1.80 |
| HIV-1 protease/U100313 | 2UPJ | 3 |
| Algorithm | Parameter | Value |
|---|---|---|
| NSGA-II | Selection | Binary Tournament |
| ssNSGA-II | Crossover | SBX (pc = 0.9; ηc = 20) |
| Mutation | Polynomial (pm = 1=n; ηm = 20) | |
| SMPSO | Archive size | 150 |
| Acceleration coefficients | ϕ1 = 1, 5; ϕ2 = 1, 5 | |
| Inertia | W = 0.9 | |
| Mutation | Polynomial (pm = 1=n; ηm = 20) | |
| GDE3 | DE variant | rand/1/bin |
| Mutation | μ = 0.5 | |
| Crossover | Cr = 0.5 | |
| MOEA/D | DE variant | rand/1/bin |
| Crossover | Cr = 1.0 | |
| Mutation | μ = 0.5; Polynomial (pm = 1=n; ηm = 20) | |
| SMS-EMOA | Selection | Random |
| Crossover | SBX (pc = 0.9; ηc = 20) | |
| Mutation | Polynomial (pm = 1=n; ηm = 20) | |
| Reference point | Maximum objective values plus offset=20 | |
| Common parameters | Population size | 150 individuals (or particles) |
| Stopping condition | 1,500,000 function evaluations | |
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Godoy, M.J.; López-Camacho, E.; García-Nieto, J.; Nebro, A.J.; Aldana-Montes, J.F. Solving Molecular Docking Problems with Multi-Objective Metaheuristics. Molecules 2015, 20, 10154-10183. https://doi.org/10.3390/molecules200610154
García-Godoy MJ, López-Camacho E, García-Nieto J, Nebro AJ, Aldana-Montes JF. Solving Molecular Docking Problems with Multi-Objective Metaheuristics. Molecules. 2015; 20(6):10154-10183. https://doi.org/10.3390/molecules200610154
Chicago/Turabian StyleGarcía-Godoy, María Jesús, Esteban López-Camacho, José García-Nieto, Antonio J. Nebro, and José F. Aldana-Montes. 2015. "Solving Molecular Docking Problems with Multi-Objective Metaheuristics" Molecules 20, no. 6: 10154-10183. https://doi.org/10.3390/molecules200610154