Vibrational Effect on Entropy Generation in a Square Porous Cavity
Abstract
:Introduction
Equations and Numerical Methods
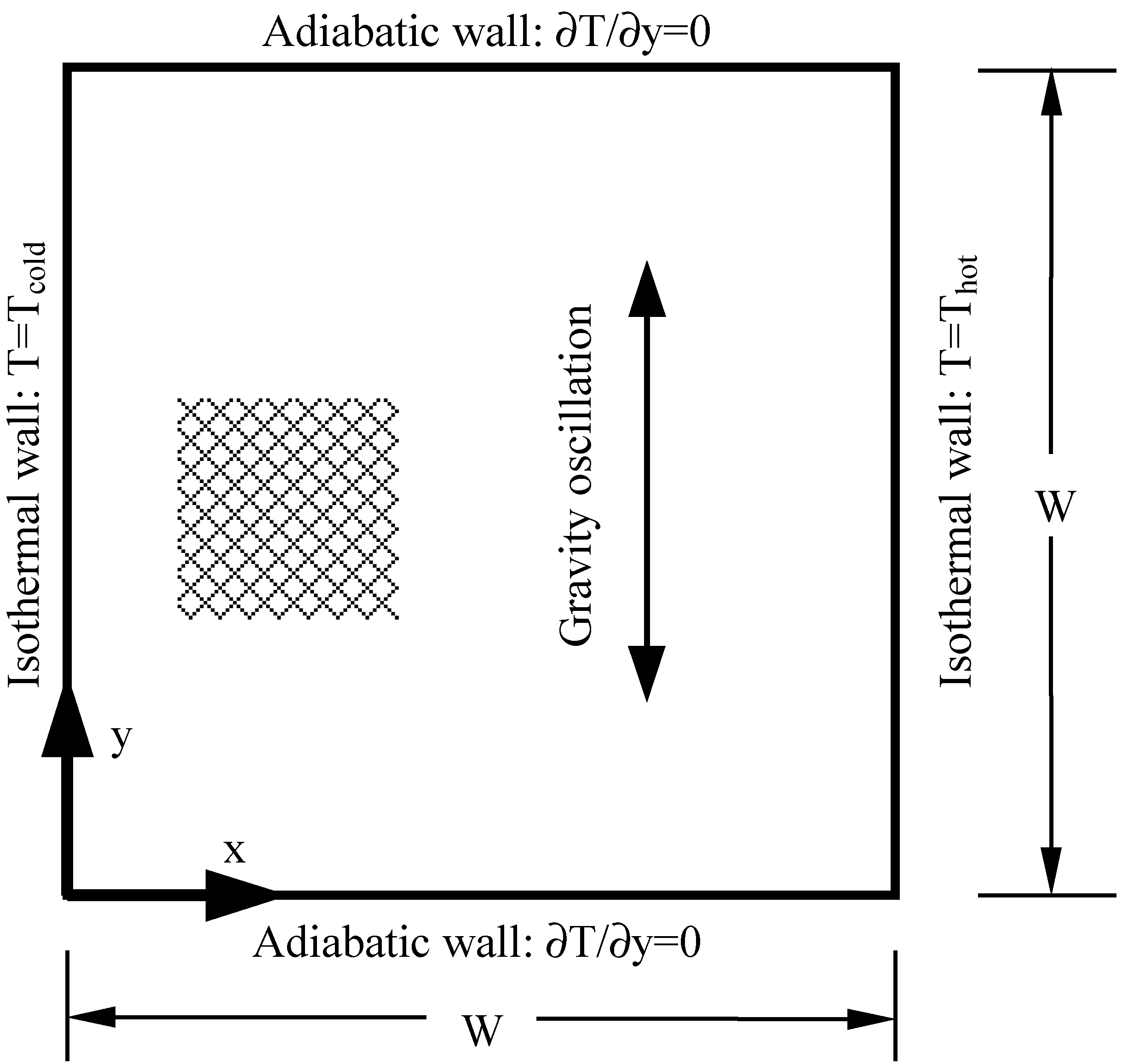
Entropy Generation
| Nuav | |||
|---|---|---|---|
| Ra=10 | Ra=100 | Ra=1000 | |
| Baytas and Pop [10] | 1.079 | 3.16 | 14.06 |
| Walker and Homsy [11] | -------- | 3.10 | 12.96 |
| Gross et al. [12] | -------- | 3.14 | 13.45 |
| Manole and Lage [13] | -------- | 3.12 | 13.64 |
| Moya et al. [14] | 1.065 | 2.80 | ------- |
| Present prediction | 1.079 | 3.14 | 13.82 |
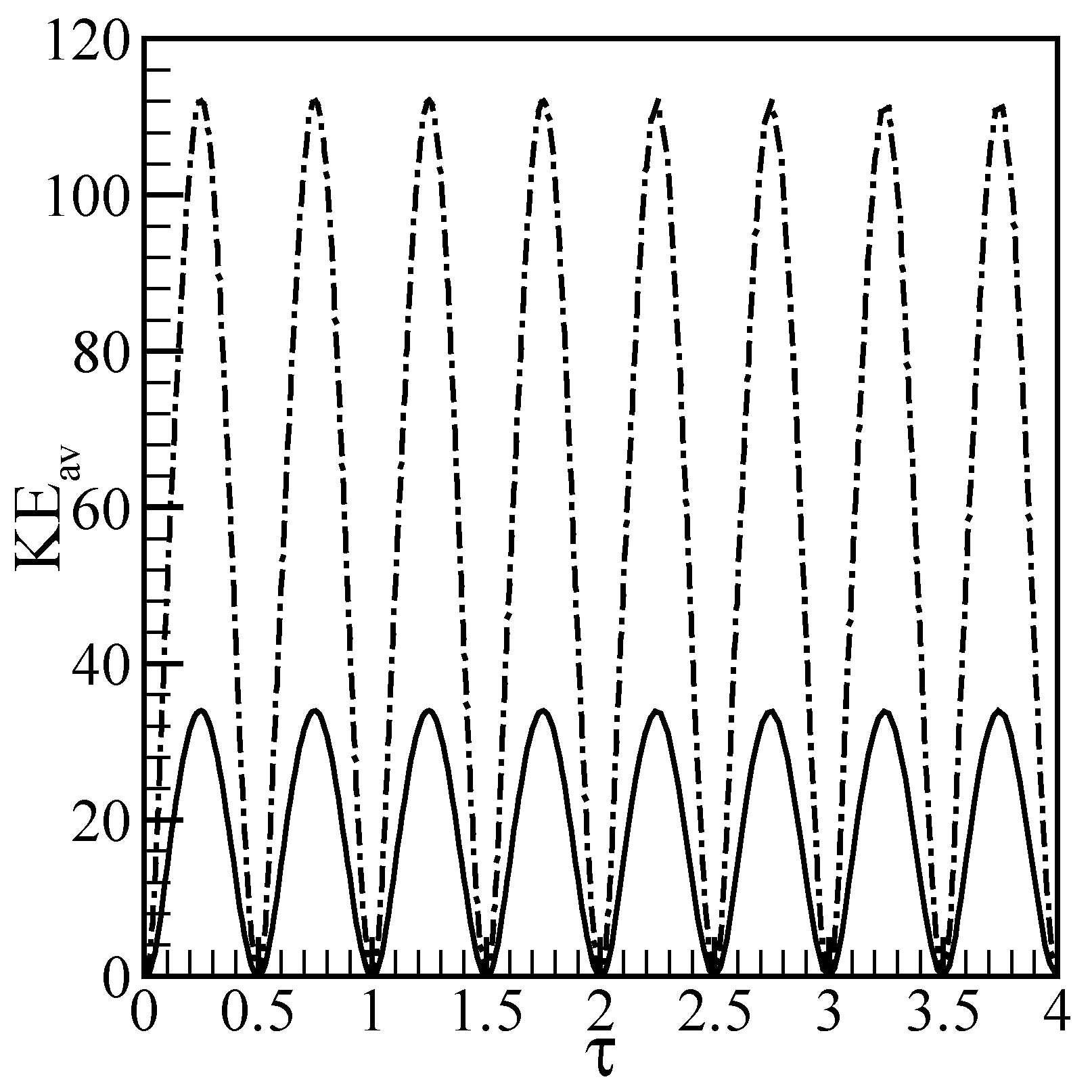
Results and discussion
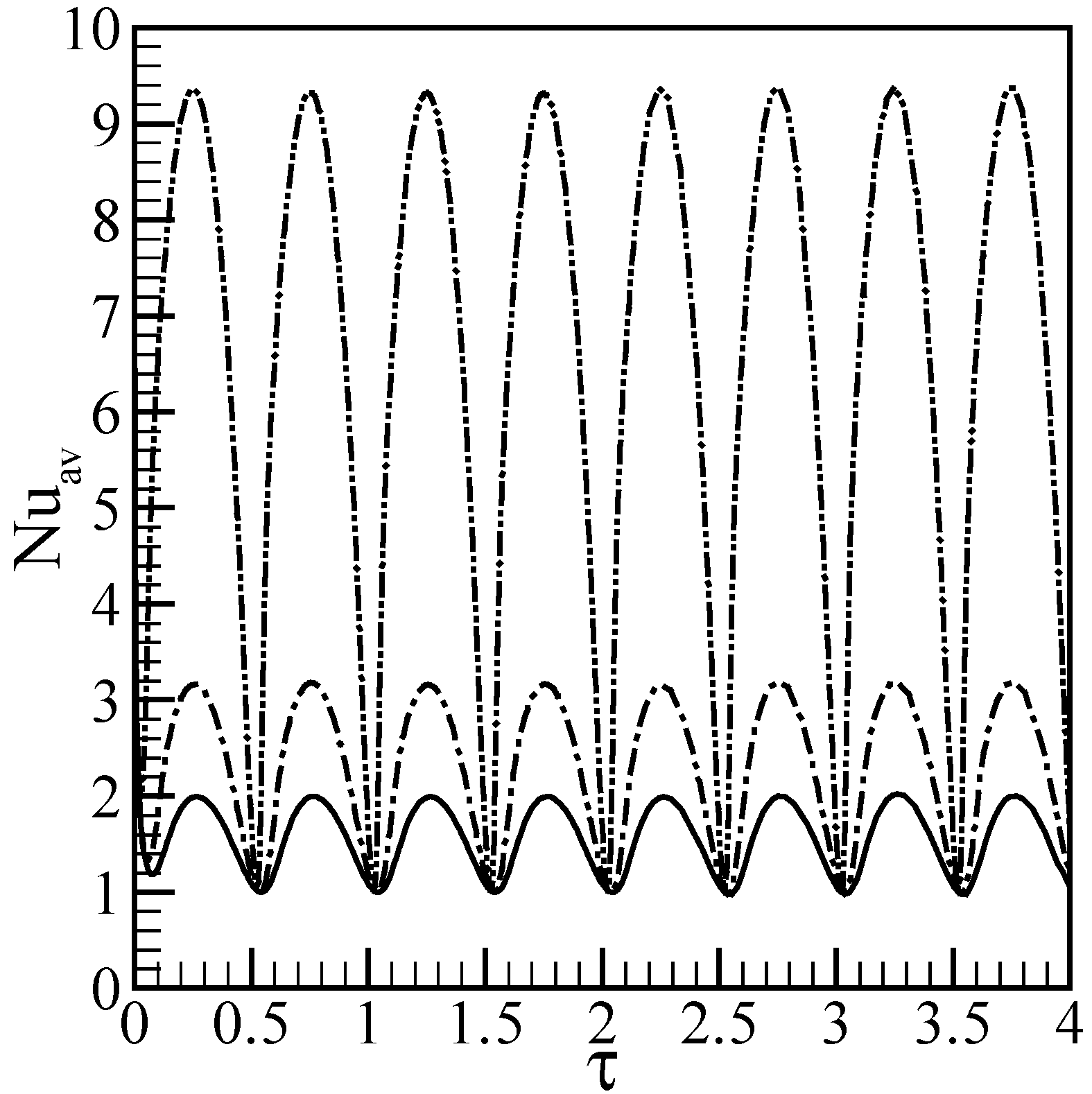
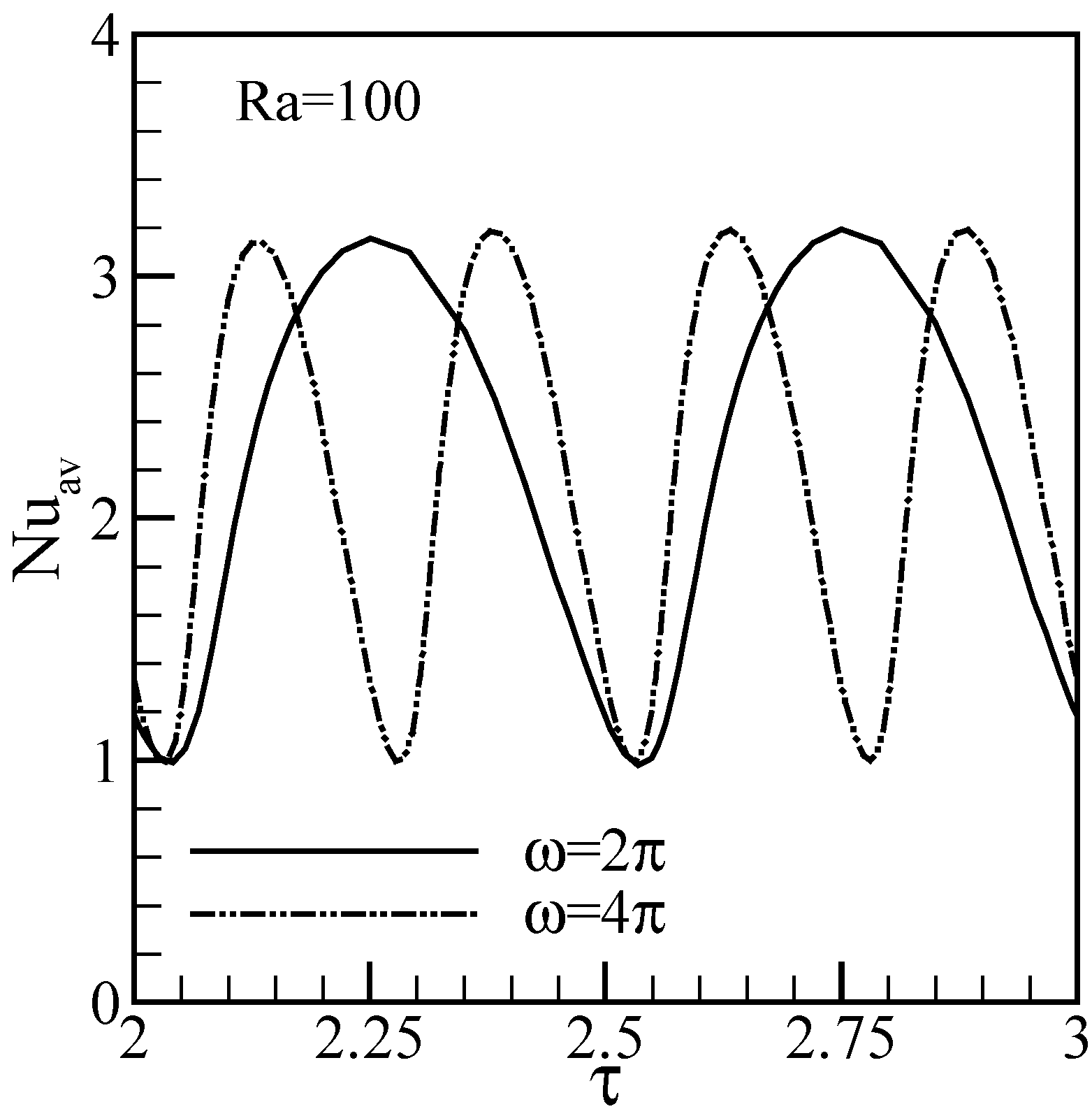
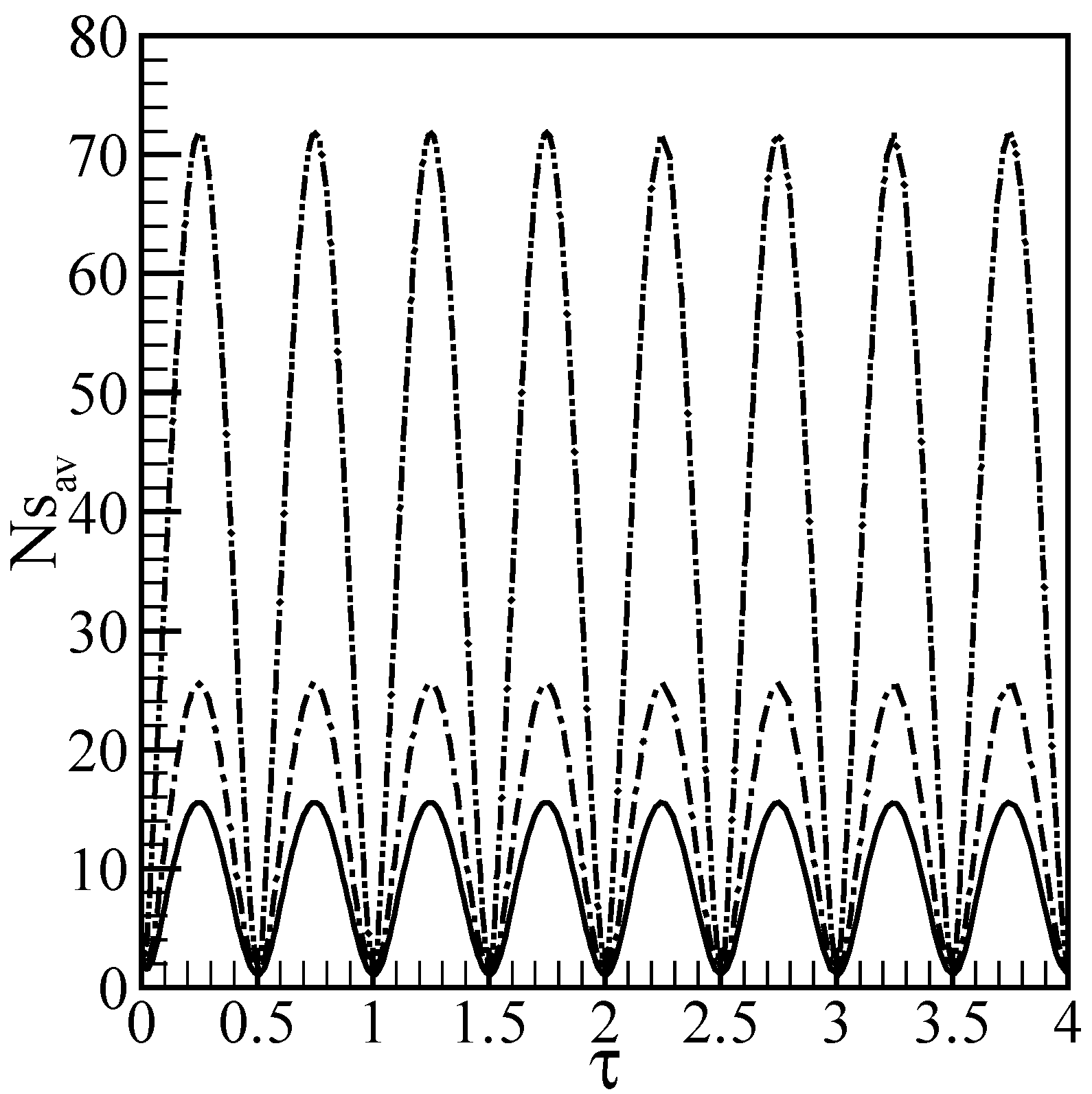
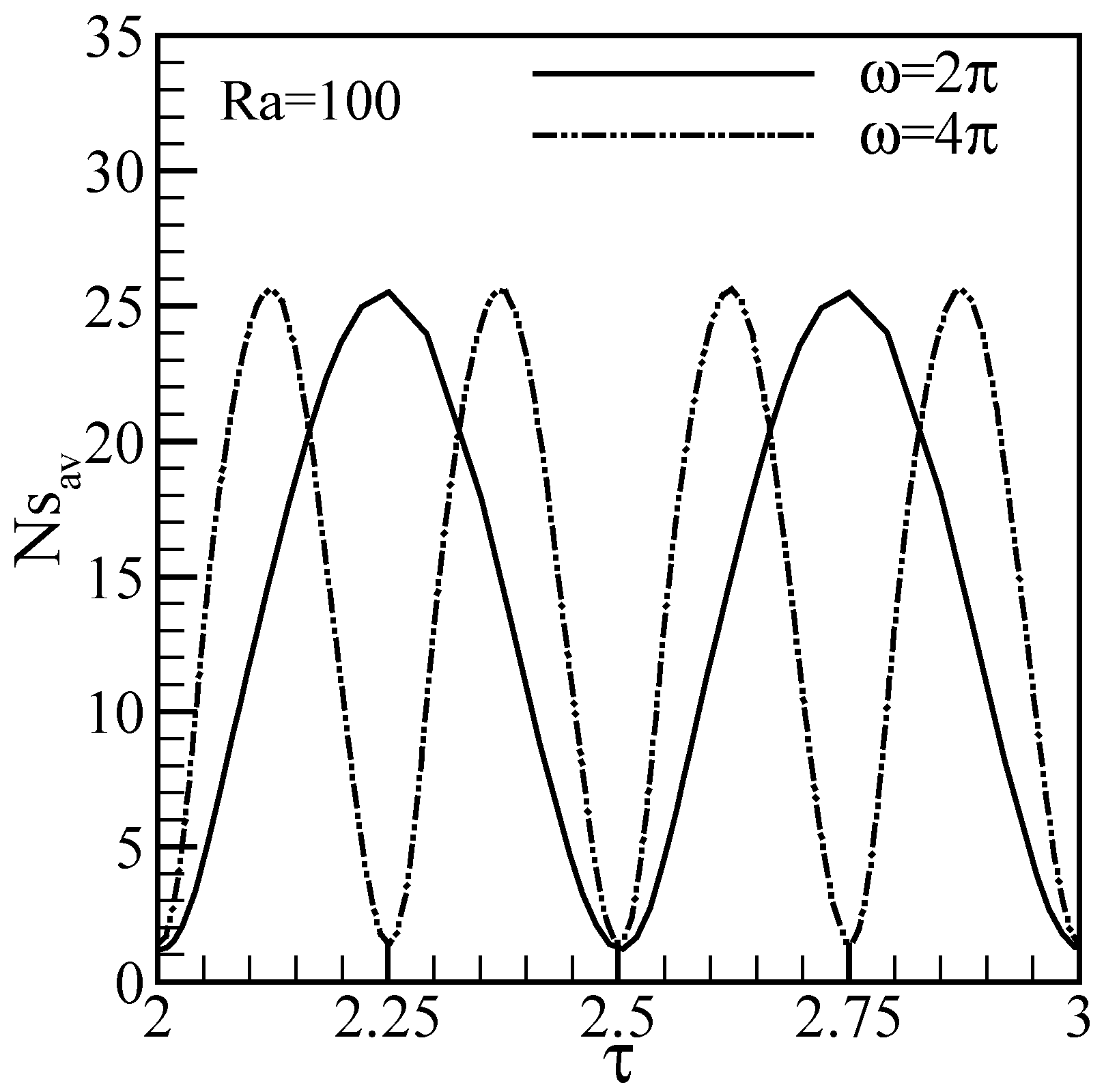
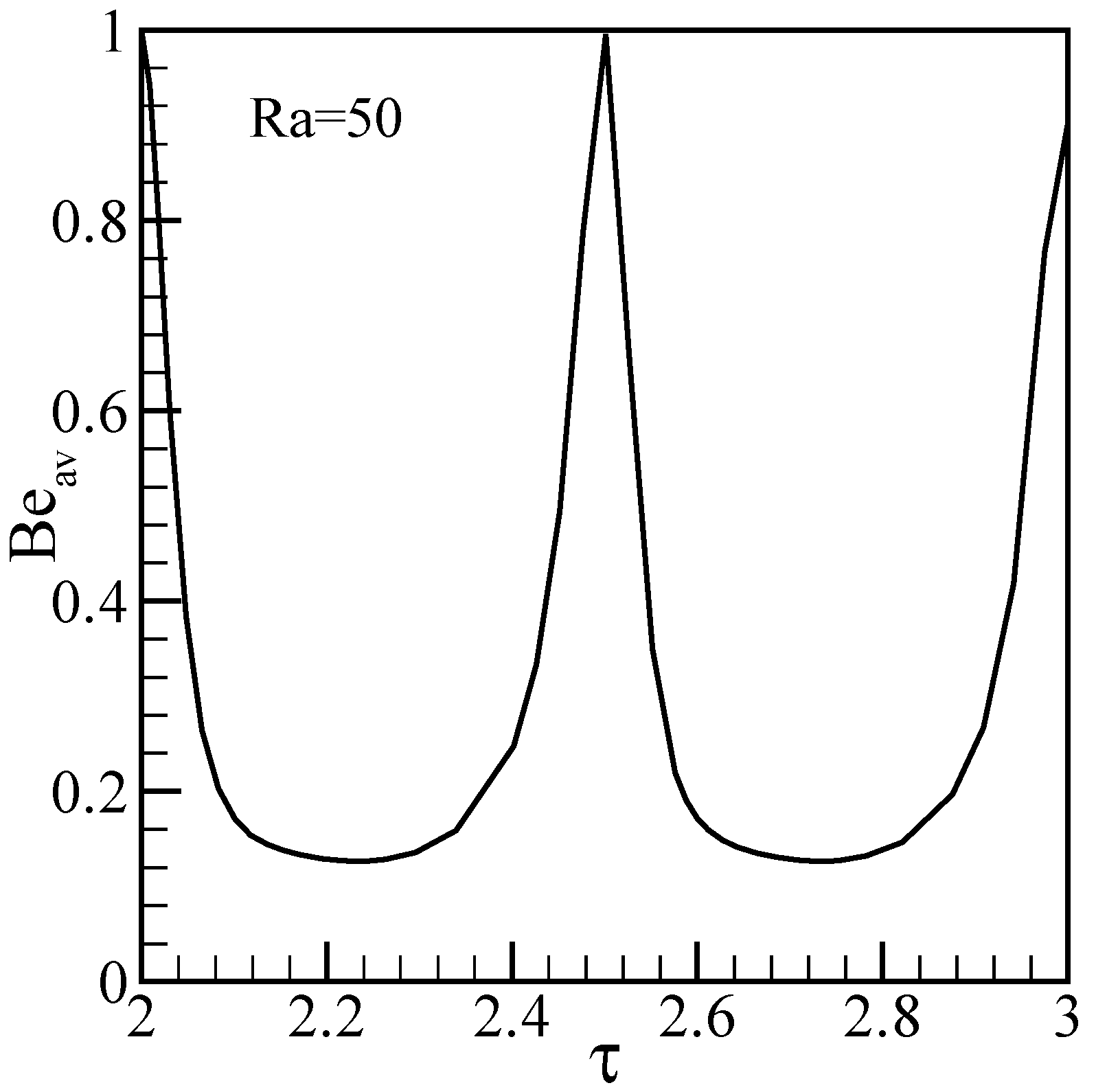
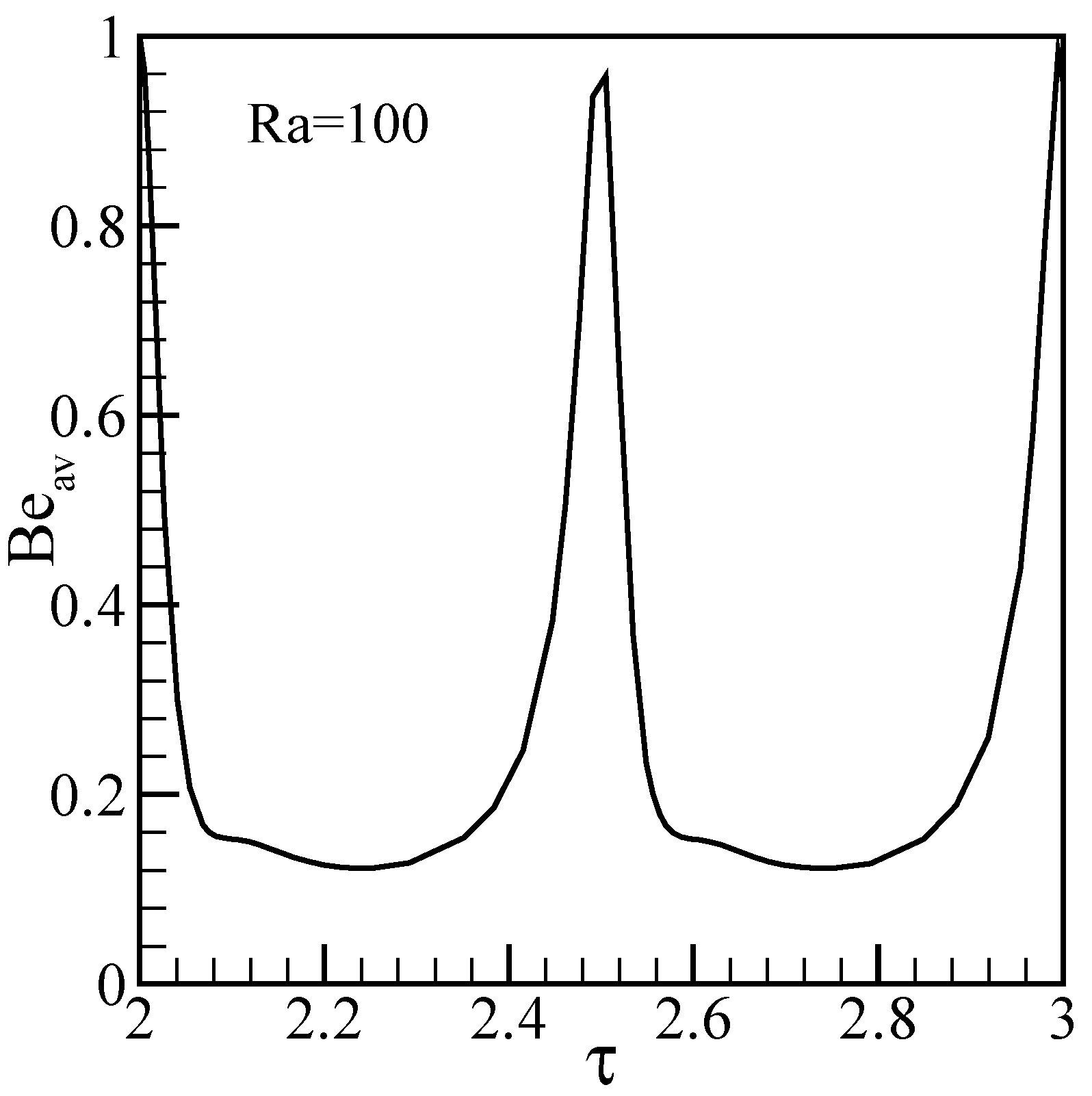
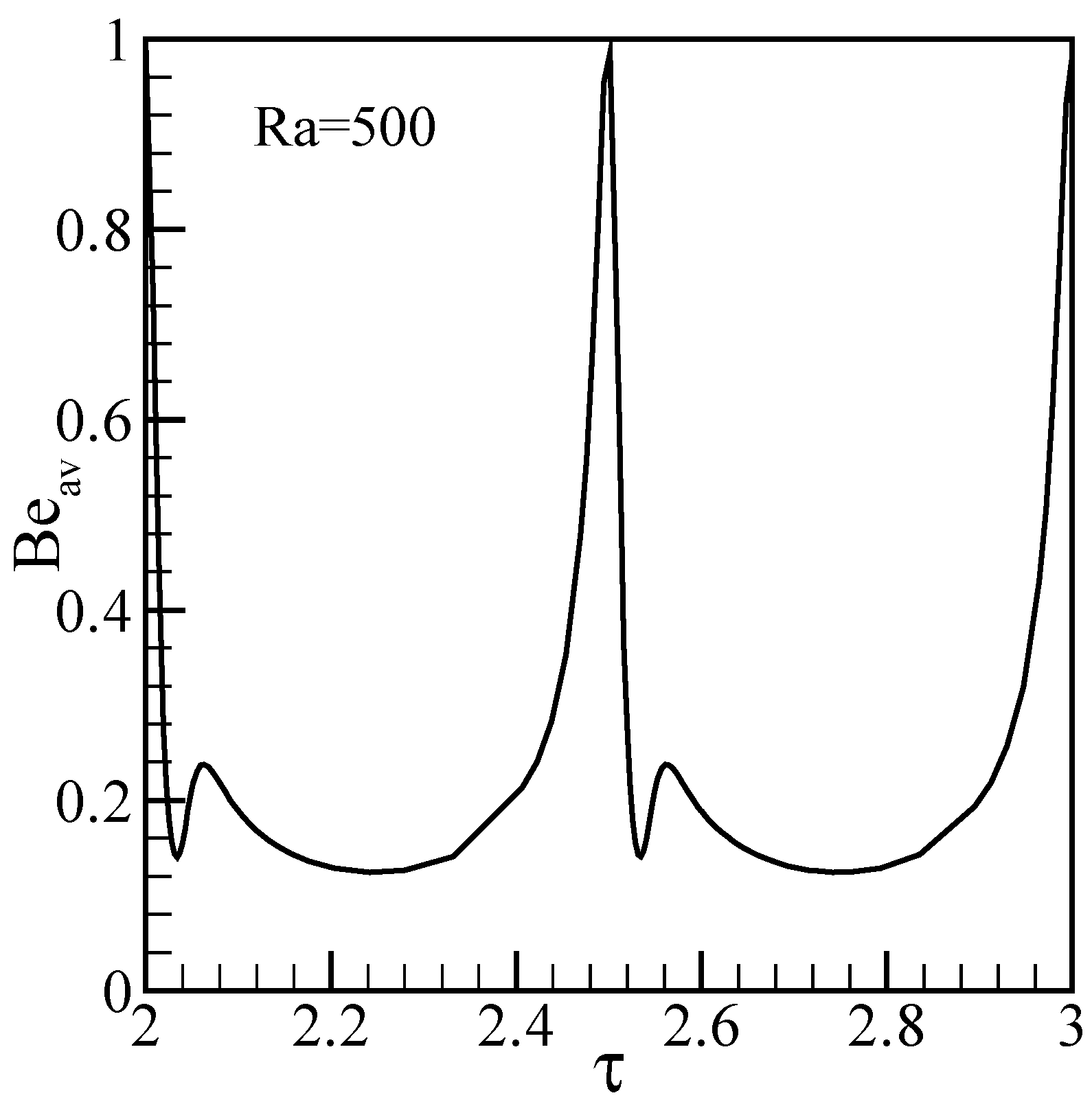
Conclusions
Nomenclature
| A | Area of the cavity, m2. |
| Be | Bejan number, (see Eq. (8)). |
| Cp | Specific heat of the fluid, J.kg-1.0C-1. |
| Cs | Specific heat of the solid matrix, J.kg-1.0C-1. |
| Ecm | Modified Eckert number = . |
| K | Permeability of the porous media, m2. |
| KE | Kinetic energy, J. |
| Ns | Entropy generation number, (see Eq. (7)). |
| Nu | Nusselt number, (see Eq. (9)). |
| Pr | Prandtl number = ν/α. |
| Ra | Rayleigh number, (see Eq. (3)). |
| Entropy generation rate, W.m-3.K-1. | |
| Characteristics entropy transfer rate, (see Eq. (5)). | |
| T | Temperature of the fluid, 0C. |
| T0 | Reference temperature, 0C. |
| t | Time, sec. |
| u* | x-component of the velocity, m.sec-1. |
| v* | y-component of the velocity, m.sec-1. |
| u | x-component of the dimensionless velocity = u*/u0. |
| v | y-component of the dimensionless velocity = v*/u0. |
| u0 | Reference velocity = α/W. |
| W | Width and height of the cavity, m. |
| x* | Horizontal distance, m. |
| y* | Vertical distance, m. |
| x | Dimensionless horizontal distance =x*/W. |
| y | Dimensionless vertical distance =y*/W. |
| Greek symbols | |
| α | Thermal diffusivity of the fluid, m2.sec-1. |
| β | Thermal expansion coefficient of the fluid, 0C-1. |
| ψ* | Streamfunction, m2.sec-1. |
| ψ | Dimensionless streamfunction = ψ*/α. |
| Θ | Dimensionless temperature = (T-T0)/ΔT. |
| ω* | Angular frequency, Hz. |
| ω | Dimensionless angular frequency, (see Eq. (3)). |
| ρ | Density of the fluid, kg.m-3 |
| ρs | Density of the solid matrix, kg.m-3 |
| τ | Dimensionless time = t.α/(W2.σ). |
| σ | Empirical constant (see Eq. (3)) |
| ν | Kinematic viscosity of the fluid, m2.sec-1. |
| ∀ | Volume of the cavity, m3. |
| ϕ | Porosity of the porous media. |
References
- A. Bejan. In Convection Heat Transfer; John Wiley & Sons: New York, 1984.
- Hirata, K.; Sasaki, T.; Tanigawa, H. Vibrational effects on convection in a square cavity at zero gravity. J. Fluid Mechanics. 2001, 445, 327–344. [Google Scholar]
- Biringen, S.; Danabasoglu, G. Computation of convective flow with gravity modulation in rectangular cavities. J. Thermophys. 1990, 4, 357–365. [Google Scholar]
- Gershuni, G.Z.; Zhukhovitskiy, Y.M. Vibration-induced thermal convection in weightlessness. Fluid Mech.–Sov. Res. 1986, 15, 63–84. [Google Scholar]
- Goldhirsch, I.; Pelz, R.B.; Orszag, S.A. Numerical simulation of thermal convection in a two-dimensional finite box. J. Fluid Mech. 1989, 199, 1–28. [Google Scholar]
- Kamotani, Y.; Prasad, A.; Ostrach, S. Thermal convection in an enclosure due to vibrations aboard spacecraft. AIAA J. 1981, 19, 511–516. [Google Scholar]
- Kondos, P.A.; Subramanian, R.S. Buoyant flow in a two-dimensional cavity due to a sinusoidal gravitational field. Microgravity Sci. Technol. 1996, 9, 143–151. [Google Scholar]
- A. Bejan. In Entropy Generation Minimization; CRC Press: New York, 1996.
- Bejan, A. Fundamental of exergy analysis, entropy generation minimization, and the generation of flow architecture. Int. J. Energy Research. 2002, 26, 545–565. [Google Scholar] [CrossRef]
- Baytas, A.C.; Pop, I. Free convection in oblique enclosures filled with a porous medium. Int. J. Heat Mass Transfer. 1999, 42, 1047–1057. [Google Scholar]
- Walker, K.L.; Homsy, G.M. Convection in a porous cavity. J. Fluid Mechanics. 1978, 87, 449–474. [Google Scholar]
- Gross, R.J.; Bear, M.R.; Hickox, C.E. The application of flux-corrected transport (FCT) to high Rayleigh number natural convection in porous medium, in: Proc. 8th International Heat Transfer Conference. San Francisco, CA; 1986. [Google Scholar]
- Manole, D.M.; Lage, J.L. Numerical benchmark results for natural convection in a porous medium cavity. HTD-Vol. 216, Heat and Mass Transfer in Porous Media, ASME Conference 1992. 55–60.
- Moya, S.L.; Ramos, E.; Sen, M. Numerical study of natural convection in a tilted rectangular porous material. Int. J. Heat Mass Transfer, 1987, 30, 741–756. [Google Scholar]
- Gershuni, G.Z.; Lyubimov, D.V. Thermal Vibrational Convection; John Wiley & Sons: New York, 1997. [Google Scholar]
- Baytas, A.C. Entropy generation for natural convection in an inclined porous cavity. Int. J. Heat and Mass Transfer 2000, 43, 2089–2099. [Google Scholar]
© 2003 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Mahmud, S.; Fraser, R.A. Vibrational Effect on Entropy Generation in a Square Porous Cavity. Entropy 2003, 5, 366-376. https://doi.org/10.3390/e5050366
Mahmud S, Fraser RA. Vibrational Effect on Entropy Generation in a Square Porous Cavity. Entropy. 2003; 5(5):366-376. https://doi.org/10.3390/e5050366
Chicago/Turabian StyleMahmud, Shohel, and Roydon Andrew Fraser. 2003. "Vibrational Effect on Entropy Generation in a Square Porous Cavity" Entropy 5, no. 5: 366-376. https://doi.org/10.3390/e5050366




