A Spacetime Foam Approach to the Schwarzschild-de Sitter Entropy

Abstract

The entropy for a black hole in a de Sitter space is approached wwithin the framework of spacetime foam. A simple model made by N wormholes in a semiclassical approximation, is taken under examination to compute the entropy for such a case. An extension to the extreme case when the black hole and cosmological horizons are equal is discussed.

1. Introduction

Black holes have many properties analogous to those of thermodynamics. In particular, four laws of black holes [1] combined with the generalized second law make up a main framework of the black hole thermodynamics. In these laws, black hole entropy is defined as

(1)

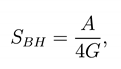
where A is the area of black hole horizon. This formula is known as Bekenstein-Hawking formula, since the concept of black hole entropy as first introduced by Bekenstein [2] as a quantity proportional to the horizon area and the proportionality coefficient as fixed by Ha king’s discovery of thermal radiation with temperature given by

(2)

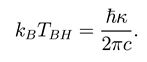
κ is the surface gravity of a background black hole. This thermal radiation and its temperature are called Hawking radiation and Hawking temperature, respectively. Let us recall basic properties of the black hole thermodynamics by taking the example of a one-parameter family of Schwarzschild black holes, parameterized by the mass M. The first la of thermodynamics [1], in this case is

(3)

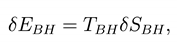
where E_BH, S_BH and T_BH are quantities that are identified with the energy, the entropy and the temperature of a black hole, respectively. The energy of the black hole is simply given by E_BH = M_BH. A simple relation exists also for the temperature T_BH. Hawking showed that a black hole with surface gravity κ emits thermal radiation of a quantum matter field (which plays the roˆle of a thermometer) at temperature given by Eq. (2) [3]. Since κ = C⁴/4GM_BH, it is natural to define the temperature of a Schwarzschild black hole with mass M_BH by

(4)

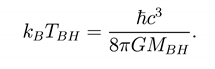
Then from Kqs.(2)-(4), we get

(5)

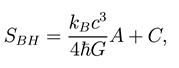
where A Ξ 16πG²$M_{\mathrm{BH}}^2$ /C⁴ is the area of the event horizon and C is some constant. Since a value of C is not essential in our discussions, we shall set hereaIter C = 0. This is a special case of the Bekenstein-Hawking formula. It can be shown that classically the area of the event horizon cannot decrease in time (the area law [4] or the second law of black hole) just as the ordinary thermodynamical entropy. This observation as the real motivation of introducing a black-hole entropy [2]. Moreover, when quantum eRects are taken into account, it is believed that a sum of the black hole entropy and matter entropy does not decrease (the generalized second law). The zeroth law of black hole thermodynamics states that surface gravity of a Killing horizon is constant throughout the horizon. This is expected for the Schwarzschild black hole, because it is a static black hole. What is unexpected is that the same result is valid also for a Kerr black hole, which is dependent by its temperature, while the surface gravity is not. Of course we could just check this result but the point is that it is. This supports the choice of the black-hole temperature. The third law does hold in the sense of Nernst: it is impossible by any process, no matter how idealized, to reduce the surface gravity to zero in a finite sequence by operations [1]. Thermodynamics has a well-established microscopic description: the quantum statistical mechanics. In the thermodynamical description, information on each microscopic degree of freedom is lost, and only macroscopic variables are concerned. However, the number of all microscopic degrees of freedom is implemented in a macroscopic variable: entropy S is related to the number of all consistent microscopic states N as

(6)

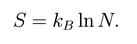
In analogy, it is expected that there might be a microscopic description of the black hole thermodynamics, too. In particular, it is widely believed that the black hole entropy might be related to a number of microscopic states. This microscopic description seems to require a yet to be developed quantum theory of gravity. Actually a microscopic derivation of the black hole entropy as given in superstring theory [5,6,7] by using the so-called D-brane technology. In this approach, the black hole entropy is identified with the logarwithm of the number of states of massless strings attached to D-branes, with D-brane configuration and total momentum of the strings along a compactified direction fixed to be consistent with the corresponding black hole [8,9]. The analysis along this line as extended to the so-called M-theory [10]. Recently a diRerent approach based on a foamy structure of space-time has been proposed [11,12]. In this approach space-time foam is described by a collection of N coherent wormholes, hose energy density (Casimir energy) at its minimum, is

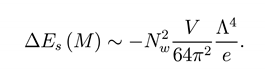
Λ is an U.V. cut-off, V is the volume of the space and N_w is the wormholes number. When we apply the wormhole model to the area, we obtain the mass quantization of the Schwarzschild black hole, namely ¹

(7)

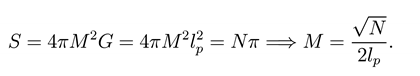
A second consequence is that in de Sitter space, the cosmological constant is quantized in terms of l_p, i.e.

(8)

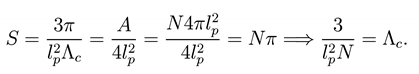
In this paper we would like to apply the same wormhole model of spacetime foam, to compute the entropy of a black hole embedded in a de Sitter space hose line element is described by the Schwarzschild-de Sitter metric (SdS). We will also look at its extreme version, the so-called Nariai metric [13]. The plan of the paper is the following: in Section 2, we will briefly report our model of space-time foam, in Section 3, we give a simple example of application of the resulting discretized (foamy) spacetime to the computation of the entropy in the Sch arzschild and in de Sitter case; in Section 4, we discuss the entropy quantization in the case of the SdS case. We summarize and conclude in Section 5.

2. Constructing the Foam

When we try to merge General Relativity with Quantum Field Theory at the Planck scale, spacetime could be subjected to topology and metric fluctuations [14]². Such a fluctuating spacetime is known under the name of ”spasetime foam“which can be taken as a model for the quantum gravitational vacuum. At this scale of lengths (or energies) quantum processes like black hole pair creation could become relevant. To establish if a foamy spacetime could be considered as a candidate for a Quantum Gravitational vacuum, we can examine the structure of the eRective potential for such a spacetime. There are some examples sho ing that flat space cannot be considered as the true ground state for General Relativity [16,17,18,19]. In the case of Ref. [19], the whole spacetime has been considered as a black hole-anti-black hole pair formed up by a black hole with positive mass M in the coordinate system of the observer and an anti black-hole with negative mass —M in the system here the observer is not present. In this way we have an energy preserving mechanism, because flat space has zero energy and the pair has zero energy too. Ho ever, in this case we have not a cosmological forse producing the pair: we have only pure gravitational fluctuations. The black hole-anti-black hole pair has also a relevant pictorial interpretation: the black hole with positive mass M and the anti black-hole with negative mass—M can be considered the components of a virtual dipole with zero total energy created by a large quantum gravitational fluctuation [20]. Note that this is the only physical process compatible with the energy conservation. The importance of having the same energy behaviour (asymptotic) is related to the possibility of having a spontaneous transition from one spacetime to another one with the same boundary condition [21]. This transition is a decay from the false vacuum to the true one [22,23]. Ho ever, if we take account of a pair of neutral black holes living in diRerent universes, there is no decay and more important no temperature is involved to change from flat to curved space. To see if this process is realizable we need to compute quantum corrections to the energy stored in the boundaries. These quantum corrections are pure gravitational vacuum excitations which can be measured by the Casimir energy, formally defined as

(9)

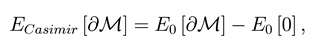
where E₀ is the zero-point energy and ∂$ℳ$ is a boundary. We begin to consider the following line element (Kinstein-Rosen bridge) related to a single wormhole

(10)

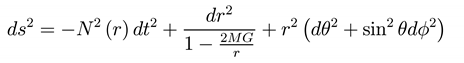
We wish to compute the Casimir-like energy

(11)

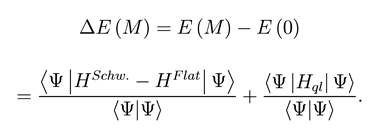
by perturbing the three-dimensional spatial metric g_ij = ${\tilde{g}}_{ij}$ + h_ij . ΔE (M) is computed in a WKB approximation, by looking at the graviton sector (spin 2 or TT tensor) in a Schrödinger representation with trial ave functionals of the Gaussian form by means of a variational approach. The Spin-two operator is defined as

(12)

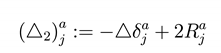
where Δ is the Laplacian on a Schwarzschild background and $R_j^a$ is the mixed Ricci tensor hose components are:

(13)

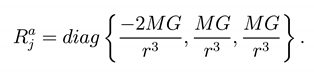
The total energy at one loop, i.e., the classical term plus the stable and unstable modes respectively, is

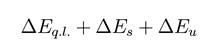
where ΔE_q.l. is the quasilocal energy. For symmetric boundary conditions with respect to the bifurcation surface S₀ (such as this case E_q.l. = E₊ − E₋ = 0. When the boundaries go to spatial infinity E_± = M_ADM . The Stable modes contribution is

(14)

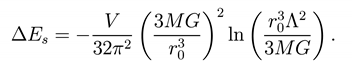
Λ is a cut-oR to keep under control the UV divergence, we can think that Λ ≤ m_p. For the unstable sector, there is only one eigenvalue in S-wave. This is in agreement with Coleman arguments on quantum tunneling: the presence of a unique negative eigenvalue in the second order perturbation is a signal of a passage from a false vacuum to a true vacuum. The RayleighRitz method joined to a numerical integration technique gives E² = −.175 41/(MG)² [19], to be compared with the value E² = −.19/(MG)² of Ref. [16]. How to eliminate the instability?

We consider N_w coherent ormholes (i.e., non-interacting) in a semiclassical approximation and assume that there exists a covering of ∑ such that ∑ = ${\cup }_{i=1}^{N_w}$∑_i, with ∑_i∩∑_j = Φ when i ≠ j. Each ∑_i has the topology S² × R^l with boundaries ∂${\sum }_i^{\pm }$ with respect to each bifurcation surface. On each surface ∑_i, quasilocal energy is zero because we assume that on each copy of the single Wormhole there is symmetry with respect to each bifurcation surface. Thus the total energy for the collection is $E_{|2}^{\mathit{tot}}$ = N_wH_|2 and the total trial ave functional is the product of N_w t.w.f.

(15)

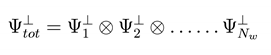
By repeating the same calculations done for the single ormhole for the N_w wormhole system, we obtain

(a)

The total Casimir energy (stable modes), at its minimum, is

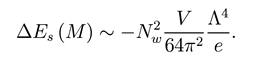
The minimum does not correspond to flat space → ΔE_s (M) ≠ 0.

(b)

The initial boundary located at R_± will be reduced to R_±/N_w.

(c)

Since the boundary is reduced there exists a critical radius ρ_c = 1.113 4 such that: ∀N ≥ N_w ∃ r_c s.t. ∀ r₀ ≤ r ≤ r_c, σ (Δ₂) = Φ. This means that the system begins to be stable [11,12]. To be compared with the value ρ_c = 1.445 obtained by B. Allen in Ref. [24].

3. Area Spectrum, Entrop) and the Cosmological constant

Bekenstein has proposed that a black hole does have an entropy proportional to the area of its horizon S_bh = const × A_hor [2]. In natural units one finds that the proportionality constant is set to 1/4G = 1/4$l_p^2$, so that the entropy becomes S = A/4G = A/4$l_p^2$. Another proposal always made by Bekenstein is the quantization of the area for nonextremal black holes a_n = α$l_p^2$(n + η) η > −1 n = 1,2,… The area is measured by the quantity

(16)

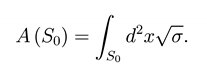
We would like to evaluate the mean value of the area

(17)

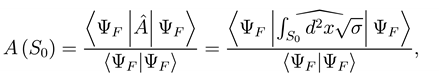
computed on the foam state

(18)

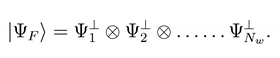
Consider σ_ab = ${\stackrel{-}{\sigma }}_{ab}$ + δ${\sigma }_{ab}$${\stackrel{-}{\sigma }}_{ab}$ is such that ʃS₀ d² x √$\stackrel{-}{\sigma }$ = 4π${\stackrel{-}{r}}^2$ and $\stackrel{-}{r}$ is the radius of S₀

(19)

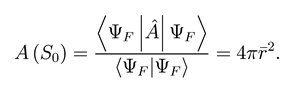
Suppose to consider the mean value of the area A computed on a given macroscopic fixed radius R. On the basis of our foam model, we obtain A = $\underset{i=1}{\overset{N}{\cup }}$ A_i, with A_i ∩ A_j = Φ when i ≠ j. Thus

(20)

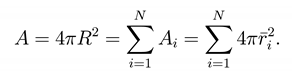
When ${\stackrel{-}{r}}_i$ → l_p, A_i → A_{l p} and [12]

(21)

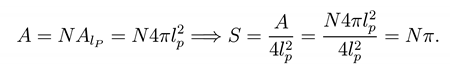
Thus the macroscopic area is represented by N microscopic areas of the Planckian size. In this sense we will claim that the area is quantized. The first consequence is the mass quantization of the Schwarzschild black hole, namely

(22)

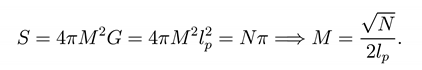
To be compared with Refs. [25,26,27,28,29,30]. A second consequence is that in de Sitter space, the cosmological constant is quantized in terms of l_p, i.e. [31,32]

(23)

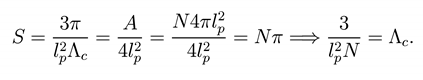
It is possible to give an estimate of the total amount of Plan ckian ormholes needed to fill the space beginning from the Planck era live (∧ ~ (10¹⁶ − 10¹⁸ GeV)²) up to the space in which we now live ∧ ≤ (10⁻⁴²GeV²)

(24)

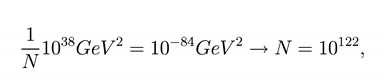
in agreement with the observational data ∧_c ≲ 10⁻¹²² $l_p^{-2}$ coming from the Friedmann-Robertson-Walker cosmology constraining the cosmological constant [33].

4. Entropy for black holes in de Sitter space

The Schwarzschild-de Sitter metric (SdS) is defined as

(25)

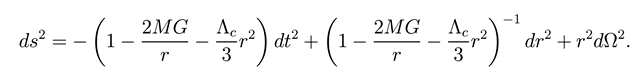
For ∧_c = 0 the metric becomes

(26)

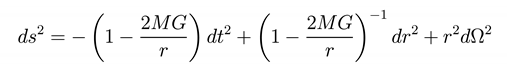
and it describes the Sch arzschild metric, hile for M = 0, we obtain

(27)

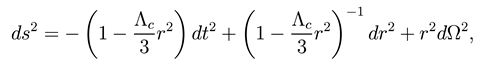
namely the de Sitter metric (dS). The gravitational potential g₀₀ (r) of (25) admits three real roots. One is negative and it is located at

(28)

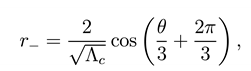
While the other ones are associated to the black hole and cosmological horizons respectively located at

(29)

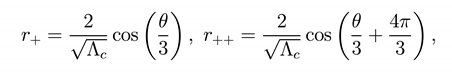
where

(30)

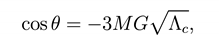
with the condition

(31)

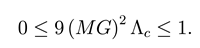
Eq.(30) implies that θ ∈ [$\frac{\pi }{2}$, $\frac{3\pi }{2}$]. In this interval r₊ is a monotonic decreasing function of θ, while r₊₊ is a monotonic increasing one wwith

(32)

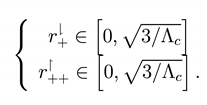
They have a common value hen r₊ = r₊₊ = 1/√∧_c , here 9(MG)²∧ = 1 and Φ = π. This means that the cosmological horizon and the black hole horizon have merged. The relation between the three roots is

(33)

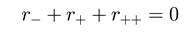
and furthermore

(34)

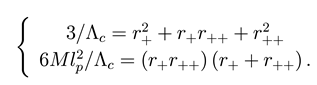
The gravitational entropy in the SdS case is

(35)

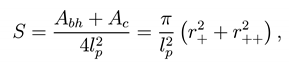
namely it is the sum of the black hole and cosmological entropy [34]. By means of Eqs.(29) one gets,

(36)

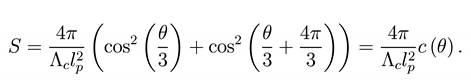
For θ ∈ [$\frac{\pi }{2}$, $\frac{3\pi }{2}$], c (Φ) ∈ [$\frac{1}{2}$, $\frac{3}{4}$] and the entropy is bounded by

(37)

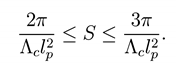
The lower bound of inequality (37) corresponds to the entropy of the Nariai metric, hose (Lorentzian) line element is

(38)

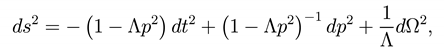
Thus the entropy in the SdS case has an upper bound represented by the de Sitter entropy and a lo er bound represented by the Nariai entropy. By means of Eq.(23), the Nariai entropy is

(39)

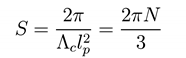
and the relative black hole mass is

(40)

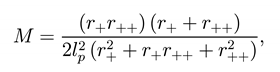
where we have used Eqs.(34) to express the mass and the cosmological constant in terms of the roots of the gravitational potential g ₀₀ (r). When r₊ = r₊₊ = $\stackrel{-}{r}$, the black hole mass is equal to the “cosmologisal mass” M_C

(41)

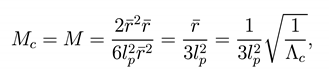
i.e. Eq. (31) for θ = π. Recalling Eq.(23) we obtain

(42)

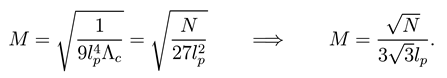
Therefore the black hole mass is bounded by

(43)

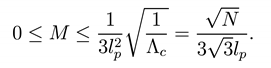
Note that the black hole mass in the Nariai case is lower than the Schwarzschild case: this is the eRect of having a spacetime with a positive cosmological constant which describes a S³ topology. This means that also the black hole radius cannot exceed the cosmological radius. Thus the black hole mass has an upper bound deriving from the extreme case.

5. Conclusions

On the basis of the model of spacetime foam described in Section 3, in this paper an attempt to compute the entropy for the Sch arzschild-de Sitter metric has been performed including also its extreme case or Nariai metric. It is known that semiclassically, one can assign a probability measure that leads to computing the logarwithm of the number of microstates as in the case of a thermal system with an entropy

(44)

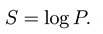
The SdS case entropy is described by Eq.(35). The associated probability is

(45)

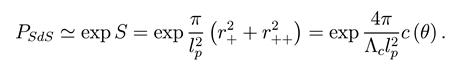
This value interposes t o special cases, as seen. The first is the de Sitter case here M = 0 and S = 3π/$l_p^2$ ^_c, i.e.

(46)

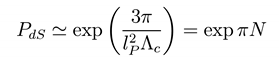
and the second is the Nariai case here M = M_c and S = 2π/$l_p^2$ ^_c with probability

(47)

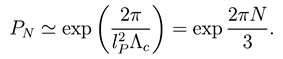
Thus the probability is an exponentially decreasing function in terms of the mass parameter and

(48)

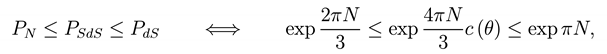
where we have expressed the probability in terms of the ormholes number. As expected the presence of the cosmological constant modifies the property of the black hole mass and consequently of its horizon. This modification is given by directly comparing the Sch arzschild metric and the Sch arzschild-de Sitter metric.Moreover from Eq.(48), we realize that the de Sitter space has the best probability to be realized hen compared with the SdS or Nariai spaces. Nevertheless, we can see that the SdS space has a probability that can be driven close to the de Sitter probability. Moreover, hen we compare P_SdS with P_N we can see that the SdS space has a major probability with respect to the extreme space, namely the Nariai space. This conclusion seems to be in conflict with the request that only regular Kuclidean Kinstein solutions close to the horizon have to be considered; in this case only the Nariai solution. A possibility that can be investigated to better understand this situation is given by the computation of the Casimir-like energy for the SdS space with the de Sitter space as a reference space. This has been done for the Sch arzschild space with flat space as a reference space in Ref. [19] and it has led to the Normhole approximation of the foam we have used to compute the entropy for the SdS and Nariai spaces. The same steps can be repeated to better understand the process of black hole pair creation in presence of a cosmological term and its consequences on the foam structure.