Chaos Synchronization Error Technique-Based Defect Pattern Recognition for GIS through Partial Discharge Signal Analysis
Abstract
:1. Introduction
2. Chaos Synchronization Error Dynamics
3. Fractal and Extension Theories
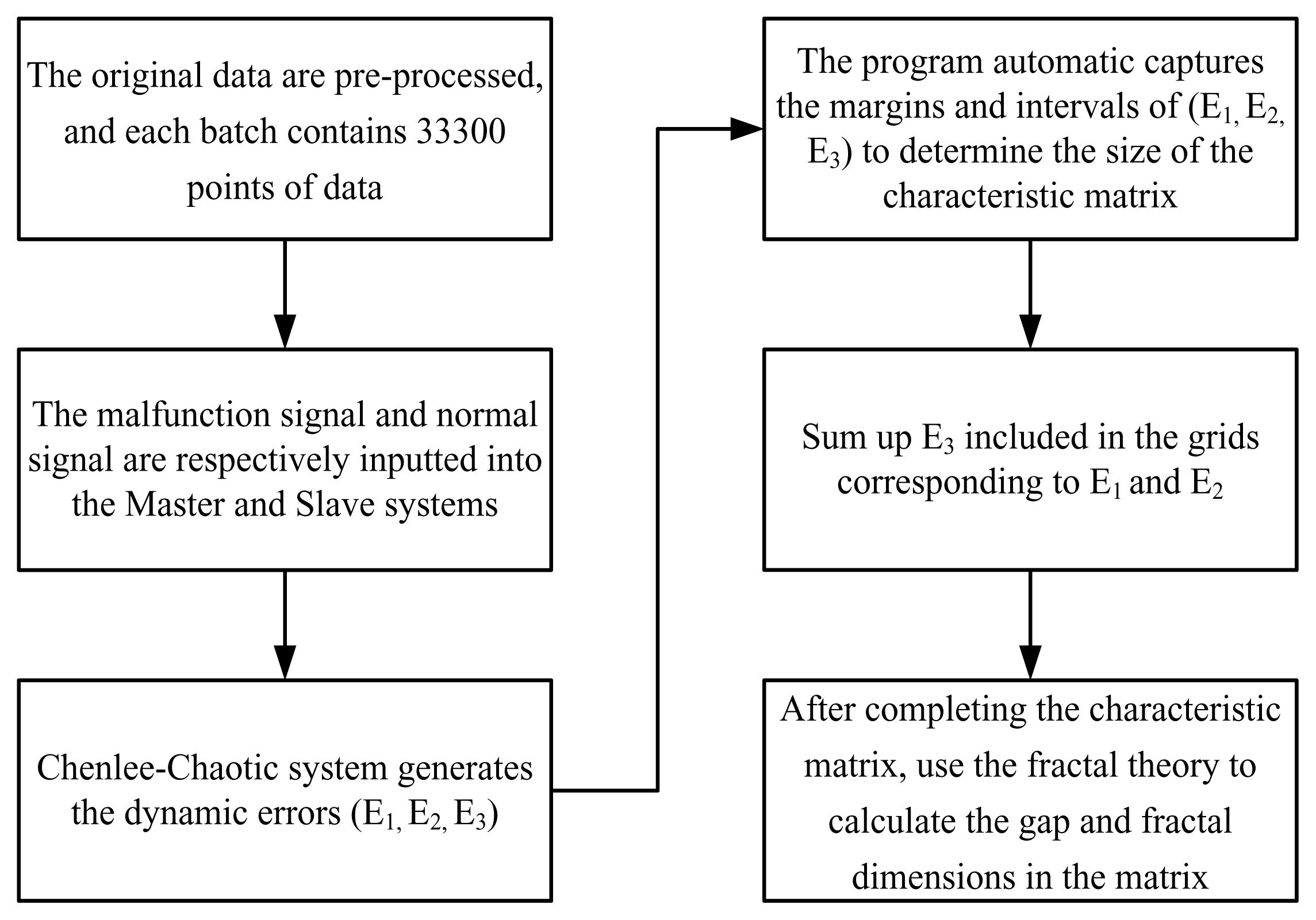
4. Method
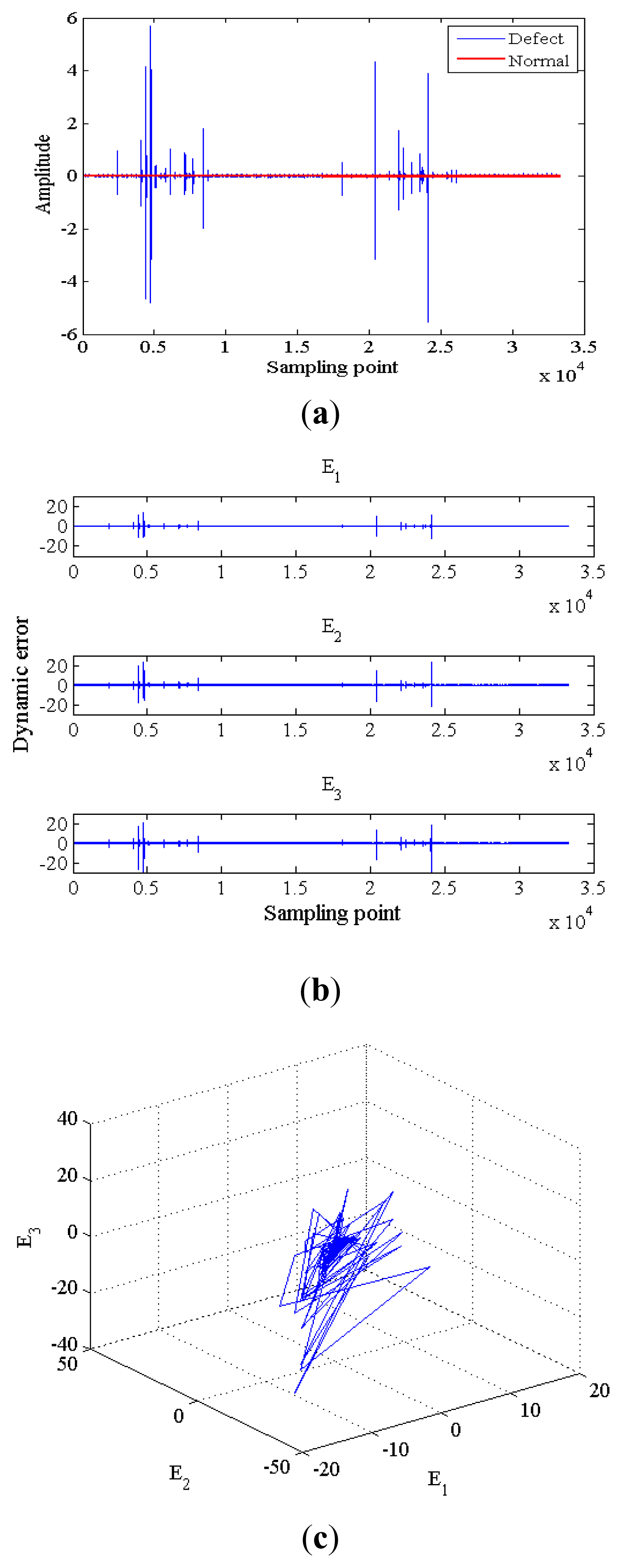
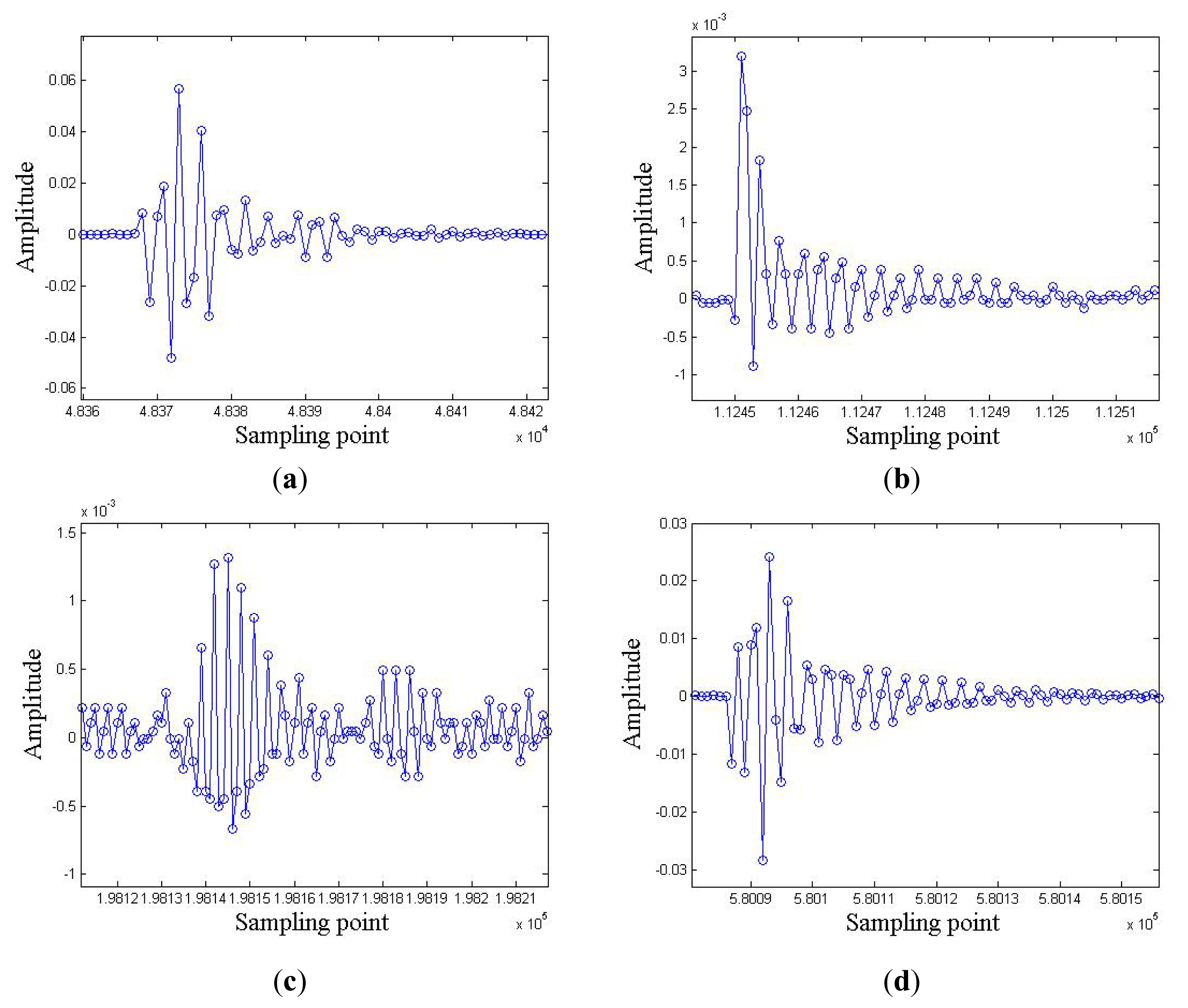
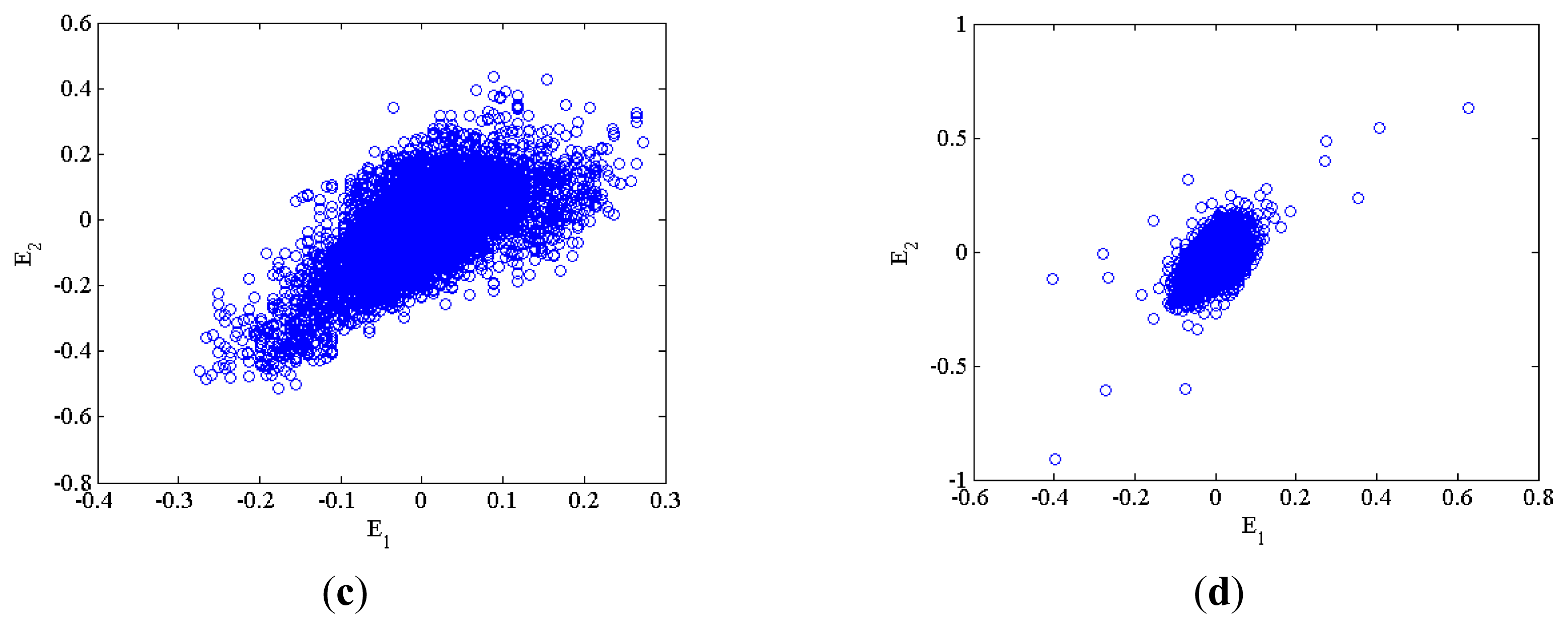
4.1. Characteristic Extraction
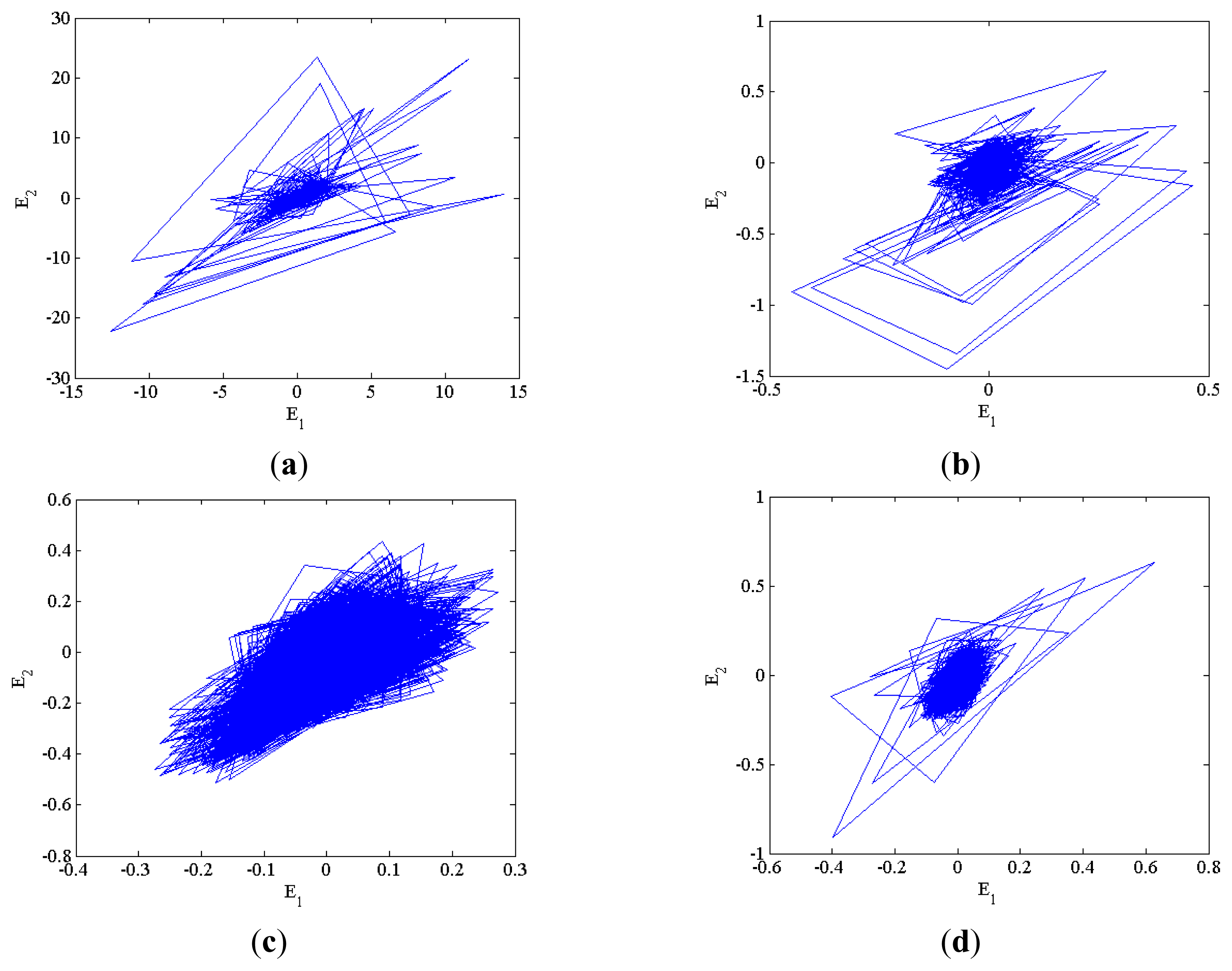
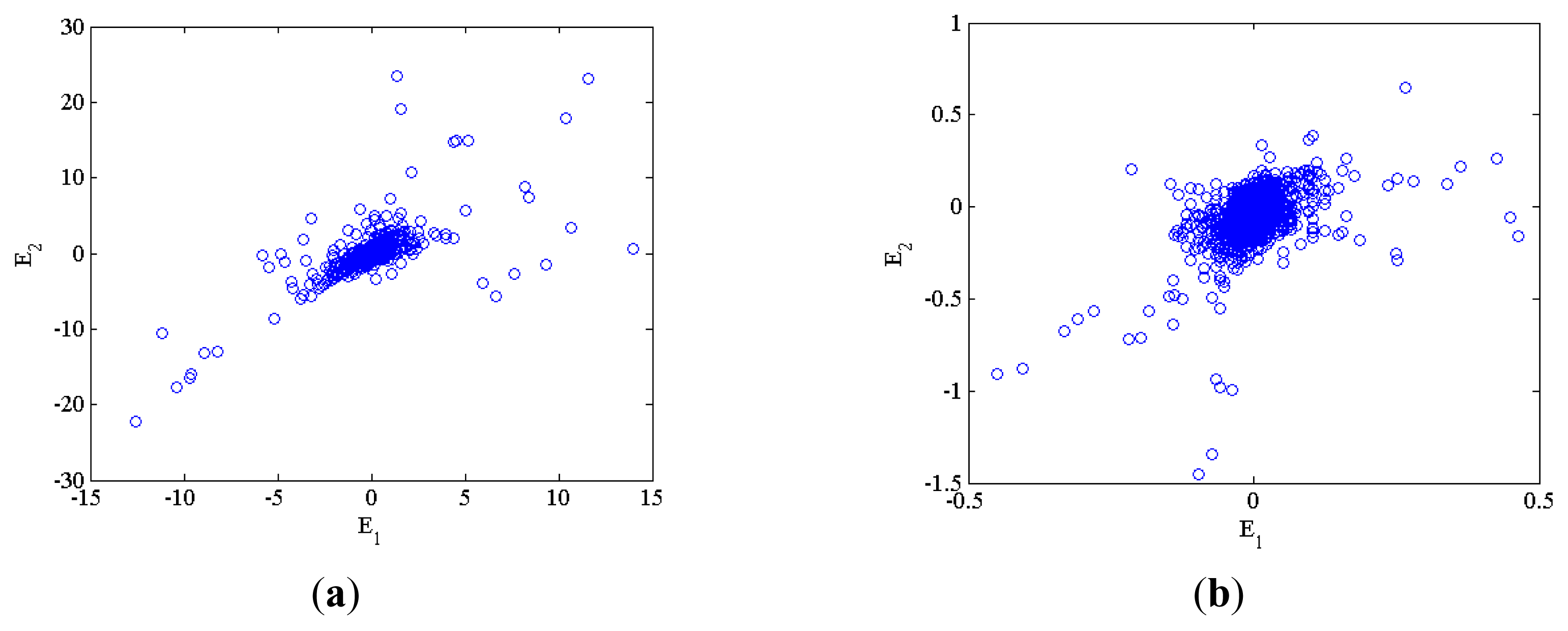
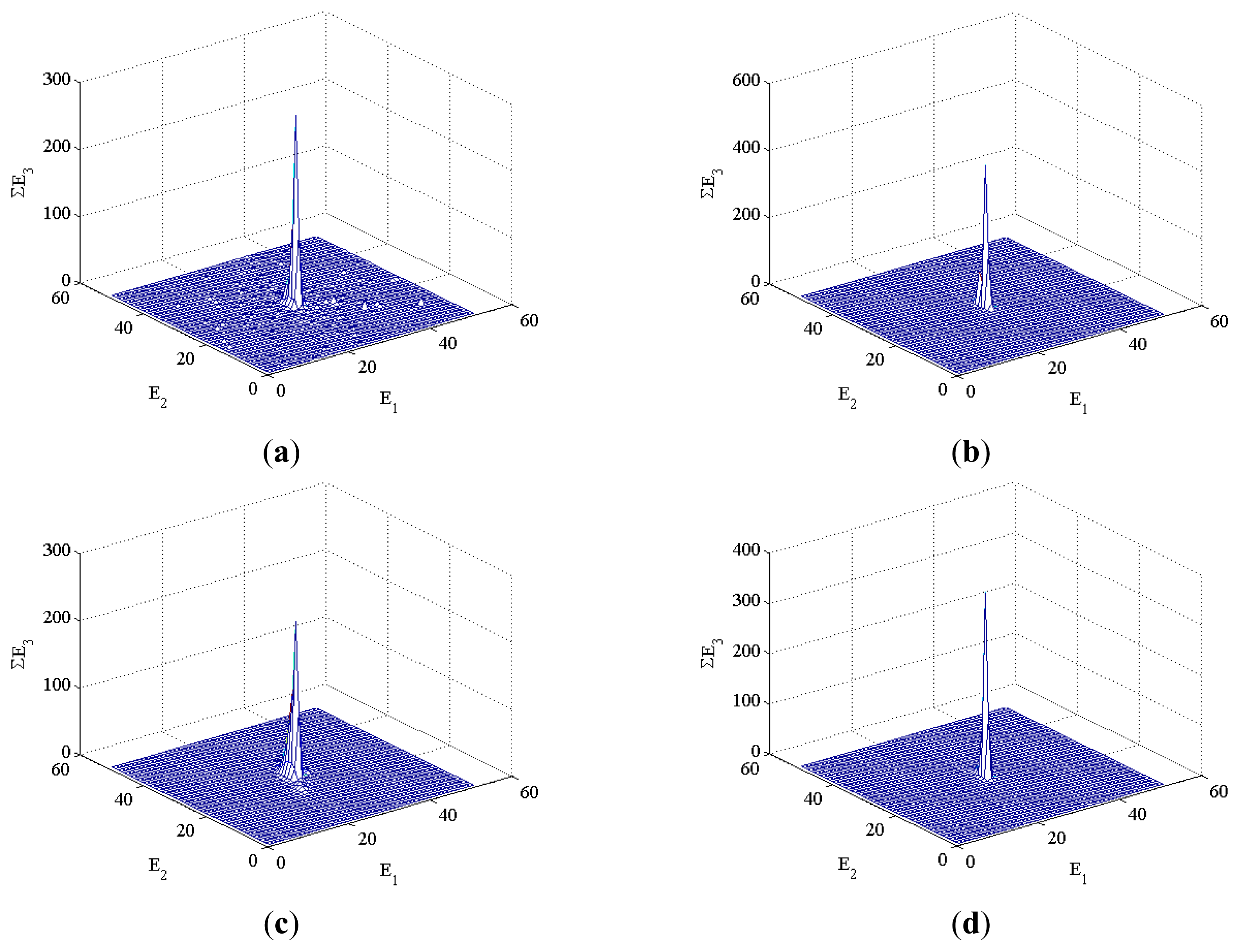
4.2. Construction of the Characteristic Matrix
4.3. Characteristic Extraction and Clustering Method
5. Experiment and Results
5.1. Experiment Models
- Type I: Porcelain bushing internal conductor containing oil grease.
- Type II: SF6 gas tank containing 5 mm × 3 mm × 1 mm metal particles.
- Type III: A welding protrusion with size approximately 5 mm × 5 mm × 2 mm on the bearing.
- Type IV: An abrasion defect with 2 mm depth and 10 mm length on a metal ring.
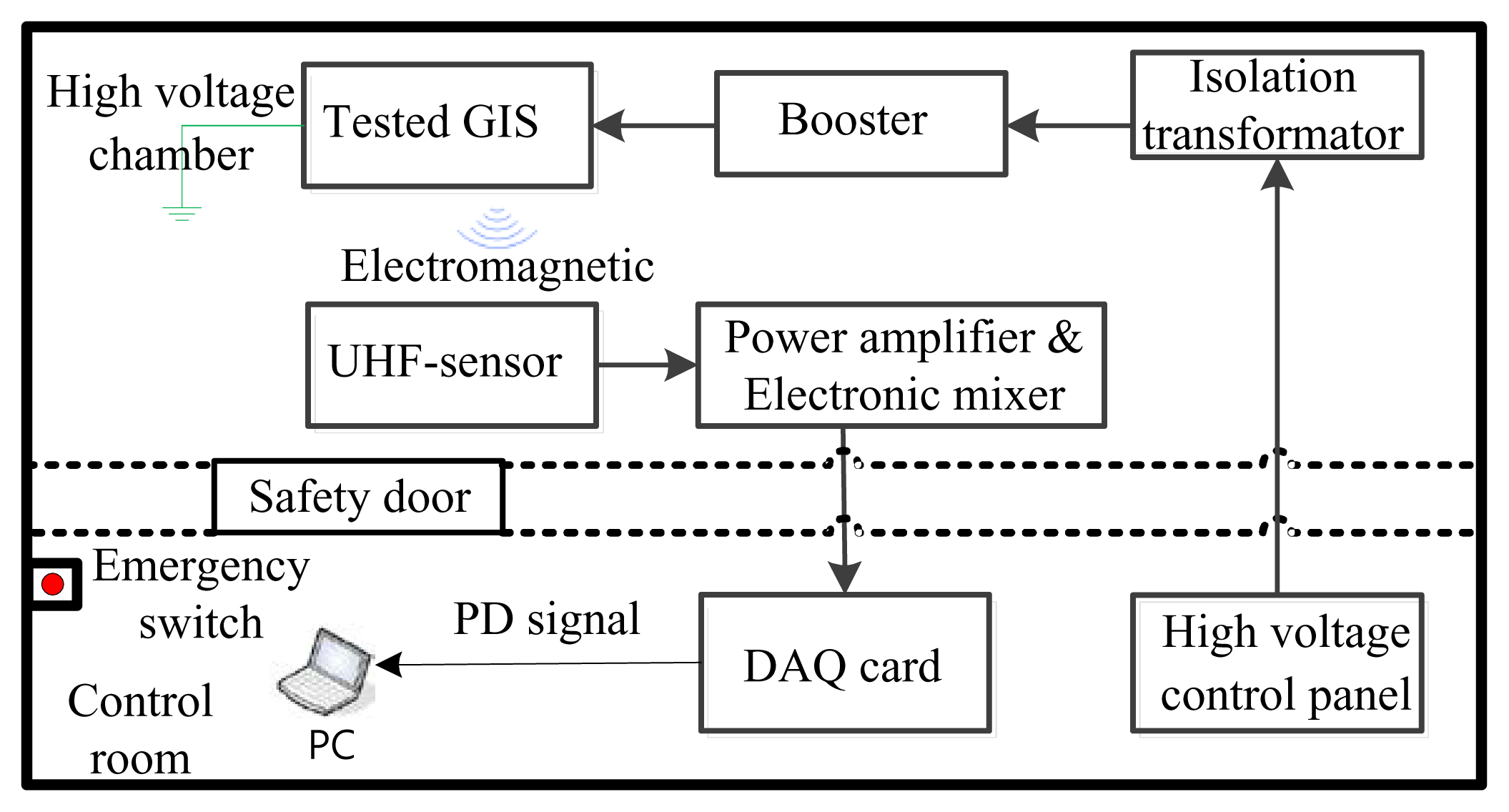
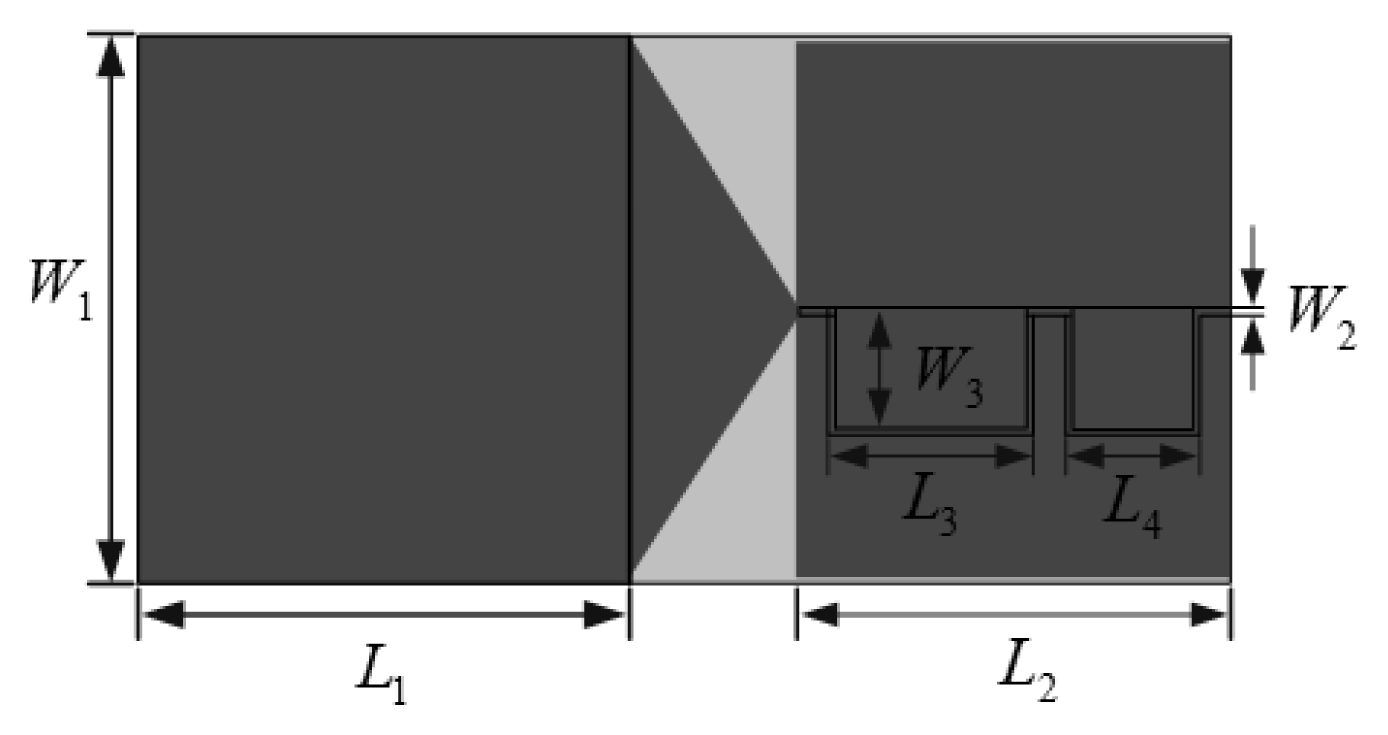
5.2. Measurement System
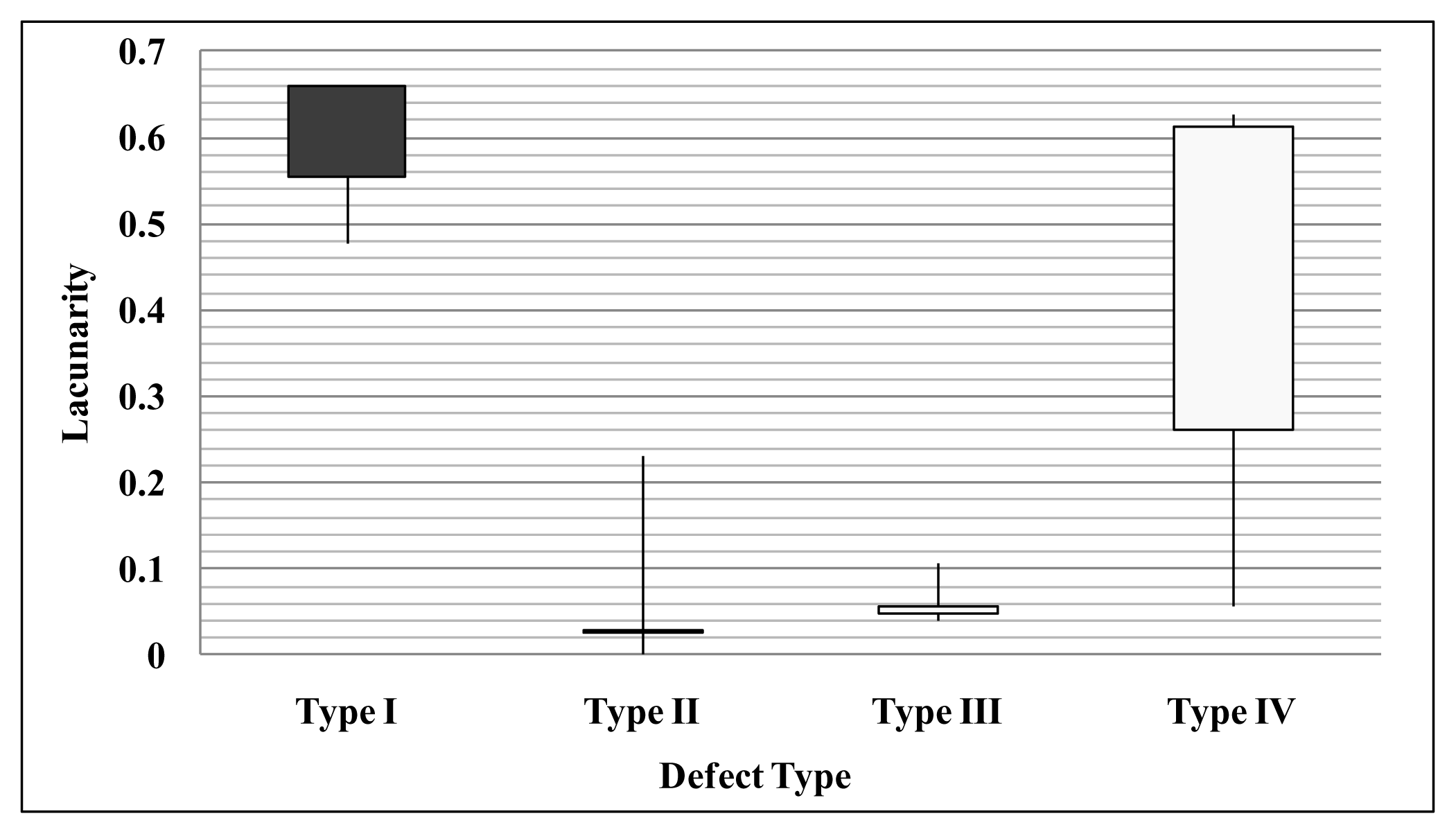
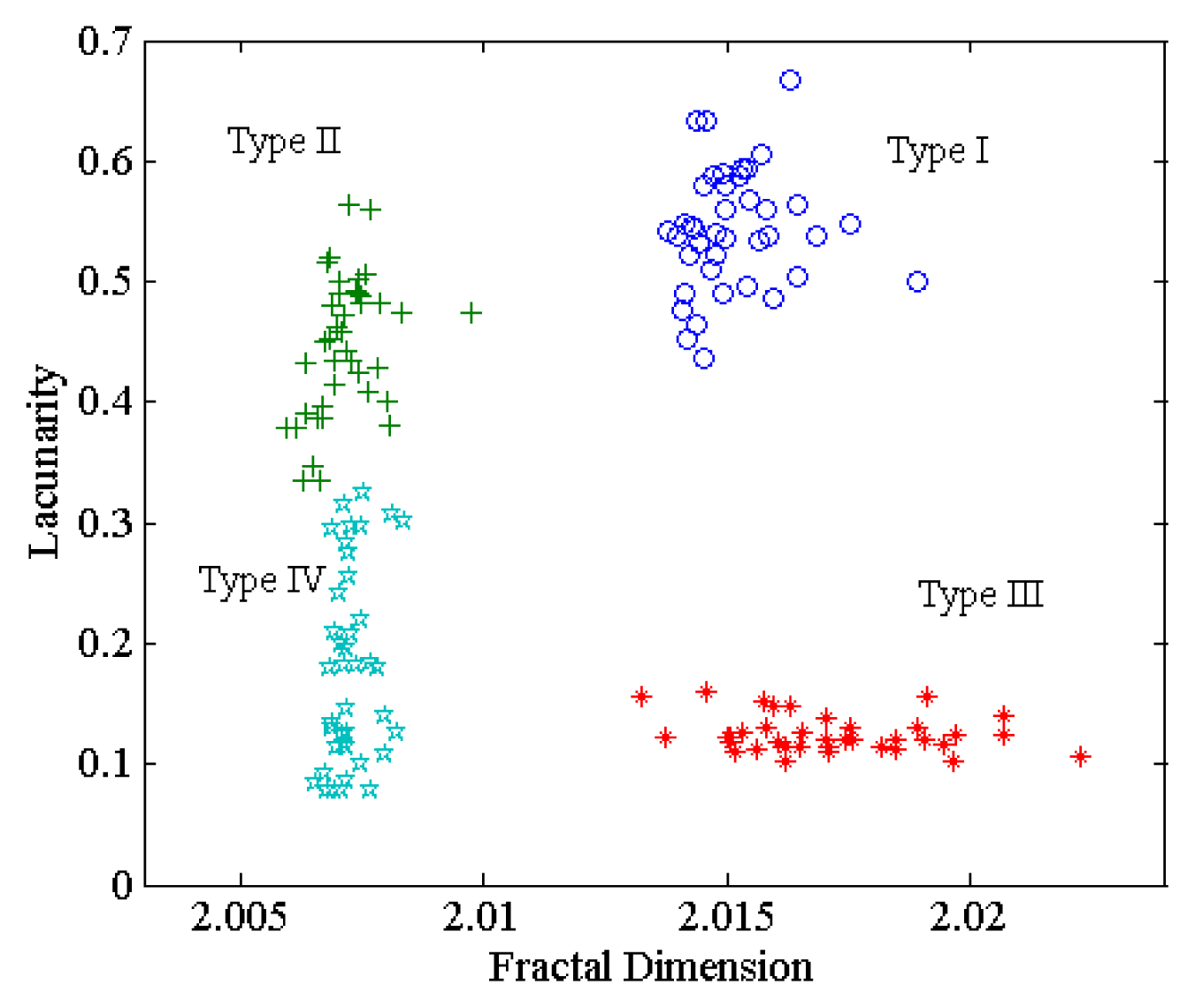
5.3. Experiment Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hampton, B.F.; Meats, R.J. Diagnostic Measurements at UHF in Gas Insulated Substations. IEE Proc. C Gener. Transm. Distrib 1988, 135, 137–144. [Google Scholar]
- Tang, J.; Xu, Z.; Zhang, X.; Sun, C. GIS partial discharge quantitative measurements using UHF microstrip antenna sensors. Proceedings of Annual Report Conference on Electrical Insulation and Dielectric Phenomena, CEIDP 2007, Vancouver, Canada, 14–17 October 2007; pp. 116–119.
- Sellars, A.G.; MacGregor, S.J.; Farish, O. Calibrating the UHF Technique of Partial Discharge Detection Using a PD Simulator. IEEE Trans. Dielectr. Electr. Insul 1995, 2, 46–53. [Google Scholar]
- Andre, H.; Khayam, U. Design of New Shape Printed Bowtie Antenna for Ultra High Frequency Partial Discharge Sensor in Gas-Insulated Substations. Proceedings of International Conference on Information Technology and Electrical Engineering, Yogyakarta, Indonesia, 7–8 October 2013; pp. 355–359.
- Chen, H.C.; Chen, B.Y.; Kou, C.C.; Chao, M.H. UHF Micro-Strip Antenna Design for Partial Discharge Detection of Gas Insulated Switch. Proceedings of 7th Asia-Pacific International Conference on Lightning, Chengdu, China, 1–4 November, 2011; pp. 590–594.
- Petzold, F.; Schlapp, H.; Gulski, E.; Seitz, P.P.; Quak, B. Advanced Solution for On-site Diagnosis of Distribution Power Cables. Proceedings of International Conference on Condition Monitoring and Diagnosis (CMD), Beijing, China, 21–24 April 2008; pp. 1145–1149.
- Wester, F.J.; Gulski, E.; Smit, J.J. Detection of Partial Discharges at Different AC Voltage Stresses in Power Cables. IEEE Electr. Insul. Mag 2007, 23, 28–43. [Google Scholar]
- Li, J.; Sum, C.; Grzybowski, S.; Taylora, C.D. Partial Discharge Image Recognition Using a New Group of Features. IEEE Trans. Dielectr. Electr. Insul 2006, 23, 1245–1253. [Google Scholar]
- Mazzetti, C.; Mascioli, F.F.; Baldini, F.; Panella, M.; Risica, R.; Bartnikas, R. Partial Discharge Pattern Recognition by Neuro-Fuzzy Networks in Heat-Shrinkable Joints and Terminations of XLPE Insulated Distribution Cables. IEEE Trans. Power Deliv 2006, 21, 1035–1044. [Google Scholar]
- Abdel-Galil, T.K.; Sharkawy, R.M.; Salama, M.M.A.; Bartnikas, R. Partial Discharge Pulse Pattern Recognition using an Inductive Inference Algorithm. IEEE Trans. Dielectr. Electr. Insul 2006, 12, 320–327. [Google Scholar]
- Qi, B.; Li, C.; Geng, B.; Hao, Z. Severity Diagnosis and Assessment of the Partial Discharge Provoked by High-Voltage Electrode Protrusion on GIS Insulator Surface. IEEE Trans. Power Deliv 2011, 26, 2363–2369. [Google Scholar]
- Mansour, D.E.; Kojima, H.; Hayakawa, N.; Endo, F.; Okubo, H. Partial Discharges and Associated Mechanisms for Micro Gap Delamination at Epoxy Spacer in GIS. IEEE Trans. Dielectr. Electr. Insul 2010, 17, 855–861. [Google Scholar]
- Gargari, S.M.; Wouters, P.A.A.F.; van der Wielen, P.C.J.M.; Steenis, E.F. Partial Discharge Parameters to Evaluate the Insulation Condition of On-line Located Defects in Medium Voltage Cable Networks. IEEE Trans. Dielectr. Electr. Insul 2011, 18, 868–877. [Google Scholar]
- Gulski, E. Digital Analysis of Partial Discharge. IEEE Trans. Dielectr. Electr. Insul 1995, 2, 822–837. [Google Scholar]
- Kreuger, F.H.; Gulski, E.; Krivda, A. Classification of Partial Discharge. IEEE Trans. Electr. Insul 1993, 28, 917–931. [Google Scholar]
- Kuo, C.L. Design of an Adaptive Fuzzy Sliding-Mode Controller for Chao Synchronization. Int. J. Nonlinear Sci. Numer. Simul 2007, 8, 631–636. [Google Scholar]
- Chen, G.; Dong, X. From Chaos to Order: Methodologies, Perspectives and Applications; World Scientific: Singapore, Singapore, 1998; pp. 12–27. [Google Scholar]
- Chen, J.H. Controlling Chaos Chaotification in the Chen-Lee System by Multiple Time Delays. Chaos Solitons Fractals 2008, 36, 843–852. [Google Scholar]
- Sheu, L.J.; Tam, L.M.; Chen, H.K.; Lao, S.K. Alternative Implementation of the Chaotic Chen-Lee System. Chaos Solitons Fractals 2009, 41, 1923–1929. [Google Scholar]
- Li, T.; Zhao, D.; Huang, Z.; Liu, C.W.; Su, S.J.; Zhang, Y.M. Blind Demodulation of Chaotic Direct Sequence Spread Spectrum Signals Based on Particle Filters. Entropy 2013, 15, 3877–3891. [Google Scholar]
- Su, R.Q.; Lai, Y.C.; Wang, X. Identifying Chaotic FitzHugh–Nagumo Neurons Using Compressive Sensing. Entropy 2014, 16, 3889–3902. [Google Scholar]
- Huang, C.H.; Lin, C.H.; Kuo, C.L. Chaos Synchronization-Based Detector for Power-Quality Disturbances Classification in a Power System. IEEE Trans. Power Deliv 2009, 26, 944–953. [Google Scholar]
- Krivda, A.; Gulski, E.; Satish, L.; Zaengl, W.S. The Use of Fractal Features for Recognition of 3D Discharge patterns. IEEE Trans. Dielectr. Electr. Insul 1995, 2, 889–898. [Google Scholar]
- Hao, N.; Dong, Z. Partial Discharge Signal Feature Extraction based on Hilbert-Huang Transform. Proceedings of 2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE), ChangChun, China, 16–18 December 2011; pp. 2398–2401.
- Liu, W.; Chen, G. A new chaotic system and its generation. Int. J. Bifurc. Chaos 2003, 13, 261–267. [Google Scholar]
- Chen, H.C.; Gu, F.C.; Lee, C.Y. A New Method Based on Extension Theory for Partial Discharge Pattern Recognition. WSEAS Trans. Syst 2008, 7, 1402–1411. [Google Scholar]
- Chen, H.C.; Gu, F.C.; Wang, M.H. A Novel Extension Neural Network Based Partial Discharge Pattern Recognition Method for High-Voltage Power Apparatus. Expert Syst. Appl 2012, 39, 3423–3431. [Google Scholar]
- Prieto, M.D.; Espinosa, A.G.; Ruiz, J.R.; Urresty, J.C.; Ortega, J.A. Feature Extraction of Demagnetization Faults in Permanent-Magnet Synchronous Motors Based on Box-Counting Fractal Dimension. IEEE Trans. Ind. Electron 2011, 58, 1594–1605. [Google Scholar]
- Du, B.X.; Ma, Z.L.; Cheng, X.X.; Liu, Y. Hydrophobicity Evaluation of Silicone Rubber Insulator Using PD-Induced Electromagnetic Wave. IEEE Trans. Dielectr. Electr. Insul 2012, 19, 1060–1067. [Google Scholar]
- Purkait, P.; Chakravorti, S. Impulse Fault Classification in Transformers by Fractal Analysis. IEEE Trans. Dielectr. Electr. Insul 2003, 10, 109–116. [Google Scholar]
- Wang, Q.; Wang, H.; Hao, K.; Dai, P. Two-Phase Flow Regime Identification Based on Cross-Entropy and Information Extension Methods for Computerized Tomography. IEEE Trans. Instrum. Meas 2011, 60, 488–495. [Google Scholar]
- Wang, M.H.; Ho, C.Y. Application of Extension Theory to PD Pattern Recognition in High-Voltage Current Transformers. IEEE Trans. Power Deliv 2005, 20, 1939–1946. [Google Scholar]
- International Electrotechnical Commission, High-Voltage Switchgear and Controlgear—Part 203: Gas-Insulated Metal Enclosed Switchgear for Rated Voltages above 52 kV; IEC 62271-203; IEC: Geneva, Switzerland, 2003.



| Noise Amount | 0% | ±10% | ±20% | ±30% |
|---|---|---|---|---|
| Defect Types | ||||
| Type I | 100 | 100 | 80 | 70 |
| Type II | 100 | 80 | 70 | 40 |
| Type III | 100 | 70 | 60 | 30 |
| Type IV | 100 | 90 | 75 | 60 |
| Noise Amount | 0% | ±10% | ±20% | ±30% |
|---|---|---|---|---|
| Defect Types | ||||
| Type I | 100 | 80 | 50 | 35 |
| Type II | 100 | 75 | 60 | 55 |
| Type III | 100 | 90 | 75 | 30 |
| Type IV | 100 | 85 | 70 | 65 |
| Noise Amount | 0% | ±10% | ±20% | ±30% |
|---|---|---|---|---|
| Defect Types | ||||
| Type I | 80 | 70 | 70 | 50 |
| Type II | 30 | 30 | 20 | 10 |
| Type III | 90 | 55 | 30 | 10 |
| Type IV | 50 | 25 | 10 | 0 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, H.-C.; Yau, H.-T.; Chen, P.-Y. Chaos Synchronization Error Technique-Based Defect Pattern Recognition for GIS through Partial Discharge Signal Analysis. Entropy 2014, 16, 4566-4582. https://doi.org/10.3390/e16084566
Chen H-C, Yau H-T, Chen P-Y. Chaos Synchronization Error Technique-Based Defect Pattern Recognition for GIS through Partial Discharge Signal Analysis. Entropy. 2014; 16(8):4566-4582. https://doi.org/10.3390/e16084566
Chicago/Turabian StyleChen, Hung-Cheng, Her-Terng Yau, and Po-Yan Chen. 2014. "Chaos Synchronization Error Technique-Based Defect Pattern Recognition for GIS through Partial Discharge Signal Analysis" Entropy 16, no. 8: 4566-4582. https://doi.org/10.3390/e16084566




