Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics
Abstract
:1. Introduction
2. Legendre Duality and Projective Duality
- If the vertices of a simple hexagon are points of a point conic, then its diagonal points are collinear: If an arbitrary six points are chosen on a conic (i.e., ellipse, parabola or hyperbola) and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon (extended if necessary) meet in three points which lie on a straight line, called the Pascal line of the hexagon.
- If the sides of a simple hexagon are lines of a line conic, then the diagonal lines are concurrent.
- - Dual Coordinates systems:
- - Dual potential functions:
3. Koszul Characteristic Function/Entropy by Legendre Duality
3.1. Koszul-Vinberg Characteristic Function and Metric for Convex Sharp Cone
Koszul-Vinberg Characteristic Function Definition
- The Bergman kernel of Ω + iRn+1 is written as KΩ(Re(z)) up to a constant where KΩ is defined by the integral:
- ψΩ is analytic function defined on the interior of Ω and ψΩ(x) → + ∞ as x → ∂Ω
- ψΩ is logarithmically strictly convex, and φΩ (x) = log(ψΩ (x)) is strictly convex.
Koszul 1-form α
Koszul 2-form β
Koszul Metric
3.2. Koszul Entropy and Its Barycenter
3.3. Relation of Koszul Density with the Maximum Entropy Principle
3.4. Crouzeix Relation on Hessian of Dual Potentials and Its Consequences
3.5. Fisher Information Geometry Metric as a Particular Case of Koszul Metric
“Le contenu de ce mémoire a formé une partie de notre cours de statistique mathématique a l’Institut Henri Poincaré pendant l’hiver 1939–1940. Il constitue l’un des chapitres du deuxième cahier (en préparation) de nos «Leçons de Statistique Mathématique», dont le premier cahier, «Introduction: Exposé préliminaire de Calcul des Probabilités” (119 pages in-quarto, dactylographiées) vient de paraitre au «Centre de Documentation Universitaire, Tournois et Constans. Paris».”[The contents of this report formed a part of our lecture of mathematical statistics at the Henri Poincaré institute during winter 1939–1940. It constitutes one of the chapters of the second exercise book (in preparation) of our “Lessons of Mathematical Statistics”, the first exercise book of which, “Introduction: preliminary Presentation of Probability theory” (119 pages quarto, typed) has just been published in the “Centre de Documentation Universitaire, Tournois et Constans. Paris”.]
3.6. Extended Results by Koszul, Vey and Sasaki
- If M/G is quasi-compact, then the universal covering manifold of M is affinely isomorphic to a convex domain Ω of an affine space not containing any full straight line.
- If M/G is compact, then Ω is a sharp convex cone.
3.7. Geodesics Equation for the Koszul Hessian Metric
3.8. Koszul Metric for Siegel Homogeneous Domains
4. Souriau Geometric Temperature and Covariant Definition of Thermodynamic Equilibriums
Souriau Theorem 1
- Temperature Vector:with:
- Unitary Mean Speed:
- Eigen Absolute Temperature:
5. Souriau-Gibbs Canonical Ensemble of Dynamical Group and Lie Group Thermodynamics
- f is a symplectic cocycle (we refer to books of Sympectic geometry for cocycle definition)
- β ∈ Ker fβ
- The following symmetric tensor gβ, defined on all values of Adβ(.) is positive definite:
Souriau Theorem 2
Souriau Theorem 3
- There exists a symmetric tensor gβ defined on the image of Adβ(.) = [.,β] such that:and:Last equation gives the structure of a positive Euclidean space.
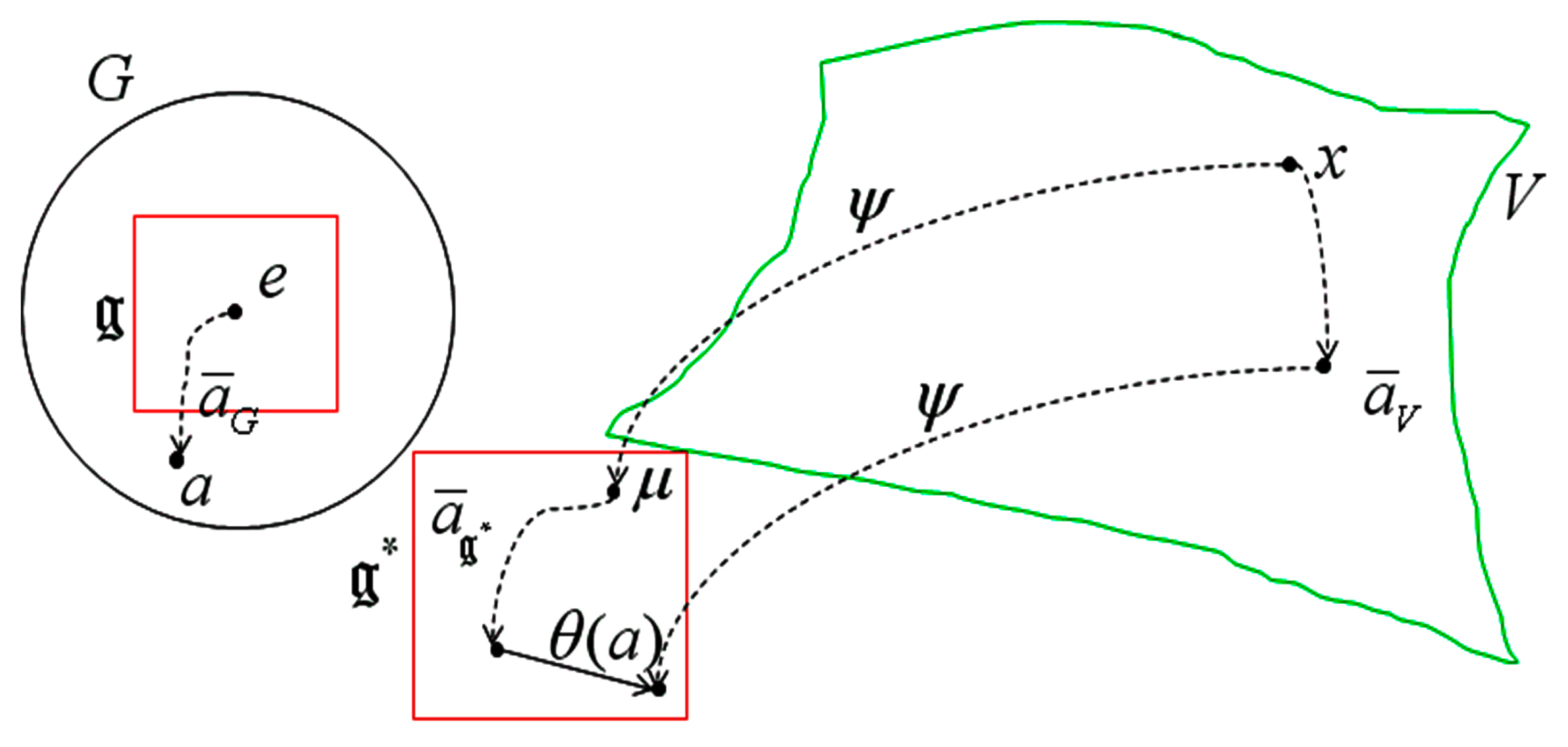
6. Synthesis of Analogies Between the Koszul Information Geometry Model and Souriau Statistical Physics Model
6.1. Comparison of Koszul and Souriau Models
6.2. Invariances in Koszul and Souriau Models
6.3. Souriau Thermometer
7. From Characteristic Function to Generative Inner Product
8. Conclusions on General Definition of Entropy by Legendre Transform
“La théorie cinétique des gaz laisse encore subsister bien des points embarrassants pour ceux qui sont accoutumés à la rigueur mathématique… L’un des points qui m’embarrassaient le plus était le suivant: il s’agit de démontrer que l’entropie va en diminuant, mais le raisonnement de Gibbs semble supposer qu’après avoir fait varier les conditions extérieures on attend que le régime soit établi avant de les faire varier à nouveau. Cette supposition est-elle essentielle, ou en d’autres termes, pourrait-on arriver à des résultats contraires au principe de Carnot en faisant varier les conditions extérieures trop vite pour que le régime permanent ait le temps de s’établir? ”Henri Poincaré « Réflexions sur la théorie cinétique des gaz », 1906[The kinetic theory of gases leaves awkward points for those who are accustomed to mathematical rigor … One of the points which embarrassed me most was the following one: it is a question of demonstrating that the entropy keeps decreasing, but the reasoning of Gibbs seems to suppose that having made vary the outside conditions we wait that the regime is established before making them vary again. Is this supposition essential, or in other words, we could arrive at opposite results to the principle of Carnot by making vary the outside conditions too fast so that the permanent regime has time to become established ?]Henri Poincaré “Reflection on The kinetic theory of gases”, 1906“Quel est l'objet de l’art ? Si la réalité venait frapper directement nos sens et notre conscience, si nous pouvions entrer en communication immédiate avec les choses et avec nous-mêmes, je crois bien que l’art serait inutile, ou plutôt que nous serions tous artistes, car notre âme vibrerait alors continuellement à l’unisson de la nature. ”Henri Bergson, Le rire, p.115, Éd. P.U.F[What is the object of art? Could reality come into direct contact with sense and consciousness, could we enter into immediate communion with things and with ourselves, probably art would be useless, or rather we should all be artists, for then our soul would continually vibrate in perfect accord with nature.]Henri Bergson, Laughter
Acknowledgments
Appendix
A1. Legendre Transform and Minimal Surface
A2. Gromov Inner Product
A3. The Cohomology of a Dynamical Group
Theorem
Conflicts of Interest
References
- Massieu, F. Sur les Fonctions caractéristiques des divers fluides. Comptes Rendus de l’Académie des Sciences 1869, 69, 858–862. (In French) [Google Scholar]
- Massieu, F. Addition au précédent Mémoire sur les Fonctions caractéristiques. Comptes Rendus de l’Académie des Sciences 1869, 69, 1057–1061. (In French) [Google Scholar]
- Massieu, F. Thermodynamique: Mémoire sur les Fonctions Caractéristiques des Divers Fluides et sur la Théorie des Vapeurs; Académie des Sciences: Paris, France, 1876; p. 92. (In French) [Google Scholar]
- Duhem, P. Sur les équations générales de la Thermodynamique. Annales Scientifiques de l’Ecole Normale Supérieure 1891, 8, 231–266. (In French) [Google Scholar]
- Duhem, P. Commentaire aux principes de la Thermodynamique—Première partie. Journal de Mathématiques pures et appliquées 1892, 8, 269–330. (In French) [Google Scholar]
- Duhem, P. Commentaire aux principes de la Thermodynamique—Troisième partie. Journal de Mathématiques pures et appliquées 1894, 10, 207–286. (In French) [Google Scholar]
- Duhem, P. Les théories de la chaleur. Revue des deux Mondes 1895, 130, 851–868. [Google Scholar]
- Gibbs, J.W. Graphical Methods in the Thermodynamics of Fluids. In The Scientific Papers of J. Willard Gibbs; Bumstead, H.A., van Name, R.G., Eds.; Dover: New York, NY, USA, 1961. [Google Scholar]
- Poincaré, H. Calcul des Probabilités; Gauthier-Villars: Paris, France, 1896. (In French) [Google Scholar]
- Poincaré, H. Thermodynamique, Cours de Physique Mathématique. Carré, G., Ed.; 1892. Available online: http://gallica.bnf.fr/ark:/12148/bpt6k2048983 (accessed on 30 July 2014). In French.
- Vinberg, E.B. Structure of the Group of Automorphisms of a Homogeneous Convex Cone. Trudy Moskovskogo Matematicheskogo Obshchestva 1965, 13, 56–83. [Google Scholar]
- Faraut, J.; Koranyi, A. Analysis on Symmetric Cones, Oxford Mathematical Monographs; The Clarendon Press, Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Lichnerowicz, A. Espaces homogènes Kähleriens. In Colloque de Géométrie Différentielle; Pub. du CNRSP: Paris, France, 1953; pp. 171–184. (In French) [Google Scholar]
- Cartan, E. Sur les domaines bornés de l’espace de n variables complexes. Abh. Math. Seminar Hamburg 1935, 1, 116–162. (In French) [Google Scholar]
- Siegel, C.L. Über der analytische Theorie der quadratischen Formen. Ann. Math 1935, 36, 527–606. (In German) [Google Scholar]
- Siegel, C.L. Symplectic geometry. Amer. J. Math 1943, 65, 1–86. [Google Scholar]
- Marle, C.M. On mechanical systems with a Lie group as configuration space. Jean Leray’99 Conference, Proceedings of the Karlskrona Conference in the Honor of Jean Leray, Kluwer, Dordrecht, The Netherlands, 2003; de Gosson, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 183–203. [Google Scholar]
- Marle, C.M. On Henri Poincaré’s note “Sur une forme nouvelle des équations de la mécanique”. J. Geom. Symmetry Phys 2013, 29, 1–38. [Google Scholar]
- Friedrich, T. Die Fisher-Information und symplektische Strukturen. Math. Nachr 1991, 153, 273–296. (In German) [Google Scholar]
- Gromov, M. In a Search for a Structure, Part 1: On Entropy. Available online: http://www.ihes.fr/~gromov/PDF/structre-serch-entropy-july5-2012.pdf (accessed on 23 June 2013).
- Gromov, M. Convex Sets and Kähler Manifolds. In Advances in Differential Geometry and Topology; Tricerri, F., Ed.; World Scientific: Singapore, Singapore, 1990; pp. 1–38. [Google Scholar]
- Gromov, M. Entropy and Isoperimetry for Linear and non-Linear Group Actions. Groups Geom. Dyn 2008, 2, 499–593. [Google Scholar]
- Gromov, M. Carnot-Carathéodory spaces seen from within. In Progress in Mathematics; Springer: Berlin/Heidelberg, Germany, 1996; Volume 144. [Google Scholar]
- Ollivier, Y.; Akimoto, Y. Objective Improvement in Information-Geometric Optimization. In Foundations of Genetic Algorithms XII; Springer: Berlin/Heidelberg, Germnay, 2013. [Google Scholar]
- Bensadon, J. Black-box optimization using geodesics in statistical manifolds. 2013. arXiv:1309.7168. [Google Scholar]
- Bennequin, D. Dualités de champs et de cordes. Séminaire N. Bourbaki 2003, 899, 117–148. (In French) [Google Scholar]
- Bennequin, D. Dualité Physique-Géométrie et Arithmétique. Avalable online: http://archive.numdam.org/ARCHIVE/SB/SB_2001-2002__44_/SB_2001-2002__44__117_0/SB_2001-2002__44__117_0.pdf (accessed on 16 June 2014).
- Chasles, M. Aperçu Historique sur L’origine et le Développement des Méthodes en Géométrie; Gauthier-Villars: Paris. France 1837. (In French) [Google Scholar]
- Gergonne, J.D. Polémique mathématique. Réclamation de M. le capitaine Poncelet (extraite du bulletin universel des annonces et nouvelles scientifiques); avec des notes. Annales de Mathématiques Pures et Appliquées 1827–1828, 18, 125. (In French) [Google Scholar]
- Poncelet, J.V. Traité des propriétés projectives des figures; Gauthier-Villars: Paris, France, 1822. (In French) [Google Scholar]
- André, Y. Dualités, Sixième séance, ENS, Séminaire MaxMux. In Leçons de Mathématiques contemporaines à l'IRCAM; ENS: Paris, France, 2009; Volume Chap. 6. (In French) [Google Scholar]
- Atiyah, M.F. Duality in mathematics and physics. Available online: https://www.fme.upc.edu/arxius/butlleti-digital/riemann/071218_conferencia_atiyah-d_article.pdf (accessed on 20 June 2014).
- Von Oettingen, A.J. Das duale System der Harmonie (Part 1). Annalen der Naturphilosophie 1902, 1, 62–75. (In German) [Google Scholar]
- Von Oettingen, A.J. Das duale System der Harmonie (Part 2). Annalen der Naturphilosophie 1903, 2, 375–403. (In German) [Google Scholar]
- Von Oettingen, A.J. Das duale System der Harmonie (Part 3). Annalen der Naturphilosophie 1904, 3, 241–269. (In German) [Google Scholar]
- Von Oettingen, A.J. Das duale System der Harmonie (Part 4). Annalen der Naturphilosophie 1905, 4, 116–152. (In German) [Google Scholar]
- Von Oettingen, A.J. Das duale System der Harmonie (Part 5). Annalen der Naturphilosophie 1906, 5, 449–503. (In German) [Google Scholar]
- Von Oettingen, A.J. Das duale Harmoniesystem; C.F.W. Siegel’s musikalienhandlung; R. Linnemann: Leipzig, Germany, 1913. (In German) [Google Scholar]
- Moreau, J.J. Fonctions convexes duales et points proximaux dans un espace hilbertien. Comptes Rendus de l’Académie des Sciences 1962, 255, 2897–2899. (In French) [Google Scholar]
- Zia, R.K.P.; Redish, E.F.; McKay, S.R. Making Sense of the Legendre Transform. 2009. arXiv:0806.1147. [Google Scholar]
- Koszul, J.L. Variétés localement plates et convexité. Osaka. J. Math 1965, 2, 285–290. (In French) [Google Scholar]
- Koszul, J.L. Exposés sur les Espaces Homogènes Symétriques; Publicação da Sociedade de Matematica de São Paulo: São Paulo, Brazil, 1959. (In French) [Google Scholar]
- Koszul, J.L. Sur la forme hermitienne canonique des espaces homogènes complexes. Can. J. Math 1955, 7, 562–576. (In French) [Google Scholar]
- Koszul, J.L. Lectures on Groups of Transformations; Tata Institute of Fundamental Research: Bombay, India, 1965. [Google Scholar]
- Koszul, J.L. Domaines bornées homogènes et orbites de groupes de transformations affines. Bull. Soc. Math. Fr 1961, 89, 515–533. (In French) [Google Scholar]
- Koszul, J.L. Ouverts convexes homogènes des espaces affines. Math. Z 1962, 79, 254–259. (In French) [Google Scholar]
- Koszul, J.L. Déformations des variétés localement plates. Ann. Inst. Fourier 1968, 18, 103–114. (In French) [Google Scholar]
- Vinberg, E.B. Homogeneous convex cones. Trans. Mosc. Math. Soc 1963, 12, 340–363. [Google Scholar]
- Vinberg, E.B. The Theory of Homogeneous Convex Cones. Trudy Moskovskogo Ma tematicheskogo Obshchestva 1963, 12, 303–358. [Google Scholar]
- Jensen, J.L.W. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math 1906, 30, 175–193. (In French) [Google Scholar]
- Needham, T. A Visual Explanation of Jensen’s Inequality. Am. Math. Mon 1993, 8, 768–777. [Google Scholar]
- Jaynes, E.T. Information Theory Statistical Mechanics. Phys. Rev. Ser. II 1957, 106, 620–630. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics II. Phys. Rev. Ser 1957, 108, 171–190. [Google Scholar]
- Jaynes, E.T. Prior Probabilities. IEEE Trans. Syst. Sci. Cybern 1968, 4, 227–241. [Google Scholar]
- Dacunha-Castelle, D.; Gamboa, F. Maximum d’entropie et problèmes des moments. Ann. Inst. H. Poincaré Prob. Stat 1990, 26, 567–596. (In French) [Google Scholar]
- Gamboa, F.; Gassiat, E. Maximum d’entropie et problème des moments: Cas multidimensionnel. Probab. Math. Stat 1991, 12, 67–83. (In French) [Google Scholar]
- Dacunha-Castelle, D.; Gamboa, F. Maximum de l’entropie sous contraintes non linéaires. Ann. Inst H. Poincaré Prob. Stat 1990, 4, 567–596. (In French) [Google Scholar]
- Krein, M.G.; Nudelman, A.A. The Markov Moment Problem And Extremal Problems; American Mathematical Society: New York, NY, USA, 1977. [Google Scholar]
- Souriau, J.M. Définition covariante des équ ilibres thermodynamiques. Suppl. Nuov. Cimento 1966, 1, 203–216. (In French) [Google Scholar]
- Crouzeix, J.P. A Relationship Between The Second Derivatives of a Convex Function and of Its Conjugate. Math. Program 1977, 3, 364–365. [Google Scholar]
- Seeger, A. Second Derivative of a Convex Function and of Its Legendre-Fenchel Transformate. SIAM J. Optim 1992, 2, 405–424. [Google Scholar]
- Hiriart-Urruty, J.B. A new set-valued second-order derivative for convex functions. In Mathematics for Optimization; Mathematical Studies Series 129; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Rao, C.R. Information and the accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc 1945, 37, 81–89. [Google Scholar]
- Fréchet, M. Sur l’extension de certaines évaluations statistiques au cas de petits échantillons. Revue de l’Institut International de Statistique 1943, 11, 182–205. (In French) [Google Scholar]
- Koszul, J.L. Trajectoires Convexes de Groupes Affines Unimodulaires. In Essays on Topology and Related Topics; Springer: Berlin, Germany, 1970; pp. 105–110. [Google Scholar]
- Vey, J. Sur les Automorphismes Affines des Ouverts Convexes Saillants. Annali della Scuola Normale Superiore di Pisa, Classe di Science 1970, 24, 641–665. (In French) [Google Scholar]
- Vey, J. Sur une notion d’hyperbolicité des variables localement plates. In Thèse de Troisième Cycle de Mathématiques Pures; Faculté des sciences de l’université de Grenoble: Grenoble, France, 1969. (In French) [Google Scholar]
- Shima, H. Geometry of Hessian Structures. In Springer Lecture Notes in Computer Science; Nielsen, F., Frederic, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8085, pp. 37–55. [Google Scholar]
- Shima, H. The Geometry of Hessian Structures; World Scientific: Singapore, Singapore, 2007. [Google Scholar]
- Byande, P.M.; Ngakeu, F.; Nguiffo Boyom, M.; Wolak, R. KV-Cohomology and Differential Geometry of Affinely Flat Manifolds. Information Geometry. Afr. Diaspora J. Math 2012, 14, 197–226. [Google Scholar]
- Sasaki, T. A Note on Characteristic Functions and Projectively Invariant Metrics on a Bounded Convex Domain. Tokyo J. Math 1985, 8, 49–79. [Google Scholar]
- Sasaki, T. Hyperbolic Affine Hyperspheres. Nagoya Math. J 1980, 77, 107–123. [Google Scholar]
- Rothaus, O.S. The Construction of Homogeneous Convex Cones. Ann. Math 1966, 83, 358–376. [Google Scholar]
- Barbaresco, F. Information Geometry of Covariance Matrix: Cartan-Siegel Homogeneous Bounded Domains, Mostow/Berger Fibration and Fréchet Median, Matrix Information Geometry; Bhatia, R., Nielsen, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 199–256. [Google Scholar]
- Arnaudon, M.; Barbaresco, F.; Yang, L. Riemannian medians and means with applications to radar signal processing. IEEE J. Sel. Top. Signal Process 2013, 7, 595–604. [Google Scholar]
- Yang, L. Médianes de Mesures de Probabilité dans les Variétés Riemanniennes et Applications à la Détection de Cibles Radar. Thales Ph.D, Thèse de l’Université de Poitiers, Poitiers, France, 2012. [Google Scholar]
- Barbaresco, F. Information/Contact Geometries and Koszul Entropy, Geometric Science of Information. In Lecture Notes in Computer Science; Nielsen, F., Barbaresco, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8085, pp. 604–611. [Google Scholar]
- Cartan, E. Le rôle de la Théorie des Groupes de Lie Dans L’évolution de la Géométrie Moderne; International Mathematical Union: Berlin, Germany, 1936. (In French) [Google Scholar]
- Souriau, J.M. Thermodynamique et géométrie. In Differential Geometrical Methods in Mathematical Physics II; Bleuler, K., Reetz, A., Petry, H.R., Eds.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 369–397. [Google Scholar]
- Souriau, J.M. Géométrie de l’espace de phases. Comm. Math. Phys 1966, 374, 1–30. (In French) [Google Scholar]
- Souriau, J.M. On Geometric Mechanics. Discret. Cont. Dyn. Syst. J 2007, 19, 595–607. [Google Scholar]
- Souriau, J.M. Structure des systèmes dynamiques; Editions Jacques Gabay: Paris, France, 1970. (In French) [Google Scholar]
- Souriau, J.M. Structure of Dynamical Systems, volume 149 of Progress in Mathematics. In A Symplectic View of Physics; Birkhäuser Boston Inc.: Boston, MA, USA, 1997. [Google Scholar]
- Souriau, J.M. Thermodynamique Relativiste des Fluides; Centre de Physique Théorique: Marseille, France, 1977. (In French) [Google Scholar]
- Souriau, J.M.; Iglesias, P. Heat Cold and Geometry. Differential Geometry and Mathematical Physics, Mathematical Physics Studies Volume; Springer: Amsterdam, The Netherlands, 1983; pp. 37–68. [Google Scholar]
- Souriau, J.M. Dynamic Systems Structure (chap.16 convexité, chap. 17 Mesures, chap. 18 Etats statistiques, Chap. 19 Thermodynamique), available in Souriau archive (document sent by C. Vallée), unpublished technical notes. 1980. [Google Scholar]
- Souriau, J.M. Géométrie Symplectique et Physique Mathématique; Éditions du C.N.R.S.: Paris, France, 1975. (In French) [Google Scholar]
- Ruelle, D. Statistical Mechanics. Rigorous Results; Imperial College Press: London, UK, 1999. [Google Scholar]
- Ruelle, D. Hasard et Chaos; Editions Odile Jacob: Paris, France, 1991. [Google Scholar]
- Ruelle, D. Thermodynamic Formalism: The Mathematical Structure of Equilibrium Statistical Mechanics, 2nd ed.; Cambridge Mathematical Library; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Vallée, C. Lois de Comportement des Milieux Continus Dissipatifs Compatibles Avec la Physique Relativiste. Ph.D Thesis, Poitiers University, Poitiers, France, 1987. [Google Scholar]
- Vallée, C. Relativistic thermodynamics of continua. Int. J. Eng. Sci 1981, 19, 589–601. [Google Scholar]
- De Saxcé, G.; Vallée, C. Bargmann group, momentum tensor and Galilean invariance of Clausius-Duhem inequality. Int. J. Eng. Sci 2012, 50, 216–232. [Google Scholar]
- Vallée, C.; Hjiaj, M.; Fortuné, D.; de Saxcé, G. Canonical and Anti-Canonical Transformations Preserving Convexity of Potentials. J. Elast 2011, 103, 247–267. [Google Scholar]
- Iglésias, P. Equilibre statistiques et géométrie symplectique en relativité générale. Annales de l'institut Henri Poincaré (A) Physique théorique 1982, 36, 257–270. (In French) [Google Scholar]
- Iglésias, P. Essai de thermodynamique rationnelle des milieux continus. Annales de l'institut Henri Poincaré (A) Physique théorique 1981, 34, 1–24. (In French) [Google Scholar]
- Dubois, F. Conservation Laws Invariants for Galileo Group; Cemracs Preliminary Results. Available online: http://hal.archives-ouvertes.fr/docs/00/55/53/13/PDF/dubois-cemracs99.janv2011.pdf (accessed on 20 June 2014).
- Roblin, T. Ergodicité et équidistribution en courbure négative. Mémoire de la Société Mathématique de France 2003, 95, 96. (In French) [Google Scholar]
- Paulin, F.; Pollicott, M.; Schapira, B. Equilibrium states in negative curvature. 2013. arXiv:1211.6242. [Google Scholar]
- Coudène, Y. Gibbs measures on negatively curved manifolds. J. Dynam. Control Syst 2003, 9, 89–101. [Google Scholar]
- Coudène, Y.; Schapira, B. Generic measures for geodesic flows on nonpositively curved manifolds. Dyn. Syst 2014. submitted. [Google Scholar]
- Haydn, N.T.A.; Ruelle, D. Equivalence of Gibbs and equilibrium states for homeomorphisms satisfying expansiveness and specification. Comm. Math. Phys 1992, 148, 155–167. [Google Scholar]
- Mohsen, O. Le bas du spectre d’une variété hyperbolique est un point selle. Ann. Sci. École Norm. Sup 2007, 40, 191–207. (In French) [Google Scholar]
- Donaldson, S.K. Scalar Curvature Stability of Toric Variety. J. Differ. Geom 2002, 62, 289–349. [Google Scholar]
- Abreu, M. Kähler geometry of toric varieties and extremal metrics. Int. J. Math 1998, 9, 641–651. [Google Scholar]
- Guan, D. On modified Mabuchi functional and Mabuchi moduli space of kahler metrics on toric bundles. Math. Res. Lett 1999, 6, 547–555. [Google Scholar]
- Guillemin, V. Kaehler structures on toric varieties. J. Differ. Geom 1994, 40, 285–309. [Google Scholar]
- Guillemin, V. Moment Maps and Combinatorial Invariants of Hamiltonian Tn-Spaces; Birkhau-ser: Basel, Switzerland, 1994. [Google Scholar]
- Atiyah, M.; Bott, R. The moment map and equivariant cohomology. Topology 1984, 23, 1–28. [Google Scholar]
- Bruguières, A. Propriétés de convexité de l’application moment. Séminaire Bourbaki 1985, 28, 63–87. (In French) [Google Scholar]
- Condevaux, M.; Dazord, P.; Molino, P. Géométrie du moment. Dans Travaux du séminaire Sud Rhodanien de Géométrie; University Lyon: Lyon, France, 1988; pp. 131–160. [Google Scholar]
- Delzant, T. Hamiltoniens périodiques et images convexes de l’application moment. Bull. Soc. Math. Fr 1988, 116, 315–339. (In French) [Google Scholar]
- Guillemin, V.; Sternberg, S. Convexity properties of the moment mapping. Inv. Math 1982, 67, 491–513. [Google Scholar]
- Kirwan, F. Convexity properties of the moment mapping. Inv.Math 1984, 77, 547–552. [Google Scholar]
- Kapranov, M. Thermodynamics and the moment map. 2011. arXiv:1108.3472v1. [Google Scholar]
- Biquard, O. Métriques Kählériennes Extrémales sur les Surfaces Toriques; Société Mathématique de France: Paris, France, 2011; p. 1018. (In French) [Google Scholar]
- Pavlov, V.P.; Sergeev, V.M. Thermodynamics from the Differential Geometry Standpoint. Theor. Math. Phys 2008, 157, 1484–1490. [Google Scholar]
- Kozlov, V.V. Heat Equilibrium by Gibbs and Poincaré. Dokl. Ross. Akad. Nauk 2002, 382, 602–606. (In French) [Google Scholar]
- Berezin, F.A. Lectures on Statistical Physics; World Scientific: Singapore, Singapore, 2007. [Google Scholar]
- Poincaré, H. Réflexions sur la théorie cinétique des gaz. J. Phys. Theor. Appl 1906, 5, 369–403. [Google Scholar]
- Carathéodory, C. Untersuchungen über die Grundlagen der Thermodynamik. Math. Ann 1909, 67, 355–386. (In German) [Google Scholar]
- Souriau, J.M. Mécanique Classique et Géométrie Symplectique. In Report ref. CPT-84/PE-1695; CNRS Centre de Physique Théorique: Marseille, France, 1984. (In French) [Google Scholar]
- Viterbo, C. Generating Functions, Symplectic Geometry and Applications. Proc. Intern. Congr. Math., Zurich 1994, 1, 537–547. [Google Scholar]
- Viterbo, C. Symplectic topology as the geometry of generating functions. Math. Ann 1992, 292, 685–710. [Google Scholar]
- Hörmander, L. Fourier integral operators I. Acta Math 1971, 127, 79–183. [Google Scholar]
- Théret, D. A complete proof of Viterbo’s uniqueness theorem on generating functions. Topol. Appl 1999, 96, 249–266. [Google Scholar]
- Chentsov, N.N. Statistical Decision Rules and Optimal Inferences (Transactions of Mathematics Monograph); American Mathematical Society: Providence, RI, USA, 1982; Volume 53. [Google Scholar]
- Villani, C. (Ir)rréversibilité et entropie/(Ir)reversibility and entropy. In Séminaire Poincaré Le temps; École Polytechnique: Paris, France, 2010. (In French) [Google Scholar]
- Ollivier, Y. Aspects de l’entropie en mathématiques et en physique. Available online: http://www.yann-ollivier.org/entropie/entropie.pdf (accessed on 1 January 2014). (In French)
- Avantaggiati, A.; Loreti, P. On Fourier Transform, Parseval Equality, and the Inversion Formula in Idempotent Analysis. Proceedings of the 2013 European Control Conference (ECC), Zürich, Switzerland, 17–19 July 2013.
- Litvinov, G.L. The Maslov Dequantization, Idempotent and Tropical Mathematics: A brief Introduction. J. Math. Sci 2007, 140, 426–444. [Google Scholar]
- Leray, J. Un prolongement de la transformation de Laplace qui transforme la solution unitaire d’un opérateur hyperbolique en sa solution élémentaire. (Problème de Cauchy. IV.). Bull. Soc. Math. Fr 1962, 90, 39–156. (In French) [Google Scholar]
- Leray, J. Le calcul différentiel et intégral sur une variété analytique complexe Problème de Cauchy, III. Bull. Soc. Math. Fr 1959, 82, 6–180. (In French) [Google Scholar]
- Maslov, V.P. Operational Methods; MIR: Moscow, Russia, 1976. [Google Scholar]
- Del Moral, P.; Doisy, M. Maslov idempotent probability calculus, I, II. Theory Probab. Appl 2000, 44, 319–332. [Google Scholar]
- Del Moral, P.; Doisy, M. On the applications of Maslov optimization theory. Math. Notes 2001, 69, 232–244. [Google Scholar]
- Laplace, P.S. Mémoire sur la probabilité des causes sur les évènements. In Mémoires de Mathématique et de Physique; De l’Imprimerie Royale: Paris, France, 1774. (In French) [Google Scholar]
- Legendre, A.M. Mémoire Sur L’intégration de Quelques Equations aux Différences Partielles; Mémoires de l’Académie des Sciences: Paris, France, 1787; pp. 309–351. (In French) [Google Scholar]
- Monge, G. Sur le Calcul Intégral des Equations aux Différences Partielles; Mémoires de l’Académie des Sciences: Paris, France, 1784; pp. 118–192. (In French) [Google Scholar]
- Darboux, G. Leçons sur la Théorie Générale des Surfaces et les Applications Géométriques du Calcul Infinitésimal: Premiere Partie (Généralités, Coordonnées Curvilignes, Surface Minima); Gauthier-Villars: Paris, France, 1887. (In French) [Google Scholar]
- Hadamard, J. Les surfaces à courbures opposées et leurs lignes géodésiques. Journal de Mathématiques Pures et Appliquées 1898, 4, 27–74. (In French) [Google Scholar]
- Vesentini, E. Geometry of Homogeneous Bounded Domains; Springer-Verlag: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bourdon, M. Structure conforme au bord et flot géodésique d’un CAT(−1)-espace. L’Enseignement Mathématique 1995, 41, 63–102. (In French) [Google Scholar]
- Deza, E.; Deza, M.M. Dictionary of Distances; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Cartan, E. Leçons sur les Invariants Intégraux; Hermann: Paris, France, 1922. (In French) [Google Scholar]
- Libermann, P.; Marle, C.M. Symplectic Geometry and Analytical Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]







| Koszul Information Geometry Model | Souriau Lie Groups Thermodynamics Model | |
|---|---|---|
| Characteristic function | ||
| Entropy | ||
| Legendre Transform | Φ*(x*) = 〈x,x*〉 − Φ(x) | s(Q) = β.Q − Φ(β) |
| Density of probability | px(ξ) = e−〈x,ξ〉 + Φ(x) | pβ(ξ) = e−β.U(ξ) + Φ(β) |
| Dual Coordinate Systems | x ∈ Ω and x* ∈ Ω* | β ∈ ℊ and Q ∈ ℊ* |
β Souriau Geometric Temperature U: Souriau Moment map Q: Mean of Souriau Moment Map or Geometric heat | ||
| and | and | |
| Hessian Metric | ds2 = −d2Φ(x) | ds2 = −d2Φ(β) |
| Fisher metric | ||
| :Souriau Geometric Capacity | ||
| Koszul Information Geometry Model | Souriau Lie Groups Thermodynamics Model | |
|---|---|---|
| Convex Cone | x∈Ω Ω convex cone | β ∈ Ω Ω convex cone: largest open subset of ℊ, Lie algebra of G, such that and are convergent integrals |
| Transformation | x→gx with g∈Aut (Ω) | β→ āℊ (β) |
| Transformation of Potential (non invariant) | ΦΩ(x) → ΦΩ(gx) = ΦΩ (x) + log(|det g|) | Φ (β) → Φ(āℊ(β)) = Φ (β) − θ(a−1)β |
| Transformation of Entropy (invariant) | with | s(Q) → s′(Q′) = β′.Q′−Φ′ = β.Q − Φ = s(Q).with β′ = āℊ (β) Φ′ = Φ(β′) = Φ(āℊ(β)) = Φ(β) − θ(a−1)β |
| Information Geometry Metric (invariant) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barbaresco, F. Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics. Entropy 2014, 16, 4521-4565. https://doi.org/10.3390/e16084521
Barbaresco F. Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics. Entropy. 2014; 16(8):4521-4565. https://doi.org/10.3390/e16084521
Chicago/Turabian StyleBarbaresco, Frédéric. 2014. "Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics" Entropy 16, no. 8: 4521-4565. https://doi.org/10.3390/e16084521
APA StyleBarbaresco, F. (2014). Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics. Entropy, 16(8), 4521-4565. https://doi.org/10.3390/e16084521





