On Spatial Covariance, Second Law of Thermodynamics and Configurational Forces in Continua
Abstract
: This paper studies the transformation properties of the spatial balance of energy equation for a dissipative material, under the superposition of arbitrary spatial diffeomorphisms. The study reveals that for a dissipative material the transformed energy balance equation has some non-standard terms in it. These terms are related to a system of microforces with its own balance equation. These microforces act during the superposition of the spatial diffeomorphism, because of the dissipative properties of the material. Moreover, it is shown that for the case in question the stress tensor is additively decomposed into a conventional part given by the standard Doyle-Ericksen formula and a non-conventional one which is related to changes in the material internal structure in the course of deformation. On the basis of the second law of thermodynamics and the integrability condition of a Pfaffian form it is shown that the non-conventional part of the stress tensor can be related not only to dissipative but also to conservative response. A further insight to this conservative response is provided by exploiting the invariance properties of the balance of energy equation within the context of the material intrinsic “physical” metric concept. In this case, it is shown that the assumption of spatial covariance yields the standard conservation and balance laws of classical mechanics but it does not yield the standard Doyle-Ericksen formula. In fact, the Doyle-Ericksen formula has an additional term in it, which is related directly to the evolution of the material internal structure, as it is determined by the (time) evolution of the material metric in the spatial configuration. A formal connection between this term and the Eshelby energy-momentum tensor is derived as well.1. Introduction
Invariance principles play a fundamental role in several branches of mechanics and physics. The basic idea relies crucially on the fact that if a quantity, underlying the response of a dynamical system, is invariant under the action of some group of transformations, then by exploiting the corresponding invariance properties one can determine relations between the system variables, which in turn may be interpreted as conservation and/or balance laws.
The study of invariance principles within the context of continuum mechanics is rather an old subject and seems to go back to Ericksen [1]. In particular, Ericksen stated that by postulating an energy balance equation and its invariance under superimposed rigid body motions, one can derive the conservation and the balance laws for a continuum theory related to liquid crystals. In that he was followed by Green and Rivlin [2], who by postulating the invariance of the global form of the spatial energy balance, under the action of rigid translations and rotations in the current configuration, derived conservation of mass, as well as the balances of linear and angular momenta of classical mechanics. Identical results to those of Green and Rivlin [2] were derived also in a paper by Noll [3], with the basic difference in Noll’s work being in the treatment of the superimposed rigid body motion, which was viewed therein as a time dependent change of coordinates. As a matter of fact, both works are based on the same idea and are related by the so called alias-alibi (e.g., see, Bishop and Goldberg ([4], p. 72) viewpoint of coordinates in differential manifolds (see also Frewer [5] for a concise discussion of the alias-alibi concept in continuum mechanics).
The concept was studied further by Marsden and Hughes ([6], pp. 154–176), who by realizing that: “Any theory (relativistic or nonrelativistic) that purports to be fundamental ought to be generalizable so that the underlying physical space is a manifold and not just Euclidean (or Newtonian) space.”, generalized the work of Green and Rivlin by replacing the (rigid) Euclidean ambient space by a Riemannian one. More precisely, these authors by postulating the covariance of the global energy balance equation, that is, its invariance under arbitrary superimposed spatial diffeomorphisms, derived not only the conservation and balance laws, but also the mechanical state equation in the form of the Doyle-Ericksen formula (Doyle and Ericksen [7]). Related to the work of Marsden and Hughes [6], is that of Simo and Marsden [8], who on the basis of the polar decomposition theorem and by postulating the existence of two different Riemannian metrics in the reference configuration, one of which remains invariant under the application of a spatial diffeomorphism while the other changes, derived an expression of the rotated stress tensor in terms of the body metric in the reference configuration.
An alternative approach was proposed by Šilhavý [9] who unlike the aforementioned works did not consider either the concept of mass, or the standard splitting of the total energy into invariant internal energy and kinetic energy. Instead, Šilhavý [9] by postulating the invariance of the global balance of energy under Galilean transformations and the boundness of energy from below derived the classical structure of Cauchy’s equations of motion together with the existence of a non-negative mass and its conservation law. Moreover, he derived the standard splitting of the total energy into internal and kinetic energies and the transformation law for external forces. Since then a lot of effort has been placed and a series of papers have appeared in the literature dealing with the concept of covariant energy balance in both a conservative (see, e.g., Yavari et al. [10]; Kanso et al. [11]; Yavari and Ozakin [12]; Yavari and Marsden [13]; Panoskaltsis and Soldatos [14]) as well as a dissipative (see, e.g., Yavari [15]; Panoskaltsis et al. [16,17]) setting.
The work which constitutes the contribution that has been preferred in the present study is that of Yavari et al. [10]. In this work, the authors besides revisiting the basic theorem of the covariance of the energy balance equation of Marsden and Hughes ([6], pp. 163–167) by clarifying some technical details in its proof and by providing a proof for its converse, they also consider the case in which the material (referential) energy balance equation is invariant under the superposition of spatial diffeomorphisms; their results are identical with those of Marsden and Hughes [6]. The authors stated that even they have initially considered their basic statement: “if a deformed body satisfies the balance of energy, any framing of it should satisfy the balance of energy as well” as a postulate, they concluded that “one can justify it (or motivate it) by the fact that the ambient space S is homogeneous”.
A similar assumption has been also made in a recent paper by Panoskaltsis et al. [17], which addresses an internal variable model of highly dissipative response. More specifically, Panoskaltsis et al. in [17] started by postulating that the spatial balance of energy equation is covariant. On the basis of this postulate, they derived mass conservation, the balance equations of linear and angular momenta and some additional conditions - related to the equilibrium properties of the material - under which, the Doyle-Ericksen formula holds. Nevertheless, in the course of their analysis Panoskaltsis et al. [17] realized that in general, for a dissipative material, the spatial balance of energy equation cannot be covariant. The authors attributed the lack of covariance to the fact that, unlike the conservative case studied in Yavari et al. [10], in the dissipative case the evolution of the body is determined not only by the deformation map—that is, by the motion of the body within the (homogeneous) ambient space—but also by the evolution of the internal variables. The internal variables under the superposition of a spatial diffeomorphism, are expected to perform work, which in turn, will result in the appearance of some non-standard terms in the expression of the transformed balance of energy equation.
This paper presents a first attempt at exploiting the transformation properties of the spatial balance of energy equation under the superposition of spatial diffeomorphisms in the case of a dissipative material. In order to accomplish this goal, after briefly reviewing some standard concepts from the tensor analysis on manifolds (see, e.g., Bishop and Goldberg [4]; Abraham et al. [18]; Szekeres, [19]) in Section 2, we revisit the approach of Yavari et al. [10] on the covariant energy balance within the context of a dissipative material in Section 3. Unlike our previous studies in Panoskaltsis et al. [16,17], where the dissipative response was modeled by means of internal variables, within the present approach we assume that the dissipative response of the body is closely tied to a system of microforces, that acts during the superimposition of an arbitrary spatial diffeomorphism by performing work. The proposed approach has its origins in the work of Gurtin [20] dealing with configurational forces, which are forces acting in the reference configuration due to changes in the material internal structure, in addition to the standard (deformational) forces. The analysis reveals that for the case in question, this system of microforces has its own balance equation, while the stress tensor is decomposed additively into a conventional part, which is given by the standard Doyle-Ericksen formula and a non-conventional one, which is related to changes in the material internal structure. In Section 4, on the basis of the second law of thermodynamics, several constitutive equations for this non-conventional part are proposed. Moreover, on the basis of the integrability condition of a Pfaffian form, it is shown that such an additive decomposition may also hold for the case of a non-dissipative material with internal structure, which evolves in the course of deformation. A further insight to this non-standard case is provided in Section 5 where the approach of Yavari et al. [10] is revisited within the context of the material intrinsic “physical” metric concept (Valanis [21]; see also Valanis and Panoskaltsis [22]; Panoskaltsis et al. [16]). In particular, by following the suggestions given in these works, it is assumed that the internal structure of the material may be modeled macroscopically by the material intrinsic metric “as seen” in the spatial configuration, while its changes may by modeled by the time evolution of this metric. In this case it is shown that the assumption of spatial covariance yields the standard conservation and balance laws of classical mechanics but does not yield the standard Doyle-Ericksen formula. In fact, the Doyle-Ericksen formula has an additional term that is related directly to the evolution of the internal structure of the material, as this is determined by the evolution of the material metric. A formal connection between this term and the Eshelby energy-momentum stress tensor “as seen” in the spatial configuration is derived as well.
2. Review of Some Basic Concepts from the Geometry of Continuum Mechanics
This section reviews some basic elements of the geometrical approach to continuum mechanics that will be used in our subsequent developments. A summary of these concepts may be found in the monograph of Marsden and Hughes [6], as well as in the survey articles by Stumpf and Hoppe [23] and Ganghoffer [24].
Accordingly, we denote by B the reference configuration of the body of interest, which is modeled as a three dimensional Riemannian manifold with (covariant) metric G and points labeled by X, and we define a motion of B as an one-parameter family of mappings φt: B → S:
A material (referential) tensor Z of type at X (or in component form ) is defined as a multilinear mapping:
The push-forward φ*Z, of the material tensor Z by the deformation mapping (1) is defined to be the spatial tensor z of type , with components:
If W1 and W2 are two tangent vectors at X, their inner product 〈W1, W2〉 is defined in terms of the material metric tensor G: TXB × TXB → R as:
In a similar manner the inner product of their images w1 = FW1 and w2 = FW2 under the mapping (1) on TxS, is defined in terms of the spatial metric g: TxS × TxS → R as:
Then, since the mapping (1) is invertible it will be W1 = F−1w1 and W2 = F−1w2 so that from Equations (3) and (7) it follows that:
In a similar manner:
The material velocity is defined as:
The material acceleration is defined as:
The (convected) Lie derivative LV (z) of a time-dependent spatial tensor z of type is obtained by pulling z back to the reference configuration, taking its time derivative by keeping X fixed and pushing-forward the result to the spatial configuration, that is:
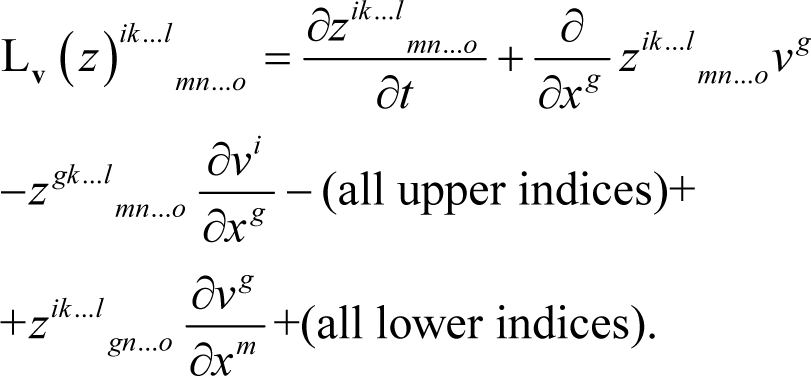
For further use we define the autonomous Lie derivative Λv(z) if we hold t fixed in z (see, e.g., Marsden and Hughes ([6], p.96) as:
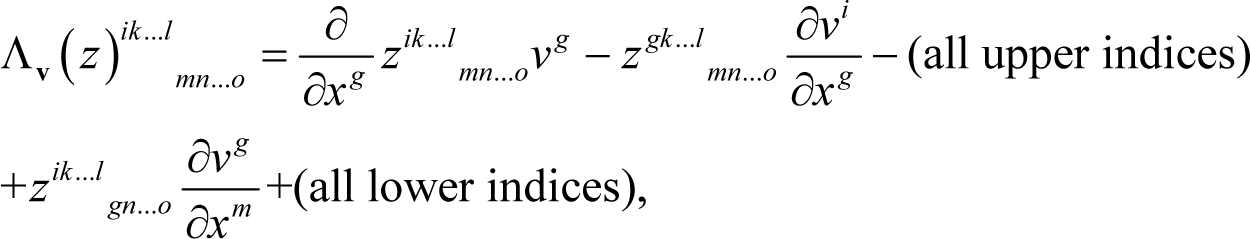
3. Transformation Formula of the Energy Balance Equation Under Spatial Diffeomorphisms for a Dissipative Process
As a point of departure in the examination of the transformation formula of the spatial energy balance for the case of a dissipative material, we consider the covariant theory of Marsden and Hughes ([6], pp. 154–176); see also Yavari et al. [10]. As a first step we consider that balance of energy holds, that is (see Marsden and Hughes ([6], pp. 163–165):
Assumption 3.1. Let xt be a fixed motion of a dissipative body, given by the deformation mapping (1), which maps the reference configuration B onto the current configuration xt(B) ⊂ S, with boundary ∂xt (B). Let ρ(x,t) denote the mass density, e(x,t) the internal energy function per unit mass, v(x,t) the spatial velocity, a(x,t) the spatial acceleration, b(x,t) the external body force per unit mass and t(x, t, n) the Cauchy traction vector, where n is the unit normal to the boundary ∂x(B). Then the principle of balance of energy for any nice subset U ⊂ B may be stated as an axiom as follows:
As a second step, unlike the classical elastic case, we assume that in the case of a dissipative material under the action of a spatial diffeomorphism, the dissipative mechanisms within the material will perform some work, a fact that will result in the appearance of some extra terms in the transformed balance of energy equation. We further assume that the dissipative mechanisms can be modeled as interactions of microscopic nature which result to a (body) microforce and a microtraction, which act in the spatial configuration by performing the aforementioned work. A similar idea has been employed in the approach of Gurtin [20] investigating the nature of the configurational forces. This idea has been also implemented within the context of an infinitesimal theory of viscoplasticity by Gurtin [25] and has been discussed further within the context of the finite theory by Gurtin and Anand [26]. A straightforward application of this concept can be also found in the paper of Yavari et al. [10], where it is used as a basis for the derivation of the transformation formula of the material (referential) energy balance equation under the superimposition of arbitrary referential diffeomorphisms. Accordingly, our second basic assumption deals with the transformation formula of the energy balance equation and may be stated as follows:
Assumption 3.2. For the fixed motion xt which satisfies the balance of energy assumption, consider an arbitrary superimposed spatial diffeomorphism ξt : S → S. Postulate that during the new motion:
Assume that there exists a microforce vector (field) and a microtraction vector (field) , acting by performing work during the superposition of ξt, so that the balance of energy equation in the barred system has the following form:
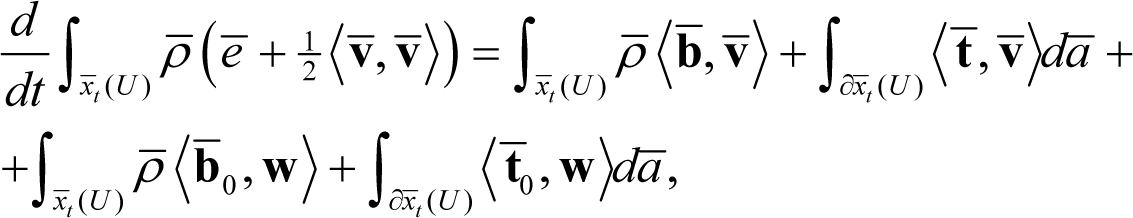
Before determining the microforce system , the following remarks are in order.
Remark 3.3. Within this approach and by following Marsden and Hughes [6, p. 163] and Yavari et al. [10], we adopt the usual (metric-dependent) definition of traction. It is noted that in general the traction t is an exterior 1-form (see, e.g., Kanso et al. [11]; Mariano [27]), a consideration which leads to a metric-independent power defined as the natural pairing between the velocity vector field and the traction 1-form.
Remark 3.4. It is noted that unlike the standard approaches to the bodies with internal structure (see, e.g., Mariano [27]; Yavari and Marsden [13]) in which an independent manifold M is attributed to the material substructure and usually the microforce b0 and the microtraction t0 are defined as 1-forms over its cotangent space (see, e.g., Mariano [27]), in the present approach the microforce systems b0 and t0 are defined in the spatial configuration of the body. The basic conceptual difference between these approaches and the present one, relies crucially in the origins of the system of microforces: within the context of bodies with substructure the microforce system is considered as existing throughout the deformation history of the body, while in the present approach the microforce system is considered as originating because of the superimposition of the spatial diffeomorphism ξ.
Remark 3.5. An alternative approach to the concept of invariance can be provided by noting the natural connection which exists between conservation laws and the symmetries of a dynamical system (see, e.g., Gotay et al. [28]; Ganghoffer [24]). In particular, if the Euler-Lagrange equations of the system are satisfied and the Lagrangian is invariant under the action of some group of transformations, Noether’s theorem establishes the existence and the precise nature of the corresponding conserved quantities. Such an approach within the context of a dissipative body has been favored by Rahuadj et al. [29,30] and Mariano [27]. A formal comparison between the two approaches, namely the covariant energy balance and the one based on Noether’s theorem, can be found, for the case of a conservative material, in Yavari et al. [10]. Related is also and the very recent paper by Romero [31].
The determination of the unknown fields b0 and t0 can be performed as in the classical elastic case (see, e.g., Marsden and Hughes, ([6], pp. 166–167) Yavari et al., [10]; Panoskaltsis and Soldatos [14]) by evaluating Equation (24) at time t = t0 for which:
The derivation to be presented here follows closely the one by Yavari et al. [10]. Accordingly, upon denoting by , the scalar quantity multiplying the 3-form in Equation (24) and by applying the transport theorem for k-forms (see, e.g., Marsden and Hughes [6, p. 121]) we derive:
Since it will be:
The Lie derivative of is determined as in Yavari et al. [10] as:
In light of Equations (25), (28) and (29) the left-hand side of Equation (24) at t = t0, can be written as:
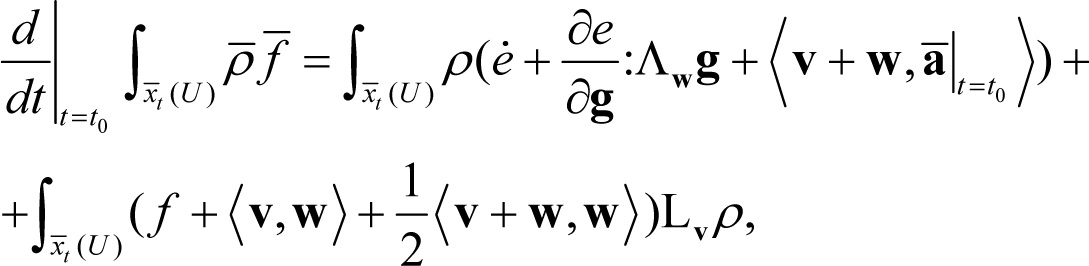
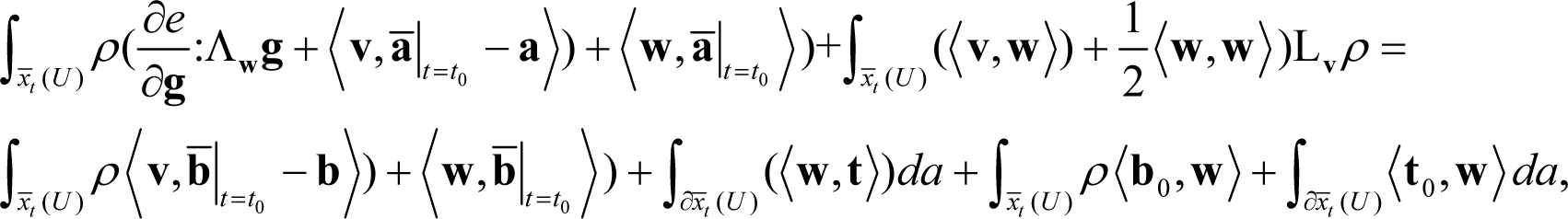
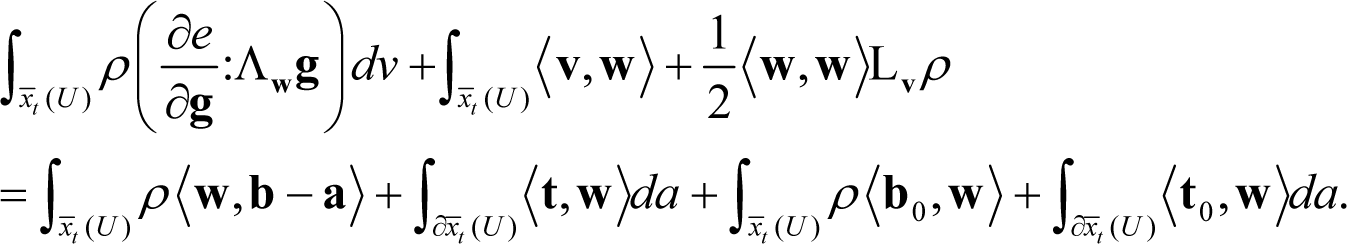
As it is noted in Yavari et al. [10], Cauchy’s theorem implies that 〈t,w〉 = 〈〈σ,n〉,w〉, where σ is the Cauchy stress tensor and n is the outward normal on ∂xt(U). In a similar manner there exists a microstress stress tensor σ0 such as 〈t0,w〉 = 〈〈σ0,n〉,w〉.
The traction terms in the right hand-side of Equation (32), by recalling the identity div(w.σ) = (divσ).w + σ : s + σ : k (see, e.g., Marsden and Hughes ([6] p. 167)), where div(·) stands for the divergence operator, for the spin and , can be written as:
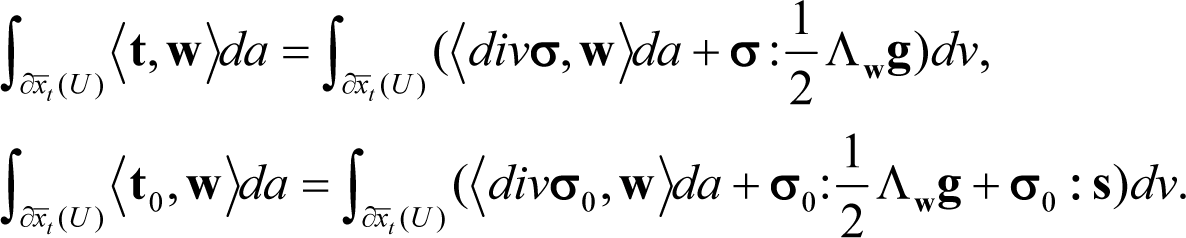
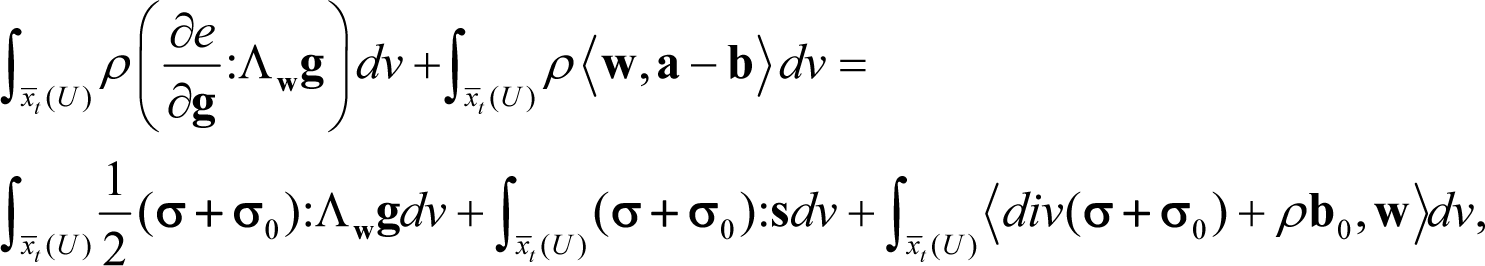
It is noted that if Equation (37) holds, Equation (36) is trivially satisfied because of the symmetry of σ and g. Thus, the unknowns of the problem, namely the body force vector b0 and the traction vector t0, have been determined as:
Therefore, we can state the following theorem:
Theorem 3.6. If assumption 3.1 holds and the spatial energy density transforms tensorially (see Equation (23)), then for a dissipative material, under the superimposition of an arbitrary spatial diffeomorphism ξt : S → S, the spatial balance of energy obeys the following transformation formula:
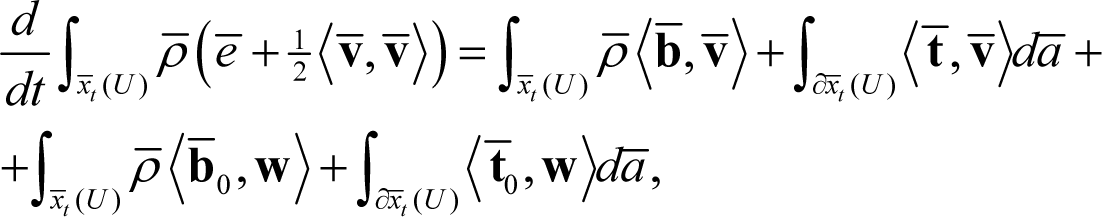
4. On the Nature of the Microforce Systems b0 and t0 and its Relationship to Thermodynamics
Our previous analysis besides establishing the transformation properties of the spatial balance of energy equation under superimposed spatial diffeomorphisms, it also determines a general material (constitutive) model, namely the model determined by the microforce balance equation (see Equation (35)) and the constitutive relation (37). Since this model is intended to be one of dissipative behavior, its compatibility with the second law of thermodynamics must be examined first.
4.1. Compatibility with the Second Law of Thermodynamics
As a first step, we note that once σ0 is known the microbody force b0 is also known from Equation (35) and therefore the (local) material state at the spatial point x is determined uniquely by the couple (g,σ0). Accordingly, it may be assumed that the corresponding state space D can be attached at the spatial point x, so that the set {x}×D is a fiber of x and since it is an open subset of S × D, it is a local manifold. Then, a local process within D may be identified by a parametrized curve C : [t1, t2] → D, so that for such a process it may be assumed that the second law of thermodynamics within the present (isothermal) setting can be expressed in the form of the (local) Clausius-Duhem inequality as:
Upon substitution of the expression for the stress tensor (see Equation (37)), the inequality (40) reduces to:
Therefore, when relation (40) holds as an inequality, σ0 constitutes indeed the dissipative part of the (spatial) stress tensor σ. Moreover, it is emphasized that in general (see Equation (37)), the stress tensor is decomposed additively in a conventional part given by the standard Doyle-Ericksen formula and a non-conventional one obeying the dissipation inequality see (Equation (42)). As a next step, we propose some constitutive equations for σ0.
4.2. Some Constitutive Equations for σ0
We start with the general case, where Equation (42) holds as an inequality and therefore the non-conventional part σ0 constitutes the dissipative part of the stress tensor. Without loss of generality, that is by imposing some restrictions in the memory of the material, a general constitutive equation for −σ0 may be written in the form:
Then in view of Equation (43), the simplest constitutive equation for the microstress tensor may be stated in the form:
Remark 4.1. An alternative expression for σ0 may be derived by means of the principle of maximum plastic dissipation, which within the present setting may be formulated (see Le and Stumpf [33]) as:
Remark 4.2. It is noted that even though the microstress tensor σ0 has not been included in the arguments of the energy density (see Equation (23)), it underlies the dissipative response of the material and accordingly may be considered as a non-conventional internal (hidden) variable. Moreover, since the present approach does not consider either the existence of any primitive kinematical measure accounting for irreversible deformation, or any decomposition of the kinematical quantities in conservative (elastic) and dissipative (plastic) parts, but instead, it is based on the additive decomposition of the stress tensor (see Equation (37)), Equation (44)—or equivalently Equations (45) or (46)—it may be particularized by a non-conventional (viscoplastic) flow rule.
4.3. A Non-Conventional Model of Conservative Response
As a next step we study the particular case in which the Clausius-Duhem inequality holds as an equality. To this end, it is noted that Lvg may be identified by a tangent vector in D at the current material state, so that the expression ω = −σ0:Lvg, constitutes in the spatial configuration a 1-form (Pfaffian form). Then, the (dissipation) inequality (42) in D may be written as:
In the limiting case where the dissipation inequality (47) holds as an equality, the integrability of the Pfaffian form ω = 0 (see, e.g., Szekeres, ([19], pp. 455–456)) asserts that there exist surfaces given in the state space by χ(g) = constant, such as:
Consequently, in this case and if both the standard Doyle-Ericksen formula and the microforce balance equation (Equation (35)) hold, the energy balance equation will be covariant. This result can be summarized in the following proposition:
Proposition 4.3. Assume that for a material with internal structure defined by a microforce vector field b0 and a microtraction vector field t0
Assumption 3.1 holds.
The spatial energy density transforms tensorially.
Conservation of mass, balances of linear and angular momenta hold.
The microforce system is self-equilibrated, that is divσ0 + ρb0 = 0, where the microstress tensor σ0 is given as t0 = σ0n.
The standard Doyle-Ericksen formula ( ) holds.
The response is conservative, that is σ0:Lvg = 0.
Then:
The balance of energy is spatially covariant.
There exists a scalar function χ of the spatial metric g and a positive constant β, such that the microstress tensor is given as:
Remark 4.4. From the present analysis we conclude that even though at the outset we had assumed that the system of microforces b0 and t0 is related to dissipative mechanisms within the material, in the course of development it turned out that may also exist identical non-conventional conservative mechanisms within the material. Clearly, these mechanisms are related to reversible changes in the material’s internal structure and result to a system of microforces identical to that appearing in the case of a dissipative material.
4.4. On the Nature of the Force System b0 and t0
In this subsection we arrive at some essential comments regarding the nature of the (spatial) microforce systems b0 and t0.
Our motivation for studying the transformation properties of the balance of energy equation in the spatial configuration, was our previous work in Panoskaltsis et al. [17], where it was realized that for a dissipative material - with the dissipative response being simulated by internal variables—the spatial balance of energy cannot be covariant. Subsequently, motivated by the works of Gurtin [20] and Yavari et al. [10], we assumed that the dissipative response, which is closely tied to changes in the internal structure of the material, may be modeled by the existence of the microforce systems b0 and t0, which act during the superposition of the spatial diffeomorphism ξ. After employing the transformation properties of the balance of energy equation and with the help of the second law of thermodynamics, we concluded that these systems of forces, besides having their own balance equations, also contribute to the stress tensor. In this sense, these systems of forces are conceptually identical to the configurational force system considered by Gurtin [20], since both b0 and t0, constitute “…basic primitive objects with their own force balance…” and are related to the evolution of the internal structure of the material with the basic difference being that while in the present work the system of forces is defined in the spatial configuration, in Gurtin [20]—see also Yavari et al. [10]—it is defined in the reference configuration. Moreover, similar to the configurational force system of Gurtin, the present microforce system has its origins in a kinematical process different from the deformation mapping, since it appears because of the superimposition of the spatial diffeomorphism ξ, which indeed is a different kinematical process from the deformation mapping. Nevertheless, after considering the constitutive restrictions imposed on the microstress tensor by the second law of thermodynamics, we concluded that the microstress tensor is work—conjugate to the external (deformation) agent Lvg. Such a result should not be surprising, since the deformation mapping is responsible for the deformation of the body, resulting in the part of the stress tensor given by the Doyle-Ericksen formula , while the external agent Lvg—with the notable exception of a relaxation process—is responsible for the changes of the internal structure of the material, resulting in the non-conventional part −σ0. A further insight of this subtle point for the conservative case will be given in the forthcoming section, where the changes in the internal structure of the material will be directly modeled by the changes of the material metric G “as seen” in the spatial configuration.
To this end, it is interesting to note further that the results derived herein are in full agreement with our interpretation of spatial covariance in Panoskaltsis et al. [34], according to which “… all configurations of the body are practically indistinguishable and the equation forming is a matter of observation.”
5. Physical Metric and Covariant Energy Balance
The basic objective of this section is to provide a link between the microstress tensor σ0 introduced and studied in the previous section and the intrinsic material “physical” metric G, by employing the invariance properties of the balance of energy equation. For this purpose, unlike the classical elastic case examined in Marsden and Hughes ([6], pp. 154–176) and Yavari et al. [10] and by following a suggestion given in Valanis [21]—see also Valanis and Panoskaltsis [22], Panoskaltsis et al. [16]—we assume that the internal energy density e, besides being a function of g, is also a function of the Finger deformation tensor c, that is e = e(g, c); (recall that c is the push-forward of the material metric G, that is, it is the metric G “as seen” in the spatial configuration). We further assume that the balance of energy holds and that in this case is covariant. Accordingly, assumption 3.1 remains essentially unaltered, while assumption 3.2 may be restated as follows:
Assumption 5.1. For the fixed motion xt which satisfies the balance of energy, consider an arbitrary superposed spatial diffeomorphism ξt : S → S. Postulate that during the new motion:
Assume further that the balance of energy is (spatially) covariant, that is
Remark 5.2. It is noted that, unlike the standard approaches to bodies with internal structure (see, e.g., Mariano [27]; Yavari and Marsden [13]; Yavari [15]) the thermodynamic force work-conjugate to c, that is , does not enter the expression of working. Accordingly, the proposed scheme resembles the standard internal variables approaches, in the sense that the material metric c in the spatial configuration does not enter explicitly the balance of energy equation.
In order to exploit the invariance properties of the balance of energy equation we evaluate Equation (50) at t = t0 (Yavari et al. [10], Panoskaltsis and Soldatos [14]). Then, by applying the standard procedure (see Section 3), the left hand side of Equation (50) reads in view of Equation (49):
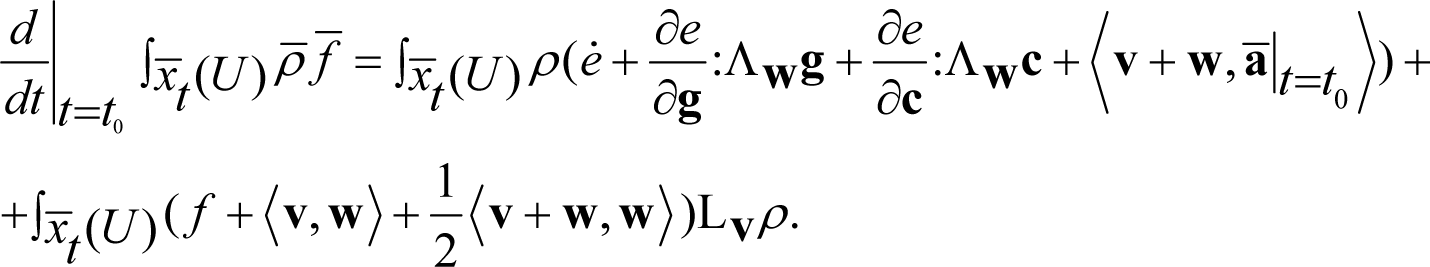
By evaluating the left-hand side of Equation (51) as in Section 3 and subtracting the result from Equation (51) we derive:
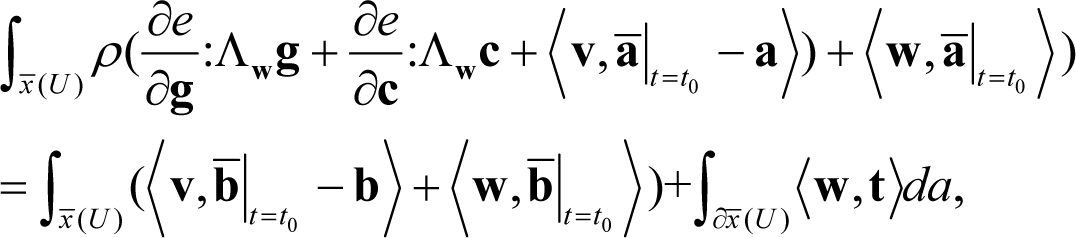
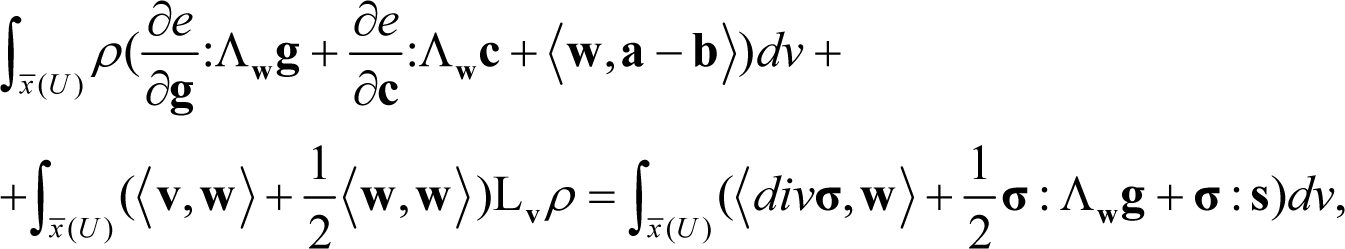
a case that must be excluded since we have assumed that e depends on c. Then, it must be considered that Λwg and Λwc must be somehow dependent. A rather simple relation expressing this dependence may be stated in the following (linear) form:
If this is the case, Equation (60) yields the following expression for the stress tensor:
As a further step we examine the compatibility of the stress tensor (62) with the second law of thermodynamics by evaluating the quantity , that is:
Our results can be summarized in the following theorem:
Theorem 5.3. If for an elastic (conservative) material with an internal energy density e of the form: e = e(x,t,g,c),
Assumptions 2.1 and 5.1 hold.
The material metric in the spatial configuration in the course of deformation is related to the spatial metric by a relation of the form:
Conservation of mass (Equation (55)),
balance of linear momentum (Equation (56)),
balance of angular momentum (Equation (57) hold, and
the stress tensor is decomposed additively into the conventional part σconv - given by the standard Doyle-Ericksen formula ( ) - and a non-conventional microstress tensor, which is related to the internal structure of the material as well as its evolution in the course of deformation, as this (i.e., the evolution of the internal structure) is embodied by the changes in the material metric. Therefore, it holds that:
Remark 5.4. It is emphasized that within the present structure, the covariant balance of energy approach does not yield explicitly any additional balance law for the microstress tensor. Nevertheless, an additional (micro) balance law does exist (see Panoskaltsis and Soldatos [14]; Panoskaltsis et al. [17]) and is given by the rate Equation (61), which may be identified as a balance type of equation between the state variables g and c, the external agent Lvg and the evolution of the material internal structure as the latter is embodied by Lvc. A further discussion on this subtle point may be found in Panoskaltsis and Soldatos [14], where an equation like (61) is considered as a first-order principle.
Remark 5.5. The statement that Equation (61) enforces elastic response inevitably means that the internal energy function e is a function of the spatial metric g alone, which in turn means that Equation (61) must be integrable. Accordingly, there must be restrictions imposed on the state function f in order to ensure integrability. The integrability conditions can be found by means of Frobenius theorem (see, e.g., Bishop and Goldberg ([4], pp. 151–153) and they have been analyzed in a material setting in Panoskaltsis and Soldatos [14].
As a further step we revisit the approach of Yavari et al. [10] within the present context in order to investigate the validity of the converse of Theorem 5.3. Accordingly, we assume that Equations (55)–(57) and (62) together with our basic assumptions 2.1 and 5.1 hold and we define the quantity:
Then the balance of energy equation will be covariant if ΔE(ξt) = 0.
By extending the approach of Yavari et al. [10] we introduce the quantities:
By evaluating the integrals in the right-hand side of Equation (65) and involving mass conservation this equation yields:
By involving assumption 5.1, the integrand in the first integral can be evaluated by noting that:
On substituting from Equation (68) and applying the divergence theorem, Equation (67) reads:
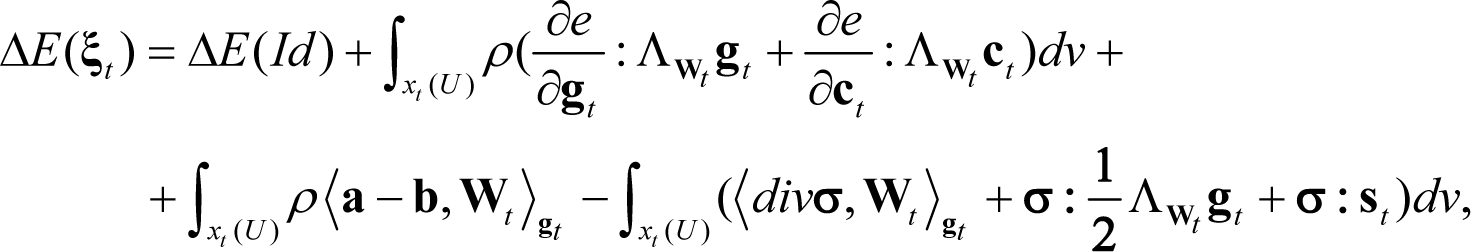
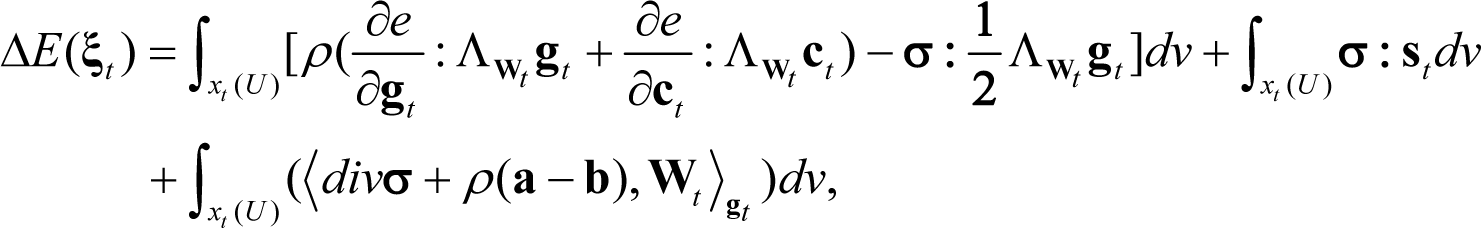
Thus, the converse of Theorem 5.3 is valid and it is stated in the form:
Theorem 5.6. (Converse of 5.3) If for the elastic (conservative) material with an internal energy density e of the form: e = e(x,t, g,c),
Assumptions 2.1 and 5.1 hold.
The material metric in the course of deformation is related to the spatial metric by a relation of the form:
Equations (55)–(57) and (62) hold:
then the spatial balance of energy equation is covariant.
As a final step in our analysis, on the basis of an idea discussed within a different context by Le and Stumpf [33], we make a formal connection between the microstress tensor σmicro derived herein and the Eshelby energy-momentum tensor (see, e.g., Eshelby [35]; Le and Stumpf [33]; Gurtin [20]; Epstein and Maugin [36]), “as seen” in the spatial configuration.
There are two basic assumptions underlying the approach to be followed. The first is that the spatial energy density has the following special form:
Then, the rate of the internal energy density can be derived as:
In light of Equation (77), Equation (53) reads:
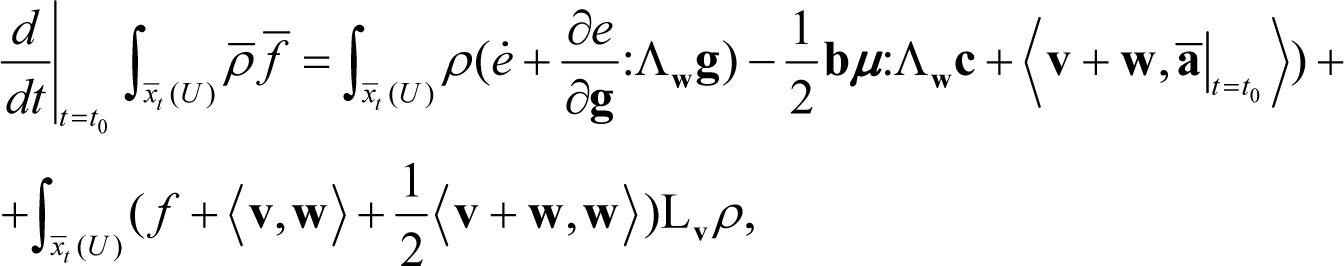
Putting all these together, we can state the following corollary.
Corollary 5.7. If for an elastic material with an internal energy density e of the form and
Assumption 2.1 holds.
The basic variables follow the standard laws of the Cartan theory of space times and the internal energy density transforms tensorially, that is , .
The material metric c (= b−1) in the course of deformation is related to the spatial one by a relation of the form:
that is:Mass conservation holds.
Then:
Balance of linear and angular momenta hold.
The stress tensor σ is given by Equation (81) where μ is identified as the Eshelby energy-momentum tensor defined in the spatial configuration as: .
6. Concluding Remarks
The basic thrust of this paper resides in the determination of the transformation properties of the spatial balance of energy equation under the superposition of arbitrary spatial diffeomorphisms and the consequent repercussions of the second law of thermodynamics, as it is expressed by the local form of the Clausius-Duhem inequality, in the response of continua with internal structure. In particular in this paper:
We have derived the transformation formula of the spatial balance of energy equation by considering a microforce system b0and t0, which acts during the spatial diffeomorphism by producing work. We have proved that this system of microforces has its own balance equation while the stress tensor is decomposed into a conventional part given by the standard Doyle-Ericksen formula and a non-conventional part, which in general is related to changes of the material internal structure in the course of deformation.
By means of the second law of thermodynamics we have proposed simple constitutive equations for the non-conventional part of the stress tensor.
We have concluded that this system of microforces, even though it is derived in the spatial configuration, is qualitatively indistinguishable from the configurational force system that acts in the reference configuration, since as in the latter system, it consists of a system of primitive objects with their own balance equations and is related to changes in the material internal structure via the non-conventional part of the stress tensor.
Moreover, in the course of our development:
On the basis of the second law of thermodynamics and the integrability condition of a Pfaffian form, we have shown that the aforementioned force system can be also associated to (non-conventional) conservative mechanisms within the material.
We have explored further these non-conventional mechanisms by revisiting the covariant energy balance method within the context of the “physical” metric concept. In particular, we have shown that in the case where the changes in the material internal structure are modeled macroscopically by a rate equation describing the time evolution of the intrinsic material metric in the spatial configuration, the stress tensor, as in the previous case, is also decomposed into conventional and non-conventional (microstress tensor) parts, with the non-conventional part related to changes in the internal structure of the material.
We have shown that, if mass conservation holds and the internal energy density has a particular form in terms of the mass density, the spatial metric and the contravariant (reciprocal) material metric, then the aforementioned non-conventional part of the stress tensor can be related to the Eshelby energy-momentum tensor “as seen” in the spatial configuration.
Author Contributions
This is a joint effort based on an idea conceived by both authors. The basic derivations performed in principle by Dimitris Soldatos, while Vassilis Panoskaltsis performed the final review and took care of the overall presentation of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ericksen, J.L. Conservation laws for liquid crystals. Trans. Soc. Rheol 1961, V, 23–34. [Google Scholar]
- Green, A.E.; Rivlin, R.S. On Cauchy’s equation of motion. Zeit. Angew. Math. Phys 1964, 15, 290–292. [Google Scholar]
- Noll, W. Lectures on the foundations of continuum mechanics and thermodynamics. Arch. Ration. Mech. Anal 1973, 52, 62–92. [Google Scholar]
- Bishop, R.L.; Goldberg, S.I. Tensor Analysis on Manifolds; Dover Publications: New York, NY, USA, 1980. [Google Scholar]
- Frewer, M. More clarity on the concept of material-frame indifference in classical continuum mechanics. Acta. Mech 2009, 202, 213–246. [Google Scholar]
- Marsden, J.E.; Hughes, T.J.R. Mathematical Foundations of Elasticity; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Doyle, T.C.; Ericksen, J.L. Nonlinear elasticity. In Advances in Applied Mechanics; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Simo, J.C.; Marsden, J.E. On the rotated stress tensor and the material version of the Doyle-Ericksen formula. Arch. Ration. Mech. Anal 1984, 86, 213–231. [Google Scholar]
- Šilhavý, M. Mass, internal energy, and Cauchy’s equations in frame-indifferent thermodynamics. Arch. Ration. Mech. Anal 1989, 107, 1–22. [Google Scholar]
- Yavari, A.; Marsden, J.E.; Ortiz, M. On spatial and material covariant balance laws in elasticity. J. Math. Phys 2006, 47, 1–53. [Google Scholar]
- Kanso, E.; Arroyo, M.; Tong, Y.; Yavari, A.; Marsden, J.E.; Desbrun, M. On the geometric character of stress in continuum mechanics. Z. Angew. Math. Phys 2007, 58, 843–856. [Google Scholar]
- Yavari, A.; Ozakin, A. Covariance in linearized elasticity. Z. Angew. Math. Phys 2008, 59, 1081–1110. [Google Scholar]
- Yavari, A.; Marsden, J.E. Covariant balance laws in continua with microstructure. Rep. Math. Phys 2009, 63, 11–42. [Google Scholar]
- Panoskaltsis, V.P.; Soldatos, D. A phenomenological constitutive model of non-conventional elastic response. Int. J. Appl. Mech 2013. [Google Scholar] [CrossRef]
- Yavari, A. A geometric theory of growth mechanics. J. Nonlinear Sci 2010, 20, 781–830. [Google Scholar]
- Panoskaltsis, V.P.; Soldatos, D.; Triantafyllou, S.P. The concept of physical metric in rate-independent generalized plasticity. Acta Mech 2011, 221, 49–64. [Google Scholar]
- Panoskaltsis, V.P.; Polymenakos, L.C.; Soldatos, D. A finite strain model of combined viscoplasticity and rate-independent plasticity without a yield surface. Acta Mech 2013, 224, 2107–2125. [Google Scholar]
- Abraham, R.; Marsden, J.E.; Ratiu, T. Manifolds, Tensor Analysis and Applications, 2nd ed; Springer-Verlag: New Work, NY, USA, 1988. [Google Scholar]
- Szekeres, P. A course in Modern Mathematical Physics: Groups, Hilbert Space and Differential Geometry; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Gurtin, M.E. The nature of configurational forces. Arch. Ration. Mech. Anal 1995, 131, 67–100. [Google Scholar]
- Valanis, K.C. The concept of physical metric in thermodynamics. Acta Mech 1995, 113, 169–184. [Google Scholar]
- Valanis, K.C.; Panoskaltsis, V.P. Material metric, connectivity and dislocations in continua. Acta Mech 2005, 175, 77–103. [Google Scholar]
- Stumpf, H.; Hoppe, U. The application of tensor algebra on manifolds to nonlinear continuum mechanics—Invited survey article. Z. Angew. Math. Mech 1997, 77, 327–339. [Google Scholar]
- Ganghoffer, J.F. Differential geometry, least action principles and irreversible processes. Rend. Sem. Mat. Univ. Pol. Torino 2007, 65, 171–203. [Google Scholar]
- Gurtin, M.E. On a framework for small-deformation viscoplasticity: Free energy, microforces, strain gradients. Int. J. Plast 2003, 19, 47–90. [Google Scholar]
- Gurtin, M.E.; Anand, L. The decomposition F=FeFp, material symmetry, and plastic irrotationality for solids that are isotropic—viscoplastic or amorphous. Int. J. Plast 2005, 21, 1686–1719. [Google Scholar]
- Mariano, P.M. Cracks in complex bodies: Covariance of tip balances. J Nonlinear Sci 2008, 18, 99–141. [Google Scholar]
- Gotay, M.J.; Isemberg, J.; Marsden, J.E.; Montgomery, R. Momentum maps and classical fields. Part I: Covariant field theory, 2004. doi: arXiv:physics/9801019v2.
- Rahuadj, R.; Ganghoffer, J.F.; Cunat, C. A thermodynamic approach with internal variables using Lagrange formalism. Part I: General framework. Mech. Res. Comm 2003, 30, 109–117. [Google Scholar]
- Rahuadj, R.; Ganghoffer, J.F.; Cunat, C. A thermodynamic approach with internal variables using Lagrange formalism. Part 2: Continuous symmetries in the case of the time-temperature equivalence. Mech. Res. Comm 2003, 30, 119–123. [Google Scholar]
- Romero, I. A characterization of conserved quantities in non-equilibrium thermodynamics. Entropy 2013, 15, 5580–5596. [Google Scholar]
- Perzyna, P. On the thermomechanical foundations of viscoplasticity. In Mechanical Behavior of Materials under Dynamic Loads; Lindolm, U.S., Ed.; Springer-Verlag: Wien, Austria; New York, NY, USA, 1968; pp. 61–76. [Google Scholar]
- Le, K.C.; Stumpf, H. Constitutive equations for elastoplastic bodies at finite strain: Thermodynamic implementation. Acta Mech 1993, 100, 155–170. [Google Scholar]
- Panoskaltsis, V.P.; Polymenakos, L.C.; Soldatos, D. On large deformation generalized plasticity. J. Mech. Mater. Struct 2008, 3, 441–457. [Google Scholar]
- Eshelby, J.D. The elastic–energy momentum tensor. J. Elast 1995, 5, 321–335. [Google Scholar]
- Epstein, M.; Maugin, G.A. On the geometrical material structure of anelasticity. Acta. Mech 1996, 115, 119–131. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Panoskaltsis, V.P.; Soldatos, D. On Spatial Covariance, Second Law of Thermodynamics and Configurational Forces in Continua. Entropy 2014, 16, 3234-3256. https://doi.org/10.3390/e16063234
Panoskaltsis VP, Soldatos D. On Spatial Covariance, Second Law of Thermodynamics and Configurational Forces in Continua. Entropy. 2014; 16(6):3234-3256. https://doi.org/10.3390/e16063234
Chicago/Turabian StylePanoskaltsis, Vassilis P., and Dimitris Soldatos. 2014. "On Spatial Covariance, Second Law of Thermodynamics and Configurational Forces in Continua" Entropy 16, no. 6: 3234-3256. https://doi.org/10.3390/e16063234



