Guided Self-Organization in a Dynamic Embodied System Based on Attractor Selection Mechanism
Abstract
: Guided self-organization can be regarded as a paradigm proposed to understand how to guide a self-organizing system towards desirable behaviors, while maintaining its non-deterministic dynamics with emergent features. It is, however, not a trivial problem to guide the self-organizing behavior of physically embodied systems like robots, as the behavioral dynamics are results of interactions among their controller, mechanical dynamics of the body, and the environment. This paper presents a guided self-organization approach for dynamic robots based on a coupling between the system mechanical dynamics with an internal control structure known as the attractor selection mechanism. The mechanism enables the robot to gracefully shift between random and deterministic behaviors, represented by a number of attractors, depending on internally generated stochastic perturbation and sensory input. The robot used in this paper is a simulated curved beam hopping robot: a system with a variety of mechanical dynamics which depends on its actuation frequencies. Despite the simplicity of the approach, it will be shown how the approach regulates the probability of the robot to reach a goal through the interplay among the sensory input, the level of inherent stochastic perturbation, i.e., noise, and the mechanical dynamics.1. Introduction
A self-organizing system is characterized by several fundamental properties: the capability to create a globally coherent pattern out of local interactions, resilience to changes in the operating enviroment, as well as non-deterministic spontaneous dynamics. On the other hand, in an engineered dynamical system, realization of a particular behavior is commonly achieved through a methodical step by step planning process with predictable outcomes. Guided self-organization (GSO) is a paradigm proposed to combine these two approaches for generating behaviors in a favorable way, i.e., how a self-organizing system can be guided to have desirable behaviors without eliminating its fundamental properties such as non-deterministic dynamics with emergent features [1,2].
Different approaches to achieve GSO have been proposed in the last several years. Based on information theory, for example, several approaches based on predictive information, and information driven evolutionary design have been proposed [3–5]. From dynamical system perspective, recent approaches of GSO based on the principle of homeokinesis have also gained a lot of attention [2,6]. In contrast to the homeostatis principle which states that behavior results from the compensation of perturbations of an internal equilibrium, a homeokinesis-based approach suggests a self-organization mechanism through amplification of intrinsic or extrinsic noise which is counterbalanced by the simultaneous maximization of the predictability of the resulting behavior [6].
On the other hand, studies in biological systems suggest that in particular cases, inherent stochasticity may indeed increase the performance of the systems. The phenomena where noise increases a particular performance metric of a nonlinear system are commonly referred to as stochastic resonance [7,8]. In biological systems, there are many studies of stochastic resonance in the context of sensing, i.e., how the amount of information received by a sensory system is enhanced by the presence of noise [9].
Recently, it has also been suggested that a proper level of inherent random dynamics may increase the performance of living beings as a whole by driving an appropriate behavior. Commonly, phenomena where stochasticity in an internal control structure drives the behavior of the system are observed at cellular and molecular level [10–13]. For example, it has been reported that noise in a chemotaxis network of Escherichia coli bacteria affects the switching events of their individual flagellar motors, causing their counterclockwise rotation interval to have a power law distribution [10]. However, there are also studies which suggest similar phenomena in simple animals. It has been suggested that the behavioral variability of Drosophila fruit flies which leads to a stochastic foraging pattern known as Levy walks is evolutionarily conserved, and there should be a general neural mechanism underlying the spontaneous behavior [14]. Along a similar line of discussion, it has also been suggested that internally generated noise which affects the turning angle distributions of Daphnia zooplankton has an evolutionary origin [15]. Most recently, it is reported that Levy walks in mussels should have evolved through interaction with their environment [16]. Several studies have also been dedicated to understand and model the balance between stochastic behavior in biological systems commonly measured by entropy, and the ability to attenuate the effect of the randomness to reveal potentially useful deterministic dynamics [11–13,17–20].
In order to understand how inherent stochastic dynamics can drive the behaviors of living beings and artificial systems like robots, it must however be noted that they are embodied systems, i.e., systems with mechanical bodies and physically embedded in the environment [21]. The behaviors of embodied system cannot be seen as merely the outcome of internal control structures, e.g., brain and central nervous system in biological systems. However, they are also affected by both the ecological niche where the system is physically embedded and the morphology, i.e., shape, size and material properties, of the system. In other words, behaviors of embodied systems must be seen as results of self-organization among the internal control structure, the body and the environment [21–24]. In fact, the emergence of distinguishable behaviors depends on the interaction among these three components [24]. Therefore, to guide the self-organizing behaviors of an embodied system towards desirable ones, the dynamics of the central control structure must be coupled with the mechanical dynamics of the body, resulting from the interaction with the environment.
The main goal of this paper is to understand how to guide self-organizing behaviors of a dynamic robot as an embodied system, by coupling the mechanical dynamics with a suitable central control structure which enables the system to balance its deterministic and stochastic dynamics. The approach taken is to use a mathematical framework known as attractor selection mechanism as the control structure [11,12,17–20]. It is hypothesized that by coupling the mechanical dynamics of the body properly with the mechanism, the corresponding embodied system should be able to gracefully switch between random and deterministic behaviors. It will also be shown that the deterministic dynamics can be represented by a number of attractors, and the tendency to gracefully change the behaviors depends on internally generated stochastic perturbation and sensory input. In order to verify the efficacy of the approach, the model is implemented in a simulated curved beam hopping robot: an embodied system with a variety of mechanical dynamics which depends on its actuation frequencies [25,26]. Despite the simplicity of the approach, it will be demonstrated that it enables the robot to perform a simple form of goal directed locomotion by knowing only the distance to a goal. More specifically, it will be shown how the probability to reach the goal is regulated through the interplay among the sensor input, the level of stochastic perturbation, i.e., noise, driving the inherent randomness, and the mechanical dynamics.
The rest of the paper will be organized as follows: the next section will present the proposed GSO approach. Afterward, we will explain the simulated curved hopping robotic system used as a paradigmatic example of the embodied system in this paper, along with the conducted experiments and the experimental results. Finally, we will conclude and discuss related future work.
2. Basic Concept of an Attractor Selection Mechanism Based Guided Self-organization
The GSO approach proposed in the manuscript is based on a coupling between the mechanical dynamics of an embodied system and a control structure known as attractor selection mechanism [11,12,17–20]. The mechanism is inspired from a noise-utilizing behavior found in various scales of biological systems like stochasticity in molecular motors, cell signaling processes, dynamic structure of proteins and recognition in brains [11,12]. Based on the observed dynamics, a simple model was proposed to explain the underlying mechanism by using a dynamical system equation with some attractors [12,17–20]. The model was referred to as the attractor selection mechanism (ASM) and represented by Langevin equation as:
where s(t) and −∇U(s(t)) are the state and dynamics of the mechanism at time t, and ε(t) is the noise term. The sensory feedback function A(t) represents sensory information which indicates the suitability of the state particular goal expressed by A(t). From the equation, U(s(t))A(t) becomes dominant when A(t) is large, and the state transition becomes more deterministic. On the other hand, when A(t) is small, ε(t) becomes dominant, and the state transition becomes more stochastic. A(t) should therefore be designed to have a large value when the state s(t) is suited to the environment and vice versa.
The potential function U(t) can be designed to have some attractors. The coupling between the attractors of the ASM and the mechanical dynamics plays a key role in the GSO approach presented in this paper. As mentioned in the Introduction section, the emergence of distinguishable behaviors depends on the interactions among the controller, the body and the environment. The nature of the ASM dynamics allows the behavior of the system to be entrained into suitable attractors, corresponding to a particular distinguishable behavior, when the state s(t) is considered suitable to bring the system towards the desirable goal, i.e., A(t) in Equation (1) has a high value. However, when s(t) is not adequately suitable, i.e., A(t) has a low value, the exploratory stochastic dynamics will let the system have more tendency to find another suitable attractor.
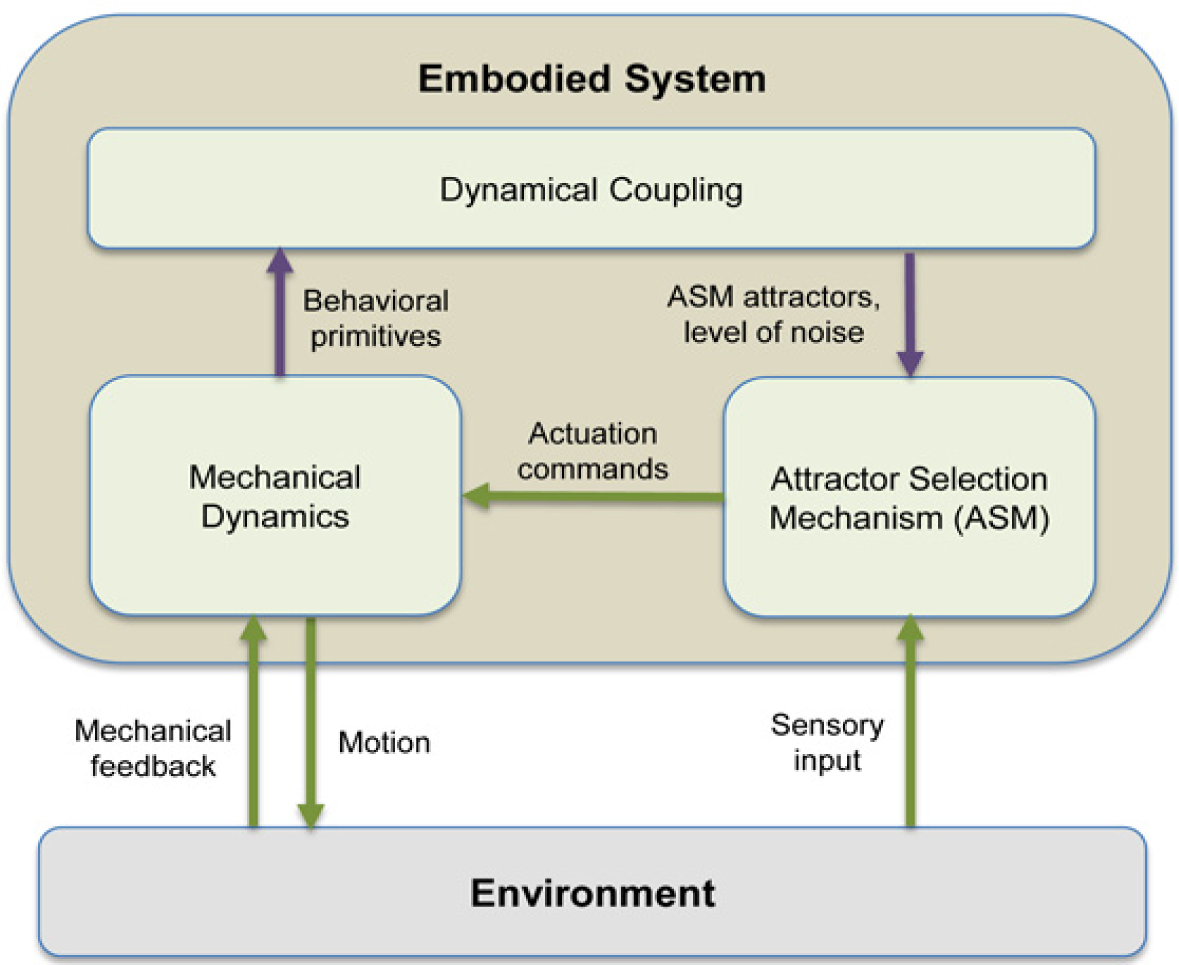
The basic concept of the GSO framework presented in this manuscript is explained further in Figure 1. The coupling between the mechanical dynamics and ASM is shown by the purple arrows. More specifically, the distinguishable behavioral “primitives” should correspond with the attractors of the ASM, modeled by U(t) in Equation (1). The noise level, i.e., size of ε(t), decides the tendency to switch between the deterministic and stochastic behaviors which allows the system to find another attractors suitable to the current situation. The state of ASM, s(t), is used as the actuation command for the system. The sensory input provides the knowledge of whether the current actuation command is suited to the environment or vice versa, and it is modeled through A(t) in Equation (1).
3. Model and Dynamics of a Curved Beam Hopping Robot
The embodied system used as a paradigmatic example in this manuscript is a simulated curved beam hopping robot used in our previous research [25,26]. The robot is ideal for our purpose, as it possesses a variety of mechanical dynamics which solely depend on its actuation frequencies. We can therefore observe whether the proposed approach is realizable by simply observing the dynamics of a single dimensional ASM state. The following sections will explain the model of the curved beam hopping robot and its mechanical dynamics.
3.1. The Model of the Curved Beam Hopping Robot
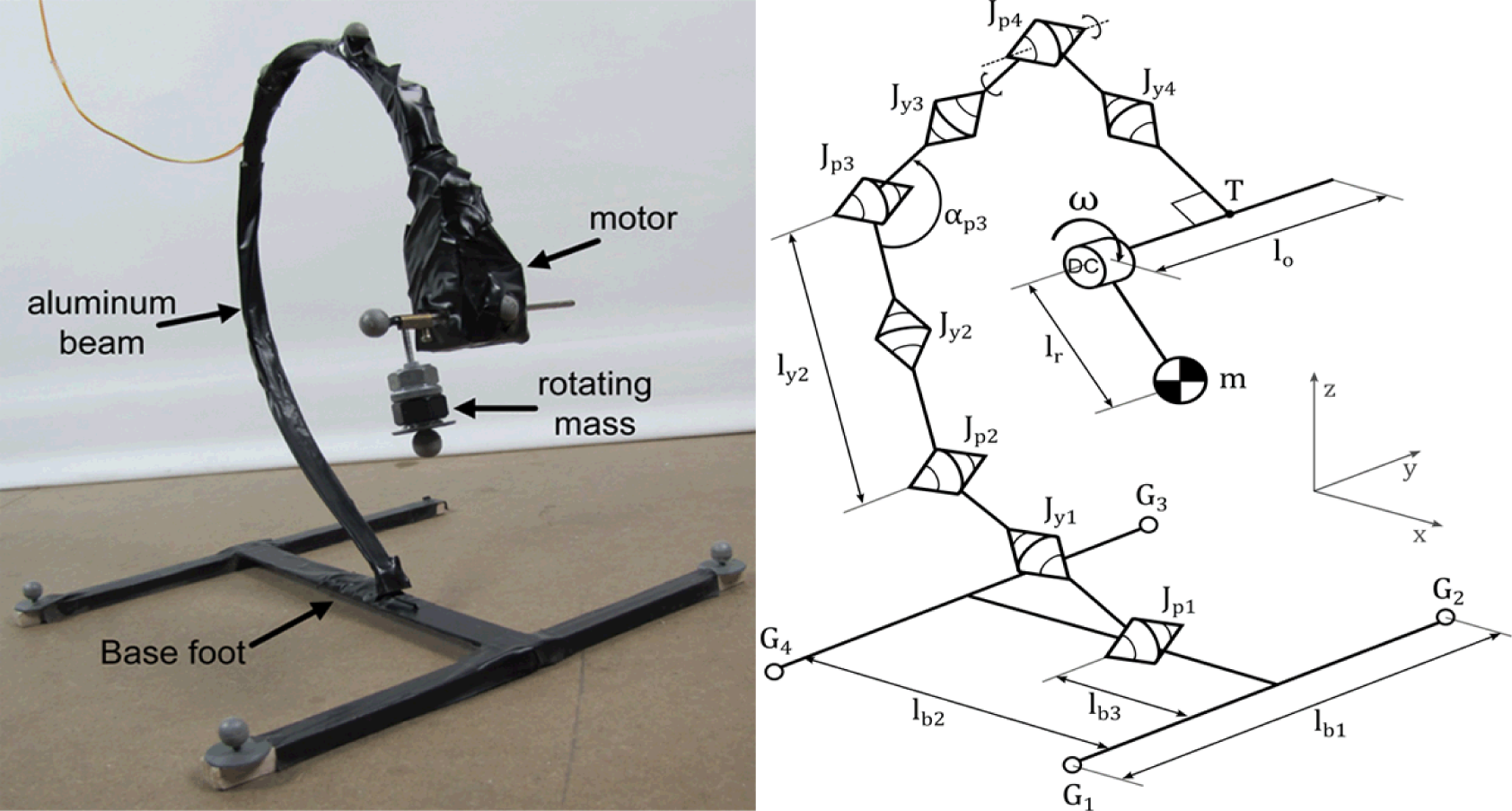
Figure 2a shows the physical curved beam hopping robot used in our previous research [25,26]. The robot consists of a large curved beam made of aluminum, which is attached to a large foot base on one end, and a DC motor with a small rotating object on the other. The rotation of the object causes the curved beam to vibrate, depending on the voltage applied to the DC motor. Due to the vibration and the interaction with the ground, the curved beam will hop at a particular range of frequencies [25,26]. Therefore, the dynamics of the robot are driven by the actuation frequency, i.e., the frequency of the rotating mass.
The model of the robot, along with the Cartesian axes used, is shown in Figure 2b. The mass of the rotating object is denoted as m. The lengths of the supplementary segments which connect the object with the motor, and the motor with tip of the beam are lr and lo, respectively. The curved beam is modeled as eight connected segments of equal lengths. The segments are alternately connected by joints which allow either pitch motion (Jp) or yaw motion (Jy). There are four pitch joints and four yaw joints, each with their corresponding spring constants. The pitch and yaw joints are denoted by Jpi=1..4 and Jyi=1..4, along with their spring constants kpi=1..4 and kyi=1..4 where smaller value of i refers to joints nearer to the foot. Two segments connected by yaw joint i have the same lengths, whose total length is defined as lyi. Figure 2(b) shows ly2 as an example. The angle between two segments connected by pitch joint i is defined as αpi Figure 2(b) shows αp3 as an example. The foot part of the robot is modeled as three connected segments with four contact points (G1..4). G1 and G2 denote the contact points of the robot’s forefoot, while G3 and G4 denotes the hindfoot’s contact point. The forefoot and hindfoot have the same length, lb1. The length of the segment that connects the forefoot and the hindfoot is denoted as lb2, while the length between the forefoot and the connection point between the beam and the foot is defined as lb3. We attempt to match the mechanical parameters as similar to the real robot as possible. The values of all the mechanical parameters used in the model are shown in Table 1, where M is the total mass of the robot. The model assumes that the ground is adequately soft, i.e., the contact points can be placed “below” the ground, and there is no pulling force exerting on Gi when the contact points are above the ground [27,28]. Here, fg is the gravitational force, kx, ky and kz are the spring coefficients in the x, y and z direction respectively, while dx, dy and dz are damper coefficients. The values for the spring and damper coefficients used in this manuscript are listed in Table 2.
The model is implemented by using standard components of MATLAB Simmechanics™ [29]. For each contact point Gi (i = 1,..4) shown in Figure 2(b), we use the following contact model:
where fzci is defined as follows:
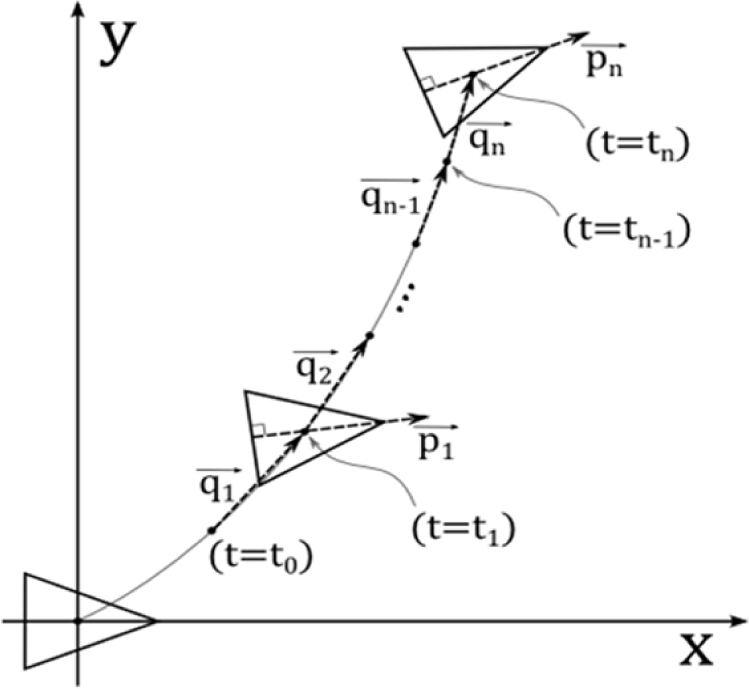
As mentioned in the Introduction, in this manuscript, we will demonstrate the proposed GSO enables the robot to perform a simple case of goal-directed locomotion. Therefore, we also build a simple model to describe the robot motion in two dimensional Cartesian space, i.e., the x-y plane. The model is shown in Figure 3. Here, is a vector which represents the robot’s orientation at time i. is therefore a unit vector whose angle is defined as ϕi. As also shown in the figure, is a displacement vector of the robot between time i-1 and i. The magnitude and angle of the vector is defined as Di and θi. The definition of the two vectors is shown in Equations (8) and (9):
In order to characterize the motion in two dimensional space, we therefore use the average of and , shown in Equations (11) and (12), where dm and Dm are the average magnitude, while θm and ϕm are the average orientation of and from time t = t0 until t = tn, i.e., i = 1…n respectively. We also define σdm, σDm, σθm, σφm as the corresponding standard deviations:
3.2. The Mechanical Dynamics of Curved Beam Hopping Robot
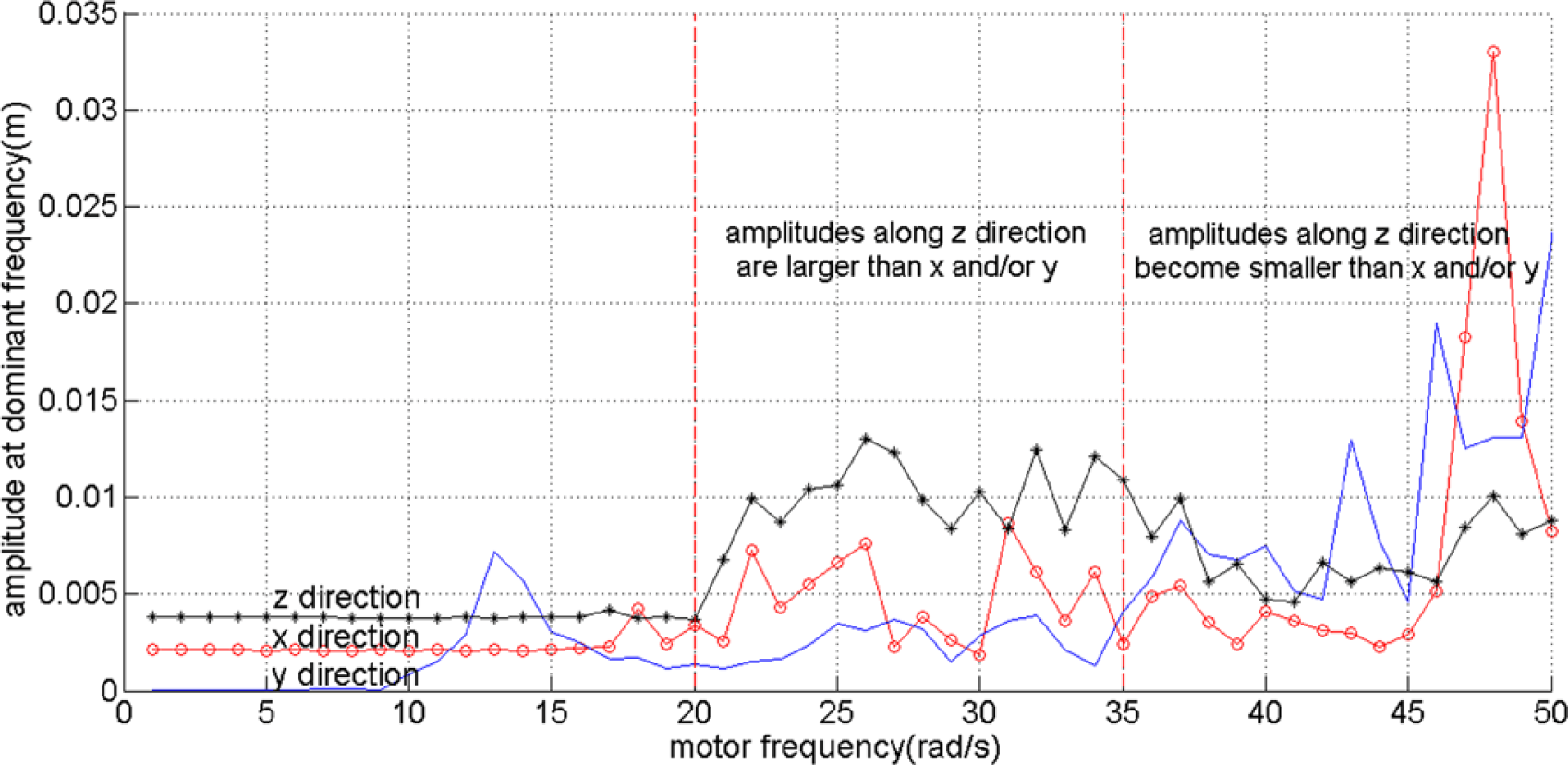
As in this paper we focus on enabling the robot to reach a goal in two dimensional spaces, we break the symmetry of the robot design by only use one rotating object on the right side of the robot as shown in Figure 2. In order to identify the behavior of the robot based on the actuation frequencies, i.e., ω, we observe the oscillation of the tip of the beam, directly connected with the DC motor. By using a Fast Fourier Transform, we collect the dominant amplitudes, i.e., amplitudes caused by the most dominant frequency, of the tip’s oscillation along the x, y and z axes. It can be seen that up until approximately ω = 20 rad/s, the oscillation can barely move the robot. However, at values larger than 20 rad/s, the amplitudes increase significantly. From approximately ω = 20 to 35 rad/s, the oscillation amplitudes along the z direction are slightly higher than along the x and y axes. However, at higher frequencies, the oscillation amplitudes along the x and y axes become much higher than those along the z direction. It is interesting to notice that these two last behaviors are similar to the torsional and longitudinal resonance shown in our previous research when there are two rotating objects attached to the DC motor [25,26]. However, because the robot is asymmetric, the power along the y axis becomes significant. Figure 4 shows the amplitudes at the dominant frequencies along x, y and z directions for different values of motor frequencies values with the red line roughly divides the frequencies based on the three explained different behaviors.
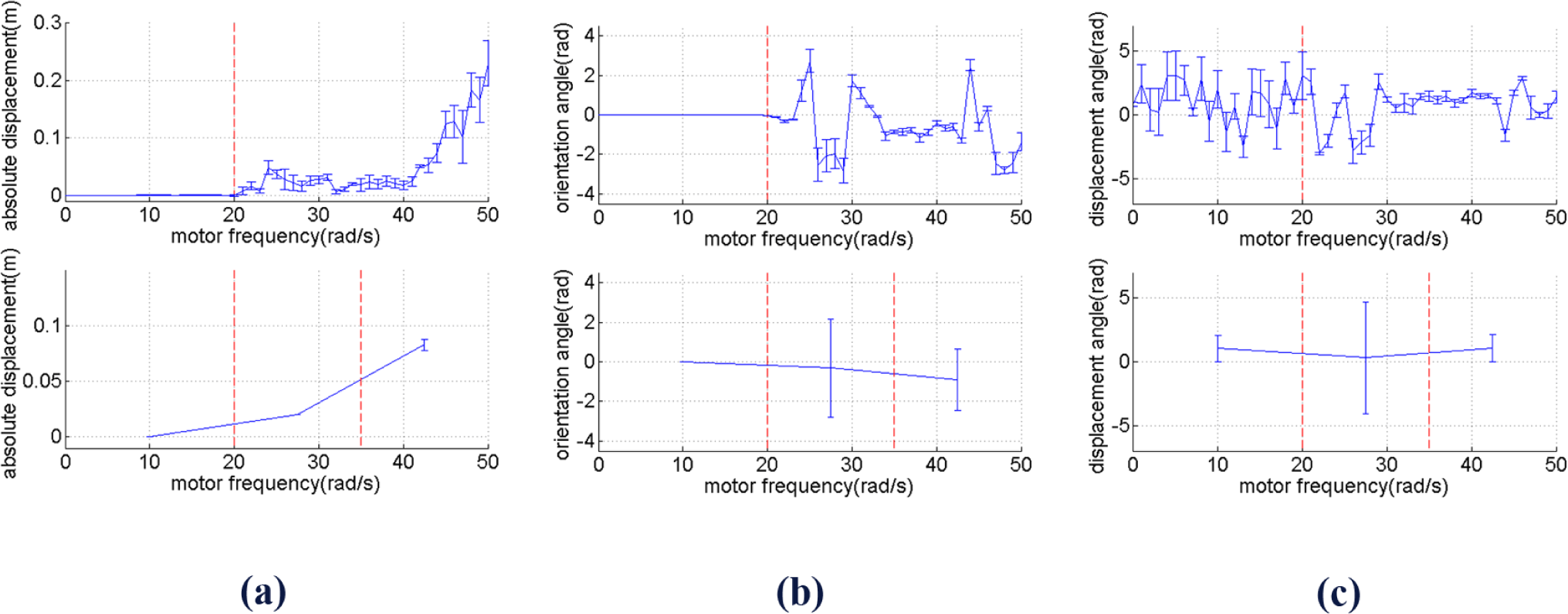
Knowing the frequency response of the tip alone is unfortunately not adequate to understand how the robot will behave in two dimensional spaces. We run several simulations for 10 s for several different frequencies and observe the trajectory in two dimensional spaces. Figure 5 shows the typical examples for the three different behaviors explained in the previous paragraph for ω = 10 rad/s, ω = 27.5 rad/s and ω = 42.5 rad/s. To further characterize the behavior, we run the simulation from ω = 0 until ω = 50 rad/s and extract the values of and in Equations (2) and (3) for i = 0…5, where t0 = 5 s and t5 = 10 s. We calculate and defined in Equations (10) and (11) and, here, we also define σDm, σθm, σφm as the standard deviation of Di, θi and ϕi for i = 0…n, respectively.
Figure 6 (top figures) shows Dm, θm, ϕm along with their standard deviation for each values of ω, while the bottom figures show them with the same partitions as Figure 4. It can be seen that Dm tends to go higher in between ω = 35 and ω = 50 rad/s. In the same range of frequency, θm also slightly increases, but σθm decreases.
A similar pattern is shown by, i.e., it increases as the frequency gets higher. It can therefore be seen that while the displacement magnitude, i.e., absolute velocity, increases as the frequency increases, the standard deviation of the displacement angle and orientation angle tend to decrease. The difference between and between the two last range of frequency is statistically significant with significance level 0.01. When the frequency gets even higher than 50 rad/s, becomes even larger, and as a result the robot becomes unstable, i.e., the tip of the beam will hit the ground after a particular period of time.
By comparing Figures 4 and 6, it can therefore be seen that we can roughly distinguish two meaningfully different behavioral types for different frequency ranges. Some references also use the term “behavioral primitives” as units of behavior above the level of motor commands which can be used as building blocks to generate more complex movement [30,31]. Ignoring the frequency range when the robot can barely move, i.e., approximately 0–20 rad/s, the two different behavioral types shown by Figure 4 and Figure 6 can be described as follows: at low frequencies, i.e., in the range of approximately 20–35 rad/s, the robot has tendency to change direction at low travelling speed. At high frequencies, i.e., approximately 35–50 rad/s, the robot has a tendency to keep going in the same direction at high travelling speed. In the next section, it will be shown that by using ASM, it is possible to take advantage of these two behavioral types which characterize the mechanical dynamics of the robot, such that the robot is able to perform goal-directed locomotion.
4. Experiment on Goal Directed Locomotion
Having described the ASM dynamics as well as the model and mechanical dynamics of the curved beam hopping robot, this section will explain how a GSO scheme can be realized by coupling the mechanical dynamics with the dynamics of the ASM. To be more specific, the next two sections will describe the experiment setting and results of a goal directed locomotion based on the proposed approach.
4.1. Experiment Setting
In order to understand whether and how the proposed GSO approach enables the robot to perform goal-directed locomotion, first, we couple the mechanical dynamics with the dynamis of ASM by having ω, the control parameter, as ASM state in Equation (1). Therefore, the dynamics of the motor frequency can be expressed by Equation (12). We also choose the potential U(ω(t)) and the sensory feedback function A(t) as shown in Equations (13) and (14):
where k = 1, and d(t) is defined as the distance between the goal and the point connecting the beam and the foot of the robot shown in Figure 2. It should be noticed that A(t) may become singular when the connection point between the beam and the foot of the robot is exactly placed at the goal, i.e., d(t) = 0. The problem is anticipated by adding a small constant value to d(t) if it equals zero, although the situation never occur in the performed experiments.
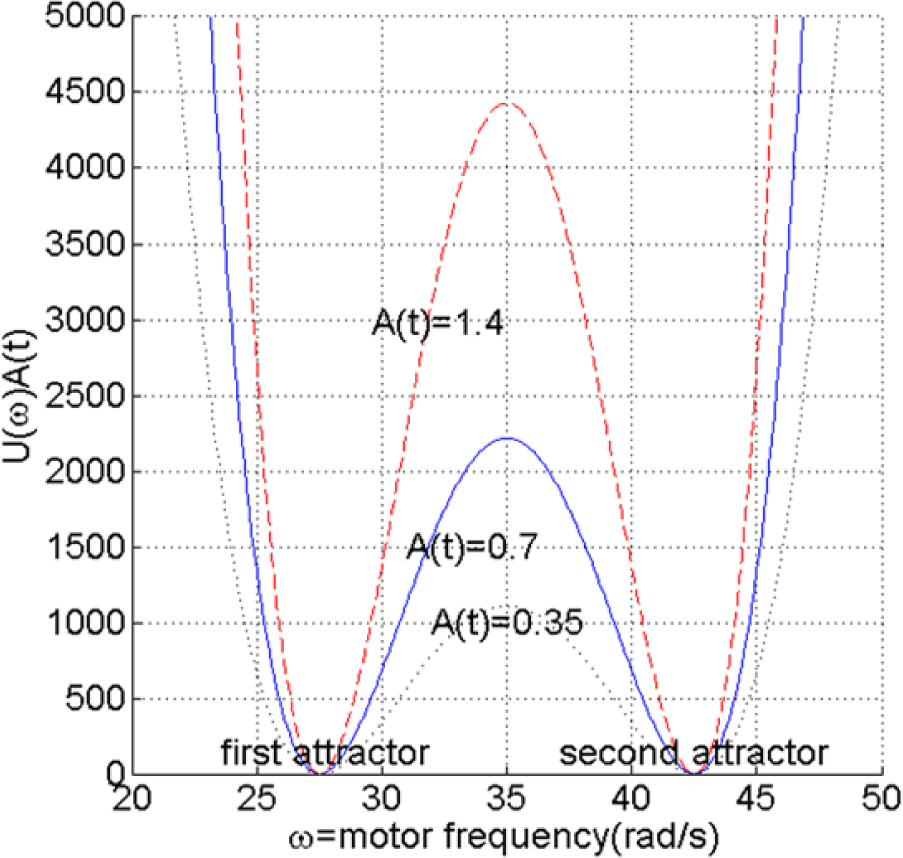
The potential function is shown in Figure 7. As can be seen from Equation (10) U(ω(t)) is a fourth order equation with two attractors at 27.5 and 42.5 rad/s. By choosing these two attractors, it is assumed that the motor frequency, ω, will adequately fluctuate between the two frequency ranges shown in Figure 5, allowing the robot to explore the two different behavioral primitives. A(t) does not give any orientation information to the robot, and the robot will simply have more tendency to keep the current behavior as long as it brings itself towards the goal, regardless of the details of the behavior. As a result, the resilience to changes in the operating enviroment, one of the fundamental properties of self-organizing system, is adequately maintained. As will be shown in the next section, it is however necessary for the robot to be able to explore the two different behavioral primitives.
For the experiment, the simulation time is set as 250 (s). The simulated robot starts at (x = 0, y = 0), facing in the positive x direction, while the goal position is set at (x = 1, y = 1). Due to the complexity of the simulation, Simmechanics™ automatically varies the sampling time depending on how complex the calculation in between two consecutive samplings is, with an average of approximately 0.05 s. The condition of the potential at the initial distance is shown in Figure 7, i.e., when A(t) ≈ 0.7. The two other values of A(t) in Figure 7 illustrate the conditions when, compared to the initial condition, the distance to the goal is doubled and cut in half.
4.2. Experimental Results
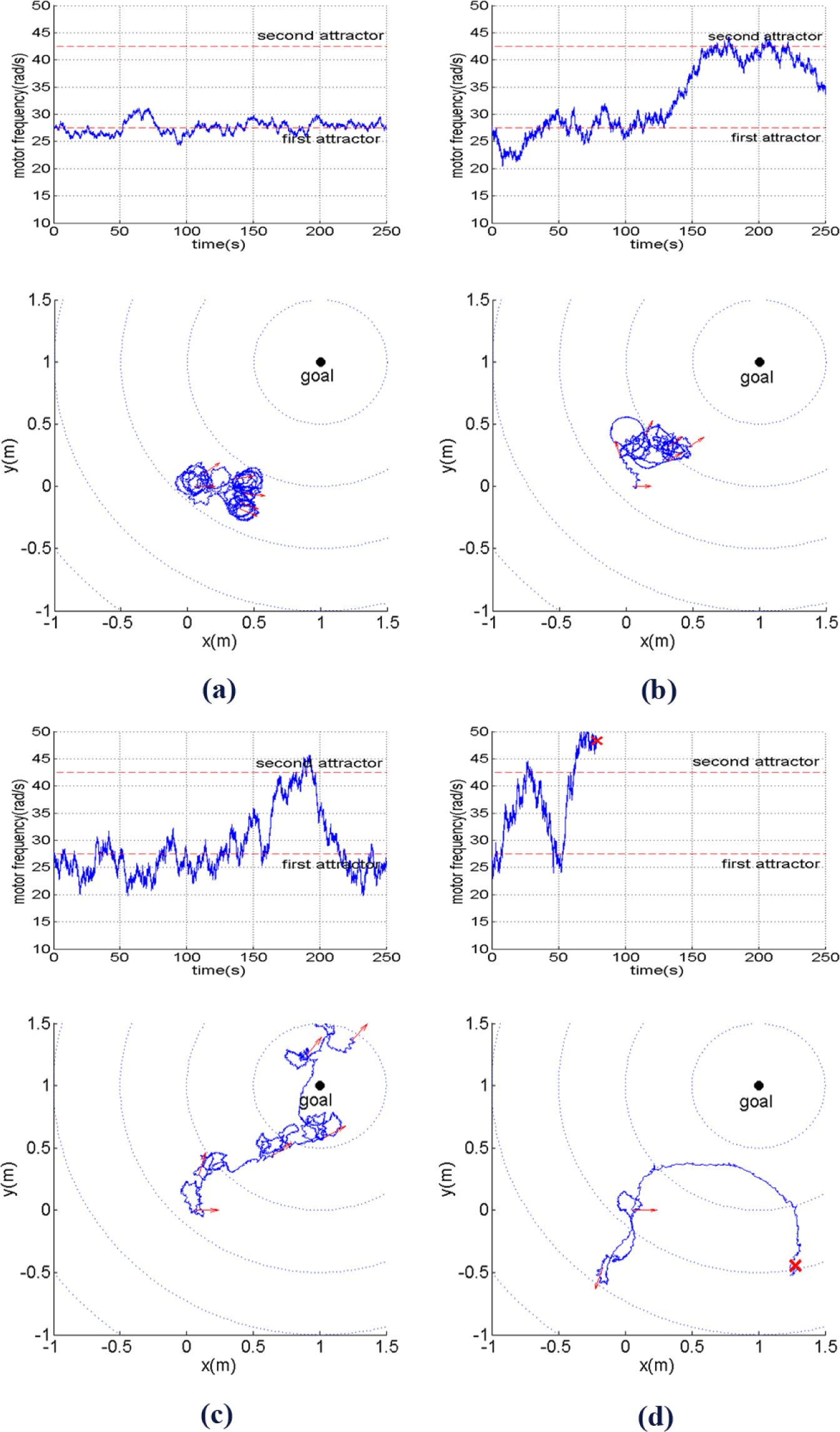
The experimental results can be summarized by Figures 8‒10. At first, we observe how different behaviors can be achieved by simply changing the level of inherent stochatic perturbation, i.e., the size of noise ε(t) defined as its standard deviation (σ(ε(t)). Figure 8 shows how the motor frequency, i.e., ω (in rad/s), changes over time along with the corresponding robot trajectory on the xy plane with different noise level. Here, ω(t) starts from the bottom of the first attractor. The arrows at the trajectories show the robot orientation, sampled every 50 s. By observing Figure 8a, it can be seen that for σ(ε(t)) = 50, ω(t) will fluctuate around the first attractor, causing the robot to explore the environment at low travelling speed while changing its directions randomly. From Figure 8b, it can be seen that at a higher noise level, i.e., (σ(ε(t)) = 100), the robot starts to be able to perform another type of behavior explained in Section 3, which is moving at higher speed while having more tendency to keep its direction.
With an approriate level of noise, i.e., σ(ε(t)) = 150, the fluctuation of ω(t) enables the robot to fully take advantage of its two behavioral primitives. As shown in Figure 8c, the robot adequately explores the two behavioral primitives in order to bring itself towards the goal. When the noise level is even larger, i.e., σ(ε(t)) = 200, ω can quickly reach very low or high values. However, due to a high probability to reach very high values of motor frequency, i.e., ω(t) > 50, the probability that the robot will become unstable, i.e., the robot tip hits the ground, also grows as shown in Figure 8d.
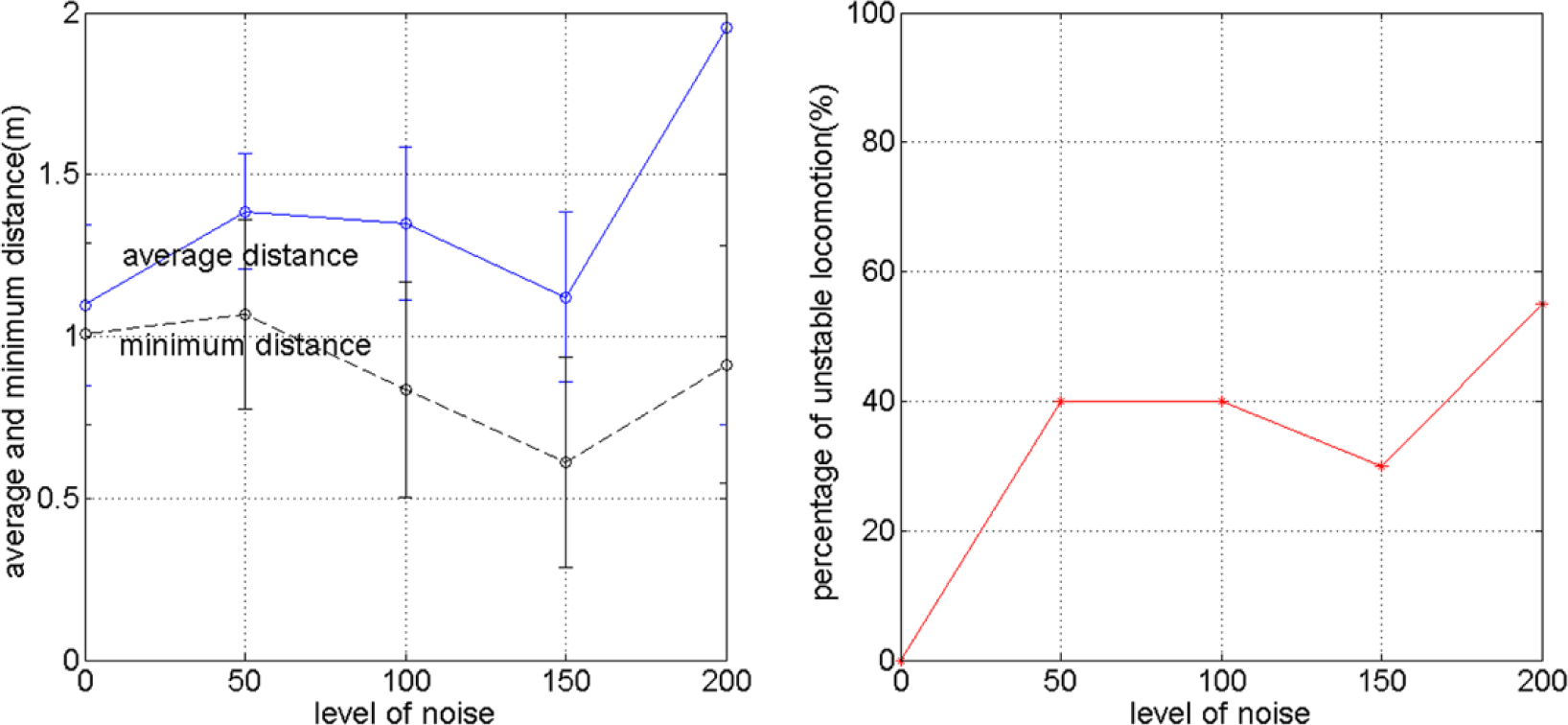
The way the different behaviors due to different noise levels affect the goal directed locomotion performance can be summarized by Figure 9, which shows that the relationship between the noise level, the average distance, minimum distance ever reached, and percentage of unstable locomotion. Each point in the figure is obtained from 20 trials of simulation explained in Section 4.1. It can be seen that for all the criteria, except for the percentage of unstable locomotion, the best performance is achieved for σ(ε(t)) = 150, which refers to the behavior shown in Figure 8c.
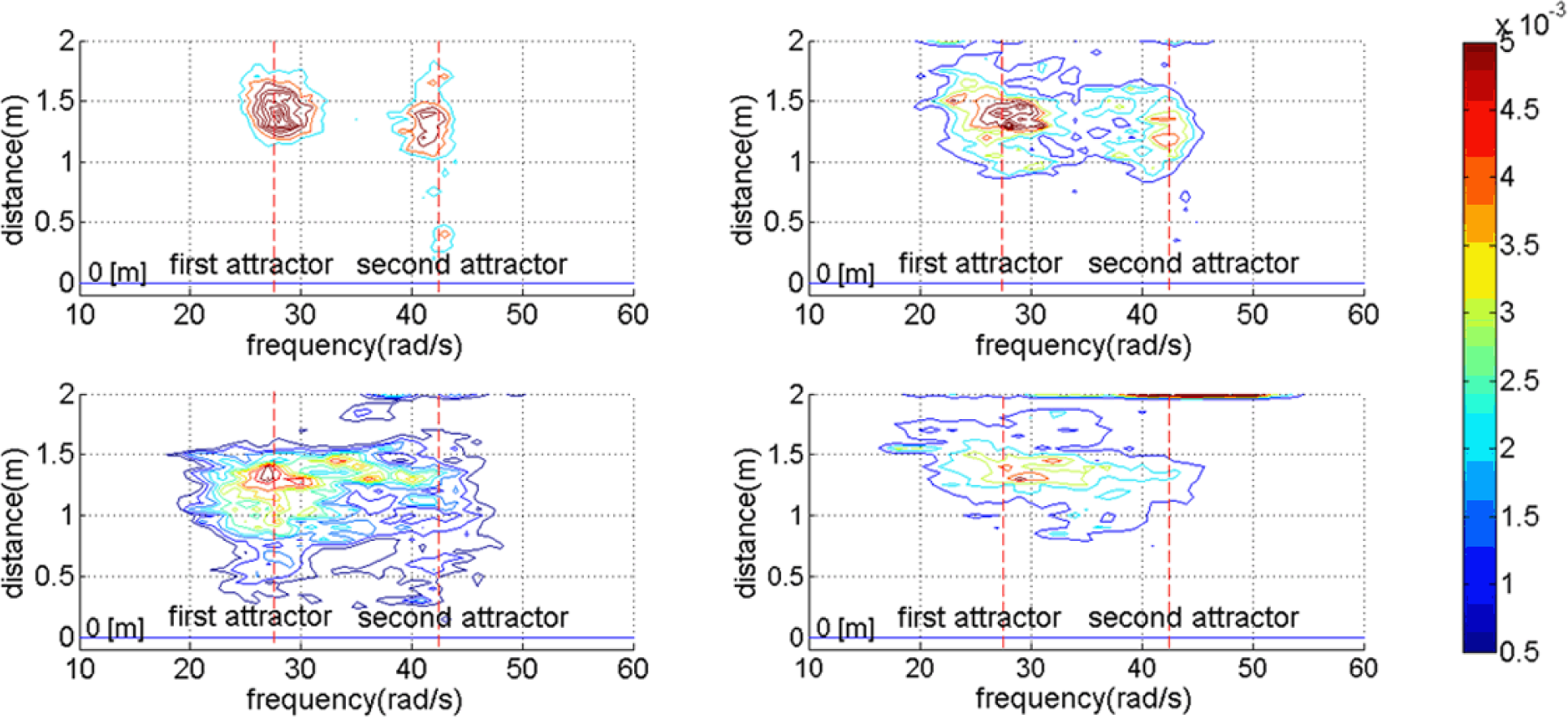
To further clarify how the different behaviors shown in Figure 8 regulate the robot’s probability to approach the goal, and therefore tune the performance shown in Figure 9, we observe the joint probability density function of the motor frequency, ω(t) and distance from the goal d(t) for all the time periods in all trials shown in Figure 10. The top left figure shows the condition when σ(ε(t)) = 50. Here, ω(t) will stay close to its initial conditions, i.e., either at the bottom of the first or second attractor. It can also be seen that due to the inability to explore another behavioral primitives, the robot generally cannot bring itself towards the goal. With higher noise levels, i.e., larger value of σ(ε(t)), the robot has a higher probability to explore the other behavioral primitive as shown in the top right and bottom left figures. For a proper noise level, i.e., σ(ε(t)) = 150, the probability to approach the goal reaches its maximum value for the chosen parameter values. When the noise level is too high, there is a higher probability for the motor frequencies to reach high values which cause the robot to become unstable and therefore the probability to approach the goal decreases as shown in the bottom right figure.
It should also be noticed that because in this manuscript A(t) is simply defined as inversely proportional to the distance from the goal, Figure 10 also shows the influence of the interplay between A(t) and the level of noise on the robot behavior. More specifically, the top left and top right figures show that even when the robot is still far from the goal, i.e., A(t) has a low value, the noise level is not high enough to make the robot alternates between the two frequency attractors to bring itself towards the goal. On the other hand, the bottom left figure of Figure 10 shows that when A(t) still has a low value due to a large distance from the goal, the robot tends to explore different behavioral primitives represented by the two attractors to bring itself towards the goal. However, when the robot approaches the goal, the frequency will settle to one of the two attractors due to a high value of A(t), observable from the two sharp edges at the bottom part of the probability density function. When the noise level is too high, despite the ability of the robot to alternate between the two attractors, the frequency can easily reach high values which cause unstable locomotion. As the noise level goes higher, it is also more difficult for the motor frequency to settle to one of the two attractors.
Another perspective to understand the robot behavior is to see it as random behavior which is biased by sensory experience through the use of A(t). In this manuscript, due to the definition of A(t), the robot does not have any explicit mechanism to orient itself toward the goal and simply has more tendency to settle to an attractor as long as the corresponding behavioral primitive reduces the distance toward the goal. In biological systems, the robot behavior is roughly comparable to bacterial chemotaxis, probably the simplest goal directed locomotion performed by animals [32]. Bacteria, such as Escherichia coli, as well as the nematode, Caenorhabditis elegans, chemotax according to a biased random walk without any direct orientation mechanism [32–34]. On the other hand, animals with a complex nervous systems show refined scent-tracking strategies, e.g., to hunt their prey, dogs move their nose back and forth across an odor trail [32,35]. More generally, it has also been explained that goal directed locomotion in vertebrata involves explicit control of their body orientation during locomotion [36].
It is also interesting to discuss how to increase the probability to reach the goal by modifying A(t). For example, it is possible to assume that the robot has at least two sensors such that it becomes explicitly aware of its orientation toward the goal. Here, A(t) can be modified such that it becomes a function of the orientation rather than the distance to the goal, which may increase the probability to reach the goal. Even based on the current implementation of A(t), the parameters involved, e.g., the value of the constant in A(t) and the noise level can be further optimized. However, the aim of the current manuscript is not to show that the proposed framework can realize goal directed locomotion in a best possible way. Instead, we simply attempt to propose a new perspective on how to achieve GSO, i.e., to guide a self-organizing system towards desirable behaviors without eliminating its fundamental properties such as non-deterministic dynamics with emergent features. Therefore, increasing the performance of the system will also be an objective of our future works.
5. Conclusions and Future Work
In this paper, we present an approach to guide the self-organization of an embodied system by coupling the mechanical dynamics of the system with an internal control structure known as attractor selection mechanism (ASM). As a paradigmatic example, the embodied system used in this paper is a simulated curved beam hopping robot: a system with a variety of mechanical dynamics which solely depends on its actuation frequencies. Due to the robot’s response to different actuation frequencies, it has been shown that the mechanical dynamics will lead into two behavioral primitives: at low frequencies, the robot has a tendency to change direction at low travelling speed, while at high frequencies, the robot has tendency to keep going in the same direction at high travelling speed. However, as the frequency becomes even higher, the probability of unstable locomotion also becomes higher.
The attractor selection mechanism takes advantage of the mechanical dynamics by considering the two behavioral primitives as different attractors. By utilizing internally generated noise, the mechanism enables the robot to gracefully shift between random and deterministic behaviors, represented by the two attractors. More specifically, if the sensory input indicates that the robot is approaching its goal, the robot will behave more deterministically by having more tendencies to keep performing the current behavior. Otherwise, the robot will behave more stochastically until it finds another suitable attractor which brings it closer to the goal. It has been shown that for a particular set of mechanical design parameters and constant in the sensory feedback function, there is a suitable level of inherent stochastic perturbation, i.e., internally generated noise, which enables the robot to adequately explore different behavioral primitives to bring itself towards a particular goal position. In other words, the probability to reach the goal is regulated by the interplay among the sensory input, the level of inherent stochastic perturbation, i.e., noise, and the mechanical dynamics.
Despite its simplicity, we have demonstrated that the proposed approach enables the robot to perform the simplest case of goal directed locomotion, i.e., random walk biased by sensory experience, without any direct orientation mechanism. We argue that the approach proposed in this paper gives us a minimalistic, yet systematic point of view on how to achieve GSO. More specifically, the general principle to achieve GSO in a dynamic embodied system based on the proposed framework is to properly couple the behavioral primitives with ASM attractors, to have proper level of noise and a to properly design the function A(t). Other mechanical system, for example, may have more numbers of distinguishable behavioral primitives than the robot shown in this manuscript. However, due to the nature of the approach, the system doesn’t need to know the detail of the behaviors. Instead, by properly coupling the ASM attractors with the behavior primitives through the function U(t) in Equation (1), the system will search and settle to an attractor which will lead to a high value of A(t). Here, A(t) should be designed based on the expected behavior of the robot. For example, by using A(t) defined in this manuscript, the robot will have more tendencies to keep executing a particular behavior primitive as long as it reduces the distance between the robot and its goal position.
In this manuscript, we have not explored the possibility of using learning algorithms to couple the mechanical and ASM dynamics. From this perspective, it is interesting to discuss the comparison between the proposed approach, and guided-self organization in general, with classical learning approaches aiming at intelligent and animal-like behavior of robot. From a time scale perspective, it is possible to classify the commonly implemented learning approaches in robotics to evolutionary robotics, reinforcement learning and developmental robotics. Inspired by biological evolution, evolutionary robotics aims to optimize robot behavior over many iterations, i.e., generations, to perform a particular task. Despite various successful implementations in robotic applications, it has not been possible to achieve an open-ended process where more and more complex behaviors emerge based on evolutionary robotics [37]. Reinforcement learning aims to obtain goal-oriented behavior from the sequences of observations makes by an agent or robot over its entire lifetime. Reinforcement learning is based on the concept of classical conditioning, which states that a reward or punishment, is associated with an earlier presented stimulus, such that the stimulus is sufficient to predict the later reward or punishment. Therefore, reinforcement learning considers robot behaviors as sequences of actions rather than as sensorimotor couplings, i.e., the coupling between the sensory and motor system, as shown by biological systems. As a result, reinforcement learning works best on discrete state and action spaces. In real world continuous time systems, it is commonly necessary to use additional methods to overcome the curse of dimensionality due to the high dimensional continuous space [38].
GSO is probably most related to developmental robotics and embodied intelligence concept. Developmental robotics is an emergent area of research at the intersection of robotics and developmental sciences, aiming at understanding the developmental mechanism which might lead to open-ended learning in embodied machines [39]. The embodied intelligence concept states that the control of robot behavior is much easier if the dynamics of interactions between the body and the environment is exploited. Therefore, complex behavior can emerge even with a fixed mapping between stimuli and actions. Homeokinesis is an important concept that relates developmental robotics and GSO. Inspired by the development of complex sensorimotor coordination through the curiosity and playful behavior of young mammals, the aim of homeokinesis is to enable robots to explore and self-organize their body capabilities and interactions with the environment for the generation of coordinated behavior without specific goal [2]. GSO can be viewed as an attempt to extend the concept, by combing developmental self-organization and goal-oriented learning. While learning has not been investigated in the approach proposed in this paper, the exploration of the body capabilities and interactions with the environment is achieved through the coupling between ASM attractors and the behavioral primitives and the stochastic perturbation, while the goal oriented behavior is achieved through the function A(t).
As future works, we plan to further explore the effect of different kinds of parameters, namely the mechanical design parameters, sensory feedback function parameters, level of noise, and the potential function representing the coupling between ASM dynamics and the mechanical dynamics. We will also explore the possibility of using learning algorithms to couple the mechanical and ASM dynamics, as well as to co-optimize the involved parameters in this approach to increase the performance.
Acknowledgments
This study was supported by the Swiss National Science Foundation Grant No. PP00P2123387/1, and the Swiss National Science Foundation through the National Centre of Competence in Research Robotics.
Author Contributions
S.G.N., X.Y. and F.I. conceived and designed the experiment; S.G.N., X.Y. and Y.K. performed experiments; S.G.N., X.Y. and Y.K. wrote the paper; S.G.N., X.Y. and Y.K. analyzed the data; F.I. read and commented on the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Prokopenko, M. Design vs. Self-organization. In Advances in Applied Self-organizing Systems; Springer-Verlag: London, UK, 2007; pp. 3–17. [Google Scholar]
- Martius, G.; Herrmann, J.M. Variants of guided self-organization for robot control. Theory Biosci 2012, 131, 129–137. [Google Scholar]
- Ay, N.; Bertschinger, N.; Der, R.; Guettler, F.; Olbrich, E. Predictive information and explorative behavior of autonomous robots. Eur. Phys. J. B 2008, 63, 329–339. [Google Scholar]
- Prokopenko, M.; Gerasimov, V.; Tanev, I. Evolving spatiotemporal coordination in a modular robotic system, In Proceedings of the 9th International Conference on the Simulation of Adaptive Behavior (SAB), Rome, Italy, 25–29 September 2006; pp. 558–569.
- Prokopenko, M.; Gerasimov, V.; Tanev, I. Measuring spatiotemporal coordination in a modular robotic system, In Proceedings of the Tenth International Conference on the Simulation and Synthesis of Living Systems, Bloomington, USA, 3–6 June 2006; pp. 185–191.
- Hesse, F.; Martius, G.J.M.; Der, R.; Herrmann, J.M. A sensor-based learning algorithm for the self-organization of robot behavior. Algorithms 2009, 2, 398–409. [Google Scholar]
- McDonnell, M.D. What is stochastic resonance? Definitions, misconceptions, debates, and its relevance to biology. PLoS Comput. Biol 2009, 5, e1000348. [Google Scholar]
- Benzi, R. Stochastic resonance: From climate to biology. Nonlin. Proces. Geophys 2010, 17, 431–441. [Google Scholar]
- Hanggi, P. Stochastic resonance in biology how noise can enhance detection of weak signals and help improve biological information processing. Chem. Phys. Chem 2002, 3, 285–290. [Google Scholar]
- Korobkova, E.; Emonet, T.; Vilar, J.M.; Shimizu, T.S.; Cluzel, P. From molecular noise to behavioral variability in a single bacterium. Nature 2004, 428, 574–578. [Google Scholar]
- Yanagida, T.; Ueda, M.; Murata, T.; Esaki, S.; Ishii, Y. Brownian motion, fluctuation and life. BioSyst 2007, 88, 228–242. [Google Scholar]
- Kashiwagi, A.; Ureba, I.; Kaneko, K.; Yomo, T. Adaptive response of a gene network to environmental changes by fitness-induced attractor selection. PLoS One 2006, 1, e49. [Google Scholar]
- Chen, B.S.; Li, C.W. On the interplay between entropy and robustness of gene regulatory networks. Entropy 2010, 12, 1071–1101. [Google Scholar]
- Maye, A.; Hsieh, C.H.; Sugihara, G.; Brembs, B. Order in spontaneous behavior. PLoS One 2007, 2, e443. [Google Scholar]
- Dees, N.D; Bahar, S.; Moss, F. Stochastic resonance and the evolution of Daphnia foraging strategy. Phys. Biol 2008, 5, 044001. [Google Scholar]
- De Jager, M.; Weissing, F.J.; Herman, P.M.J.; Nolet, B.A.; van de Koppel, J. Levy Walks evolve through interaction between movement and environmental complexity. Science 2011, 332, 1551–1553. [Google Scholar]
- Nurzaman, S.G.; Matsumoto, Y.; Nakamura, Y.; Shirai, K.; Koizumi, S.; Ishiguro, H. From Levy to Brownian: A computational model based on biological fluctuation. PLoS One 2010, 6, e16168. [Google Scholar]
- Nurzaman, S.G.; Matsumoto, Y.; Nakamura, Y.; Shirai, K.; Ishiguro, H. Bacteria-inspired underactuated mobile robot based on a biological fluctuation. Adapt. Behav 2012, 20, 225–236. [Google Scholar]
- Nurzaman, S.G.; Matsumoto, Y.; Nakamura, Y.; Koizumi, S.; Ishiguro, H. “Yuragi-based” adaptive mobile robot search with and without gradient sensing: From bacterial chemotaxis to a Levy walk. Adv. Robot 2011, 25, 2019–2037. [Google Scholar]
- Nurzaman, S.G.; Matsumoto, Y.; Nakamura, Y.; Koizumi, S.; Ishiguro, H. Attractor selection based biologically inspired navigation system, In Proceedings of the 39th International Symposium on Robotics (ISR), Seoul, Korea, 15–17 October 2008; pp. 837–842.
- Pfeifer, R.; Lungarella, M.; Iida, F. Self-organization, embodiment and biologically inspired robotics. Science 2007, 318, 1088–1093. [Google Scholar]
- Hoffmann, M.; Pfeifer, R. The implications of embodiment for behavior and cognition: animal and robotic case studies. In The Implications of Embodiment: Cognition and Communication; Tschacher, W., Bergomi, C., Eds.; Imprint Academic: Exeter, UK, 2012; pp. 31–58. [Google Scholar]
- Füchslin, R.M.; Dzyakanchuk, A.; Hauser, H.; Hunt, K.J.; Luchsinger, R.H.; Reller, B.L.; Scheidegger, S.; Walkter, R.; Scheidegger, S.; Walker, R. Morphological computation and morphological control: Steps toward a formal theory and applications. Artif. Life 2013, 19, 9–34. [Google Scholar]
- Iida, F.; Preifer, R. Sensing through body dynamics. Rob. Auton. Syst 2006, 54, 631–640. [Google Scholar]
- Reis, M.; Iida, F. An energy efficient hopping robot based on a free vibration of a curved beam. IEEE/ASME Trans. Mechatronics 2013, 19, 300–311. [Google Scholar]
- Yu, X.; Iida, F. Minimalistic models of an energy-efficient vertical-hopping robot. IEEE Trans. Ind. Electron 2013, 61, 1035–1062. [Google Scholar]
- Brubaker, M.A.; Sigal, L.; Fleet, D.J. Estimating contact dynamics, In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2389–2396.
- Naf, D. Quadruped Walking/Running Simulation. Semester-Thesis, ETH Zurich, Zurich, Switzerland, May 2011. [Google Scholar]
- MathWorks Official Homepage, Available online: http://www.mathworks.com/products/simmechanics/ (accessed on 27 January 2014).
- Bentivegna, D.; Cheng, G.; Atkeson, C. Learning from observation and from practice using behavioral primitives. In Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 551–560. [Google Scholar]
- Jenkins, O.C.; Mataric, M.J. Deriving action and behavior primitives from human motion data, In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; pp. 2551–2556.
- Gomez-Marin, A.; Stephens, G.J.; Louis, M. Active sampling and decision making in Drosophila chemotaxis. Nat. Commun 2011, 2, 1–10. [Google Scholar]
- Berg, H.C. Motile behavior of bacteria. Phys. Today 2000, 53, 24–29. [Google Scholar]
- Pierce-Shimomura, J.T.; Morse, T.M.; Lockery, S.R. The fundamental role of pirouettes in Caenorhabditis elegans chemotaxis. J. Neurosci 1999, 19, 9557–9569. [Google Scholar]
- Thesen, A.; Steen, J.B.; Doving, K.B. Behaviour of dogs during olfactory tracking. J. Exp. Biol 1993, 180, 247–251. [Google Scholar]
- Grillner, S.; Wallen, P.; Saitoh, K.; Kozlov, A.; Robertson, B. Neural bases of goal-directed locomotion in vertebrates—An overview. Brain Res. Rev 2008, 57, 2–12. [Google Scholar]
- Bianco, R.; Nolfi, S. Toward open-ended evolutionary robotics: Evolving elementary robotic units able to self-assemble and self-reproduce. Conn. Sci 2011, 16, 227–248. [Google Scholar]
- Doya, K. Reinforcement learning in continuous time and space. Neural Comput 2000, 12, 219–245. [Google Scholar]
- Lungarella, M.; Metta, G.; Pfeifer, R.; Sandini, G. Developmental robotics: A survey. Conn. Sci 2003, 15, 151–190. [Google Scholar]

| Name | Value | Name | Value |
|---|---|---|---|
| lo | 0.160 (m) | αp1 | 2.554 (rad) |
| lr | 0.030 (m) | αp2 | 2.570 (deg) |
| lb1 | 0.305 (m) | αp3 | 1.665 (deg) |
| lb2 | 0.275 (m) | αp4 | 1.803 (deg) |
| lb3 | 0.082 (m) | kp1 | 15 (N/rad) |
| ly1 | 0.151 (m) | kp2~kp4 | 13 (N/rad) |
| ly2 | 0.141 (m) | ky1~ky4 | 3.517 (N/rad) |
| ly3 | 0.135 (m) | m | 0.030 (kg) |
| ly4 | 0.145 (m) | M | 0.331 (kg) |
| Name | Value | Name | Value |
|---|---|---|---|
| kx | 10 (N/m) | dx | 10 (Ns/m) |
| ky | 10 (N/m) | dy | 10 (Ns/m) |
| kz | 105 (N/m) | dz | 10 (Ns/m) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nurzaman, S.G.; Yu, X.; Kim, Y.; Iida, F. Guided Self-Organization in a Dynamic Embodied System Based on Attractor Selection Mechanism. Entropy 2014, 16, 2592-2610. https://doi.org/10.3390/e16052592
Nurzaman SG, Yu X, Kim Y, Iida F. Guided Self-Organization in a Dynamic Embodied System Based on Attractor Selection Mechanism. Entropy. 2014; 16(5):2592-2610. https://doi.org/10.3390/e16052592
Chicago/Turabian StyleNurzaman, Surya G., Xiaoxiang Yu, Yongjae Kim, and Fumiya Iida. 2014. "Guided Self-Organization in a Dynamic Embodied System Based on Attractor Selection Mechanism" Entropy 16, no. 5: 2592-2610. https://doi.org/10.3390/e16052592




