Abstract
We apply measures of complexity, emergence, and self-organization to an urban traffic model for comparing a traditional traffic-light coordination method with a self-organizing method in two scenarios: cyclic boundaries and non-orientable boundaries. We show that the measures are useful to identify and characterize different dynamical phases. It becomes clear that different operation regimes are required for different traffic demands. Thus, not only is traffic a non-stationary problem, requiring controllers to adapt constantly; controllers must also change drastically the complexity of their behavior depending on the demand. Based on our measures and extending Ashby’s law of requisite variety, we can say that the self-organizing method achieves an adaptability level comparable to that of a living system.1. Introduction
We live in an increasingly urbanized world [–]. Cities offer several advantages and thus attract dwellers [–]. This growth, however, also generates problems for which we do not have a clear solution. One of these problems is inefficient mobility [], which is influenced by several factors ([], pp. 404–405). Efficient traffic light coordination is related to some of these factors, as mobility capacity can be increased by changes in infrastructure and technology.
Given its inherent complexity, traffic varies constantly [], as vehicles, citizens, and traffic lights interact. As many urban problems, traffic is non-stationary []. For this reason, several adaptive approaches to traffic light coordination have been proposed [–]. Some of these approaches have shown considerable improvements over static methods, which is understandable due to the non-stationary nature of the problem. Certain proposals can be described as using self-organization to achieve traffic light coordination. A question remains: how should self-organization be guided to achieve efficient traffic flow? This can be explored under the nascent field of guided self-organization [–].
Non-stationary problems change constantly. Which should be their desired regime? Would this also change? How can these be measured? We explore these questions in the context of traffic light coordination, applying recently proposed measures of complexity, emergence and self-organization based on information theory []. These measures, being simple and general, give insights on the underlying properties of the traffic light controllers, in a similar way as temperature gives an insight on the kinetic energy of molecules.
In the next section, we present our working framework: a city traffic model, the traffic light coordination methods compared, and the proposed measures. The city traffic model is based on elementary cellular automata, allowing us to detect precisely several phase transitions. The traffic light coordination methods studied are “green-wave” and “self-organizing”. The former attempts to optimize expected flows and is used in many cities. The latter has been recently proposed and adapts to immediate traffic demands. The measures are based on information theory and aim at being general and simple. Results of applying our measures to both traffic light coordination methods in our city traffic model follow under different boundary conditions: cyclic and non-orientable. The discussion focusses on the usefulness of our measures and the insights they give in the system studied. A future work section outlines possible improvements, refinements and extensions. Conclusions close the paper. Appendixes include axioms of the proposed measures, details of how data is processed, and preliminary results using a realistic open source traffic simulator.
2. Methods
We performed our study on a simulation developed in NetLogo [], available at[] including its source code. In the next subsections, we present our traffic model, the traffic light coordination methods compared, and the novel measures used on them.
2.1. Traffic Model
We used a previously proposed city traffic model [] based on elementary cellular automata [,]. This is an abstract model (deterministic, time and space are discrete, velocity is either one or zero, acceleration is infinite) allowing to identify clearly different dynamical phases. The purpose of this model is not predictive, but descriptive [].
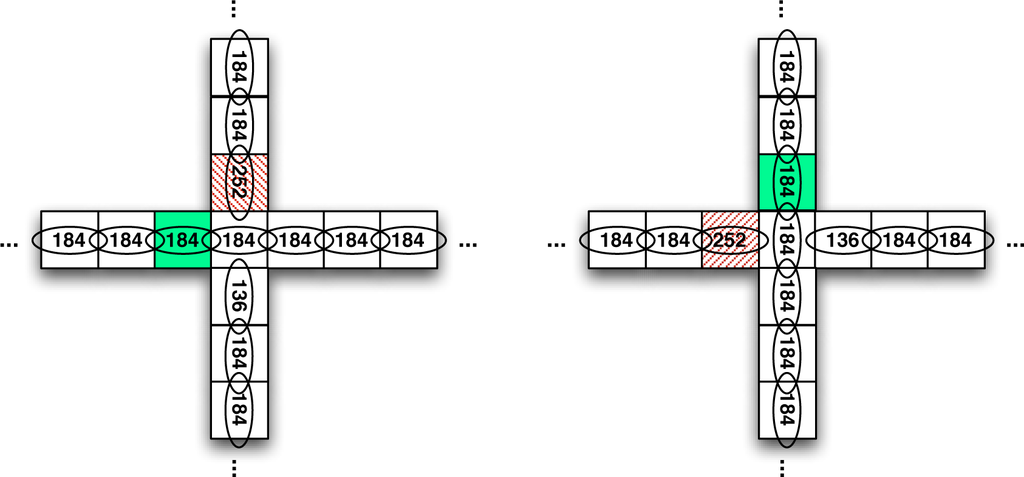
Each street is represented as an elementary cellular automaton (ECA), coupled at intersections. Each ECA contains a number of cells which can take values of zero (empty) or one (vehicle). The state of cells is updated synchronously taking into consideration their previous state and the previous state of their closest neighbors. Most cells simply allow a vehicle to advance if there is a free space ahead. This behavior is modeled with ECA rule 184, which is one of the simplest highway traffic models (See Table 1). ECA 184 models vehicles moving to the right. Other directions are obtained by changing the positions of neighbors while using the same rule. At intersections, two other rules are used. Before a red light, vehicles do not advance, modeled with ECA rule 252. After a red light, crossing vehicles should not enter the street, modeled with ECA rule 136. The street with the green light uses only ECA rule 184. The intersection cells change neighbourhood to cells on the street with the green light, as shown in Figure 1.

This city traffic model is conservative, i.e., the density of vehicles ρ (proportion of cells with a value of one) is constant in time. It is straightforward to extend such a model to an hexagonal grid, allowing for more complex intersections [].
The average velocity υ is simple to calculate: it is given by the number of cells that changed from zero to one (movement occurred between time t and t + 1) divided by the total number of vehicles (cells with one). υ = 0 if no vehicle moves, while υ = 1 when all vehicles are moving.
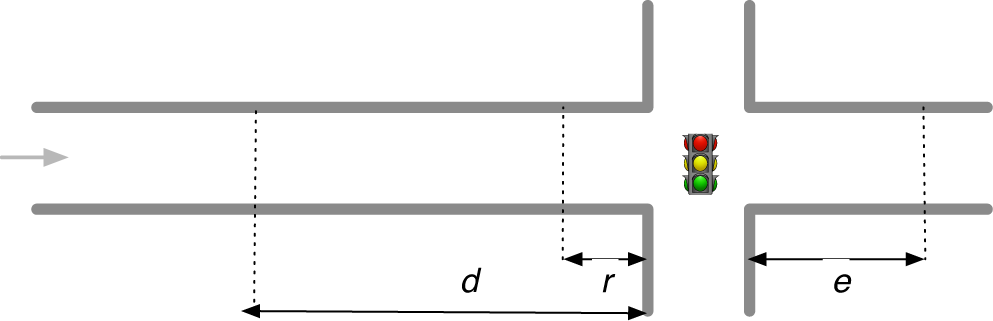
Flow J is defined as the velocity υ multiplied by the density ρ, i.e., J = υ · ρ. J = 0 when there is no flow: either there are no vehicles in the simulation (ρ = 0) or all vehicles are stopped (υ = 0). A maximum J occurs when all intersections are being crossed by vehicles. In the studied scenarios, Jmax = 0.25. This is because, for a single street (ECA rule 184), vehicles need a space to advance, limiting Jmax = 0.5. However, when two streets intersect, one of them has to stop while the other flows, halving Jmax to 0.25.
Theoretically, the optimum υ and J for a given ρ in a traffic light coordination problem should be the same as optimal υ and J for isolated intersections, i.e., an upper limit. This implies that each intersection interacting with its neighbors is as efficient as one without interactions. This can be shown with optimality curves (defined as the best possible performance for an isolated intersection for different densities minus the actual performance of the traffic system []), visually and analytically comparing results of different methods with theoretical optima.
Non-Orientable Boundaries
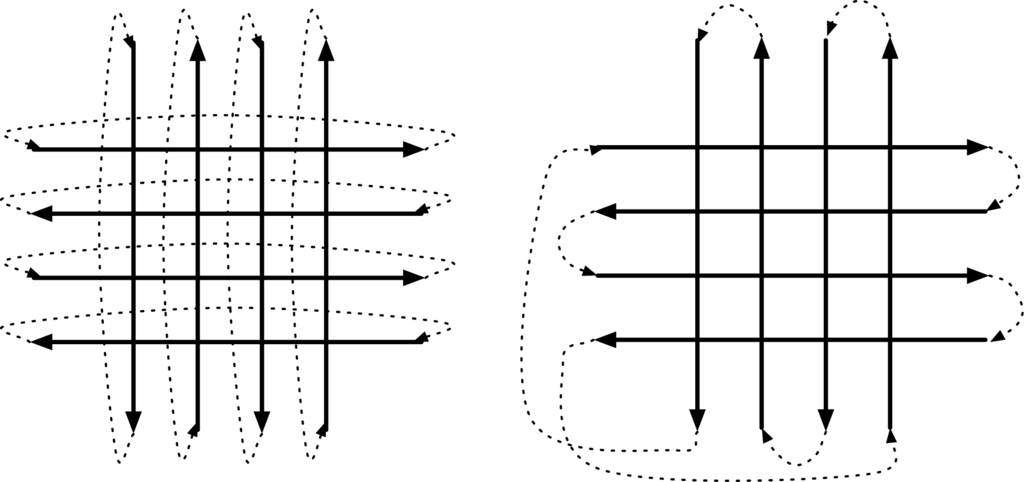
Our previous studies have assumed cyclic boundaries, as is usual with ECA. However, this can lead to a quick stabilization of the system for certain densities, as vehicle trajectories become repetitive (assuming no turning probabilities, the model is deterministic).
Following a suggestion by Masahiro Kanai [], we changed the boundary conditions to be non-orientable (as in a Möbius strip or a Klein bottle), maintaining incoming vehicle distributions, constant density, and determinism but in practice destroying the correlations that were formed with cyclic boundaries.
Kanai [] studied an isolated intersection, also using ECA. Instead of having two cyclic ECA, he used a single self-intersecting ECA where vehicles exiting on the east enter from the north and vehicles exiting on the south enter from the west. Using a similar approach, changing the boundaries we transformed a ten-by-ten street scenario (20 cyclic streets with 100 intersections) to a single street self-intersecting 100 times. An example of this change of boundaries is shown in Figure 2.
2.2. Traffic Light Coordination
The problem of coordinating traffic lights is EXPTIME-complete []. This implies that optimization for large traffic networks is unfeasible. Moreover, the precise traffic conditions change constantly (each cycle a different number of vehicles arrive at each intersection), so the problem is non-stationary. Even if we find an optimal solution, this will become obsolete in seconds. Thus, an alternative to optimization becomes adaptation, being self-organization a useful method for building adaptive systems [].
In this work, we compare a traditional method which tries to optimize expected flows with a self-organizing method. These are described in detail in [] and have been replicated in a parallel implementation, also available with source code at [].
2.2.1. Green-Wave Method
Many cities employ the “green-wave” method to coordinate traffic lights []. Traffic lights have the same period and the phase (offset) is adjusted so that green lights switch at the expected velocity of vehicles. In this way, once vehicles get a green light, they should not get any red light. This is better than having no coordination. However, due to mathematical constraints, at most two directions can have a green-wave at the same time. Thus, vehicles driving in the opposite direction find anti-correlated phases and have high waiting times, leading to long queue formation already for medium densities. Moreover, if the vehicles do not go at the expected velocity (as it is the case when densities change), then vehicles will not be able to go at the speed of the green-wave and will have to stop.
In [] we studied the green-wave method in the traffic model described in the previous subsection. We found only two dynamical phases: intermittent (some vehicles stop, some move) and gridlock (all vehicles are stopped).
2.2.2. Self-Organizing Method
We have proposed and refined a self-organizing method for traffic light coordination where each intersection follows simple local rules, reaching close to optimal global coordination [,,,]. The algorithm follows six simple rules, listed in Table 2. Rules with higher numbers override rules with lower numbers, e.g., rule 4 overrides rule 1.

Rule 1 gives preference to streets with higher demand (few vehicles wait more than several) and promotes the formation of platoons (few vehicles waiting may be joined by more to form larger groups, which reaching further intersections can trigger the green light before decreasing their speed). Rule 2 maintains a minimum green time to prevent fast switching of traffic lights in high densities. Rule 3 maintains platoons together, although allowing the splitting of large platoons. Rule 4 is useful for low densities, allowing few vehicles to trigger a green light if there is no vehicle approaching the current green. Rules 5 and 6 are useful for high densities, switching lights to red if there are cars stopped downstream of the intersection, preventing its blockage. The pseduocode of the algorithm extended for multiple directions can be found in [].
In [] we found seven dynamical phases of the self-organizing method in our traffic model (with cyclic boundaries) as the density ρ increases: free-flow (no vehicle stops, υ = 1), quasi-free-flow (almost no vehicle stops), underutilized-intermittent (some vehicles stop, intersections do not reach maximum flow Jmax), full-capacity-intermittent (some vehicles stop, Jmax i.e., all intersections have vehicles using them always), overutilized-intermittent (some vehicles stop, intersections have to restrict both streams to prevent blockages using rule 6), quasi-gridlock (almost all vehicles are stopped, but “platoons” of spaces form and move in the direction opposite of streets), and gridlock (all vehicles are stopped, i.e., υ = 0, as intersections get blocked from initial conditions). Their respective phase transitions occur approximately at ρ values of 0.15, 0.22, 0.38, 0.63, 0.77, and 0.95.
2.3. Measures
We recently proposed measures of emergence, self-organization, and complexity based on information theory in [] and refined them and based them on axioms in []. These axioms are included in Appendix A.1 for quick reference. There are no agreed definitions—or even notions—of complexity, emergence, or self-organization. The ones we have proposed aim at being most general and most simple, with the possibility of containing other measures and definitions as special cases.
The concept of emergence has been controversial for centuries (for a comprehensive overview, see []). Many notions of emergence are compatible with the idea of describing emergence as novelty (between scales, in time, or within a process). There is a well-studied equation which measures novelty. Shannon defined a measure of information [], equivalent to Boltzmann’s entropy, depending of the probabilities pi for all i symbols in a finite alphabet:
where K is a positive constant. In this work, we consider the log in Equation 1 to be of base two.
In its most general form, emergence can be understood as information produced by a process or system []. As Shannon’s information already measures this, we defined
Minimum E = 0 is given for regular, predictable strings (no new information produced), while maximum E = 1 is given for irregular, pseudorandom strings (each symbol is new information). To bound E to the interval [0, 1] we simply consider
where b is the base used, i.e., the length of the alphabet (possible symbols which can occur in a string). For example, if b = 2, then Equation (1) can be rewritten as:
since K = 1. In this work, we use base ten,i.e., b = 10 (See Appendix A.2 for details). In our experience, a slight change of b does not affect qualitatively the measures.
Having the same equation to measure emergence, information, and entropy could be questioned. However, different phenomena such as gravity and electrostatic force are also described with the same equation. Still, this does not mean that gravitation and charge are the same. In the same fashion, there are differences between emergence, information, and entropy, which depend more on their usage and interpretation than on the equation describing them. Thus, it is justified to use the same expression to measure different phenomena.
For example, in cellular automata, it is considered that patterns such as gliders (spatial dynamic structures) are emergent []. In previous work [], we showed that elementary cellular automata with gliders have higher E than those which produce static patterns (ordered dynamics). Also, gliders can be seen as “more information” in Shannon’s sense than static patterns. But chaotic patterns have an even higher E. This is analogous to Boltzmann’s entropy—also equivalent to Equation (1)—as equal probabilities of symbols imply more possible microstates, leading to higher entropy and information ([], Ch. 3), and thus emergence.
Self-organization, just like emergence, has many notions, definitions, and measures. In its most general form, it can be seen as a reduction of entropy [].
Since E is analogous to Boltzmann’s entropy, we define
which satisfies the axioms listed in Appendix A.1. With this measure of self-organization, static patterns have the highest S, i.e., lowest entropy. Living systems have to reduce thermodynamic entropy to maintain themselves, which has been described with the concept of self-organization [].
It might seem counterintuitive to define self-organization as the opposite of emergence, being both properties of complex systems. However, when taken to their limits, emergence is maximal in chaotic systems (E = 1, S = 0) and self-organization is maximal in static (ordered) systems (S = 1, E = 0). It is when these are balanced that we can have complexity. Following López-Ruiz et al. [], we define
where the 4 is included as a normalizing constant, bounding C to [0, 1].
Historically, Shannon defined information as entropy [] (equivalent to our E), while Wiener [] and von Bertanalffy [] defined information as its opposite, negentropy (equivalent to our S). Our measure of complexity C reconciles these two opposing views, as a balance between order and chaos is maximal with a high C. Dynamical systems such, cellular automata [], random Boolean networks [,,], and Ising models [] have a maximal C in the region their dynamics are considered most complex []. Since living systems also require a balance between adaptivity (E) and stability (S) [,], C can be used to characterize living systems, especially when comparing their C with that of their environment []. If we want artificial systems to exhibit the properties of living systems [,,], then these should also have a high C compared with that of their environment.
In this work, we measure the E, S, and C of three different time series: of switching intervals, of vehicle intervals at an intersection, and of vehicle intervals at a street. These series measure the time between light switches or between vehicles crossing a point. If these are completely regular, then E = C = 0 and S = 1. If these were maximally chaotic, then S = C = 0 and E = 1. Complex patterns are indicated by high C values.
3. Results
Results in this section were obtained simulating a ten-by-ten street grid, each equidistant street representing 800m, i.e., 80 m per block. A cell represents 5 m (the distance between the front ends of stopped vehicles), and a time step one third of a second. Thus, υ = 1 represents 54 km/h.
Simulations were performed for one hundred densities ρ between 0.01 and 1, fifty runs per density value (5000 runs total with random initial conditions). Standard deviations are shown in figures, although these were minimal, except for some regions near phase transitions. Each run consisted of ten thousand time steps, of which only the second half were considered for generating the statistics.
All figures in the Results and Discussion sections show phase transitions of the self-organizing method for the cyclic boundary scenario with vertical dotted lines for comparison. Preliminary results of a more realistic simulation are presented in Appendix A.3.
3.1. Cyclic Boundaries
As reported in [], the performance—based on υ and J—of the self-organizing method is superior to the green-wave method for all densities, as it can be seen in Figure 3. Here we include optimality curves [], showing that the self-organizing method achieves or reaches a performance close to the theoretical optimum for a given density. The full-capacity-intermittent phase is optimal by definition, as well as the free-flow phase. Small improvements can still be made in the underutilized and overutilized phases, as well as the quasi-gridlock and gridlock phases.
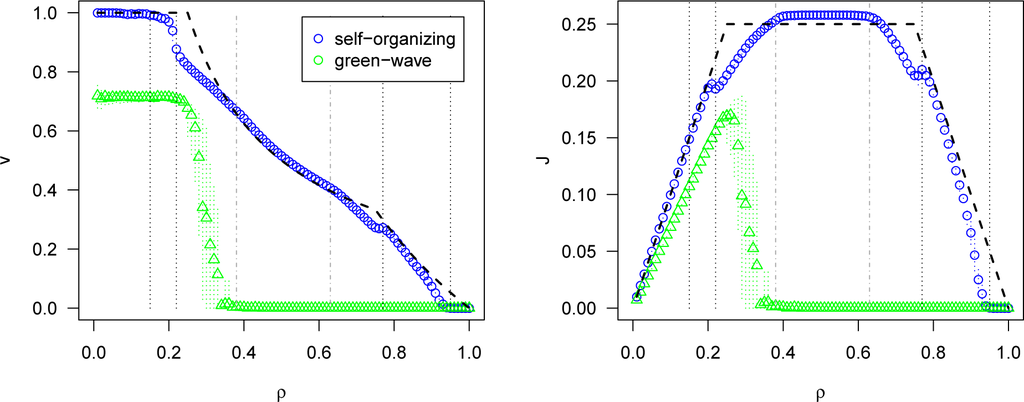
It can be seen that the self-organizing method goes above the optimality curve in the full-capacity-intermittent phase (J > Jmax = 0.25, see Section 2.1). This is an artifact of the traffic model, because it allows a vehicle of a street which just got a green light to advance without leaving a space between it and the last vehicle on the street which just got a red light.
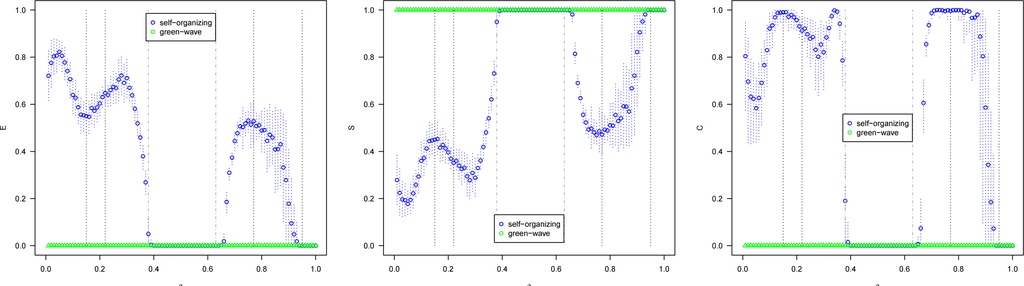
Figure 4 shows results of measures for switching intervals of intersections.
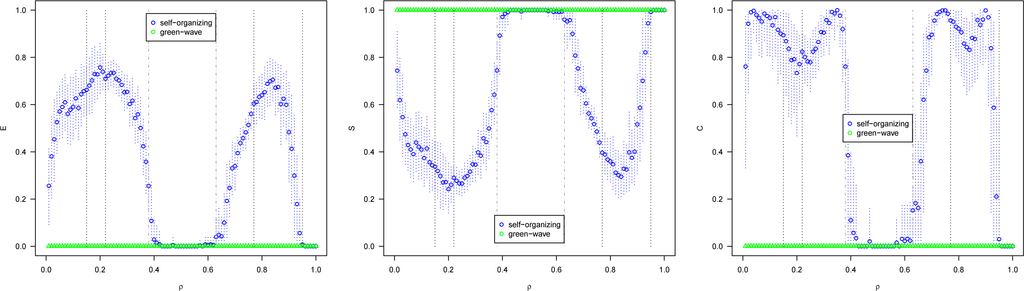
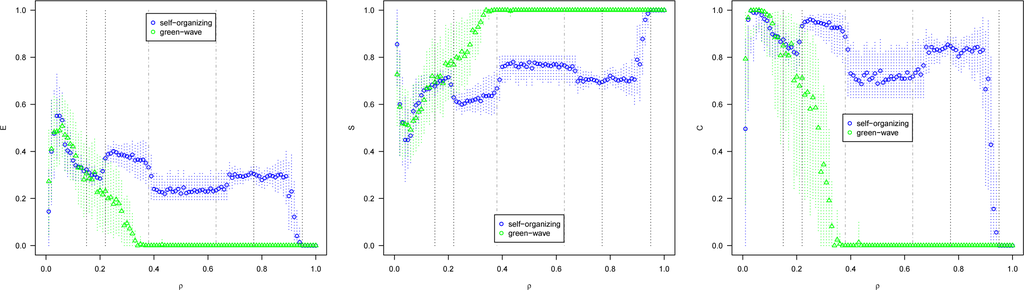
Since the green-wave method has periodic cycles, for their switching E = C = 0 and S = 1. Note that our S measure does not distinguish whether the organization is internal (self-) or external, as it is the case for this method which depends on a central controller. Having extreme S = 1, it cannot adapt to changes in traffic flow. It might seem paradoxical that the green-wave method has a higher S for several densities than the self-organizing method. Given the generality and simplicity of S, as just mentioned, it cannot distinguish between a self-organized system (e.g., by an external controller) and a self-organizing system, which adapts constantly to changing demands. This is similar to temperature, which does not indicate whether heat is generated internally or externally of the system being studied, but is useful nevertheless. S, as any measure, has to be interpreted properly in a specific context to be useful.
The self-organizing method adapts constantly to changes in demand, as it can be seen from the measures variation for different densities. The switching is most irregular (greatest E, lowest S) in the quasi-free-flow and quasi-gridlock phases, while it achieves a regular switching (minimal E and C, maximal S) for the full-capacity-intermittent phase, as there is always demand to be served from all directions. C is high for all phases but full-capacity-intermittent and gridlock, exhibiting similar measures as the green-wave method for these two phases.
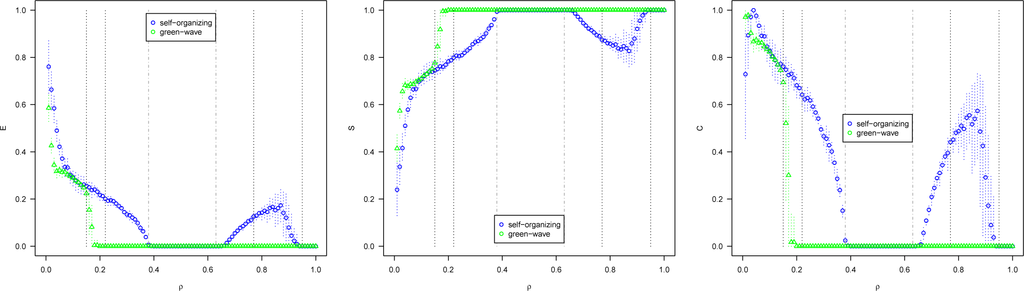
The measures of vehicles crossing at an intersection, as seen in Figure 5, are similar for the full-capacity-intermittent and gridlock phases, as there are either vehicles constantly crossing the intersection (there is a space between moving vehicles, so the intervals are constantly two time steps) or no vehicles moving (gridlock). E and C are high for low densities for both methods, and these become more regular (S increases) with ρ until reaching a maximum in the full-capacity-intermittent phase for the self-organizing method and the gridlock phase in the green-wave method. The self-organizing method increases again E and C until the quasi-gridlock phase, as vehicle crossings become less regular and “space platoons” are formed, only to decrease again towards the gridlock phase.
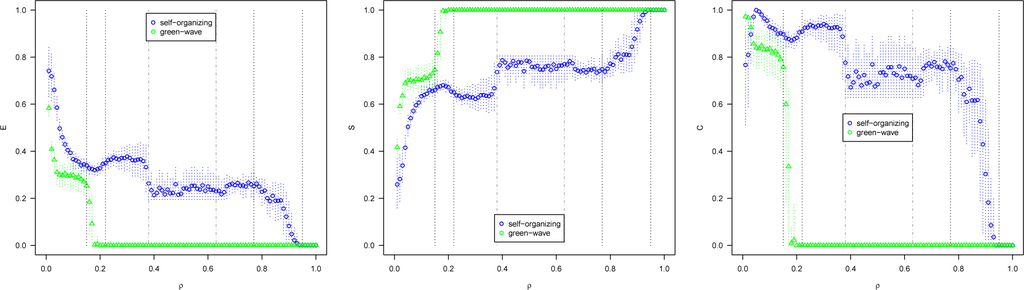
Vehicle intervals are measured at different street locations (not intersections) chosen randomly each run. These measures are similar to those from intersections described above, although they reach maximum S = 1 only for the gridlock phase. There seems to be a minimum E ≈ 0.2 for the full-capacity-intermittent phase. Long platoons are formed, so most crossing intervals are two time steps. However, between two platoons there are long spaces which imply a single long interval between the last vehicle of a platoon and the first one of the next platoon, giving a lower bound to the irregularity of the time series. Notice that C is high for all phases except gridlock, for both methods, i.e., urban traffic flow is complex. Nevertheless, differences can be clearly identified between some phases of the self-organizing method. In other words, the dynamical phase can have a direct impact on E, S, and C, which potentially could also be used to identify dynamical phases in more realistic traffic models, where transitions are not as crisp as in ours and thus could be difficult to identify.
3.2. Non-Orientable Boundaries
We performed similar simulations as the ones described in the previous subsection but with non-orientable boundaries. Results for υ and J are shown in Figure 7, which indicates with dotted lines the phase transitions of the self-organizing method for the cyclic boundaries scenario for comparison.
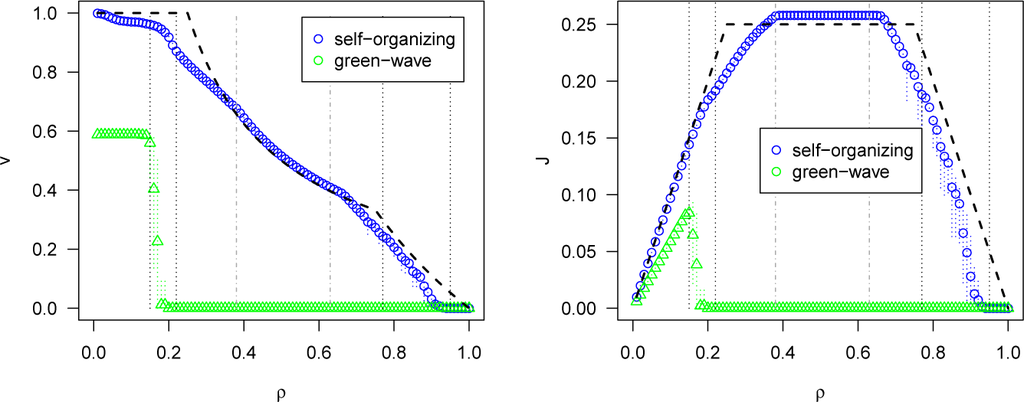
Compared to the cyclic boundaries scenario, the green-wave method has a lower υ for its intermittent phase and transitions into the gridlock phase at a lower density.
For the self-organizing method, there is no free-flow phase, as this depends on the correlations formed by the looping platoons which are destroyed with the non-orientable boundaries. The transition between the quasi-free-flow and underutilized-intermittent phases occurs at a lower density. The full-capacity-intermittent phase is expanded for higher densities, transitioning later into the quasi-gridlock phase. The transition between the quasi-gridlock and gridlock phases occurs at a slightly lower density.
In general, the self-organizing method maintains itself at or near the optimality curves, showing that its performance is not strongly dependent on the boundary conditions studied here.
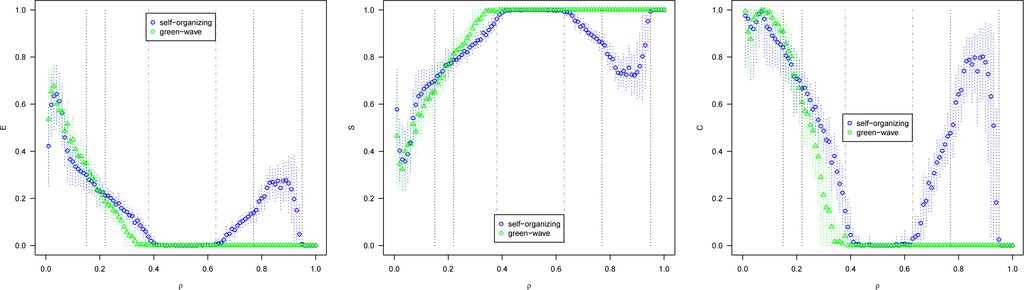
As for the measures of E, S, and C for switching intervals (Figure 8), vehicle intervals at intersections (Figure 9) and vehicle intervals at streets (Figure 10), there are no qualitative differences for the same dynamical phases between the cyclic and non-orientable boundary conditions.
4. Discussion
E, S, and C values reflect different operation schemes of traffic lights, which also impact the values obtained for vehicles. Changes in values of C, S, or E can be used to detect phase transitions, as these can change radically for different phases. This detection can also be achieved with other measures, such as Fisher information []. However, it cannot be said whether a specific value of our measures is good or bad independently of density. There are traffic regimes where high regularity (S) of traffic lights is required to achieve optimal performance (full-capacity-intermittent phase), precisely when there is a regular traffic flow at the intersection. However, there are other regimes where a high adaptability (C) is necessary, precisely when the traffic demand is irregular. This reflects the non-stationary nature of urban systems [], where no single solution is efficient for all situations, as these change constantly.
Not only do traffic lights have to adapt their duration at the seconds scale to match the scale at which traffic demand changes; traffic lights must also adapt their regime at the scale at which density shifts from phase to phase. Extending Ashby’s law of requisite variety [], it can be said that there is a requisite complexity [] that a controller must have in order to cope with the complexity of the system it attempts to control ([], p. 47). This is similar to the “matching complexity” proposed by []. Our self-organizing method seamlessly achieves this, giving insights on the requirements of other self-organizing systems which might be used for addressing non-stationary problems.
It might be possible to define measures which capture this requisite complexity and how it should match the complexity of the controlled/environment at different scales. One possibility can be with a measure of autopoiesis A [] which is defined as the ratio between the C of a system (controller) and the C of its environment (controlled). Further work is required in this direction, especially because in the self-organizing method, traffic lights control vehicles, but vehicles also control traffic lights to a certain degree.
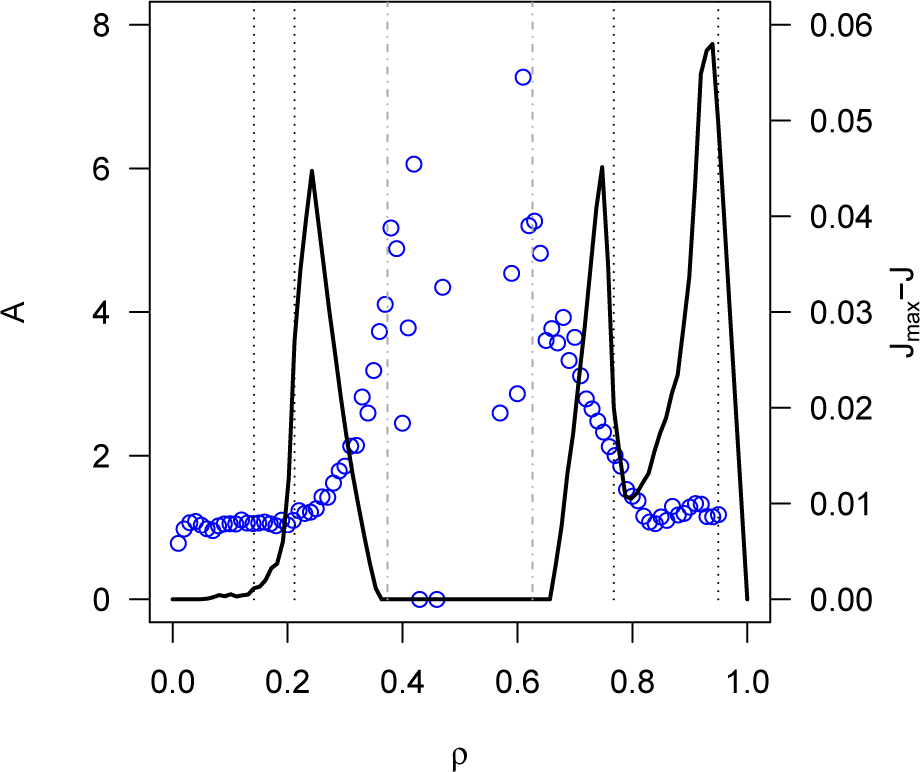
As an initial exploration, we compared the C ratio between the switching intervals with vehicle intervals at intersections to obtain A for the self-organizing method, shown in Figures 11 and 12. Missing points are those where there is a division by zero. The green-wave method is not considered here, since A = 0 for all densities. This is because C = 0 for the switching intervals, as these are always regular. The switching C is almost always greater than or equal to the C of vehicles at intersections (not always at streets), leading to A ≥ 1. The highest A values occur close to the phase transitions bordering the full-capacity-intermittent phase. These regions require a complex switching, and the self-organizing method manages to achieve this to regulate vehicle flow. Figures 11 and 12 also include the difference between the optimality flow curve Jmax and the actual J of the self-organizing method (defined as interference curve in []), to show where the method can still be improved. As mentioned previously, this is near the phase transitions between the quasi-free-flow and underutilized-intermittent phases and those around the quasi-gridlock phase. It could be speculated that to improve these regions A should be further increased, either by augmenting the C of the switching intervals or by decreasing the C of the vehicle intervals. However, having already A ≥ 1 suggests that the lack of optimality for the specific densities close to the three mentioned phase transitions is due to inherent constraints in the problem. We conjecture that to reach Jmax around ρ = 0.25 and ρ = 0.75, it is necessary to have a homogeneous demand on all streets, so as to prevent “idling” of some intersections due to some streets having densities different from these values, which do vary in our simulations as initial conditions are random. A similar reasoning can be made for the region around the quasi-gridlock to gridlock phase transition: In order to allow vehicles on a single street with very high ρ > 0.95 to have J > 0, initial conditions must be such that all of the intersecting streets must have a space available for the intersection and not others. This is highly unlikely for large grids with random initial conditions. Both constraints are dependent on the problem and beyond the traffic light coordination method.

From this study, we can generalize the use of our measures for guiding self-organization of other systems. We have seen that a desired value of C depends on the regime which a system requires. If the system benefits from high regularity, then a high S should be sought. If randomness or chaos are desired, then a high E can be covetable. If adaptation is needed, then a high C is advisable. In a control system, from our initial explorations of A, a minimum required value of the C of the controller will depend on the C of the controlled.
5. Future Work
The results presented in this paper are promising, but there are several points that should be further explored.
The relationship between dynamical phases and measures should be studied in greater detail.
The phase transitions in the non-orientable scenario can be further investigated, relating the performance measures such as υ and J with the measures C, E, and S.
We plan to perform similar studies with a more realistic traffic model [], adapted to city traffic.
Massive simulations with hundreds of streets and thousands of intersections are intended to better observe the dynamical phases and their transitions.
We have calculated the optimality curves for υ and J. What would be the optimality curves for C, S and E? These cannot be simply extrapolated from the C, S and E obtained for an optimal switching of an isolated intersection.
Can our measures be used to guide the self-organization of traffic lights even closer towards optimality?
Can our measures be used to guide the self-organization of other systems?
6. Conclusions
In this work we applied measures of emergence, self-organization, and complexity to an abstract city traffic model and compared two traffic light coordination methods. Varying boundary conditions yielded similar results. The measures reflect why the self-organizing method is much better than the green-wave method: for certain dynamical phases regular behavior is required, while for others adaptive, complex behavior is most efficient. The green-wave method by definition has only regular behavior, and thus is unable to adapt to constantly shifting demands. The self-organizing method has enough “requisite complexity” to cope with different behaviors required by changes in demand. Having an autopoiesis greater than one, it can be said that the self-organizing traffic lights have (computationally) the properties of a living system [,], which also require to have a greater C than their environment. Still, there are some regions that are not optimal. Whether these can be reached with a different method or they are computationally unfeasible (and our method then would be optimal in practice) still has to be explored.
This work shows an example of the usefulness of our proposed measures to guide the self-organization of systems, which are being applied in other areas as well [–]. Since everything can be described as information [], there is the potential of measuring C, E, and S of every phenomena. Certainly, interpreting the meaning of a specific value at a particular scale is the real challenge.
Acknowledgments
C.G. was partially supported by SNI membership 47907 of CONACyT, Mexico. We are grateful to three anonymous reviewers who provided useful comments.
Author Contributions
D.Z., N.F., J.A., D.A.R. and C.G. designed research; D.Z., G.C. L.D.A., J.Z., N.F., and C.G. performed research and analyzed data; D.Z., N.F., J.A., D.A.R. and C.G. wrote the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix
A.1. Axioms
Further discussion and justification of these axioms can be found in [].
Emergence has the same axioms as Shannon’s information. Quoting Shannon [] (and replacing Shannon’s H for I):
Suppose we have a set of possible events whose probabilities of occurrence are p1, p2, …, pn. These probabilities are known but that is all we know about the event that might occur. Can we find a measure of how much “choice” is involved in the selection of the event or how uncertain we are of the outcome? If there is such a measure, say (p1, p2, …, pn) it is reasonable to require of it the following properties:
- (1)
I should be continuous in each pi.
- (2)
If all the pi are equal, pi = 1/n, then I should be a monotonic increasing function of n. With equally n likely events there is more choice, or uncertainty, when there are more possible events.
- (3)
If a choice be broken down into two successive choices, the original I should be the weighted sum of the individual values of I.
with these few axioms, Shannon demonstrates that the only function I satisfying the three above is Equation (1). Thus, a measure of emergence is also satisfied by this equation.
A measure of self-organization S should be a function S: Σ → ℝ (where Σ = Aℕ) with the following properties:
- (1)
The range of S is the real interval [0, 1].
- (2)
S(X) = 1 if and only if X is deterministic, i.e., we know beforehand the value of the process.
- (3)
S(X) = 0 if and only if X has a uniform distribution, i.e., any state of the process is equally likely.
- (4)
S(X) has a negative correlation with emergence E.
It is straightforward to check that Equation (5) fulfills the axioms stated. Nevertheless it is not unique. However, it is the only affine (linear) function which fulfills the axioms. For simplicity, we propose the use of 5 as a measure of self-organization.
The complexity function C: Σ → ℝ should have the following properties:
- (1)
The range is the real interval [0, 1].
- (2)
C = 1 if and only if S = E.
- (3)
C = 0 if and only if S = 0 or E = 0.
It is natural to consider the product of S and I to satisfy the last two requirements. Again for simplicity, Equation (6) is proposed as a measure of complexity.
A.2. Base transformation
For calculating E, S, and C, data were transformed into base ten before using Equation (1). For a list of intervals (switching or vehicles), each point was mapped into one of ten bins which were defined by dividing equally the range between the maximum and minimum values.
For example, if the maximum value is 121 and the minimum value is 11, then all points between 11 and 21 are mapped to the symbol ‘0’, points between 22 and 32 are mapped to the symbol ‘1’, and so on until the bin between 111 and 121, corresponding to the symbol ‘9’.
A.3. Results wIth a More Realistic Traffic Model
We present here preliminary results of simulations performed in SUMO (Simulation of Urban MObility) [], which implements Krause’s microscopic traffic model [,].
A grid of ten-by-ten streets was also used in this simulation. However, each street had two lanes with opposite directions. The distance between intersections was of 150 meters. The boundary conditions of these simulation were open. This is different from the ECA model, where density could be conserved. Each street was injected with traffic from the incoming lanes with a different rate of seconds between cars. The values in the simulations were from two to 40 s between vehicles, using only even numbers, and one car per second for the highest density achieved. This was performed eight times with 4000 cars in each simulation for each method. Since the number of cars was fixed, the total time for the simulations was different. For the higher densities, the duration was around 400 s and approximately 4000 s for the lower densities. The density was measured by the average number of cars in the simulation, between the exit of the first car from the network and the entrance of the last car to the network, divided by the maximum number of cars that could be in the network. High densities could not be reached because traffic in entry lanes does not allow more vehicles to flow to the central streets of the network. In future work, we will increase the density by starting the simulation with cars inside the network instead of only injecting traffic.
Results for velocity and flow are shown in Figure A1. Even when these results are limited, they confirm the ones we obtained with our ECA model. In this scenario, only the underutilized-intermittent dynamical phase was found for the self-organizing method. There are no free-flow or quasi-free-flow phases because vehicles exiting the simulation do not reenter, and thus platoons are not conserved. There is no full-capacity-intermittent phase because the SUMO’s method of injecting vehicles limits higher densities. The shape of the decrease in υ and increase in J for the self-organizing method in this scenario is similar to the ones presented in Section 3, focussing only on the underutilized-intermittent phase, although the precise densities differ. For low densities, the self-organizing method achieves high velocities, even when entering vehicles have a Poisson distribution, which is changed quickly by traffic lights by promoting platoon formation. Velocities decrease as density increases. Velocities are less indicative for higher densities, as we could not obtain densities higher than ρ = 0.23 for the self-organizing method. This can be explained with Figure A1B, where the same values of flow J are obtained with the self-organizing method for lower densities than those with the green-wave method. We speculate that we cannot obtain higher densities because there is a limitation of the flux in this scenario Jmax ≈ 0.08.
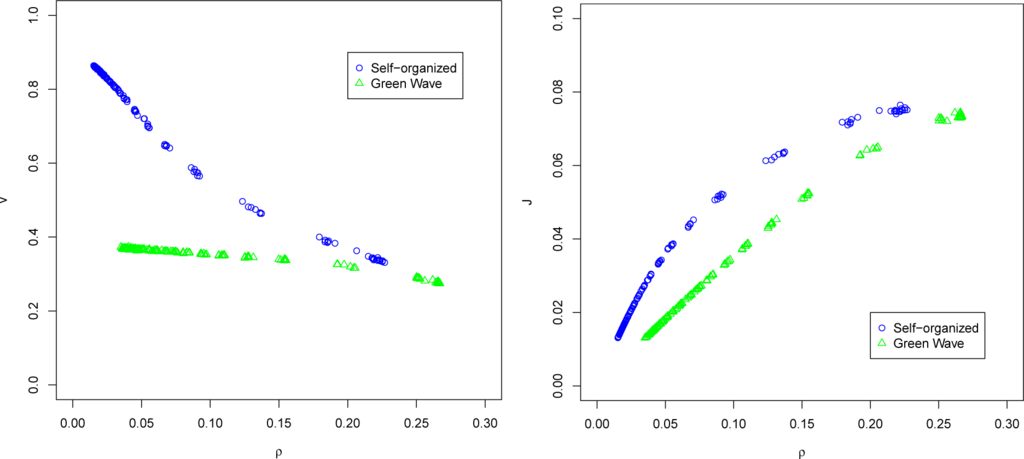
The green-wave method has only an intermittent phase, which offers almost the same υ for all densities. There is no gridlock phase because SUMO prevents intersections from being blocked (vehicles stop before the intersection—even if they have a green light—if they are unable to cross), a feature which is not realistic for cities such as Mexico.
Since the preliminary results presented in this Appendix correspond only to densities 0.2 <≈ ρ <≈ 0.4 of our ECA results, we compare the obtained E, S, and C with this density region only.
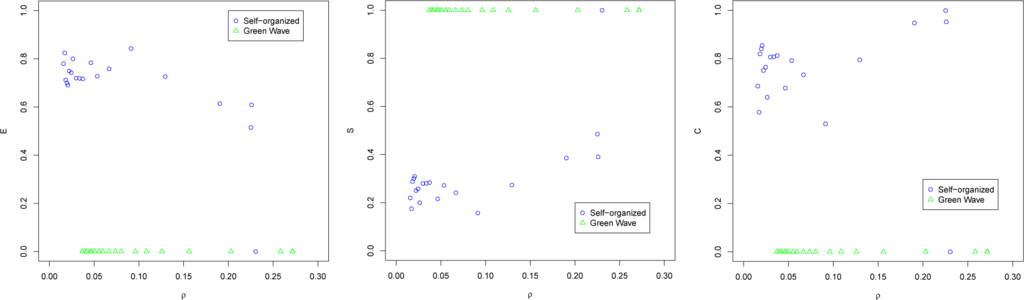
Figure A2 shows measures of switching intervals. The results are similar to those obtained with the ECA model. The green-wave method has a fixed period, so E = C = 0 and S = 1 independently of ρ. The self-organizing method, being in the underutilized-intermittent dynamical phase, decreases its E and increases its S and C (which is C > 0.5 for all densities). One point was obtained with E = C = 0 and S = 1, characteristic of the full-capacity-intermittent dynamical phase, indicating that the density limitations of this scenario are near the phase transition.
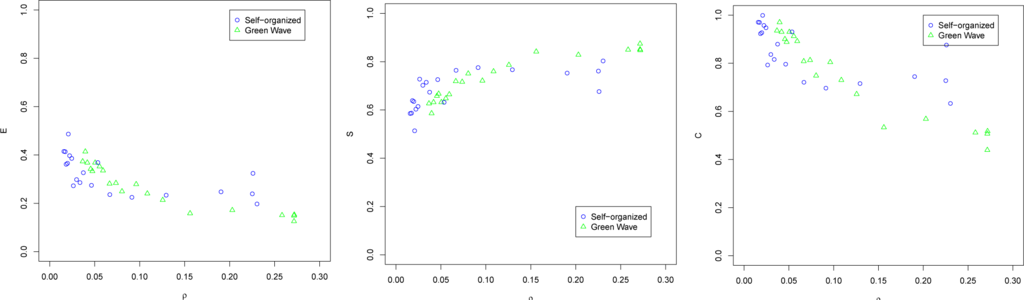
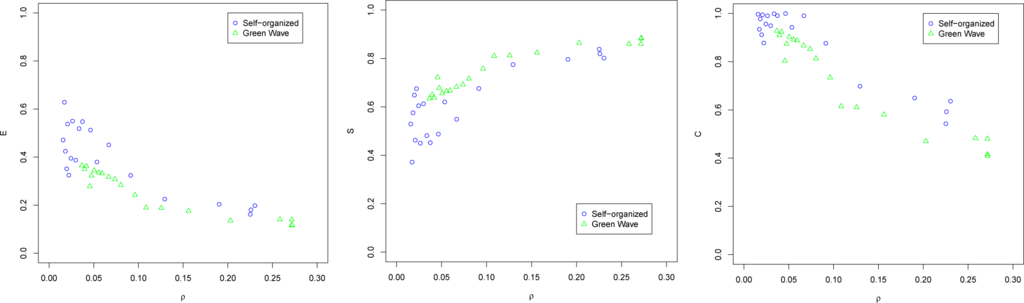
Measures of intervals of vehicles at an intersection are shown in Figure A3. For both methods, E decreases and S increases with density, consistent with the ECA results. C also decreases with density, but the values are higher than those of the ECA scenarios. This is probably because in SUMO intersections handle four directions, while in ECA only two. The same observations just described apply for the measures of intervals of vehicles at streets, shown in Figure A4. C is close to maximal for low densities for the self-organizing method, probably also because streets have two directions instead of one.
Further work with SUMO will involve studying higher densities, calculating optimality curves, removing the blockage restriction, and evaluation in simulations based on real cities.
References
- Cohen, J.E. Human Population: The Next Half Century. Science 2003, 302, 1172–1175. [Google Scholar]
- Butler, D. Cities: The century of the city. Nature 2010, 467, 900–901. [Google Scholar]
- Roberts, L. 9 Billion? Science 2011, 333, 540–543. [Google Scholar]
- Glaeser, E. Cities, Productivity, and Quality of Life. Science 2011, 333, 592–594. [Google Scholar]
- Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar]
- Bettencourt, L.; West, G. A unified theory of urban living. Nature 2010, 467, 912–913. [Google Scholar]
- Gyimesi, K.; Vincent, C.; Lamba, N. Frustration Rising: IBM 2011 Commuter Pain Survey; IBM: Armonk, NY, USA, 2011. [Google Scholar]
- Gershenson, C. Living in Living Cities. Artif. Life 2013, 19, 401–420. [Google Scholar]
- Gershenson, C. The Implications of Interactions for Science and Philosophy. Found. Sci 2013, 18, 781–790. [Google Scholar]
- Gershenson, C. Self-organizing urban transportation systems. In Complexity Theories of Cities Have Come of Age: An Overview with Implications to Urban Planning and Design; Portugali, J., Meyer, H., Stolk, E., Tan, E., Eds.; Springer: Berlin Heidelberg, Germany, 2012; pp. 269–279. [Google Scholar]
- Federal Highway Administration, Traffic Control Systems Handbook; U.S. Department of Transportation: Washington, D.C., USA, 2005.
- Henry, J.; Farges, J.; Tuffal, J. The PRODYN real time traffic algorithm, Proceedings of the International Federation of Automatic Control (IFAC) Conference, San Francisco, CA, USA, June 1983.
- Mauro, V.; di Taranto, D. UTOPIA, Proceedings of the 6th IFAC/IFIP/IFORS Symposium on Control Computers and Communication in Transportation, Paris, France, 1990.
- Robertson, D.; Bretherton, R. Optimizing networks of traffic signals in real time—the SCOOT method. Veh. Technol. IEEE Trans 1991, 40, 11–15. [Google Scholar]
- Faieta, B.; Huberman, B.A. Firefly: A Synchronization Strategy for Urban Traffic Control; Technical Report SSL-42; Xerox PARC: Palo Alto, CA, USA, 1993. [Google Scholar]
- Gartner, N.H.; Pooran, F.J.; Andrews, C.M. Implementation of the OPAC Adaptive Control Strategy in a Trafffic Signaling Network, Proceedings of the IEEE Intelligent Transportation Systems Conference, Oakland, CA, USA, 25–29 August 2001; pp. 195–200.
- Diakaki, C.; Dinopoulou, V.; Aboudolas, K.; Papageorgiou, M.; Ben-Shabat, E.; Seider, E.; Leibov, A. Extensions and New Applications of the Traffic Signal Control Strategy TUC. Transp. Res. Rec 2003, 1856, 202–211. [Google Scholar]
- Fouladvand, M.E.; Sadjadi, Z.; Shaebani, M.R. Optimized Traffic Flow at a Single Intersection: Traffic Responsive Signalization. J. Phys. A: Math. Gen 2004, 37, 561–576. [Google Scholar]
- Mirchandani, P. RHODES to Intelligent Transportation Systems. IEEE Intell. Syst 2005, 20, 10–15. [Google Scholar]
- Bazzan, A.L.C. A. A Distributed Approach for Coordination of Traffic Signal Agents. Auton. Agents Multiagent Syst 2005, 10, 131–164. [Google Scholar]
- Helbing, D.; Lämmer, S.; Lebacque, J.P. Self-organized control of irregular or perturbed network traffic. In Optimal Control and Dynamic Games; Deissenberg, C., Hartl, R.F., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 239–274. [Google Scholar]
- Gershenson, C. Self-Organizing Traffic Lights. Complex Syst 2005, 16, 29–53. [Google Scholar]
- Prokopenko, M. Guided self-organization. HFSP J 2009, 3, 287–289. [Google Scholar]
- Ay, N.; Der, R.; Prokopenko, M. Guided self-organization: Perception–action loops of embodied systems. Theory Biosci 2012, 131, 125–127. [Google Scholar]
- Polani, D.; Prokopenko, M.; Yaeger, L.S. Information and Self-organization of Behavior. Adv. Complex Syst 2013, 16, 1303001. [Google Scholar]
- Prokopenko, M., Ed.; Guided Self-Organization: Inception; Emergence, Complexity and Computation; Springer: Berlin Heidelberg, Germany, 2014; Volume 9.
- Fernández, N.; Maldonado, C.; Gershenson, C. Information Measures of Complexity, Emergence, Self-organization, Homeostasis, and Autopoiesis. In Guided Self-Organization: Inception; Emergence, Complexity and Computation; Prokopenko, M., Ed.; Springer: Berlin Heidelberg, Germany, 2014; Volume 9, pp. 19–51. [Google Scholar]
- Wilensky, U. NetLogo, Center for connected learning and computer-based modeling; Northwestern University, 1999. [Google Scholar]
- Gershenson, C. TrafficCA Simulation, http://tinyurl.com/trafficCA Last accessed: 2014-04-23.
- Rosenblueth, D.A.; Gershenson, C. A model of city traffic based on elementary cellular automata. Complex Syst 2011, 19, 305–322. [Google Scholar]
- Wuensche, A.; Lesser, M. The Global Dynamics of Cellular Automata; An Atlas of Basin of Attraction Fields of One-Dimensional Cellular Automata; Santa Fe Institute Studies in the Sciences of Complexity; Addison-Wesley: Reading, MA, USA, 1992. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA; 2002. [Google Scholar]
- Gershenson, C.; Rosenblueth, D.A. Self-organizing traffic lights at multiple-street intersections. Complexity 2012, 17, 23–39. [Google Scholar]
- Kanai, M. Calibration of the Particle Density in Cellular-Automaton Models for Traffic Flow. J. Phys. Soc. Jpn 2010, 79, 075002. [Google Scholar]
- Papadimitriou, C.H.; Tsitsiklis, J.N. The Complexity of Optimal Queuing Network Control. Math. Oper. Res 1999, 24, 293–305. [Google Scholar]
- Gershenson, C. Design and Control of Self-organizing Systems; CopIt Arxives: Mexico City, Mexico, 2007; Available online: http://tinyurl.com/DCSOS2007 (accessed on 2014-04-23). [Google Scholar]
- Zapotecatl, J. QtTrafficLights, https://github.com/Zapotecatl/Traffic-Light Last accessed: 2014-04-23.
- Gershenson, C.; Rosenblueth, D.A. Adaptive self-organization vs. static optimization: A qualitative comparison in traffic light coordination. Kybernetes 2012, 41, 386–403. [Google Scholar]
- Török, J.; Kertész, J. The green wave model of two-dimensional traffic: Transitions in the flow properties and in the geometry of the traffic jam. Phys. A 1996, 231, 515–533. [Google Scholar]
- Cools, S.B.; Gershenson, C.; D’Hooghe, B. Self-organizing traffic lights: A realistic simulation. In Self-Organization: Applied Multi-Agent Systems; Prokopenko, M., Ed.; Springer: London, UK, 2007; Chapter 3; pp. 41–49. [Google Scholar]
- Gershenson, C.; Fernández, N. Complexity and Information: Measuring Emergence, Self-organization, and Homeostasis at Multiple Scales. Complexity 2012, 18, 29–44. [Google Scholar]
- Bedau, M.A., Humphreys, P., Eds.; Emergence: Contemporary Readings in Philosophy and Science; MIT Press: Cambridge, MA, USA, 2008.
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J 1948, 27. [Google Scholar]
- Bedau, M.A. Weak Emergence. In Philosophical Perspectives: Mind, Causation, and World; Tomberlin, J., Ed.; Blackwell: Malden, MA, USA, 1997; Volume 11, pp. 375–399. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Gershenson, C.; Heylighen, F. When Can We Call a System Self-Organizing? In Advances in Artificial Life, 7th European Conference, ECAL 2003 LNAI 2801; Banzhaf, W., Christaller, T., Dittrich, P., Kim, J.T., Ziegler, J., Eds.; Springer: Berlin, Germany, 2003; pp. 606–614. [Google Scholar]
- Kauffman, S.A. The Origins of Order; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Lopez-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar]
- Wiener, N. Cybernetics; or, Control and Communication in the Animal and the Machine; Wiley and Sons: New York, NY, USA, 1948. [Google Scholar]
- von Bertalanffy, L. General System Theory: Foundations, Development, Applications; George Braziller: New York, NY, USA, 1968. [Google Scholar]
- Langton, C. Computation at the Edge of Chaos: Phase Transitions and Emergent Computation. Phys. D 1990, 42, 12–37. [Google Scholar]
- Kauffman, S.A. Metabolic Stability and Epigenesis in Randomly Constructed Genetic Nets. J. Theor. Biol 1969, 22, 437–467. [Google Scholar]
- Gershenson, C. Introduction to Random Boolean Networks. In Workshop and Tutorial Proceedings, Ninth International Conference on the Simulation and Synthesis of Living Systems (ALife IX); Bedau, M., Husbands, P., Hutton, T., Kumar, S., Suzuki, H., Eds.; 2004; pp. 160–173. [Google Scholar]
- Glauber, R.J. TimeDependent Statistics of the Ising Model. J. Math. Phys 1963, 4, 294–307. [Google Scholar]
- Balleza, E.; Alvarez-Buylla, E.R.; Chaos, A.; Kauffman, S.; Shmulevich, I.; Aldana, M. Critical Dynamics in Genetic Regulatory Networks: Examples from Four Kingdoms. PLoS One 2008, 3, e2456. [Google Scholar]
- Bedau, M.A.; McCaskill, J.S.; Packard, N.H.; Rasmussen, S. Living Technology: Exploiting Life’s Principles in Technology. Artif. Life 2009, 16, 89–97. [Google Scholar]
- Bedau, M.A.; McCaskill, J.S.; Packard, N.H.; Parke, E.C.; Rasmussen, S.R. Introduction to Recent Developments in Living Technology. Artif. Life 2013, 19, 291–298. [Google Scholar]
- Prokopenko, M.; Lizier, J.T.; Obst, O.; Wang, X.R. Relating Fisher information to order parameters. Phys. Rev. E 2011, 84, 041116. [Google Scholar]
- Ashby, W.R. An Introduction to Cybernetics; Chapman & Hall: London, UK, 1956. [Google Scholar]
- Gershenson, C. The World as Evolving Information. In Unifying Themes in Complex Systems; Minai, A., Braha, D., Bar-Yam, Y., Eds.; Springer: Berlin Heidelberg, Germany, 2012; Volume VII, pp. 100–115. [Google Scholar]
- Tononi, G.; Sporns, O.; Edelman, G.M. A complexity measure for selective matching of signals by the brain. Proc. Natl. Acad. Sci. USA 1996, 93, 3422–3427. [Google Scholar]
- Lárraga, M.E.; Aacute;lvarez-Icaza, L. Cellular automaton model for traffic flow based on safe driving policies and human reactions. Phys. A: Stat. Mech. Appl 2010, 389, 5425–5438. [Google Scholar]
- Amoretti, M.; Gershenson, C. Measuring the Complexity of Ultra-Large-Scale Evolutionary Systems. Submitted.
- Fernández, N.; Gershenson, C. Measuring Complexity in an Aquatic Ecosystem. In Advances in Computational Biology; Advances in Intelligent Systems and Computing; Castillo, L.F., Cristancho, M., Isaza, G., Pinzón, A., Corchado Rodríguez, J.M., Eds.; Springer: Cham Heidelberg New York Dordrecht London, 2014; Volume 232, pp. 83–89. [Google Scholar]
- Febres, G.; Jaffe, K.; Gershenson, C. Complexity measurement of natural and artificial languages. Complexity 2014. In Press. [Google Scholar]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent Development and Applications of SUMO - Simulation of Urban MObility. Int. J. Adv. Syst. Meas 2012, 5, 128–138. [Google Scholar]
- Krauss, S.; Wagner, P.; Gawron, C. Metastable states in a microscopic model of traffic flow. Phys. Rev. E 1997, 55, 5597–5602. [Google Scholar]
- Krauss, S. Microscopic Modeling of Traffic Flow: Investigation of Collision Free Vehicle Dynamics. PhD Thesis, Universität zu Köln, Cologne, Germany, 1998. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).