1. Introduction
The supramolecular order of water, be it water clusters [
1–
3], coherent domains [
4], exclusion zone water [
5] and other similar phenomena is still controversial, despite various theoretical considerations and positive results obtained from numerous different experiments. Among the many methods that are being used in this research, the droplet evaporation method (DEM) used with water or some other solvent or liquid, is a very promising—though not a simple—one. It implies the evaluation of certain features of evaporated water drops monitored by dark field microscopy. This method has several modalities and applications. For example, it can be used to monitor diseases via blood drops evaporation [
6], for salt induced protein self-assembly research [
7],
etc. The method can be highly sensitive to even the most minuscule concentrations of substances that water was exposed to prior to evaporation, as shown by the fact that one can even differentiate between various wheat cultivars [
8].
Despite being a non-linear and highly complex process, the evaporation of water droplets also found physical descriptions in terms of mathematical models, where the formation of droplet remnant pattern (DRP) is described in terms of the so-called self pinning of colloidal drops theory [
9,
10]. It seems that a complex and dynamic process is taking place during evaporation, providing an immensely rich variety of DRPs that are partially defined by the concentration of colloidal particles, their average size, velocity of evaporation,
etc. [
11,
12]. Consequently, certain properties of DRP are strongly influenced by the material composition of the solution to-be-evaporated (like viscosity, composition, total dissolved solids – TDS) and by certain ambient parameters as for example temperature, moisture, pressure
etc. [
12,
13].
Furthermore, it seems that the properties of DRP are also influenced by the subtle physical characteristics of solution. Thus, DEM has also been used to research the still controversial special characteristics of ultra-high diluted aqueous solutions [
14]. It proved capable of demonstrating differences in subtle influences of a ultra-high dilution (around 10
−47 M, practically “pure” water) of As
2O
3 (UDH As) on common wheat seeds. DRP originating from the UHD As with immersed wheat seeds demonstrated more complex and symmetrical formations than the control (DRP from water with immersed wheat seeds). This method is therefore capable of transferring certain not yet fully understood or generally accepted subtle physical characteristics [
15–
17] of the solution to the remnant patterns after drop evaporation.
It is therefore highly probable that some stable supramolecular water structures, such as the ones from the theory of exclusion-zone (EZ) water [
18] or those known as the autothixotropic phenomenon [
19,
20], can also be transferred and “coded” into the droplets. Such proof of transfer of a hidden order from the solution to the DRPs could further strengthen the still controversial theories and empirical findings concerning the evidence of a high level supramolecular order in liquid water. We know that ordinary physics and chemistry consider water to be more or less subject only to Brownian motion, which represents the negation of any true order or long range correlations.
In our previous experiments with aqueous solutions of NaHCO
3 [
21], we found higher electrical conductivity in the aged solutions than in the chemically analogous fresh (one day old) ones. The phenomenon was discovered in distilled water or water solutions left undisturbed for longer periods of time (~1 year). Most likely, the dissolved ions, as well as the contact with hydrophilic surfaces, played an essential role. In our research, we found that the higher conductivity was proportional to the higher surface
vs. volume ratio. This finding corroborated those of Vybiral and Voráček [
19] concerning the autothixotropic nature of water, when the latter is subject to aging with minimal disturbance.
Because of the length (duration) of exposure to glass-surfaces as well as the size of these surfaces proved to be important, we designed a new set of experiments using DEM. We exposed spring water of known quality and characteristics to various glass surfaces and monitored the DRPs through a specifically designed computer program. The decision to use spring water stemmed partially from the conclusion found in the work of Vybiral [
22] that the autothixotropic phenomenon depends on ions dissolved in water, which was further elaborated by Yakhno [
23] and partially from our experience with such water. From our experience with DEM on one hand and the already known self-ordering capacities of water solutions on the other [
21], our working hypothesis was that both aging and surface contact would result in some sort of higher order of the DRPs. We therefore designed a series of experiments that were intended to examine characteristics of water (via DRPs) one hour (t
h), one day (t
d), one week (t
w) and one month (t
m) after filling the vials with spring water of known origin and with well researched characteristics of its DRPs. For simultaneous testing of different surface/volume (S/V) ratios one third of the vials were filled only with water (basic surface, S
0), another third with large glass beads (larger surface area, S
1) and the final third with smaller beads (yielding the largest surface area, S
2)—for details see Experimental Section.
2. Results and Discussion
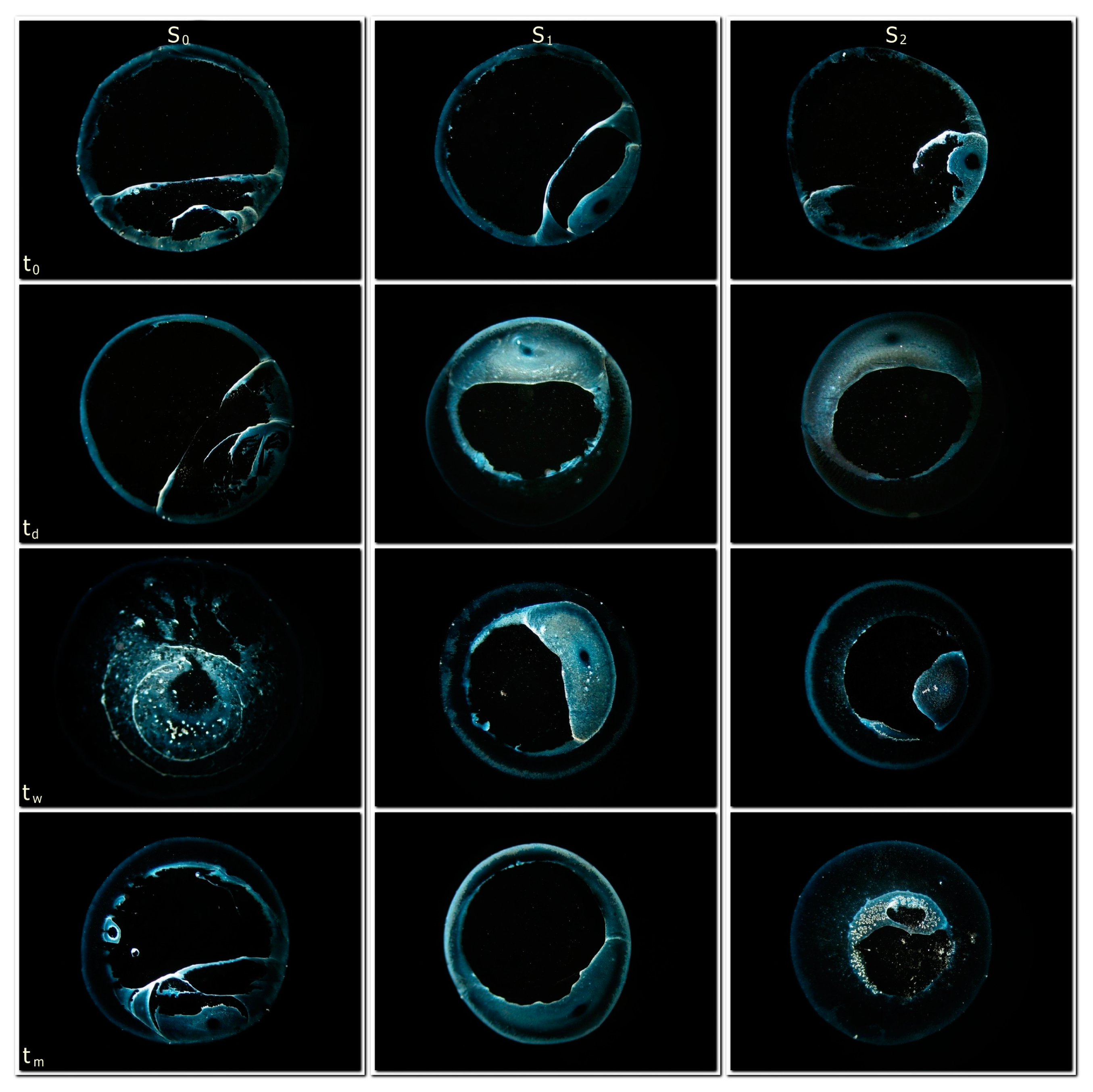
The first result of the DEM is a representation of DRP. Certain types of water provide relatively similar images, while others show more variety. The DRPs of the water used in the present study have typical forms, and are bluish in color—often revealing a “black-hole”-like center.
Figure 1 shows representations of our 12 different treatments (three S/V-ratios as a time-series of four separate sampling and drying events (four incubation time points)). Visual assessment of the DRPs involves an examination of the border line, the ring region and the central region. Distinctness of the border line is prominent in all treatments. Difference in thickness of the ring region and the formation of additional structures can be observed at t
d, t
w and t
m. After the last incubation time point (t
m), the DRPs of all three S/V-ratios display greater diversity. The majority of the central regions remains without mineral deposits or any special structures, the mechanism of which is well described in Deegan
et al. [
11]. Since the images vary a lot, the parameters and algorithms (computer programs) have to be selected very carefully, in order to enable us to glance at some of the more orderly structures and dependences (significant correlations).
The DRP images are usually highly complex and can be analyzed in numerous ways. Some authors look for the differences in contrast, fractal dimension [
8,
24], while others find the symmetry of DRP images to be an important parameter for the measuring of differences using DEM [
14,
25]. A possible way to group the ways of pattern evaluation is also the one used in [
26] which distinguishes between the sizing parameters and shape-descriptors. Of course, such analysis can only reveal one subset of DRP characteristics, meaning that even though it is sophisticated, it is still subject to limitations. The first limitation in our investigation was the fact that our special software computed and yielded only the frequency distribution of distances between illuminated pixels. A further limitation resides in the fact that we used only one specific point of the frequency graphs, namely the maximal frequency. There are many other possible characteristics of the frequency graphs that could be abstracted for further analysis, but we concluded that they would all be more arbitrary than the one we selected. And besides, d
max proved itself as a relatively robust parameter.
We assume that some more advanced analysis with a more sophisticated method of research—for instance performing Fourier analysis of the images—would yield more refined and richer results, and would provide a deeper insight into the orderliness behind DRPs. However, even with the relatively simple software available and with only one cardinal point per graph (see
Figure 5), we obtained statistically significant results that at least roughly corresponded to our working hypothesis. Even though we took only one point per graph, taking many such graphs together enabled us to monitor three different parameters with their statistical characteristics: D
max, FR
max (see Experimental Section) and the dependence between the two (involving d
max and fr
max), while also taking into account the four points of incubation and the three different S/V ratios.
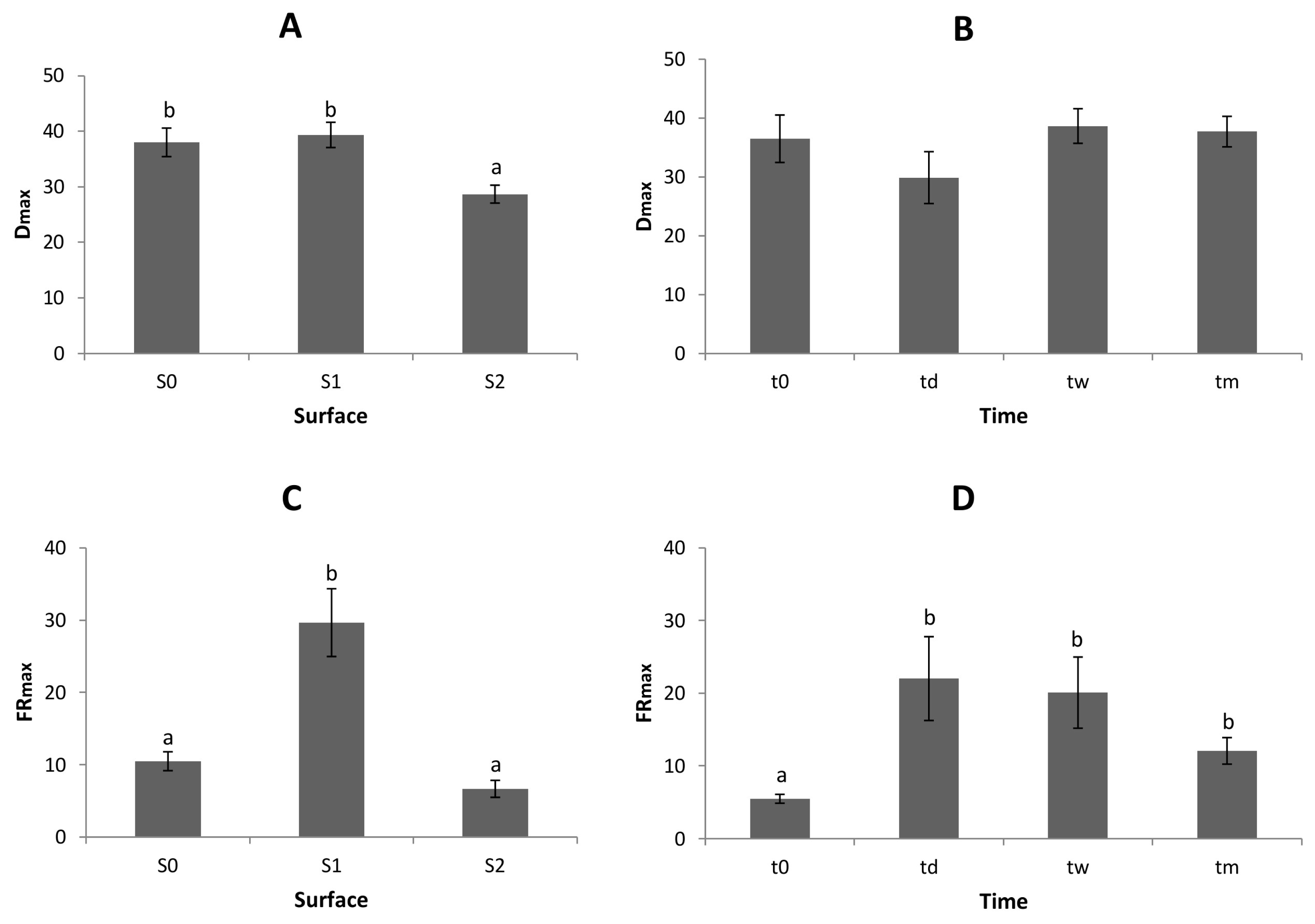
As to the distance itself, the statistical analysis shows a significant difference between S
0 and S
1 on the one hand and S
2 on the other (one-way ANOVA;
p = 0.0077, see
Figure 2A). Therefore it seems that the S/V-ratio had an effect on the water that was then further transferred to the structure of the droplet remnants themselves—namely, D
max (through all incubation times) of S
2 was significantly smaller than the other two. The direct physical interpretation of the results in terms of the processes behind these effects would be too far-fetched, at least at the present state of research.
On the other hand, we could see no significant effect of the water incubation time (t
i) (one-way ANOVA,
p = 0.2928) and even if we neglected this statistical evaluation, we see no clear trend, since the smallest D
max was achieved after 1 day of incubation and the highest after 1 week (see
Figure 2B). Perhaps this independence of D
max (and also FR
max, see
Figure 2D) from time is a sign that our analysis was insensitive to a possible silicate or Na
+ dissolution (even if very minuscule) from the glass into the water, since it is not only a function of S, but also of time.
The analogous results concerning FR
max also yielded statistically significant results in the S
j domain, as revealed by Kruskal–Wallis test of medians (
p = 0.001, see
Figure 2C). A significant difference was observed between S
0 and S
1 on one hand as well as between S
1 and S
2 on the other. Surface S
1 demonstrated a much higher average frequency than either S
0 or S
2. Even though the result seems to be a bit misleading, it clearly delineates S
1 from S
2, with S
0 in between (closer to S
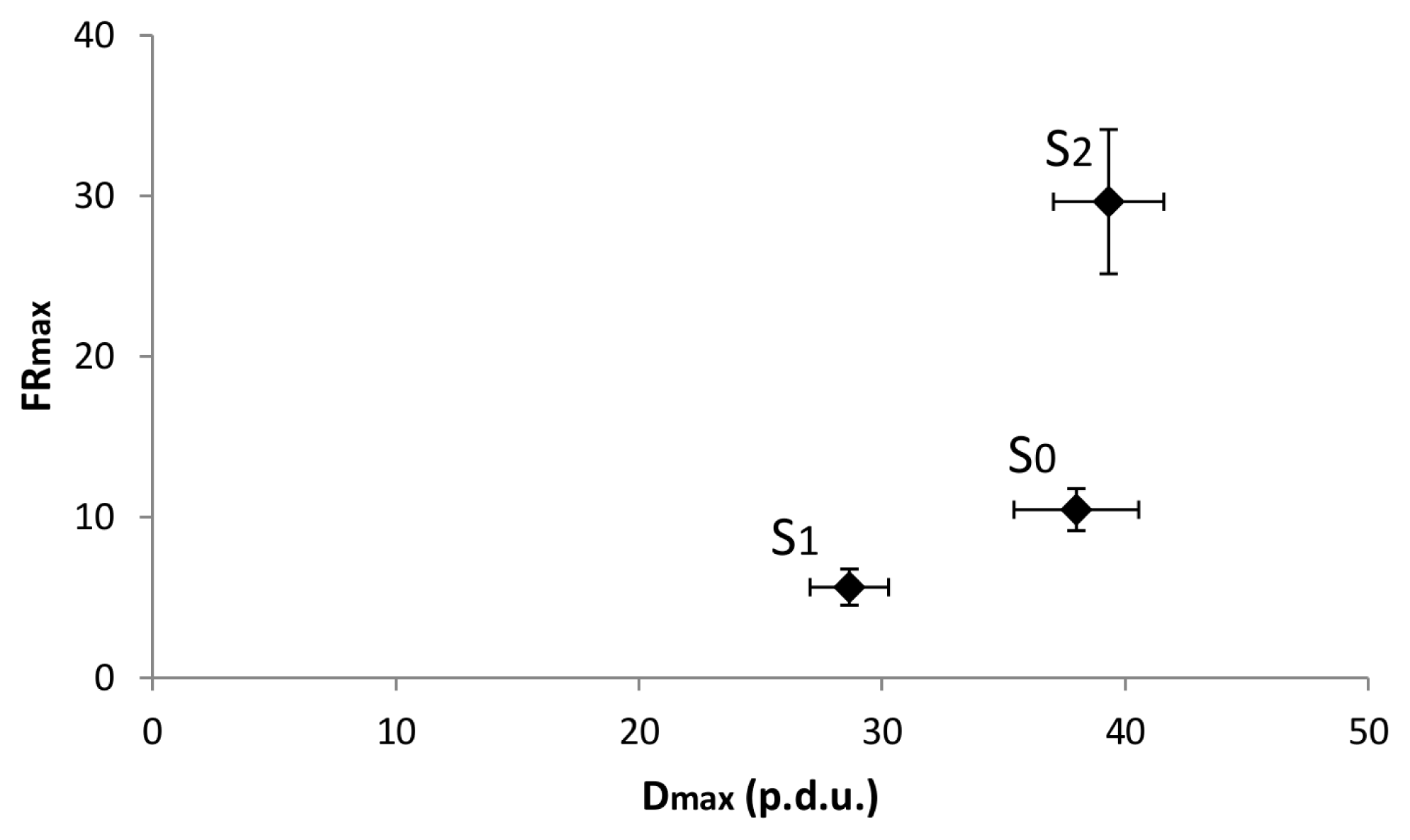
2). It also seems that a high S (S
1) determines a high D
max and a high FR
max, while a very high S (S
2) influences the evaporation in the direction of very small distances as well as very small frequencies (
Figure 3).
For incubation time (
ti) FR
max results show a significant difference between the starting point (
t0) and the other three points (
td,
tw,
tm) (Kruskal–Wallis test,
p = 0.0166) (see
Figure 2D). It seems that shortly after the start of the incubation certain processes began that resulted in a high frequency, while afterwards the frequency shows a trend towards the starting level (FR
max(t
d) > FR
max(t
w) > FR
max(t
m) > FR
max(t
0).
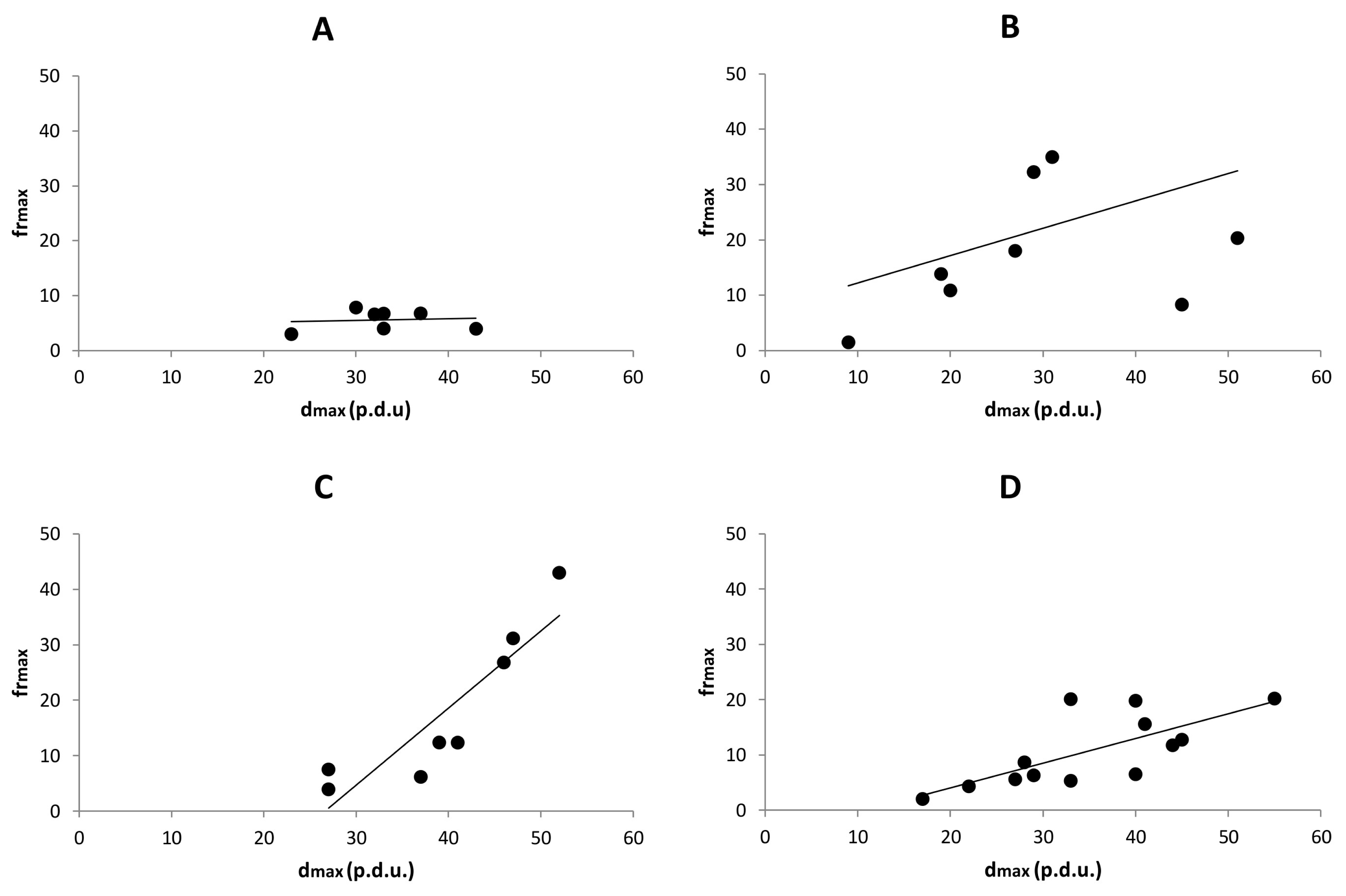
Taking all these results into account, we can conclude that the DRPs demonstrate differences in either Sj or ti domain via at least one parameter. But there is still no clear evidence as to whether some hidden order comes to the fore through time or via S/V-ratio. To clarify this important issue, we calculated the dependence between the two parameters: dmax and frmax with linear regression analysis. We assumed that the dependence is based on two factors: the correlation between the two parameters and the significance of the given linear regression line.
We did not find any dependence in the S
j domain, but we discovered an increasing dependence in the
ti domain, as demonstrated in
Figure 4 and
Table 1, achieving relatively high correlation and high significance of the linear regression line at
tm. This dependence shows an increase in order throughout the incubation time. In other words, a certain relation is gradually established during incubation, so that when d
max increases, so does the corresponding fr
max. However, considering that the results show no big difference between
tm and
tw, we could conclude that the dependence (order) was formed somewhere before or at least at one week incubation time and then remained more or less constant.
Is this all that can be said about the DRP images? No, because, as previously stated, there are many other analyses of the images possible, which could demonstrate other dependencies and other features of incubation time as well as the S/V-ratio. Even our selection of typical images (see
Figure 1) displays some general differences between the variously treated waters (different S
j or/and
ti) that are mostly neglected by our present algorithm.
3. Experimental Section
3.1. Droplets Evaporation Method
The method of monitoring dried water drops by dark field microscopy was discovered in the previous century by German artist Ruth Kübler [
27] and further developed by Kröplin, Hein [
28], Heusel [
29] and Schröcker [
30,
31]. The method consists of creating drops of different solutions on clean microscope slides and drying them under defined conditions. Dry residues are then observed under the microscope and the anomalously dried drops (evidently non-circular form, ripped up or interrupted edges) or drops with fibers or dust-like particles (occasionally stemming from previous cleaning of slides) incorporated in dry residues are eliminated from further analysis. Properly dried drops with no additional artifacts are photographed and analyzed by visual assessment and software.
3.2. Experimental Protocol
Bottled spring water from a well known source (Spring Living water from the Tunjice Natural Health Resort; Na—1.7 mg/L, K—0.46 mg/L, Mg—1.6 mg/L, Ca—40.2 mg/L, I—0.05 mg/L, HCO3—119 mg/L, SiO2—9.2 mg/L, dry residue 180 °C—137 mg/L, pH—7.6; Analysis: The Institute of Public Health Kranj, 2005) was incubated in 20 mL transparent glass bottles (Wheaton, Millville, NJ, USA). The surface of water in contact with glass was increased using glass beads (3 mm or 10 mm, Assistent, Glaswarenfabrik Karl Hecht KG, Sondheim, Germany). The sampled volume of spring water incubated in the bottles without glass beads was 20 mL, and 10 mL in the bottles filled with glass beads. During the experiment, all bottles were tightly sealed, stored in the dark and put to rest, at room temperature. We disregarded the potential effects of impurities released from the glass of the bottles.
Structural changes in water were evaluated using the evaporation method after one hour (t0), one day (td), one week (tw) and one month (tm) of incubation. From each bottle 14–16 water drops (3 μL each) were placed on clean microscope slides (Assistant) with an automatic pipette and then dried under laboratory conditions (temperature 22–25 °C, moisture 44–48%.). Microscopic slides were previously cleaned with 70% ethanol and rinsed with distilled water. The patterns of individual droplet residues were observed under dark field microscope (Euromex ME 2665, Euromex, Arnhem, The Netherlands) at 40× magnification after approximately 1 hour of evaporation. Properly dried drops were photographed by a digital camera (2048 × 1536 resolution) and analyzed.
3.3. Experimental Design
We studied the influence of three different surface sizes (S
j) and four different incubation times (
ti) at maximum distance (d
max) and maximum frequency (fr
max). Three different surface sizes (S
j) were designated as S
0, S
1, S
2 (see
Table 2). As previously stated, water drops were prepared at 4 different times. Time
t0 is considered as a starting point, where the water was still considerably disturbed, at least while filling the bottles. All subsequent procedures (at
td,
tw and
tm) left the water almost undisturbed. All three S
j variants were prepared at all four times. Experiments were performed in triplicates,
i.e., three parallel bottles were prepared (A, B and C) and analyzed for each set of samples S
i. Drops from each bottle were placed on one microscope slide, except at t
m where drops were placed on three different slides from each A parallel (triplicate of A) and on one slide from the parallels B and C. This is the reason that there are more data for the t
m than for other t
i.
3.4. Evaluation of Droplet Remnant Patterns
DRP images were analyzed with a computer software developed especially for our DEM. The program divides the diameter size into 200 equal intervals (designated as p.d.u.-s, procedure defined units). Then the algorithm of the program performs a frequency analysis of all distances between all illumined pixels (representing dry residues within the droplet remnants perimeter). Therefore all the distances between pixels of a DRP image are arranged into one of 200 possible intervals. The frequency distribution analysis roughly captures some structural features of a DRP.
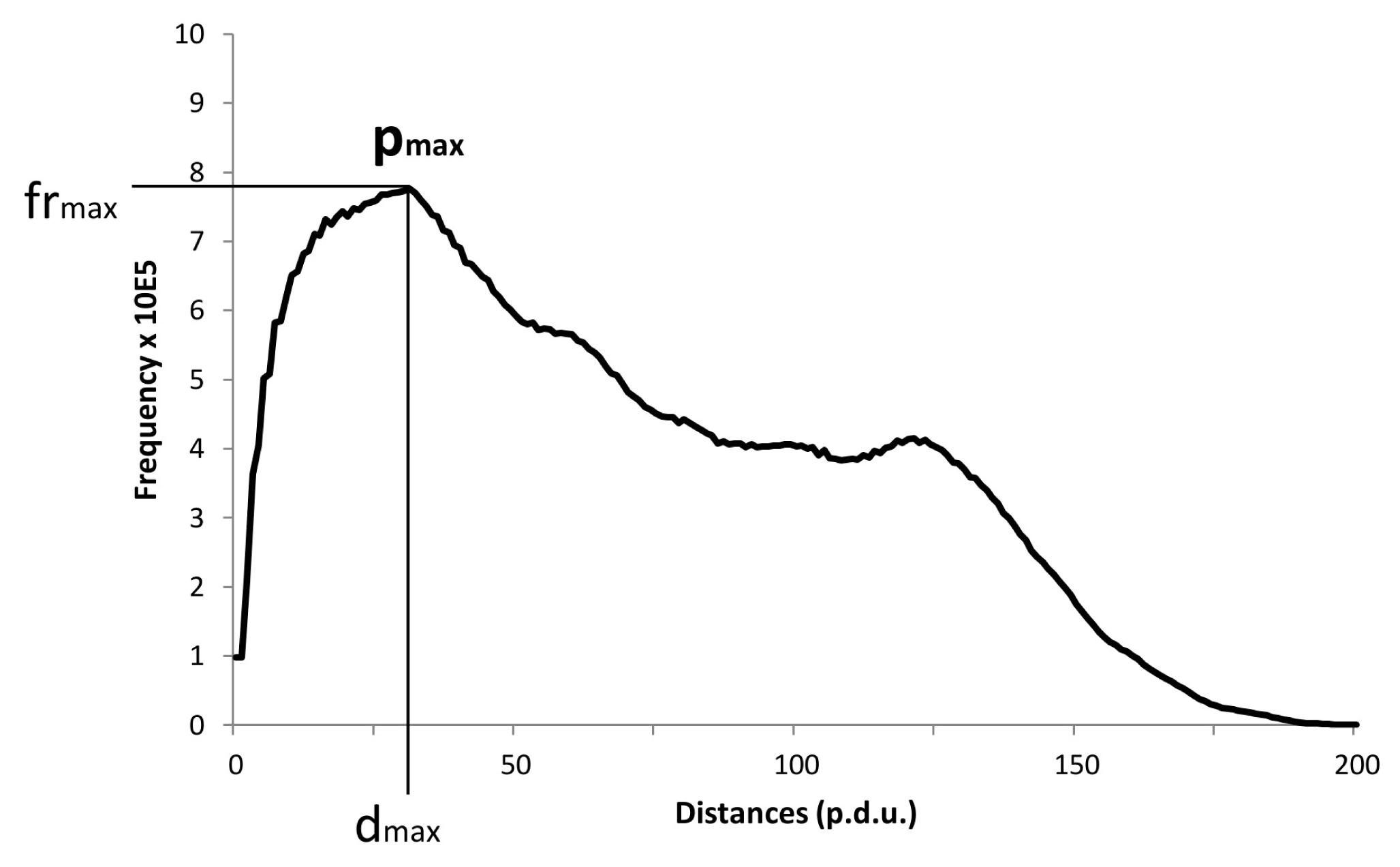
Many different features of the frequency analysis can be used to seek some characteristics or a hidden order behind the DRPs. In this study, we used a clearly defined cardinal point of the average frequency distribution graph of all correctly formed drops form one slide (14–16 drops), namely, its peak and the corresponding maximal frequency (designated as
pmax) (see
Figure 5).
Thus we have two variables at our disposal for every graph: the distance (dmax) and the frequency (frmax). The parameter dmax therefore represents the distance at the maximal frequency (frmax). In order to seek out statistical differences among the various groups, we had to group all pertaining distances (dmax) and frequencies (frmax) based on Sj or ti. We designated the averages of these treatments as Dmax and FRmax; for instance since there are three Sj we have three Dmax values and three FRmax values (grouping triplets from all given incubation times—ti).
3.5. Statistical Analysis
Results are expressed as average ± SE. The difference in each group was evaluated by one-way ANOVA (with Duncan’s multiple range test) or Kruskal–Wallis test for non-normal distributed data. Linear regression by the least-squares method was carried out. All statistical tests were performed with Statgraphics Centurion XV (StatPoint Technologies, Warrenton, VA, USA). Value of p < 0.05 was considered as statistically significant.
4. Conclusions
In conclusion, we can say that the evaporation method with our special frequency analysis showed statistically significant differences in both: the incubation time domain (
ti) and the S/V-ratio domain (S
j), though they were more pronounced with FR
max than D
max. These results speak only about the differences of some water features when certain parameters (time, S/V-ratio) change, but they do not directly reveal any higher (supramolecular) order. The latter was found in an increasing dependence in the t
i domain, thus further corroborating the hypothesis of water self-ordering capacities that are at least partially covered by the term autothixotropy, researched by other methods—mechanical [
19] and electrical conductivity measurements [
21]. This further confirmation of the self-ordering nature of water (with ions) is not only important to physical chemistry, but—as stated by Vybiral [
22]—it may be also very important for biology, since there are so many surfaces, especially on the subcellular level, that could influence water in the direction of increased (by resting) or decreased (by moving) orderliness. This investigation did not disclose any such increasing order depending on S/V-ratio, however, as already stated, our method was very limited and some other method could reveal some measure of self-ordering capacity also here, as it was discovered by Verdel
et al. [
21]. Further studies along this line should follow.