Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review
Abstract
:1. Introduction
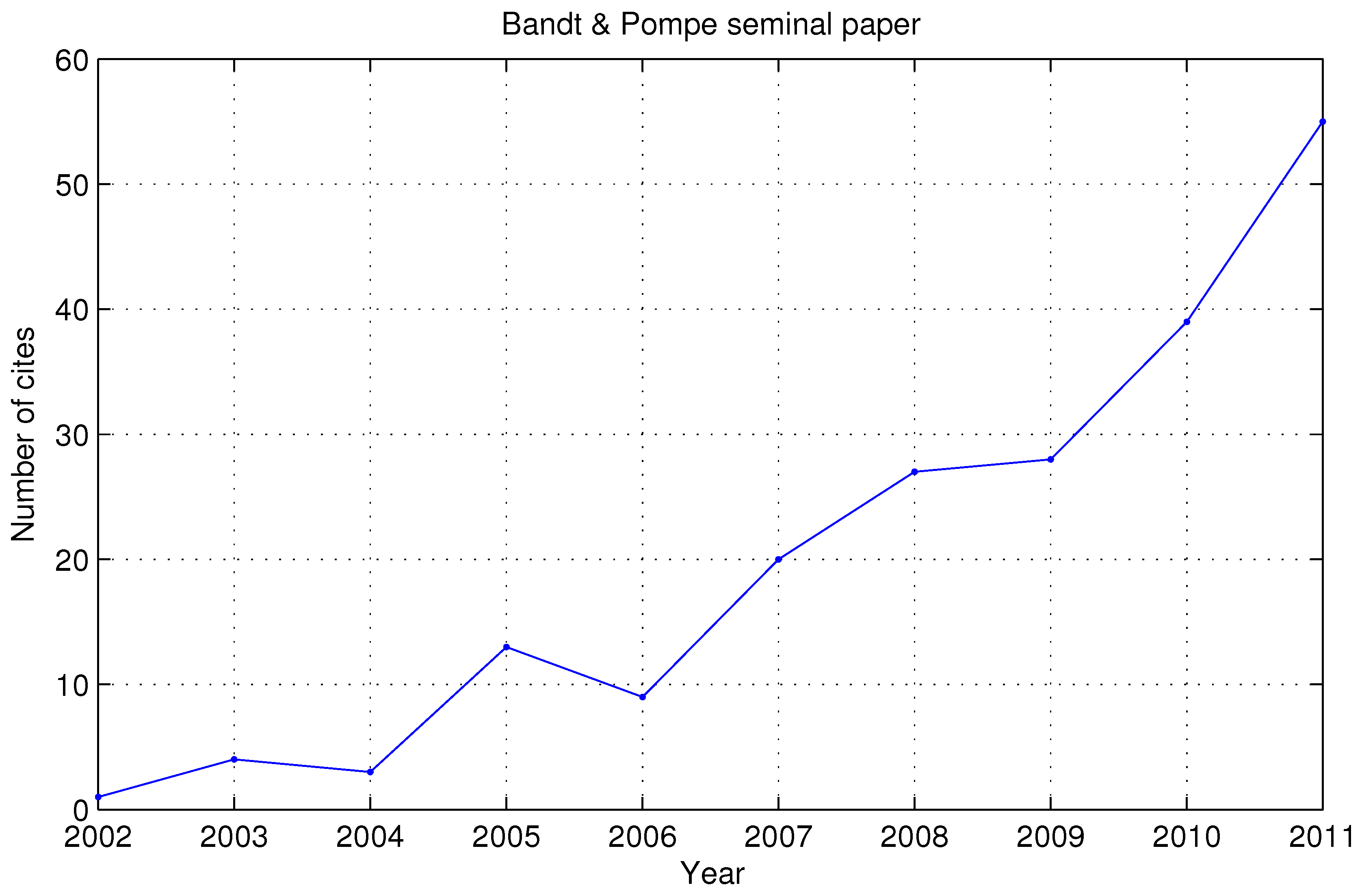
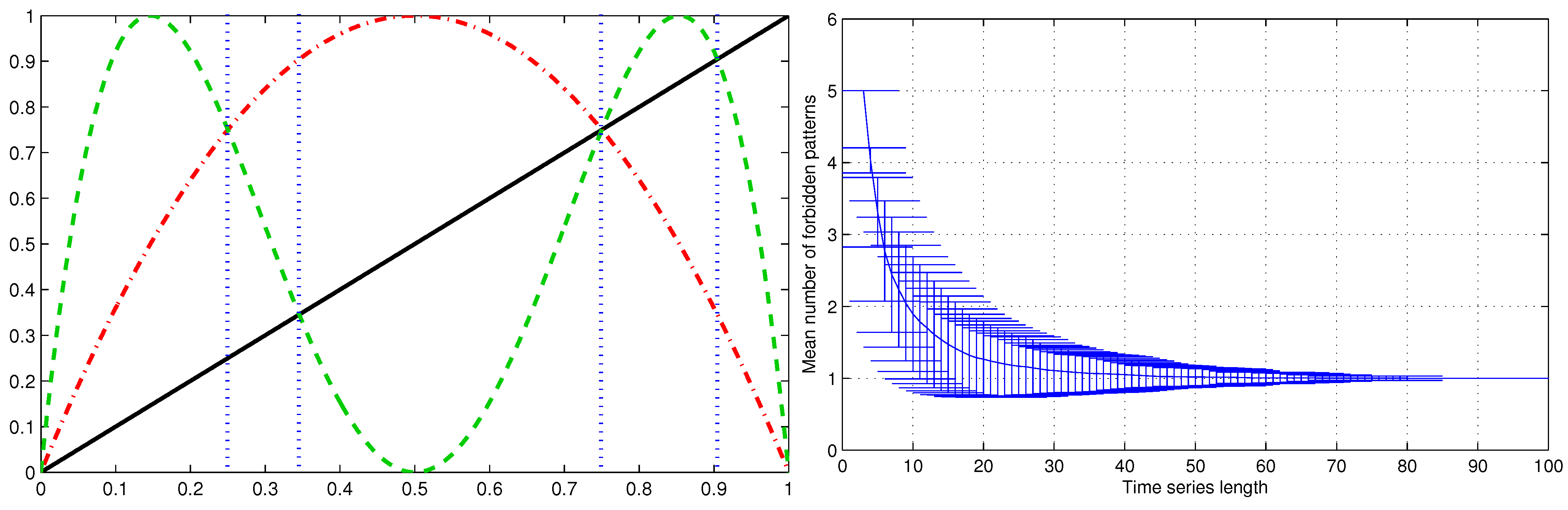
2. The Permutation Entropy

3. Applying Permutation Entropy
3.1. Distinguishing Noise from Chaos
3.2. The Statistical Complexity and the Complexity-Entropy Plane
3.3. Identification of Time Scales
3.4. Dependences between Time Series
3.5. Some Improvements on the PE Definition
4. Biomedical Applications
4.1. Epilepsy Studies
4.1.1. Classification
4.1.2. Determinism Detection
4.1.3. Detection of Dynamic Change
4.1.4. Prediction
4.1.5. Spatio-Temporal Dynamics
4.2. Anesthesia
4.3. Cognitive Neuroscience
4.4. Heart Rhythms
5. Econophysics Applications
6. Conclusions
Acknowledgments
References
- Gray, R.M. Entropy and Information Theory; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Brissaud, J.B. The meaning of entropy. Entropy 2005, 7, 68–96. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Rosso, O.A.; Craig, H.; Moscato, P. Shakespeare and other English renaissance authors as characterized by Information Theory complexity quantifiers. Physia A 2009, 388, 916–926. [Google Scholar] [CrossRef]
- De Micco, L.; González, C.M.; Larrondo, H.A.; Martín, M.T.; Plastino, A.; Rosso, O.A. Randomizing nonlinear maps via symbolic dynamics. Physia A 2008, 387, 3373–3383. [Google Scholar] [CrossRef]
- Mischaikow, K.; Mrozek, M.; Reiss, J.; Szymczak, A. Construction of symbolic dynamics from experimental time series. Phys. Rev. Lett. 1999, 82, 1144–1147. [Google Scholar] [CrossRef]
- Powell, G.E.; Percival, I.C. A spectral entropy method for distinguishing regular and irregular motion of hamiltonian systems. J. Phys. A: Math. Gen. 1979, 12, 2053–2071. [Google Scholar] [CrossRef]
- Rosso, O.A.; Blanco, S.; Jordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Başar, E. Wavelet entropy: A new tool for analysis of short duration brain electrical signals. J. Neurosci. Meth. 2001, 105, 65–75. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102:1–174102:4. [Google Scholar] [CrossRef]
- Martín, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Physia A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martín, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102:1–154102:4. [Google Scholar] [CrossRef]
- Rosso, O.A.; Carpi, L.C.; Saco, P.M.; Ravetti, M.G.; Plastino, A.; Larrondo, H.A. Causality and the entropy-complexity plane: Robustness and missing ordinal patterns. Phys. A 2012, 391, 42–55. [Google Scholar] [CrossRef]
- Rosso, O.A.; De Micco, L.; Larrondo, H.; Martín, M.T.; Plastino, A. Generalized statistical complexity measure. Int. J. Bifurc. Chaos 2010, 20, 775–785. [Google Scholar] [CrossRef]
- Parlitz, U.; Berg, S.; Luther, S.; Schirdewan, A.; Kurths, J.; Wessel, N. Classifying Cardiac Biosignals Using Pattern Statistics and Symbolic Dynamics. In Proceedings of the 6th ESGCO, Berlin, Germany, 12–14 April 2010.
- Parlitz, U.; Berg, S.; Luther, S.; Schirdewan, A.; Kurths, J.; Wessel, N. Classifying cardiac biosignals using ordinal pattern statistics and symbolic dynamics. Comput. Biol. Med. 2012, 42, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Peitgen, H.O.; Jürgens, H.; Saupe, D. Chaos and Fractals, New Frontiers of Science; Springer-Verlag: New York, NY, USA, 1992. [Google Scholar]
- Frank, B.; Pompe, B.; Schneider, U.; Hoyer, D. Permutation entropy improves fetal behavioural state classification based on heart rate analysis from biomagnetic recordings in near term fetuses. Med. Biol. Eng. Comput. 2006, 44, 179–187. [Google Scholar] [CrossRef] [PubMed]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Rosso, O.A. Bandt-Pompe approach to the classical-quantum transition. Phys. D 2007, 233, 21–31. [Google Scholar] [CrossRef]
- Bandt, C. Ordinal time series analysis. Ecol. Model. 2005, 182, 229–238. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Fischer, I.; Rosso, O.A.; Mirasso, C.R. Permutation-information-theory approach to unveil delay dynamics from time-series analysis. Phys. Rev. E 2010, 82, 046212:1–046212:9. [Google Scholar] [CrossRef]
- Soriano, M.C.; Zunino, L.; Rosso, O.A.; Fischer, I.; Mirasso, C.R. Time scales of a chaotic semiconductor laser with optical feedback under the lens of a permutation information analysis. IEEE J. Quantum Electron. 2011, 47, 252–261. [Google Scholar] [CrossRef]
- Soriano, M.C.; Zunino, L.; Larger, L.; Fischer, I.; Mirasso, C.R. Distinguishing fingerprints of hyperchaotic and stochastic dynamics in optical chaos from a delayed opto-electronic oscillator. Opt. Lett. 2011, 36, 2212–2214. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Kocarev, L.; Szczepanski, J. Order patterns and chaos. Phys. Lett. A 2006, 355, 27–31. [Google Scholar] [CrossRef]
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A.F. True and false forbidden patterns in deterministic and random dynamics. Europhys. Lett. 2007, 79. [Google Scholar] [CrossRef]
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A.F. Combinatorial detection of determinism in noisy time series. Europhys. Lett. 2008, 83. [Google Scholar] [CrossRef]
- Amigó, J.M. Permutation Complexity in Dynamical Systems; Springer-Verlag: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Bandt, C.; Shiha, F. Order patterns in time series. J. Time Ser. Anal. 2007, 28, 646–665. [Google Scholar] [CrossRef]
- Carpi, L.C.; Saco, P.M.; Rosso, O.A. Missing ordinal patterns in correlated noises. Phys. A 2010, 389, 2020–2029. [Google Scholar] [CrossRef]
- Feldman, D.P.; McTague, C.S.; Crutchfield, J.P. The organization of intrinsic computation: Complexity-entropy diagrams and the diversity of natural information processing. Chaos 2008, 18. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, P.W.; Martín, M.T.; Plastino, A.; Rosso, O.A. Intensive entropic nontriviality measure. Phys. A 2004, 334, 119–131. [Google Scholar] [CrossRef]
- Rosso, O.A.; Masoller, C. Detecting and quantifying stochastic and coherence resonances via information-theory complexity measurements. Phys. Rev. E 2009, 79, 040106R:1–040106R:4. [Google Scholar] [CrossRef]
- Rosso, O.A.; Masoller, C. Detecting and quantifying temporal correlations in stochastic resonance via information theory measures. Eur. Phys. J. B 2009, 69, 37–43. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Rosso, O.A.; Casas, M. Distances in probability space and the statistical complexity setup. Entropy 2011, 13, 1055–1075. [Google Scholar] [CrossRef]
- Grosse, I.; Bernaola-Galván, P.; Carpena, P.; Román-Roldán, R.; Oliver, J.; Stanley, H.E. Analysis of symbolic sequences using the Jensen-Shannon divergence. Phys. Rev. E 2002, 65. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Complexity-entropy causality plane: A useful approach to quantify the stock market inefficiency. Phys. A 2010, 389, 1891–1901. [Google Scholar] [CrossRef]
- Zunino, L.; Tabak, B.M.; Serinaldi, F.; Zanin, M.; Pérez, D.G.; Rosso, O.A. Commodity predictability analysis with a permutation information theory approach. Phys. A 2011, 390, 876–890. [Google Scholar] [CrossRef]
- Masoller, C.; Rosso, O.A. Quantifying the complexity of the delayed logistic map. Philos. Trans. Roy. Soc. A 2011, 369, 425–438. [Google Scholar] [CrossRef] [PubMed]
- Lepri, S.; Giacomelli, G.; Politi, A.; Arecchi, F.T. High-dimensional chaos in delayed dynamical systems. Phys. D 1994, 70, 235–249. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Xiang, S.; Pan, W.; Luo, B.; Yan, L.; Zou, X.; Jiang, N.; Yang, L.; Zhu, H. Conceal time-delay signature of chaotic vertical-cavity surface-emitting lasers by variable-polarization optical feedback. Opt. Commun. 2011, 284, 5758–5765. [Google Scholar] [CrossRef]
- Wu, J.G.; Wu, Z.M.; Xia, G.Q.; Feng, G.Y. Evolution of time delay signature of chaos generated in a mutually delay-coupled semiconductor lasers system. Opt. Express 2012, 20, 1741–1753. [Google Scholar] [CrossRef] [PubMed]
- Matilla-García, M.; Ruiz Marín, M. A non-parametric independence test using permutation entropy. J. Econom. 2008, 144, 139–155. [Google Scholar] [CrossRef]
- López, F.; Matilla-García, M.; Mur, J.; Ruiz Marín, M. A non-parametric spatial independence test using symbolic entropy. Reg. Sci. Urban Econ. 2010, 40, 106–115. [Google Scholar] [CrossRef]
- Matilla-García, M.; Ruiz Marín, M. Spatial symbolic entropy: A tool for detecting the order of contiguity. Geogr. Anal. 2011, 43, 228–239. [Google Scholar] [CrossRef]
- Herrera Gómez, M.; Ruiz Marín, M.; Mur, J.; Paelinck, J. A non-parametric approach to spatial causality. In 9mes Journées Internationales dEconometrie et de Statistique Spatiales, Orléans, France, 24–25 June 2010.
- Cánovas, J.S.; Guillamón, A.; Ruíz, M.C. Using permutations to detect dependence between time series. Phys. D 2011, 240, 1199–1204. [Google Scholar] [CrossRef]
- Freeman, G.H.; Halton, J.H. Note on an exact treatment of contingency, goodness of fit and other problems of significance. Biometrika 1951, 38, 141–149. [Google Scholar] [CrossRef] [PubMed]
- Bahraminasab, A.; Ghasemi, F.; Stefanovska, A.; McClintock, P.V.E.; Kantz, H. Direction of coupling from phases of interacting oscillators: A permutation information approach. Phys. Rev. Lett. 2008, 100, 084101:1–084101:4. [Google Scholar] [CrossRef]
- Liu, X.-F.; Wang, Y. Fine-grained permutation entropy as a measure of natural complexity for time series. Chin. Phys. B 2009, 18, 2690–2695. [Google Scholar]
- Bian, C.; Qin, C.; Ma, Q.D.Y.; Shen, Q. Modied permutation-entropy analysis of heartbeat dynamics. Phys. Rev. E 2012, 85, 021906:1–021906:7. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Hausdorff, J.M.; Ivanov, P.; Peng, C.K.; Stanley, H.E. Fractal dynamics in physiology: Alterations with disease and aging. Proc. Natl. Acad. Sci. USA 2002, 99, 2466–2472. [Google Scholar] [CrossRef] [PubMed]
- Kenet, T.; Bibitchkov, D.; Tsodyks, M.; Grinvald, A.; Arieli, A. Spontaneously emerging cortical representations of visual attributes. Nature 2003, 425, 954–956. [Google Scholar] [CrossRef] [PubMed]
- Beggs, J.; Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [PubMed]
- Dragoi, G.; Tonegawa, S. Preplay of future place cell sequences by hippocampal cellular assemblies. Nature 2011, 469, 397–401. [Google Scholar] [CrossRef] [PubMed]
- Schindler, K.; Gast, H.; Stieglitz, L.; Stibal, A.; Hauf, M.; Wiest, R.; Mariani, L.; Rummel, C. Forbidden ordinal patterns of periictal intracranial EEG indicate deterministic dynamics in human epileptic seizures. Epilepsia 2011, 52, 1771–1780. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.J. Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar] [CrossRef] [PubMed]
- Pereda, E.; Quiroga, R.Q.; Bhattacharya, J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 2005, 77, 1–37. [Google Scholar] [CrossRef] [PubMed]
- Groth, A. Visualization of coupling in time series by order recurrence plots. Phys. Rev. E 2005, 72, 046220:1–046220:8. [Google Scholar] [CrossRef]
- Cao, Y.; Tung, W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70. [Google Scholar] [CrossRef]
- Keller, K.; Wittfeld, K. Distances of time series components by means of symbolic dynamics. Int. J. Bifurc. Chaos 2004, 14, 693–703. [Google Scholar] [CrossRef]
- Veisi, I.; Pariz, N.; Karimpour, A. Fast and Robust Detection of Epilepsy in Noisy EEG Signals Using Permutation Entropy. In Proceedings of the 7th IEEE International Conference on Bioinformatics and Bioengineering, Boston, MA, USA, 14–17 October 2007; pp. 200–203.
- Li, X.; Ouyang, G.; Richards, D.A. Predictability analysis of absence seizures with permutation entropy. Epilepsy Res. 2007, 77, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, G.; Li, X.; Dang, C.; Richards, D.A. Deterministic dynamics of neural activity during absence seizures in rats. Phys. Rev. E 2009, 79, 041146:1–041146:8. [Google Scholar] [CrossRef]
- Ouyang, G.; Dang, C.; Richards, D.A.; Li, X. Ordinal pattern based similarity analysis for EEG recordings. Clin. Neurophysiol. 2010, 121, 694–703. [Google Scholar] [CrossRef] [PubMed]
- Bruzzo, A.A.; Gesierich, B.; Santi, M.; Tassinari, C.; Birbaumer, N.; Rubboli, G. Permutation entropy to detect vigilance changes and preictal states from scalp EEG in epileptic patients: A preliminary study. Neurol. Sci. 2008, 29, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Jordan, D.; Stockmanns, G.; Kochs, E.F.; Pilge, S.; Schneider, G. Electroencephalographic order pattern analysis for the separation of consciousness and unconsciousness: An analysis of approximate entropy, permutation entropy, recurrence rate, and phase coupling of order recurrence plots. Anesthesiology 2008, 109, 1014–1022. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Cui, S.M.E.; Voss, L.J. Using permutation entropy to measure the electroencephalographic effect of sevoflurane. Anesthesiology 2007, 109, 448–456. [Google Scholar] [CrossRef] [PubMed]
- Olofsen, E.; Sleigh, J.W.; Dahan, A. Permutation entropy of the electroencephalogram: A measure of anaesthetic drug effect. Br. J. Anaesth. 2008, 101, 810–821. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.; Cardoso-Cruz, H.; Silva, F.; Galhardo, V.; Antunes, L. Comparison of anesthetic depth indexes based on thalamocortical local field potentials in rats. Anesthesiology 2010, 112, 355–363. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.; Campos, S.; Monteiro, J.; Venâncio, C.; Costa, B.; Guedes de Pinho, P.; Antunes, L. Performance of anesthetic depth indexes in rabbits under propofol anesthesia. Anesthesiology 2011, 115, 303–314. [Google Scholar] [CrossRef] [PubMed]
- Schinkel, S.; Marwan, N.; Kurths, J. Order patterns recurrence plots in the analysis of ERP data. Cogn. Neurodyn. 2007, 1, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Schinkel, S.; Marwan, N.; Kurths, J. Brain signal analysis based on recurrences. J. Physiol. 2009, 103, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Berg, S.; Luther, S.; Lehnart, S.E.; Hellenkamp, K.; Bauernschmitt, R.; Kurths, J.; Wessel, N.; Parlitz, U. Comparison of Features Characterizing Beat-to-Beat Time Series. In Proceedings of Biosignal, Berlin, Germany, 14–16 July 2010.
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on Permutation Entropy and Support Vector Machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Li, H.; Muskulus, M.; Heusdens, R.; Wolters, L. Analysis and Synthesis of Pseudo-Periodic Job Arrivals in Grids: A Matching Pursuit Approach. In Proceedings of the Seventh IEEE International Symposium on Cluster Computing and the Grid, Rio De Janeiro, Brazil, 14–17 May 2007; pp. 183–196.
- Wendling, F.; Chauvel, P.; Biraben, A.; Bartolomei, F. From intracerebral EEG signals to brain connectivity: Identification of epileptogenic networks in partial epilepsy. Front. Syst. Neurosci. 2010, 4. [Google Scholar] [CrossRef] [PubMed]
- Staniek, M.; Lehnertz, K. Symbolic transfer entropy. Phys. Rev. Lett. 2008, 100, 158101:1–158101:4. [Google Scholar] [CrossRef]
- Li, X.; Ouyang, G. Estimating coupling direction between neuronal populations with permutation conditional mutual information. Neuroimage 2010, 52, 497–507. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, X.; Liang, Z.; Voss, L.J.; Sleigh, J.W. Multiscale permutation entropy analysis of EEG recordings during sevoflurane anesthesia. J. Neural Eng. 2010, 7. [Google Scholar] [CrossRef] [PubMed]
- Nicolaou, N.; Georgiou, J. Permutation Entropy: A New Feature for Brain-Computer Interfaces. In Proceedings of the IEEE Biomedical Circuits and Systems Conference, Paphos, Cyprus, 3–5 November 2010; pp. 49–52.
- Zanin, M. Forbidden patterns in financial time series. Chaos 2008, 18. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Forbidden patterns, permutation entropy and stock market inefficiency. Phys. A 2009, 388, 2854–2864. [Google Scholar] [CrossRef]
- Zunino, L.; Bariviera, A.F.; Guercio, M.B.; Martinez, L.B.; Rosso, O.A. On the efficiency of sovereign bond markets. Phys. A 2012, 391, 4342–4349. [Google Scholar] [CrossRef]
- Ruiz, M.C.; Guillamón, A.; Gabaldón, A. A new approach to measure volatility in energy markets. Entropy 2012, 14, 74–91. [Google Scholar] [CrossRef]
- Amigó, J.M.; Kennel, M.B.; Kocarev, L. The permutation entropy rate equals the metric entropy rate for ergodic information sources and ergodic dynamical systems. Phys. D 2005, 210. [Google Scholar] [CrossRef]
- Saco, P.M.; Carpi, L.C.; Figliola, A.; Serrano, E.; Rosso, O.A. Entropy analysis of the dynamics of El Niño/Southern oscillation during the holocene. Phys. A 2010, 389, 5022–5027. [Google Scholar] [CrossRef]
- Rosso, O.A.; Zunino, L.; Pérez, D.G.; Figliola, A.; Larrondo, H.A.; Garavaglia, M.; Martín, M.T.; Plastino, A. Extracting features of Gaussian self-similar stochastic processes via the Bandt-Pompe approach. Phys. Rev. E 2007, 76, 061114:1–061114:6. [Google Scholar] [CrossRef]
- Zunino, L.; Pérez, D.G.; Martín, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Permutation entropy of fractional Brownian motion and fractional Gaussian noise. Phys. Lett. A 2008, 372, 4768–4774. [Google Scholar] [CrossRef]
- Zunino, L.; Pérez, D.G.; Kowalski, A.; Martín, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Fractional Brownian motion, fractional Gaussian noise, and Tsallis permutation entropy. Phys. A 2008, 387, 6057–6068. [Google Scholar] [CrossRef]
- Tiana-Alsina, J.; Torrent, M.C.; Rosso, O.A.; Masoller, C.; Garcia-Ojalvo, J. Quantifying the statistical complexity of low-frequency fluctuations in semiconductor lasers with optical feedback. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
- Tiana-Alsina, J.; Buldu, J.M.; Torrent, M.C.; Garcia-Ojalvo, J. Quantifying stochasticity in the dynamics of delay-coupled semiconductor lasers via forbidden patterns. Philos. Trans. Roy. Soc. A 2010, 368, 367–377. [Google Scholar] [CrossRef] [PubMed]
- Xiang, S.; Pan, W.; Yan, L.; Luo, B.; Zou, X.; Jiang, N.; Wen, K. Influence of polarization mode competition on chaotic unpredictability of vertical-cavity surface-emitting lasers with polarization-rotated optical feedback. Opt. Lett. 2011, 36, 310–312. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Rosso, O.A.; Soriano, M.C. Characterizing the hyperchaotic dynamics of a semiconductor laser subject to optical feedback via permutation entropy. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 1250–1257. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Zunino, L. Information flow during the quantum-classical transition. Phys. Lett. A 2010, 374, 1819–1826. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Zunino, L.; Plastino, A.; Casas, M. The quantum-classical transition as an information flow. Entropy 2010, 12, 148–160. [Google Scholar] [CrossRef]
- Kowalski, A.M.; Martín, M.T.; Plastino, A.; Rosso, O.A. Chaos and complexity in the classical-quantum transition. Int. J. Appl. Math. Stat. 2012, 26, 67–80. [Google Scholar]
- Suyal, V.; Prasad, A.; Singh, H.P. Hysteresis in a solar activity cycle. Solar Phys. 2012, 276, 407–414. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Zunino, L.; Mendes, R.S.; Lenzi, E.K. Complexity-entropy causality plane: A useful approach for distinguishing songs. Phys. A 2012, 391, 2421–2428. [Google Scholar] [CrossRef]
- Li, X.; Ouyang, G.; Liang, Z. Complexity measure of motor current signals for tool flute breakage detection in end milling. Int. J. Mach. Tools Manuf. 2008, 48, 371–379. [Google Scholar] [CrossRef]
- Nair, U.; Krishna, B.M.; Namboothiri, V.N.N.; NaMpoori, V.P.N. Permutation entropy based real-time chatter detection using audio signal in turning process. Int. J. Adv. Manuf. Technol. 2010, 46, 61–68. [Google Scholar] [CrossRef]
- Sun, X.; Zou, Y.; Nikiforova, V.; Kurths, J.; Walther, D. The complexity of gene expression dynamics revealed by permutation entropy. BMC Bioinform. 2010, 11. [Google Scholar] [CrossRef] [PubMed]
- Larrondo, H.A.; González, C.M.; Martín, M.T.; Plastino, A.; Rosso, O.A. Intensive statistical complexity measure of pseudorandom number generators. Phys. A 2005, 356, 133–138. [Google Scholar] [CrossRef]
- Larrondo, H.A.; Martín, M.T.; González, C.M.; Plastino, A.; Rosso, O.A. Random number generators and causality. Phys. Lett. A 2006, 352, 421–425. [Google Scholar] [CrossRef]
- De Micco, L.; Larrondo, H.A.; Plastino, A.; Rosso, O. Quantifiers for randomness of chaotic pseudo-random number generators. Philos. Trans. Roy. Soc. A 2009, 367, 3281–3296. [Google Scholar] [CrossRef] [PubMed]
- De Micco, L.; Petrocelli, R.A.; Rosso, O.A.; Plastino, A.; Larrondo, H.A. Mixing chaotic maps and electromagnetic interference reduction. Int. J. Appl. Math. Stat. 2012, 26, 106–120. [Google Scholar]
- De Micco, L.; Fernández, J.G.; Larrondo, H.A.; Plastino, A.; Rosso, O.A. Sampling period, statistical complexity, and chaotic attractors. Phys. A 2012, 391, 2564–2575. [Google Scholar] [CrossRef]
- Rosso, O.A.; Vicente, R.; Mirasso, C.R. Encryption test of pseudo-aleatory messages embedded on chaotic laser signals: An Information Theory approach. Phys. Lett. A 2008, 372, 1018–1023. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy 2012, 14, 1553-1577. https://doi.org/10.3390/e14081553
Zanin M, Zunino L, Rosso OA, Papo D. Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy. 2012; 14(8):1553-1577. https://doi.org/10.3390/e14081553
Chicago/Turabian StyleZanin, Massimiliano, Luciano Zunino, Osvaldo A. Rosso, and David Papo. 2012. "Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review" Entropy 14, no. 8: 1553-1577. https://doi.org/10.3390/e14081553
APA StyleZanin, M., Zunino, L., Rosso, O. A., & Papo, D. (2012). Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy, 14(8), 1553-1577. https://doi.org/10.3390/e14081553




