Maximum Entropy Gibbs Density Modeling for Pattern Classification
Abstract
:1. Introduction
2. Density Estimation by Constrained Maximum Entropy
3. Gibbs Pattern Density Modeling by a Kohonen Network
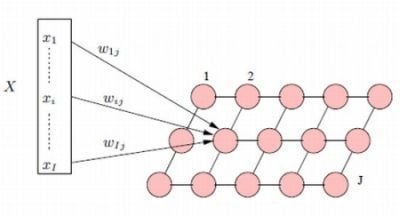
3.1. The Traditional Kohonen Network
3.2. The Gibbsian Kohonen Network

| - Initialize the potential functions to small random values, . | |||
| - Initialize patterns in nodes . | |||
| - For , do | |||
| - For each training pattern Γ do | |||
| - Compute the vectors of representation and , . | |||
| - determine , | |||
| - Update the potential functions: | |||
| - Synthesize new patterns by MCMC using the potential functions | |||
3.3. The Main Differences and Similarities
4. An Experimental Validation
4.1. The Database
4.2. Feature Extraction
4.3. Evaluation
| Fold | Gibbsian network | Kohonen network | Difference |
|---|---|---|---|
| 1 | 95.1 % | 94.4 % | +0.7 |
| 2 | 94.0 % | 92.1 % | +1.9 |
| 3 | 94.7 % | 92.4 % | +2.3 |
| Mean | 94.6% | 92.9 % | +1.7 |
4.4. Test of Statistical Significance
5. Conclusions
Appendix
A. MCMC Shape Sampling Algorithm
| Given a shape | |||
| - For , with being the maximum sweep number | |||
| - For ,with being the point number on shapes | |||
| - For , | |||
| with being the number of | |||
| directions | |||
| - move according to d directions | |||
| to obtain a set of new shapes , | |||
| - Compute by Equation (6). | |||
| - Keep which maximizes and affect it to . | |||
| - Compute . | |||
| - Draw a random number from a uniform distribution | |||
| - If , replace Γ by . | |||
References
- Duda, P.O.; Hart, P.E.; Stork, D.G. Pattern Classification. New York, NY, USA, 2001. [Google Scholar]
- Jain, A.; Duin, R.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Recognit. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Zhu, S. Embedding gestalt laws in Markov random fields. IEEE Trans. Pattern Recognit. Mach. Intell. 1999, 21, 1170–1187. [Google Scholar]
- Zhu, S.C.; Mumford, D. Prior learning and Gibbs reaction-diffusion. IEEE Trans. Pattern Recognit. Mach. Intell. 1997, 19, 1236–1250. [Google Scholar]
- Zhu, S.C.; Wu, Y.; Mumford, D. Minimax entropy principle and its application to texture modeling. Neural Comput. 1997, 9, 1627–1660. [Google Scholar] [CrossRef]
- Zhu, S.C.; Wu, Y.; Mumford, D. Filters, Random Fields and Maximum Entropy (FRAME): Towards a unified theory for texture modeling. Int. J. Comput. Vision 1998, 27, 107–126. [Google Scholar] [CrossRef]
- Mezghani, N.; Mitiche, A.; Cheriet, M. Bayes classification of online arabic characters by Gibbs modeling of class conditional densities. IEEE Trans. Pattern Recognit. Mach. Intell. 2008, 30. [Google Scholar] [CrossRef] [PubMed]
- Kohonen, T. Self-organizing Maps; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Kaski, S.; Kangas, J.; Kohonen, T. Bibliography of Self-Organizing Map SOM papers: 1981–1997. Neural Comput. Surveys 1998, 1, 102–350. [Google Scholar]
- Oja, M.; Kaski, S.; Kohonen, T. Bibliography of Self-Organizing Map SOM papers: 1998–2001 addendum. Neural Comput. Surveys 2003, 3, 1–156. [Google Scholar]
- Lippman, R. An introduction to computing with neural networks. IEEE ASSP Mag. 1987, 3, 4–22. [Google Scholar] [CrossRef]
- Ritter, H.; Schulten, K. 1988. Kohonen Self-Organizing Maps: Exploring Their Computational Capabilities. In Proceedings of the IEEE International Joint Conference on Neural Networks, Piscataway, NJ, USA, 1988; IEEE Service Center. Volume I, pp. 109–116.
- LeBail, E.; Mitiche, A. Quantification vectorielle d’images par le réseau neuronal de kohonen. Traitement du Signal 1989, 6, 529–539. [Google Scholar]
- Sabourin, M.; Mitiche, A. Modeling and classification of shape using a Kohonen associative memory with selective multiresolution. Neural Netw. 1993, 6, 275–283. [Google Scholar] [CrossRef]
- Anouar, F.; Badran, F.; Thiria, S. Probabilistic self-organizing map and radial basis function. J. Neurocomput. 1998, 20, 83–96. [Google Scholar] [CrossRef]
- Mezghani, N.; Mitiche, A.; Cheriet, M. On-line Recognition of Handwritten Arabic Characters Using a Kohonen Neural Network. In Proceedings of the 8th International Workshop on Frontiers in Handwriting Recognition, Niagara-on-the-Lake, Canada, 6–8 August 2002; pp. 490–495.
- Mezghani, N.; Mitiche, A.; Cheriet, M. A new representation of shape and its use for superior performance in on-line Arabic character recognition by an associative memory. Int. J. Doc. Anal. Recognit. 2005, 7, 201–210. [Google Scholar] [CrossRef]
- Mitiche, A.; Aggarwal, J. Pattern category assignement by neural networks and the nearest neighbors rule. Int. J. Pattern Recognit. Artif. Intell. 1996, 10, 393–408. [Google Scholar] [CrossRef]
- Descombes, X.; Morris, R.; Zerubia, J.; Berthod, M. Maximum Likelihood Estimation of Markov Random Field Parameters Using Markov Chain Monte Carlo Algorithms. In Proceedings of the Internalional Workshop on Energy Minimization Methods, Venice, Italy, 21–23 May 1998.
- Ritter, H.; Kohonen, T. Self-organizing semantic maps. Biol. Cybern. 1989, 61, 241–254. [Google Scholar] [CrossRef]
- Mezghani, N.; Phan, P.; Mitiche, A.; Labelle, H.; de Guise, J. A Kohonen neural network description of scoliosis fused region and their corresponding lenke classification. Int. J. Comput. Assist. Radiol. Surgery 2012, 7, 157–264. [Google Scholar] [CrossRef] [PubMed]
- Spall, J.C. Estimation via Markov Chain Monte Carlo. IEEE Control Syst. Mag. 2003, 23, 34–45. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mezghani, N.; Mitiche, A.; Cheriet, M. Maximum Entropy Gibbs Density Modeling for Pattern Classification. Entropy 2012, 14, 2478-2491. https://doi.org/10.3390/e14122478
Mezghani N, Mitiche A, Cheriet M. Maximum Entropy Gibbs Density Modeling for Pattern Classification. Entropy. 2012; 14(12):2478-2491. https://doi.org/10.3390/e14122478
Chicago/Turabian StyleMezghani, Neila, Amar Mitiche, and Mohamed Cheriet. 2012. "Maximum Entropy Gibbs Density Modeling for Pattern Classification" Entropy 14, no. 12: 2478-2491. https://doi.org/10.3390/e14122478
APA StyleMezghani, N., Mitiche, A., & Cheriet, M. (2012). Maximum Entropy Gibbs Density Modeling for Pattern Classification. Entropy, 14(12), 2478-2491. https://doi.org/10.3390/e14122478