D. Proofs
Preliminary remark :
Let us note that if , a simple reductio ad absurdum enables us to to infer that . Therefore, through an induction, we immediately obtain that, for any k, . Thus, for any k and from a certain rank n, we derive that .
Proof of Lemma D.1.
Lemma D.1. We have .
Putting , let us determine f in basis A. Let us first study the function defined by , We can immediately say that ψ is continuous and since A is a basis, its bijectivity is obvious. Moreover, let us study its Jacobian.
By definition, it is
since
A is a basis. We can therefore infer :
i.e., Ψ (resp.
y) is the expression of
f (resp of
x) in basis
A, namely
, with
and
being the expressions of
n and
h in basis
A. Consequently, our results in the case where the family
is the canonical basis of
, still hold for Ψ in basis
A—see
Section 2.1. And then, if
is the expression of
g in basis
A, we have
,
i.e.,
.
Proof of Lemma D.2.
Lemma D.2. Should there exist a family such that with , with f, n and h being densities, then this family is an orthogonal basis of .
Using a reductio ad absurdum, we have . We can therefore conclude.
Lemma D.3. is reached when the ϕ-divergence is greater than the distance as well as the distance.
Indeed, let G be and be for all c>0. From Lemmas A.1, A.2 and A.3 (see page 1605), we get is a compact for the topology of the uniform convergence, if is not empty. Hence, and since property A.2 (see page 1605) implies that is lower semi-continuous in for the topology of the uniform convergence, then the infimum is reached in . (Taking for example Ω is necessarily not empty because we always have ). Moreover, when the divergence is greater than the distance, the very definition of the space enables us to provide the same proof as for the distance.
Proof of Lemma D.4.
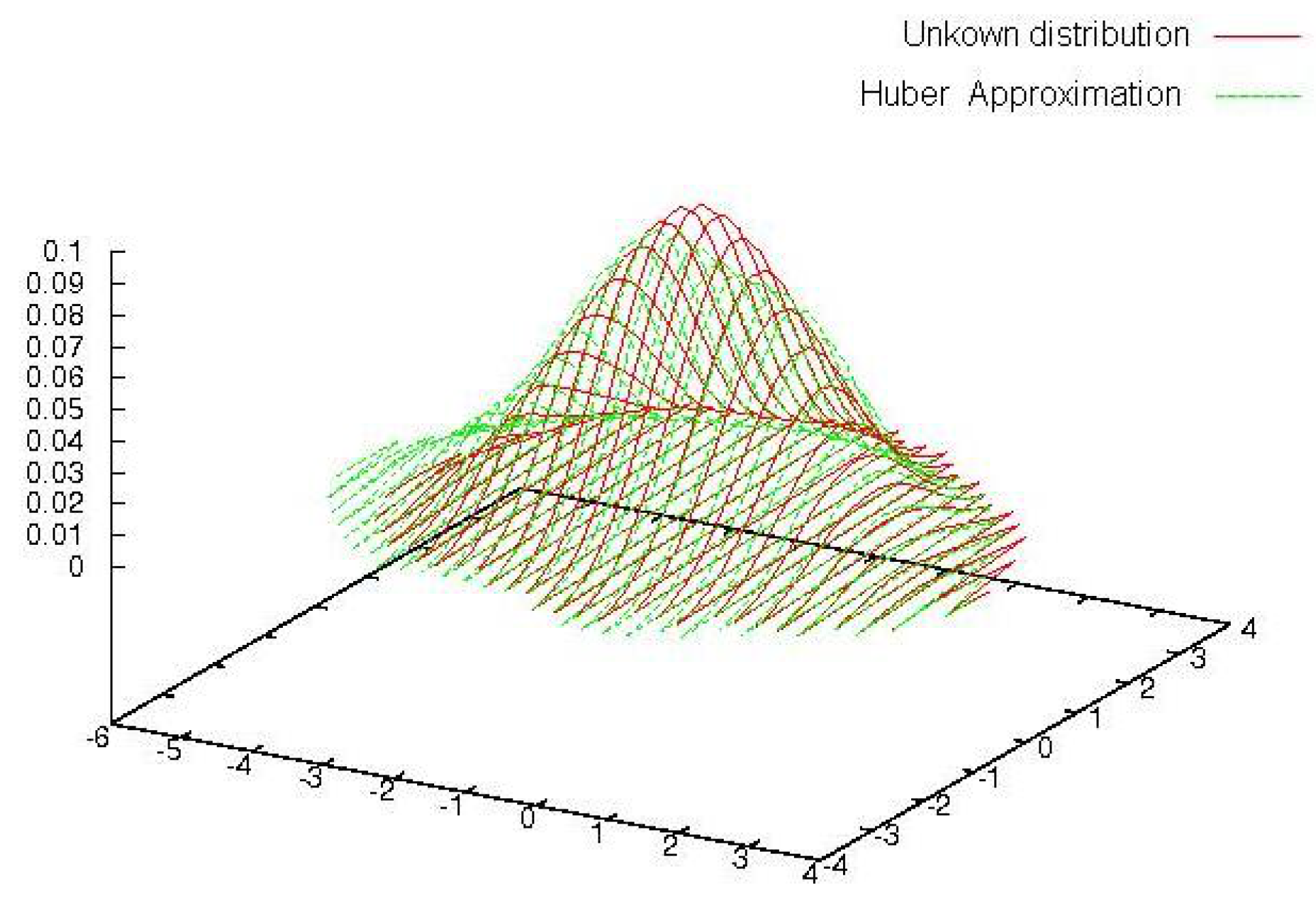
Lemma D.4. For any , we have —see Huber’s analytic method -, —see Huber’s synthetic method - and —see our algorithm.
As it is equivalent to prove either our algorithm or Huber’s, we will only develop here the proof for our algorithm. Assuming, without any loss of generality, that the , , are the vectors of the canonical basis, since we derive immediately that . We note that it is sufficient to operate a change in basis on the to obtain the general case.
Proof of Lemma D.5.
Lemma D.5. If there exits p, , such that , then the family of —derived from the construction of —is free and orthogonal.
Without any loss of generality, let us assume that and that the are the vectors of the canonical basis. Using a reductio ad absurdum with the hypotheses and , where , we get and . Hence It consequently implies that since . Therefore, , i.e., which leads to a contradiction. Hence, the family is free. Moreover, using a reductio ad absurdum we get the orthogonality. Indeed, we have . The use of the same argument as in the proof of Lemma D.2, enables us to infer the orthogonality of .
Proof of Lemma D.6.
Lemma D.6. If there exits p, , such that , where is built from the free and orthogonal family ,...,, then, there exists a free and orthogonal family of vectors of , such that and such that .
Through the incomplete basis theorem and similarly as in Lemma D.5, we obtain the result thanks to the Fubini’s theorem.
Proof of Lemma D.7.
Lemma D.7. For any continuous density f, we have .
Defining
as
, we have
. Moreover, from page 150 of Scott [
15], we derive that
where
. Then, we obtain
. Finally, since the central limit theorem rate is
, we infer that
.
Proof of Proposition 3.1.
Without loss of generality, we reason with in lieu of .
Let us define . We remark that g and present the same density conditionally to . Indeed, .
We can therefore prove this proposition.
First, since
f and
g are known, then, for any given function
, the application
T, which is defined by
is measurable.
Second, the above remark implies that
Consequently, property A.3 page 1605 infers:
, by the very definition of T.
, which completes the proof of this proposition.
Proof of Proposition 3.3. Proposition 3.3 comes immediately from Proposition B.1 page 1606 and Lemma A.1 page 1605.
Proof of Theorem 3.1. First, by the very definition of the kernel estimator converges towards g. Moreover, the continuity of and and Proposition 3.3 imply that converges towards . Finally, since, for any k, , we conclude by an immediate induction.
Proof of Theorem 3.2. First, from Lemma D.7, we derive that, for any x, . Then, let us consider , we have i.e., since and . We can therefore conclude similarly as in the proof of Theorem A.2.
Proof of Theorem D.1.
Theorem D.1. In the case where f is known and under the hypotheses assumed in Section 3.1, it holds and where , and First of all, let us remark that hypotheses to imply that and converge towards in probability. Hypothesis enables us to derive under the integrable sign after calculation, , and consequently which implies,
The very definition of the estimators and , implies that i.e. i.e.
Under and , and using a Taylor development of the (resp. ) equation, we infer there exists (resp. ) on the interval such that (resp. ) with . Thus we get Moreover, the central limit theorem implies: , , since , which leads us to the result.
Proof of Theorem 3.3. We derive this theorem through Proposition B.1 and Theorem D.1.
Proof of Theorem 3.4. We recall that is the kernel estimator of . Since the Kullback–Leibler divergence is greater than the -distance, we then have
Moreover, the Fatou’s lemma implies that
and Through Lemma A.4, we then obtain that , i.e., that . Moreover, for any given k and any given n, the function is a convex combination of multivariate Gaussian distributions. As derived at Remark 2.1 of page 1585, for all k, the determinant of the covariance of the random vector—with density —is greater than or equal to the product of a positive constant times the determinant of the covariance of the random vector with density f. The form of the kernel estimate therefore implies that there exists an integrable function φ such that, for any given k and any given n, we have .
Finally, the dominated convergence theorem enables us to say that , since converges towards f and since .
Proof of Corollary 3.1. Through the dominated convergence theorem and through Theorem 3.4, we get the result using a reductio ad absurdum.
Proof of Theorem 3.5. Through Proposition B.1 and Theorem A.3, we derive theorem 3.5.