Entropy: The Markov Ordering Approach
Abstract
:1. Introduction
1.1. A Bit of History: Classical Entropy
- The energy of the Universe is constant.
- The entropy of the Universe tends to a maximum.
1.2. Key Points
- In Markov processes probability distributions monotonically approach equilibrium : divergence monotonically decrease in time.
- In most applications, conditional minimizers and maximizers of entropies and divergences are used, but the values are not. This means that the system of level sets is more important than the functions’ values. Hence, most of the important properties are invariant with respect to monotonic transformations of entropy scale.
- The system of level sets should be the same as for additive functions: after some rescaling the divergences of interest should be additive with respect to the joining of statistically independent systems.
- The system of level sets should after some rescaling the divergences of interest should have the form of a sum (or integral) over states , where the function f is the same for all states. In information theory, divergences of such form are called separable, in physics the term trace–form functions is used
1.3. Structure of the Paper
- Entropy should be a Lyapunov function for continuous-time Markov processes;
- Entropy is additive with respect to the joining of independent systems;
- Entropy is additive with respect to the partitioning of the space of states (i.e., has the trace–form).
- 2’.
- There exists a monotonic transformation which makes entropy additive with respect to the joining of independent systems (Section 4.1);
- 3’.
- There exists a monotonic transformation which makes entropy additive with respect to the partitioning of the space of states (Section 4.2).
2. Non-Classical Entropies
2.1. The Most Popular Divergences
2.1.1. Csiszár–Morimoto Functions
2.1.2. Required Properties of the Function
2.1.3. The Most Popular Divergences
- Let be the step function, if and if . In this case,The quantity is the number of non-zero probabilities and does not depend on . Sometimes it is called the Hartley entropy.
- ,this is the -distance between P and .
- ,this is the usual Kullback–Leibler divergence or the relative BGS entropy;
- ,this is the relative Burg entropy. It is obvious that this is again the Kullback–Leibler divergence, but for another order of arguments.
- Convex combinations of and also produces a remarkable family of divergences: (),The convex combination of divergences becomes a symmetric functional of for . There exists a special name for this case, “Jeffreys’ entropy".
- ,This is the quadratic term in the Taylor expansion of the relative Botzmann–Gibbs-Shannon entropy, , near equilibrium. Sometimes, this quadratic form is called the Fisher entropy.
- For the CR family in the limits only the maximal terms “survive". Exactly as we get the limit of norms for , we can use the root for and write in these limits the divergences:The existence of two limiting divergences seems very natural: there may be two types of extremely non-equilibrium states: with a high excess of current probability above and, inversely, with an extremely small current probability with respect to .
- The Tsallis relative entropy [27] corresponds to the choice , .For this family we use notation .
2.1.4. Rényi Entropy
2.2. Entropy Level Sets
2.3. Minima and Normalization
2.4. Symmetrization
3. Entropy Production and Relative Entropy Contraction
3.1. Lyapunov Functionals for Markov Chains
3.2. “Lyapunov Divergences" for Discrete Time Markov Chains
4. Definition of Entropy by its Properties
4.1. Additivity Property
- The BGS relative entropy .
- The Burg entropy . It is obvious that a convex combination of the Shannon and Burg entropies has the same additivity property.
- The Rényi entropy . For the Min-entropy also inherites this property.
4.2. Separation of Variables for Partition of the State Space
4.3. “No More Entropies" Theorems
- To provide the separation of variables for incompatible events together with the symmetry property we assume that the divergence is separable, possibly, after a scaling transformation: there exists such a function of two variables and a monotonic function of one variable that . This formula allows us to define for all n.
- is a Lyapunov function for the inverse Kolmogorov equation (22) for any Markov chain with equilibrium . (One can call these functions the universal Lyapunov functions because they do not depend on the kinetic coefficients directly, but only on the equilibrium distribution .)
- To provide separation of variables for independent subsystems we assume that is additive (possibly after a scaling transformation): there exists such a function of one variable that the function is additive for the union of independent subsystems: if , , , then .
5. Markov Order
5.1. Entropy: a Function or an Order?
5.2. Description of Markov Order
- On a given space of states an “equilibrium distribution" is given. If we deal with the probability distribution in real kinetic processes then it means that without any additional restriction the current distribution will relax to . In that sense, is the most disordered distribution. On the other hand, may be considered as the “most disordered" distribution with respect to some a priori information.
- We do not know the current distribution P, but we do know some linear functionals, the moments .
- We do not want to introduce any subjective arbitrariness in the estimation of P and define it as the “most disordered" distribution for given value and equilibrium . That is, we define P as solution to the problem:Without the condition the solution should be simply .
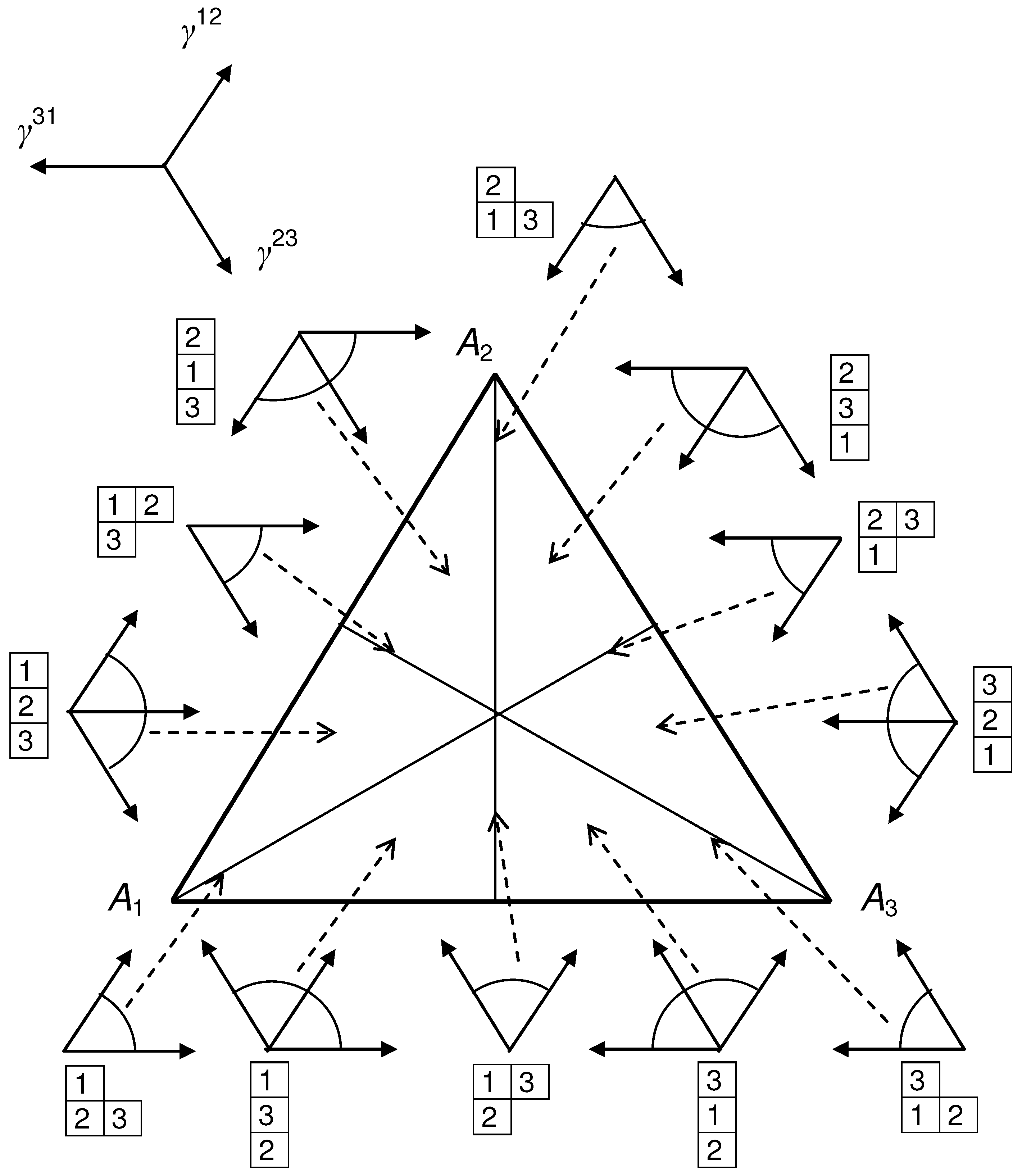
5.3. Combinatorics of Local Markov Order
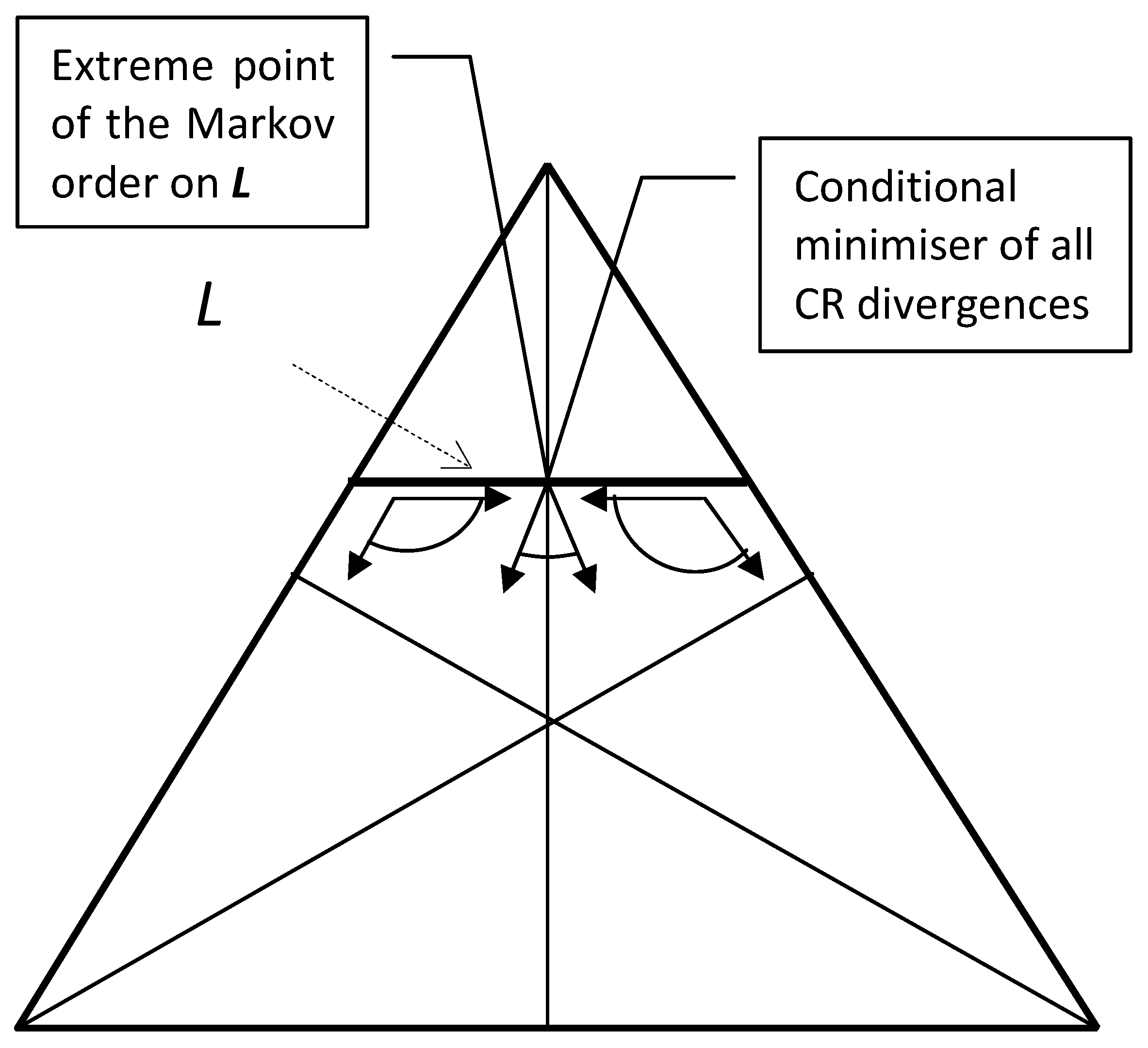
6. The “Most Random" and Conditionally Extreme Distributions
6.1. Conditionally Extreme Distributions in Markov Order
6.2. How to Find the Most Random Distributions?
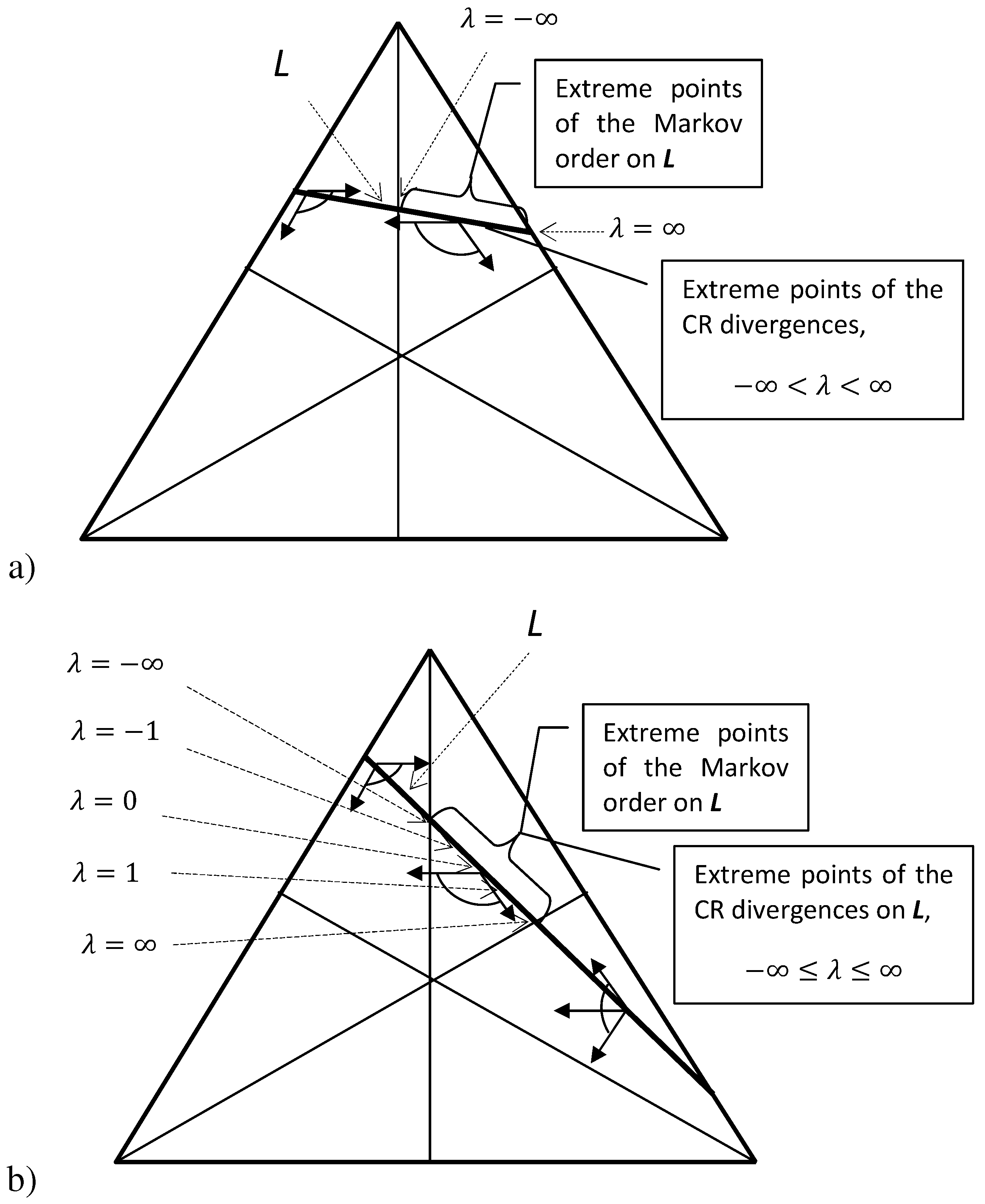
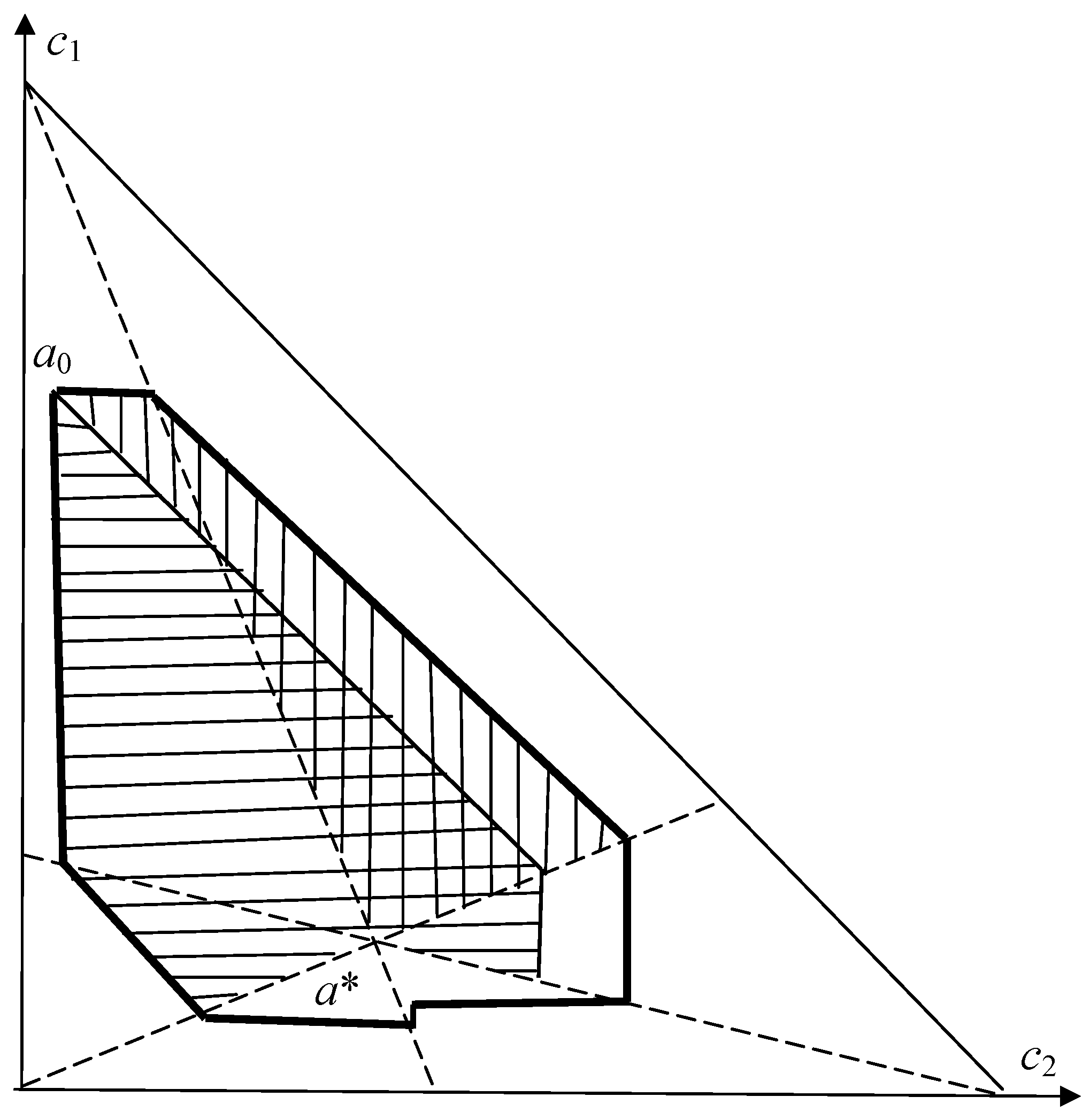
7. Generalized Canonical Distribution
7.1. Reference Distributions for Main Divergences
7.2. Polyhedron of Generalized Canonical Distributions for the Markov Order
8. History of the Markov Order
8.1. Continuous Time Kinetics
- The list of components (in chemical kinetics) or populations (in mathematical ecology) or states (for general Markov chains);
- The list of elementary processes (the reaction mechanism, the graph of trophic interactions or the transition graph), which is often supplemented by the lines or surfaces of partial equilibria of elementary processes;
- The reaction rates and kinetic constants.
8.2. Discrete Time Kinetics
9. Conclusion
- They are Lyapunov functions for all Markov chains;
- They become additive with respect to the joining of independent systems after a monotone transformation of scale;
- They become additive with respect to a partitioning of the state space after a monotone transformation of scale.
Acknowledgements
References
- Clausius, R. Über vershiedene für die Anwendungen bequeme Formen der Hauptgleichungen der Wärmetheorie. Poggendorffs Annalen der Physic und Chemie 1865, 125, 353–400. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the equilibrium of heterogeneous substance. Trans. Connect. Acad. 1875–1876, 108–248, 1875–1876, 343–524. [Google Scholar] [CrossRef]
- Boltzmann, L. Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen. Sitzungsberichte der keiserlichen Akademie der Wissenschaften 1872, 66, 275–370. [Google Scholar]Translation: Further studies on the thermal equilibrium of gas molecules. In Kinetic Theory of Gases: An Anthology of Classic Papers With Historical Commentary; Brush, S.G.; Hall, N.S. (Eds.) Imperial Colledge Press: London, UK, 2003; pp. 362–368.
- Gibbs, J.W. Elementary Principles in Statistical Mechanics; Ox Bow Press: New York, NY, USA, 1981. [Google Scholar]
- Villani, C. H-theorem and beyond: Boltzmann’s entropy in today’s mathematics. In Boltzmann’s Legacy; Gallavotti, G., Reiter, W.L., Yngvason, J., Eds.; EMS Publishing House: Zürich, Switzerland, 2008; pp. 129–145. [Google Scholar]
- Jaynes, E.T. Gibbs versus Boltzmann entropy. Am. J. Phys. 1965, 33, 391–398. [Google Scholar] [CrossRef]
- Goldstein, S.; Lebowitz, J.L. On the (Boltzmann) entropy of non-equilibrium systems. Physica D 2004, 193, 53–66. [Google Scholar] [CrossRef]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Hartley, R.V.L. Transmission of information. Bell Syst. Tech. J. 1928, July, 535–563. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. Proof of the uniqueness of the solution of the equations of the law of mass action. In Selected Works of Yakov Borisovich Zeldovich; Ostriker, J.P., Ed.; Princeton University Press: Princeton, NJ, USA, 1996; Volume 1, pp. 144–148. [Google Scholar]
- Yablonskii, G.S.; Bykov, V.I.; Gorban, A.N.; Elokhin, V.I. Kinetic Models of Catalytic Reactions, Series: Comprehensive Chemical Kinetics; Elsevier: Amsterdam, The Netherlands, 1991; Volume 32. [Google Scholar]
- Hangos, K.M. Engineering model reduction and entropy-based lyapunov functions in chemical reaction kinetics. Entropy 2010, 12, 772–797. [Google Scholar] [CrossRef]
- Burg, J.P. Maximum entropy spectral analysis. In Proceedings of the 37th meeting of the Society of Exploration Geophysicists, Oklahoma City, OK, USA, 1967; Reprinted in Modern Spectrum Analysis. Childers, D.G., Ed.; IEEE Press: New York, NY, USA, 1967; pp. 34–39. [Google Scholar]
- Burg, J.P. The relationship between maximum entropy spectra and maximum likelihood spectra. Geophysics 1972, 37, 375–376. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Harremoës, P.; Topsøe, F. Maximum entropy fundamentals. Entropy 2001, 3, 191–226. [Google Scholar] [CrossRef]
- Beck, C. Generalized information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Mittelhammer, R.; Judge, G.; Miller, D. Econometric Foundations; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Van Akkeren, M.; Judge, G.; Mittelhammer, R. Generalized moment based estimation and inference. J. Econom. 2002, 107, 127–148. [Google Scholar] [CrossRef]
- Myers, T.S.; Daniel, N.; Osherson, D.N. On the psychology of ampliative inference. Psychol. Sci. 1992, 3, 131–135. [Google Scholar] [CrossRef]
- Esteban, M.D.; Morales, D. A summary of entropy statistics. Kybernetica 1995, 31, 337–346. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability 1960, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Abe, S.; Okamoto, Y. (Eds.) Nonextensive Statistical Mechanics and its Applications; Springer: Heidelberg, Germany, 2001.
- Cressie, N.; Read, T. Multinomial goodness of fit tests. J. R. Stat. Soc. Ser. B 1984, 46, 440–464. [Google Scholar]
- Read, T.R.; Cressie, N.A. Goodness of Fit Statistics for Discrete Multivariate Data; Springer: New York, NY, USA, 1988. [Google Scholar]
- Bagci, G.B.; Tirnakli, U. On the way towards a generalized entropy maximization procedure. Phys. Lett. A 2009, 373, 3230–3234. [Google Scholar] [CrossRef]
- Cho, A. A fresh take on disorder, or disorderly science? Science 2002, 297, 1268–1269. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.-K. Diversity and entropy. Entropy 1999, 1, 1–3. [Google Scholar] [CrossRef]
- Gorban, A.N. Equilibrium Encircling. Equations of Chemical kinetics and their Thermodynamic Analysis; Nauka: Novosibirsk, Russia, 1984. [Google Scholar]
- Gorban, A.N.; Karlin, I.V. Family of additive entropy functions out of thermodynamic limit. Phys. Rev. E 2003, 67, 016104. Available online: http://arxiv.org/abs/cond-mat/0205511 (accessed on 4 May 2010). [Google Scholar] [CrossRef] [PubMed]
- Gorban, A.N.; Karlin, I.V.; Öttinger, H.C. The additive generalization of the Boltzmann entropy. Phys. Rev. E 2003, 67, 067104. Available online: http://arxiv.org/abs/cond-mat/0209319 (accessed on 4 May 2010). [Google Scholar] [CrossRef] [PubMed]
- Nonextensive statistical mechanics and thermodynamics: bibliography. Available online: http://tsallis.cat.cbpf.br/TEMUCO.pdf (accessed on 4 May 2010).
- Petz, D. From f-divergence to quantum quasi-entropies and their use. Entropy 2010, 12, 304–325. [Google Scholar] [CrossRef]
- Cachin, C. Smooth entropy and Rényi entropy. In Proceedings of EUROSCRIPT’97; Fumy, W., et al., Eds.; LNCS; Springer: New York, NY, USA, 1997; Volume 1233, pp. 193–208. [Google Scholar]
- Davis, J.V.; Kulis, B.; Jain, P.; Sra, S.; Dhillon, I.S. Information-theoretic metric learning. ICML 2007, 227, 209–216. [Google Scholar]
- Rényi, A. Probability Theory; North-Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Abe, S. Axioms and uniqness theorem for Tsallis entropy. Phys. Lett. A 2000, 271, 74–79. [Google Scholar] [CrossRef]
- Aczel, J. Measuring information beyond communication theory. Inf. Process. Manage. 1984, 20, 383–395. [Google Scholar] [CrossRef]
- Aczel, J.; Daroczy, Z. On Measures of Information and Their Characterizations; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Csiszár, I. Information measures: A critical survey. In Transactions of the Seventh Prague Conference on Information Theory, Statistical Decision Functions and the Eighth European Meeting of Statisticians, Prague, Czech Republic, 18 August–23 August 1974; Academia: Prague, Czech Republic, 1978; Volume B, pp. 73–86. [Google Scholar]
- Gorban, P. Monotonically equivalent entropies and solution of additivity equation. Physica A 2003, 328, 380–390. Available online: http://arxiv.org/abs/cond-mat/0304131 (accessed on 4 May 2010). [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221–260. [Google Scholar] [CrossRef]
- Morimoto, T. Markov processes and the H-theorem. J. Phys. Soc. Jap. 1963, 12, 328–331. [Google Scholar] [CrossRef]
- Csiszár, I. Eine informationstheoretische Ungleichung und ihre Anwendung auf den Beweis der Ergodizitat von Markoffschen Ketten. Magyar. Tud. Akad. Mat. Kutato Int. Kozl. 1963, 8, 85–108. [Google Scholar]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970; reprint 1997. [Google Scholar]
- Liese, F.; Vajda, I. Convex Statistical Distances; Teubner: Leipzig, Germany, 1987. [Google Scholar]
- Dobrushin, R.L. Central limit theorem for non-stationary Markov chains I, II. Theory Probab. Appl. 1956, 1, 163–80, 329–383. [Google Scholar]
- Seneta, E. Nonnegative Matrices and Markov Chains; Springer: New York, USA, 1981. [Google Scholar]
- Cohen, J.E.; Derriennic, Y.; Zbaganu, G.H. Majorization, Monotonicity of relative entropy and stochastic matrices. Contemp. Math. 1993, 149, 251–259. [Google Scholar]
- Cohen, J.E.; Iwasa, Y.; Rautu, G.; Ruskai, M.B.; Seneta, E.; Zbaganu, G. Relative entropy under mappings by stochastic matrices. Linear. Alg. Appl. 1993, 179, 211–235. [Google Scholar] [CrossRef]
- Del Moral, P.; Ledoux, M.; Miclo, L. On contraction properties of Markov kernels. Probab. Theory Relat. Field 2003, 126, 395–420. [Google Scholar] [CrossRef]
- Amari, S. Divergence, Optimization, Geometry . In Proceedings of the 16th International Conference on Neural Information Processing, Bangkok, Thailand, 1 December–5 December 2009; Leung, C.S., Lee, M., Chan, J.H., Eds.; Springer: Berlin, Germany, 2009. LNCS 5863. pp. 185–193. [Google Scholar]
- Bregman, L.M. The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Itakura, F.; Saito, S. Analysis synthesis telephony based on the maximum likelihood method. In Proceedings of the 6th International Congress on Acoustics, Tokyo, Japan, 1968; pp. C17–C20. Reprinted in Speech Synthesis; Flanagan, J.L.; Rabiner, L.R. (Eds.) Dowden, Hutchinson & Ross: Stroudsburg, PA, USA, 1973; pp. 289–292.
- Gorban, A.N. Invariant sets for kinetic equations. React. Kinet. Catal. Lett. 1979, 10, 187–190. [Google Scholar] [CrossRef]
- Gorban, A.N.; Kaganovich, B.M.; Filippov, S.P.; Keiko, A.V.; Shamansky, V.A.; Shirkalin, I.A. Thermodynamic Equilibria and Extrema: Analysis of Attainability Regions and Partial Equilibria; Springer: New York, NY, USA, 2006. [Google Scholar]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Edwards, R.E. Functional Analysis: Theory and Applications; Dover Publications: New York, NY, USA, 1995. [Google Scholar]
- Kolmogorov, A.N. Sulla teoria di Volterra della lotta per l’esistenza. Giornale Instituto Ital. Attuari 1936, 7, 74–80. [Google Scholar]
- May, R.M.; Leonard, W.J. Nonlinear aspects of competition between three species. SIAM J. Appli. Math. 1975, 29, 243–253. [Google Scholar] [CrossRef]
- Bazykin, A.D. Nonlinear Dynamics of Interacting Populations; World Scientific Publishing: Singapore, 1998. [Google Scholar]
- Sigmung, K. Kolmogorov and population dynamics. In Kolmogorovs Heritage in Mathematics; Charpentier, É., Lesne, A., Nikolski, N.K., Eds.; Springer: Berlin, Germany, 2007; pp. 177–186. [Google Scholar]
- Horn, F. Attainable regions in chemical reaction technique. In The Third European Symposium on Chemical Reaction Engineering; Pergamon Press: London, UK, 1964; pp. 1–10. [Google Scholar]
- Glasser, D.; Hildebrandt, D.; Crowe, C. A geometric approach to steady flow reactors: the attainable region and optimisation in concentration space. Am. Chem. Soc. 1987, 26, 1803–1810. [Google Scholar] [CrossRef]
- Filippi-Bossy, C.; Bordet, J.; Villermaux, J.; Marchal-Brassely, S.; Georgakis, C. Batch reactor optimization by use of tendency models. Comput. Chem. Eng. 1989, 13, 35–47. [Google Scholar] [CrossRef]
- Hildebrandt, D.; Glasser, D. The attainable region and optimal reactor structures. Chem. Eng. Sci. 1990, 45, 2161–2168. [Google Scholar] [CrossRef]
- Feinberg, M.; Hildebrandt, D. Optimal reactor design from a geometric viewpoint–I. Universal properties of the attainable region. Chem. Eng. Sci. 1997, 52, 1637–1665. [Google Scholar] [CrossRef]
- Hill, M. Chemical product engineering—the third paradigm. Comput. Chem. Eng. 2009, 33, 947–953. [Google Scholar] [CrossRef]
- Smith, R.L.; Malone, M.F. Attainable regions for polymerization reaction systems. Ind. Eng. Chem. Res. 1997, 36, 1076–1084. [Google Scholar] [CrossRef]
- Metzger, M.J.; Glasser, D.; Hausberger, B.; Hildebrandt, D.; Glasser, B.J. Use of the attainable region analysis to optimize particle breakage in a ball mill. Chem. Eng. Sci. 2009, 64, 3766–3777. [Google Scholar] [CrossRef]
- McGregor, C.; Glasser, D.; Hildebrandt, D. The attainable region and Pontryagin’s maximum principle. Ind. Eng. Chem. Res. 1999, 38, 652–659. [Google Scholar]
- Kauchali, S.; Rooney, W. C.; Biegler, L. T.; Glasser, D.; Hildebrandt, D. Linear programming formulations for attainable region analysis. Chem. Eng. Sci. 2002, 57, 2015–2028. [Google Scholar] [CrossRef]
- Manousiouthakis, V.I.; Justanieah, A.M.; Taylor, L.A. The Shrink-Wrap algorithm for the construction of the attainable region: an application of the IDEAS framework. Comput. Chem. Eng. 2004, 28, 1563–1575. [Google Scholar] [CrossRef]
- Gorban, A.N. Methods for qualitative analysis of chemical kinetics equations. In Numerical Methods of Continuum Mechanics; Institute of Theoretical and Applied Mechanics: Novosibirsk, USSR, 1979; Volume 10, pp. 42–59. [Google Scholar]
- Gorban, A.N.; Yablonskii, G.S.; Bykov, V.I. Path to equilibrium. In Mathematical Problems of Chemical Thermodynamics; Nauka: Novosibirsk, USSR, 1980; pp. 37–47. (in Russian); English translation: Int. Chem. Eng. 1982, 22, 368–375 [Google Scholar]
- Gorban, A.N.; Yablonskii, G.S. On one unused possibility in planning of kinetic experiment. Dokl. Akad. Nauk SSSR 1980, 250, 1171–1174. [Google Scholar]
- Zylka, Ch. A note on the attainability of states by equalizing processes. Theor. Chim. Acta 1985, 68, 363–377. [Google Scholar] [CrossRef]
- Krambeck, F.J. Accessible composition domains for monomolecular systems. Chem. Eng. Sci. 1984, 39, 1181–1184. [Google Scholar] [CrossRef]
- Shinnar, R.; Feng, C.A. Structure of complex catalytic reactions: thermodynamic constraints in kinetic modeling and catalyst evaluation. Ind. Eng. Chem. Fundam. 1985, 24, 153–170. [Google Scholar] [CrossRef]
- Shinnar, R. Thermodynamic analysis in chemical process and reactor design. Chem. Eng. Sci. 1988, 43, 2303–2318. [Google Scholar] [CrossRef]
- Bykov, V.I. Comments on “Structure of complex catalytic reactions: thermodynamic constraints in kinetic modeling and catalyst evaluation”. Ind. Eng. Chem. Res. 1987, 26, 1943–1944. [Google Scholar] [CrossRef]
- Alberti, P.M.; Uhlmann, A. Stochasticity and Partial Order—Doubly Stochastic Maps and Unitary Mixing (Mathematics and its Applications 9); D. Reidel: London, UK, 1982. [Google Scholar]
- Alberti, P.M.; Crell, B.; Uhlmann, A.; Zylka, C. Order structure (majorization) and irreversible processes. In Vernetzte Wissenschaften—Crosslinks in Natural and Social Sciences; Plath, P.J., Hass, E.-Chr., Eds.; Logos Verlag: Berlin, Germany, 2008; pp. 281–290. [Google Scholar]
- Harremoës, P. A new look on majorization. In Proceedings ISITA 2004, Parma, Italy, 2004; IEEE/SITA: Washington, DC, USA, 2004; pp. 1422–1425. [Google Scholar]
- Harremoës, P.; Tishby, N. The information bottleneck revisited or how to choose a good distortion measure. In Proceedings ISIT 2007, Nice, France, 2007; IEEE Information Theory Society: Washington, DC, USA, 2007; pp. 566–571. [Google Scholar]
- Aczél, J. Lectures on Functional Equations and Their Applications; Academic Press: New York, NY, USA, 1966. [Google Scholar]
Appendix
- , , and are real or complex-conjugate numbers.
- .
- . After substitution of this into (71) and calculations we getThis means that , or , or , or and the solution of this kind can have only the form .
- . After substitution of this into (71) and some calculations if we getThis means that either and the solution is or and the solution is .
- ,
- , , there are two possibilities:
- 1.1)
- . Then , , ;
- 1.2)
- . Then , and here are also two possibilities:
- 1.2.1)
- . Then ;
- 1.2.2)
- . Then ;
- ; ; ;
- , , ,
- .
- Universality: H is a Lyapunov function for Markov chains (22) with a given equilibrium for every possible values of kinetic coefficients .
- H is a trace–form function.where f is a differentiable function of two variables.
- H is additive for composition of independent subsystems. It means that if and then .
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Gorban, A.N.; Gorban, P.A.; Judge, G. Entropy: The Markov Ordering Approach. Entropy 2010, 12, 1145-1193. https://doi.org/10.3390/e12051145
Gorban AN, Gorban PA, Judge G. Entropy: The Markov Ordering Approach. Entropy. 2010; 12(5):1145-1193. https://doi.org/10.3390/e12051145
Chicago/Turabian StyleGorban, Alexander N., Pavel A. Gorban, and George Judge. 2010. "Entropy: The Markov Ordering Approach" Entropy 12, no. 5: 1145-1193. https://doi.org/10.3390/e12051145
APA StyleGorban, A. N., Gorban, P. A., & Judge, G. (2010). Entropy: The Markov Ordering Approach. Entropy, 12(5), 1145-1193. https://doi.org/10.3390/e12051145




