Engineering Model Reduction and Entropy-based Lyapunov Functions in Chemical Reaction Kinetics

Abstract

In this paper, the structural properties of chemical reaction systems obeying the mass action law are investigated and related to the physical and chemical properties of the system. An entropy-based Lyapunov function candidate serves as a tool for proving structural stability, the existence of which is guaranteed by the second law of thermodynamics. The commonly used engineering model reduction methods, the so-called quasi equilibrium and quasi steady state assumption based reductions, together with the variable lumping are formally defined as model transformations acting on the reaction graph. These model reduction transformations are analysed to find conditions when (a) the reduced model remains in the same reaction kinetic system class, (b) the reduced model retains the most important properties of the original one including structural stability. It is shown that both variable lumping and quasi equilibrium based reduction preserve both the reaction kinetic form and the structural stability of reaction kinetic models of closed systems with mass action law kinetics, but this is not always the case for the reduction based on quasi steady state assumption.

1. Introduction

Chemical Reaction Networks (CRNs) form a wide class of positive (or non-negative) systems attracting significant attention not only among chemists but in numerous other fields such as physics, or even pure and applied mathematics where nonlinear dynamical systems are considered [1]. Beside pure chemical reactions, CRNs are often used to model the dynamics of intracellular processes, metabolic or cell signalling pathways [2]. The increasing interest towards reaction networks as a well-defined special class of positive nonlinear systems is clearly shown by recent tutorial and survey papers [3,4,5] in the systems and control community.

The above approach of general systems and control theory can be usefully complemented with a thermodynamic approach taking into account that reaction kinetic systems are special types of process systems [6], where most often stability is well-established in the thermodynamic approach to analyse their dynamical properties (see e.g., [7,8,9]). The thermodynamic approach recognizes, that the reaction kinetic equations originate from dynamic conservation balances constructed for component masses, and utilizes the second law of thermodynamics [10] to associate an entropy-based Lyapunov function candidate to investigate the stability of the system.

The traditional way of describing the structure of a reaction kinetic system for the purpose of analysing its dynamic properties originate from the classical work of Feinberg (see e.g., [11,12]), who introduced the notion of deficiency that is based upon the structure of the so-called reaction graph.

Based on the above interdisciplinary foundations, the aim of this work is to precisely define and analyse model reduction schemes based on the thermodynamic and system theoretical understanding, combined with engineering intuition.

Mathematical models of reaction kinetic systems based on detailed kinetic studies are most often too large for dynamic analysis, model-based control, diagnosis or parameter estimation purposes. Therefore, the need arises to derive more simple versions from these detailed dynamic models that can be handled by the tools and techniques of nonlinear systems and control theory, and possess the same dynamic properties. These detailed dynamic models are simplified by reducing the number of their state (concentration) variables using engineering judgement and operating experience on the relative time constants of the different reaction steps present in the system. The most common model reduction or model simplification steps applied in practice include the removal of variables being in quasi steady state and lumping together variables with similar dynamics.

The model reduction based on quasi steady state approximation is well-studied in biochemical kinetics, because this is the dominant way of obtaining simpler equations. The applicability of quasi steady state approximation was investigated by Tzafiri and Edelman [13] for enzyme kinetics, but they disregard the conservation of reaction kinetic forms of the equations. This type of model reduction was also analysed in signal transduction pathways [14]. It is clear from the studies of quasi steady state approximation that this simplification method changes not only the reaction kinetic form of the equations resulting in reaction rate expressions in rational function form, but also the dynamic properties of the model as well. One of the motivations of the present work is to theoretically analyse the conditions that lead to the distortion of dynamical properties during model reduction.

The model reduction using variable lumping is less popular in practice, but relatively well-defined mathematically. Linear kinetic lumping schemes were defined and analysed by Farkas [15], while general nonlinear lumping in chemical kinetics was investigated by Lee et al. [16]. Although both of the above model reduction methods are quite widespread, none of them has been analysed from a thermodynamic or from a system theoretical viewpoint yet.

The outline of the paper is as follows. First the considered reaction kinetic model classes obeying the mass action law are described, and then their structural properties are briefly discussed. The model reduction using variable lumping, quasi equilibrium and quasi steady state assumptions are presented in the following sections. Finally conclusions are given.

2. Reaction Kinetic Model Classes

In this section, the characteristic structural properties of various reaction kinetic model classes are identified. The structural dynamic properties of reaction kinetic models are determined by two sets of descriptors, the so called General (G) and Reaction (R) descriptors, introduced in this section and used for the analysis of the model reduction schemes in the second part of the paper.

Basic assumptions The original physical and chemical picture underlying the reaction kinetic system class is a closed system under isothermal and isobaric conditions, where chemical components or species ${\mathbf{X}}_i,i=1,...,n$ take part in $r^{\prime }$ chemical reactions. The system is assumed to be perfectly stirred, i.e. concentrated parameter in the simplest case. The concentrations $x_i,i=1,...,n$ of the chemical components form the state vector, the elements of which are positive by nature.

For the sake of simplicity, physico-chemical properties are assumed to be constant. Because the system is assumed to be thermodynamically closed, its total mass (and its volume because of the constant density) is also constant. In addition, the closed system assumption enables to use the principles of the classical and irreversible thermodynamics [10] when analysing the equilibrium state(s) and their stability (see later in Section 3).

Chemical reactions A complex chemical reaction mechanisms is composed of elementary reaction steps in the following form:

$$\sum _{i=1}^n{\alpha }_{ij}{X}_i\to \sum _{i=1}^n{\beta }_{ij}{X}_{i}j=1,...,r^{\prime }$$

(1)

where ${\alpha }_{ij}$ is the so-called stoichiometric coefficient of component $X_i$ in the jth reaction, i.e. the number of colliding $X_i$ molecules, and ${\beta }_{i\ell }$ is the stoichiometric coefficient of the product $X_{\ell }$. Note that the stoichiometric coefficients are always non-negative integers in classical reaction kinetic systems.

The set of components with non-zero stoichiometric coefficients ${\alpha }_{ij}$ or ${\beta }_{ij}$ on a side of a reaction form a so-called complex $C_k,k=1,...,m$ with m being the number of complexes, that is, $C_k={\sum }_{i=1}^n{\alpha }_{ij}{\mathbf{X}}_i$ or $C_k={\sum }_{i=1}^n{\beta }_{ij}{\mathbf{X}}_i$ for some j. The vector ${\nu }^{\left(k\right)}$ consisting of the stoichiometric coefficients ${\alpha }_{ij}$ or ${\beta }_{ij}$ ($i=1,...,n$) characterizes the complex $C_k$. In the general case one may have less complexes than reactions when some of the reactions have the same reactant complex.

The zero complex is a special complex with a zero stoichiometric vector ${\nu }^{\left(k\right)}=0$. This appears in the reaction schemes where one considers either an external source or sink of some components, i.e. elementary reaction steps of the form

$$\varnothing \to \sum _{i=1}^n{\beta }_{ij}{\mathbf{X}}_i\mathrm{or}\sum _{i=1}^n{\alpha }_{ij}{\mathbf{X}}_i\to \varnothing$$

Note that the zero complex is not component specific: there is only a single sink or source term for all components that represent component mass inflows and outflows. In these cases the systems is thermodynamically open, therefore the conservation of the total mass in the describing reaction kinetic system model does not hold.

Descriptors (G) The above number of components, reactions and complexes (n, $r^{\prime }$ and m) form the first group of descriptors of reaction kinetic systems. The stoichiometric coefficient vectors ${\nu }^{\left(k\right)},k=1,...,m$ of the complexes belong also to this group.

2.1. General reaction kinetic differential equations

In the most general case the dynamics of a reaction kinetic system in the concentration (state) space can be described with the following set of ordinary differential equations (ODEs) that originate from the dynamic conservation balance equations [6] constructed for component masses:

$$\frac{d{x}_i}{dt}=F_i\left(x\right)=-x_i{f}_i\left(x\right)+g_i\left(x\right),i=1,...,n$$

(2)

where $f_i$ and $g_i$ are non-negative polynomials, i.e., polynomials with positive coefficients, and $F_i$ is a polynomial right-hand side (RHS) function [1,17].

Although this is the most general class of reaction kinetic systems, it can be shown that a model (2) can always be realized with a reaction kinetic system obeying the mass action law [17]. Note however, that the zero complex may appear in the realization, so the closed system assumption does not always hold in this general case.

2.2. Mass action law (MAL) kinetics

The mass action law is based on the extended collision picture of the elementary reaction steps, where a reaction occurs if the reactants collide. Thus the rate of the above elementary reaction steps can be described as

$${\rho }_j=k_j\prod _{i=1}^n{\left[X_i\right]}^{{\alpha }_{ij}}=k_j\prod _{i=1}^n{x}_i^{{\alpha }_{ij}},j=1,...,r^{\prime }$$

(3)

where $\left[X_i\right]=x_i$ is the concentration of the component $X_i$, and $k_j>0$ is the reaction rate constant of the jth reaction, that is always positive (see [18]).

Algebraic characterization The reaction rates are described using the so-called reaction monomials associated to the complexes in the form

$${\phi }_j\left(x\right)=\prod _{i=1}^n{x}_i^{y_{ij}}$$

(4)

where the elements of the matrix Y are the stoichiometric coefficients of the components $i,i=1,...,n$ in the complexes $j,j=1,...,m$, such that the stoichiometric vector of the jth complex forms the jth column of matrix Y, i.e. ${\left[Y\right]}_{·,j}={\nu }^{\left(j\right)}$.

Note that the stoichiometric coefficients ${\alpha }_{ij}$ of the reactants in the irreversible reaction steps (1) appear in matrix Y , while the reaction monomials are the principal factors in the MAL reaction rate expression (3).

The reaction graph The vertices V of the reaction graph $G=(V,E)$ correspond to the complexes, and the edges E to the reactions. Two complexes $C_k$ and $C_{\ell }$ are connected by a directed edge, if a reaction in the form of

$$C_k\to C_{\ell }$$

(5)

exists. Edge weights can be associated to the edges that are the reaction rate constants $k_{k\ell }>0$, thus the reaction graph is a weighted directed graph.

The Kirchhoff matrix of the reaction graph $A_{\mathbf{k}}\in {\mathbb{R}}^{m\times m}$ uniquely describes the reaction graph with

$${\left[A_{\mathbf{k}}\right]}_{ij}=\left\{\begin{array}{ccc}-\sum _{l=1}^m{k}_{il}& \mathrm{if}\hfill & i=j\hfill \\ k_{ji}& \mathrm{if}\hfill & i\ne j\mathrm{and}\exists C_j\to C_i\hfill \\ 0& \mathrm{otherwise}\hfill \end{array}\right.$$

(6)

The Kirchhoff matrix $A_{\mathbf{k}}$ is a column conservation matrix with non-positive diagonal and non-negative off-diagonal, where the sum of the elements in a column is equal to zero.

The reaction kinetic equations In order to construct the dynamic state equations of a reaction kinetic system, the information on the composition of the complexes that are coded in the stoichiometric matrix Y is needed together with the Kirchhoff matrix $A_{\mathbf{k}}$. The dynamic model that describes the evolution of the reaction kinetic system in its component or state space is given by

$$\frac{dx}{dt}=Y·A_k·\phi \left(x\right)=N·\phi \left(x\right)$$

(7)

It is important to note that the matrices Y and $A_{\mathbf{k}}$ uniquely determine the reaction kinetic system, because the stoichiometric coefficients in Y determine the reaction monomials in $\phi \left(x\right)$.

It should be remarked that the solution of the inverse realization problem, i.e., to find matrices Y and $A_{\mathbf{k}}$ to a given state matrix N in (7) such that they describe a reaction kinetic system, is not at all unique for systems with higher than zero deficiency, see e.g., in [19].

Descriptors (R) The general descriptors (G) determine the matrix Y , therefore only the Kirchhoff matrix $A_{\mathbf{k}}$ constitutes the group of the reaction network descriptors.

One can form a complex combinatorial structure that uniquely describes a reaction kinetic system with MAL kinetics if vertex weights are also associated to the vertices of the reaction graph in such a way that the column of the matrix Y that belongs to the complex $C_j$ is associated to the vertex as its weight. Then any formal transformation applied to the reaction kinetic system can be described as a graph transformation applied to the vertex weighted reaction graph.

2.3. MAL kinetics with reversible reactions

A special class of reaction kinetic systems is the case of reversible reactions, the rate equations of which obey the mass action law (MAL). This case was first investigated by Bykov et al. [20].

The reaction scheme consists of r reversible reactions of the form

$$\sum _{i=1}^n{\alpha }_{ij}{X}_i\rightleftarrows \sum _{i=1}^n{\beta }_{ij}{X}_{i}j=1,...,r$$

(8)

Here we have $2r$ complexes from which there can be identical ones, i.e., $k=1,...,m,m\le 2r$. Note that the reversible (8) can be realized as $r^{\prime }=2r$ irreversible reaction steps in the form of (1).

The mass action law type reaction rates can also be applied to this reversible case by considering the rate of the jth reversible step in the form:

$$W_j\left(x\right)=W_j^{+}\left(x\right)-W_j^{-}\left(x\right)=k_j^{+}\prod _{i=1}^n{x}_i^{{\alpha }_{ij}}-k_j^{-}\prod _{x=1}^n{x}_i^{{\beta }_{ij}}$$

(9)

Here both reaction rate constants $k_j^{+}>0$ and $k_j^{-}>0$ are strictly positive. The terms $W_j^{+}\left(x\right)$ and $W_j^{-}\left(x\right)$ are the reaction rates of the forward and backward directed reaction steps, respectively.

The reaction kinetic equations of a reaction kinetic system with reversible MAL kinetics are in the form

$$\frac{dx}{dt}=\mathcal{N}W\left(x\right)$$

(10)

where $\mathcal{N}\in {\mathbb{R}}^{n\times r}$ is the stoichiometric matrix, and $W\in {\mathbb{R}}^r$ is the reaction rate vector described in Equation (9).

The stoichiometric matrix $\mathcal{N}$ is constructed form the stoichiometric coefficients ${\alpha }_{ij}$ and ${\beta }_{ij}$ in the following way. To each complex $C_k$ a column vector ${\nu }^{\left(k\right)}\in {\mathbb{R}}^n$ is associated in the usual way, as in the stoichiometric matrix Y . Note that precisely two complexes take part in a reaction (see Equation (8)), thus one can form two matrices ${\mathcal{N}}^{\left(\alpha \right)}$ from the complexes of the left hand sides of the r reactions, and ${\mathcal{N}}^{\left(\beta \right)}$ from that of the right hand sides by collecting the column vectors ${\nu }^{\left(k\right)}$ of the corresponding complexes. Thus $\mathcal{N}$ is simply the difference of the two, i.e., $\mathcal{N}={\mathcal{N}}^{\left(\beta \right)}-{\mathcal{N}}^{\left(\alpha \right)}$ where the jth column vector of $\mathcal{N}$, ${\mu }^{\left(j\right)}\in {\mathbb{R}}^n$ contains the difference of the stoichiometric coefficients of the jth reaction.

Note that the parameters that describe a reaction kinetic system with reversible MAL kinetics are given by the stoichiometric matrix $\mathcal{N}$ and the reaction rate coefficients $k^{+}={[k_1^{+}...k_r^{+}]}^T$ and $k^{-}={[k_1^{-}...k_r^{-}]}^T$.

2.4. Examples

Three simple yet characteristic examples are introduced here for illustrating the concepts and algorithms in the later sections.

Linear kinetics Let us consider a simple reaction kinetic system consisting of two reversible first order steps and three components

$$X_1\rightleftarrows X_2\rightleftarrows X_3$$

Figure 1. Reaction graph of the linear kinetics system

Figure 1. Reaction graph of the linear kinetics system

The reaction graph consisting of a single connected component is seen in Figure 1.

The dynamic state equations are as follows.

$$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_1{x}_1+k_2{x}_2\hfill \\ \frac{d{x}_2}{dt}\hfill & =& k_1{x}_1-k_2{x}_2-k_3{x}_2+k_4{x}_3\hfill \\ \frac{d{x}_3}{dt}\hfill & =& k_3{x}_2-k_4{x}_3\hfill \end{array}$$

(11)

From this the representation matrices and vectors are easy to derive

$$\begin{array}{ccc}\phi \left(x\right)=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right],& Y=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],& N=A_{\mathbf{k}}=\left[\begin{array}{ccc}-k_1& k_2& 0\\ k_1& -(k_2+k_3)& k_4\\ 0& k_3& -k_4\end{array}\right]\end{array}$$

(12)

The system consists of only reversible reactions, thus the reversible representation form also exists with $r=2$ and

$$\begin{array}{cc}W\left(x\right)=\left[\begin{array}{c}-k_1{x}_1+k_2{x}_2\\ -k_3{x}_2+k_4{x}_3\end{array}\right],& \mathcal{N}=\left[\begin{array}{cc}-1& 0\\ 1& -1\\ 0& 1\end{array}\right]\end{array}$$

(13)

Descriptors The general descriptors of this example are

$$m=n=3,r^{\prime }=4,r=2$$

(14)

and the reaction descriptor is in Equation (12).  ☐

Michealis–Menten kinetics The Michaelis–Menten kinetics is the simplest example of an enzyme kinetic reaction that is widely used for kinetic and model reduction studies. The overall reaction equation is

$$E+S\rightleftarrows E+P$$

(15)

where E is the enzyme, S is the substrate and P is the product of the reaction. The enzyme acts as a catalyst. The mechanism assumes that the substrate forms a complex $ES$ with the enzyme in a reversible reaction step that can react further to form the product P and giving back the unchanged enzyme E. There is a substrate inhibition step in the scheme, too.

The kinetic scheme consists of three reversible reactions

$$E+S\rightleftarrows ESES\rightleftarrows E+PES+S\rightleftarrows ESS$$

(16)

The reaction kinetic model now consists of the component mass balances for the species S, E, $ES$, $ESS$ and P. These can be written in the following ODE form with $x={\left[x_1,x_2,x_3,x_4,x_5\right]}^T={\left[\left[E\right],\left[S\right],\left[ES\right],\left[ESS\right],\left[P\right]\right]}^T$.

$$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_1^{+}{x}_1{x}_2+k_1^{-}{x}_3-k_2^{-}{x}_1{x}_5+k_2^{+}{x}_3\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\frac{d{x}_2}{dt}\hfill & =& -k_1^{+}{x}_1{x}_2+k_1^{-}{x}_3-k_3^{+}{x}_2{x}_3+k_3^{-}{x}_4\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\frac{d{x}_3}{dt}\hfill & =& +k_1^{+}{x}_1{x}_2-k_1^{-}{x}_3+k_2^{-}{x}_1{x}_5-k_2^{+}{x}_3-\hfill \\ & & -k_3^{+}{x}_2{x}_3+k_3^{-}{x}_4\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\frac{d{x}_4}{dt}\hfill & =& +k_3^{+}{x}_2{x}_3-k_3^{-}{x}_4\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\frac{d{x}_5}{dt}\hfill & =& -k_2^{-}{x}_1{x}_5+k_2^{+}{x}_3\hfill \end{array}$$

(21)

The reaction graph consisting of two connected components is seen in Figure 2.

Figure 2. Reaction graph of the Michaelis-Menten kinetic scheme

Figure 2. Reaction graph of the Michaelis-Menten kinetic scheme

Descriptors The general descriptors of this example are

$$m=n=5,r^{\prime }=6,r=3$$

(22)

The stoichiometric and Kirchhoff matrices are in the form

$$Y=\left[\begin{array}{ccccc}1& 0& 1& 0& 0\\ 1& 0& 0& 1& 0\\ 0& 1& 0& 1& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 1& 0& 0\end{array}\right],A_{\mathbf{k}}=\left[\begin{array}{ccccc}-k_1^{+}& k_1^{-}& 0& 0& 0\\ k_1^{+}& -(k_1^{-}+k_2^{-})& k_2^{-}& 0& 0\\ 0& k_2^{-}& -k_2^{-}& 0& 0\\ 0& 0& 0& -k_3^{+}& k_3^{-}\\ 0& 0& 0& k_3^{+}& -k_3^{-}\end{array}\right]$$

(23)

 ☐

Sequential reactions A reaction network of three consecutive reaction steps are considered, the reaction graph of which is depicted in Figure 3.

Figure 3. Reaction graph of the sequential kinetic scheme

Figure 3. Reaction graph of the sequential kinetic scheme

The kinetic equations are as follows using the concentration vector $x={\left[x_1,x_2,x_3,x_4,a,b\right]}^T={\left[\left[X_1\right],\left[X_2\right],\left[X_3\right],\left[X_4\right],\left[A\right],\left[B\right]\right]}^T$

$$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_1^{+}{x}_1+k_1^{-}{x}_{2}a\hfill \\ \frac{d{x}_2}{dt}\hfill & =& k_1^{+}{x}_1-k_1^{-}{x}_{2}a-k_2^{+}{x}_{2}a+k_2^{-}{x}_{3}b=\frac{da}{dt}\hfill \\ \frac{d{x}_3}{dt}\hfill & =& k_2^{+}{x}_{2}a-k_2^{-}{x}_{3}b-k_3^{+}{x}_{3}b+k_3^{-}{x}_4=\frac{db}{dt}\hfill \\ \frac{d{x}_4}{dt}\hfill & =& k_3^{+}{x}_{3}b-k_3^{-}{x}_4\hfill \end{array}$$

(24)

 ☐

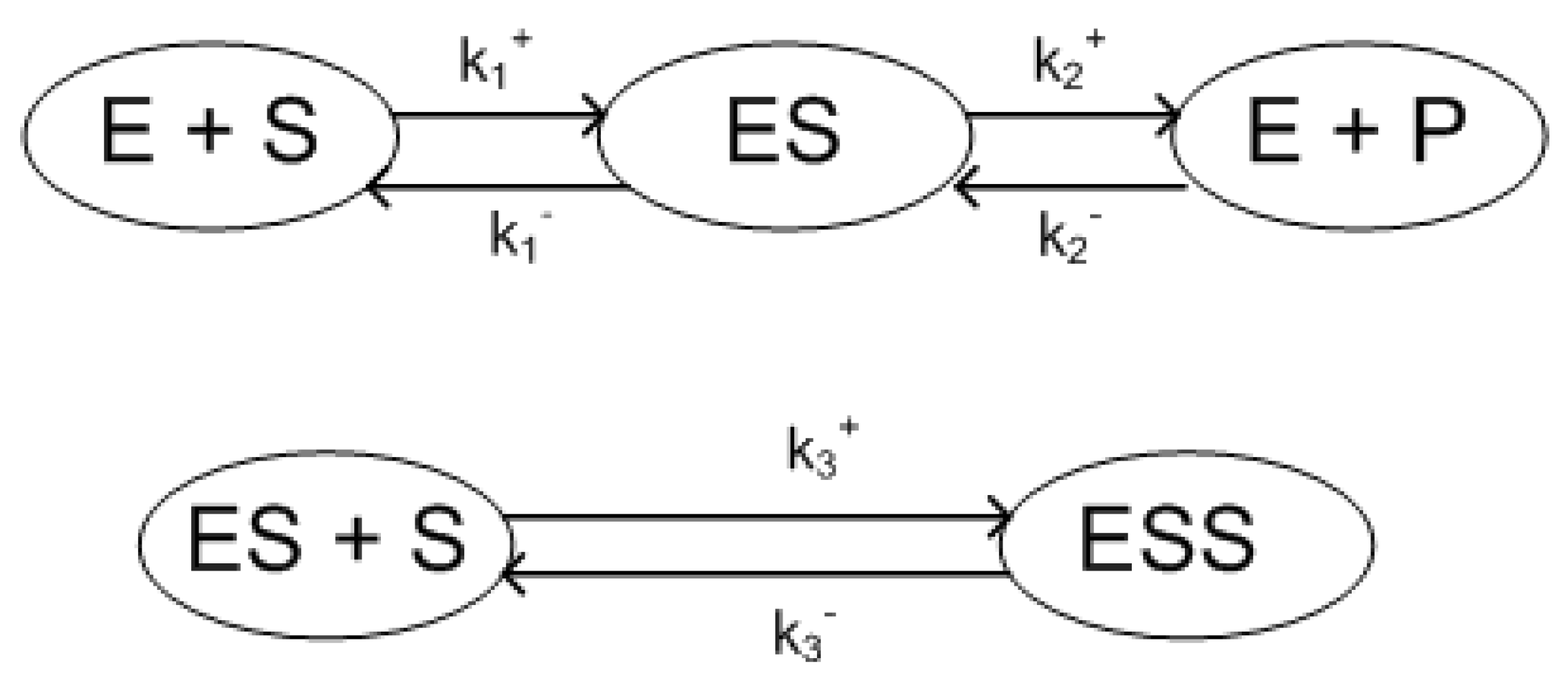
3. Properties of Reaction Kinetic Models

The most important properties and their physical and chemical background is presented in this section, which will be used later when analysing the effect of the engineering model reduction transformations. As is well-known, the reaction rate equations (2) originate from the component mass balances [6] of the underlying lumped process system, while there is no need for any energy balance because of the constant temperature and pressure assumption.

3.1. Basic properties

It can be shown that all MAL reaction kinetic models are non-negative, i.e., they remain in the positive orthant or on its boundary if the initial conditions are non-negative [5]. A reaction network is said to be persistent if it starts in the positive orthant and does not approach the boundary of the orthant, in other words, if provided that every species is present at the start of the reaction, no species will tend to be eliminated in the course of the reaction. Conditions for persistence are given by Angeli et al. [21].

Originally, the theory of reaction network was developed for closed and isothermal systems where the conservation of overall mass holds. Open systems can be described by using the zero complex that describes an infinite source or sink representing the environment. If a zero complex is present in a reaction kinetic model, it implies that the systems is open, and thus the conservation of the overall mass does not hold.

Reversibility is a property of the reaction graph as a directed graph. A reaction network is reversible, if for every reaction $C_j\to C_k$ the system contains its reverse, $C_k\to C_j$. Weak reversibility is a weaker notion, which requires that each complex $C_k$ lies on a directed circle in the reaction graph.

The stability of reaction networks (10) can be examined using the notion of deficiency (see [3,11,18]). It is an integer number that depends on the properties of matrix Y and the structure of the reaction graph. The deficiency $\delta$ is defined as:

$$\delta =m-L-s$$

(25)

where m is the number of complexes and L is the number of connected components (linkage classes) in the reaction graph, while s is the dimension of the stoichiometric sub-space, i.e., $s=rank\left(\mathcal{R}\right)$. The stoichiometric subspace $\mathcal{R}$ is spanned by the so-called reaction vectors ${\epsilon }_k,k=1,...,r^{\prime }$, that are associated to the reaction $C_i\to C_j$ such that

$${\epsilon }_k={\left[Y\right]}_{·,j}-{\left[Y\right]}_{·,i}$$

where ${\left[Y\right]}_{·,j}$ is the jth column of matrix Y.

Note that precisely the reaction vectors, one from a pair of the reversible reaction pairs, appear in matrix $\mathcal{N}$ of Equation (10) in the case of reversible MAL kinetics.

3.2. Conservations and first integrals

Given the dynamic state equations of a reaction kinetic system obeying the mass action law (7), it is easy to show that the solution of it remains on a linear manifold, on the so-called reaction simplex determined by the initial conditions, assuming that all stoichiometric coefficients are non-negative. Each vector $e\in ker\left(N^T\right)$ generates a linear invariant for the system (10) since

$$e^{T}N=0\Rightarrow e^T\frac{dx}{dt}=0\Rightarrow e^{T}x\left(t\right)=const=e^T{x}_0$$

The linear invariants correspond to conservation of the overall mass or that of another species (e.g., atoms of a given type). Therefore, closed reaction kinetic systems have at least one linear invariant describing the conservation of the overall mass. The form of this invariant is determined by the unit of the component concentrations $x_i$. If $x_i$ is in mole per unit mass (or volume), then ${\sum }_{i=1}^n{\gamma }_i{x}_i=M=\mathrm{const}$, where M is the overall mass of the components that take part in the chemical reactions (there may be inert components present) and ${\gamma }_i$ is their molecular weight. If $x_i$ is measured in mole fractions, then M is simply equal to 1, assuming that no inert component is present.

In addition to the linear invariants, there can be other nonlinear algebraic equations that determine the manifold on which the system dynamics evolves. These are nonlinear first integrals of the reaction equations, and can be consequences of model reduction transformations, as we shall see later.

3.3. Stability

With the thermodynamically closed system assumption, the most important property characterizing the qualitative behaviour of the time evolution of the system is its stability. Stability is related to the number of equilibrium (steady state) points, as only systems with a single unique equilibrium point can be globally asymptotically stable.

Unlike many other nonlinear systems that exhibit different stability properties depending on the value of their parameters, the global stability of a reaction kinetic system with zero deficiency does not depend on the value of its parameters, i.e., on the value of its reaction rate constants, but only on its structural descriptors. Therefore, its stability can be called structural stability.

The deficiency zero theorem [11] gives a condition for reaction kinetic systems with zero deficiency to be structurally stable, i.e., globally stable irrespectively of the actual values of its reaction rate constants. If the reaction network with zero deficiency is (weakly) reversible then there exists within each reaction simplex precisely one equilibrium, and that equilibrium is asymptotically stable if the dynamics is restricted to the reaction simplex to which the equilibrium point belongs. Consequently, the original system in the concentration space is globally stable in the positive orthant. Therefore, having zero deficiency is a very strong structural property.

Since reversible reaction kinetic systems with MAL kinetics and with independent reaction vectors fall into the deficiency zero class, they are proved to be structurally stable in agreement with [11].

The entropy-based Lyapunov function The structural stability of reversible reaction networks is proved by using a Lyapunov function of thermodynamic origin in [20]. This is applied to the dynamic state equation of a closed reaction kinetic system with reversible reactions given in the form of (10), where $dimker\left(\mathcal{N}\right)=0$. This means that the reaction vectors, which form the columns of the matrix $\mathcal{N}$, one from each pair of a reversible reaction, are linearly independent, which—together with the closed nature of the system with reversible reactions—guarantees the existence of a unique positive equilibrium point $x^{*}$ in the concentration (state) space.

The structural stability theorem states that the equilibrium point $x^{*}$ of such a system is globally stable with the Lyapunov function

$$B_{x^{*}}\left(x\right)=\sum _{i=1}^n{x}_i\left(ln\left(\frac{x_i}{x_i^{*}}\right)-1\right)+x_i^{*}=\sum _{i=1}^n{x}_i\left(ln{x}_i-ln{x}_i^{*}\right)-\left(x_i-x_i^{*}\right)$$

(26)

The basic idea behind the above function is to use the second law of thermodynamics [8] to derive a Lyapunov function of the form

$$\mathcal{L}={\overline{Z}}^T{w}^{*}-\overline{S}$$

(27)

where $\overline{Z}$ is the vector of conserved extensive variables (internal energy, volume, and component mass of chemical constituents) expressed as a deviation from the reference state $\overline{Z}=Z-Z^{*}$, $w^{*}=\frac{\partial S}{\partial Z}{|}_{Z=Z^{*}}$ is the vector of intensive driving force variables (temperature, pressure and chemical potential) evaluated at the reference state $Z^{*}$, and $\overline{S}$ is the entropy deviation from the reference state. The reference state is usually chosen as a thermodynamic equilibrium state.

In the case of isothermal, isobaric and closed reaction kinetic systems only the masses of components and their chemical potential appear in Z and w, respectively, and the elements of these vectors can be expressed as functions of the component concentrations $x_i$ as $Z_i=M{x}_i$ with M being the total constant mass of the system, and $w_i=-C_{w}ln{x}_i$ with the constant $C_w=RT$ where T is the constant temperature and R is the universal gas constant. Note that one has to assume perfect mixing and ideal mixtures for such a simple expression for the chemical potentials [10].

The entropy of the system can then be given as

$$S=-C_w\sum _{i=1}^n{x}_{i}ln{x}_i=-C_w\sum _{i=1}^n{x}_i{\mu }_i$$

(28)

where ${\mu }_i=ln{x}_i$. With the above expression, the thermodynamically motivated Lyapunov function (27) becomes

$$\mathcal{L}\left(x\right)=-C_w\left(\sum _{i=1}^n(x_i-x_i^{*}){\mu }_i^{*}-(x_i{\mu }_i-x_i^{*}{\mu }_i^{*})\right)=C_w\left(\sum _{i=1}^n{x}_i(ln{x}_i-ln{x}_i^{*})\right)$$

(29)

This shows that $\mathcal{L}$ contains the driving force of the reactions $(ln{x}_i-ln{x}_i^{*})$ for each component, which also appears in the Lyapunov function (26) of the structural stability theorem.

Note that the above Lyapunov functions can be seen as thermodynamic analogues of relative entropies or divergences defined in the theory of stochastic processes (see [22]).

In order to show the identity of the two Lyapunov functions $\mathcal{L}\left(x\right)$ and $B_{x^{*}}\left(x\right)$, one can use the fact that in closed systems ${\sum }_{i=1}^n{x}_i={\sum }_{i=1}^n{x}_i^{*}=1=\mathrm{const}$ if $x_i$ is measured in mole fractions. With this, Equation (26) can be transformed to the form

$$B_{x^{*}}\left(x\right)=\sum _{i=1}^n{x}_i\left(ln{x}_i-ln{x}_i^{*}\right)-\left(\sum _{i=1}^n{x}_i-\sum _{i=1}^n{x}_i^{*}\right)=\sum _{i=1}^n{x}_i\left(ln{x}_i-ln{x}_i^{*}\right)$$

The proof of the structural stability theorem [20] sheds light to the thermodynamic background of the Lyapunov function (26). Here we assume the so called detailed balance condition [23], i.e., reversible reactions with independent reaction vectors, and we first define the auxiliary vector $\mu$ as

$$\mu \left(x\right)={\left[ln\left(x_1\right),...,ln\left(x_1\right)\right]}^T$$

that is the chemical potential vector (up to a multiplicative constant), and denote the jth column of the stoichiometric matrices ${\mathcal{N}}^{\left(\alpha \right)}$ by ${\alpha }^{\left(j\right)}$ and ${\mathcal{N}}^{\left(\beta \right)}$ by ${\beta }^{\left(j\right)}$, respectively. The relations

$$\begin{array}{ccc}{\mu }^T{\beta }^{\left(j\right)}\hfill & =& {\beta }_1^{\left(j\right)}ln\left(x_1\right)+...+{\beta }_n^{\left(j\right)}ln\left(x_n\right)=ln\left(x_1^{{\beta }_1^{\left(j\right)}}...x_n^{{\beta }_n^{\left(j\right)}}\right)=ln\left(\frac{1}{k_j^{-}}{W}_j^{-}\left(x\right)\right)\hfill \\ {\mu }^T{\alpha }^{\left(j\right)}\hfill & =& ln\left(\frac{1}{k_j^{+}}{W}_j^{+}\left(x\right)\right)\hfill \end{array}$$

(30)

are used to compute the time-derivative of $B_{x^{*}}$ as

$$\begin{array}{ccc}\frac{d{B}_{x^{*}}}{dt}\hfill & =& \frac{\partial B_{x^{*}}}{\partial x}\mathcal{N}W\left(x\right)={(\mu -{\mu }^{*})}^T\sum _{j=1}^r({\beta }^{\left(j\right)}-{\alpha }^{\left(j\right)})(W_j^{+}\left(x\right)-W_j^{-}\left(x\right))\hfill \end{array}$$

(31)

$$\begin{array}{ccc}& =& \sum _{j=1}^r\left({\mu }^T{\beta }^{\left(j\right)}-{\mu }^T{\alpha }^{\left(j\right)}-{\mu }^{*T}{\beta }^{\left(j\right)}+{\mu }^{*T}{\alpha }^{\left(j\right)}\right)(W_j^{+}\left(x\right)-W_j^{-}\left(x\right))\hfill \end{array}$$

(32)

$$\begin{array}{ccc}& =& \sum _{j=1}^{r}ln\left(\frac{W_j^{-}}{W_j^{+}}\right)(W_j^{+}\left(x\right)-W_j^{-}\left(x\right))\le 0\hfill \end{array}$$

(33)

3.4. Properties of the example kinetic systems

Linear kinetics This simple reaction kinetic system is closed, it contains reversible reactions in a single linkage class. Its deficiency is zero, and it has a single linear invariant $M=x_1+x_2+x_3$ corresponding to the conservation of the overall mass in the system.

Therefore, the system is structurally stable because of the deficiency zero theorem.

Michealis–Menten kinetics This kinetic system is a closed, reversible system, and its deficiency is zero.

Linear invariants It is easy to see from the physical interpretation that there exists linear conservation invariants for the “E” and the “S” type groups as follows:

$${\left[E\right]}^{tot}=\left[E\right]+\left[ES\right]+\left[ESS\right]=x_1+x_3+x_4$$

(34)

$${\left[S\right]}^{tot}=\left[S\right]+\left[ES\right]+2\left[ESS\right]+\left[P\right]=x_2+x_3+2x_4+x_5$$

(35)

where ${\left[E\right]}^{tot}$ and ${\left[S\right]}^{tot}$ are constants, besides the linear invariant for the overall mass conservation.

Structural stability The system is structurally stable because of the deficiency zero theorem.

4. Model Reduction Using Variable Lumping

Model reduction aims at finding a “reduced” or “more simple” model to a dynamic system that describes its dynamical behaviour (relatively) well but with a smaller number of dynamic variables and/or equations. One possible and quite widespread way of reducing the number of variables is to lump them together, i.e., to consider only an aggregate “averaged” variable instead of at least two original ones in the reduced dynamic model.

Variable lumping in the above sense is widely used in reducing reaction kinetic and other process models. Farkas [15] has analysed kinetic lumping schemes consisting of linear projective transformation of the original concentrations, and gave conditions for the transformation and its pseudo-inverse that preserve the reaction kinetic form of the reduced model. The general nonlinear exact and approximate lumping of reaction kinetic models has been analysed by Li and co-workers [16], who also treated the model reduction as a nonlinear projective model transformation.

For cascade type lumped process models Leitold et al. [24] developed and analysed the variable lumping transformation. The transformation is represented as context sensitive graph transformation acting on the structure graphs of the dynamic process models. In the paper [24] it was shown that the variable lumping transformation preserves the structural controllability and observability of process models, but nothing was reported about the stability of the reduced model.

Following this line, the variable lumping transformation is treated in this paper as a graph transformation acting on the vertex-weighted reaction graph by identifying its effect on the describing matrices Y and $A_{\mathbf{k}}$. This allows us to detect if this transformation preserves the structural stability of the reduced reaction kinetic system model.

4.1. Mathematical and physical characterization

The engineering two-variable version of variable lumping can be applied when the dynamic response of two concentration variables ($x_i$ and $x_j$) are of the same character. Then both of them can be substituted by a single one ${\overline{x}}_i$ such that

$$x_i\left(t\right)={\chi }_i{\overline{x}}_i\left(t\right),x_j\left(t\right)={\chi }_j{\overline{x}}_i\left(t\right)$$

(36)

where both ${\chi }_i$ and ${\chi }_j$ are constants. The above relations imply that $x_i\left(t\right)=\mathrm{const}·x_j\left(t\right)$.

A kinetic lumping scheme in the sense of [15] arises when ${\chi }_i={\chi }_j=\frac{1}{2}$. Assume that we perform a permutation of the concentration variables such that the two variables to be lumped are $x_n$ and $x_{n-1}$ , i.e., they are the last two ones. The so-called lumping matrix forms the reduced set of concentration variables $\overline{x}=\mathcal{M}x$, with $dim\overline{x}=dimx-1$. Then the lumping matrix and its generalized inverse are of the form

$$\mathcal{M}=\left[\begin{array}{ccc}{\varnothing }^T& 1& 1\\ I& 0& 0\end{array}\right],\overline{\mathcal{M}}=\left[\begin{array}{cc}\varnothing & I\\ \frac{1}{2}& 0\\ \frac{1}{2}& 0\end{array}\right]$$

(37)

where I is the $(n-2)\times (n-2)$ unit matrix and $\varnothing$ is a $(n-2)$-dimensional zero column vector.

It is important to note that the generalized inverse of a lumping matrix is not unique, the one we selected in (37) reflects the assumption $x_i\left(t\right)=x_j\left(t\right)$ that is behind the lumping of the two variables.

The lumped new concentration variable ${\overline{x}}_{n-1}$ and the RHS of its kinetic equation can be computed as

$${\overline{x}}_{n-1}=x_{n-1}+x_n,\frac{d{\overline{x}}_{n-1}}{dt}=\frac{d{x}_{n-1}}{dt}+\frac{d{x}_n}{dt}=F_{n-1}\left(x\right)+F_n\left(x\right)$$

(38)

while

$$x_n=\frac{1}{2}{\overline{x}}_{n-1},x_{n-1}=\frac{1}{2}{\overline{x}}_{n-1}$$

(39)

With these equations the model reduction transformation consists of three consecutive steps.

L1

Substitute ${\overline{x}}_{n-1}$ for $x_n$ and $x_{n-1}$ into the RHS of the kinetic equations whenever they appear using Equation (39).

L2

Form the RHS of the kinetic equation of the lumped variable ${\overline{x}}_{n-1}$ as

$${\overline{F}}_{n-1}\left(\overline{x}\right)=F_{n-1}\left(\overline{x}\right)+F_n\left(\overline{x}\right)$$

from Equation (38).

L3

Replace the last two equations, the nth and $(n-1)$th ones, of the original model with the newly formed equation

$$\frac{d{\overline{x}}_{n-1}}{dt}={\overline{F}}_{n-1}\left(\overline{x}\right)$$

The primary effect of variable lumping is that one component disappears from the equations, i.e., $\overline{n}=n-1$.

4.2. Effect on the model properties

The effect of the three transformation steps L1, L2 and L3 is analysed both on the Y and $A_{\mathbf{k}}$ matrices.

L1

By substituting the lumped variable into the two original ones, each complex that contains them will change. Formally, the nth row ${\left[Y\right]}_{n,·}$ is added to the $(n-1)$th one, and the nth is deleted, while the number of columns in Y does not change.

L2,L3

These steps do not influence the structure of the matrices Y and $A_{\mathbf{k}}$ but implement the changes in the reaction equations caused by step L1. Note that the reaction rate constants in $A_{\mathbf{k}}$ will change.

In degenerate special cases it may happen, that some columns of Y become identical, i.e., some complexes may become identical. Then the number of complexes also decreases, and the dimension of the stoichiometric space s may decrease, too. This case requires that the two vertices corresponding to these identical complexes be condensed (united) in the reaction graph. As the new vertex inherits all directed edges from the ones it is condensed from, the reversibility of the reaction graph remains unchanged.

Effect on structural stability If no condensation of the reaction complexes occurs, then neither the structure of the reaction graph nor the dimension of the stoichiometric space change. These facts imply that the structural stability of the reaction kinetic system remains unchanged during this model reduction transformation.

The condensation of some of the vertices in the reaction graph does not change its reversibility, but may change its deficiency. Therefore, the conservation of structural stability can only be guaranteed in the reversible case.

4.3. Examples

Variable lumping is performed on both of the examples introduced in subSection 2.4, and the properties of the reduced model are investigated.

Linear kinetics Let us lump components $X_2$ and $X_3$. This implies

$${\overline{x}}_2=x_2+x_3,x_2=\frac{1}{2}{\overline{x}}_2,x_3=\frac{1}{2}{\overline{x}}_2$$

Substituting this into the original model (11) we obtain

$$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_1{x}_1+\frac{1}{2}{k}_2{\overline{x}}_2\hfill \\ \frac{d{\overline{x}}_2}{dt}\hfill & =& k_1{x}_1-\frac{1}{2}{k}_2{\overline{x}}_2\hfill \end{array}$$

(40)

The reduced reaction graph is in the form

$$X_1\leftrightarrows {\overline{X}}_2$$

The structural descriptors change to $\overline{n}=n-1=2$, $\overline{m}=m-1=2$ and ${\overline{r}}^{\prime }=r^{\prime }-2=2$. The representation matrices and vectors are also easy to derive

$$\begin{array}{ccc}\phi \left(x\right)=\left[\begin{array}{c}{x}_2\\ x_3\end{array}\right],& Y=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],& N=A_{\mathbf{k}}=\left[\begin{array}{cc}-k_1& \frac{1}{2}{k}_2\\ k_1& -\frac{1}{2}{k}_2\end{array}\right]\end{array}$$

(41)

The deficiency of the reduced model with reversible reactions is zero, thus it remains structurally stable.

Michaelis–Menten kinetics The two intermediate components $ES$ and $ESS$ with similar dynamics are lumped to form the lumped pseudo-component $E_S$ with concentration ${\overline{x}}_3=\left[E_S\right]$. Then the equations needed for the transformation are

$${\overline{x}}_3=x_3+x_4,x_3=\frac{1}{2}{\overline{x}}_3,x_4=\frac{1}{2}{\overline{x}}_3$$

and the concentration variable $x_4$ is left out from the model.

The reduced kinetic equations are

$$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_1^{+}{x}_1{x}_2+\frac{1}{2}{k}_1^{-}{\overline{x}}_3+\frac{1}{2}{k}_2^{+}{\overline{x}}_3-k_2^{-}{x}_1{x}_5\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\frac{d{x}_2}{dt}\hfill & =& -k_1^{+}{x}_1{x}_2+\frac{1}{2}{k}_1^{-}{\overline{x}}_3+\frac{1}{2}{k}_3^{-}{\overline{x}}_3-\frac{1}{2}{k}_3^{+}{x}_2{\overline{x}}_3\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\frac{d{\overline{x}}_3}{dt}\hfill & =& k_1^{+}{x}_1{x}_2-\frac{1}{2}{k}_1^{-}{\overline{x}}_3-\frac{1}{2}{k}_2^{+}{\overline{x}}_3+k_2^{-}{x}_1{x}_5\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\frac{d{x}_5}{dt}\hfill & =& \frac{1}{2}{k}_2^{+}{\overline{x}}_3-k_2^{-}{x}_1{x}_5\hfill \end{array}$$

(45)

It is important to note that the number of complexes has also been reduced by one, as both $ES$ and $ESS$ formed complexes that were replaced by a new complex formed by $E_S$. Thus the new stoichiometric matrix Y is in the form

$$Y=\left[\begin{array}{cccc}1& 0& 0& 0\\ 1& 0& 0& 1\\ 0& 1& 0& 1\\ 0& 0& 1& 0\end{array}\right]$$

and the reaction graph is depicted in Figure 4

Figure 4. Reaction graph of the lumped Michaelis-Menten scheme

Figure 4. Reaction graph of the lumped Michaelis-Menten scheme

Deficiency and structural stability Because of the condensation of two complexes, the number of complexes is now $\overline{m}=4$, and the number of linkage classes is also reduced by one, i.e., $\overline{L}=1$. The dimension of the stoichiometric space remains $s=3$, therefore the reduced model is of zero deficiency, and therefore it is structurally stable.

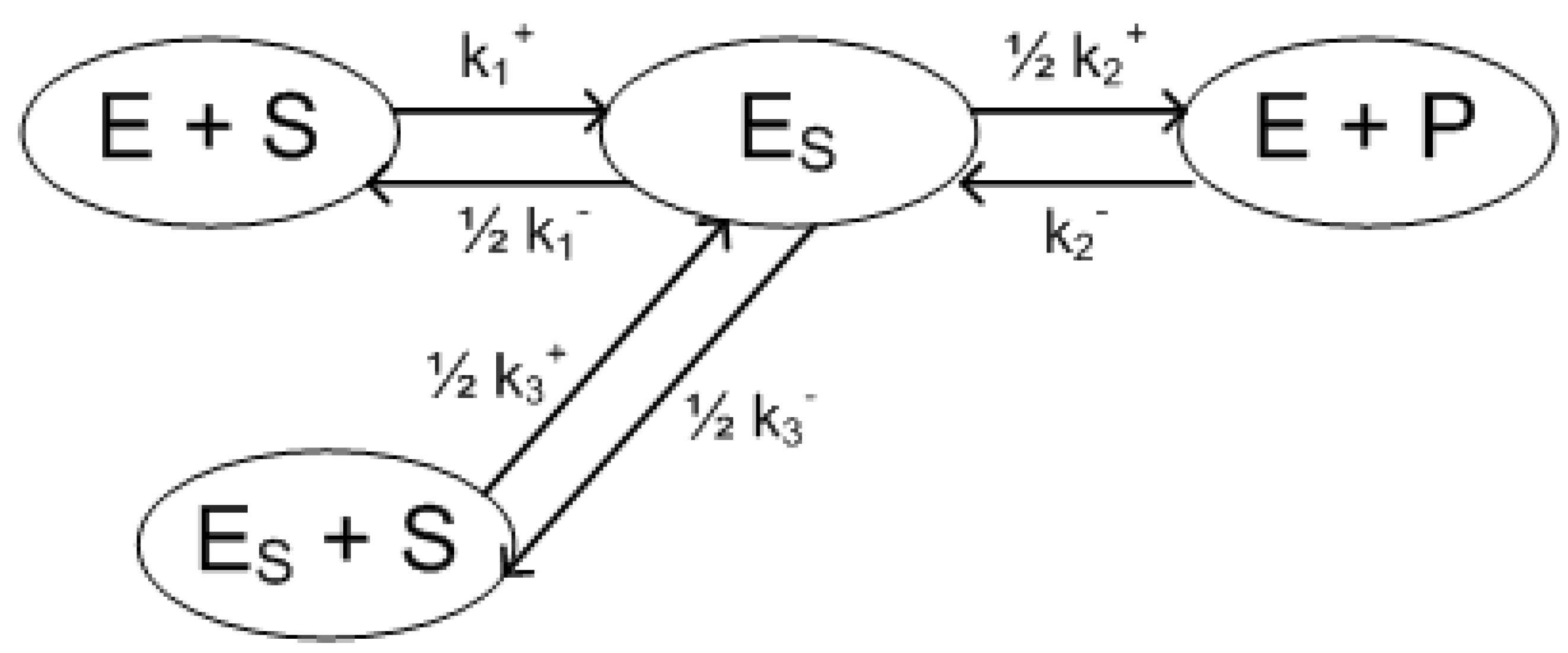
5. Model Reduction Using Quasi Equilibrium and Quasi Steady State Assumptions

For both the quasi equilibrium and quasi steady state assumptions, the underlying physical picture determines the conditions under which it can be applied. Similar to the case of variable lumping, this is translated into a mathematical description in the form of a model reduction transformation that is then formally applied to the reaction kinetic model.

5.1. Mathematical and physical characterization

The model reduction transformations using quasi equilibrium and quasi steady state assumptions are closely related and imply each other in certain cases. In both of the cases one adds polynomial type algebraic equation(s) to the original differential ones, and possibly omits a differential equation from the original model in case of the quasi steady state assumption. The additional algebraic equations can be considered as nonlinear first integrals that restrict the dynamic evolution of the system in the state (concentration) space to a lower dimensional manifold determined by these first integrals.

It is important to note, however, that the reaction kinetic form may be, and in most of the cases will be, destroyed when one simply eliminates one of the concentration variables by expressing it from the algebraic equations, and substitutes the resulting expression into the differential ones. Therefore, this substitution will be circumvented here by choosing carefully the model reduction transformation.

Quasi equilibrium Here one assumes that there exists a fast (compared to the others) reversible reaction step consisting of the jth and $\ell$th irreversible reaction step for which

$$k_j\prod _{i=1}^n{x}_j^{{\alpha }_{ij}}=k_j{\phi }_j\left(x\right)=k_{\ell }{\phi }_{\ell }\left(x\right)=k_{\ell }\prod _{i=1}^n{x}_{\ell }^{{\alpha }_{i\ell }}$$

(46)

The condition when this assumption can be applied is that both reaction rate coefficients $k_j$ and $k_{\ell }$ are at least several orders of magnitude larger than all the other ones such that the reaction steps in both directions can take place much faster than the other reaction steps.

Formally one adds the defining Equation (46) to the kinetic equations that constrains its dynamics to a manifold determined by this equation. Equation (46) can be considered as a additional nonlinear first integral of the system. However, it is important to note that the substitution of $k_{\ell }{\phi }_{\ell }\left(x\right)$ into the term $k_j{\phi }_j\left(x\right)$ may result in a negative cross-effect if the complex behind $k_j{\phi }_j\left(x\right)$ appears in other reaction(s) but the one in quasi equilibrium, too. This implies that the reduced model will loose its reaction kinetic form.

In order to preserve the reaction kinetic form of the reduced model, the reduction transformation is performed in an unusual way by introducing a new variable that forms a complex itself instead of the two complexes that appear in the reaction in quasi equilibrium. Therefore, the following transformation sub-steps are to be carried out:

E1

introducing a new pseudo concentration variable $x_{j\ell }$ in the form of

$$x_{j\ell }=k_{\ell }{\phi }_{\ell }\left(x\right)=k_j{\phi }_j\left(x\right)$$

(47)

E2

substituting the new concentration variable into the terms $k_{\ell }{\phi }_{\ell }\left(x\right)$ and $k_j{\phi }_j\left(x\right)$ whenever they appear,

E3

condensing (uniting) the complexes $C_{\ell }$ and $C_j$ into a new complex $C_{j\ell }$ corresponding to the new variable $x_{j\ell }$ in the reaction graph, and forming a new pseudo component mass balance, i.e. a kinetic equation for $x_{j\ell }$ by adding together all the RHS functions $F_k\left(\overline{x}\right)$ where any of the terms $k_{\ell }{\phi }_{\ell }\left(x\right)$ and $k_j{\phi }_j\left(x\right)$ appear, and taking its negative.

It is to be noted that the defining Equation (47) can be interpreted as introducing the new pseudo variable as

$$x_{j\ell }={\left(k_{\ell }{\phi }_{\ell }\left(x\right)·k_j{\phi }_j\left(x\right)\right)}^{1/2}$$

This, together with the equality (46) leads to the defining equation, but shows a rationale for the complex vertex condensation in the reaction graph performed in step E3 above.

The primary effect of this reduction transformation is that two complexes and one reaction-pair disappear from the reaction kinetic system, and one complex and one component appear. The descriptors will change accordingly, thus

$$\overline{m}=m-1,\overline{n}=n+1,{\overline{r}}^{\prime }=r^{\prime }-2$$

(48)

It will be seen later in the examples, however, that the number of components may even decrease if a component forms a complex itself and takes part only in the reaction that is in quasi equilibrium.

Quasi equilibrium example on the sequential kinetic scheme The above reduction transformation is applied to the sequential kinetic scheme with kinetic equations (24) and reaction graph in Figure 3 assuming quasi steady state for the reaction $X_2+A\leftrightarrows X_3+B$. The equilibrium assumption implies to introduce the pseudo component concentration

$$x_{23}=k_2^{+}{x}_{2}a=k_2^{-}{x}_{3}b$$

The reduced kinetic equations are

$$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_1^{+}{x}_1+\frac{k_1^{-}}{k_2^{+}}{x}_{23}\hfill \\ \frac{d{x}_4}{dt}\hfill & =& \frac{k_3^{+}}{k_2^{-}}{x}_{23}-k_3^{-}{x}_4\hfill \\ \frac{d{x}_{23}}{dt}\hfill & =& k_1^{+}{x}_1-\frac{k_1^{-}}{k_2^{+}}{x}_{23}+k_3^{-}{x}_4-\frac{k_3^{+}}{k_2^{-}}{x}_{23}\hfill \end{array}$$

(49)

Here 4 original components, $X_2$, $X_2$, A and B disappear, and one new, $X_{23}$ appears. Thus there are only 3 complexes and 3 components in the reduced model that are connected by 4 reactions. The resulting reaction graph is seen in Figure 5.

Figure 5. Reaction graph of the reduced sequential kinetic scheme

Figure 5. Reaction graph of the reduced sequential kinetic scheme

☐

As a side effect of a quasi equilibrium assumption, the component(s) that only appear in the complexes $C_j$ or $C_{\ell }$ will be in quasi steady state, because their component mass balance will have the form

$$\frac{d{x}_i}{dt}=k_j{\phi }_j\left(x\right)-k_{\ell }{\phi }_{\ell }\left(x\right)=0$$

(50)

that implies $x_i=\mathrm{const}$. In this case the number of components will decrease, too, giving rise to $\overline{n}\le n$.

Quasi steady state This is the most “popular” engineering model reduction assumption [6], when the concentration of a certain component in the model, say the jth one is assumed to be constant, formally

$$\frac{d{x}_j}{dt}=0,x_j=x_j^{*}=\mathrm{const}$$

(51)

The physical picture behind this assumption is that there exists a reservoir of infinite capacity attached to the system that can enforce the concentration to be constant; in other words, the component $X_j$ is “in great excess”. This normally contradicts to the conservation of the overall mass in the system, thus to the closed system assumption.

The model reduction transformation consists of two consecutive formal steps:

SS1

eliminating the component $X_j$ by setting its concentration $x_j$ to a constant $x_j^{*}$ whenever it appears,

SS2

substituting the resulting algebraic equation from Equation (51), e.g., $F_j\left(x\right)=0$ into the differential ones.

Without the second step SS2, the resulting reduced system would have an additional nonlinear first integral described by the algebraic equation

$$F_j\left(x\right)=0=\sum _{j=1}^m{\left[Y\right]}_{ij}\sum _{\ell }^m{\left[A_{\mathbf{k}}\right]}_{j\ell }{\phi }_{\ell }\left(x\right)$$

(52)

and the system would evolve on a manifold determined by this first integral.

The usual way of substituting the above algebraic equation to the differential ones is to express one concentration from it, and substitute the resulting expression—a fraction of two polynomials in the general case—into the expressed concentration. This way, the number of components can be further reduced, but on the price of obtaining a differential equation with non-polynomial right-hand sides (e.g., see [13,14]). This means that the reduced model will no longer belong to the reaction kinetic class.

Another possible way proposed here is to express a whole reaction monomial $k_{\ell *}{\phi }_{\ell *}\left(x\right)$ from Equation (52) and substitute this expression, a polynomial, whenever it appears in the equations. This way the number of components will not decrease further but the polynomial form of the right-hand sides remain. Unfortunately, it can happen that the reduced model will contain negative cross-effects as a results of this substitution, so it will not be reaction kinetic any more. On the price of an increased number of complexes, however, one can transform this polynomial equation into a reaction kinetic form [25] using a simple state-dependent time-rescaling [26].

The primary effect of this model reduction transformation is that one component disappears from the equations, i.e., $\overline{n}=n-1$.

5.2. Effect on the model properties

The effect of the two model reduction transformation is related, and they may imply each other in special cases.

Quasi equilibrium Both complexes $C_j$ and $C_{\ell }$ and one reaction pair $C_j\leftrightarrows C_{\ell }$ (say the $\kappa$th reaction pair) disappear from the reaction network, and a new complex $C_{j\ell }$ appears, which is in itself a new component $X_{j\ell }$. Therefore

• the columns ${\left[Y\right]}_{·,j}$ and ${\left[Y\right]}_{·,\ell }$ are deleted from matrix Y, and a new column ${\left[Y\right]}_{·,j\ell }$ is inserted being a unit column vector,
• the vertices $C_j$ and $C_{\ell }$ in the reaction graph are condensed (united), such that the united remaining vertex $C_{j\ell }$ inherits every incoming and outgoing directed edges (all reactions) that were adjacent to $C_j$ and $C_{\ell }$. Formally this can be performed by adding the jth row to the $\ell$th one in the Kirchhoff matrix $A_{\mathbf{k}}$, and the jth column to the $\ell$th one (except for the diagonal entries), and then delete the jth row and column (and recompute ${\left[A_{\mathbf{k}}\right]}_{\ell \ell }$).

A special “degenerate” case arises if any of the components, say the ith, appear only in the reaction pair in quasi equilibrium, because then this component will be in quasi-steady state, and its row ${\left[Y\right]}_{i,·}$ is deleted from matrix Y, too.

Because of the above vertex condensation in the reaction graph, the reversibility of the reaction network does not change, while the number of connected components L either remains unchanged or decreases by one. The dimension of the stoichiometric space s may also decrease by one in the non-degenerate case, because precisely one reversible reaction, a pair of reaction vectors (${\epsilon }_{\kappa }$, $-{\epsilon }_{\kappa }$) is deleted, where $\kappa$ identifies the the reaction pair $C_j\leftrightarrows C_{\ell }$. As the number of complexes m is also decreased by one, the deficiency of the reaction kinetic system may change.

Quasi steady state The effect of the two transformation steps SS1 and SS2 is analysed on both the Y and $A_{\mathbf{k}}$ matrices.

SS1

The row ${\left[Y\right]}_{k,·}$ belonging to the component in quasi steady state is deleted from the matrix Y.

SS2

The substitution of one reaction monomial $k_{\ell *}{\phi }_{\ell *}\left(x\right)$ into the RHSs using Equation (52) decreases the number of complexes, which implies to delete the column ${\left[Y\right]}_{·,\ell *}$ from the matrix Y, to omit the vertex belonging to $C_{\ell *}$ from the reaction graph, and to introduce directed edges into the graph.

Step SS1 may result in identical transformed columns, ${\left[Y\right]}_{·,j}$ and ${\left[Y\right]}_{·,i}$, i.e., identical transformed complexes ${\overline{C}}_j$ and ${\overline{C}}_i$ in degenerate special cases. In addition, the zero complex may also appear in the transformed matrix $\overline{Y}$, when the deleted component formed a complex itself. In the general non-degenerate cases, however, neither the number of complexes m nor the reaction vectors change, thus the dimension of the stoichiometric space s remains unchanged as a result of this step.

Step SS2 results in a decrease of the number of complexes and in a drastic change of the reaction graph that may destroy its reversibility.

Effect on structural stability The effect of the quasi equilibrium model reduction transformation on the basic properties shows that it preserves structural stability in the general non-degenerate cases.

This is, unfortunately, not the case for the quasi steady state transformation when we cannot guarantee that structural stability remains unchanged.

5.3. Examples

Model reduction is performed on both of the examples introduced in subSection 2.4 using a quasi equilibrium and a quasi steady state assumption.

Linear kinetics Let us assume first quasi equilibrium for the reaction $X_1\leftrightarrows X_2$. This implies

$$k_1{x}_1=k_2{x}_2$$

Substituting this to the original model (11) we obtain

$$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& 0,x_1=\mathrm{const}\hfill \\ \frac{d{x}_2}{dt}\hfill & =& -k_3{x}_2+k_4{x}_3\hfill \\ \frac{d{x}_3}{dt}\hfill & =& k_3{x}_2-k_4{x}_3\hfill \end{array}$$

(53)

It is important to observe that the quasi equilibrium assumption implies the quasi steady state for the component $X_1$, because it only participates in the reaction for which the equilibrium assumption holds.

The reduced reaction graph is in the form

$$X_2\leftrightarrows X_3$$

The structural descriptors change to $\overline{n}=n-1=2$, $\overline{m}=m-1=2$ and ${\overline{r}}^{\prime }=r^{\prime }-2=2$ The representation matrices and vectors are also easy to derive

$$\begin{array}{ccc}\phi \left(x\right)=\left[\begin{array}{c}{x}_2\\ x_3\end{array}\right],& Y=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],& N=A_{\mathbf{k}}=\left[\begin{array}{cc}-k_3& k_4\\ k_3& -k_4\end{array}\right]\end{array}$$

(54)

The resulting reduced model preserves its structural stability.

Michaelis–Menten kinetics First two quasi equilibrium assumptions are investigated.

• Quasi equilibrium for the reaction $E+S\leftrightarrows ES$
  The equation to be used is $k_1^{+}{x}_1{x}_2=k_1^{-}{x}_3$, the complex $(E+S)$ is eliminated. The resulting reduced model is in a reaction kinetic form

  $$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_2^{-}{x}_1{x}_5+k_2^{+}{x}_3\hfill \end{array}$$

  (55)

  $$\begin{array}{ccc}\frac{d{x}_2}{dt}\hfill & =& -k_3^{+}{x}_3{x}_2+k_3^{-}{x}_4\hfill \end{array}$$

  (56)

  $$\begin{array}{ccc}\frac{d{x}_3}{dt}\hfill & =& k_2^{-}{x}_1{x}_5-k_2^{+}{x}_3-k_3^{+}{x}_3{x}_2+k_3^{-}{x}_4\hfill \end{array}$$

  (57)

  $$\begin{array}{ccc}\frac{d{x}_4}{dt}\hfill & =& k_3^{+}{x}_3{x}_2-k_3^{-}{x}_4\hfill \end{array}$$

  (58)

  $$\begin{array}{ccc}\frac{d{x}_5}{dt}\hfill & =& -k_2^{-}{x}_1{x}_5+k_2^{+}{x}_3\hfill \end{array}$$

  (59)

  that remains structurally stable.
• Quasi equilibrium for the reaction $ES+S\leftrightarrows ESS$
  Here we use the equation $k_3^{+}{x}_3{x}_1=k_3^{-}{x}_4$ for the reduction, that implies quasi steady state for the component $ESS$, that is, $x_4=\left[ESS\right]=x_4^{*}$. In addition, as the reaction $ES+S\leftrightarrows ESS$ forms a connected component in the reaction graph in itself, this connected component disappears from the reaction graph completely. Performing the reduction formally, one obtains the following reduced model in reaction kinetic form

  $$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_1^{+}{x}_1{x}_2+k_1^{-}{x}_3-k_2^{-}{x}_1{x}_5+k_2^{+}{x}_3\hfill \end{array}$$

  (60)

  $$\begin{array}{ccc}\frac{d{x}_2}{dt}\hfill & =& -k_1^{+}{x}_1{x}_2+k_1^{-}{x}_3\hfill \end{array}$$

  (61)

  $$\begin{array}{ccc}\frac{d{x}_3}{dt}\hfill & =& k_1^{+}{x}_1{x}_2-k_1^{-}{x}_3+k_2^{-}{x}_1{x}_5-k_2^{+}{x}_3\hfill \end{array}$$

  (62)

  $$\begin{array}{ccc}\frac{d{x}_5}{dt}\hfill & =& -k_2^{-}{x}_1{x}_5+k_2^{+}{x}_3\hfill \end{array}$$

  (63)

  that preserves it structural stability.

The reduced reaction graphs are seen in Figure 6.

Figure 6. Reaction graph of the reduced Michelis–Menten kinetics, (a) quasi equilibrium for $E+S\leftrightarrows ES$ and (b) quasi equilibrium for $ES+S\leftrightarrows ESS$

Figure 6. Reaction graph of the reduced Michelis–Menten kinetics, (a) quasi equilibrium for $E+S\leftrightarrows ES$ and (b) quasi equilibrium for $ES+S\leftrightarrows ESS$

It is easy to check using the deficiency zero theorem that both of the above reduced models have structural stability.

Finally, model reduction using two quasi steady state assumptions is presented.

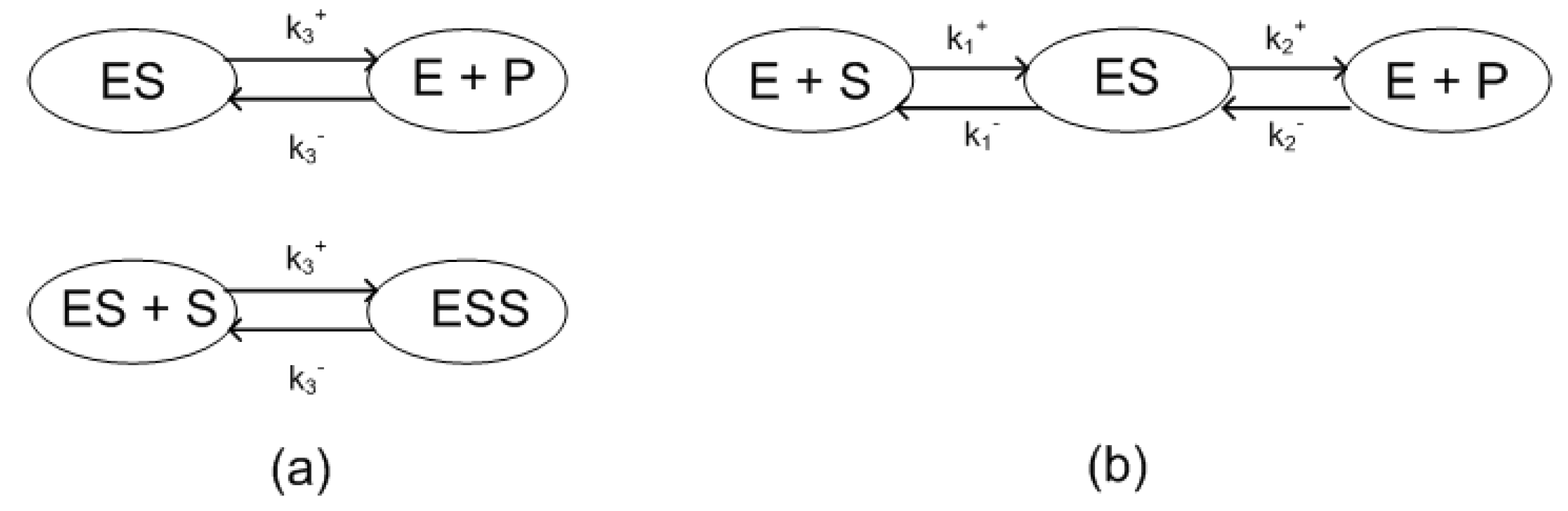
• Quasi steady state for the component $ES$
  Let us denote the steady state value of component $ES$ by $x_3^{*}$, and let us notice that $ES$ forms a complex in itself. Therefore, the reduced stoichiometric matrix $\overline{Y}$ becomes

  $$\overline{Y}=\left[\begin{array}{ccccc}1& 0& 1& 0& 0\\ 1& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 1& 0& 0\end{array}\right]$$

  that shows that the zero complex appears in the reaction kinetic system (see 2nd column of $\overline{Y}$). The reduced kinetic equations are

  $$\begin{array}{ccc}\frac{d{x}_1}{dt}\hfill & =& -k_1^{+}{x}_1{x}_2+{\overline{k}}_1^{-}-k_2^{-}{x}_1{x}_5+{\overline{k}}_2^{+}\hfill \end{array}$$

  (64)

  $$\begin{array}{ccc}\frac{d{x}_2}{dt}\hfill & =& -k_1^{+}{x}_1{x}_2+{\overline{k}}_1^{-}-{\overline{k}}_3^{+}{x}_2+k_3^{-}{x}_4\hfill \end{array}$$

  (65)

  $$\begin{array}{ccc}\frac{d{x}_4}{dt}\hfill & =& {\overline{k}}_3^{+}{x}_2-k_3^{-}{x}_4\hfill \end{array}$$

  (66)

  $$\begin{array}{ccc}\frac{d{x}_5}{dt}\hfill & =& -k_2^{-}{x}_1{x}_5+{\overline{k}}_2^{+}\hfill \end{array}$$

  (67)

  where the new reaction rate constants are formed as ${\overline{k}}_i^{\pm }=k_i^{\pm }{x}_3^{*}$. For the zero complex that appears in the place of $ES$ there is no component mass balance, but the presence of constant positive terms indicate that the systems becomes open. The reaction graph of the reduced system is seen in Figure 7. It is important to note that structural stability of the reduced model cannot be guaranteed.

Figure 7. Reaction graph of the reduced Michelis–Menten kinetics with $ES$ in quasi steady state

Figure 7. Reaction graph of the reduced Michelis–Menten kinetics with $ES$ in quasi steady state

2

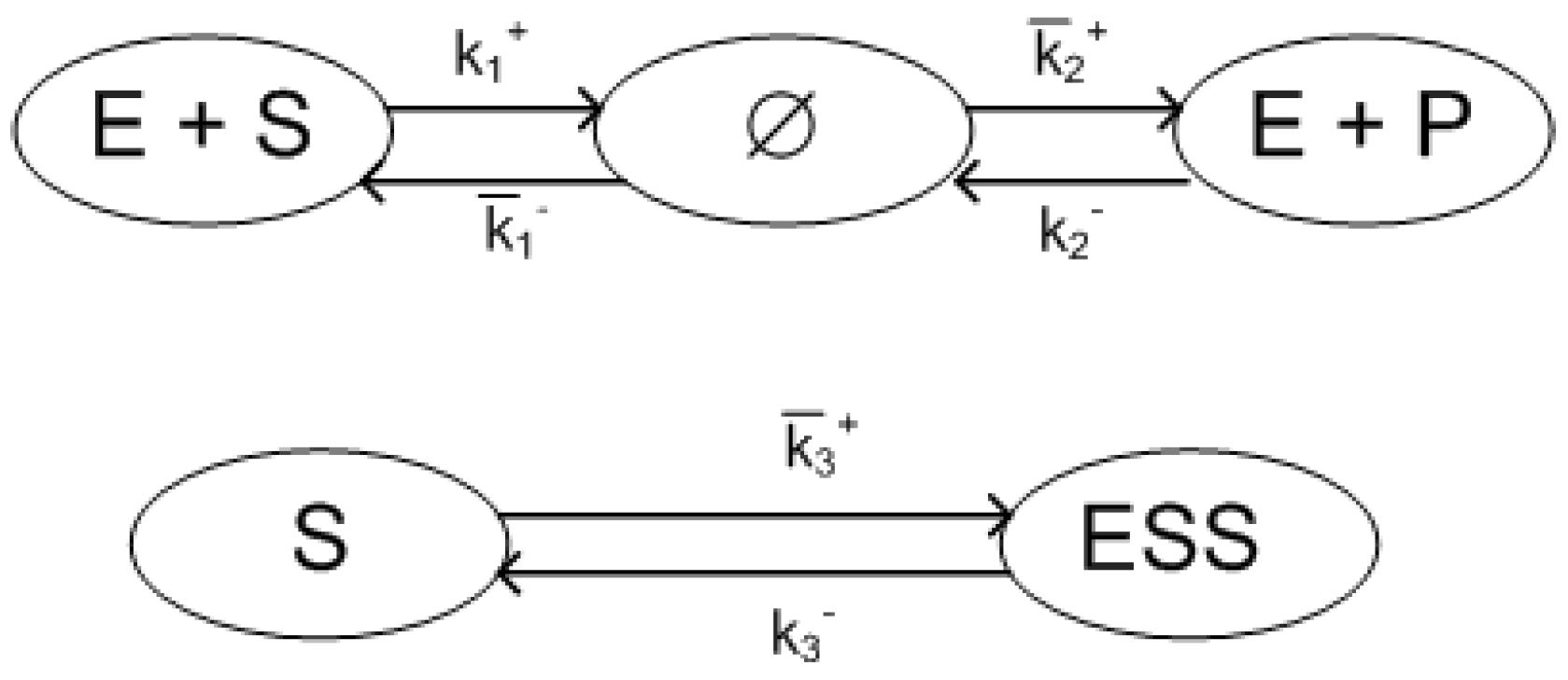
Quasi steady state for the component E

With the steady state value $x_1^{*}$ of component E the transformed reaction rate constants are formed as ${\overline{k}}_i^{\pm }=k_i^{\pm }{x}_1^{*}$, and the reduced kinetic equations are as follows.

$$\begin{array}{ccc}0\hfill & =& -{\overline{k}}_1^{+}{x}_2+k_1^{-}{x}_3+k_2^{+}{x}_3-{\overline{k}}_2^{-}{x}_5\hfill \end{array}$$

(68)

$$\begin{array}{ccc}\frac{d{x}_2}{dt}\hfill & =& -{\overline{k}}_1^{+}{x}_2+k_1^{-}{x}_3-k_3^{+}{x}_2{x}_3+k_3^{-}{x}_4\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\frac{d{x}_3}{dt}\hfill & =& {\overline{k}}_1^{+}{x}_2-k_1^{-}{x}_3-k_3^{+}{x}_2{x}_3+k_3^{-}{x}_4\hfill \end{array}$$

(70)

$$\begin{array}{ccc}\frac{d{x}_4}{dt}\hfill & =& k_3^{+}{x}_2{x}_3-k_3^{-}{x}_4\hfill \end{array}$$

(71)

$$\begin{array}{ccc}\frac{d{x}_5}{dt}\hfill & =& -{\overline{k}}_2^{-}{x}_5+k_2^{+}{x}_3\hfill \end{array}$$

(72)

The reduced stoichiometric matrix is now

$$\overline{Y}=\left[\begin{array}{ccccc}1& 0& 0& 1& 0\\ 0& 1& 0& 1& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 1& 0& 0\end{array}\right]$$

It can be easily seen that the algebraic equation (68) restricts the system dynamics to a 3-dimensional manifold in the 4-dimensional component space. However, the reaction kinetic form would be lost if one expresses a variable from Equation (68) and substitutes it into the differential ones because of the appearance of negative cross-effects.

At the same time, structural stability of the model remains unchanged, because the reduced “unrestricted model” (Equations (69)–(72)) is in a reaction kinetic form with reversible reactions.

6. Conclusions

In this paper, the structural properties of chemical reaction systems obeying the mass action law were investigated and related to the physical and chemical properties of the system. An entropy-based Lyapunov function candidate serves as a tool for proving structural stability for closed reaction kinetic system obeying the MAL. The equivalence of the special form of this Lyapunov function used in reaction kinetics [20] was shown to be equivalent to the thermodynamically motivated Lyapunov function used in process systems engineering [7,8].

The commonly used engineering model reduction methods, the so-called quasi equilibrium and quasi steady state assumption based reductions, together with the variable lumping, were formally defined as model transformations acting on the reaction graph, and their effect on the structural descriptors and on structural stability were investigated.

It was shown that both variable lumping and quasi equilibrium based reduction preserves both the reaction kinetic form and the structural stability of reaction kinetic models of closed systems, but this is not always the case for the reduction based on quasi steady state assumption.