Turing Systems, Entropy, and Kinetic Models for Self-Healing Surfaces
Abstract
:1. Introduction
2. Turing System and Self-Organization Processes
- −
- if then a short external influence on the system gives a rise to static or pulse auto-waves;
- −
- if then auto-waves and wave structures appear without external influence.
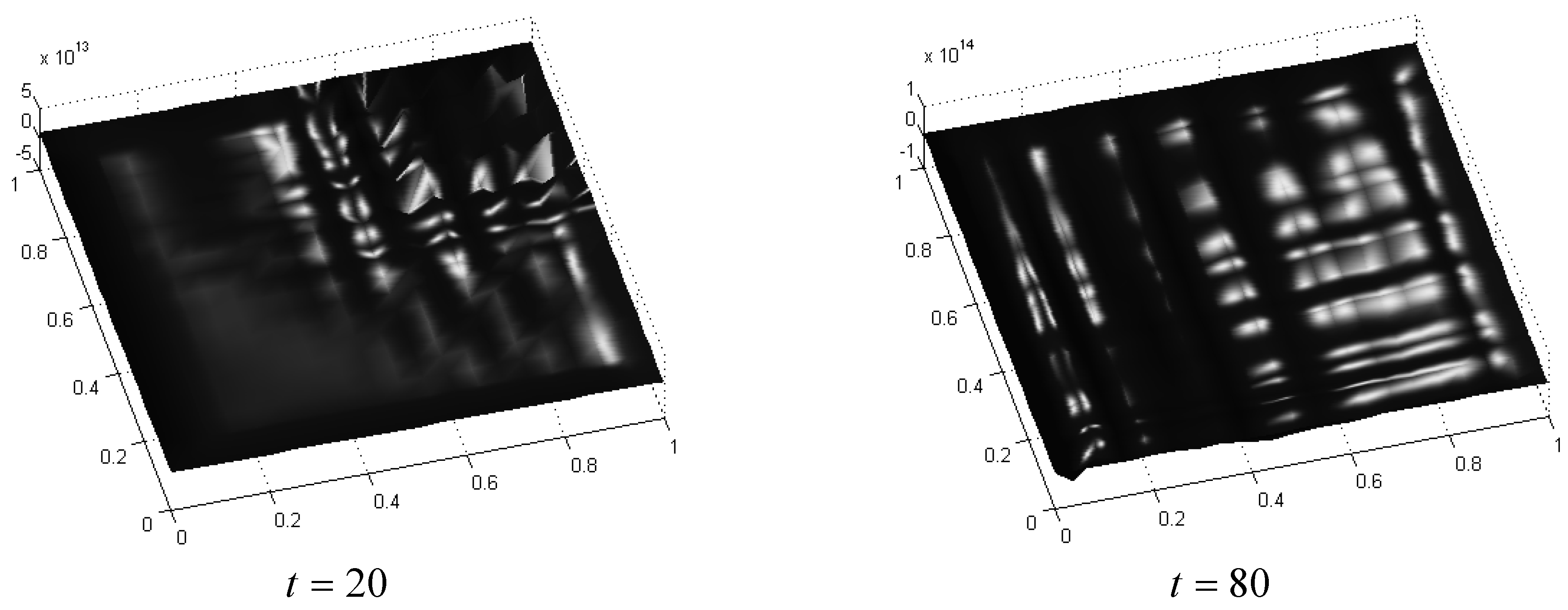
3. Kinetic Models and Entropy
3.1. Concentrated Turing System
- Chaotic behavior that holds while and . Then
- Threshold state with . Then
- Generating regime while and . Then
3.2. Distributed Turing System

- −
- for any time-moment t,
- −
- , that follows form conventional assumption that ,
- −
- for any μ, Kullback-Leibler distance is continuous in time, that follows from continuality of distribution μ and energy E.
4. Remarks on Wave Behavior
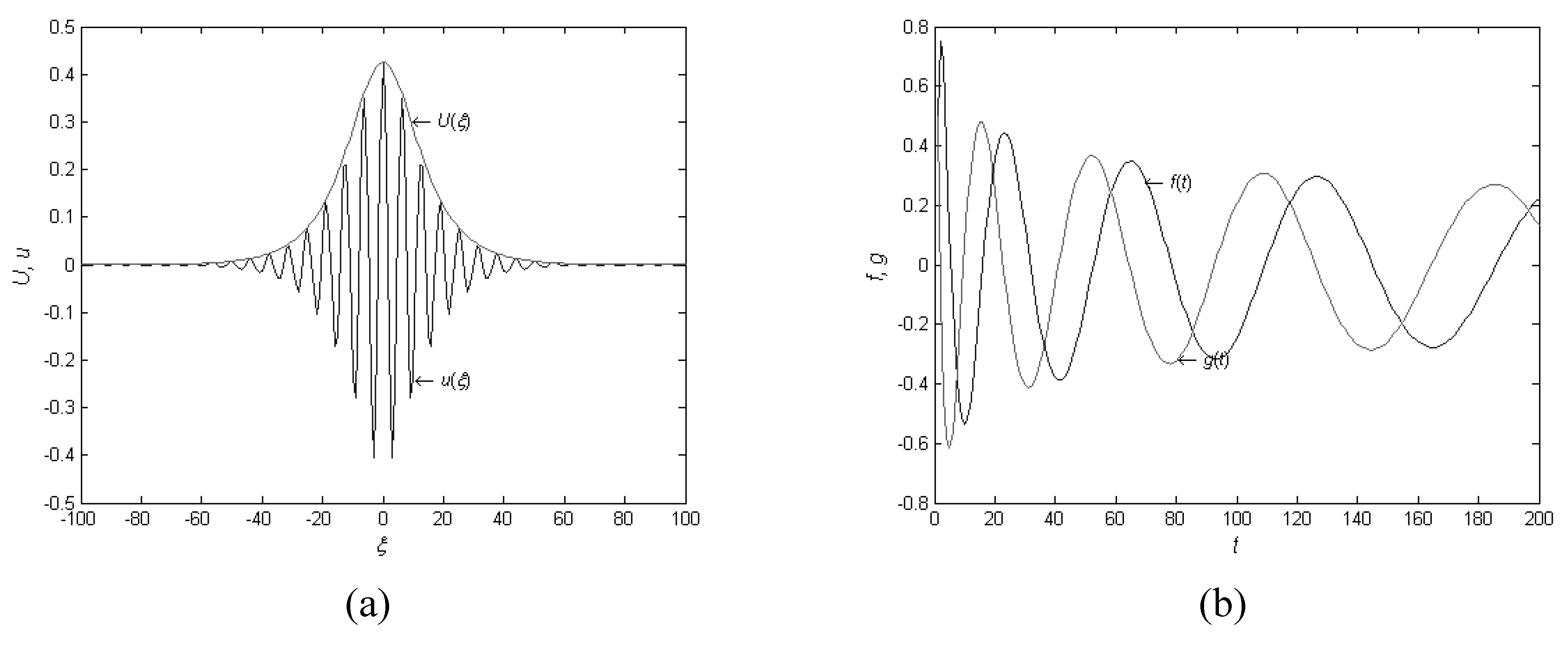
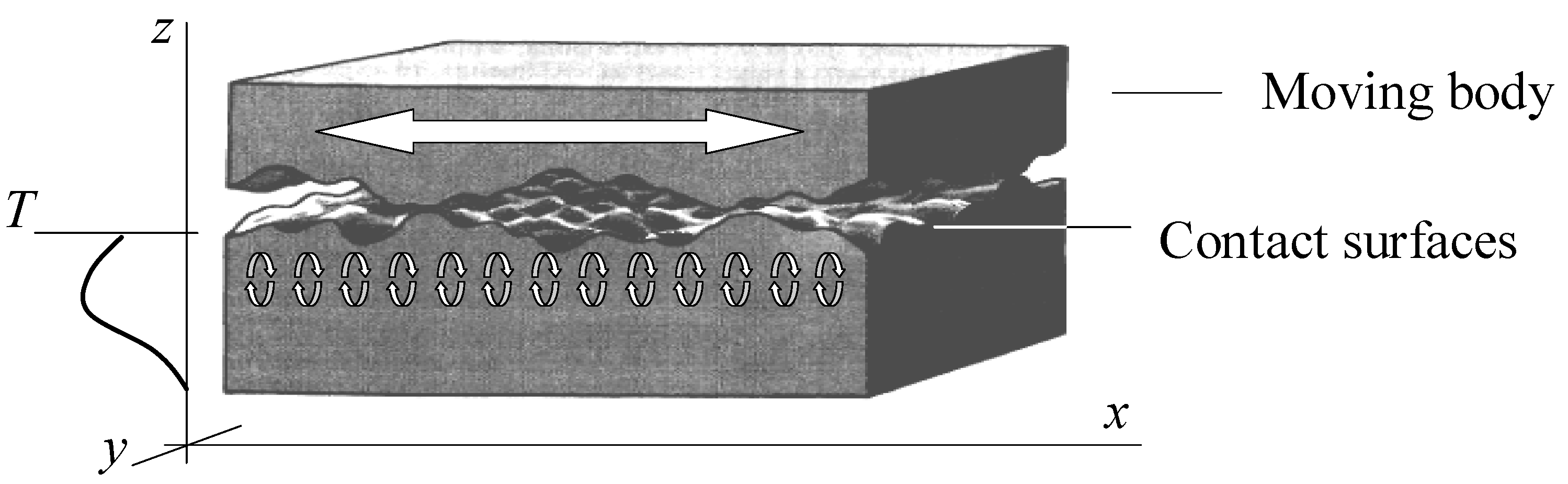
5. Friction-Inspired Self-Organization on Surfaces

6. Conclusion
Acknowledgements
References
- Van der Zwaag, S. (Ed.) Self Healing Materials. An Alternative Approach to 20 Centuries of Materials Science; Springer-Verlag: Dordrecht, Netherlands, 2007.
- Fox-Rabinovich, G.S.; Totten, G.E. (Eds.) Self-Organization During Friction. Advanced Surface-Engineered Materials and Systems Design; Taylor & Francis: Boca Raton, FL, USA, 2007.
- Hayes, S.A.; Zhang, W.; Branthwaite, M.; Jones, F.R. Self-healing of damage in fibre-reinforces polymer-matrix composites. J. R. Soc. Interface 2007, 4, 381–387. [Google Scholar] [CrossRef] [PubMed]
- White, S.R.; Sottos, N.R.; Geubelle, P.H.; Moore, J.S.; Kessler, M.R.; Sriram, S.R.; Brown, E.N.; Viswanathan, S. Autonomic healing of polymer surfaces. Nature 2001, 409, 794–797. [Google Scholar] [CrossRef] [PubMed]
- Balazs, A.C. Modeling self-healing materials. Materials Today 2007, 10, 18–23. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Bhushan, B. Multiscale Dissipative Mechanisms and Hierarchical Surfaces; Springer-Verlag: Berlin, Heidelberg, 2008. [Google Scholar]
- Nosonovsky, M.; Bhushan, B. Thermodynamics of surface degradation, self-organization and self-healing for biomimetic surfaces. Phil. Trans. R. Soc. A 2009, 367, 1607–1627. [Google Scholar] [CrossRef] [PubMed]
- Varley, R.J.; Zwaag, S.van der. Towards an understanding of thermally activated self-healing of an ionomer system during ballistic penetration. Acta Materialia 2008, 56, 5737–5750. [Google Scholar]
- Gerde, E.; Marder, M. Friction and fracture. Nature 2001, 413, 285–288. [Google Scholar] [CrossRef] [PubMed]
- Gershman, I.S.; Bushe, N.A. Elements of thermodynamics and self-organization during friction. In Self-Organization during Frict; Fox-Rabinovich, G.S., Totten, G.E., Eds.; Taylor & Francis: Boca Raton, FL, USA, 2007; Chapter 2; pp. 13–56. [Google Scholar]
- Haken, H. Synergetics. An Introduction. Nonequilibrium Phase Transitions in Physics, Chemistry and Biology, 3rd ed.; Springer-Verlag: New York, NY, USA, 1983. [Google Scholar]
- Nikolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems; John Willey & Sons: New York, NY, USA, 1977. [Google Scholar]
- Prigogine, I. Thermodynamics of Irreversible Processes; John Willey & Sons: New York, NY, USA, 1968. [Google Scholar]
- Fox-Rabinovich, G.; Gershman, I.S.; Yamamoto, K.; Veldhuis, S.; Agguire, M.; Beake, B.; Kovalev, A.; Biksa, A. Self-organization during friction in complex surface engineered tribo-systems. Entropy 2010, 12, 275–288. [Google Scholar] [CrossRef]
- Gaponov-Grekhov, A.V.; Rabinovich, M.I. Auto-structures. Chaotic dynamics of ensembles. In Non-linear Waves. Structures and Bifurcations; Gaponov-Grekhov, A.V., Rabinovich, M.I., Eds.; Nauka: Moscow, Russia, 1987; pp. 7–44. [Google Scholar]
- Gaponov-Grekhov, A.V.; Lomov, A.S.; Osipov, G.V.; Rabinovich, M.I. Creation and dynamics of two-dimensional structures in non-stable dissipative medias. In Non-linear Waves. Structures and Bifurcations; Gaponov-Grekhov, A.V., Rabinovich, M.I., Eds.; Nauka: Moscow, Russia, 1988; pp. 61–83. [Google Scholar]
- Vasiliev, V.A.; Romanovskii, Yu.M.; Chernavskii, D.S.; Yakhno, V.G. Auto-wave Processes in Kinetic Systems: Spatial and Temporal Self-organization in Physics, Chemistry, Biology, and Medicine; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Klimontovich, Yu.L. Problems in the statistical theory of open systems: criteria for the relative degree of order in self-organization processes. Sov. Phys. Usp. 1989, 32, 416–433. [Google Scholar] [CrossRef]
- Klimontovich, Yu.L. Turbulent Motion and the Structure of Chaos; Kluwer Academic Publishers: New York, NY, USA, 1991. [Google Scholar]
- Turing, A.M. The chemical basis of morphogenesis. Phil. Trans. R. Soc. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Landa, P.S. Nonlinear Oscillations and Waves in Dynamical Systems; Kluwer Academic Publishers: Dordrecht, Boston, London, 1996. [Google Scholar]
- Kerner, B.S.; Osipov, V.V. Autosolitons. Uspehi Fiz. Nauk 1989, 157, 201–206. [Google Scholar] [CrossRef]
- Kagan, E. A Model of concentration structures on the semiconductor’s surface. Izvestiya TREI 1995, 1, 43–45. [Google Scholar]
- Kagan, E. On the realization of controlled patterns’ formation on the semiconductor surface. In Proceedings of the Third International Arctic Seminar on Physics and Mathematics IAS’98, Murmansk State Pedagoical University, Murmansk, Russia, 1998; pp. 48–51.
- Kagan, E. Stability of turing patterns in a reaction-diffusion system with boundary control. In Nanomaterials: Methods and Approaches; Belonenko, M.B., Ed.; PrinTerra: Volgograd, Russia, 2008; pp. 134–147. [Google Scholar]
- Balkarey, Yu.I.; Elinson, M.I.; Evtikhov, M.G. Auto-waves and dissipative structures in two-layers medium of Van der Pol Oscillators connected by diffusion. J. Theor. Phys. 1987, 57, 209–218. [Google Scholar]
- Balkarey, Yu.I.; Elinson, M.I.; Evtikhov, M.G. Auto-waves, Dissipative structures and storing information in multi-layers medium with diffusion. Microelectronics 1988, 17, 313–320. [Google Scholar]
- Leppänen, T. Computational Studies of Pattern Formation in Turing Systems. PhD Dissertation, Helsinki University of Technology, Espoo, Finland, 2004. [Google Scholar]
- Leppänen, T. The theory of turing pattern formation. In Current Topics in Physics; Kaski, K., Bario, R.A., Eds.; Imperial College Press: London, UK, 2005; pp. 190–227. [Google Scholar]
- Shoji, H.; Yamada, K.; Ueyama, D.; Ohta, T. Turing patterns in three dimensions. Phys. Rev. E 2007, 75, 046212. [Google Scholar] [CrossRef] [Green Version]
- Mihalache, D.; Mazilu, D.; Lederer, F.; Malomed, B.A.; Crasovan, L.-C.; Kartashov, Y.V.; Torner, L. Stable Three-dimensional solitons in Attractive Bose-Einstein Condensates loaded in an optical lattice. Phys. Rev. A 2005, 021601(R). [Google Scholar] [CrossRef]
- Klimontovich, Yu.L. Entropy evolution in self-organization processes H-theorem and S-theorem. Physica A 1987, 142, 390–404. [Google Scholar] [CrossRef]
- Frank, T.D. Nonlinear Fokker-Planck Equations. Fundamentals and Applications; Springer-Verlag: Berlin, Germany, 2005. [Google Scholar]
- Risken, H. The Fokker-Planck Equation. Methods of Solution and Applications; Springer-Verlag: Berlin, Germany, 1989. [Google Scholar]
- Sirazetdinov, T.K. Stability of Distributed Systems; Nauka: Novosibirsk, Russia, 1987. [Google Scholar]
- Berkovich, I.I.; Gromakovsky, D.G. Tribology; Samara State University of Technology Press: Samara, Russia, 2000. [Google Scholar]
- Garkunov, D.N. Triboengineering (Wear and Non-Wear); Moscow Agricultural Academy Press: Moscow, Russia, 2000. [Google Scholar]
- Armazov, B.N.; Mukhina, G.G. (Eds.) Materials Theory; Moscow State Technical University (MSTU n. a. N. E. Bauman) Press: Moscow, Russia, 2005.
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kagan, E. Turing Systems, Entropy, and Kinetic Models for Self-Healing Surfaces. Entropy 2010, 12, 554-569. https://doi.org/10.3390/e12030554
Kagan E. Turing Systems, Entropy, and Kinetic Models for Self-Healing Surfaces. Entropy. 2010; 12(3):554-569. https://doi.org/10.3390/e12030554
Chicago/Turabian StyleKagan, Eugene. 2010. "Turing Systems, Entropy, and Kinetic Models for Self-Healing Surfaces" Entropy 12, no. 3: 554-569. https://doi.org/10.3390/e12030554



