A Bi-Objective Scheduling Problem in a Home Care Business ^†

Abstract

In this work we study a routing and scheduling problem for a home care business. The problem is composed of two conflicting objectives, therefore we study it as a bi-objective one. We obtain the Pareto frontier for small size instances using the AUGMECON2 method and, for bigger cases, we developed an heuristic algorithm. We also obtained some preliminary results that show the algorithm has good behaviour.

1. Introduction

Home care services aim to help elderly, sick or dependent people maintain their quality of life without having to leave their homes. The goal of a Home Care Scheduling Problem is to obtain the routes that the company’s employees must follow, as well as the times at which each service has to be carried out.

In our problem, the users are the company’s clients, and they require a number of services that need to be carried out, by the company’s employees, throughout the week. To correctly address the users’ needs it is essential that they define the characteristics of the services they request: the day of the week they belong to, their duration, a hard time window and a soft time window. These time windows are necessary because they are used to determine the schedule of each service. Hard time windows state the times within which services must be completed, to have a feasible plan. Soft time windows represent when the user prefers to be attended, even though it is not necessary to uphold them.

The caregivers are the company’s employees and their work consists of visiting users at their homes to carry out the tasks required by them. Every caregiver has a contract, which states the maximum number of hours they can work during each day, and the number of hours that they are hired to work during the week. Caregivers’ working days start at the beginning of the first service and end when the last one is finished. All breaks that caregivers have during the day are considered worked time, with the exception of the largest one—if it lasts two or more hours.

To maintain the users satisfaction, the company works with a list of 6 affinity levels that establish the compatibility between users and caregivers.

2. The Problem

The purpose of this work is to provide the company with the caregivers’ schedules for the week. In the interest of achieving the best possible schedules, we consider two clearly differentiated objectives: the cost of the schedule and the users’ welfare.

The cost of the schedule represents the expenses associated with the caregivers carrying out their routes, and it is composed of two elements:

• The overtime of the caregivers. This is caused by allowing the caregivers to work more hours during the week than initially agreed, while still adhering to their daily maximum allowed working time, which results in an extra cost for the company.
• The total working time of the caregivers. This is the sum of the daily working time of each caregiver according to the schedules, and by reducing them we are saving the company money while also optimizing the caregivers time.

The users’ welfare represents the degree of well being and satisfaction that users present according to the schedule, and combines two elements:

• The affinity between caregivers and the users they attend. By maximizing the affinity, we try to ensure that users will be attended by caregivers they are most comfortable with.
• The penalization for carrying out a service before, or after, its soft time window. Minimizing this value means that the services will be scheduled as close as possible to their soft time windows.

For the schedules to be feasible, the company requires that: each service has to be carried out within its hard time window by one caregiver, the caregivers’ daily scheduled time cannot surpass their maximum working hours, the largest break a caregiver has during the day will not be considered as working time.

3. Resolution Methods

The problem has two conflicting objectives, which means that there is not a single solution that optimizes both of them at the same time. In a multi-objective problem with p objectives we say that x dominates y if $f_k\left(x\right)\le f_k\left(y\right)$$\forall k\in \{1,\dots ,p\}$ and $f_k\left(x\right)<f_k\left(y\right)$ for at least one $k\in \{1,\dots ,p\}$. To solve our problem we look for the Pareto frontier, which is a set composed by the non-dominated solutions.

We modelled the problem as a Mixed Integer Programming (MIP) one and used it to obtain non-dominated solutions with the AUGMECON2 method [1]. However, because this problem is a complex one, we can only solve small instances with the AUGMECON2 method. Therefore, it is necessary to develop an heuristic algorithm to generate good approximations of the non-dominated set for instances of bigger size.

The algorithm presented in this problem is divided into three steps:

Step 1 

We initiate the sets by obtaining the best solutions for each of the objectives (considering a lexicographic objective function) using the Adaptive Large Neighbourhood Search (ALNS) [2].

Step 2 

We obtain a set of multiple solutions with different routes. This is done by applying the ALNS to a solution chosen at random from the ones already found.

Step 3 

The set of non-dominated solutions is obtained by randomly choosing a solution and then modifying its schedule in order to improve one of the objectives. In order to modify the schedule of a solution the method randomly selects a service and an objective. Then the service is advanced or delayed in order to improve the objective under consideration.

4. Results

In this section we present the preliminary computational results obtained to check the behaviour of the heuristic algorithm. The instances we solved are the ones presented in [3], which were adapted to the characteristics of our problem.

In Figure 1 and Figure 2 we present the Pareto front obtained by the AUGMECON2 method (blue colour) as well as two approximations of the non-dominated set obtained by different configurations of the algorithm. These configurations depend of the number of iterations used, and are described in Table 1.

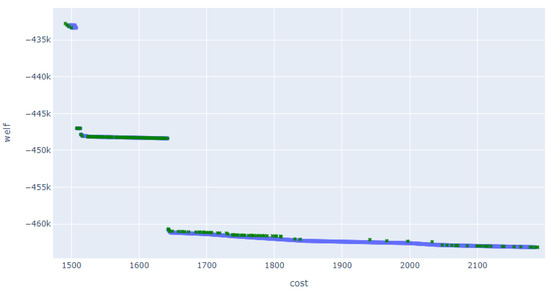
Figure 1. Approximation of the Pareto frontier—Configuration 1.

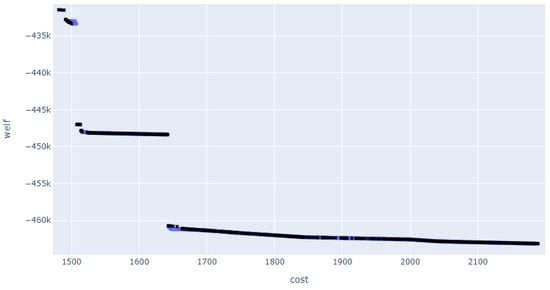
Figure 2. Approximation of the Pareto frontier—Configuration 2.

Table 1. Configurations of the experiments.

	Step 1	Step 2	Step 3
Configuration 1	1000	1000	10,000
Configuration 2	1000	500	100,000

We can see that the approximation presented in Figure 2 (black) is better than the one in Figure 1 (green), because it is closer to the Pareto frontier. In fact, Figure 2 shows that our algorithm can provide good approximations of the Pareto frontier.