Foam Formation by Compression/Decompression Cycle of Soft Porous Media
Abstract
:1. Introduction
2. Materials and Methods
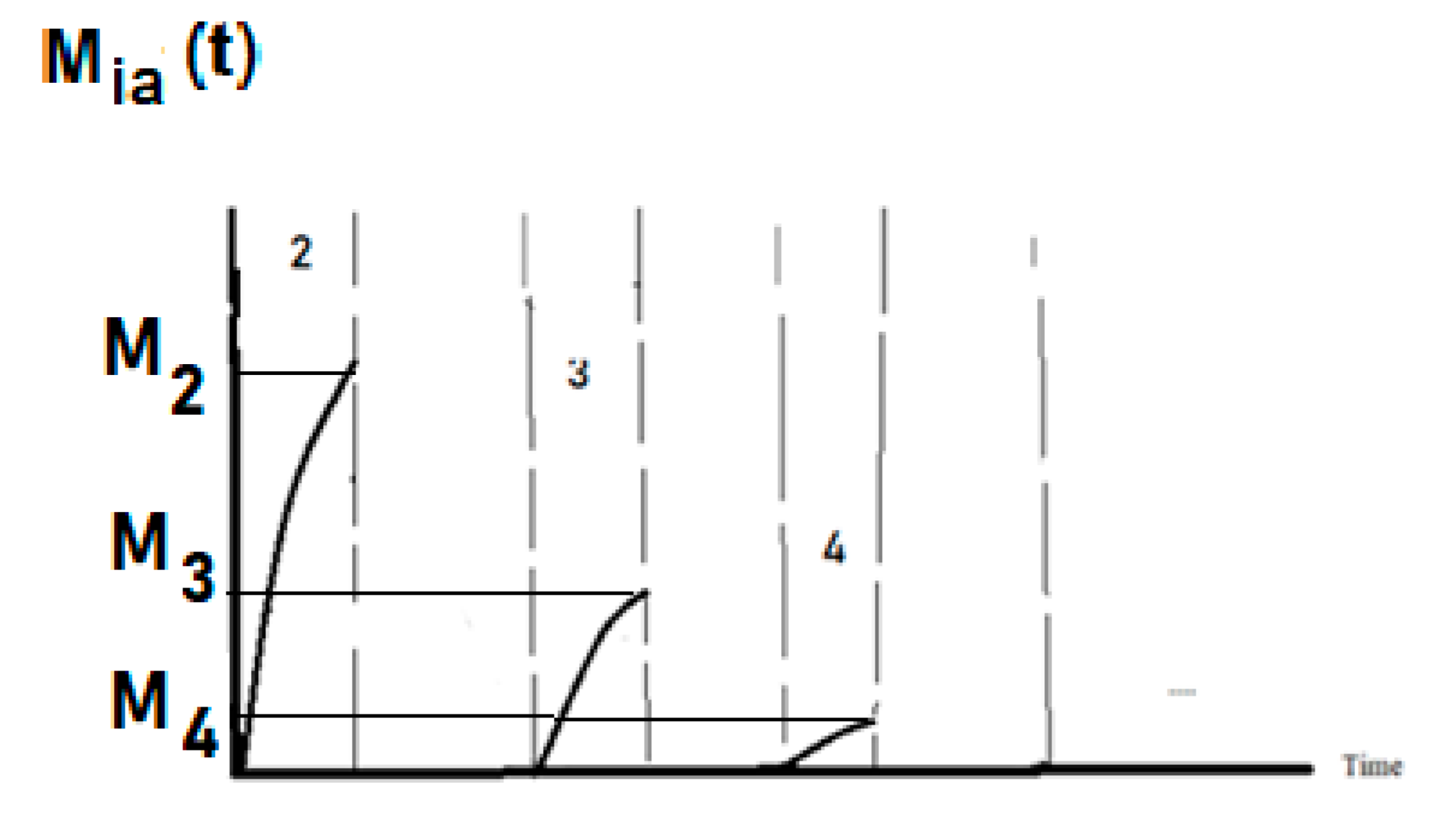
3. Theory
Modelling of Sponge Squeezing
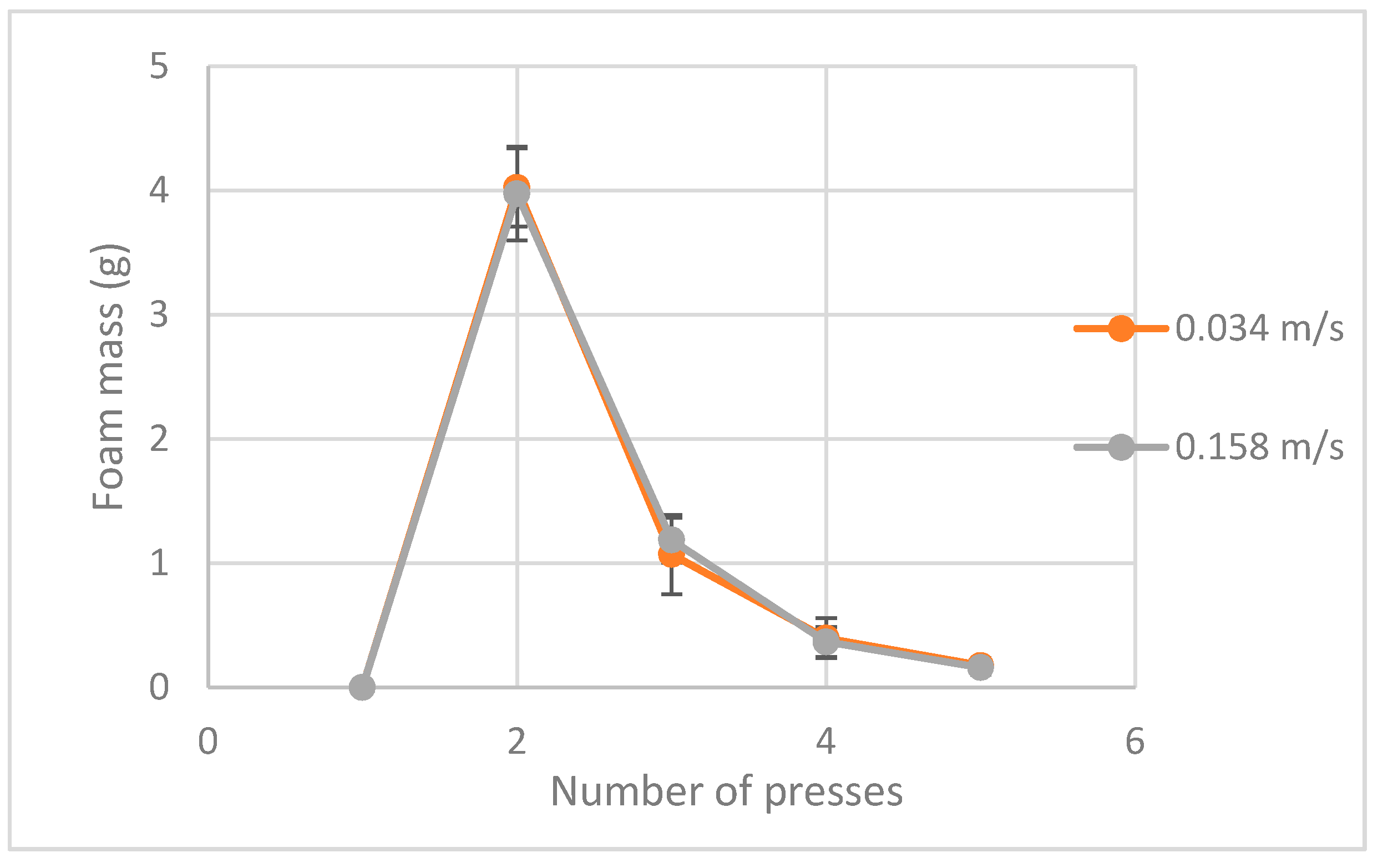
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schramm, L.L.; Wassmuth, F. Foams: Basic principies. Adv. Chem. Ser. 1994, 242, 3. [Google Scholar]
- Wasan, D.T.; Nikolov, A.D.; Lobo, L.A.; Koczo, K.; Edwards, D.A. Foams, thin films and surface rheological properties. Prog. Surf. Sci. 1992, 39, 119–154. [Google Scholar] [CrossRef]
- Małysa, K. Wet foams: Formation, properties and mechanism of stability. Adv. Colloid Interface Sci. 1992, 40, 37–83. [Google Scholar] [CrossRef]
- Heard, J.; Harvey, E.; Johnson, B.B.; Wells, J.D.; Angove, M.J. The effect of filamentous bacteria on foam production and stability. Colloids Surf. B Biointerfaces 2008, 63, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Schilling, K.; Zessner, M. Foam in the aquatic environment. Water Res. 2011, 45, 4355–4366. [Google Scholar] [CrossRef] [PubMed]
- Weaire, D.; Hutzler, S. The Physics of Foams; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Stevenson, P. Foam Engineering: Fundamentals and Applications; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Gauglitz, P.A.; Friedmann, F.; Kam, S.I.; Rossen, W.R. Foam generation in homogeneous porous media. Chem. Eng. Sci. 2002, 57, 4037–4052. [Google Scholar] [CrossRef]
- Drenckhan, W.; Saint-Jalmes, A. The science of foaming. Adv. Colloid Interface Sci. 2015, 222, 228–259. [Google Scholar] [CrossRef] [PubMed]
- Pugh, R.J. Foaming, foam films, antifoaming and defoaming. Adv. Colloid Interface Sci. 1996, 64, 67–142. [Google Scholar] [CrossRef]
- Johnson, P.; Routledge, T.; Trybala, A.; Vaccaro, M.; Starov, V. Wetting and Spreading of Commercially Available Aqueous Surfactants on Porous Materials. Colloids Interfaces 2019, 3, 14. [Google Scholar] [CrossRef] [Green Version]
- Johnson, P.; Vaccaro, M.; Donnell, C.O.; Trybala, A.; Starov, V. Foamability of soft porous media using compression. Colloids Surf. A 2019, 579, 123569. [Google Scholar] [CrossRef]



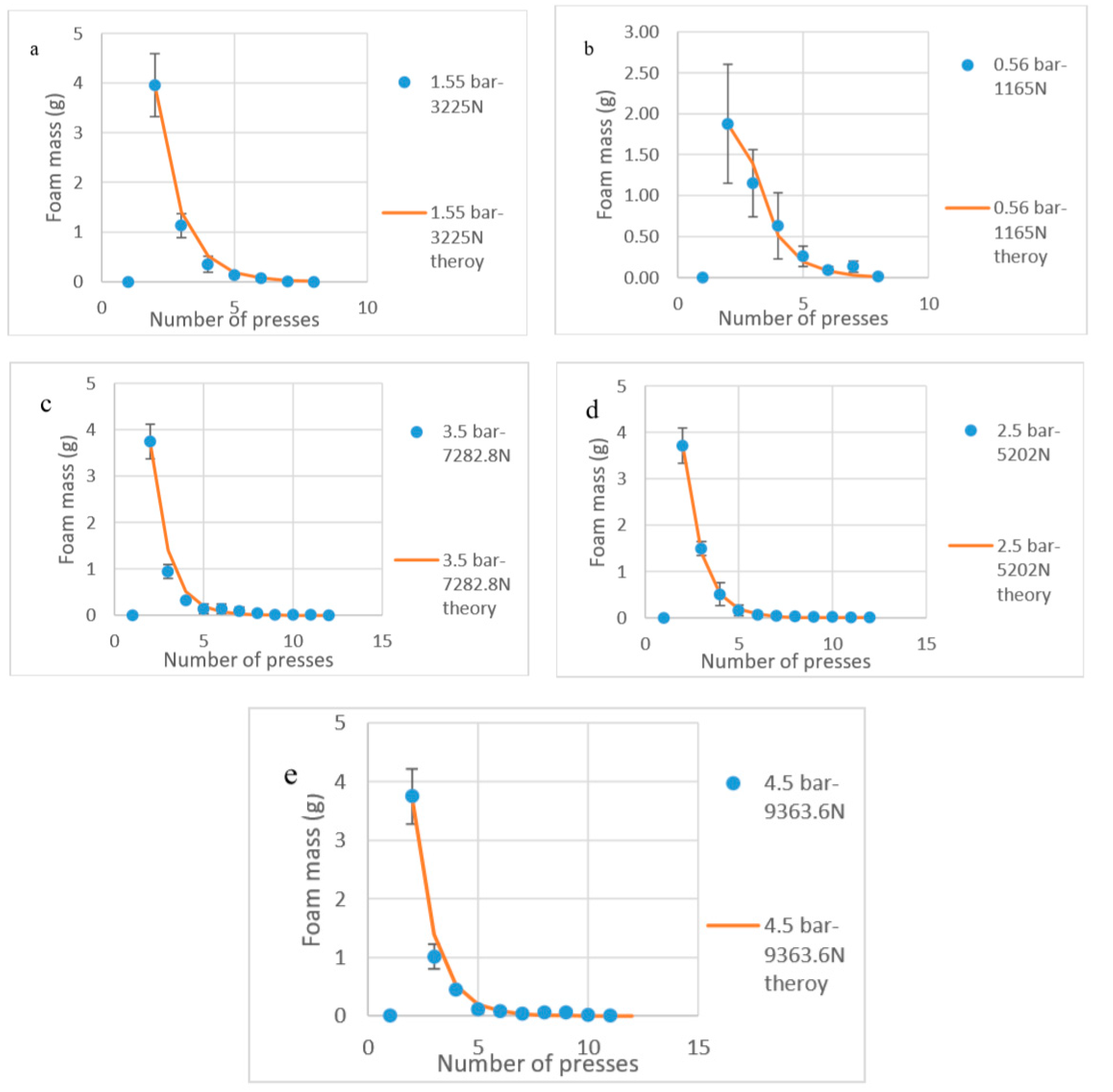

| Pressure (bar) | h (cm) | α (1/cm) | 1/h (1/cm) |
|---|---|---|---|
| 0.56 | 0.4 | 2.5 | 2.5 |
| 1.55 | 0.3 | 3.33 | 3.33 |
| 2.5 | 0.2 | 5 | 5 |
| 3.5 | 0.1 | 10 | 10 |
| 4.5 | 0.1 | 10 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johnson, P.; Vaccaro, M.; Starov, V.; Trybala, A. Foam Formation by Compression/Decompression Cycle of Soft Porous Media. Colloids Interfaces 2020, 4, 31. https://doi.org/10.3390/colloids4030031
Johnson P, Vaccaro M, Starov V, Trybala A. Foam Formation by Compression/Decompression Cycle of Soft Porous Media. Colloids and Interfaces. 2020; 4(3):31. https://doi.org/10.3390/colloids4030031
Chicago/Turabian StyleJohnson, Phillip, Mauro Vaccaro, Victor Starov, and Anna Trybala. 2020. "Foam Formation by Compression/Decompression Cycle of Soft Porous Media" Colloids and Interfaces 4, no. 3: 31. https://doi.org/10.3390/colloids4030031






