Optimization of Fiber Factors on Flexural Properties for Carbon Fiber Reinforced Polypropylene
Abstract
:1. Introduction
2. Experimental
2.1. Material
2.2. Fiber Length and Fiber Orientation
2.3. Composite Fabrication
2.4. Design of Experiment
2.5. Characterization
3. Results and Discussion
3.1. Experimental Results
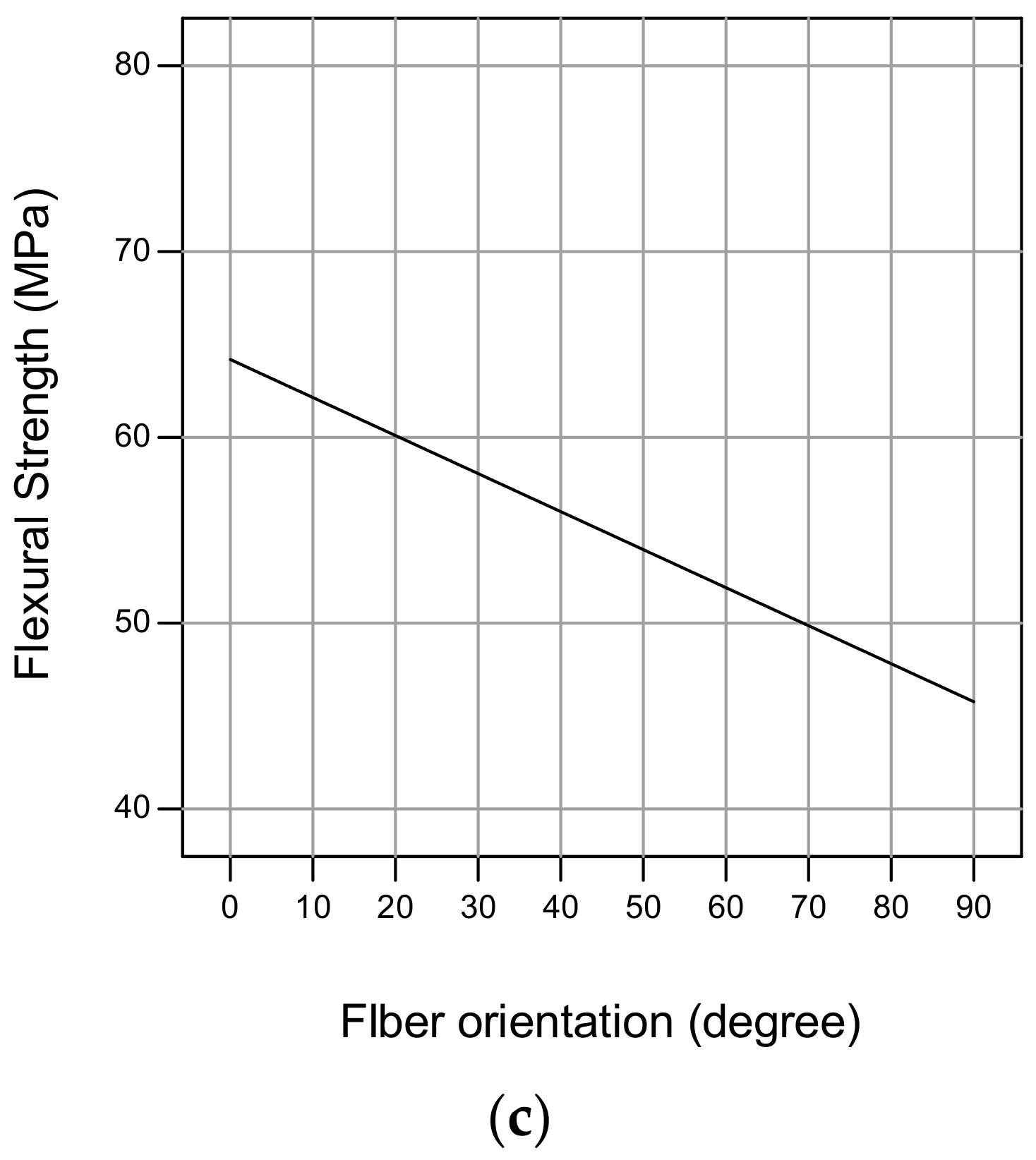
3.2. Analysis of Flexural Strength
3.3. Analysis of Flexural Modulus
3.4. Optimization and Confirmation
4. Conclusions
- The RSM-ANOVA models of the flexural strength and modulus have been developed and statistically validated.
- The RSM optimization technique reduces the experimental time, improves the flexural performance of the composite, improves reliability, and achieves robustness of the composite.
- The orientation of the fibers has the most significant effect on the flexural strength of the composite.
- All fiber factors influenced flexural modulus significantly, with fiber orientation being the most significant factor.
- Applying the optimal fiber factors can improve the flexural strength and modulus of carbon fiber reinforced polypropylene.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Singh, J.; Kumar, M.; Kumar, S. Properties of glass-fiber hybrid composites: A review. Polym. Plast. Technol. Eng. 2017, 56, 455–469. [Google Scholar] [CrossRef]
- Kugler, S.K.; Kech, A.; Cruz, C. Fiber Orientation Predictions—A Review of Existing Models. J. Compos. Sci. 2020, 4, 69. [Google Scholar] [CrossRef]
- Hirano, N.; Muramatsu, H.; Inoue, T. Study of fiber length and fiber-matrix adhesion in carbon-fiber-reinforced polypropylenes. Adv. Compos. Mater. 2014, 23, 2–151. [Google Scholar] [CrossRef]
- Piggott, M.R. Load Bearing Fibre Composites, 2nd ed.; MERP: Toronto, ON, Canada, 2016. [Google Scholar]
- Zhou, Y.; Mallick, P.K. A non-linear damage model for the tensile behavior of an injection molded short E-glass fiber reinforced polyamide-6,6. Mater. Sci. Eng. 2005, 393, 303–309. [Google Scholar] [CrossRef]
- Werken, N.V.; Reese, M.S.; Taha, M.R.; Tehrani, M. Investigating the effects of fiber surface treatment and alignment on mechanical properties of recycled carbon fiber composites. Compos. Part A 2019, 119, 38–47. [Google Scholar] [CrossRef]
- Teixeira, D.; Giovanela, M.; Gonella, L.B. Influence of injection molding on the flexural strength and surface quality of long glass fiber-reinforced polyamide 6.6 composites. Mater. Des. 2015, 85, 695–706. [Google Scholar] [CrossRef]
- Kumaresan, M.; Satish, S.; Karthi, N. Effect of Fiber Orientation on Mechanical Properties of Sisal Fiber Reinforced Epoxy Composites. J. Appl. Sci. Eng. 2015, 18, 289–294. [Google Scholar] [CrossRef]
- Fu, S.; Lauke, B. Effect of Fiber Length and Fiber Orientation Distributions on the Tensile Strength of Short-Fiber-Reinforced Polymers. Compos. Sci. Technol. 1996, 56, 1179–1190. [Google Scholar] [CrossRef]
- Rezaei, F.; Yunus, R.; Ibrahim, N.A. Effect of fiber length on thermomechanical properties of short carbon fiber reinforced polypropylene composites. Mater. Des. 2009, 30, 260–263. [Google Scholar] [CrossRef]
- Harper, L.T.; Turner, T.A.; Warrior, N.A.; Rudd, C.D. Characterisation of random carbon fibre composites from a directed fibre preforming process: The effect of fibre length. Compos. Part A 2006, 37, 1863–1878. [Google Scholar] [CrossRef]
- Ksouri, I.; Guermazi, N.; Haddar, N.; Ayedi, H.F. Effects of Processing Steps and Hygrothermal Ageing on Mechanical Performance of PA6GF30 Composite: Interfacial Shear Strength. Polym. Compos. 2018, 36, 504–512. [Google Scholar] [CrossRef]
- Karsli, N.G.; Aytac, A.; Deniz, V. Effects of initial fiber length and fiber length distribution on the properties of carbon-fiber-reinforced-polypropylene composites. J. Reinf. Plast. Compos. 2012, 3, 1053–1060. [Google Scholar] [CrossRef]
- Rohde, M.; Ebel, A. Influence of Processing Parameters on the Fiber Length and Impact Properties of Injection Molded Long Glass Fiber Reinforced Polypropylene. Intern. Polym. Process. 2011, 26, 292–303. [Google Scholar] [CrossRef]
- Warrier, A.; Godara, A.; Rochez, O.; Mezzo, L.; Luizi, F.; Gorbatikh, L.; Verpoest, I. The effect of adding carbon nanotubes to glass/epoxy composites in the fibre sizing and/or the matrix. Compos. Part A 2010, 41, 532–538. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, F.; Zhang, C.; Wang, J.; Jia, Z.; Hui, D.; Qiu, Y. Tensile and interfacial properties of polyacrylonitrile-based carbon fi ber after different cryogenic treated condition. Compos. Part B 2016, 99, 358–365. [Google Scholar] [CrossRef]
- Li, W.; Zheng, L.; Gao, Y.; Xu, F. Interfacial Bonding Enhancement between Cryogenic Conditioned Carbon Fiber and Epoxy Resin Characterized by the Single-Fiber Fragmentation Method. AATCC J. Res. 2020, 8, 24–30. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, F.; Liu, W.; Zhou, M.; Li, W.; Hui, D. Influence of cryogenic treatment on mechanical and interfacial properties of carbon nanotube fiber/bisphenol-F epoxy composite. Compos. Part B. 2017, 125, 195–202. [Google Scholar] [CrossRef]
- Sumitomo Chemical. Cosmoplene® AW564 Technical Data Sheet; The Polyolefin Company: Singapore, 2019. [Google Scholar]
- Torayca. T700S Data Sheet No. CFA-005; Torayca: Santa Ana, CA, USA, 2018. [Google Scholar]
- Mortazavian, S.; Fatemi, A. Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber reinforced polymer composites. Compos. Part B Eng. 2015, 72, 116–129. [Google Scholar] [CrossRef]
- Burn, D.T.; Harper, L.T.; Johnson, M.; Warrior, N.A.; Yang, L.; Thomason, J. The Influence of Coupling Agent, Fibre Sizing and Matrix Degradation on the Interfacial Shear Strength between Carbon FIbre and Polypropylene. In Proceedings of the ECCM-16TH European Conference On Composite Materials, Seville, Spain, 22–26 June 2014. [Google Scholar]
- Budiyantoro, C.; Rochardjo, H.S.B.; Nugroho, G. Effects of Processing Variables of Extrusion—Pultrusion Method on the Impregnation Quality of Thermoplastic Composite Filaments. Polymers 2020, 12, 2833. [Google Scholar] [CrossRef]
- ASTM D790; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. ASTM Internasional: West Conshohocken, PA, USA, 2013.
- Fu, T.; Haworth, B. Analysis of process parameters related to the single-screw extrusion of recycled polypropylene blends by using design of experiments. J. Plast. Film Sheeting 2017, 32, 168–190. [Google Scholar] [CrossRef] [Green Version]
- Pal, S.; Gauri, S.K. A desirability functions-based approach for simultaneous optimization of quantitative and ordinal response variables in industrial processes. Int. J. Eng. Sci. Technol. 2018, 10, 76–87. [Google Scholar] [CrossRef] [Green Version]
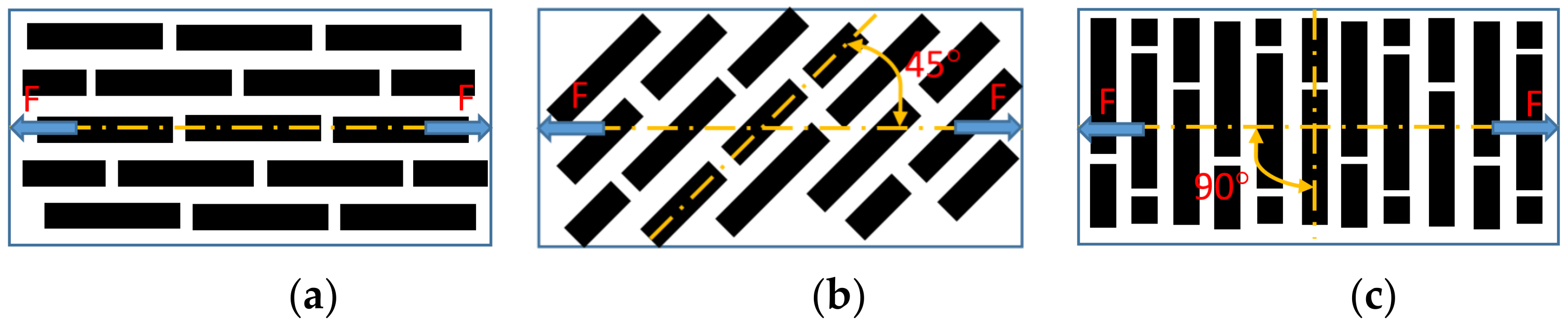




| Material | Properties | Values |
|---|---|---|
| Carbon fiber (T700SC 12K) | Filament diameter (µm) | 7 |
| Tow diameter (mm) | 0.85 | |
| Density (g/cm3) | 1.8 | |
| Tensile strength (MPa) | 4900 | |
| Cosmoplene AW564 | Density (g/cm3) | 0.9 |
| Melting temperature (°C) | 190–230 | |
| Tensile strength at yield (MPa) | 27.5 | |
| Tensile strength at break (MPa) | 23 | |
| Liquid nitrogen | Boiling point (°C) | −196 |
| Density, Liquid @ BP, 1 atm (kg/m3) | 808.5 | |
| Specific Gravity, Liquid (water = 1) @ 20 °C, 1 atm | 0.808 |
| Factors | Coding | Actual Level | ||
|---|---|---|---|---|
| Low (−1) | Middle (0) | High (+1) | ||
| Fiber immersion time (min) | A | 10 | 15 | 20 |
| Fiber length (mm) | B | 1.5 | 3 | 4.5 |
| Fiber orientation (°) | C | 0 | 45 | 90 |
| Run | Code | Actual | ||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| 1 | −1 | 0 | −1 | 10 | 3 | 0 |
| 2 | 0 | −1 | −1 | 15 | 1.5 | 0 |
| 3 | 0 | 0 | 0 | 15 | 3 | 45 |
| 4 | −1 | 1 | 0 | 10 | 4.5 | 45 |
| 5 | −1 | 0 | 1 | 10 | 3 | 90 |
| 6 | 0 | −1 | 1 | 15 | 1.5 | 90 |
| 7 | 0 | 1 | −1 | 15 | 4.5 | 0 |
| 8 | −1 | −1 | 0 | 10 | 1.5 | 45 |
| 9 | 0 | 1 | 1 | 15 | 4.5 | 90 |
| 10 | 0 | 0 | 0 | 15 | 3 | 45 |
| 11 | 1 | −1 | 0 | 20 | 1.5 | 45 |
| 12 | 1 | 0 | 1 | 20 | 3 | 90 |
| 13 | 0 | 0 | 0 | 15 | 3 | 45 |
| 14 | 1 | 0 | −1 | 20 | 3 | 0 |
| 15 | 1 | 1 | 0 | 20 | 4.5 | 45 |
| Run | Factors | Average Flexural Strength (MPa) | Average Flexural Modulus (MPa) | ||
|---|---|---|---|---|---|
| A | B | C | |||
| 1 | 10 | 3 | 0 | 63.87 | 1326.7 |
| 2 | 15 | 1.5 | 0 | 55.7 | 2630 |
| 3 | 15 | 3 | 45 | 58.6 | 1409 |
| 4 | 10 | 4.5 | 45 | 46.8 | 1540 |
| 5 | 10 | 3 | 90 | 45.3 | 345 |
| 6 | 15 | 1.5 | 90 | 44.1 | 240 |
| 7 | 15 | 4.5 | 0 | 78.43 | 3426.7 |
| 8 | 10 | 1.5 | 45 | 62.6 | 439.7 |
| 9 | 15 | 4.5 | 90 | 47.9 | 658 |
| 10 | 15 | 3 | 45 | 59.1 | 1400.2 |
| 11 | 20 | 1.5 | 45 | 45.27 | 1079.7 |
| 12 | 20 | 3 | 90 | 50.5 | 1283.3 |
| 13 | 15 | 3 | 45 | 58.27 | 1403.3 |
| 14 | 20 | 3 | 0 | 63.5 | 2740 |
| 15 | 20 | 4.5 | 45 | 50.43 | 1680 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Note |
|---|---|---|---|---|---|---|
| Model | 692.22 | 3 | 230.74 | 3.84 | 0.0419 | significant |
| A-Cryogenic Immersion | 1.03 | 1 | 1.03 | 0.017 | 0.8982 | |
| B-Fiber length | 12.23 | 1 | 12.23 | 0.20 | 0.6606 | |
| C-Fiber orientation | 678.96 | 1 | 678.96 | 11.30 | 0.0063 | significant |
| Residual | 660.66 | 11 | 60.06 | |||
| Pure Error | 0.26 | 2 | 0.13 | |||
| Mean | 53.75 | |||||
| R-Squared | 0.5117 | |||||
| Adj R-Squared | 0.3785 | |||||
| Pred R-Squared | −0.0427 | |||||
| Model Precision | 5.222 |
| Calculation Run | Factor Entry | Calculated Flexural Strength (MPa) | ||
|---|---|---|---|---|
| Fiber Immersion Time (min) | Fiber Length (mm) | Fiber Orientation (°) | ||
| 1 | 10 | 32 | 0 | 87 |
| 2 | 10 | 14.14 | 45 | 63 |
| 3 | 10 | 10 | 90 | 51 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Note |
|---|---|---|---|---|---|---|
| Model | 9.503 × 106 | 3 | 3.168 × 106 | 17.08 | 0.0002 | significant |
| A-Cryogenic Immersion | 1.226 × 106 | 1 | 1.226 × 106 | 6.61 | 0.0260 | significant |
| B-Fiber length | 1.062 × 106 | 1 | 1.062 × 106 | 5.73 | 0.0357 | significant |
| C-Fiber orientation | 7.214 × 106 | 1 | 7.214 × 106 | 38.90 | <0.0001 | significant |
| Residual | 2.040 × 106 | 11 | 1.855 × 105 | |||
| Pure Error | 39.85 | 2 | 19.92 | |||
| Mean | 1440.11 | |||||
| R-Squared | 0.8233 | |||||
| Adj R-Squared | 0.7750 | |||||
| Pred R-Squared | 0.6218 | |||||
| Model Precision | 12.060 |
| Calculation Run | Factor Entry | Calculated Flexural Modulus (MPa) | ||
|---|---|---|---|---|
| Fiber Immersion Time (min) | Fiber Length (mm) | Fiber Orientation (°) | ||
| 1 | 10 | 32 | 0 | 9043 |
| 2 | 10 | 14.14 | 45 | 3755 |
| 3 | 10 | 10 | 90 | 1799.6 |
| 4 | 15 | 32 | 0 | 9435 |
| 5 | 15 | 14.14 | 45 | 4146.5 |
| 6 | 15 | 10 | 90 | 2191.1 |
| 7 | 20 | 32 | 0 | 9826.5 |
| 8 | 20 | 14.14 | 45 | 4537.9 |
| 9 | 20 | 10 | 90 | 2582.5 |
| Trial | Flexural Strength (MPa) | Flexural Modulus (MPa) | ||
|---|---|---|---|---|
| Confirmation | Predictive | Confirmation | Predictive | |
| 1 | 70.3 | 64 | 3200 | 3145.6 |
| 2 | 74 | 3580 | ||
| 3 | 64.3 | 3170 | ||
| Average | 69.5 | 3316 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nugroho, G.; Budiyantoro, C. Optimization of Fiber Factors on Flexural Properties for Carbon Fiber Reinforced Polypropylene. J. Compos. Sci. 2022, 6, 160. https://doi.org/10.3390/jcs6060160
Nugroho G, Budiyantoro C. Optimization of Fiber Factors on Flexural Properties for Carbon Fiber Reinforced Polypropylene. Journal of Composites Science. 2022; 6(6):160. https://doi.org/10.3390/jcs6060160
Chicago/Turabian StyleNugroho, Gesang, and Cahyo Budiyantoro. 2022. "Optimization of Fiber Factors on Flexural Properties for Carbon Fiber Reinforced Polypropylene" Journal of Composites Science 6, no. 6: 160. https://doi.org/10.3390/jcs6060160






