1. Introduction
Reversible single-stage axial fans are largely employed in tunnel and metro ventilation systems, to supply and extract air from the tunnels. State-of-the-art solutions include the use of dedicated fans for air supply and extraction, but in general the use of reversible fan rotors, characterized by truly reversible blade sections, has been established as the most convenient [
1,
2,
3].
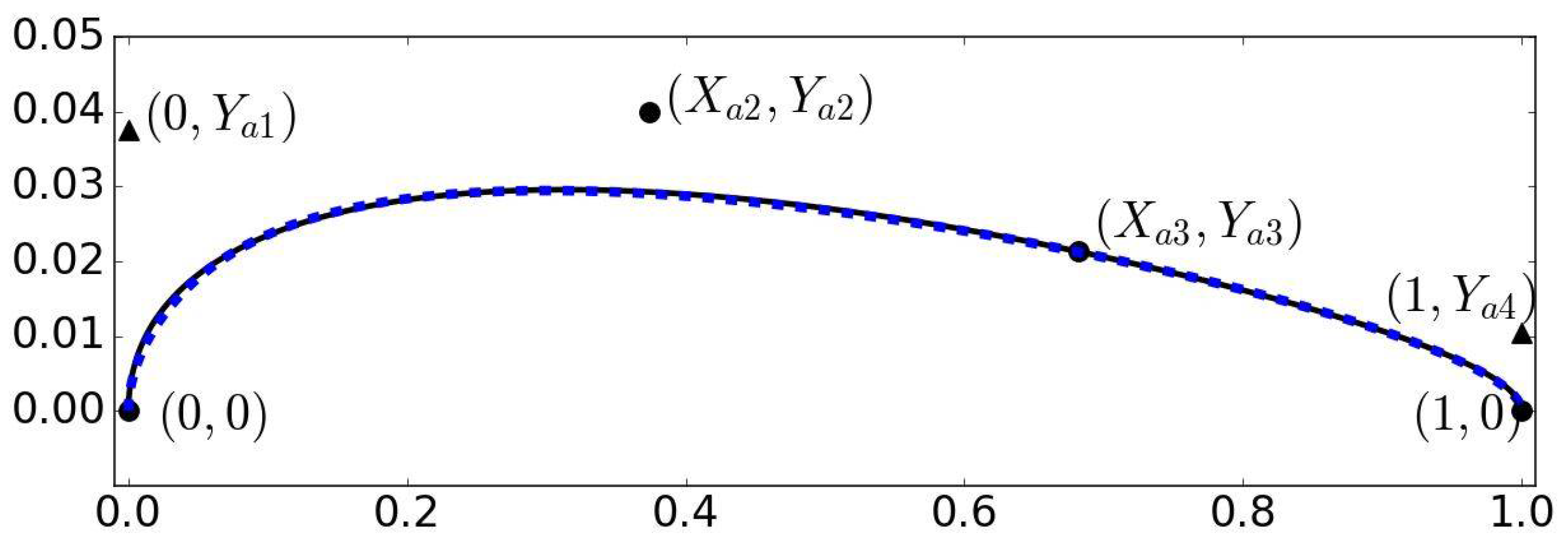
Traditionally, truly reversible aerofoils have been generated by flipping the pressure side of a non-cambered aerofoil and joining the suction side trailing edge with the pressure side leading edge, and vice versa (
Figure 1). Therefore, the aerofoil has periodic aerodynamic performance in terms of lift and drag coefficients every 180 degrees of angle of attack. However, the unnecessary thickness in the trailing edge coming from this approach (
Figure 1) reduces the performance when compared with standard aerofoils used for turbomachinery blades. As a global effect, the average aerodynamic efficiencies of reversible profiles reach just up to 95% of the correspondent non-reversible geometry [
4].
Since 2012, the new legislation introduced minimum efficiency grades, imposing stricter efficiency constraints on fan designers during the design of a new reversible fan, challenging them toward revised reversible aerofoil concepts. In the past, this process relied mainly on two-dimensional cascades wind tunnel data [
5] or fully three-dimensional annular cascades data [
6]. Nevertheless, experimental reversible cascade data are seldom available to industrial fan designers.
When looking at optimization strategies, several multi-objective optimization problems (MOOPs) have been presented in the open literature and the choice depends upon various aspects, in particular the level of knowledge of the objective function and the fitness landscape [
7]. Among these methods, evolutionary algorithms (EAs) often perform well in approximating solutions to all types of problems. They ideally do not make any assumption about the underlying fitness landscape and they are able to find a good spread of solutions in the obtained set of solutions. Furthermore, genetic methods are independent from the level of knowledge of the objective function and the fitness landscape, and are consequently less sensitive to numerical noise. Over the past decade, a number of multi-objective evolutionary algorithms (MOEAs) have been proposed [
8,
9,
10,
11,
12,
13,
14], primarily because of their ability to find multiple Pareto-optimal solutions in one single simulation run. Among the number of different EAs, the most popular belong to the family of genetic algorithms (GAs) and among these, we focused on non-dominated sorting genetic algorithm (NSGA)-II [
15].
When dealing with engineering optimization problems, the number of calls of the objective function to find a good solution can be high. Furthermore, in optimization problems based on computer experiments, where the simulation acts as the objective function, the computational cost of each run can severely restrict the number of available calls to the fitness function. Therefore, to reduce these computational efforts, the introduction of SMs has been proposed. Traditionally, the use of SMs in MOEAs has been classified according to the type of surrogate model at hand [
16,
17,
18]. However, these works have shelved MOEAs’ point of view concerning the integration of SM into the evolutionary process. Jin [
19] and Manríquez [
20] proposed a classification based on the way EAs or MOEAs incorporate the SMs (focusing on the optimization loop). This taxonomy is called working style classification and allows for finding similar optimization problems, putting a greater emphasis on the methodology followed and not on the SM used. According to such a classification, the approaches are divided into direct fitness replacement (DFR) methods and indirect fitness replacement (IFR) methods [
20].
This paper presents a study on the SM-based methodology to obtain a set of optimized aerofoil shapes for use in reversible fan blading. The work investigates the possibility to speed up the MOOP based on a non-dominated sorted genetic algorithm proposed by Deb [
15], by means of SMs. In this view, meta-models created by a least square interpolation surface and artificial neural network were used to replace aerodynamic performance predicted by XFoil [
21]. Even if the use of the boundary element method (BEM) can lead to non-optimal solutions, it is still a good replacement (mostly customary in design phase) of an expensive tool, such as computational fluid dynamic (CFD), to perform a preliminary study on this topic and to define guidelines to replicate the study in cascade configuration by means of CFD [
22]. Each meta-model was used in two different optimization strategies, namely, (i) a simple-level characterized by a no evolution control (NEC) approach, and (ii) an indirect fitness replacement (IFR) bi-level. To have the maximum control on each step of the MOOP solution, the entire optimization framework and the meta-models development were in-house coded in Python [
23]. In conclusion, differences between the use of different meta-models and different optimization strategies are discussed by means of quality metrics typical of optimization schemes.
3. Surrogate Model-Based Optimizations
If the final objective is to compute a stable solution for the MOOP, more accurate and computationally expensive fitness estimators need to be deployed into the MOEA framework, increasing the time to solution. As a compromise, the established framework to address such challenging optimization problems is the use of surrogate-based optimization, in which a meta-model approximates the fitness function and leads the optimizer with local or global extrema values at a much lower computational cost [
8,
9]. In this work, the least square method (LSM) and artificial neural networks (ANNs) were used as surrogate models (SM) of the original BEM solution (i.e., the XFoil-based fitness function) in the MOOP.
Two meta-model optimization approaches were considered. Namely, the simple-level approach, in which the optimization is entirely driven by the SMs, and the bi-level approach, in which the reference solution (original fitness function) is used to evaluate the surrogate optimum designs.
Following the classification proposed by Jin [
32] and Manríquez [
20], the simple-level is also called the direct fitness replacement (DFR) method or no evolution control (NEC), and it is considered the most straightforward SM approach. The simple-level framework is illustrated in
Figure 4, where MOEAs calculate the solutions using the SMs without any assessment against the original fitness function. NEC has proven to be adequate in problems with low dimensionality in both decision and objective space, and is established in turbomachinery applications [
11,
12,
13,
14]. However, in more challenging problems [
12,
20], this approach can converge to false or sub-optima, which in a MOOP, is a Pareto front not corresponding to the Pareto front estimated by the original function.
The bi-level framework (or
in-fill criterion), also known as the indirect fitness replacement (IFR) method [
24,
33], advocates the use of the fitness function during the EA process, adding new sample points to the current data set, while one or more components of the MOEA (typically the variation operators) are assessed in the SM. The IFR method is clearly a two-stage approach, as illustrated in
Figure 5. A number of solutions are produced, evaluated, and compared using the SM. Among them,
n best solutions are then delivered to the parent approach and evaluated against the original fitness function to enrich, iteration by iteration, the sampling data set from which meta-models are derived. Therefore, it is expected to keep the optimization towards the true Pareto front, and at the same time reduce the risk of convergence to false optima [
16,
34]. Most of the existing works in this category use the MOEA in a direct coarse grain search, while the SM intervenes in a local search, providing candidate solutions, which are then assessed in the real function. Therefore, the IFR approach uses the SM for exploitation purposes, while the MOEA is employed for design space exploration.
3.1. Data Sampling
In both of the optimization frameworks, the initial meta-models were trained by means of selected samples inside the design space. In this work, the design space includes
s = 8 parameters (i.e., 6 airfoil geometry parameters,
Re and
CLS), and the vector of independent variables reads as follows:
Usually, a full factorial design of experiment is used to test all possible combinations of variables (factors). Such an approach would require a large number of experimental trials, specifically 3
8 = 6561. To reduce the number of trials, we use a central composite design, and in particular the rotatable central composite inscribed (CCI). CCI is full factorial, to which 2
s axial trials and center point trials are added [
35,
36]. Axial points are located at factors levels −1 and 1, while factorial points are brought into the interior of the design space and located at distance 1/
ν from the center point. Here,
ν is the distance from the center of the design space to a star point. To ensure the rotatability of the design [
37],
ν was set to the following:
where
s is the number of factors. As a consequence, the number of factorial runs is 2
8 = 256, with
ν set to 4 to keep rotatability. The operating ranges for all the factors and the levels at which they were tested are shown in
Table 3.
The total number of experimental trials was equal to
N = 2
s + 2
s + 1 = 273. All 273 examples were tested by means of XFoil to calculate the vector of design objectives that reads as follows:
Notably, the entire sampling task required approximately 1.5 h on a 4 cores i7 laptop.
3.2. Least Square Method (LSM)
The model fitness function was approximated using a second-order polynomial response surface, which reads as follows:
A least square method fit approach enables the estimation of the polynomial coefficients, or regressors, so that it best fits the CCI data set. The polynomials (8) quantify the relationship between the vector
O of the objective functions,
ε and
α, respectively, and the factors.
ζι are the regressors and
q is an error associated with the model. This first surrogate model is suitable for optimization processes and can handle noisy optimization landscapes, as reported in the works of [
33,
38].
3.3. Artificial Neural Network (ANN)
The neural network developed was a multilayer perceptron (MLP), commonly used in regression problems [
39]. A series of tests on the architecture of the MLP was carried out to identify the best tradeoff architecture to ensure accuracy and limit the computational costs. Following these tests, the selected configuration MLP included one hidden layer, 25 neurons, a
logsig activation function on the hidden layer, and a linear function on the output layer. Tests were done using 10 to 60 neurons, and 1 and 2 hidden layer(s), for a total of 6 tests on a single layer network and 36 tests on a double layer network. The architecture with one hidden layer and 25 neurons had the best surrogate model coefficient of determination. The MLP is illustrated in
Figure 6.
The neural network was trained using a Bayesian optimization algorithm, randomly initializing weights and biases between 1 and −1. To avoid convergence into a local minimum and detect overfitting, the sampling dataset was re-organized into five different datasets; each was then split into a “training dataset” containing 80% of the total samples, and a “test dataset” with the remaining samples. The ANN was then trained on each dataset and the accuracy was evaluated by means of the coefficient of determination R/1, calculated above the entire normalized prevision set; ε and α.
3.4. Pareto Front Properties
To further analyze the SM-assisted multi-objective optimization performance, the quality of results was assessed using the following Pareto front properties: (i) the number of Pareto optimal solutions in the set; (ii) the accuracy of the solution in the set (i.e., measured by closeness to the theoretical Pareto-front solution); and (iii) the distribution and (iv) spread of the solutions [
40]. To quantify these properties, we computed a set of performance indices. Specifically; (i) Overall Non-dominated Vector Generation Ratio (
ONVGR); (ii) Hyperarea (
H); and (iii) Spacing (
Sp) and Overall Pareto Spread (
OS).
ONVGR is a cardinality-based index derived from the one defined in Okabe et al. [
40], and it is linked to the number of non-dominated solutions in the Pareto front. To compute this index, all the elements that populate the optimized solution sets (from all optimization framework; MOEA and SMs assisted optimizations) were combined in a unique Pareto front for each test case, according to the non-dominated sorting algorithm of NSGA-II.
ONVGR defines the percentage of unique Pareto front elements that are generated from metamodel-assisted optimization, or using XFoil as fitness function.
H identifies the area of objective space subtended by the Pareto solution set.
Sp identifies the distance between the elements that populate the solution set.
OS quantifies how widely the optimized solution set spreads over the objective space. In a two objectives optimization, it is computed as the ratio of the rectangle that is defined selecting the good and bad points (according to each objective functions), and the rectangle that has two vertices on the Pareto front extreme points. A solution set presenting higher
OS value is characterized by wider spread.
4. Results
Standard MOEA results are first illustrated. The results from the developed SMs are then presented and compared against MOEA.
4.1. MOEA
The fitness function selected to compute the objective functions
ε and
α during NSGA-II algorithm was based on BEM modelling of the airfoil (i.e. XFoil). This model was selected as it is customary in the prediction of aerofoil lift and drag polars [
41,
42]. Moreover, RANS-based numerical models were found to be affected by noise as a consequence of turbulence modelling discontinuous variations in calculating objective functions and discretization, as indicated by Giunta et al. [
43] and Madsen et al. [
44,
45].
Figure 7 shows the objective function values of the initial given population P
t for
Re = 1.05 × 10
6 and
CLS ranging between 0.1 and 0.9.
We analysed the initial population using XFoil with the aim to find an initial frontier. We sorted the tested individuals according to fast non-dominated sorting algorithm, suggested by Deb [
15], obtaining the front depicted by filled symbols. Any optimization technique should move this imaginary frontier (dotted line) towards higher efficiencies and stall margins.
Figure 8 shows the results for all
Re and
CLS combinations of the MOEA test matrix after 20 generations.
Each graph illustrates the initial frontier (dotted line) and the final frontier obtained by a selection of elements on the Pareto fronts. Irrespective of the configuration, the frontier shifts as a result of a major improvement in efficiency, lowering the stall margin.
4.2. No Evolution Control (NEC) or Single-Level Approach
MOOP was solved using NSGA-II algorithm assisted by developed meta-models. SMs’ accuracy in terms of coefficient of determination
R/1 for the least square method and artificial neural networks is reported in
Table 4.
In this method, there is no call to the original fitness function-based BEM, and the optimization was stopped after 20 generations. To assess the results of the SM-assisted optimization, solutions on the Pareto fronts were retested with XFoil.
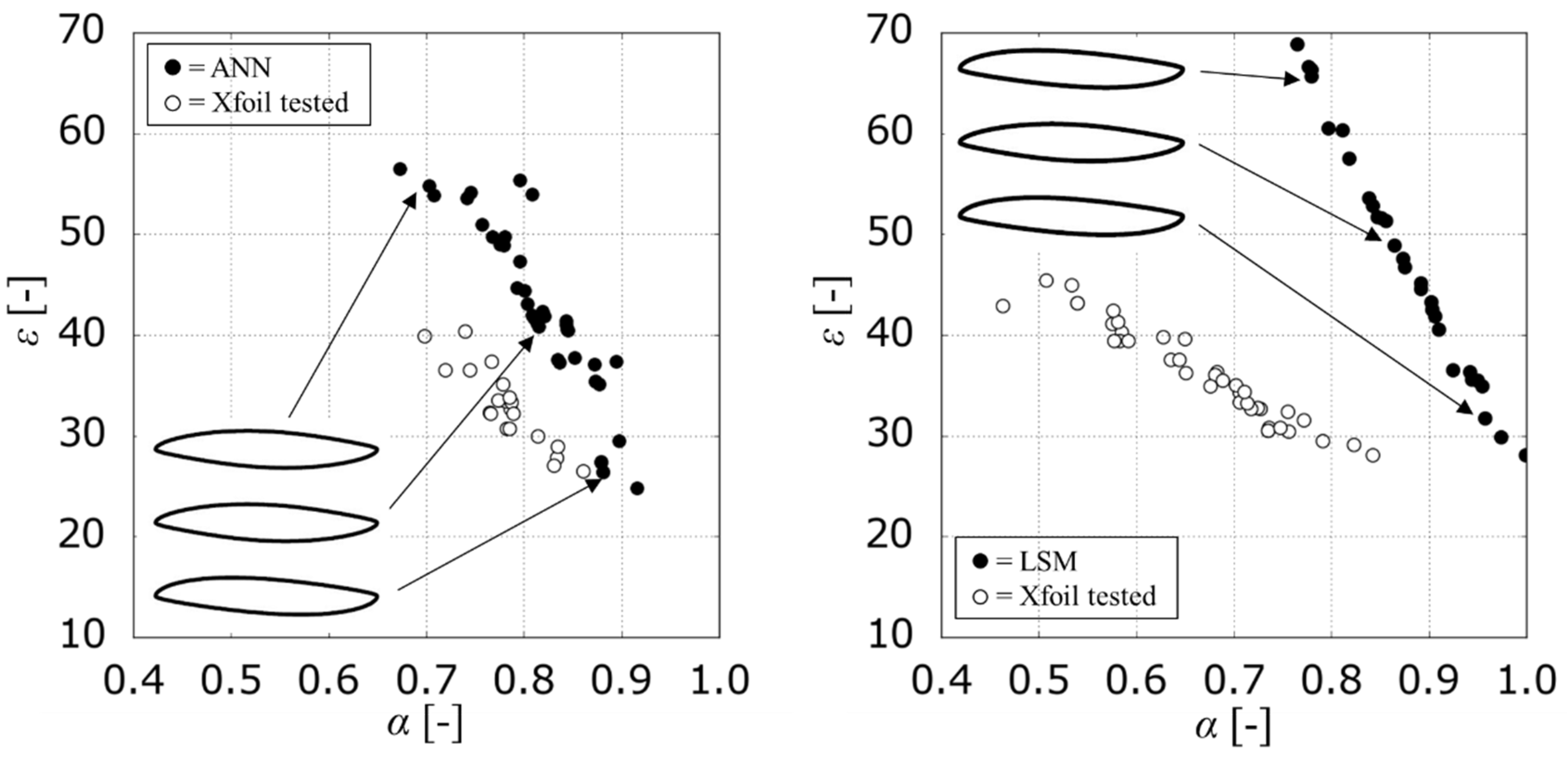
Figure 9 shows the results of such an assessment for
Re = 1.05 × 10
6 and C
LS = 0.5. Irrespective of the value of Reynolds number and C
LS, the use of SMs to drive the optimization result was inadequate with the NEC approach. In fact, a consistent discrepancy was observed between the meta-model predicted aerodynamic performance (black dots) and the performance obtained testing the same individuals with the BEM function (white dots).
A geometrical analysis made on a few geometries of the SMs’ Pareto fronts confirms that the geometrical trends, previously found with MOEA, are not reproduced. In addition, as described in
Figure 9, each Pareto front given by SMs provides similar aerofoil shape, in contrast to the flow physics, which suggest the finding of thinner aerofoils in zones with high efficiency and low stall margin, and conversely an increased thickness in the zone with low efficiency and high stall margin.
To quantify the underlined departure of SMs’ optimization, the prediction capability (
Pc) was plotted against the number of iterations in
Figure 10 (i.e.,
Re = 1.05 × 10
6,
CLS = 0.5). Notably, the prediction capability
Pc is an index similar to the coefficient of determination
R/1, computed as follows:
where
εBEM,i is the aerodynamic efficiency (objective function) of the
ith individual of Pareto front tested with the
BEM function, and
ε,i is the efficiency predicted by the surrogate model. Using the same criteria, we have computed
Pc,α.
Irrespective of the SMs, after an initial phase of five or six iterations, in which the meta-model prediction is above 90%, Pc quickly drops for both objectives ε and α. Despite that Pc trends in ANN and LSM are similar, the optimization behaviors are totally different. In the test matrix, ANN tends to empathize a geometrical feature that generates distorted or unrealistic geometries that are hard or impossible to simulate by means of XFoil, while this trend was seldom recorded for LSM.
The inability of meta-model based optimized geometry to replicate the behaviour of aerofoils is strongly connected to the incorrect prediction of elements in the intermediate regions of the sampled design space for SMs’ instruction. This circumstance was already documented in highly dimensional problems (as in the present case owing to the selected aerofoil parameterization) when using the single-level NEC approach [
12,
46].
4.3. Indirect Fitness Replacement (IFR) or Bi-Level Approach
In view of the poor performance of the NEC approach, the IFR framework was implemented for the solution of the MOOP. In this case, the initial sampling was used to train the first iteration of both meta-models. Then, meta-model assisted NSGA-II was invoked for five generations. The genetic algorithm was kept identical to the original formulation used in the reference MOEA optimization. After the NSAG-II completion, the 40 best new members are evaluated using the original fitness objective function, and then stored to enrich the SMs training pool. To this end, a limit of 10 calls to the objective function was set, in order to control the computational cost of the optimization process.
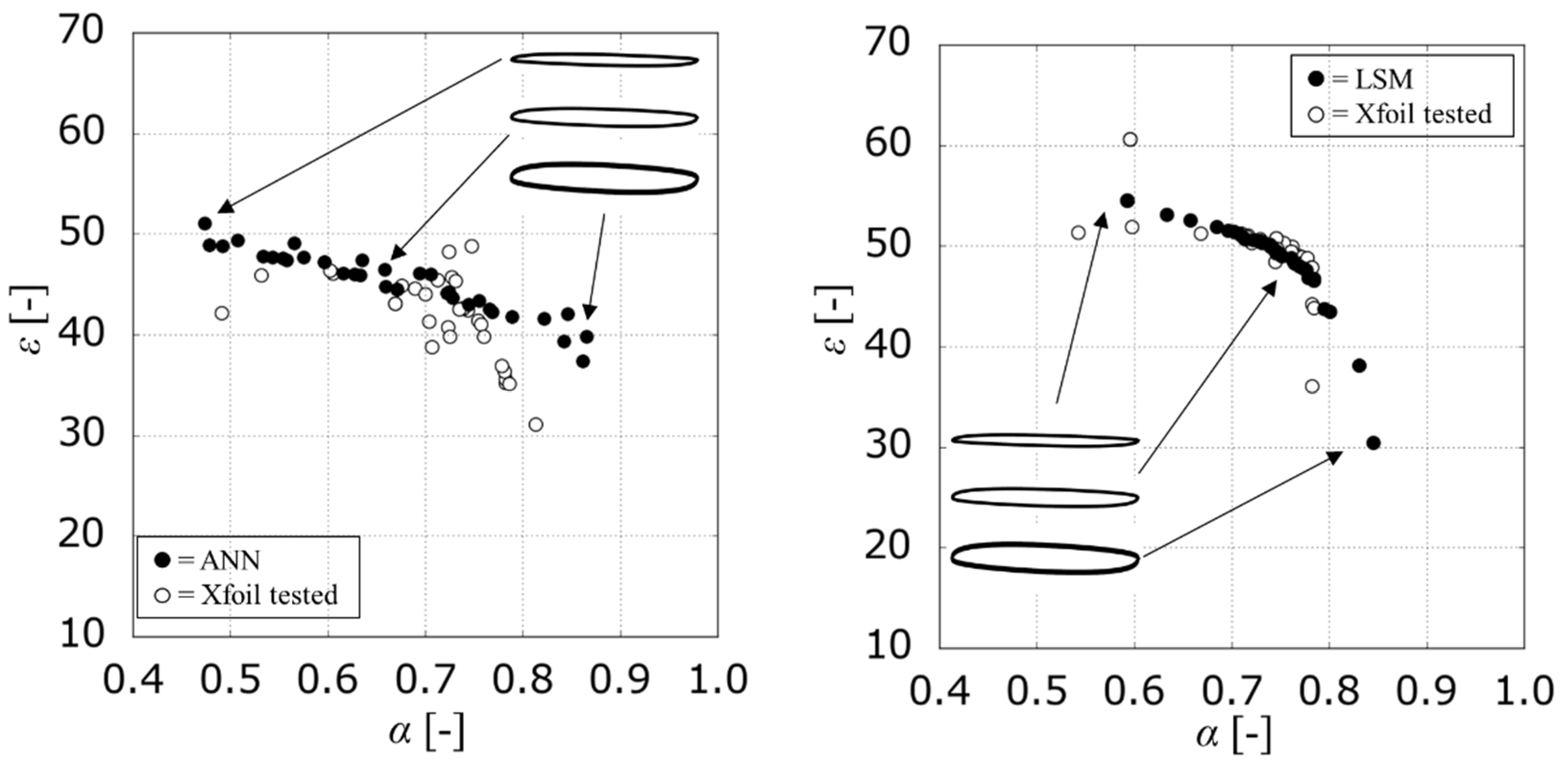
Figure 11 illustrates the results of the final iteration loop again for the combination
Re = 1.05 × 10
6,
CLS = 0.5, already used in the NEC exploration. In the IFR approach, aerodynamic performance predictions are in good agreement with XFoil predictions, with a significant gap reduction between Pareto fronts estimated by the meta-models and by the original fitness function. In addition, it is possible to infer that the aerofoil flow physics is well represented in both SM-based optimizations, by the change in the aerofoils geometry. Thinner aerofoils populate the upper left region of Pareto front, where the efficiency increases to the detriment of stall margin, as expected and confirmed by MOEA analysis.
Figure 12 shows the overall comparison of SM-assisted optimizations against the standard MOEA for five different configurations of the test matrix. Notably, in
Figure 12, the dotted lines indicate the base-line aerofoil performance for the specified
Re and
CLS values. To give additional hints about the ANN-based surrogate,
Figure 12 also shows the results of a reduced complexity level artificial neural network with only 10 neurons per hidden layer. Because the results obtained with the IFR approach demonstrates that the complexity of SMs had low impact on the quality of the obtained Pareto fronts, we performed the optimization with a simplified version of the ANN to reduce the computational effort required. At a glance, these results give the indication of the quality of SM-assisted optimizations implemented in a IFR test-bed, using half of the computational effort required by the MOEA. It is also worth noting that, when comparing the two meta-models, the quality of the Pareto front solutions is close, indicating a reduced influence of the optimization process to the specific meta-modelling algebra.
Table 5 reports the values of the indexes described in
Section 3.4. In each column, the best case is in
bold, and the worst case is in
italic.
According to the values of
ONVGR listed in
Table 5, the SM-assisted optimizations resulted in a larger number of non-dominated elements in the set when compared with MOEA. The only exception concerns the central test case in the matrix (
Re = 105000,
CLS = 0.5), where MOEA optimization reaches 33.3% of non-dominated elements. However, we can obtain the same result using LSM as the fitness function.
As per H, the use of ANN determines a wider dominated area in the objective space, although LSM has very close values for the same test cases. As observed above, also in this case, worse results have been obtained using the MOEA approach. Concerning SP values, the analysis shows that ANN, even with 10 neurons, in general have Pareto fronts characterized by the minimum distance between the elements that populate the solution. The values of OS tend to confirm that ANN Pareto sets present a wider spread over the objective space, in line with the H quality.
As a final comment, it is impossible to say that the overall quality of solution sets for MOOP cannot be accounted for by means of a single performance index, especially if the shape of Pareto front is extremely different. In the end, because in this study the declared final objective was to move as much as possible the technological frontier on the α–ε chart, the effectiveness was assessed by means of ONGVR index, concluding that SMs-assisted optimization can be equivalent, or even better in this case, with respect to that based on XFoil and surrogate models.
5. Conclusions
This paper presents an investigation of surrogate-based optimization of truly reversible profile family for axial fans. The multi-objective optimization problem (MOOP) is based on the NSGA-II, an evolutionary algorithm able to find multiple Pareto-optimal solutions in one simulation run. The MOOP has been firstly solved using the XFoil software, avoiding the modelling and use of any SMs. These results have been compared with those obtained by implementing different SMs in the MOOP, considering two different optimization frameworks, namely NEC and IFR.
The use of SMs to assist MOEAs is a complex matter that requires an exhaustive analysis of the entire optimization framework and how the SMs are embedded in the considered optimization algorithm.
This work has shown that, for this problem, an IFR approach has to be preferred to an NEC approach. In fact, an NEC approach has produced false Pareto-fronts in all of the tested configurations. In particular, the NEC optimization has been not able to explore the entire design space in between the sampling points. The genetic algorithm led the optimizer to candidate solutions that were, during every iteration, more and more distant from the corresponding true value. This interpretation was suggested by the decreasing value of prediction capability associated with the increase of unrealistic geometries and thick profile.
An IFR approach has produced more reliable results, providing a good prediction capability during the iterations, and hence reducing the distance between estimated and true Pareto fronts. The optimization was able to cover the entire design space, providing a geometry along the Pareto fronts similar to those experienced by the MOEA optimization. The IFR method required a more complex and computationally expensive optimization framework based on a bi-level approach, with the infill criterion based on the results of the GA.
An analysis of the ONVGR index has shown that, in most cases, the IFR optimization was able to produce better results (individuals) than the XFoil-based optimization.
Regarding the SMs used in this work (an LSM and ANN with different number of neurons), the IFR results show the independence of the MOEA to the SM considered. This is considered an important outcome; LSM being an easier and faster to model when compared with an ANN. On the other side, the NEC approach results do not present any relevant differences between the two SMs, even though different prediction accuracies were reached.
The different reliability of the results obtained by adopting a NEC and IFR approach scales down the role and importance of the initial sampling in SMs-based optimization. In fact, it is evident that an NEC approach is totally favourable to exploitation, on the contrary, not being able to correctly explore the design space. An IFR approach, which involves an infill criterion, overcomes the difficulties and limitations related to the correct initial sampling creation, by iteratively adding optimized solutions evaluated with XFoil to the initial sampling. This approach ensures a better balance between exploration and exploitation of the design space.
The results shown for the IFR approach demonstrated that, in the selected cases, a consistent reduction of MOOP computational cost is possible. In the specific case, according to the metric selected to judge the Pareto frontiers, the calls to the expensive objective function were reduced by 50%, in all cases producing a reliable set of better solutions in comparison with the standard MOEA approach.
In conclusion, this study clarified the strong impact of the optimization framework on the reliability of the obtained Pareto fronts in a SM-based design optimization for an industrial fan benchmark problem. With an IFR approach, the use of the considered SMs can significantly reduce the computational time needed to solve the MOOP by reducing the call of the fitness function, while ensuring the creation of the same, or even better, Pareto fronts when compared with those obtained using only XFoil. The solutions obtained by the IFR method present higher values of Pareto quality indexes when compared with MOEA (see
Table 5). The major improvement is associated with the
ONVGR index, which assesses that the elements populating the Pareto front obtained with the SMs-assisted optimization dominate the solution obtained with the MOEA.