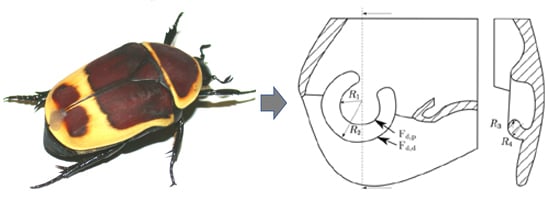
The Topology of the Leg Joints of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) and Its Implication for the Tribological Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1 Sample Preparation
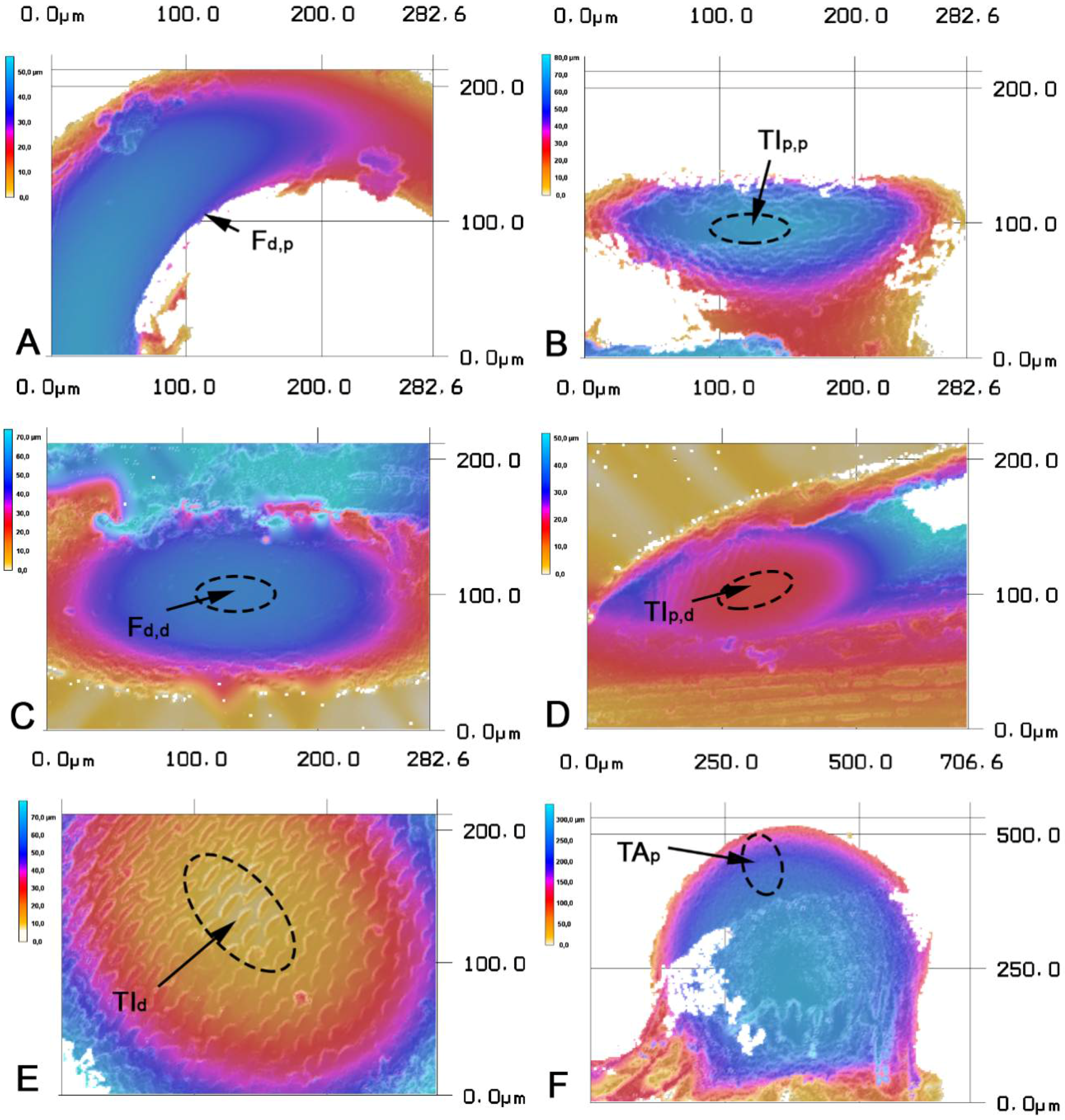
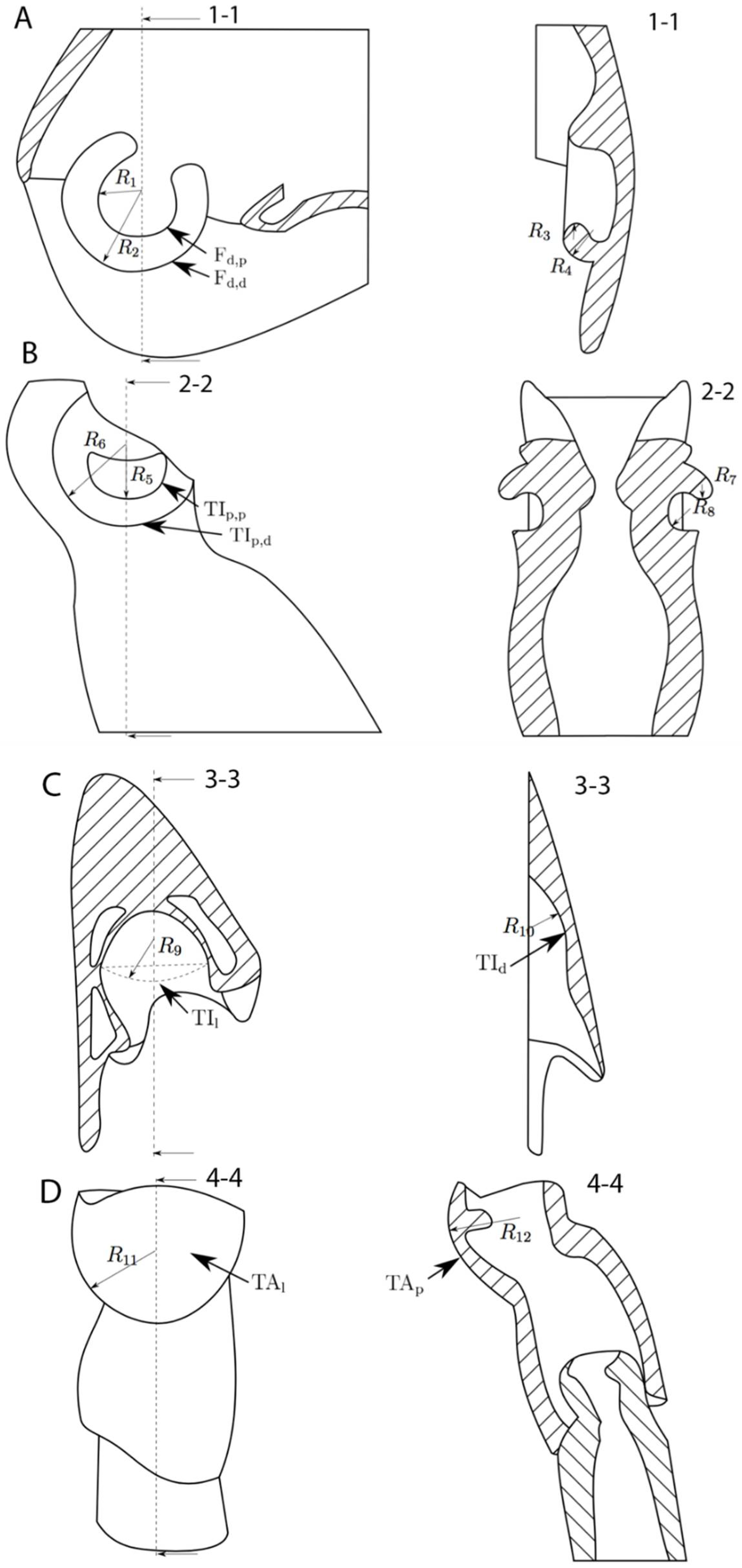
2.2 Confocal Laser Scanning Microscopy and White Light Interferometry
2.3 Nanoindentation
2.4 Statistical Analysis
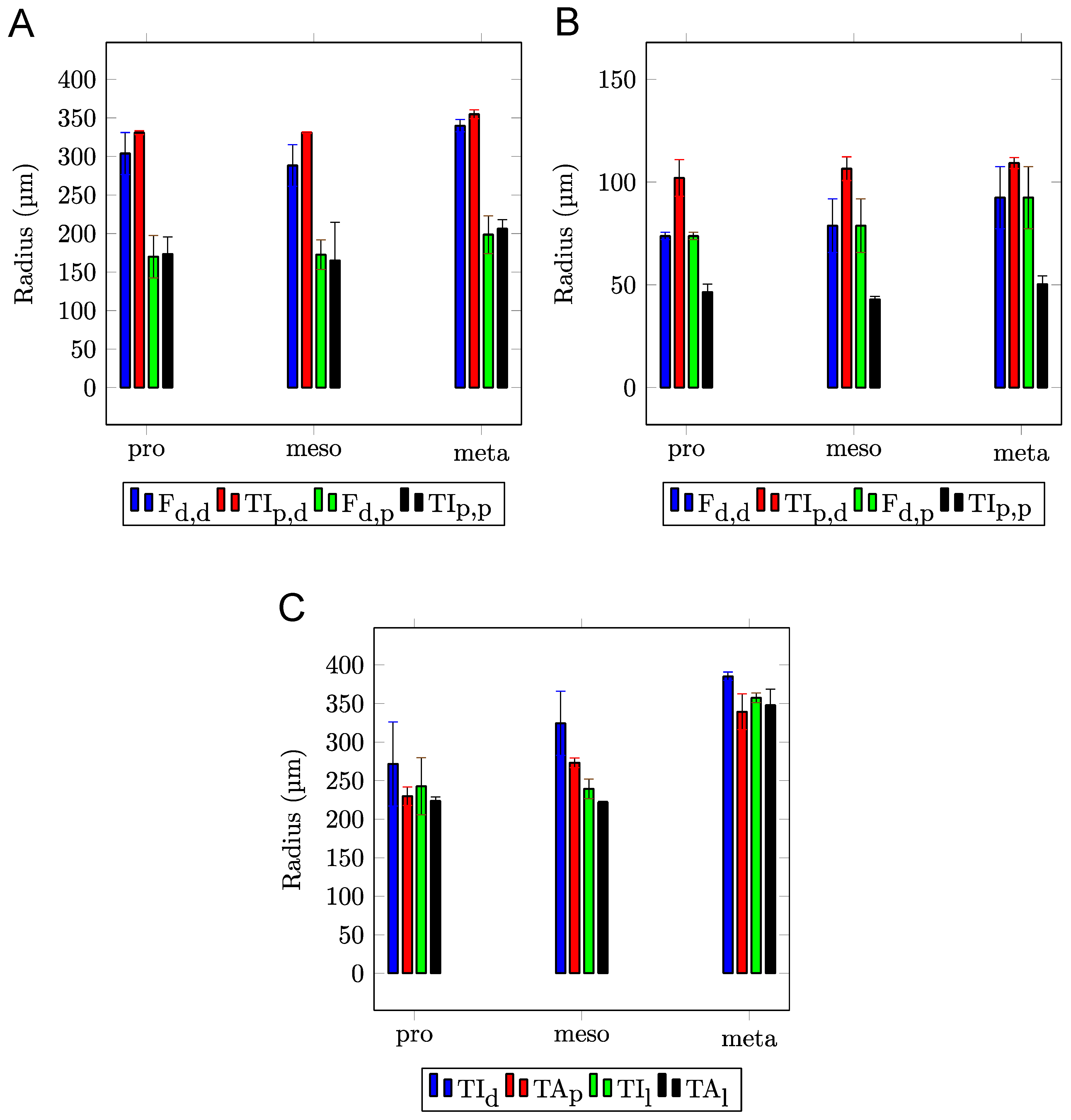
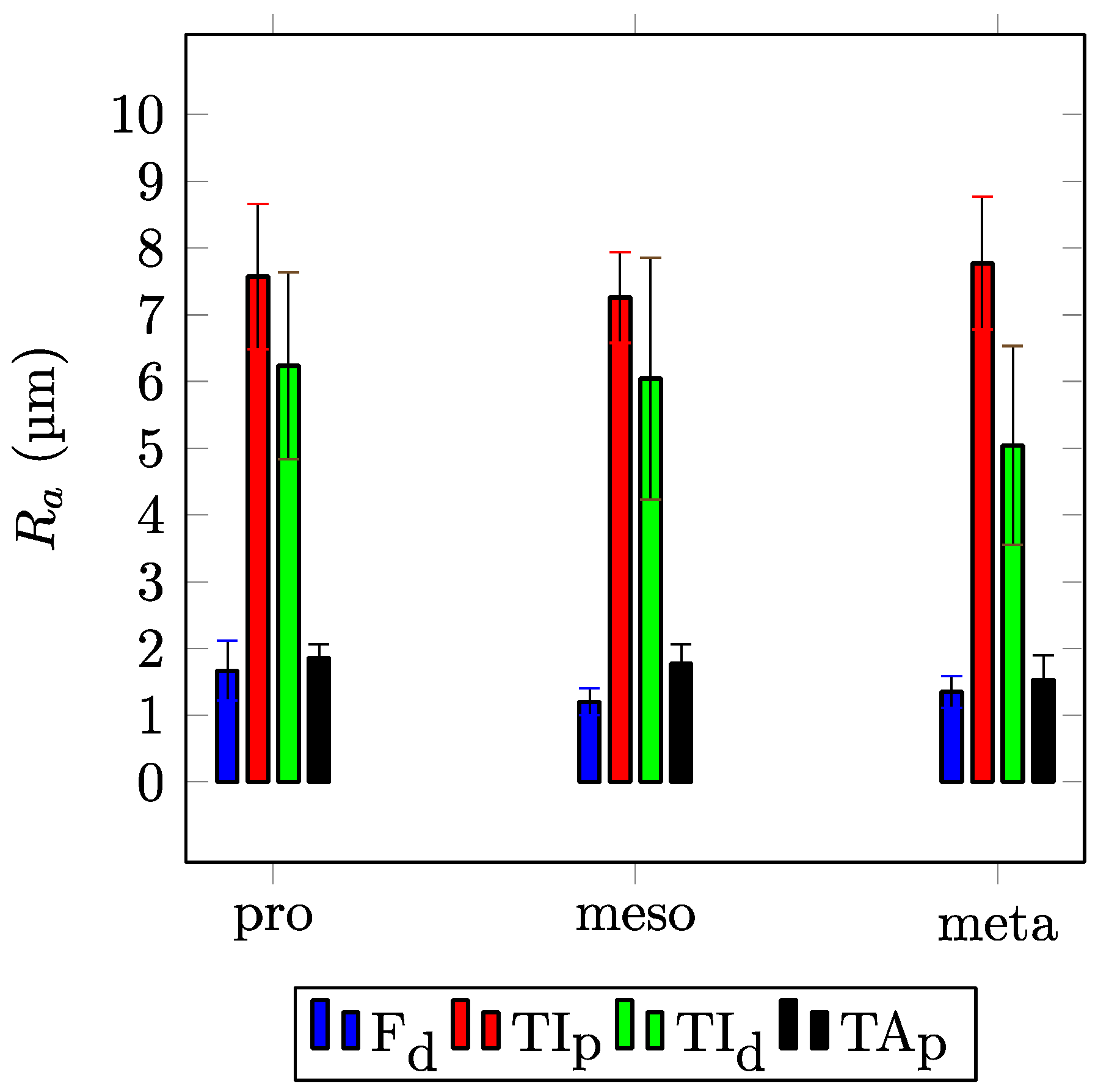
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Scherge, M.; Gorb, S.N. Biological Micro- and Nanotribology; Springer Science & Business: Berlin, Germany, 2001. [Google Scholar]
- Persson, B.N.J. Sliding Friction: Physical Principles and Applications; Springer Science & Business: Berlin, Germany, 2013. [Google Scholar]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues, 2nd ed.; Springer: Berlin, Germany, 1993. [Google Scholar]
- Date, K. Scanning electron microscope studies on the synovial membrane. Arch. Histol. Jap. 1979, 42, 517–531. [Google Scholar] [CrossRef] [PubMed]
- Leach, D.H.; Caldwell, S.J.; Ferguson, J.G. Ultrastructural study of synovial membrane from the antebrachiocarpal joint of calves. Cells Tissues Organs 1988, 133, 234–246. [Google Scholar] [CrossRef]
- Mow, V.C.; Ateshian, G.A. Lubrication and wear of diathrodial joints. Basic Orthop. Biomech. 1997, 2, 275–315. [Google Scholar]
- Smeathers, J. Cartilage and joints. In Biomechanics—Materials: A Practical Approach; Vincent, J.F.V., Ed.; IRL Press: Oxford, UK, 1992; pp. 99–132. [Google Scholar]
- Clark, J.M.; Norman, A.G.; Kaab, M.J.; Notzli, H.P. The surface contour of articular cartilage in an intact, loaded joint. J. Anat. 1999, 195, 45–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorb, S.N. Attachment devices of insect cuticle; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Dai, Z.; Gorb, S.N. Micro-structure and frictional characteristics of beetle’s joint. Sci. China Ser. G Phys. Mech. Astron. 2004, 47, 99–106. [Google Scholar] [CrossRef]
- Barbakadze, N.; Enders, S.; Gorb, S.N.; Arzt, E. Local mechanical properties of the head articulation cuticle in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae). J. Exp. Biol. 2006, 209, 722–730. [Google Scholar] [CrossRef] [PubMed]
- Kheireddin, B.A.; Wiliams, T.C.; Akbulut, M. Tribological properties of femur-tibia articulation of lubber grasshopper. Tribol. Int. 2012, 50, 76–81. [Google Scholar] [CrossRef]
- Enders, S.; Barbakadze, N.; Gorb, S.N.; Arzt, E. Exploring biological surfaces by nanoindentation. J. Mater. Res. 2004, 19, 880–887. [Google Scholar] [CrossRef]
- Gorb, S.N. Functional Surfaces in Biology: Little Structures with Big Effects; Springer: New York, NY, USA, 2009. [Google Scholar]
- Hazel, J.; Stone, M.; Grace, M.S.; Tsukruk, V.V. Nanoscale design of snake skin for reputation locomotions via friction anisotropy. J. Biomech. 1999, 32, 477–484. [Google Scholar] [CrossRef]
- Baum, M.J.; Heepe, L.; Fadeeva, E.; Gorb, S.N. Dry friction of microstructured polymer surfaces inspired by snake skin. Beilstein J. Nanotechnol. 2014, 5, 1091–1103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suh, N.P.; Mosleh, M.; Howard, P.S. Control of friction. Wear 1999, 175, 151–158. [Google Scholar] [CrossRef]
- Mosleh, M.; Laube, S.J.P.; Suh, N.P. Friction of undulated surfaces coated with MoS2 by pulsed laser deposition. Tribol. Trans. 1999, 42, 495–502. [Google Scholar] [CrossRef]
- Volchok, A.; Halperin, G.; Etsion, I. The effect of surface regular microtopography on fretting fatigue life. Wear 2002, 253, 509–515. [Google Scholar] [CrossRef]
- Ryk, G.; Kligerman, Y.; Etsion, I. Experimental investigation of laser surface texturing for reciprocating automative components. Tribol. Trans. 2002, 45, 444–449. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G.; Brizmer, V.; Kligerman, Y. Experimental investigation of laser surface textured parallel thrust bearings. Tribol. Lett. 2004, 17, 295–300. [Google Scholar] [CrossRef]
- Kligerman, Y.; Etsion, I.; Shinkarenko, A. Improving tribological performance of piston rings by partial surface texturing. J. Tribol. 2005, 127, 632–638. [Google Scholar] [CrossRef]
- Vagts, S.; Schlattmann, J.; Busshardt, P.; Kleinteich, T.; Gorb, S.N. The application of multi-body simulation approach in the kinematic analysis of beetle leg joints. Artif. Life Robot. 2017, 22, 412–420. [Google Scholar] [CrossRef]
- Vagts, S.; Schlattmann, J. General Systems Theory in a Horizontal and Vertical Action Process for Cross-Disciplinary Knowledge Transfer. In Proceedings of the ASME IMECE 2013, San Diego, CA, USA, 15–21 November 2013. [Google Scholar] [CrossRef]
- Thchstreet. DIN EN ISO 25178-6; Thchstreet: Carol Stream, IL, USA, 2010. [Google Scholar]
- Pharr, G.M.; Oliver, W.C. Measurement of thin film mechanical properties using nanoindentation. MRS Bull. 1992, 17, 28–33. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Contact mechanics. In Nanoindentation; Springer: New York, NY, USA, 2011; pp. 1–19. [Google Scholar]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Czichos, H. Tribology: A Systems Approach to the Science and Technology of Friction, Lubrication and Wear; Elsevier Science: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Archard, J.F. Elastic deformation and the laws of friction. Proc. R. Soc. Lond. A 1957, 243, 190–205. [Google Scholar] [CrossRef]
- Popov, V.L. Contact Mechanics and Friction; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Sondhauss, J.; Fuchs, H.; Schirmeisen, A. Frictional properties of a mesoscopic contact with engineered surface roughness. Tribol. Lett. 2011, 42, 319–324. [Google Scholar] [CrossRef]
- Baum, M.J.; Heepe, L.; Gorb, S.N. Friction behavior of a microstructured polymer surface inspired by snake skin. Beilstein J. Nanotechnol. 2014, 5, 83–97. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marchetto, D.; Rota, A.; Calabri, L.; Gazzadi, G.C.; Menozzi, C.; Valeri, S. AFM investigation of tribological properties of nano-patterned silicon surface. Wear 2008, 265, 577–582. [Google Scholar] [CrossRef]
- Yu, C.; Wang, Q.J. Friction anisotropy with respect to topographic orientation. Sci. Rep. 2012, 2, 988. [Google Scholar] [CrossRef] [PubMed]
- Gachot, C.; Rosenkranz, A.; Reinert, L.; Ramos-Moore, E.; Souza, N.; Muser, M.H.; Mucklich, F. Dry friction between laser-patterned surfaces: Role of alignment, structural wavelength and surface chemistry. Tribol. Lett. 2013, 49, 193–202. [Google Scholar] [CrossRef]
- Filippov, A.; Gorb, S.N. Frictional-anisotropy-based systems in biology: Structural diversity and numerical model. Sci. Rep. 2013, 3, 1240. [Google Scholar] [CrossRef] [PubMed]


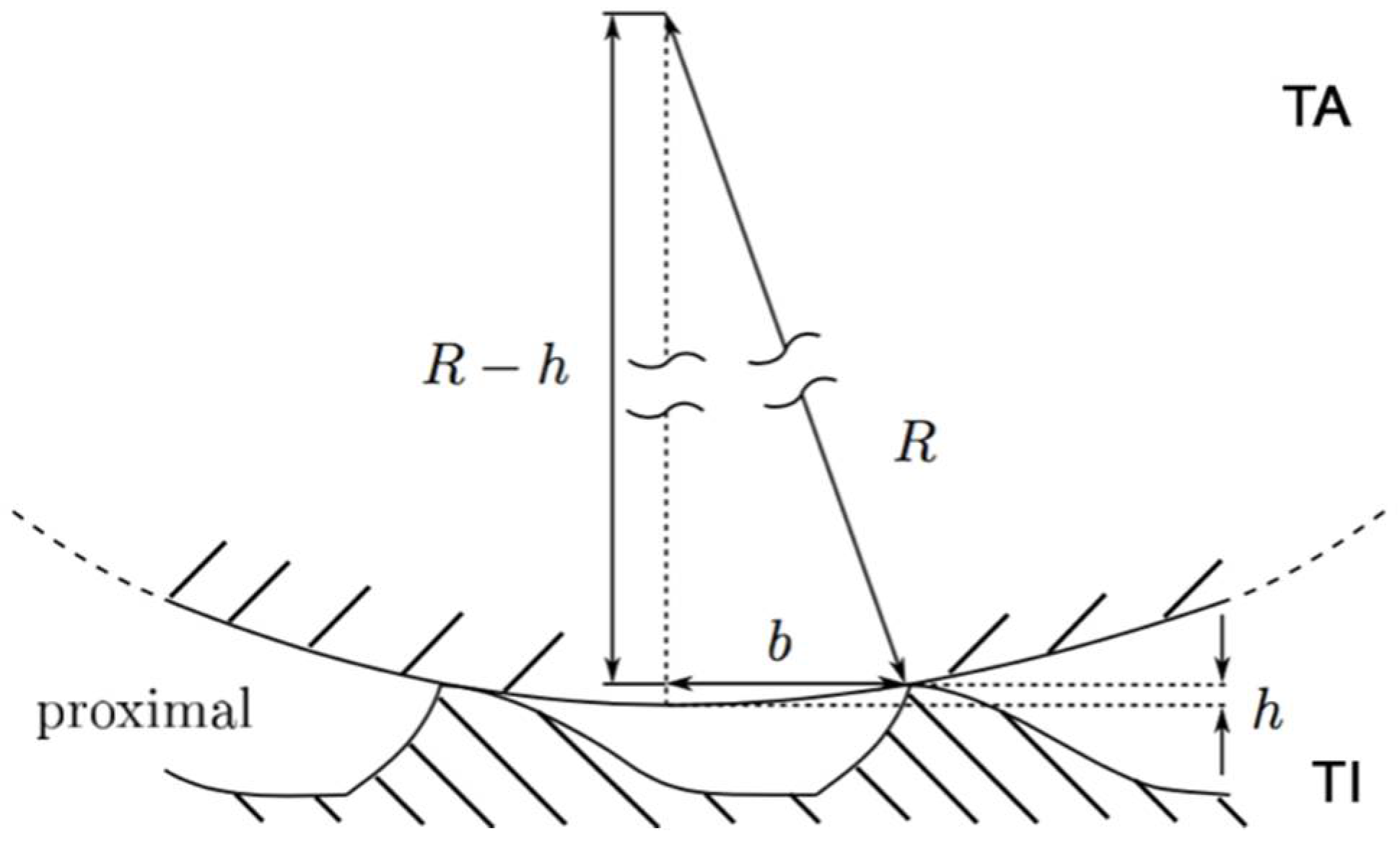

| Width (µm) | Length (µm) | Height (µm) | Δp,d (µm) | Δl (µm) | |
|---|---|---|---|---|---|
| Pro | - | - | - | - | - |
| Meso | 6.52 ± 0.60 | 20.88 ± 1.03 | 3.21 ± 0.24 | 14.10 ± 2.45 | 29.40 ± 10.02 |
| Meta | 7.00 ± 0.31 | 21.43 ± 1.78 | 3.50 ± 0.39 | 14.72 ± 2.04 | 28.84 ± 4.09 |
| E (GPa) | H (GPa) | |
|---|---|---|
| Fd,d | 4.74 ± 2.97 | 0.10 ± 0.03 |
| TIp,p | 0.84 ± 0.17 | 0.03 ± 0.01 |
| TIp,d | 1.80 ± 0.92 | 0.05 ± 0.03 |
| TId | 0.47 ± 0.30 | 0.04 ± 0.04 |
| TAp | 2.06 ± 0.95 | 0.10 ± 0.02 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vagts, S.; Schlattmann, J.; Kovalev, A.; Gorb, S.N. The Topology of the Leg Joints of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) and Its Implication for the Tribological Properties. Biomimetics 2018, 3, 12. https://doi.org/10.3390/biomimetics3020012
Vagts S, Schlattmann J, Kovalev A, Gorb SN. The Topology of the Leg Joints of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) and Its Implication for the Tribological Properties. Biomimetics. 2018; 3(2):12. https://doi.org/10.3390/biomimetics3020012
Chicago/Turabian StyleVagts, Steffen, Josef Schlattmann, Alexander Kovalev, and Stanislav N. Gorb. 2018. "The Topology of the Leg Joints of the Beetle Pachnoda marginata (Scarabaeidae, Cetoniinae) and Its Implication for the Tribological Properties" Biomimetics 3, no. 2: 12. https://doi.org/10.3390/biomimetics3020012