Implementing an Agent-Based Modeling Approach for Protein Glycosylation in the Golgi Apparatus
Abstract
:1. Introduction
2. Theoretical Background
3. Procedure
4. Agent-Based Modeling
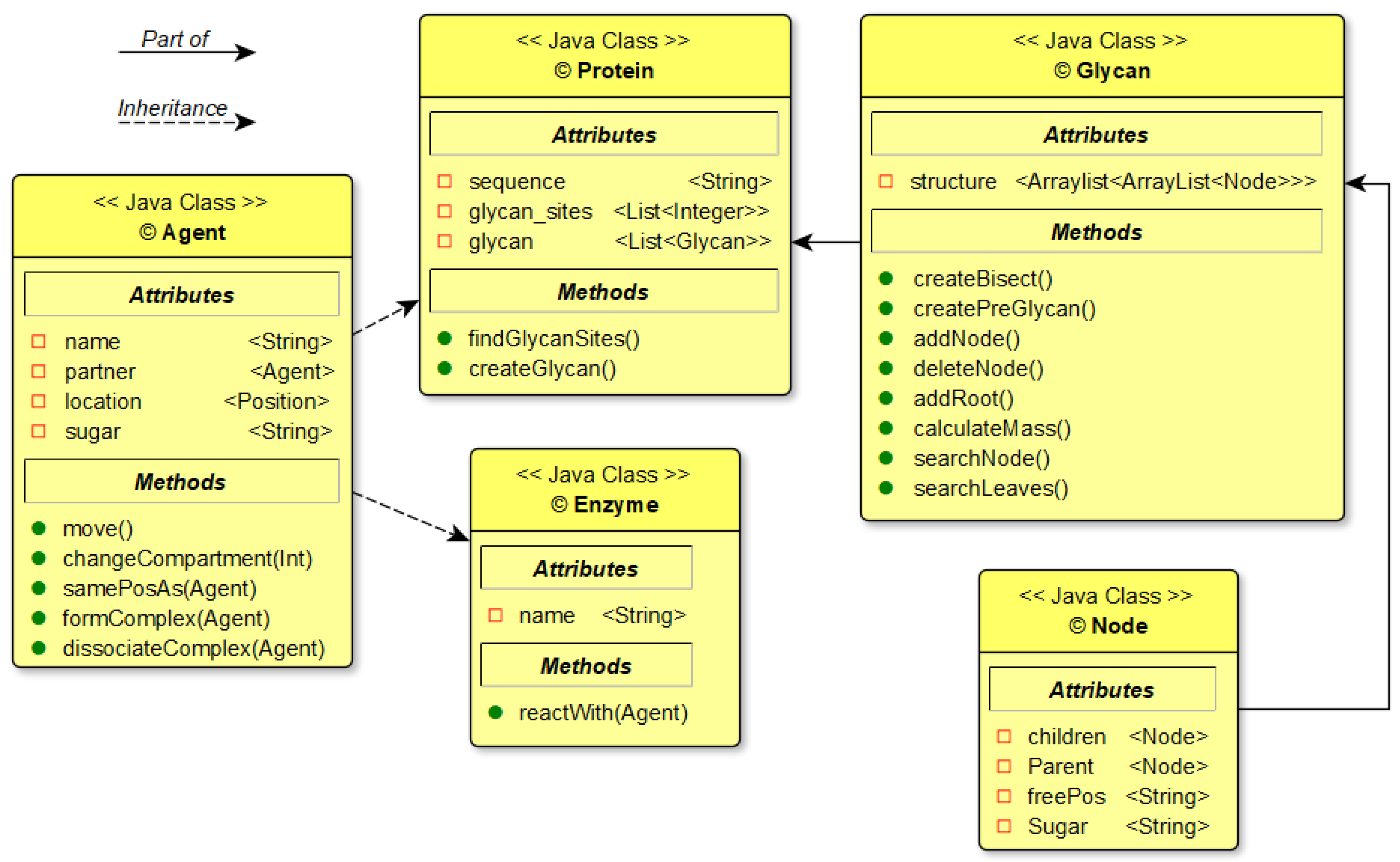
4.1. Java for ABM
4.2. Java Class Structure
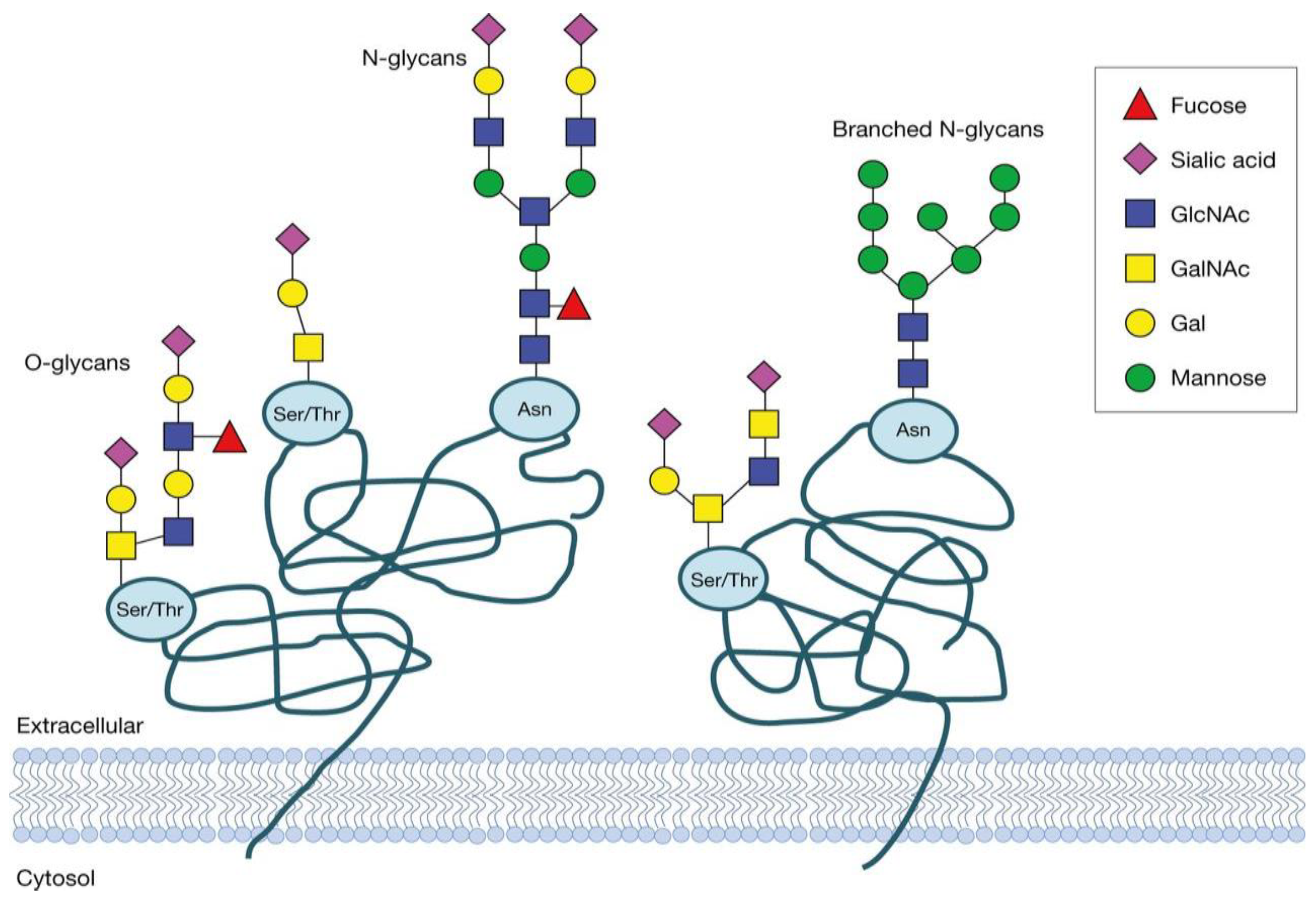
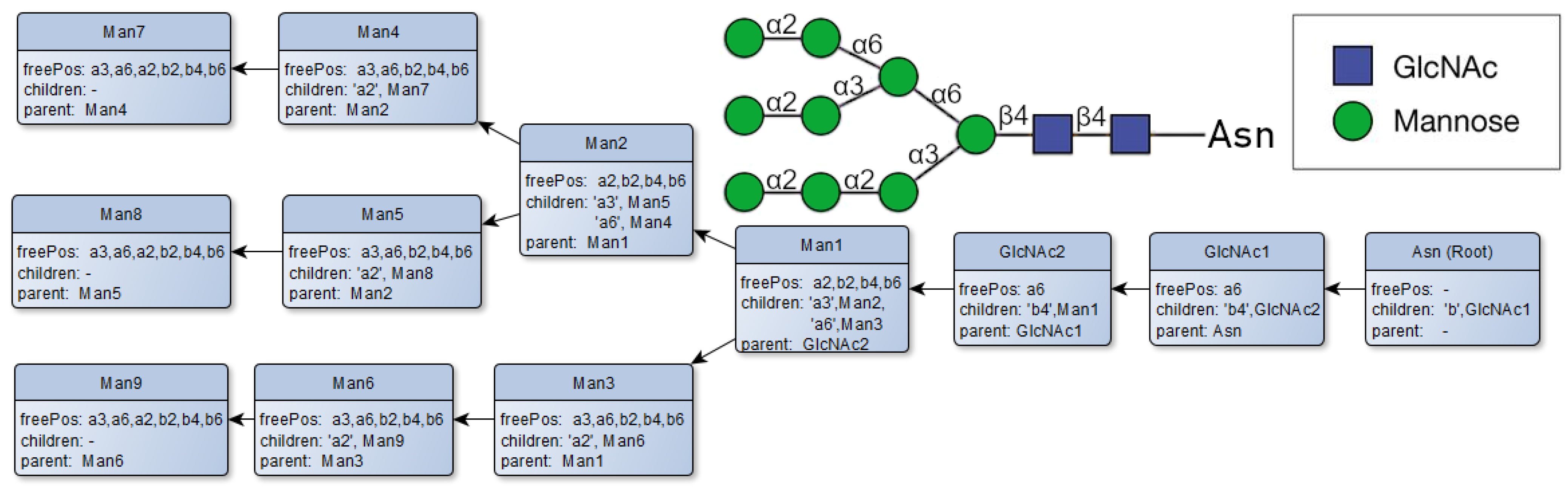
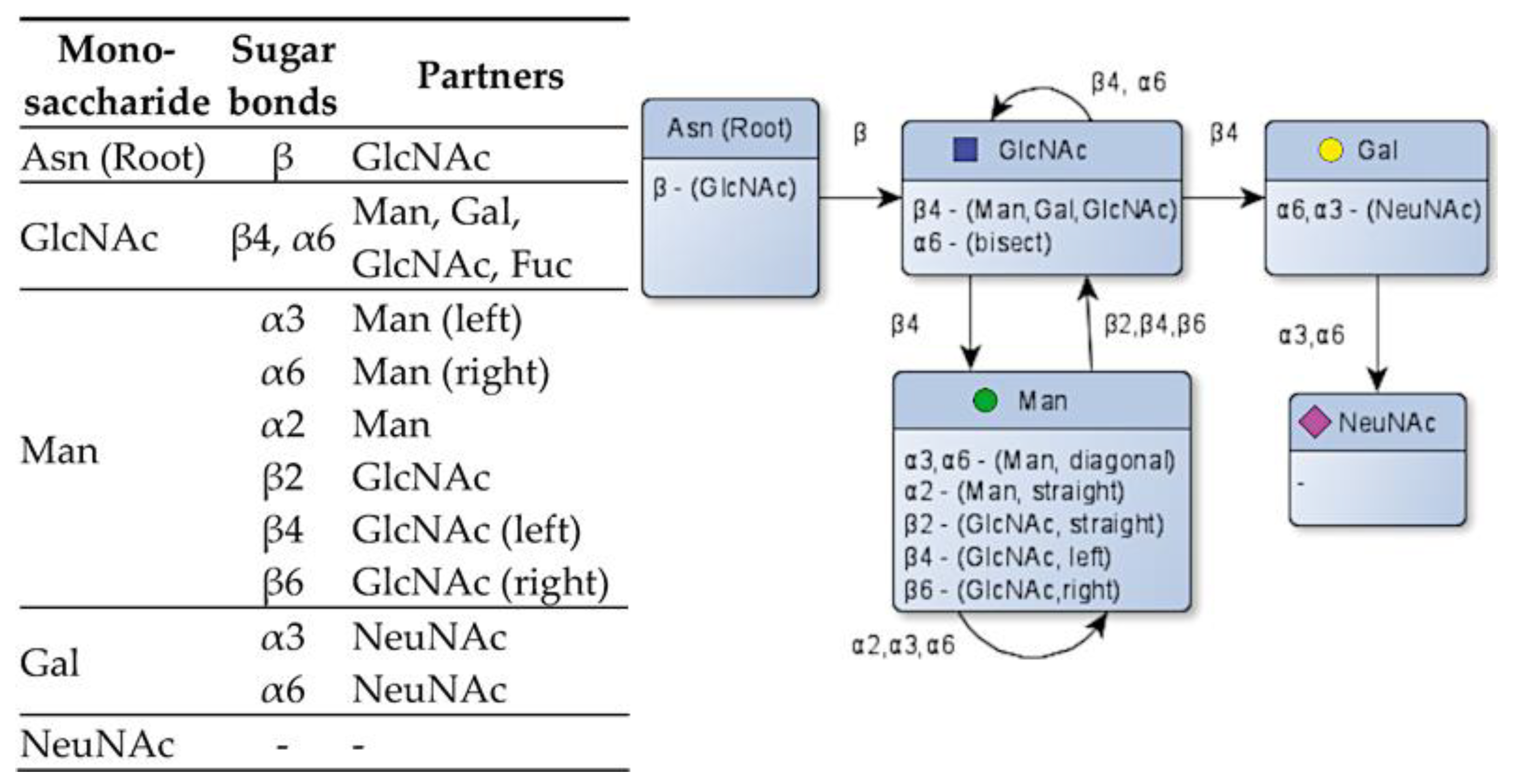
4.3. Structure of the Glycans
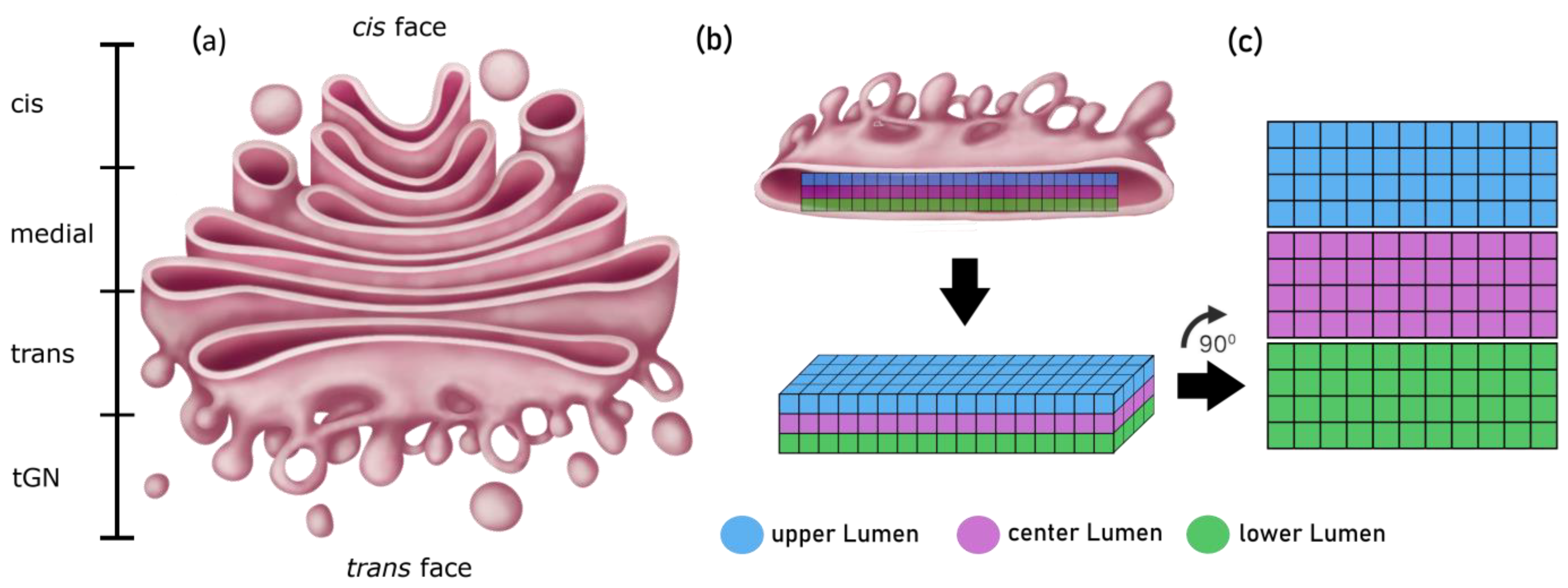
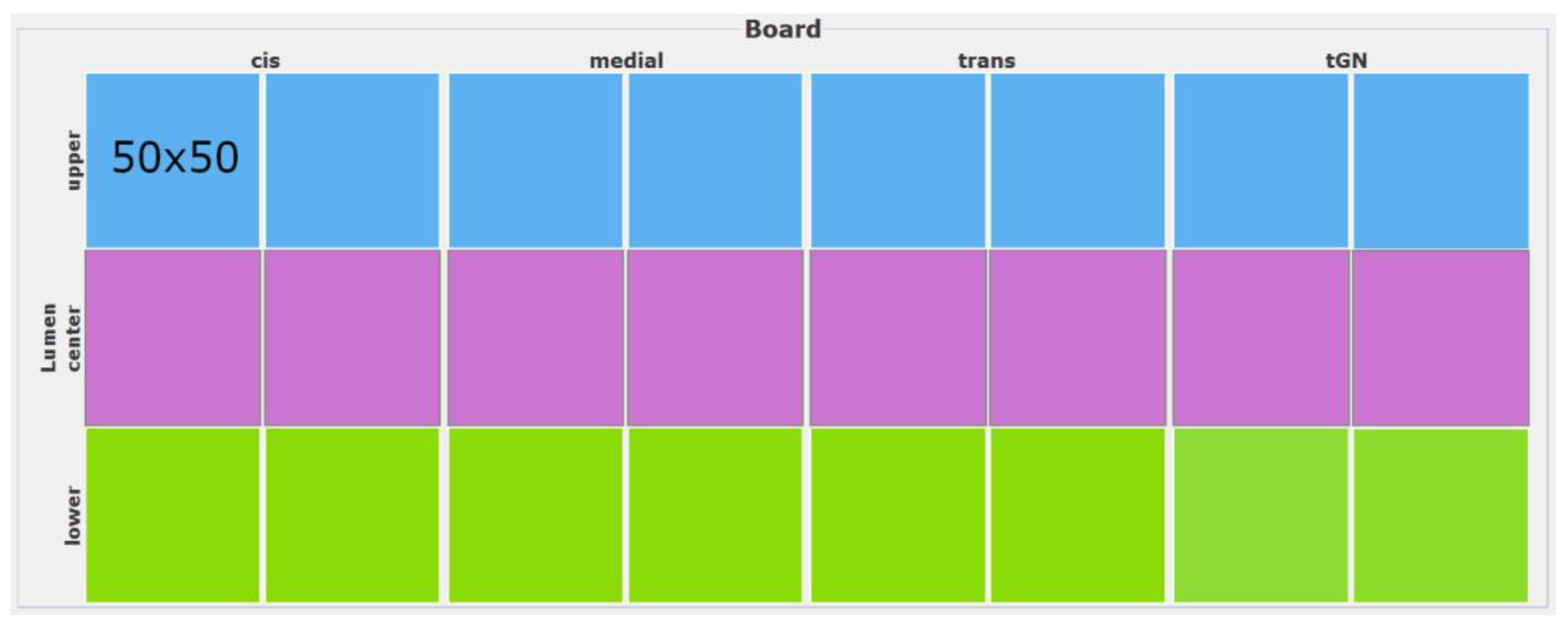
5. The Environment: The Golgi Apparatus
Enzymes
6. Simulation Process
- Movement of the proteins;
- Complex formation;
- Reaction;
- Dissociation.
6.1. Movement of the Proteins
6.2. Complex Formation
6.3. Reaction
6.4. Dissociation
6.5. Simulation Output
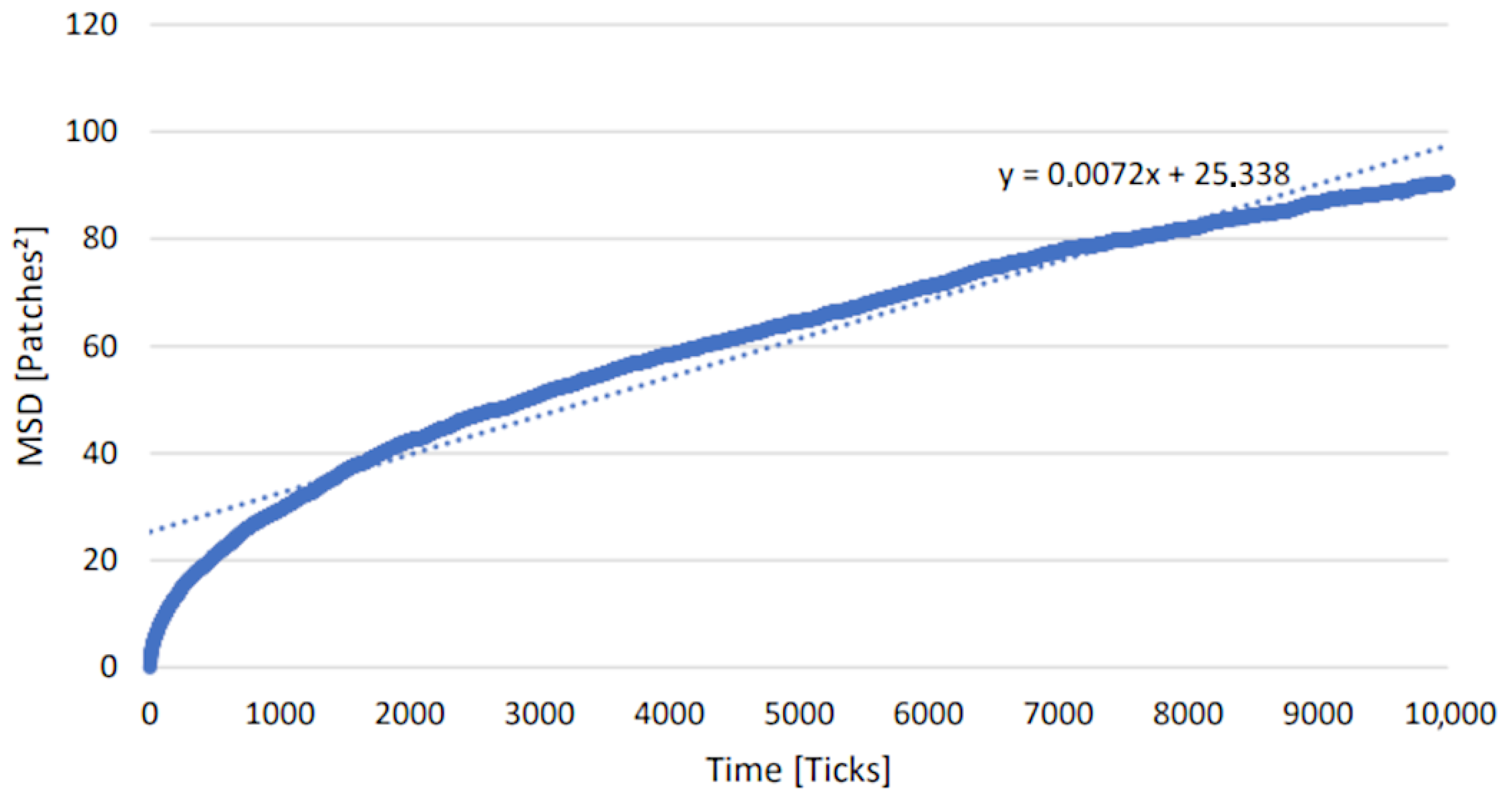
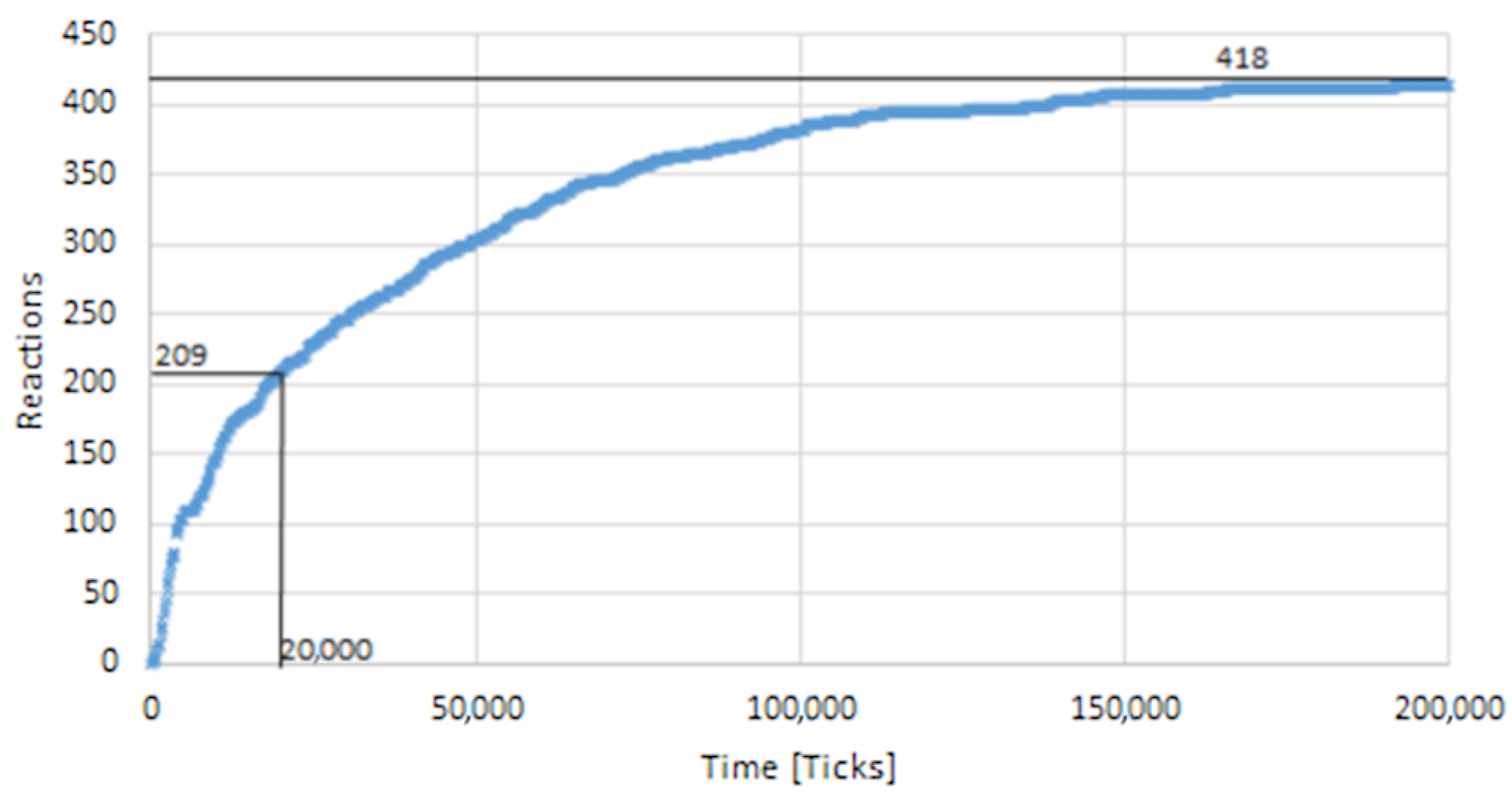
7. Results
8. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Solá, R.J.; Griebenow, K. Glycosylation of therapeutic proteins: An effective strategy to optimize efficacy. BioDrugs 2010, 24, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Liu, W.; Li, Y.; Ma, B.; Shang, S.; Tan, Z. Impact of N-Linked Glycosylation on Therapeutic Proteins. Molecules 2022, 27, 8859. [Google Scholar] [CrossRef] [PubMed]
- Frank, M.; Schloissnig, S. Bioinformatics and molecular modeling in glycobiology. Cell. Mol. Life Sci. 2010, 67, 2749–2772. [Google Scholar] [CrossRef]
- Lin, L.; Kightlinger, W.; Prabhu, S.K.; Hockenberry, A.J.; Li, C.; Wang, L.X.; Jewett, M.C.; Mrksich, M. Sequential Glycosylation of Proteins with Substrate-Specific N-Glycosyltransferases. ACS Cent. Sci. 2020, 6, 144–154. [Google Scholar] [CrossRef]
- Wang, S.; He, Q.; Ye, J.; Kang, Z.; Zheng, Q.; Liu, S.; He, J.; Sun, L. N-linked Glycosylation and its Potential Application in Drug Development. Health Sci. J. 2020, 14, 743. [Google Scholar] [CrossRef]
- Roth, Z.; Yehezkel, G.; Khalaila, I. Identification and Quantification of Protein Glycosylation. Int. J. Carbohydr. Chem. 2012, 2012, 640923. [Google Scholar] [CrossRef]
- Phoomak, C.; Cui, W.; Hayman, T.J.; Yu, S.H.; Zhao, P.; Wells, L.; Steet, R.; Contessa, J.N. The translocon-associated protein (TRAP) complex regulates quality control of N-linked glycosylation during ER stress. Sci. Adv. 2021, 7, eabc6364. [Google Scholar] [CrossRef]
- Reynders, E.; Foulquier, F.; Annaert, W.; Matthijs, G. How Golgi glycosylation meets and needs trafficking: The case of the COG complex. Glycobiology 2011, 21, 853–863. [Google Scholar] [CrossRef]
- Krambeck, F.J.; Betenbaugh, M.J. A mathematical model of N-linked glycosylation. Biotechnol. Bioeng. 2005, 92, 711–728. [Google Scholar] [CrossRef]
- Aebi, M. N-linked protein glycosylation in the ER. Biochim. Biophys. Acta 2013, 1833, 2430–2437. [Google Scholar] [CrossRef]
- Apweiler, R.; Hermjakob, H.; Sharon, N. On the frequency of protein glycosylation, as deduced from analysis of the SWISS-PROT database. Biochim. Biophys. Acta 1999, 1473, 4–8. [Google Scholar] [CrossRef] [PubMed]
- Munkley, J. Glycosylation is a global target for androgen control in prostate cancer cells. Endocr. Relat. Cancer 2017, 24, R49–R64. [Google Scholar] [CrossRef] [PubMed]
- Huxley, K.E.; Willems, L.I. Chemical reporters to study mammalian O-glycosylation. Biochem. Soc. Trans. 2021, 49, 903–913. [Google Scholar] [CrossRef] [PubMed]
- Zlatina, K.; Galuska, S.P. The N-glycans of lactoferrin: More than just a sweet decoration. Biochem. Cell Biol. 2021, 99, 117–127. [Google Scholar] [CrossRef]
- Peixoto, A.; Relvas-Santos, M.; Azevedo, R.; Santos, L.L.; Ferreira, J.A. Protein Glycosylation and Tumor Microenvironment Alterations Driving Cancer Hallmarks. Front. Oncol. 2019, 9, 380. [Google Scholar] [CrossRef]
- Reily, C.; Stewart, T.J.; Renfrow, M.B.; Novak, J. Glycosylation in health and disease. Nat. Rev. Nephrol. 2019, 15, 346–366. [Google Scholar] [CrossRef]
- Stanley, P. Golgi glycosylation. Cold Spring Harb. Perspect. Biol. 2011, 3, a005199. [Google Scholar] [CrossRef]
- Lowenthal, M.S.; Davis, K.S.; Formolo, T.; Kilpatrick, L.E.; Phinney, K.W. Identification of Novel N-Glycosylation Sites at Noncanonical Protein Consensus Motifs. J. Proteome Res. 2016, 15, 2087–2101. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y. Glycosylation Quality Control by the Golgi Structure. J. Mol. Biol. 2016, 428, 3183–3193. [Google Scholar] [CrossRef]
- Manske, M. “The Endomembrane System and Proteins: Figure 1” by OpenStax College, Biology (CC BY 3.0). Available online: https://openstax.org/books/biology-2e/pages/4-4-the-endomembrane-system-and-proteins (accessed on 12 June 2023).
- Nilsson, T.; Au, C.E.; Bergeron, J.J. Sorting out glycosylation enzymes in the Golgi apparatus. FEBS Lett. 2009, 583, 3764–3769. [Google Scholar] [CrossRef]
- Auchincloss, A.H.; Garcia, L.M. Brief introductory guide to agent-based modeling and an illustration from urban health research. Cad. Saude Publica 2015, 31 (Suppl. S1), 65–78. [Google Scholar] [CrossRef] [PubMed]
- Laubenbacher, R.; Hinkelmann, F.; Oremland, M. Agent-based models and optimal control in biology: A discrete approach. In Mathematical Concepts and Methods in Modern Biology; Academic Press: Cambridge, MA, USA, 2013; pp. 143–178. [Google Scholar]
- Macal, C.M.; North, M.J. Agent-based modeling and simulation. In Proceedings of the 2009 Winter Simulation Conference (WSC), Austin, TX, USA, 13–16 December 2009; pp. 86–98. [Google Scholar]
- Phelps, S. Applying Dependency Injection to Agent-Based Modeling: The JABM Toolkit; Working Paper Series (CCFEA) #WP056-12; CCFEA: Colchester, UK, 2013. [Google Scholar]
- Bandini, S.; Manzoni, S.; Vizzari, G. Agent Based Modeling and Simulation: An Informatics Perspective. J. Artif. Soc. Soc. Simul. 2009, 12, 4. [Google Scholar]
- Mironov, A.A.; Beznoussenko, G.V. Algorithm for Modern Electron Microscopic Examination of the Golgi Complex. Methods Mol. Biol. 2023, 2557, 161–209. [Google Scholar] [CrossRef] [PubMed]
- Mogelsvang, S.; Marsh, B.J.; Ladinsky, M.S.; Howell, K.E. Predicting function from structure: 3D structure studies of the mammalian Golgi complex. Traffic 2004, 5, 338–345. [Google Scholar] [CrossRef] [PubMed]
- Tachikawa, M.; Mochizuki, A. Golgi apparatus self-organizes into the characteristic shape via postmitotic reassembly dynamics. Proc. Natl. Acad. Sci. USA 2017, 114, 5177–5182. [Google Scholar] [CrossRef] [PubMed]
- Stanley, P.; Schachter, H.; Taniguchi, N. N-Glycans. In Essentials of Glycobiology, 2nd ed.; Varki, A., Cummings, R.D., Esko, J.D., Freeze, H.H., Stanley, P., Bertozzi, C.R., Hart, G.W., Etzler, M.E., Eds.; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2009; Chapter 8. [Google Scholar]
- Opat, A.S.; van Vliet, C.; Gleeson, P.A. Trafficking and localisation of resident Golgi glycosylation enzymes. Biochimie 2001, 83, 763–773. [Google Scholar] [CrossRef]
- Gu, F.; Crump, C.M.; Thomas, G. Trans-Golgi network sorting. Cell. Mol. Life Sci. 2001, 58, 1067–1084. [Google Scholar] [CrossRef]



| Enzyme | Condition | Reaction |
|---|---|---|
| Man I (α2-mannosidase I) mannosyl-oligosaccharid-1,2-α-mannosidase | Free α(1,2)-Man | Removes the α(1,2)-Man |
| GnT I (β2-GlcNAc-transferase I) α-1,3-mannosylglycoprotein-2-β-N-acetylglucosaminyltransferase | No α(1,2)-Man present | Adds a β(1,2)-GlcNAc to the α(1,3)-core-Man |
| Man II (α3/6-mannosidase II) mannosyl-oligosaccharid-1,3-1,6-α-mannosidase | Free α(1,3 and 6)-Man at α(1,6)-core-Man and GlcNAc at α(1,3)-core-Man; Inhibited by bisecting β(1,4)-GlcNAc | Removes α(1,3)-Man and α(1,6)-Man |
| GnT II (β2-GlcNAc-transferase II) α-1,6-mannosylglycoprotein 2-β-N-acetylglucosaminyltransferase | β(1,2) GlcNAc at α(1,3)-core-Man; Inhibited by bisecting β(1,4) GlcNAc; Inhibited, if Gal is present | Adds a β(1,2)-GlcNAc to the α(1,6)-core-Man |
| GnT III (β4-GlcNAc-transferase III) β-1,4-mannosylglycoprotein-4-β-N-acetylglucosaminyltransferase | β(1,2) GlcNAc at α(1,3)-core-Man; Inhibited, if Gal is present | Adds bisecting β(1,4) GlcNAc; |
| GnT IV (β4-GlcNAc-transferase IV) α-1,3-mannosylglycoprotein-4-β-N-acetylglucosaminyltransferase | β(1,2)-GlcNAc at α(1,3)-core-Man; Inhibited if β(1,4) Gal is at α(1,3)-Man-branch; Inhibited, if no Man or GlcNAc is at α(1,6)-core-Man; Inhibited by bisecting β(1,4)-GlcNAc | Adds a β(1,4)-GlcNAc to the α(1,3)-Man |
| GnT V (β6-GlcNAc-Transferase V) α-1,6-mannosylglycoprotein-6-β-N-acetylglucosaminyltransferase | β(1,2) GlcNAc at α(1,6)-core-Man Inhibited, if β(1,4) Gal is at α(1,6)-Man-branch; Inhibited by bisecting β(1,4)-GlcNAc | Adds a β(1,6)-GlcNAc to the α(1,6)-Man |
| GalT (β4-Gal-transferase) β-N-acetylglucosaminylglycopeptide-β-1,4-galactosyltransferase | Free GlcNAc | Adds β(1,4)-Gal to GlcNAc |
| α6-FucT (α6-Fuc-transferase) glycoprotein 6-α-L-fucosyltransferase | At least one GlcNAc added; Inhibited by bisecting β(1,4)-GlcNAc; Inhibited by a branch ending with Gal | Adds α(1,6)-core-Fuc |
| SiaT (α3/6-sialyl-transferase) β-galactosid-α-2,3/6-sialyltransferase | Free β(1,4)-Gal | Adds α(1,3)-NeuNAc to Gal |
| α3-FucT (α3-Fuc-transferase) glycoprotein 3-α-L-fucosyltransferase | β(1,4)-Gal at β(1,2)-GlcNAc | Adds antennary α(1,3)-Fuc |
| GnT VII (β3-GlcNAc-transferase VII) N-acetyl-lactosaminid-β-1,3-N-acetylglucosaminyltransferase | β(1,4)-Gal at β(1,2)-GlcNAc | Adds β(1,3)-GlcNAc to Gal |
| GalNAcT II (β4-GalNAc-transferase II) N-acetylneuraminylgalactosylglucosylceramide β-1,4-N-acetylgalactosaminyltransferase | α(1,3)-NeuNAc at β(1,4)-Gal | Adds β(1,4)-GalNAc to Gal |
| GalNAcT III (β4-GalNAc-transferase III) β-N-acetylglucosaminylglycopeptide β-1,4-N-acetylgalactosaminyltransferase | Free GlcNAc | Adds β(1,4)-GalNAc to GlcNAc |
| Enzyme | Fraction in Compartment (%) | |||
|---|---|---|---|---|
| Cis | Medial | Trans | tGN | |
| Man I | 90 | 10 | 0 | 0 |
| GnT I | 20 | 50 | 30 | 10 |
| Man II | 10 | 50 | 30 | 10 |
| GnT II | 10 | 50 | 30 | 10 |
| GnT III | 10 | 50 | 30 | 10 |
| GnT IV | 10 | 50 | 30 | 10 |
| GnT V | 10 | 50 | 30 | 10 |
| GalT | 0 | 10 | 20 | 70 |
| SialT | 0 | 10 | 20 | 70 |
| α6-FucT | 10 | 50 | 30 | 10 |
| α3-FucT | 0 | 0 | 30 | 70 |
| GnTVII | 0 | 0 | 30 | 70 |
| GalNAcTII | 0 | 0 | 30 | 70 |
| GalNAcTIII | 0 | 0 | 30 | 70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jetschni, C.; Götz, P. Implementing an Agent-Based Modeling Approach for Protein Glycosylation in the Golgi Apparatus. Fermentation 2023, 9, 849. https://doi.org/10.3390/fermentation9090849
Jetschni C, Götz P. Implementing an Agent-Based Modeling Approach for Protein Glycosylation in the Golgi Apparatus. Fermentation. 2023; 9(9):849. https://doi.org/10.3390/fermentation9090849
Chicago/Turabian StyleJetschni, Christian, and Peter Götz. 2023. "Implementing an Agent-Based Modeling Approach for Protein Glycosylation in the Golgi Apparatus" Fermentation 9, no. 9: 849. https://doi.org/10.3390/fermentation9090849





