DFT Study on the Interaction of the Smallest Fullerene C20 with Lithium Ions and Atoms
Abstract
:1. Introduction
2. Results and Discussion
2.1. C20–Li+
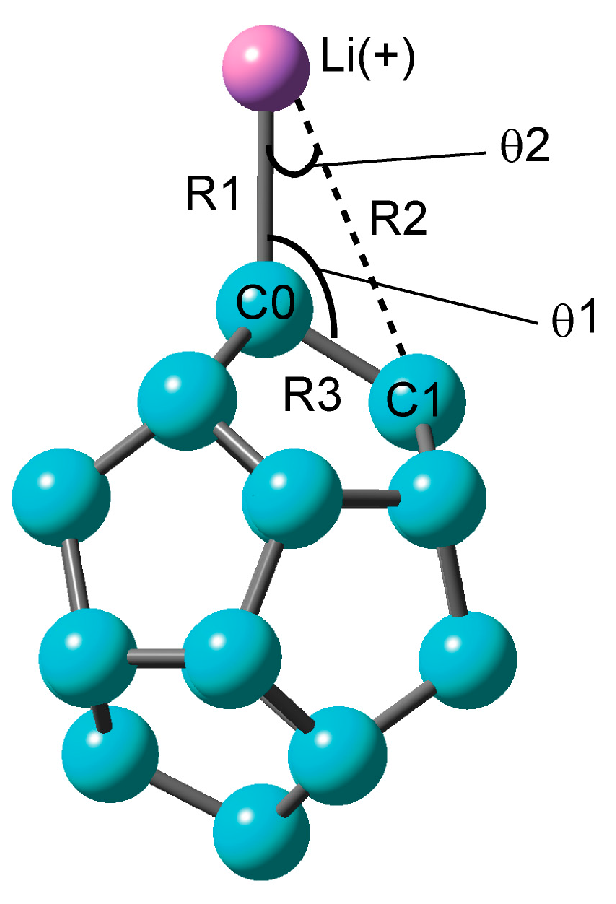
2.1.1. Optimized Structure of the C20–Li+ System
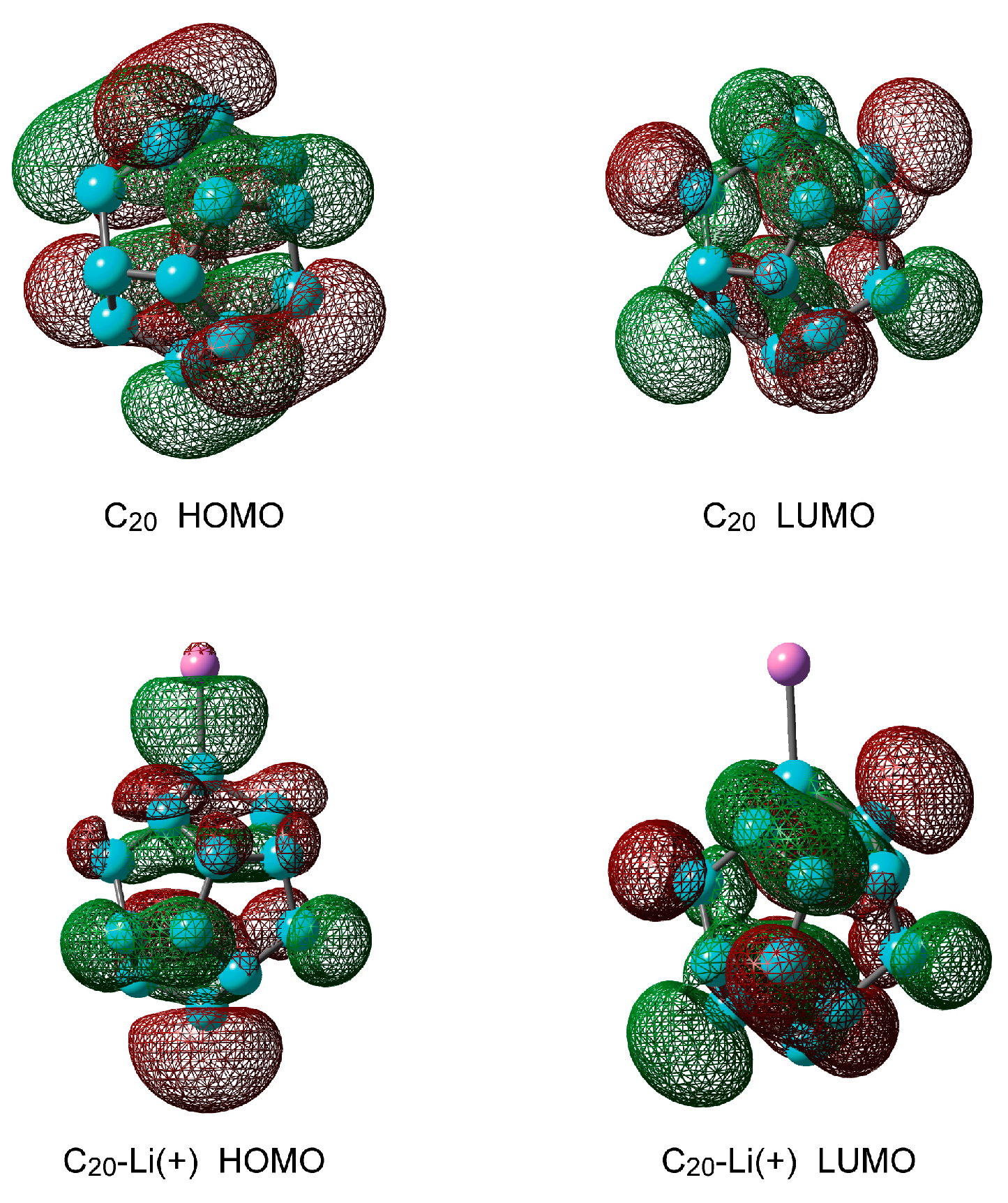
2.1.2. Electronic Structures of Pure C20 and C20–Li+
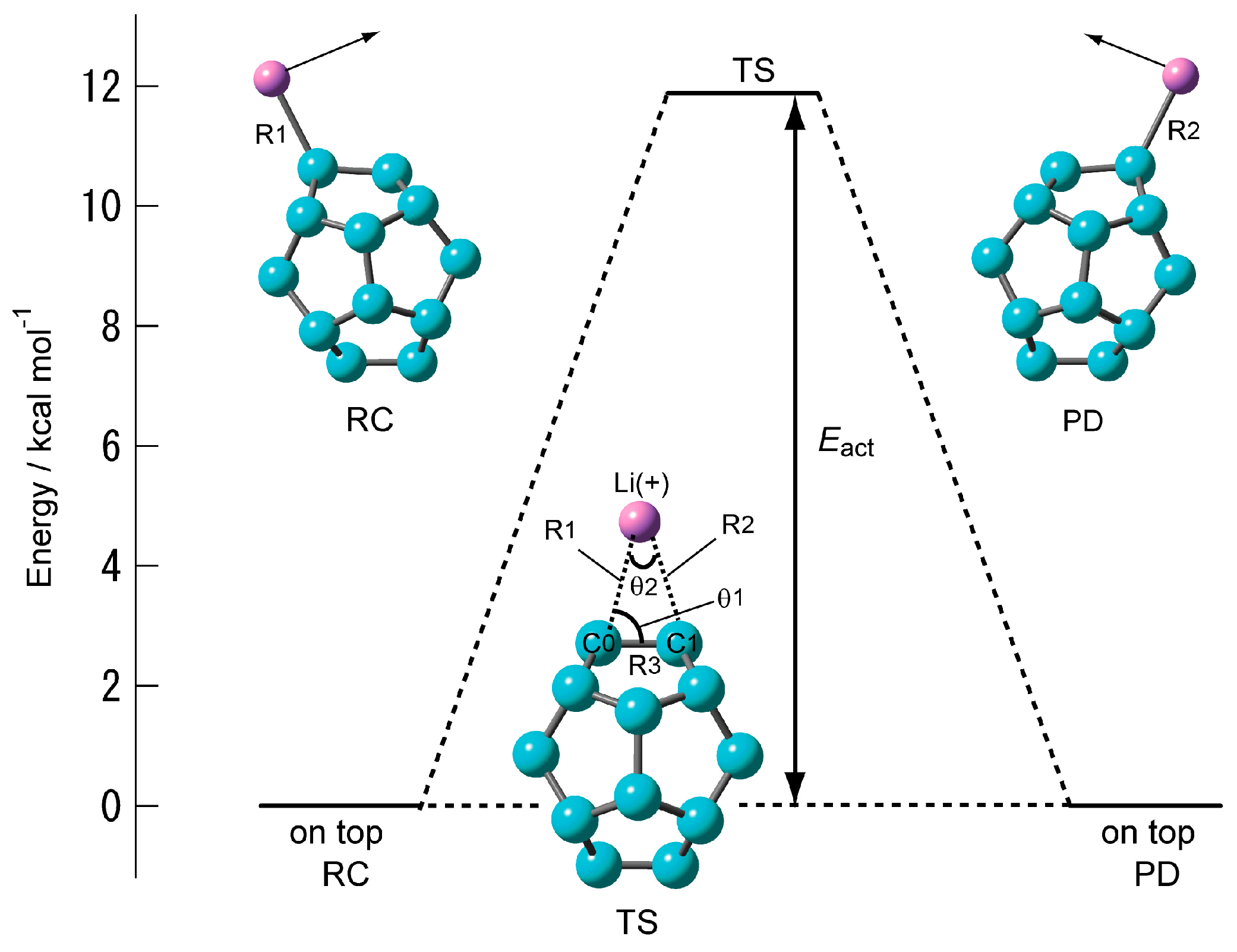
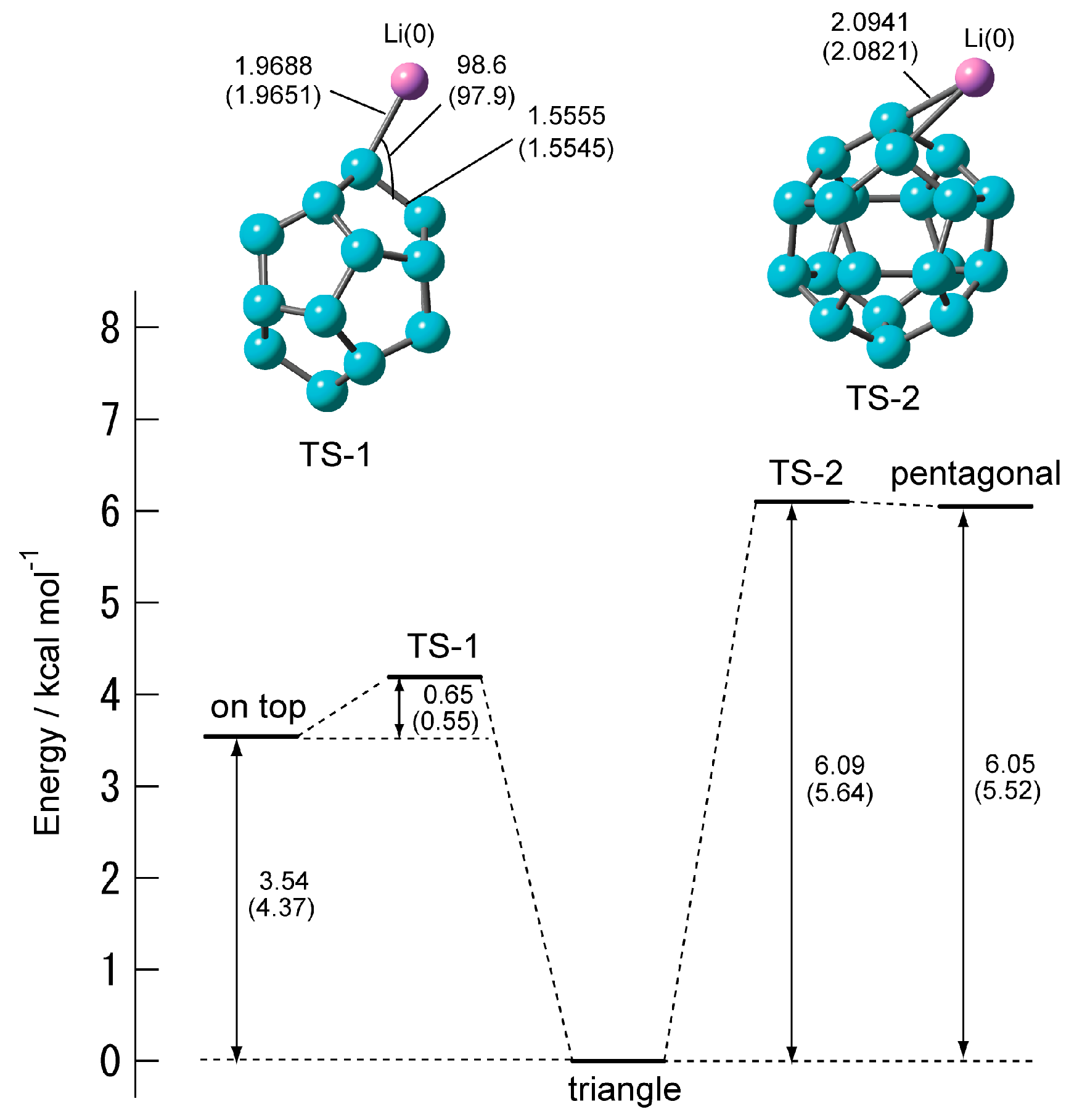
2.1.3. Transition State of C20–Li+ and the Movement Path of the Li Ion on the Surface of C20
2.2. C20–Li
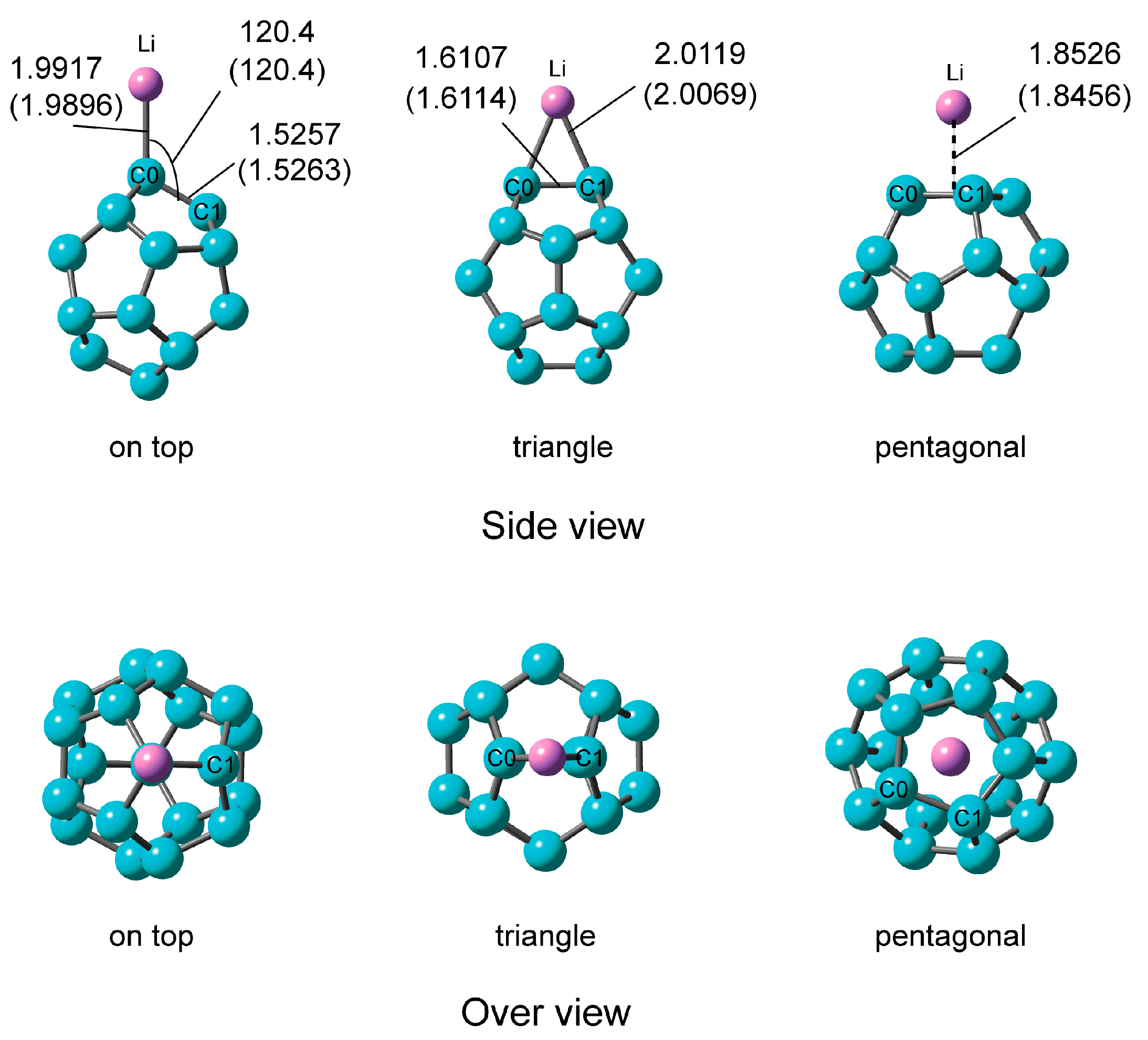
2.2.1. Optimized Structure of C20–Li
2.2.2. Transition State of C20–Li and the Movement Path of the Li atom on the Surface of C20
3. Method of Calculation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qin, L.-C.; Zhao, X.; Hirahara, K.; Miyamoto, Y.; Ando, Y.; Iijima, S. The smallest carbon nanotube. Nature 2000, 408, 50. [Google Scholar] [CrossRef] [PubMed]
- Parasuk, V.; Almof, J. C20: The smallest fullerene? Chem. Phys. Lett. 1991, 184, 187–190. [Google Scholar] [CrossRef]
- Prinzbach, H.; Weiler, A.; Landenberger, P.; Wahl, F.; Wörth, J.; Scott, L.T.; Gelmont, M.; Olevano, D.; Issendorff, B.V. Gas-phase production and photoelectron spectroscopy of the smallest fullerene, C20. Nature 2000, 407, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Kurokawa, S.; Yamamoto, D.; Hirashige, K.; Sakai, A. Possible formation of one-dimensional chains of C20 fullerenes observed by scanning tunneling microscopy. Appl. Phys. Express 2016, 9, 045102. [Google Scholar] [CrossRef]
- Lüssem, B.; Riede, M.; Leo, K. Doping of organic semiconductor. Phys. Status. Solidi. A 2013, 210, 9–43. [Google Scholar]
- Salzmann, I.; Heimel, G. Toward a comprehensive understanding of molecular doping organic semiconductors. J. Electron Spectrosc. Relat. Phenom. 2015, 204, 208–222. [Google Scholar] [CrossRef]
- Holczer, K.; Whetten, R.L. Superconducting and normal state properties of the A3C60 compounds. Carbon 1992, 30, 1261–1276. [Google Scholar] [CrossRef]
- Moriyama, H.; Kobayashi, H.; Kobayashi, A.; Watanabe, T. ESR spectra on single crystals of alkali metal fulleride complexes by means of wet-chemical synthesis. Chem. Phys. Lett. 1995, 238, 116–121. [Google Scholar] [CrossRef]
- Dalchiele, E.A. Rosolen. J.M.; Decker, F. Electrochemically intercalated MxC60 thin films in a solid state cell (M = Li, K): Optical and photoelectrochemical characterization. Appl. Phys. A Mater. Sci. 1996, 63, 487–494. [Google Scholar]
- Zhang, Z.; Chen, C.C.; Kelty, S.P.; Dai, H.J.; Lieber, C.M. The superconducting energy gap of Rb3C60. Nature 1991, 353, 333–335. [Google Scholar] [CrossRef]
- Cazorla, C.; Shevlin, S.A.; Guo, Z.X. Calcium-based functionalization of carbon materials for CO2 capture: A first-principles computational study. J. Phys. Chem. C 2011, 115, 10990–10995. [Google Scholar] [CrossRef]
- Cazorla, C. Ab initio study of the binding of collagen amino acids to graphene and A-doped (A = H, Ca) graphene Original Research Article. Thin Solid Films 2010, 518, 6951–6961. [Google Scholar] [CrossRef]
- Abe, S.; Kawano, S.; Toida, Y.; Nakamura, M.; Inoue, S.; Sano, H.; Yoshida, Y.; Kawabata, H.; Tachikawa, H. Electronic states of alkyl-radical-functionalized C20 fullerene using density functional theory. Jpn. J. Appl. Phys. 2016, 55, 03DD03. [Google Scholar] [CrossRef]
- Iyama, T.; Abe, S.; Tachikawa, H. Density functional theory (DFT) study on the addition of hydroxyl radical (OH) to C20. Mol. Cryst. Liq. Cryst. 2012, 567, 200–206. [Google Scholar] [CrossRef]
- Fukuzumi, T.; Tachikawa, H.; Azumi, K. DFT Study on the interaction of carbon nano-materials with sodium ion and atom. Mol. Cryst. Liq. Cryst. 2011, 538, 61–66. [Google Scholar] [CrossRef]
- Tachikawa, H. Diffusion of the Li+ Ion on C60: A DFT and Molecular Dynamics Study. J. Phys. Chem. C 2011, 115, 20406–20411. [Google Scholar] [CrossRef]
- Tachikawa, H. Diffusion dynamics of the Li ion on C60: A direct molecular orbital−molecular dynamics study. J. Phys. Chem. C 2007, 111, 13087–13091. [Google Scholar] [CrossRef]
- Tachikawa, H.; Shimizu, A. Diffusion Dynamics of the Li+ Ion on a Model Surface of Amorphous Carbon: A direct molecular orbital dynamics study. J. Phys. Chem. B 2005, 109, 13255–13262. [Google Scholar] [CrossRef] [PubMed]
- Gaussian 09, Revision D.01, Gaussian, Inc.: Wallingford CT, 2013.
- Kobayashi, R.; Amos, R.D. The application of CAM-B3LYP to the charge-transfer band problem of the zincbacteriochlorin–bacteriochlorin complex. Chem. Phys. Lett. 2006, 420, 106–109. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange—Correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Cazorla, C.; Shevlin, S.A. Accuracy of density functional theory in the prediction of carbon dioxide adsorbent materials. Dalton Trans. 2013, 42, 4670–4676. [Google Scholar] [CrossRef] [PubMed]
- Cazorla, C. The role of density functional theory methods in the prediction of nanostructured gas-adsorbent materials. Coordination Chem. Rev. 2015, 300, 142–163. [Google Scholar] [CrossRef]
- Tachikawa, H.; Kawabata, H. Electronic states of alkali metal-NTCDA complexes: A DFT study. Solid State Sci. 2015, 48, 141–146. [Google Scholar] [CrossRef]
- Iyama, T.; Kawabata, H.; Tachikawa, H. Origin of Spectrum Shifts of Benzophenone-Water Clusters: DFT Study J. Solution Chem. 2014, 43, 1676–1686. [Google Scholar] [CrossRef]
| Method | Structural Parameter | NPA Atomic Charge | Ebind(a)/kcal mol−1 | |||||
|---|---|---|---|---|---|---|---|---|
| R1/Å | R2/Å | θ1/° | θ2/° | νC0–Li+/cm−1 | C0 | Li+ | ||
| CAM-B3LYP/6-311G(d) | 2.0548 | 3.1288 | 121.0 | 24.7 | 399 | −0.630 | 0.957 | 43.24 (41.31) |
| CAM-B3LYP/6-311+G(d) | 2.0547 | 3.1293 | 121.0 | 24.7 | 399 | −0.621 | 0.955 | 42.36 (40.40) |
| System | Structural Parameter | Eact/kcal·mol–1 | ||||
|---|---|---|---|---|---|---|
| R1/Å | R3/Å | θ1/° | θ2/° | νC0–Li+/cm–1 | ||
| CAM-B3LYP/6-311G(d) | 2.2856 | 1.4347 | 71.7 | 36.6 | 399 i | 11.94 (11.34) |
| CAM-B3LYP/6-311+G(d) | 2.2884 | 1.4352 | 71.7 | 36.5 | 400 i | 11.88 (11.31) |
| System | Ebind (b)/kcal·mol−1 | NPA Atomic Charge | ||
|---|---|---|---|---|
| Part of C20 | C(0) | Li | ||
| On-top | 49.42 (49.32) | –0.934 | –0.662 | +0.934 |
| Triangle | 52.96 (52.85) | –0.869 | +0.869 | |
| Pentagonal | 46.89 (47.95) | –0.823 | +0.823 | |
| State | Eact/kcal mol−1 | νi/cm−1 |
|---|---|---|
| TS-1 | 0.65 (0.55) | 252 i (182 i) |
| TS-2 | 0.04 (0.12) | 110 i (120 i) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawabata, H.; Tachikawa, H. DFT Study on the Interaction of the Smallest Fullerene C20 with Lithium Ions and Atoms. C 2017, 3, 15. https://doi.org/10.3390/c3020015
Kawabata H, Tachikawa H. DFT Study on the Interaction of the Smallest Fullerene C20 with Lithium Ions and Atoms. C. 2017; 3(2):15. https://doi.org/10.3390/c3020015
Chicago/Turabian StyleKawabata, Hiroshi, and Hiroto Tachikawa. 2017. "DFT Study on the Interaction of the Smallest Fullerene C20 with Lithium Ions and Atoms" C 3, no. 2: 15. https://doi.org/10.3390/c3020015





