On Description of Acceleration of Spinless Electrons in Law of Heat Conduction a capite ad calcem in Temperature
Abstract
:1. Introduction
- (i)
- the microscopic theory of reversibility of Onsager [2] is violated;
- (ii)
- it neglects the time needed for the acceleration of heat flow by free electrons (Sharma, [9]);
- (iii)
- (iv)
- the development of Fourier’s law was from observations at steady state;
- (v)
- (vi)
- Landau and Lifshitz observed the contradiction of the infinite speed of propagation of heat with Einstein’s light speed barrier [23];
- (vii)
- Fourier’s law breaks down at the Casimir limit [24].
2. Materials and Methods
2.1. Free Electron Theory
2.2. Derivation of Alternate Non-Fourier Conduction Equation
2.3. Entropy Production Term
2.4. Transport Parameters
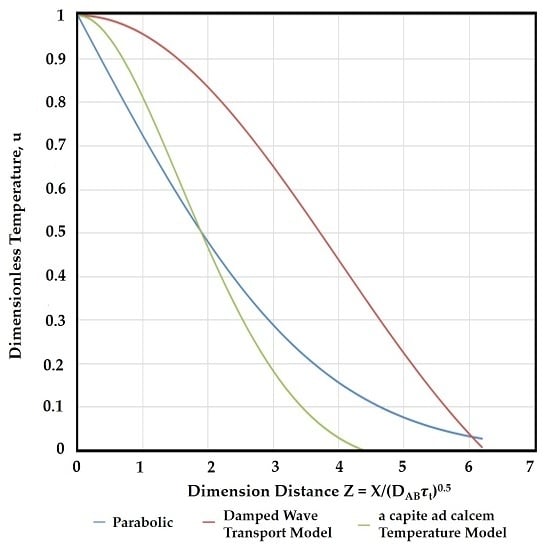
3. Results and Discussion

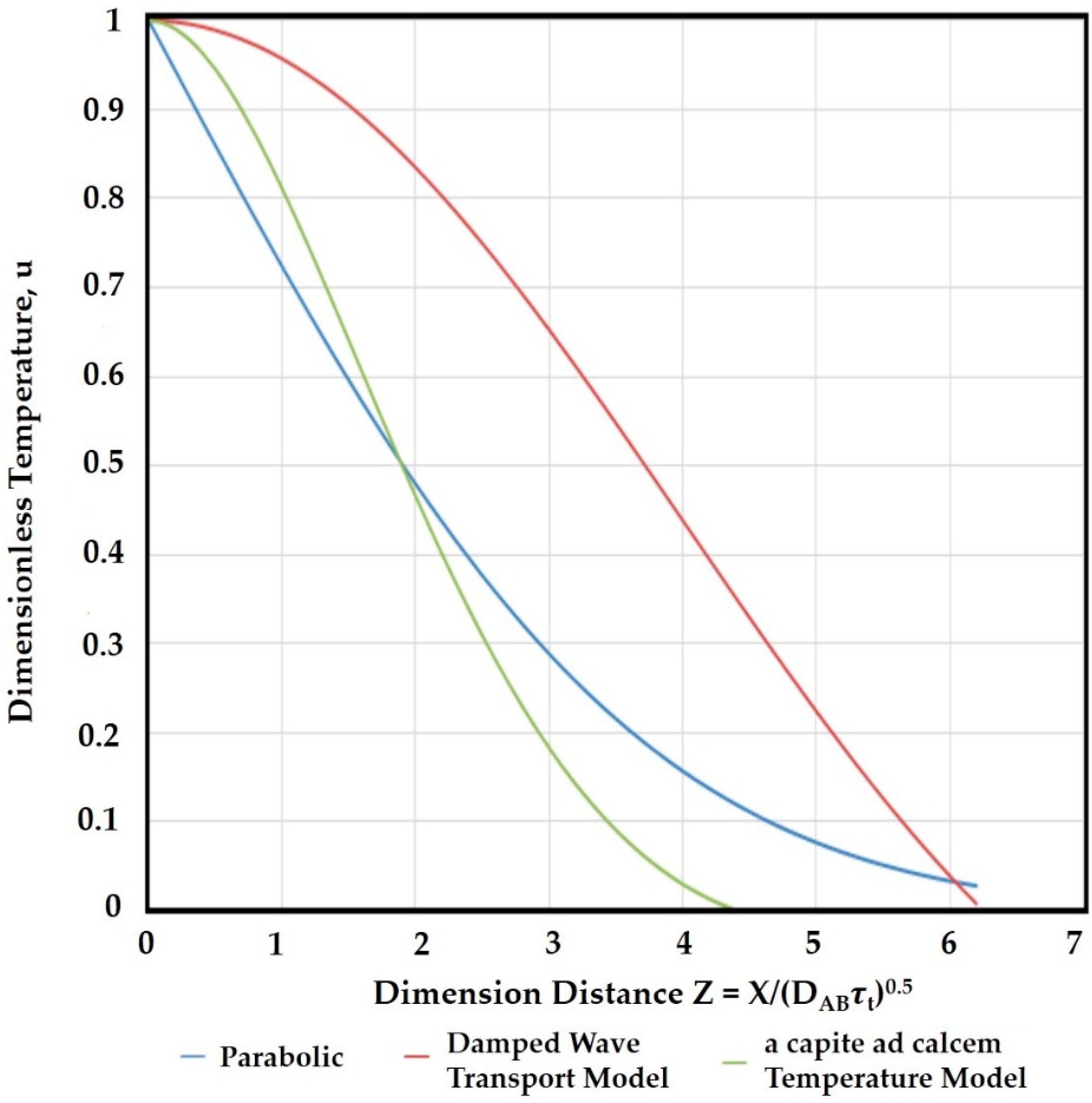
4. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| AN | Avagadro Number (6.023 × 1023 molecules/mole) |
| A | cross-sectional area across which transport occurs (m2) |
| CA | concentration of species A (mol/m3) |
| CB | concentration of species B (mol/m3) |
| Cp | heat capacity of material at constant pressure (J/mole/K) |
| Cv | heat capacity of material at constant volume (J/mole/K) |
| DAB | binary diffusion coefficient of species A in B (m2/s) |
| erf(z) | error function of z. |
| f | molecular drag coefficient (kg/s/molecule) |
| k | thermal conductivity of the material (W/m/K) |
| kB | Boltzmann Constant (J/molecule/K) |
| H | enthalpy (J/mole) |
| J″ | area averaged molar flux (mole/m2/s) |
| Jp(x) | Bessel function of the pth order and first kind |
| Ip(x) | modified Bessel function of the pth order and first kind |
| t | time (s) |
| T | Temperature ( °K) |
| m | mass of the molecule (kg) |
| N | molecular weight of oligonucleotide (kg/mole) |
| qz | heat flux (area averaged) (W/m2) |
| n | electron density (# of electrons/m3) |
| R | universal molar gas constant (J/mole/K) |
| R0 | radius of solute molecule (m) |
| S | entropy (J/mole/K) |
| u | dimensionless concentration, |
| u(s) | temperature in Laplace domain |
| ve | velocity of electron (m/s) |
| vA | velocity of solute molecule (m/s) |
| vy | velocity of fluid in y cartesian direction (m/s) |
| vm | velocity of mass (m/s) |
| z | z Cartesian distance (m) |
| Z | dimensionless distance |
| vh | velocity of heat (m/s) |
| Zpen | dimensionless penetration distance |
Greek
| σ | Entropy production term (W/m3/K) |
| α | thermal diffusivity of material (m2/s) |
| t | collision time of the electron and obstacle (seconds) |
| τ | Dimensionless time in governing equation |
| τr | relaxation time (heat) of material (s) |
| τmr | relaxtion time (mass) of material (s) |
| ρ | density of material (kg/m3) |
| τxy | tangential shear stress (N/m2) |
| τmom | relaxtion time (momentum) (s) |
| µA | chemical potential (J/molecule) |
| µ | viscosity (kg/m/s) |
| λ2 | retardation time (s) |
| xA | mole fraction of species A |
References
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 3rd ed.; Springer Verlag: Berlin, Germany, 2001. [Google Scholar]
- Onsager, L. Reciprocal Relations in Irreversible Processes. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Fourier, J.B. Theorieanalytique de la Chaleur; Freeman, A., Translator; Dover Publications: New York, NY, USA, 1955. [Google Scholar]
- Fick, A. Annalen der Physik; Wiley: Leipzig, Germany, 1855; Volume 170, p. 59. [Google Scholar]
- Ohm, G.S. GrundlinienzueinerzweckmäßigenBehandlung dereometriealshöherenBildungsmittelsanvor bereitendenLehranstalten/entworfen (Guidelines for an Appropriatetreatment of Geometry in Higher Education at Preparatory Institutes/Notes); Palm und Enke: Erlangen, Germany, 1817. [Google Scholar]
- Newton, I. Philosophiae Naturalis Principia Mathematica; Edmund Halley: London, UK, 1687. [Google Scholar]
- Sharma, K.R. Damped Wave Conduction and Relaxation in Cylindrical and Spherical Coordinates. J. Thermophys. Heat Transf. 2007, 21, 688–693. [Google Scholar] [CrossRef]
- Sharma, K.R. On the Solution of Damped Wave Conduction and Relaxation Equation in a Semi-Infinite Medium Subject to Constant Wall Flux. Int. J. Heat Mass Transf. 2008, 51, 25–26, 6024–6031. [Google Scholar] [CrossRef]
- Sharma, K.R. A Fourth Mode of Heat Transfer called Damped Wave Conduction. In Proceedings of the 42nd Annual Convention of Chemists Meeting, Santiniketan, India, 10 February 2006.
- Sharma, K.R. Damped Wave Transport and Relaxation; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Renganathan, K. Correlation of Heat Transfer with Pressure Fluctuations in Gas-Solid Fluidized Beds to Immersed Surfaces. Ph.D. Dissertation, West Virginia University, Morgantown, WV, USA, 1990. [Google Scholar]
- Sharma, K.R. Storage Coefficient of Substrate in a 2 GHz Microprocessor. In Proceedings of the 225th ACS National Meeting, New Orleans, LA, USA, 23–27 March 2003.
- Sharma, K.R. Bioinformatics:Sequence Alignment and Markov Models; McGraw Hill: NewYork, NY, USA, 2009. [Google Scholar]
- Sharma, K.R. Errors in Gel Acrylamide Electrophoresis Due to Effect of Charge. In Proceedings of the 231st ACS National Meeting, Atlanta, GA, USA, 26–30 March 2006.
- Sharma, K.R. Polymer Thermodynamics: Blends, Copolymers and Reversible Polymerization; CRC Press/Taylor & Francis Group: Baco Raton, FL, USA, 2012. [Google Scholar]
- Sharma, K.R. On Analytical Solutions during Damped Wave Conduction and Relaxation in a Finite Slab Subject to the Convective Boundary Condition. Int. J. Thermophys. 2010, 31, 430–443. [Google Scholar] [CrossRef]
- Sharma, K.R. Transport Phenomena in Biomedical Engineering: Artificial Organ Design and Development and Tissue Design; McGraw Hill Professional: New York, NY, USA, 2010. [Google Scholar]
- Sharma, K.R. On Damped Wave Diffusion of Oxygen in Islets of Langerhans: Part I Comparison of Parabolic and Hyperbolic Models in a Finite Slab. In Proceedings of the 102nd AIChE Annual Meeting, Salt Lake City, UT, USA, 12 November 2010.
- Sharma, K.R. Nanostructuring Operations in Nanoscale Science and Engineering; McGraw Hill Professional: New York, NY, USA, 2010. [Google Scholar]
- Sharma, K.R. Solution Methods and Applications for Generalized Fick’s Law of Diffusion. In 43rd Annual Conventtion of Chemists; Indian Chemical Society: Aurangabad, Gujarat, India, 2006. [Google Scholar]
- Sharma, K.R. Comparison of Solutions from Parabolic and Hyperbolic Models for Transient Heat Conduction in Semi-Infinite Medium. Int. J. Thermophys. 2009, 30, 1671–1687. [Google Scholar] [CrossRef]
- Sharma, K.R.; Turton, R. Mesoscopic Approach to Correlate Surface Heat Transfer Coefficients with Pressure Fluctuations in Dense Gas-Solid Fluidized Beds. Powder Technol. 1998, 99, 109–118. [Google Scholar] [CrossRef]
- Landau, L.; Liftshitz, E.M. Fluid Mechanics; Publisher: Pergamon, UK, 1987. [Google Scholar]
- Casimir, H.B.G. Note on the Conduction of Heat in Crystals. Physica 1938, 5, 495–500. [Google Scholar] [CrossRef]
- Cattaneo, C. A Form of Heat Conduction which Eliminates the Paradox of Instantaneous Propagation. Comptes Rendus 1958, 247, 431–433. [Google Scholar]
- Vernotte, P. Les Paradoxes de la Theorie Continue de l’equation de la Chaleur. C. R. Acad. Sci. Paris 1958, 246, 3154–3155. [Google Scholar]
- Maxwell, J.C. On the Dynamical Theory of Gases. Phil. Trans. Roy. Soc. 1867, 157, 49–88. [Google Scholar] [CrossRef]
- Joseph, D.D.; Preziosi, L. Heat Waves. Rev. Mod. Phys. 1989, 61, 41–73. [Google Scholar] [CrossRef]
- Ozisik, M.N.; Tzou, D.Y. On the Wave Theory of Heat Conduction. ASME J. Heat Transf. 1994, 116, 526–535. [Google Scholar] [CrossRef]
- Sharma, K.R. Continuous Process, Dynamics, Stability, Automation and Control, Nova Science; Nova Science: Happauge, NY, USA, 2015. [Google Scholar]
- Sharma, K.R. Analytical Solution of Damped Wave Conduction and Relaxation in a Finite Sphere and Cylinder. J. Thermophys. Heat Transf. 2008, 22, 783–786. [Google Scholar] [CrossRef]
- Sharma, K.R. Lecture Notes in Computational Molecular Biology; SASTRA Press: Kumbakonam, India, 2004. [Google Scholar]
- Sharma, K.R. Transport Phenomena in Biomedical Engineeirng: Artifical Organ Design and Development and Tissue Design; McGraw Hill Professionl: New York, NY, USA, 2010. [Google Scholar]
- Taitel, Y. On the Parabolic, Hyperbolic and Discrete Formulation of Heat Conduction Equation. Int. J. Heat Mass Transf. 1972, 15, 369–371. [Google Scholar] [CrossRef]
- Bai, C.; Lavine, A.S. On Hyperbolic Heat Conduction and Second Law of Thermodynamics. J. Heat Transf. 1995, 117, 256–263. [Google Scholar] [CrossRef]
- Zanchini, E. Hyperbolic Heat Conduction Theories and non-Decreasing Entropy. Phy. Rev. B 1999, 60, 991–997. [Google Scholar] [CrossRef]
- Lorentz, H.A. La Théorieelectromagnétique de Maxwell et sonapplication aux corps mouvants, Archives néerlandaises des sciences exactes et naturelles. Intern. Arch. 1892, 25, 363–552. (In French) [Google Scholar]
- Drude, P. ZurElektronentheorie der metalle. Ann. Physik 1900, 306, 566–613. (In German) [Google Scholar] [CrossRef]
- Boltzmann, L. Über die Natur der Gasmoleküle (On the nature of gas molecules). WienerBerichte 1876, 74, 553–560. [Google Scholar]
- Sharma, K.R. On the Derivation of an Expression for Relaxation Time from Stokes-Einstein Relation. In Proceedings of the 233rd ACS National Meeting, Chicago, IL, USA, 25–29 March 2007; American Chemical Society: Washington, DC, USA, 2007. [Google Scholar]
- Sharma, K.R. Manifestation of Acceleration during Transient Heat Conduction. J. Thermophys. Heat Transf. 2006, 20, 799–808. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Sharma, K.R. Microarray Analysis: Biochips and Eradication of All Diseases; Momentum Press: New York, NY, USA, 2015. [Google Scholar]
- Sharma, K.R. Principles of Mass Transfer; Prentice Hall of India: New Delhi, India, 2007. [Google Scholar]
- Baumeister, K.J.; Hamill, T.D. Hyperbolic Heat Conduction Equation–A Solution for the Semi-Infinite Body Problem. ASME J. Heat Transf. 1971, 93, 126–128. [Google Scholar] [CrossRef]
- Mickley, H.S.; Sherwood, T.K.; Reid, C.E. Applied Mathematics in Chemical Engineering; McGraw Hill: New York, NY, USA, 1957. [Google Scholar]
© 2015 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, K.R. On Description of Acceleration of Spinless Electrons in Law of Heat Conduction a capite ad calcem in Temperature. C 2016, 2, 1. https://doi.org/10.3390/c2010001
Sharma KR. On Description of Acceleration of Spinless Electrons in Law of Heat Conduction a capite ad calcem in Temperature. C. 2016; 2(1):1. https://doi.org/10.3390/c2010001
Chicago/Turabian StyleSharma, Kal Renganathan. 2016. "On Description of Acceleration of Spinless Electrons in Law of Heat Conduction a capite ad calcem in Temperature" C 2, no. 1: 1. https://doi.org/10.3390/c2010001
APA StyleSharma, K. R. (2016). On Description of Acceleration of Spinless Electrons in Law of Heat Conduction a capite ad calcem in Temperature. C, 2(1), 1. https://doi.org/10.3390/c2010001