A Computational Study of Amensalistic Control of Listeria monocytogenes by Lactococcus lactis under Nutrient Rich Conditions in a Chemostat Setting
Abstract
:1. Introduction
2. Governing Equations
- : population size of L. monocytogenes,
- : population size of L. lactis,
- C: concentration of lactic acids,
- P: concentration of hydrogen ions,
- M: malate concentration.
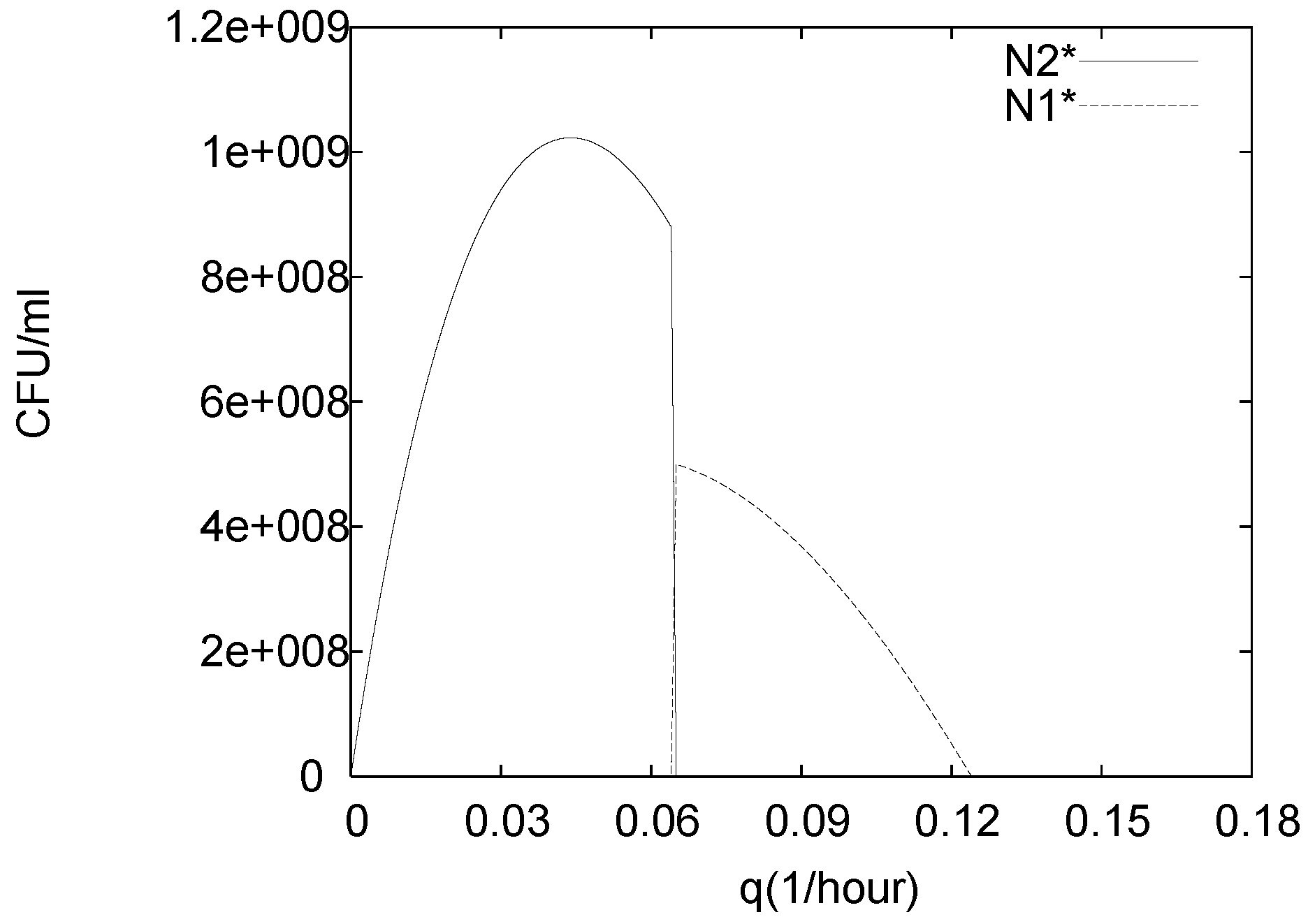
3. Analysis of the Single Species Pathogen Sub-Model
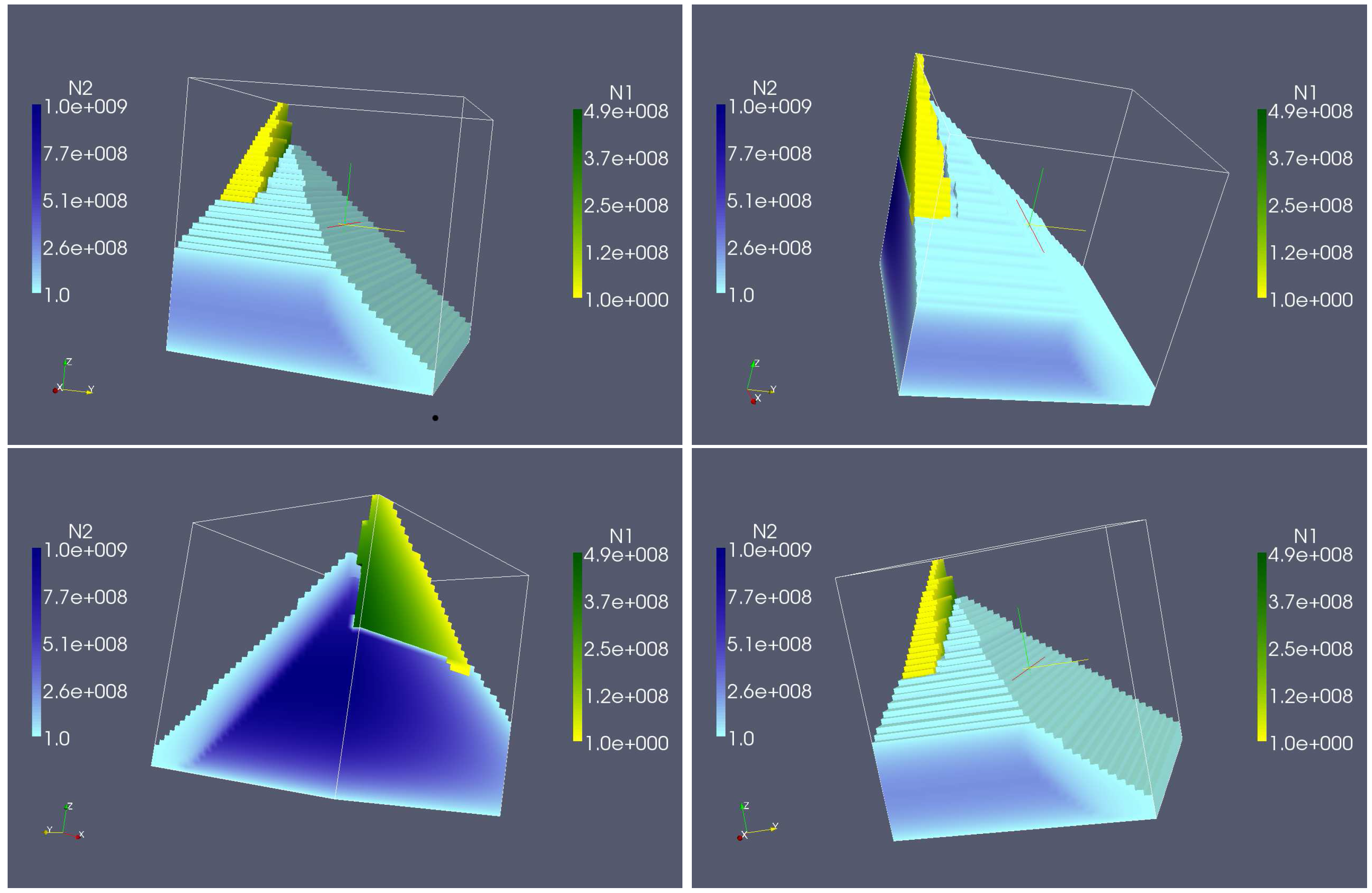
4. Numerical Experiments for the Complete Dual Species Biocontrol Model
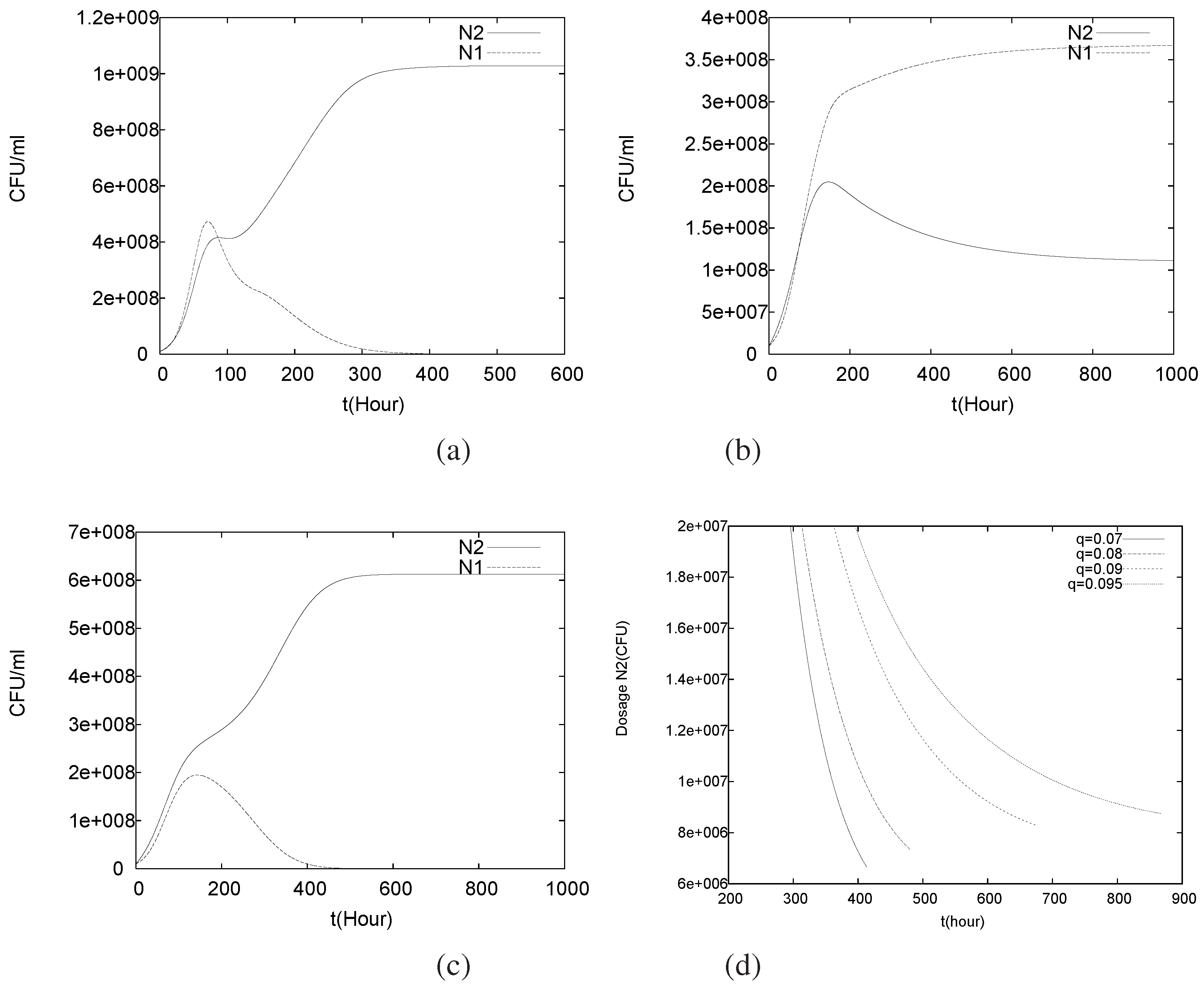
4.1. Batch Cultures
4.2. Longterm Behavior of the Full Chemostat Model
4.3. Continuously Adding Control Agents to Eradicate the Pathogens
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stiles, M.E. Biopreservation by lactic acid bacteria. Antonie Van Leeuwenhoek 1996, 70, 331–345. [Google Scholar] [CrossRef] [PubMed]
- Breidt, F.; Fleming, H.P. Modeling of the competitive growth of Listeria monocytogenes and Lactococcus lactis in vegetable broth. Appl. Environ. Microbiol. 1998, 64, 3159–3165. [Google Scholar] [PubMed]
- Gombas, D.E. Biological competition as a preserving mechanism. J. Food Saf. 1989, 10, 107–117. [Google Scholar] [CrossRef]
- Holzapfel, W.H.; Geisen, R.; Geisen, U.; Schillinger, U. Biological preservation of foods with reference to protective cultures, bacteriocins and food-grade enzymes. Int. J. Food Microbiol. 1995, 24, 343–362. [Google Scholar] [CrossRef]
- Ray, B.; Bhunia, A. Fundamental Food Microbiology; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Government of Canada. Listeriosis Investigative Review. Available online: http://epe.lac-bac.gc.ca/100/206/301/aafc-aac/listeriosis_review/2012-06-28/www.listeriosi s-listeriose.investigation-enquete.gc.ca/index_e.php (accessed on 27 May 2016).
- Canadian Food Insepction Agency. Complete Listing of All Recalls and Allergy Alerts. Available online: http://www.inspection.gc.ca/about-the-cfia/newsroom/food-recall-w arnings/complete-listing/eng/1351519587174/1351519588221?ay=2016&fr=22&fc=0&fd=0&ft=1 (accessed on 27 May 2016).
- Aryani, D.A.; den Besten, H.M.W.; Hazeleger, W.C.; Zwietering, M.H. Quantifying strain variability in modeling growth of Listeria monocytogenes. Int. J. Food Microbiol. 2015, 208, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Augustin, J.C.; Carlier, V. Mathematical modelling of the growth rate and lag time for Listeria monocytogenes. Int. J. Food Microbiol. 2000, 56, 29–51. [Google Scholar] [CrossRef]
- Carrasco, E.; Valero, A.; Pérez-Rodríguez, F.; García-Gimeno, R.M.; Zurera, G. Management of microbiological safety of ready-to-eat meat products by mathematical modelling: Listeria monocytogenes as an example. Int. J. Food Microbiol. 2007, 114, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Ferrier, R.; Hezard, B.; Lintz, A.; Stahl, V.; Augustin, J.C. Combining Individual-Based Modeling and Food Microenvironment Descriptions To Predict the Growth of Listeria monocytogenes on Smear Soft Cheese. Appl. Environ. Micobiol. 2013, 79, 5870–5881. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.K.; Yoon, W.B.; Huang, L.; Yuk, H.G. Predictive Modeling for Growth of Non- and Cold-adapted Listeria monocytogenes on Fresh-cut Cantaloupe at Different Storage Temperatures. J. Food Sci. 2014, 79, 1168–1174. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Lee, H.; Lee, J.Y.; Skandamis, P.; Park, B.Y.; Oh, M.H.; Yoon, Y. Mathematical Models To Predict Kinetic Behavior and Growth Probabilities of Listeria monocytogenes on Pork Skin at Constant and Dynamic Temperatures. J. Food Prot. 2013, 76, 1868–1872. [Google Scholar] [CrossRef] [PubMed]
- Passos, F.V.; Fleming, H.P.; Ollis, D.F.; Hassan, H.M.; Felder, R.M. Modeling the specific growth rate of Lactobacillus plantarum in cucumber extract. Appl. Microbiol. Biotechnol. 1993, 40, 143–150. [Google Scholar] [CrossRef]
- Sant’Ana, A.S.; Franco, B.D.G.M.; Schaffner, D.W. Modeling the growth rate and lag time of different strains of Salmonella enterica and Listeria monocytogenes in ready-to-eat lettuce. Food Microbiol. 2012, 30, 267–273. [Google Scholar] [CrossRef] [PubMed]
- Theys, T.E.; Geeraerd, A.H.; van Impe, J.F. Evaluation of a mathematical model structure describing the effect of (gel) structure on the growth of Listeria innocua, Lactococcus lactis and Salmonella Typhimurium. J. Appl. Microbiol. 2009, 107, 775–784. [Google Scholar] [CrossRef] [PubMed]
- Valero, A.; Hervas, C.; Garcia-Gimeno, R.M.; Zurera, G. Searching for New Mathematical Growth Model Approaches for Listeria monocytogenes. J. Food Sci. 2007, 72, 16–25. [Google Scholar] [CrossRef] [PubMed]
- Cornu, M.; Billoir, E.; Bergis, H.; Beaufort, A.; Zuliani, V. Modeling microbial competition in food: Application to the behavior of Listeria monocytogenes and lactic acid flora in pork meat products. Food Microbiol. 2011, 28, 629–647. [Google Scholar] [CrossRef] [PubMed]
- Delbon, R.R.; Yang, H.M. Dinamica Populacional Aplicada a Conservacao de Alimentos: Interacao entre Listeria Monocytogenes e Bacterias Lacticas. Tends Appl. Comput. Math. 2008, 9, 375–384. [Google Scholar] [CrossRef]
- Fgaier, H.; Kalmokoff, M.; Ellis, T.; Eberl, H.J. An allelopathy based model for the Listeria overgrowth phenomenon. Math. Biosci. 2014, 247, 13–26. [Google Scholar] [CrossRef] [PubMed]
- Smith, H.L.; Waltman, P. The Theory of the Chemostat; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Fgaier, H.; Eberl, H.J. Antagonistic control of microbial pathogens under iron limitations by siderophore producing bacteria in a chemostat setup. J. Theor. Biol. 2011, 273, 103–114. [Google Scholar] [CrossRef] [PubMed]
- El Hajji, M.; Haramnd, J.; Chaker, H.; Lobry, C. Association between competition and obligate mutualism in a chemostat. J. Biol. Dyn. 2009, 3, 635–647. [Google Scholar] [CrossRef] [PubMed]
- Sari, T.; El Hajji, M.; Harmand, J. The mathematical analysis of a syntrophic relationship between two microbial species in a chemostat. Math. BioscI. Eng. 2012, 9, 627–645. [Google Scholar] [CrossRef] [PubMed]
- Macfarlane, G.T.; Macfarlane, S.; Gibson, G.R. Co-culture of Bifidobacterium adolescentis and Bacteroides thetaiotaomicron in arabinogalactan-limites chemostats: Effects of dilution rate and pH. Anaerobe 1995, 1, 275–281. [Google Scholar] [CrossRef] [PubMed]
- FAO/WHO Working Group. Guidelines for the Evaluation of Probiotics in Food; FAO/WHO: London, ON, Canada, 2002. [Google Scholar]
- Hogben, L. Handbook of Linear Algebra, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013; p. 1904. [Google Scholar]
- Jeffries, C. Qualitative stability and digraphs in model ecosystems. Ecology 1974, 55, 1415–1419. [Google Scholar] [CrossRef]
- May, R.M. Quantitative stability in model ecosystems. Ecology 1973, 54, 638–641. [Google Scholar] [CrossRef]
- Sari, T.; Harmand, J. A model of a syntrophic relationship between two microbial species in a chemostat including maintenance. Math. Biosci. 2016, 275, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Eberl, H.J.; Khassehkhan, H.; Demaret, L. A mixed-culture model of a probiotic biofilm control system. Comput. Math. Methods Med. 2010, 11, 99–118. [Google Scholar] [CrossRef] [PubMed]
- Khassehkhan, H.; Eberl, H.J. Modeling and simulation of a bacterial biofilm that is controlled by pH and protonated lactic acids. Comput. Math. Methods Med. 2008, 9, 47–67. [Google Scholar] [CrossRef]
- Khassehkhan, E.; Efendiev, M.A.; Eberl, H.J. A degenerate diffusion-reaction model of an amensalistic probiotic biofilm control system: Existence and simulation of solutions. Discrete Contin. Dyn. Syst. B 2009, 12, 371–388. [Google Scholar] [CrossRef]
- Rahman, K.A.; Sudarsan, R.; Eberl, H.J. A Mixed Culture Biofilm Model with Cross-Diffusion. Bull. Math. Biol. 2015, 77, 2086–2124. [Google Scholar] [CrossRef] [PubMed]
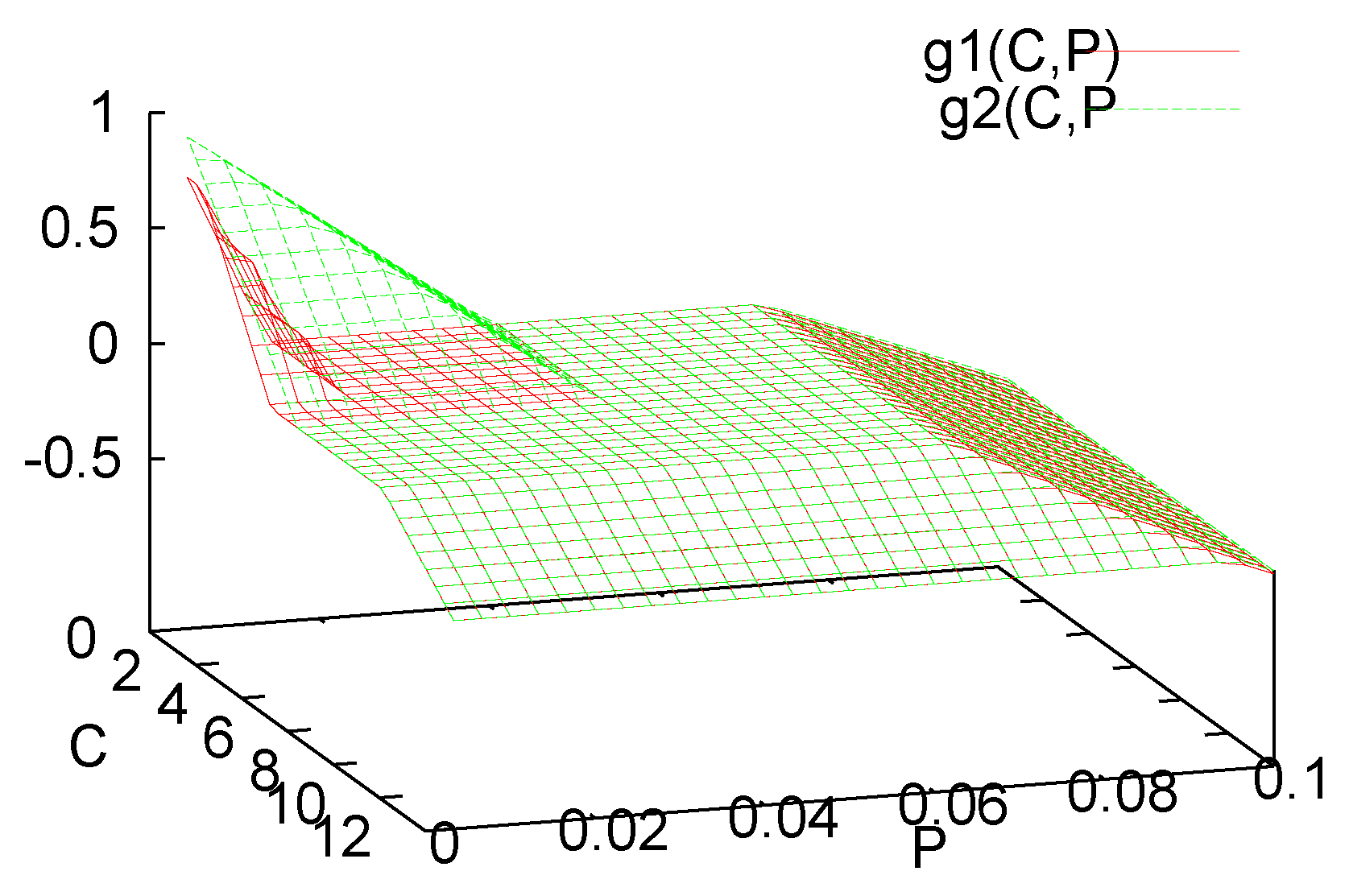


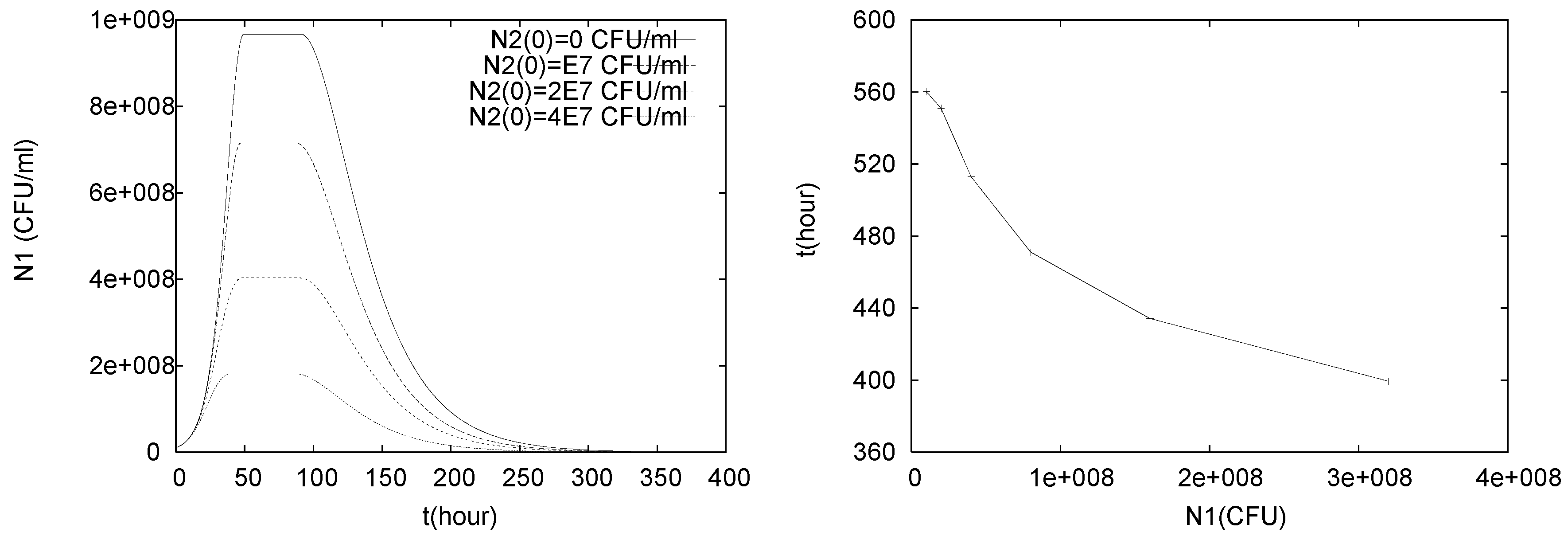

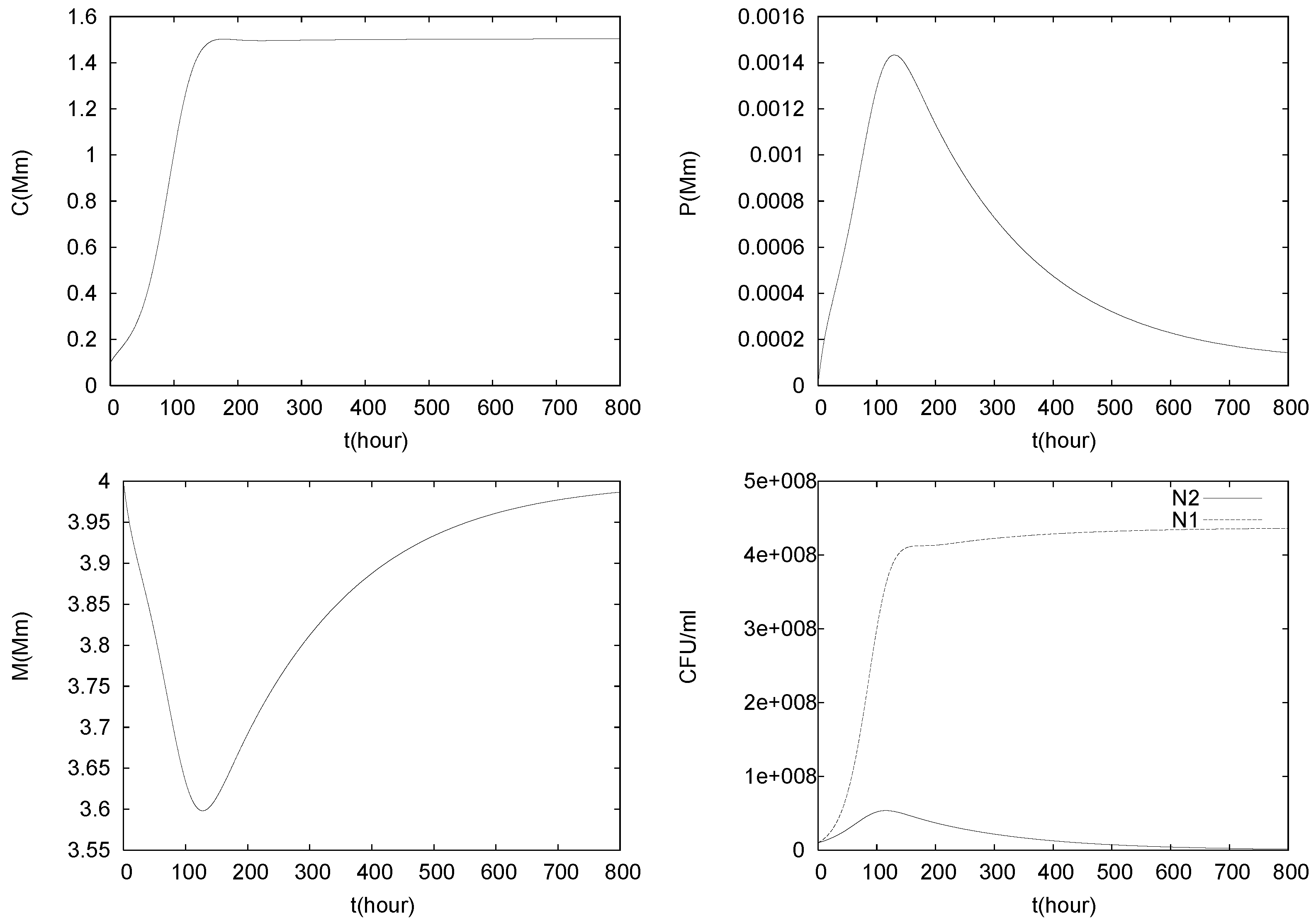
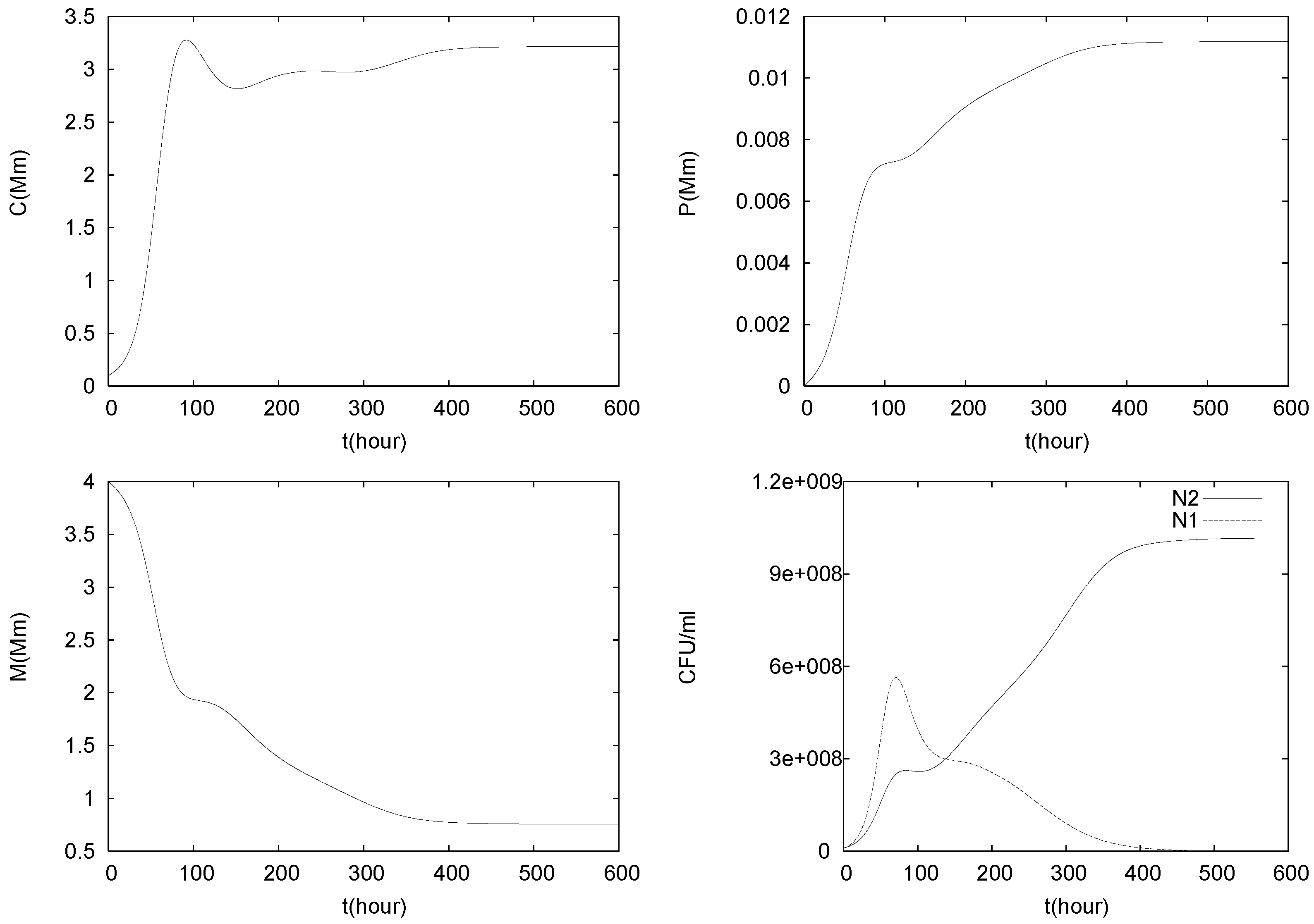
| Parameter | Symbol | Unit | L. lactis | L. monocytogenes |
|---|---|---|---|---|
| Specific growth rate | h−1 | 0.1049 | 0.1471 | |
| Protonated acid production rate | Milimoles CFU−1·h−1 | 1.7 * 10−10 | 2.95 * 10−10 | |
| MIC acid (growth) | Milimolar | 5.2 | 4.058 | |
| MIC acid (metabolism) | Milimolar | 8.907 | 8.908 | |
| Maximum acid concentration | Milimolar | 11.5 | 11.65 | |
| MIC proton ion (growth) | Milimolar | 10−1.405 | 10−1.892 | |
| MIC proton ion (metabolism) | Milimolar | 10−1.147 | 10−1.151 | |
| Maximum proton ion concentration | Milimolar | 10−1.12 | 10−1.132 | |
| Malate decay rate | θ | Milimole CFU−1·h−1 | 1.69 * 10−10 | 0 |
| Malate utilization rate | κ | Milimole−1 | 10−5.33 | 10−5.33 |
| proton concentration change rate | ρ | Moles CFU−1·h−1 | 10−5.472 | 10−5.472 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khassehkhan, H.; Eberl, H.J. A Computational Study of Amensalistic Control of Listeria monocytogenes by Lactococcus lactis under Nutrient Rich Conditions in a Chemostat Setting. Foods 2016, 5, 61. https://doi.org/10.3390/foods5030061
Khassehkhan H, Eberl HJ. A Computational Study of Amensalistic Control of Listeria monocytogenes by Lactococcus lactis under Nutrient Rich Conditions in a Chemostat Setting. Foods. 2016; 5(3):61. https://doi.org/10.3390/foods5030061
Chicago/Turabian StyleKhassehkhan, Hassan, and Hermann J. Eberl. 2016. "A Computational Study of Amensalistic Control of Listeria monocytogenes by Lactococcus lactis under Nutrient Rich Conditions in a Chemostat Setting" Foods 5, no. 3: 61. https://doi.org/10.3390/foods5030061





